텔레스코픽 붐형 지게차의 붐 최적 설계

1. 서론

다양한 산업의 발전과 함께, 건설기계는 오늘날에도 끊임없이 발전하고 있다. 특히 화물의 운반, 하역 및 이송을 담당하는 대표적인 건설기계에 있어서, 지게차가 널리 사용되고 있다. 하지만 종래의 지게차는 랙(Rack)이나 파렛트(Pallet)와 같은 고정적인 환경 및 정형적인 운반물의 취급에는 유용하지만, 비고정적인 환경과 비정형적인 운반물들이 즐비한 환경에서는 지게차의 작업 성능이 비효율적이다.

이러한 단점에 대응하여 구동 성능 및 작업 장치 등을 특화시킨 험지용 지게차(Rough Terrain Forklift) 및 텔레스코픽 핸들러(Telescopic Hanlder)와 같은 특수한 지게차들이 출현하고 있다. 하지만 차체의 대형화, 가격적인 요소 등으로 인해 대중화에는 실패하고 있다.

Hong¹ 등은 고소작업차의 붐 조인트를 최적화하기 위해서 실험계획법을 위한 5개의 인자를 선정하고 직교배열법을 실시하여 2개의 유의하지 않은 인자를 제거한 후 3개의 인자를 통해서 완전요인배치법과 반응표면분석을 하고 최대등가응력을 32.33% 감소시켰다. Yoo²는 실험계획법을 이용해서 휠 로더 전 차축의 최적 형상을 도출하였고 피로한계응력과 비교를 통해서 피로 파손을 예측하였다. Batdelger³는 두 번의 실험계획법과 다중 반응 최적화를 통해서 구조물의 강성 강화 및 중량 감소화를 실시하였다. Kwon⁴ 등은 미니로더의 구조 안전성을 평가하고 최적화하는 방법을 체계화하였고 반응표면분석을 통해서 Main Frame의 중량을 거의 변화시키지 않고 응력을 47.2% 감소하였다. Choi⁵ 등은 특장차용 텔레스코픽 붐의 단면 형상에 따른 구조해석을 실시하고 팔각형 단면에서 응력이 가장 적게 걸리는 것을 확인하였고 모서리 수가 증가함에 따라 변형량이 커지는 것을 확인하였다. Kim⁶은 반응표면법을 사용하고 다중 반응 최적화를 통해서 자동차 링크 모듈을 경량화했다. Hong⁷은 두께, 형상, 위상의 최적화를 통해서 텔레스코픽 붐대 및 프레임의 강성을 증가시키는 동시에 경량화시켰다. So⁸는 텔레스코픽 붐대와 패드의 접촉 조건과 마찰을 고려하고 패드의 두께와 면적 변화에 따른 응력의 변화를 해석했다.

본 논문은 상기의 사용 환경과 가격요소를 고려한 새로운 형태인 텔레스코픽 붐형 지게차의 구조해석을 위해서 상용 FEM(Finite Element Method) 프로그램인 ANSYS WORKBENCH를 사용하여 텔레스코픽 붐의 취약 부분을 예측하였으며, 해당 부분의 응력을 최소화하기 위해서 상용 통계 프로그램인 Minitab을 이용하여 실험계획법을 실시하였다. 본 논문의 내용은 추후 텔레스코픽 붐형 지게차의 개발 과정에 도움이 될 것이라 판단한다.

2. 유한요소해석(Finite Element Analysis)

2.1 텔레스코픽 붐의 모델

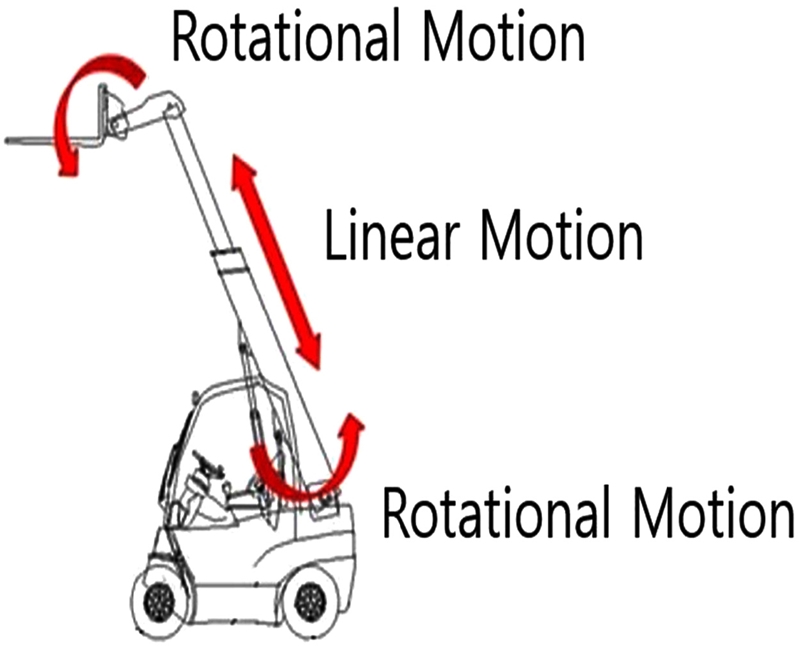
텔레스코픽 붐형 지게차의 실제 모습은 Fig. 1과 같으며 두개의 회전운동과 한 개의 직선운동으로 총 3개의 자유도를 가진다.

Fig. 1

Photo of telescopic boom type forklift truck

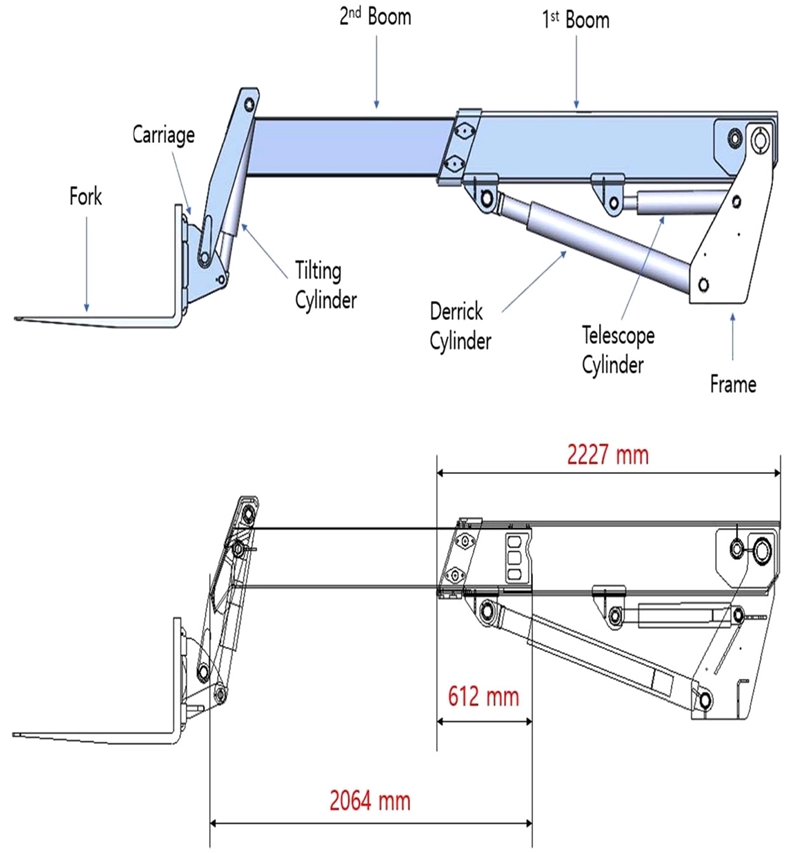
텔레스코픽 붐의 구조해석을 위한 3D 모델은 Fig. 2와 같이 캐리지(Carriage), 포크(Fork), 1st 붐, 2nd 붐, 데릭 실린더(Derrick Cylinder), 텔레스코프 실린더(Telescope Cylinder), 틸팅 실린더(Tilting Cylinder)와 프레임(Frame)으로 구성되어있으며 붐의 형상 정보도 Fig. 2를 통해 확인할 수 있다.

Fig. 2

Parts and shape information of telescopic boom

유한요소해석을 위한 모델은 2nd 붐에 최대응력이 가해지는 각도인 0^o로 설정 후 구조해석을 진행하였다.

2.2 전처리 과정(Pre-Process)

2.2.1 모델 단순화

붐의 최적화를 위해서 해석모델을 단순화할 필요가 있다. 본 연구에서는 최적화의 대상으로 텔레스코픽 붐을 선정했다. 따라서 프레임을 제거한 후 프레임과 연결되는 유압실린더와 핀(Pin)을 제거하여 모델을 단순화한 후 해석을 진행했다.

2.2.2 경계조건(Boundary Conditions)

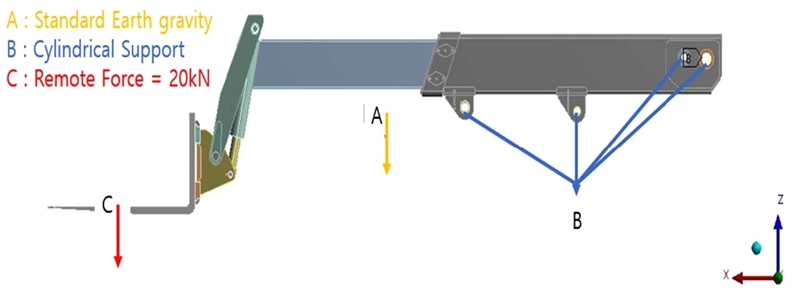
경계조건과 하중은 Fig. 3과 같다. 핀을 대체할 조건으로 원통형 지지 조건(Cylindrical Support)을 주었고 원주(Radial)방향을 제외한 모든 자유도를 구속했다. 그 이유는 실제 유압실린더가 존재할 경우 유압실린더가 플레이트의 핀홀을 지지하는 역할을 수행하기 때문이다. 그리고 자중을 고려한 중력을 주었고 텔레스코픽 붐형 지게차의 정격 하중인 2.0 ton을 고려하여 20 kN을 캐리지의 포크 중심에 가했다.

Fig. 3

Boundary & Load conditions

2.2.3 Mesh

요소(Element)는 Tetra Mesh이며, 자동 요소 생성 기능을 이용했다. Mesh 수렴을 확인하기 위한 과정으로서 응력 값의 허용변화율 2% 이내인 1.65%의 변화를 보여 수렴을 확인하였으며 요소의 크기는 10 mm로서, 그 결과 요소의 개수는 292,805개 절점(Nodes)은 581,044개로 분할되었다.

2.3 구조해석 결과

2.3.1 초기 모델

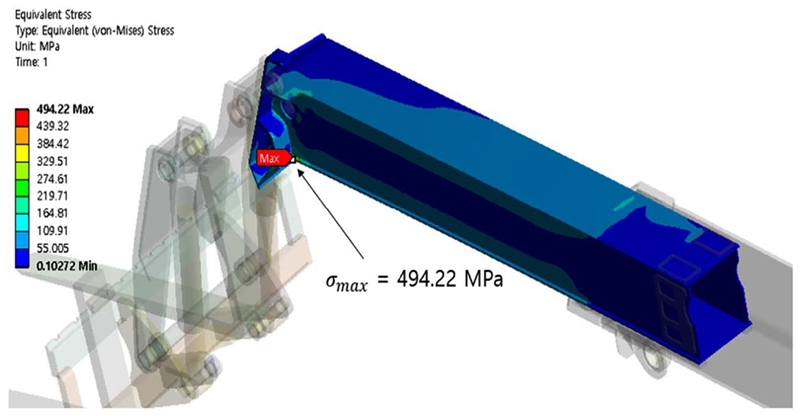
구조해석의 결과 Fig. 4에서 볼 수 있듯이 2nd 붐에서 최대등가응력(Maximum Von-Mises Stress) 494.22 MPa 발생했다. 이는 설계 관련 표준 ‘크레인-하중 및 조합 하중에 관한 설계원리’ KSB ISO 8686-1(일반)과 -2(이동식크레인)를 준용해 안전율 1.48을 붐의 재료인 ATOS80에 적용하여 구한 허용응력인 456.08 MPa을 초과하기 때문에 붐이 파손될 수 있다고 판단했다.

Fig. 4

Maximum von-mises stress for initial model

2.3.2 보강 모델

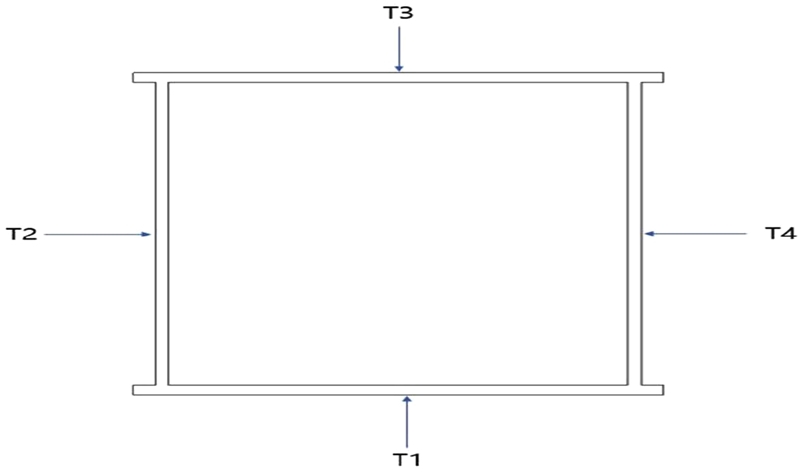
Fig. 4에서 본 바와 같이, 최대 494.22 MPa의 응력이 발생하여 허용응력 456.08 MPa보다 높으므로 파괴의 위험이 있다. 따라서 Fig. 5와 같이 차체의 정면에서 봤을 때를 기준으로 붐의 하단 플레이트를 T1으로 하여 시계방향으로 T4까지 플레이트의 두께를 설계변수로 설정했다. 응력을 감소시키기 위하여 Table 1과 같이 각 플레이트의 두께를 2 mm씩 증가시켜 구조해석을 실시하였다.

Fig. 5

Name of factors

Table 1

Modified Factors

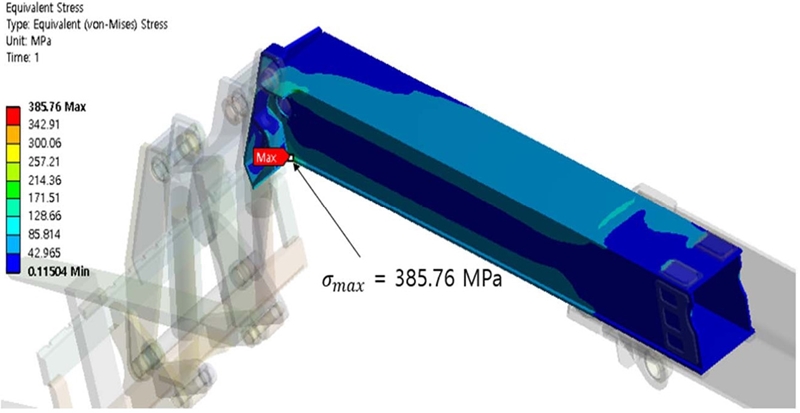
구조해석 결과는 Fig. 6과 같이 2nd 붐에서 최대 385.76 MPa의 응력이 발생했다. 이는 붐의 허용응력 456.08 MPa보다 낮으므로 파괴의 위험이 없다고 판단할 수 있다. 따라서 붐의 두께가 응력에 영향을 끼친다고 판단하여 플레이트 4개를 인자로 선정해 실험계획법을 실시했다.

Fig. 6

Maximum von-mises stress for modified model

3. 실험계획법

상기한 내용과 같이 2nd 붐의 플레이트 4개를 인자로 선정했다. 붐의 실험계획법을 진행하면서 지게차의 경량화도 고려해야 할 대상이므로 최적화해야 할 목적함수로 최대등가응력과 함께 질량도 반응 값으로 설정했다.

인자의 수준은 Table 2와 같이 초기 값에 ± 2 mm로 상한과 하한을 설정하였으며 완전요인배치법을 통해 선형회귀분석을 실시하였다. 완전요인배치법에서 곡면성이 확인될 경우에는 반응표면분석법을 통해 비선형 효과를 고려하여야 한다.

Table 2

Levels of factors

3.1 완전요인배치법

반응 값이 인자의 수준에 따라 어떻게 반응하는지 알아보기 위하여 Table 3과 같이 4인자 2 수준의 실험을 수행하였고, 곡면성을 확인하기 위해 중앙점을 포함하여 진행하였다. Y1과 Y2는 각각의 경우에서 구한 질량과 최대등가응력의 반응 값이다.

Table 3

Results of experiments

3.1.1 응력에 대한 분산분석

Table 3의 응력에 대한 분산분석 결과는 Table 4와 같다. 여기서 DF는 자유도를 나타내며, Adj SS는 제곱합(Sum of Square)으로 이는 인자 수준에 따른 변동성을 나타내며, Adj MS는 평균 제곱(Mean Square)으로 각 항의 제곱 합을 자유도로 나눈 값이다. Error는 인자들의 효과만으로는 설명이 되지 않는 변동성을 뜻한다. F-Value는 각 항의 평균 제곱을 Error의 평균 제곱으로 나눈 값으로써 F-Value의 값이 클수록 P-Value의 값이 작아지게 된다. P-Value의 값이 유의 수준인 0.05를 넘게 되면, 그 인자는 반응에 영향을 미치지 못한다고 판단한다.

Table 4

Analysis of variance for stress

Table 4는 신뢰도 95%를 기준으로 P-Value의 값이 0.05를 초과하는 항을 오차항에 포함시킨 후 검정하는 풀링(Pooling) 작업을 수행한 결과다.

목적함수인 질량, 즉 반응 값 Y1과 설계변수들 간의 관계를 나타내는 회귀방정식은 식(1)과 같다.

$\[ \mathrm{Y}1=1022.7-35.83{\mathrm{T}}_1-17.73{\mathrm{T}}_2-10.35{\mathrm{T}}_3-6.25{\mathrm{T}}_4-15.1\mathrm{C}\mathrm{P} \]$

(1)

회귀방정식이 모형을 나타내는 정도를 결정계수 R²이라하고, 100%에 가까울수록 모형을 잘 설명한다고 할 수 있으며, 식(1)에 대한 R² 값은 97.29%로써 모형을 잘 설명한다고 할 수 있다.

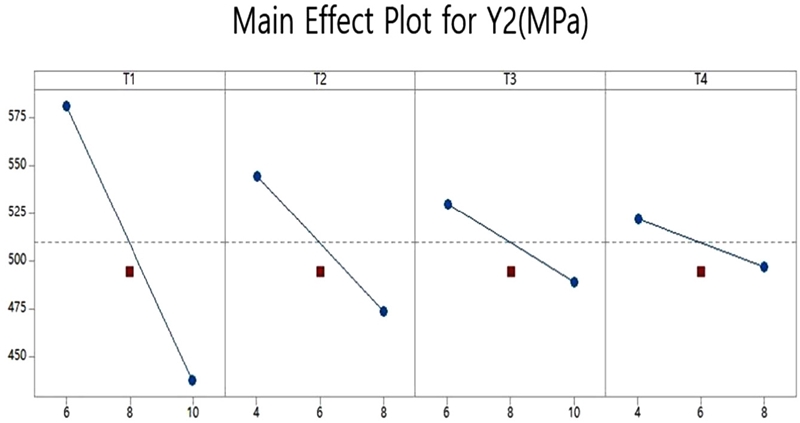
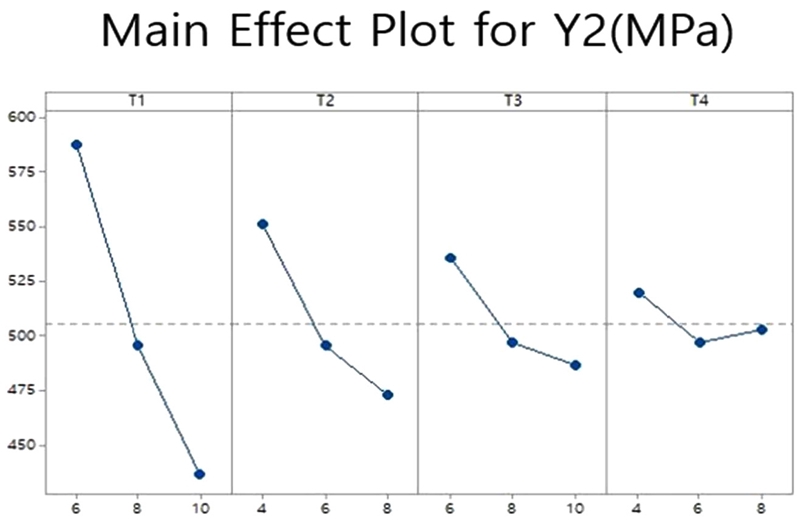
또 다른 목적함수인 최대등가응력, 즉 반응 값 Y2에 대한 주효과도는 Fig. 7과 같으며 y축은 각 인자의 수준에 따른 응력을 나타내고 x축은 각 인자의 수준을 나타낸다. 주효과도의 기울기를 통해서 T1, T2, T3, T4 순으로 반응 값에 큰 영향을 미친다고 해석할 수 있다. 또한 중앙점이 주효과도의 직선상에서 벗어난 것을 볼 수 있다. 이를 통해서 반응 값이 비선형적이라고 판단할 수 있으며 더 높은 차수의 실험을 계획할 필요가 있다. 따라서 추가적인 실험인 반응표면분석법이 필요하다.

Fig. 7

Main effect plot for stress

3.2 반응표면분석법

완전요인배치법을 통해 곡면성이 확인되었으므로 고차의 실험인 반응표면분석법을 실시하였다. 반응표면을 생성하기 위하여 면 중심의 중심합성법을 통해 실험을 계획하였다. 면 중심의 중심합성법을 통해 실험을 계획한 이유는 수준에 제한이 있을 경우 수준의 범위를 초과하지 않고 실험을 계획할 수 있기 때문이다. 실험을 수행한 결과는 Table 5와 같다. Y1과 Y2는 각각의 경우에서 구한 질량과 최대등가응력의 반응 값이다.

Table 5

Central composite design

3.2.1 질량에 대한 분산분석

Minitab을 이용하여 Table 5의 질량에 대한 분산분석을 실시한 결과는 Table 6과 같다. 풀링 작업을 수행하는데 있어서 한번에 하나씩 유의하지 않은 인자를 제외해야한다. 한번에 2개 이상의 인자를 제외하면 그 인자 간에 종속되는 효과가 있을 수 있기 때문에 하나씩 제외하는 절차의 값과 다를 수 있다.

Table 6

Analysis of variance for mass

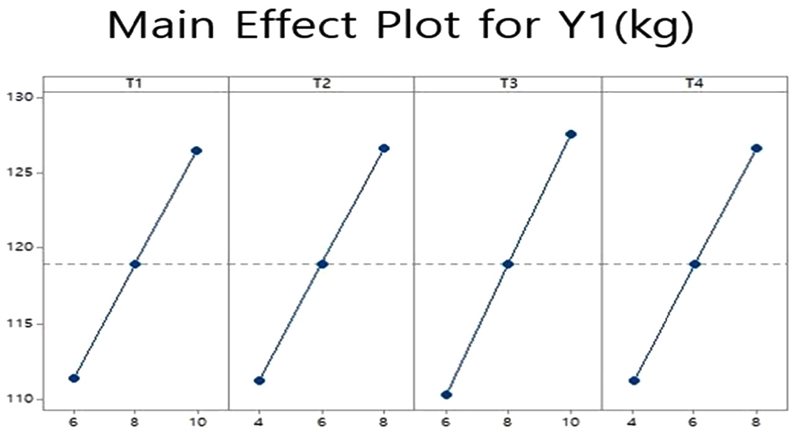
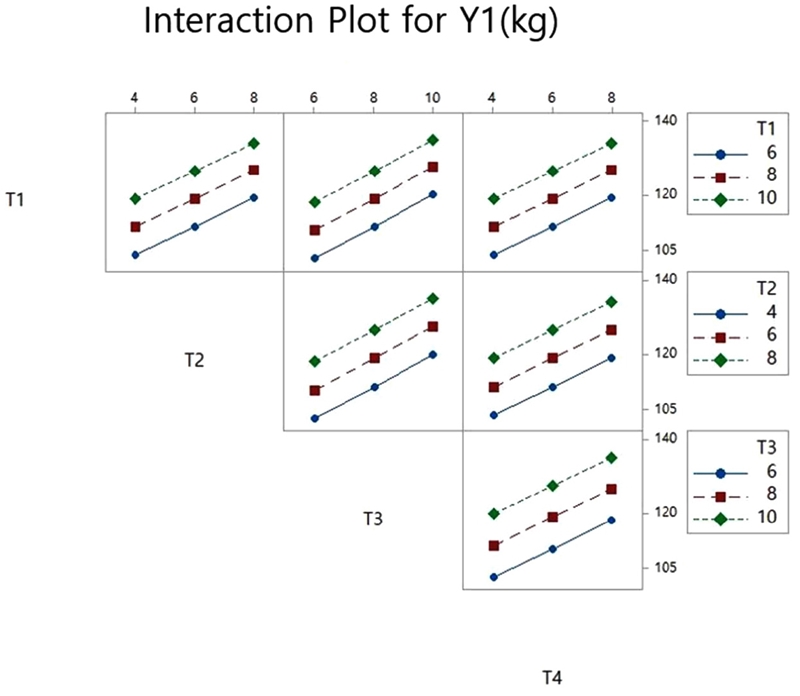
인자가 질량, 즉 반응 값 Y1에 미치는 영향을 나타내는 주효과도 및 교호작용도는 각각 Figs. 8과 9와 같이 나타났다. 4개의 인자 모두 비슷한 정도로 반응 값에 영향을 미치며 교호작용은 거의 없는 것으로 확인되었다.

Fig. 8

Main effect plot for mass

Fig. 9

Interaction plot for mass

분산분석을 통해 확인한 유의한 인자는 T1, T2, T3, T4, T1*T1, T3*T3, T1*T2, T1*T3, T1*T4, T2*T3, T3*T4이며 이를 통해 도출한 반응 값 Y1에 대한 회귀방정식은 식(2)와 같다.

$\[ \begin{array}{l}\mathrm{Y}1=3.9791+4.0687{\mathrm{T}}_1-4.12833{\mathrm{T}}_2-4.6296{\mathrm{T}}_3-4.12833{\mathrm{T}}_4-\\ 0.00279{\mathrm{T}}_1{\mathrm{T}}_1-0.00279{\mathrm{T}}_3{\mathrm{T}}_3-0.016438{\mathrm{T}}_1{\mathrm{T}}_2-0.007375{\mathrm{T}}_1{\mathrm{T}}_3-\\ 0.016438{\mathrm{T}}_1{\mathrm{T}}_4-0.018{\mathrm{T}}_2{\mathrm{T}}_3-0.018{\mathrm{T}}_3{\mathrm{T}}_4\end{array} \]$

(2)

식(2)에 대한 R² 값은 100%로서 모형을 잘 설명한다고 할 수 있다.

3.2.2 응력에 대한 분산분석

Minitab을 이용하여 Table 5의 응력에 대한 분산분석을 실시한 결과는 Table 7과 같다. 마찬가지로 인자 간에 종속되는 효과가 있을 수 있기 때문에 차례대로 하나씩 제외시키며 풀링 작업을 수행하였다.

Table 7

Analysis of variance for stess

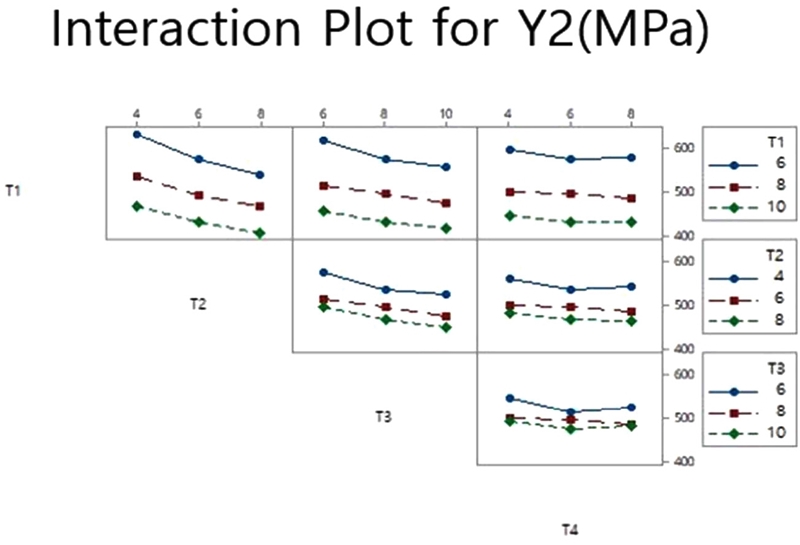
인자가 최대등가응력, 즉 반응 값 Y2에 미치는 영향을 나타내는 주효과도 및 교호작용도는 각각 Figs. 10과 11과 같이 나타났다. T1, T2, T3, T4 순으로 반응 값에 대해 영향을 크게 미치며 곡면 효과가 있는 것을 확인할 수 있다. 교호 효과는 크지 않은 것으로 확인되었다.

Fig. 10

Main effect plot for stress

Fig. 11

Interaction plot for stress

분산분석을 통해 확인한 유의한 인자는 T1, T2, T3, T4, T1*T1, T2*T2, T1*T2, T1*T3이며 이를 통해 도출한 최대등가응력, 즉 반응 값 Y2에 대한 회귀방정식은 식(3)과 같다.

$\[ \begin{array}{l}\mathrm{Y}2=1459.1-101.81{\mathrm{T}}_1-59.93{\mathrm{T}}_2-23.66{\mathrm{T}}_3-4.131{\mathrm{T}}_4+\\ 2.591{\mathrm{T}}_1{\mathrm{T}}_1+2.124{\mathrm{T}}_2{\mathrm{T}}_2+1.862{\mathrm{T}}_1{\mathrm{T}}_2+1.434{\mathrm{T}}_1{\mathrm{T}}_3\end{array} \]$

(3)

식(3)에 대한 R² 값은 99.72%로써 모형을 잘 설명한다고 할 수 있다.

3.3 반응최적화

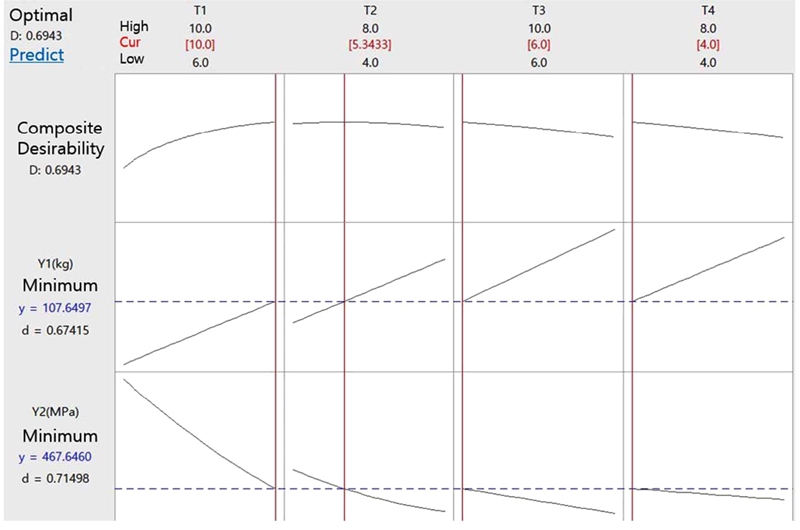
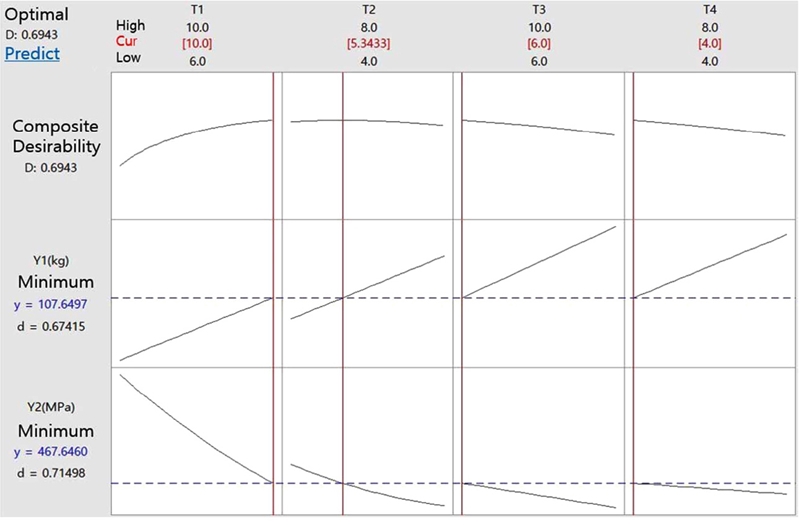
회귀방정식 식(2)와 식(3)을 통해서 질량과 응력을 모두 최적화할 수 있는 다중 반응 최적화를 실시했고 그 결과는 Fig. 12 와 같다.

Fig. 12

Optimization plot 1

그 결과는 Fig. 12와 같이 T1 = 10 mm, T2 = 5.3433 mm, T3 = 6 mm, T4 = 4 mm일 때 질량 107.6497 kg, 응력 467.65 MPa이 발생하는 것으로 예측되었다. 하지만 이는 ATOS 80의 허용 응력인 456.08 MPa을 초과하는 값이므로 파손의 위험이 있다고 판단되었다. 따라서 질량은 초기 모델의 값인 118 kg을 초과하지 않는 수준으로 목표값을 제한하고 응력의 최소화를 실시했고 그 결과는 Fig. 13과 같다.

Fig. 13

Optimization plot 2

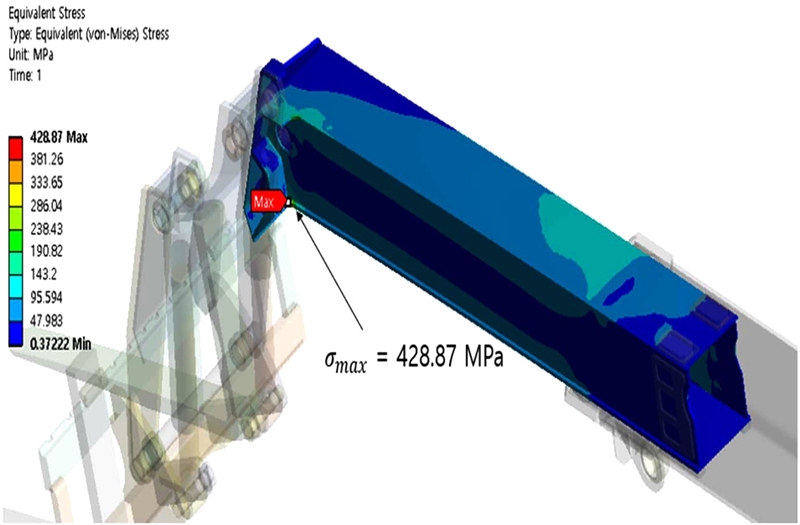
Fig. 13과 같이 T1 = 10, T2 = 8, T3 = 6.0247, T4 = 4 mm일 때 질량 118 kg, 응력 432.96 MPa이 발생하는 것으로 예측되었다. T3의 최적화 수준이 6.0247 mm로 계산되었으나 실제 제품의 수치로 사용하기에 부적절하므로 6 mm로 수정 후 구조해석을 실시하였고 그 결과는 Fig. 14와 같다.

Fig. 14

Maximum von-mises stress at optimum case

붐은 좌우대칭의 형상을 갖지만 지게차의 Fork는 좌측에 치중되어 하중이 비대칭적으로 가해진다. 따라서 좌측의 플레이트 두께가 더 두껍게 설계되어 비대칭으로 최적화됨을 확인할 수 있다.

Minitab에서 예측한 결과와 실제 구조해석 결과와의 비교는 Table 8과 같다.

Table 8

Results of optimization

그 결과 Minitab에서 제시된 결과와 99% 이상 일치하는 결과를 보였다. 또 초기 모델에서 발생한 응력인 494.22 MPa에 비해 13.22% 감소된 428.87 MPa이 발생했으며 이는 허용응력 456.08 MPa 미만의 값이므로 안전한 것으로 판단된다.

4. 결론

본 논문에선 텔레스코픽 붐형 지게차의 붐 구조를 유한요소해석 프로그램인 ANSYS를 이용하여 해석하였다. 그 결과 2nd 붐에서 재료의 허용응력인 456.08 MPa을 초과한 494.22 MPa이 발생하므로 파괴된다고 판단했고, 이를 해결하기 위해서 실험계획법을 이용한 최적화를 실시했다.

본 연구를 통해서 종래의 지게차의 한계를 극복할 수 있는 새로운 형태의 지게차 개발에 기여할 수 있으며, 험지용 지게차 및 텔레스코픽 핸들러 등 특수한 형태의 지게차 개발에 활용될 수 있을 것으로 판단된다.

붐의 두께를 보강하여 구조해석을 실시한 결과 응력의 감소를 보였다. 따라서 붐의 두께 T1, T2, T3, T4 총 4개의 인자를 선정하여 실험계획법을 실시했다. 인자의 상한과 하한을 설정해 중간점을 포함한 4인자 2 수준의 완전요인배치법을 실시하였다. 응력에 대한 분산분석을 실시한 결과, 반응 값에 곡면성이 있음이 확인되어 고차의 실험인 반응표면분석법을 실시하였다.

반응표면분석법의 실시를 통하여 응력에 대한 인자들의 곡면성을 구체적으로 확인했으며, 특히 T1이 가장 영향이 큰 인자로 확인되었다. 각 반응 값에 대한 분산분석을 통해서 얻은 회귀방정식을 통해서 질량과 응력을 모두 최적화하는 반응최적화를 실시했고, 그 결과 467.65 MPa이 발생하는 것으로 예측되었다. 이는 허용응력인 456.08 MPa을 초과하는 결과다.

허용응력을 초과하지 않는 결과를 도출하기 위하여 질량은 초기값인 118 kg으로 목표값을 제한하고 응력을 최소화할 수 있는 다중 반응 최적화를 실시하였다. 그 결과 432.96 MPa이 발생하는 것으로 예측되었으며, 실제 구조해석 결과 428.87 MPa의 응력이 발생하였다. 이는 기존 모델에 비해 응력이 13.22% 감소된 결과이며, 허용응력 456.08 MPa 미만의 값이므로 안전할 것으로 판단된다.

Acknowledgments

본 연구는 ‘텔레스코픽 붐형 하이브리드 4륜구동 지게차(중소벤처기업부 과제번호 No. 201701100014)’ 과제를 통해 수행되었으며, 2019년도 한국산업기술대학교 연구년에 의하여 연구되었음.

References

• Hong, J. M. and Lee, J. H., “Optimal Design of Boom Joint for 2.5 ton Class Aerial Lift Truck Using Design of Experiments,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 8, pp. 769-775, 2018. [https://doi.org/10.7736/KSPE.2018.35.8.769]
• Yoo, D. W. and Lee, J. H., “A Study on the Optimal Shape Design of Front Axle of Wheel Loader Using the Design of Experiments,” Journal of the Korean Society for Precision Engineering, Vol. 29, No. 2, pp. 193-200, 2012. [https://doi.org/10.7736/KSPE.2012.29.2.193]
• Batdelger, O., “Structural Analysis and Optimal Design of a Hydraulic Press Using Design of Experiment,” M.Sc. Thesis, Korea Aerospace University, 2016.
• Kwon, K. B. and Shin, D. Y., “Optimal Design of a Mini-Loader based on the Design of Experiments,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 35, No. 6, pp. 693-699, 2011. [https://doi.org/10.3795/KSME-A.2011.35.6.693]
• Choi, Y., Lee, S., Park, S., and Ryu, Y., “Structural Analysis of Telescopic Boom in a Special Vehicle,” Proc. of the KSME Fall Conference, pp. 451-455, 2009.
• Kim, S. K., “Optimal Design for Lightweight of Rear Link Module in Sports Utility Vehicle Using the Response Surface Method,” M.Sc. Thesis, Tongmyong University, 2010.
• Hong, S. K., “Structural Optimum Design for the Lightweight of an Aerial Work Platform Truck’s Telescopic Boom and Frame System,” M.Sc. Thesis, Sejong University, 2012.
• So, J. W., “Finite Element Analysis of Boom Structure of an Aerial Lift Truck Considering Friction and Contact Condition between the Elastic Bodies,” M.Sc. Thesis, Jeonbuk National University, 2015.