공진 주파수 등방성 향상을 위한 2-자유도 직렬 위치 결정 스테이지의 연성 해석과 설계 최적화

1. 서론

정밀 위치 결정 스테이지는 서브미크론(Sub-Micron)급이나 서브나노(Sub-Nano)급의 분해능으로 물체를 위치시키거나 조작을 수행하는 장치이다. 그리고 수행해야 하는 작업의 특성에 따라 다양한 자유도를 필요로 한다. 일반적으로 평면 위치 결정을 위해서는 낮은 자유도를 요구하는 반면 셀 조작이나 마이크로/나노 가공, 웨이퍼 기반 성형 가공, 광학 정렬 등을 위해서는 높은 자유도를 요구하는 경우가 많다.^1,2 특히 원자현미경, 전자현미경에서는 샘플을 정밀하게 위치시키고 빠르게 스캐닝하기 위해 높은 분해능뿐 아니라 빠른 속도 성능을 지닌 위치 결정 스테이지를 필요로 한다.^3,4 이와 같이 특수한 작업을 위해서는 주로 PZT 구동기와 플렉셔 힌지(Flexure Hinge)를 적용한 스테이지가 많이 사용된다.^5,6 모터를 구동기로 사용하고 조립된 링크의 상대 운동을 통해 운동을 전달하는 전통적인 방식으로는 유격, 마모, 분진 등의 문제로 인해 적용상의 한계가 있다. PZT 구동기는 이론적으로 무한의 분해능과 빠른 응답성을 지니며 플렉셔 힌지의 경우 유격이 전혀 존재하지 않고 재료의 미세한 변형을 통해 매우 정밀한 운동을 전달해 줄 수 있다.⁷

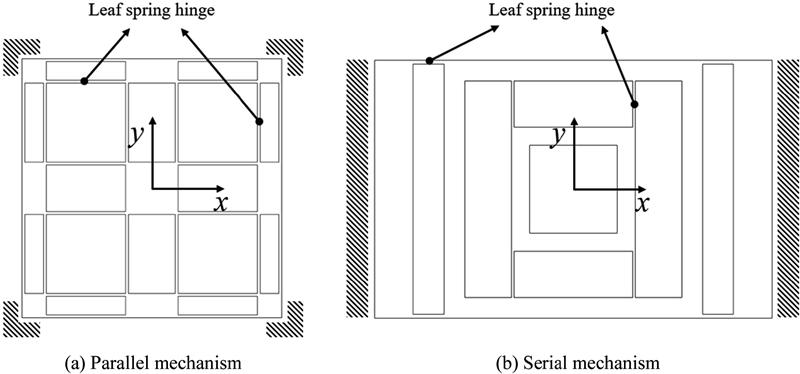
플렉셔 힌지 기반의 위치 결정 스테이지는 크게 병렬 기구(Parallel Mechanism) 방식과 직렬 기구(Serial Mechanism) 방식으로 나뉜다. Fig. 1과 같이 병렬 기구는 각 축이 하나의 엔드 이펙터(End-Effector)에 연결되어있어 높은 강성을 지니며 1, 2차 공진 주파수가 동일한 설계가 가능하다는 장점이 있지만, 간섭된 운동(Coupled Motion)이 발생할 수 있고 구조가 복잡하다는 단점이 존재한다. 반면 직렬 기구는 각 축이 적층되는 방식으로 구조가 단순하여 설계하기에 용이하고 제작 비용 측면에서 장점이 있지만 운동 질량(Moving Mass)의 누적으로 인해 1차 공진 주파수(First Resonance Frequency)가 2차 공진 주파수(Second Resonance Frequency)에 비해 확연히 낮은 편이다. 이는 제어 시스템의 대역폭을 좁게 하여 빠른 제어를 어렵게 하며 원자현미경에서의 고속 샘플 스캐닝과 같은 공정에 적용상의 한계가 있다. 게다가 병렬 기구와 달리 축별로 동적 성능이 달라서 제어 파라미터의 튜닝이 축별로 다르게 이루어져야 한다는 단점이 존재한다.⁸ 특정 분야에서는 이러한 특성이 장점으로 작용하기도 하지만 일반적으로 낮은 1차 공진 주파수는 직렬 기구의 적용 영역을 제한시킨다. 그러므로 고속 스캐닝 및 위치 결정에 적합하도록 직렬 기구의 장점을 살리면서도 동적 성능을 향상시킬 수 있는 직렬 기구 기반 위치 결정 스테이지의 설계 최적화에 대한 연구가 필요하다.

Fig. 1

Schematic diagrams of parallel and serial mechanisms with leaf spring hinges

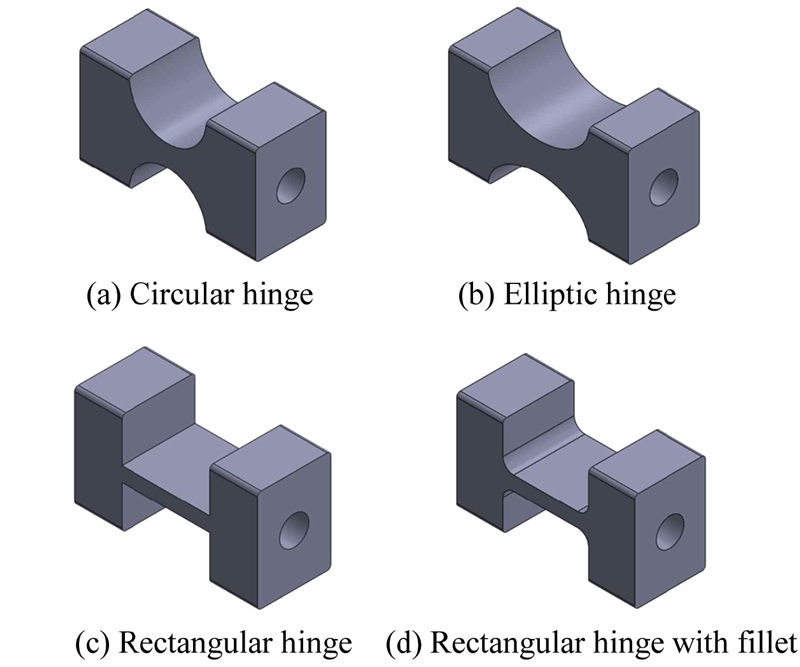
플렉셔 힌지는 모션 가이드(Motion Guide)의 역할과 더불어 부가적으로 PZT 구동기에 예압 하중(Preload)을 가하여 예상치 못한 인장에 의한 파손을 방지해주는 역할을 한다.⁹ 주로 1 -자유도 및 2-자유도가 사용되며 그 중에서도 1 -자유도를 지닌 형태가 가장 많이 사용된다. Fig. 2 는 대표적인 4가지 형태의 플렉셔 힌지를 보여주고 있다. 원형 힌지(Circular Hinge)는 회전 중심이 일정하게 유지되며 다른 형태의 힌지보다 정확한 운동 전달이 가능하다. 타원형 힌지(Elliptic Hinge)는 원형보다는 회전 중심이 부정확하지만 굽힘 하중이 낮게 분포하는 편이다. 직사각형 힌지(Rectangular/Leaf Spring Hinge)는 대부분의 길이에 걸쳐 변형이 이루어지므로 대변형에 유리하고 굽힘 하중이 적게 발생한다는 장점이 있다. 마지막으로 필렛 처리된 직사각형 힌지(Rectangular Hinge with Fillet)는 힌지부 양단에 필렛을 넣어줌으로써 응력 집중을 막기 위해 고안된 힌지이다.¹⁰

Fig. 2

Shapes of typical flexure hinges

플렉셔 힌지 기반의 위치 결정 스테이지는 공진 주파수, 구동기의 요구 추력, 변형에 따른 응력 계산을 위해 반드시 연성 해석(Compliance Analysis)을 수행해야 한다. 대표적인 연성 해석 방법으로는 Pseudo Rigid Body (PRB) 방법과 Nonlinear Modeling 방법, Matrix 기반 방법 등이 있다. Pseudo Rigid Body (PRB) 방법의 경우 힌지를 단순화시켜서 운동이 일어나는 방향의 힌지 연성만을 고려하여 해석하는 방법이다. 단순화된 수식을 얻을 수 있지만 모든 방향의 강성이 고려되지 않음으로 인해 실제와 오차가 발생하기 쉽다.¹¹ Nonlinear Modeling 방법의 경우 인장, 압축, 굽힘 및 비틀림 등의 변형을 모두 고려할 수 있으나 적분 과정이 필요하고 수식이 복잡해진다. Matrix 기반 방법은 후크의 법칙(Hooke’s Law)을 적용하여 각 방향의 변형과 관련된 연성 해석이 가능하고 주로 행렬 형태의 연산이 이루어지기 때문에 계산이 효율적이다.^12,13

본 연구에서는 원자현미경 내에서 고속 샘플 스캐닝에 활용할 수 있는 2-자유도 위치 결정 스테이지를 설계 및 최적화하고자 한다. 효율적인 최적화를 위해 연성 해석을 바탕으로 한 스테이지의 연성 모델을 도출하고 이것을 바탕으로 다양한 설계 변수에 대한 최적화를 수행함으로써 축별 동특성을 최대화하는 설계를 진행하고자 한다. 구체적으로 직사각형 힌지를 적용한 직렬 기구 2-자유도 위치 결정 스테이지의 1차 공진 주파수 특성을 향상시키며 동시에 축별 동적 특성의 균일화를 달성하고자 한다. 이를 위해 1차와 2차 공진 주파수의 비로 나타낸 공진 주파수 등방성(Resonance Frequency Isotropy, RFI)의 개념을 적용하여 이를 최대화하는 과정을 소개한다. 먼저 2-자유도 위치 결정 스테이지에 대한 연성 해석을 Matrix 기반 방법으로 수행하고, 이 결과를 바탕으로 공진 주파수 등방성 인덱스를 새롭게 고안한다. 민감도 해석을 거쳐 최적화를 이론식에 근거하여 수행하고 이론적인 해석의 결과를 검증하기 위해 유한요소해석(Finite Element Analysis, FEA)을 수행하여 결과를 비교 제시한다.

2. 연성 해석과 공진 주파수 등방성 인덱스

2.1 연성 행렬 및 연성 해석 절차

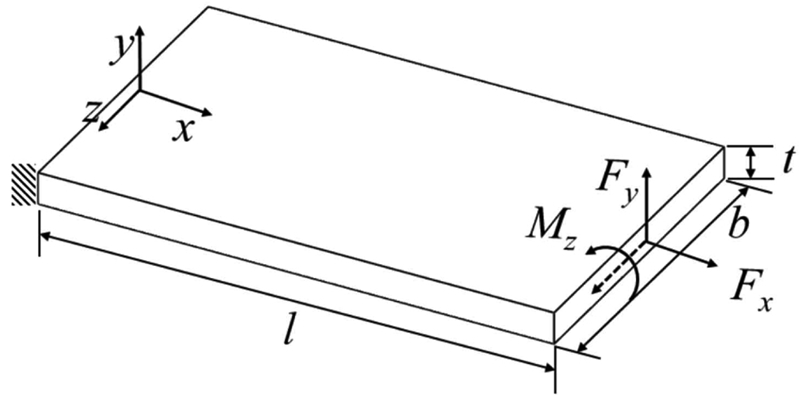
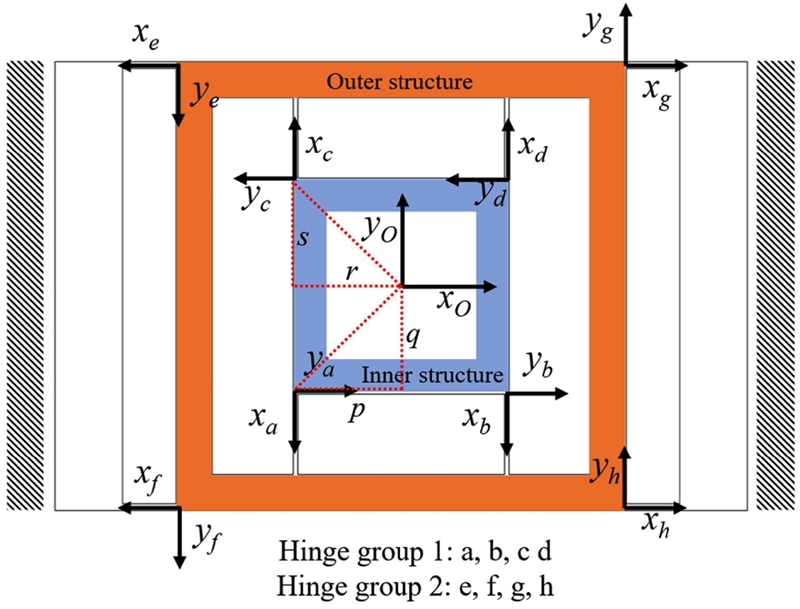
본 연구에서는 Matrix 기반 방법을 적용하여 연성 해석을 수행한다. 플렉셔 힌지 기반의 직렬 2-자유도 위치 결정 스테이지의 연성 해석은 다음의 순서로 이루어진다. 먼저 각 플렉셔 힌지에 지역 좌표계(Local Coordinate System)를 할당한다. 일반적으로 Fig. 3과 같이 힌지의 길이 방향을 x-축, 두께 방향을 y-축, 폭 방향을 z-축으로 설정한다. 이렇게 설정했을 때 적용할 수 있는 연성 행렬식이 식(1)에 나타나 있다. E는 재료의 종탄성계수를, G는 전단탄성계수를, l은 힌지의 길이를, b는 힌지의 폭을, t는 힌지의 두께를 각각 나타낸다. 연성 행렬과 변위, 외력의 관계는 식(2)에 표현되어 있다. 변위 벡터(X)는 연성 행렬과 외력 벡터(F)의 곱으로 구할 수 있다. 변위 벡터의 성분은 각각 x, y-축 직선 변위와 z-축 회전 변위를 나타내고 외력 벡터의 성분은 각각 x, y-축 힘과 z-축 모멘트를 나타낸다. Fig. 4에는 직렬 위치 결정 스테이지에 속한 모든 내부/외부 힌지에 할당된 좌표계를 나타내고 있다. 이 중에서 스테이지의 x-축 방향 운동에 관여하는 힌지(Hinge Group 1)를 내부 힌지라 하고, y-축 방향 운동에 관여하는 힌지(Hinge Group 2)를 외부 힌지라고 부르기로 한다.

$\[ C=\left[\begin{array}{ccc}\frac{1}{Ebt}& 0& 0\\ 0& \frac{4l^3}{Eb{t}^3}+\frac{1}{Gbt}& \frac{6l^2}{Eb{t}^3}\\ 0& \frac{6l^2}{Eb{t}^3}& \frac{12l}{Eb{t}^3}\end{array}\right] \]$

(1)

$\[ \begin{array}{l}X=CF\\ X={\left[u_x u_y {\theta }_z\right]}^T, F={\left[F_x F_y M_z\right]}^T\end{array} \]$

(2)

Fig. 3

Coordinate system and design parameters of the leaf spring hinge

Fig. 4

Inner and outer hinges and their assigned coordinate systems

그 후에는 각 지역 좌표계를 기준으로 표현된 연성 행렬을 기준이 되는 하나의 공통 좌표계로 변환한다. 본 연구에서 공통 좌표계는 Fig. 4의 중앙에 나타나 있는 {O} 좌표계이다. 좌표계 변환이 완료된 후에 마지막으로 공통 좌표계로 표현된 각 힌지의 연성 행렬을 더해주는데 식(3)과 같이 힌지가 직렬로 연결되어 있을 경우 연성 행렬을 더하고 병렬로 연결되어 있을 경우 연성 행렬의 역행렬인 강성 행렬을 더하여 다시 역을 취한다.

$\[ \begin{array}{l}Serial connection:\\ C_{serial}=\sum _{i=1}^m{C}_i\left(i=1~m\right)\\ parallel connection:\\ C_{parallel}=\sum _{j=1}^n{\left(\frac{1}{C_j}\right)}^{-1}\left(j=1~n\right)\end{array} \]$

(3)

본 연구에서는 Table 1과 같이 플렉셔 힌지 기반 위치 결정 스테이지에서 주로 사용되는 AL7075 재료의 물성 값을 적용했다. AL7075는 질량 대비 종탄성계수가 큰 편이며 내부식 특성이 좋다는 장점이 있다.

Table 1

Physical properties of the AL7075

3. 설계 최적화 및 유한요소해석을 통한 검증

3.1 최적화 수행 조건 및 민감도 해석

이번 장에서는 앞서 도출된 연성 해석 결과와 공진 주파수 등방성 인덱스를 적용하여 직렬 위치 결정 스테이지의 설계 최적화를 진행하고자 한다. 원자현미경 내 샘플 스캐닝에 적용할 수 있도록 2-자유도 평면형 구조를 지니도록 설계하고 목표 작업 영역은 15 × 15 μm이다. 설계 변수는 모두 7개이며 Table 2에 나타나 있다. 스테이지의 가로와 세로 크기(150 × 100 mm) 및 두께(15 mm)는 고정하고 내부의 구조와 힌지에 대한 설계 변수만을 최적화 변수로 설정하였다. 두께의 경우 가공 시 발생할 수 있는 휨 등의 제한 사항과 가공 비용을 고려하여 정하였다. 최적화의 목적은 1차 공진 주파수 특성을 향상시키며 공진 주파수 등방성을 최대화하는 설계 변수를 찾는 것이다. 이를 위해 1차 공진 주파수의 경우 원자현미경 내에서의 샘플 스캐닝(50 Hz 이상)에 필요한 사양인 500 Hz를 최소 제한 조건으로 반영했다.¹⁴ 또한, 힌지에 영구 변형이 발생하지 않도록 AL7075 재료의 항복 강도에 안전계수 3을 반영한 응력 제한 조건을 구동기의 강성 대비 스테이지의 강성이 10% 이내를 만족하도록 하기 위한 제한 조건을 추가했다. 최적화 목적과 제한 조건이 식(17)에 표현되어 있다.

$\[ \begin{array}{l}\mathrm{O}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}: to maximize \mathrm{R}\mathrm{F}\mathrm{I}\\ \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}:\\ stress of hinge\left({\sigma }_{max}\right)\le \frac{yield strength\left(503MPa\right)}{safety factor\left(3\right)}\\ 1^{st} resonance frequency\ge 500Hz,\\ stiffness of each axis\le \frac{actuator stiffness\left(90N/\mu m\right)}{10}\end{array} \]$

(17)

Table 2

Orthogonal array and design parameters

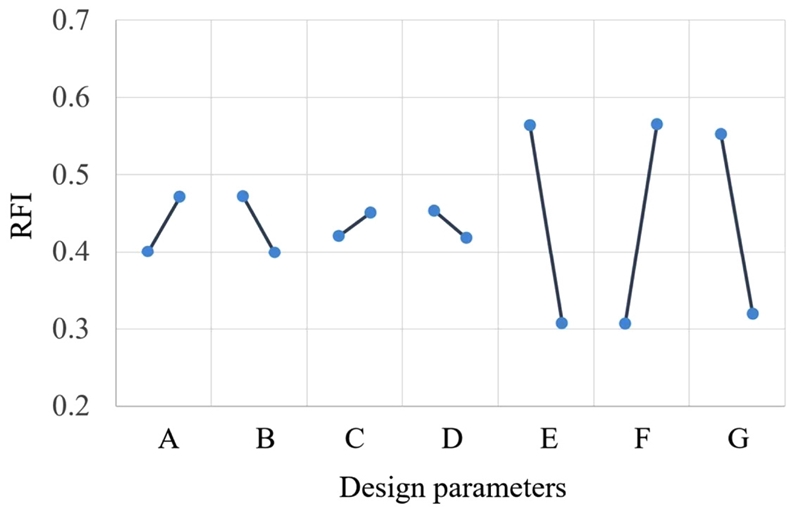
효율적인 최적화 수행을 위해 설계 변수의 탐색 간격을 정해야 하는데, 이를 위해 각 설계 변수에 대한 민감도 해석을 수행하였다(Fig. 5 참조). 그 결과 설계 변수 E, F, G의 민감도가 다른 설계 변수보다 훨씬 크게 나타났다. 그래서 다른 설계 변수보다 설계 변수 E, F, G에 대해 탐색 간격을 더 좁게 설정하여 최적화를 진행하였다.

Fig. 5

Sensitivity analysis graph

식(17)에 적용된 응력 모델을 식(18)에 참고로 나타내었다. K는 응력 집중 계수이며 2를 적용했다. δ_max는 힌지의 최대변위를, n은 안전계수를, σ_Y는 재료의 항복강도를 의미한다. 최대변위는 스테이지가 지지해야 하는 하중 조건(200 N)을 가했을 때의 힌지 변형량을 계산하여 적용했다.

$\[ {\sigma }_{max}=K\frac{2{\delta }_{max}Et}{l^2}\le \frac{{\sigma }_Y}{n} \]$

(18)

3.3 최적화 결과

최적화 결과의 제시를 위해 초기 설계 변수와 최적 설계 변수 값이 Table 3에 나타나 있다. 최적화 과정에서 전체 스테이지의 크기 및 외부 구조의 크기는 고정하였고 나머지 변수에 대해 최적화를 수행하였다.

Table 3

Comparison between initial and optimal design cases in theoretical analysis

초기 설계에서의 1, 2차 공진 주파수는 일반적인 직렬 위치 결정 스테이지의 특성을 잘 보여준다. 운동 질량의 누적으로 인해 별도의 최적화 과정을 거치지 않으면 1차가 2차 공진 주파수에 비해 크게 낮음을 알 수 있고 결과적으로 공진 주파수 등방성도 매우 낮은 수준임을 알 수 있다. 이에 비해 최적화된 설계 변수를 보면 힌지의 길이와 두께 및 내부/외부 힌지의 수가 달라졌음을 알 수 있다. 내부/외부 힌지의 수가 1개씩 많아지고 외부 구조를 지지하는 외부 힌지의 두께가 0.3 mm만큼 두꺼워짐으로 인해 강성이 향상되고 1차 공진 주파수가 높아졌음을 알 수 있다. 연성 해석 수식에 근거하여 수행한 최적화를 통해 1차 공진 주파수는 50.8%, 공진 주파수 등방성은 80.2%가 향상되었음을 볼 수 있다. 그러므로 직렬 기구 기반의 위치 결정 스테이지의 적절한 활용을 위해서는 활용 목적에 맞는 최적화 과정이 반드시 수반되어야 함을 확인할 수 있다.

3.4 유한요소해석을 통한 최적화 결과의 검증

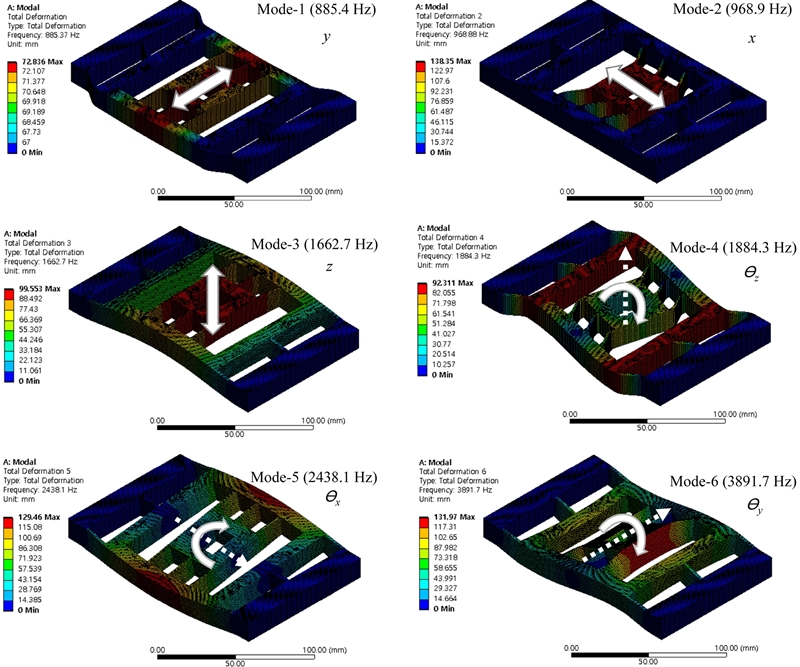
이론적인 연성 해석 및 최적화 결과의 타당성을 검증하기 위해 유한요소해석을 수행하여 그 결과를 Fig. 6에 제시하였다. 유한요소해석 도구로 ANSYS의 Modal 해석 모듈을 활용하였으며 이론해석과 동일한 조건의 재료(AL7075)를 적용하고 자유 진동 상태에서 모드별 공진 주파수와 각 모드 형상(Mode Shape)을 도출하였다. 격자 생성과 관련해서는 선행 연구 조건(Node 수: 18,603개, Element 수: 3,060개)과 달리 힌지 부위의 격자수를 두께 방향으로 2배 많게 설정하고 스테이지 전체적으로 격자 수를 증가시켰을 때(Node 수: 591,162개, Element 수: 130,800개), 공진 주파수의 변화(1-6차)가 최소 0.25%에서 최대 2.54% 차이나는 것을 확인했다. 본 연구에서는 보다 정확한 결과를 제시하기 위해 격자 수를 증가시킨 결과를 수록하였다. 유한요소해석에서는 2개의 축에 해당하는 2가지 모드에 대해서만 계산한 이론해석과 달리 총 6가지의 모드 형상과 공진 주파수가 도출된 것을 볼 수 있다.

Fig. 6

Results of modal analysis using FEA

유한요소해석 결과를 확인해 보면 각 모드는 6-자유도에 해당하는 움직임이 보이고 특히 2차 공진 주파수(968.9 Hz)와 3차 공진 주파수(1662.7 Hz)의 차이가 분명하여 최적화된 2-자유도 위치 결정 스테이지의 거동이 x-축과 y-축 위주로 일어나고 그 외의 방향으로의 거동이 일어나기가 어려움을 알 수 있다.

Table 4에는 이론해석과 유한요소해석 결과에 대한 구체적인 비교가 나타나 있다. 공진 주파수에서 각 해석 결과의 차이가 발생하는 주된 이유는 이론해석에서는 힌지의 질량이 고려되지 않았고, 식(1)의 연성 행렬 내에 포함된 수식이 실제보다 단순화되었기 때문이며, 연성 해석이 낮은 자유도의 모델을 바탕으로 수행되었기 때문이라고 판단된다. 또한, Fig. 6의 1, 2 모드에 대한 해석 결과에서 보이듯이 이론해석에서는 내부와 외부 구조를 강체로 가정하였으나 유한요소해석에서는 내부와 외부 구조의 일부분에서 미소한 변형이 발생하고 있는 것을 확인할 수 있다. 이러한 요인들이 종합적으로 오차를 발생시키고 있는 것을 보인다. 그러나 전반적으로 이론해석과 유한요소해석 결과의 차이가 오차 범위 내에 존재함을 볼 수 있고 본 연구에서 제시한 공진 주파수 등방성 인덱스를 적용하고 설계 최적화를 수행함으로써 직렬 기구 스테이지의 성능이 크게 향상될 수 있음을 알 수 있다.

Table 4

Comparison between theoretical analysis and FEA results

4. 결론

본 논문에서는 2-자유도 직렬 위치 결정 스테이지의 설계 변수 최적화를 통해 1차 공진 주파수를 높이고 공진 주파수 등방성을 최대화하는 연구를 수행하였다. 이를 위해 먼저 Matrix 기반 방법을 적용한 연성 해석을 수행하여 전체 축에 대한 연성 행렬을 도출하고 모드 해석에 활용하여 공진 주파수를 구했다. 1차와 2차 공진 주파수의 비를 공진 주파수 등방성 인덱스로 정의하여 설계 변수 민감도 해석 및 최적화를 수행하였다. 또한 이론해석과 유한요소해석 결과를 비교하여 이론해석 및 최적화의 타당성을 검증하였다. 이러한 최적화를 통해 1차 공진 주파수와 공진 주파수 등방성이 모두 향상된 설계 변수를 찾아낼 수 있었다. 본 연구에서 제시한 공진 주파수 등방성 개념을 확장하면 향후 3-자유도 이상의 위치 결정 스테이지 최적화에도 적용할 수 있을 것으로 생각된다.

Acknowledgments

본 논문은 2019년도 동양미래대학교 교내 학술 연구 과제의 연구 지원과 정부(교육부)의 재원으로 한국연구재단 기초연구사업(No. NRF-2018R1D1A1B07044104)의 지원을 받아 수행된 것임.

References

• Polit, S. and Dong, J., “Development of a High-Bandwidth XY Nanopositioning Stage for High-Rate Micro-/Nanomanufacturing,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 4, pp. 724-733, 2010. [https://doi.org/10.1109/TMECH.2010.2052107]
• Li, C. X., Gu, G. Y., Yang, M. J., and Zhu, L. M., “Design, Analysis and Testing of a Parallel-Kinematic High-Bandwidth XY Nanopositioning Stage,” Review of Scientific Instruments, Vol. 84, No. 12, Paper No. 125111, 2013. [https://doi.org/10.1063/1.4848876]
• Gu, G. Y., Zhu, L. M., Su, C. Y., and Ding, H., “Motion Control of Piezoelectric Positioning Stages: Modeling, Controller Design, and Experimental Evaluation,” IEEE/ASME Transactions on Mechatronics, Vol. 18, No. 5, pp. 1459-1471, 2012. [https://doi.org/10.1109/TMECH.2012.2203315]
• Li, Y., Huang, J., and Tang, H., “A Compliant Parallel XY Micromotion Stage with Complete Kinematic Decoupling,” IEEE Transactions on Automation Science and Engineering, Vol. 9, No. 3, pp. 538-553, 2012. [https://doi.org/10.1109/TASE.2012.2198466]
• Lai, L. J. and Zhu, Z. N., “Design, Modeling and Testing of a Novel Flexure-Based Displacement Amplification Mechanism,” Sensors and Actuators A: Physical, Vol. 266, pp. 122-129, 2017. [https://doi.org/10.1016/j.sna.2017.09.010]
• Roy, N. K. and Cullinan, M. A., “Design and Characterization of a Two-Axis, Flexure-Based Nanopositioning Stage with 50 mm Travel and Reduced Higher Order Modes,” Precision Engineering, Vol. 53, pp. 236-247, 2018. [https://doi.org/10.1016/j.precisioneng.2018.04.007]
• Cai, K., Tian, Y., Liu, X., Zhang, D., Shang, J., et al., “Development and Control Methodologies for 2-DOF Micro/Nano Positioning Stage with High Out-of-Plane Payload Capacity,” Robotics and Computer-Integrated Manufacturing, Vol. 56, pp. 95-105, 2019. [https://doi.org/10.1016/j.rcim.2018.08.007]
• Leang, K. K. and Fleming, A. J., “High-Speed Serial-Kinematic AFM Scanner: Design and Drive Considerations,” Proc. of the American Control Conference, pp. 3188-3193, 2008. [https://doi.org/10.1109/ACC.2008.4586983]
• Yong, Y., Moheimani, S. R., Kenton, B. J., and Leang, K., “Invited Review Article: High-Speed Flexure-Guided Nanopositioning: Mechanical Design and Control Issues,” Review of Scientific Instruments, Vol. 83, No. 12, Paper No. 121101, 2012. [https://doi.org/10.1063/1.4765048]
• Tian, Y., Shirinzadeh, B., Zhang, D., and Zhong, Y., “Three Flexure Hinges for Compliant Mechanism Designs based on Dimensionless Graph Analysis,” Precision Engineering, Vol. 34, No. 1, pp. 92-100, 2010. [https://doi.org/10.1016/j.precisioneng.2009.03.004]
• Pei, X., Yu, J., Zong, G., and Bi, S., “An Effective Pseudo-Rigid-Body Method for Beam-Based Compliant Mechanisms,” Precision Engineering, Vol. 34, No. 3, pp. 634-639, 2010. [https://doi.org/10.1016/j.precisioneng.2009.10.001]
• Pham, H. H. and Chen, I. M., “Stiffness Modeling of Flexure Parallel Mechanism,” Precision Engineering, Vol. 29, No. 4, pp. 467-478, 2005. [https://doi.org/10.1016/j.precisioneng.2004.12.006]
• Jiang, Y., Li, T. M., and Wang, L. P., “Stiffness Modeling of Compliant Parallel Mechanisms and Applications in the Performance Analysis of a Decoupled Parallel Compliant Stage,” Review of Scientific Instruments, Vol. 86, No. 9, Paper No. 095109, 2015. [https://doi.org/10.1063/1.4930884]
• Fleming, A. J. and Leang, K. K., “Design, Modeling and Control of Nanopositioning Systems,” Springer, 2014. [https://doi.org/10.1007/978-3-319-06617-2]