풍하중을 고려한 100 kW급 태양광 발전 설비 지지구조물의 응력해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The photovoltaic power generation facility is usually installed outdoors and is extensively impacted by snow and wind power as well as external contact friction caused by snow and rain. In particular, since there is a markedly high possibility of damage from devastating wind power such as a typhoon, an overall safety evaluation is essential. However, most studies are conducted using cell-level stress analysis rather than cluster-wide stress analysis. Thus, in this study, a finite element analysis was performed on the entire support structure of the photovoltaic power generation facility, wherein the wind load was applied, and the portion wherein extensive stress was generated was identified. The results of the analysis showed that the stress in the rear side was relatively higher than in the front side of the support structure for the horizontal wind. Additionally, it was confirmed that a relatively high stress occurs in the lower side than the upper side of the support structure.
Keywords:
Finite element analysis, Solar power structure, Wind load, Von-mises stress, Maximum principal stress키워드:
유한요소해석, 태양광 발전 구조물, 풍하중, 폰 미세스 응력, 최대주응력1. 서론
국제적으로 에너지사용에 관한 환경오염 문제가 심각하여 온실가스 절감 및 대체에너지산업 진흥 정책에 관심이 집중되고있다. ‘기후변화에 대한 국제연합 기본협약(United Nations Framework Convention on Climate Change)’ 및 파리기후협약('16.11 발효, '21. 01부터 적용)이 체결되었으며, 지구온난화 현상 원인을 제거하기 위한 노력의 일환으로 신재생 에너지 사용이 부각되고 있다. 그 중 우리나라에서는 신재생 에너지 중 수소에너지, 연료전지, 풍력 에너지, 태양광 에너지 등을 위주로 하여 정부의 정책 및 지원을 바탕으로 꾸준히 발전되어 왔다.1-4
최근 신재생 에너지 중 상대적으로 설치가 용이한 태양광 에너지 발전 관련 자재 수급률 및 발전 점유율이 급격하게 상승하면서 현재 전국에 약 23만개소 이상의 태양광 발전소를 두고 있다.5 이러한 태양광 발전시스템은 크게 태양광 모듈(태양전지, 축전지 및 전력 변환 장치)과 설치구조물 2가지로 구성된다. 과거에는 태양광 발전 기술 분야 중 전기를 생산하는 태양광 집광 패널 및 모듈 기술이 중점적으로 발전되었고,6,7 현재는 태양광 발전 기술 분야 중 모듈을 지지하는 연결부 및 지지구조물에 대한 연구개발도 상당 부분 진행된 상태이다. 하지만, 대부분의 태양광 발전 설비 지지구조물에 관한 연구는 클러스터 단위에 해당하는 전체 지지구조물의 응력해석보다 셀 단위의 단일구조물에 대한 응력해석이 이루어지고 있는 실정이다.8-11 셀 단위의 단일구조물에 대한 응력해석은 주로 패널 1 개체에 작용하는 풍하중에 대한 응력해석을 말한다.
옥외에 설치되는 태양광 발전 설비 특성상 기후(눈비에 의한 외부 접촉 마찰과 더불어 적설 및 풍력)에 많은 영향을 받으며, 특히 태풍과 같은 강한 풍력에 의해 파손될 가능성이 매우 크므로 패널 1 개체에 대한 응력해석뿐만 아니라 전체구조물에 대한 응력해석 및 안정성 평가는 필수적이다.12-14
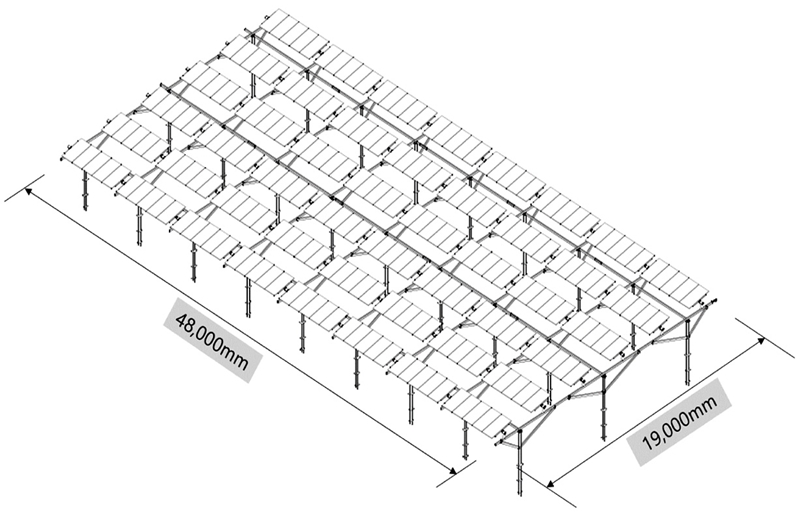
이에 본 논문에서는 클러스터 단위의 응력해석을 위하여 풍하중이 작용하는 전체 태양광 발전 설비 지지구조물에 대하여 응력해석을 수행하였다. 본 논문에 이용된 태양광 발전 구조물의 전체 3D 형상은 Fig. 1과 같다.
PV (Photovoltaic) structure dimension
2. 유한요소해석
본 연구에서 연구대상 모델은 태양광 발전 설비 지지구조물이다. 모델링을 통하여 모델 전체의 3차원 유한요소해석을 실시하였고, 구조물에 풍하중을 적용하여 태양광 발전 지지구조물에 발생하는 응력을 확인하였다. 구조물의 모델링은 구조 평면도와 설치구조물 개발로 보여진 모델을 바탕으로 하여 설계 프로그램인 Inventor 2018을 이용하였고, 3차원 유한요소해석은 상용 소프트웨어인 ANSYS Workbench 18.1을 이용하였다.
2.1 모델
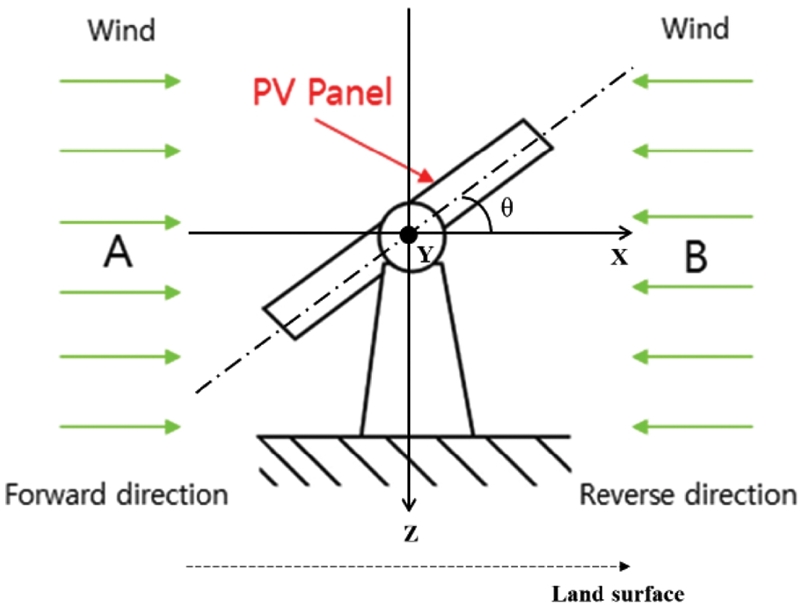
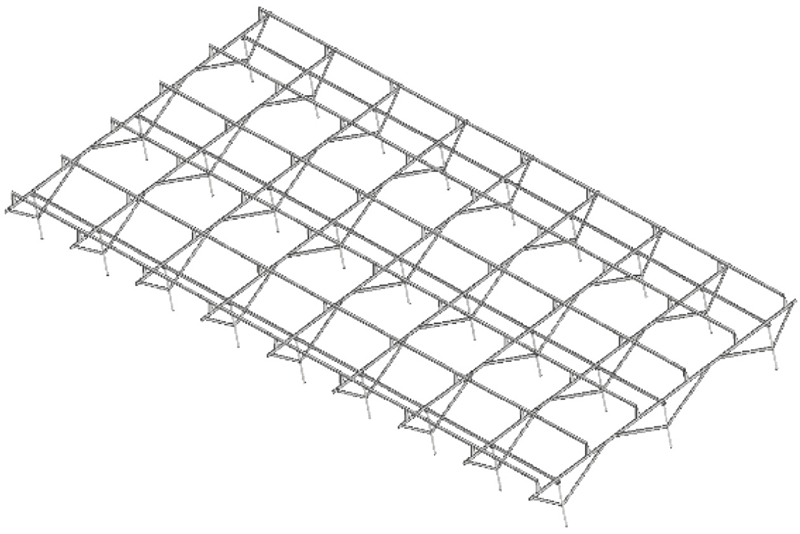
풍하중이 주요 작용하는 작용점은 지표면 기준 28o의 경사로 설치된 240장의 태양광 패널이며, 본 연구에서 다루는 태양광 발전 설비 구조물의 전체 치수(폭 × 길이 × 높이 = 19,000 × 48,000 × 5,000 mm) 및 풍향은 각각 Figs. 1과 2와 같다. 클러스터 단위의 태양광 발전 설비 지지구조물의 응력해석을 위하여 전체구조물을 하나의 개체로 모델링하였으며, 해석프로그램의 특성을 고려하여 패널을 생략하고 패널에 작용하는 풍하중을 상단 패널 지지대(Top Panel Support)에 동일하게 적용하였다. 패널을 생략한 최소화 모델은 Fig. 3과 같이 나타내었다. 지반에 고정되는 기둥은 외경 100, 두께 4.5 mm의 원형 파이프이며, 나머지 구조물은 가로 × 세로(125 × 75 mm), 두께 2.6 mm의 사각 파이프로 구성되었다. 구조물의 재질은 내식성 및 강성을 위해 SS400 재질을 사용하였으며, 이에 대한 물성은 Table 1에 나타내었다.
Wind direction
Minimization model
Material property of structure steel (SS400)
2.2 해석 조건
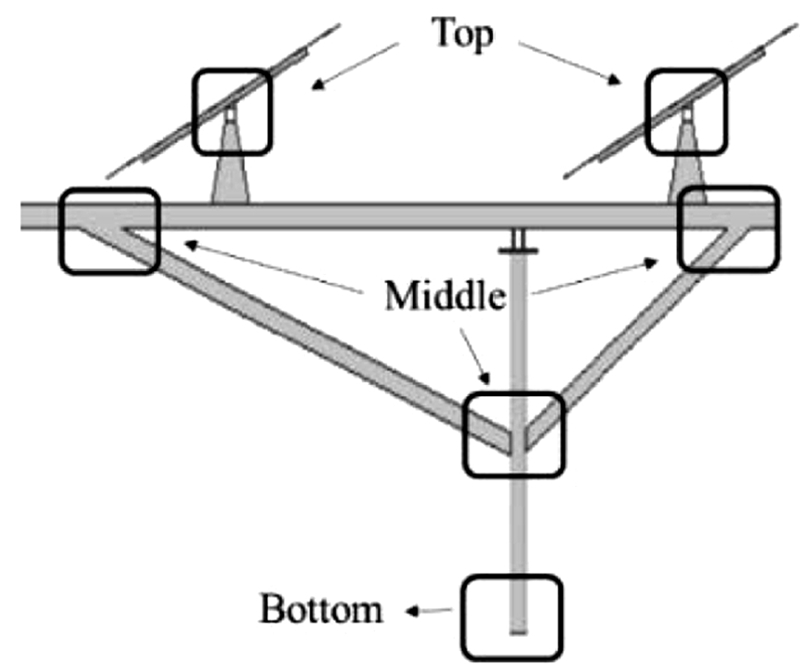
구조물의 정적 구조해석을 위해 4-Node Tetrahedron 요소로 Mesh를 구성하였으며, 이때 Node 및 Element 수는 각각 559,091 및 279,136개이다. 1개의 클러스터에는 총 6열의 태양광 패널이 존재하며 각 열에는 총 40(5 × 8)개의 패널이 존재한다. 구조물에 작용하는 외력은 패널에 작용하는 자중 및 풍하중이며, 이를 6열에 해당하며 패널이 거치되는 6개의 상단 패널 지지대에 각각 설정하였다. 1개의 패널의 무게는 약 25 kg으로 1개열에 올라가는 패널 무게는 1,000 kg(25 × 40)이고, 총 6열의 전체 패널 무게는 6,000 kg이다. 또한, 표준 중력가속도 9.80665 m/s2을 부여하였다. 패널에 가장 큰 영향을 미치는 서로 상반된 수평 방향(지표면 기준) 풍하중에 대한 해석 조건을 설정하였으며, 이를 Fig. 2에 나타내었다. 또한, 하중이 구조물에 크게 작용될 것으로 예상되는 구간에 발생하는 응력을 알아보기 위하여 3개의 구간(Top · Middle · Bottom)으로 나누어 총 6개의 Case (Fig. 4 및 Table 2 참조)로 정리하였다.
Structure fastening 3 part
Stress and reaction analysis 6 cases
2.3 풍하중 조건
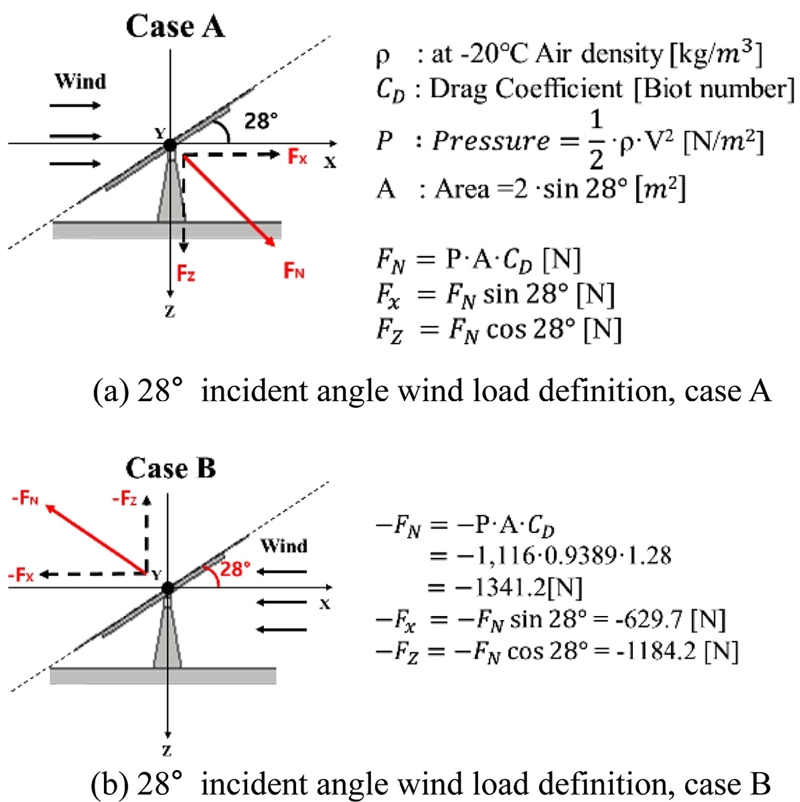
풍하중 방향에 따른 구조물의 응력분포를 확인하기 위해 실제 태풍 및 바람이 작용할 때와 같은 유사한 하중 조건을 부여하였다.15-18 태풍에 준하는 40 m/s 속도의 바람이 작용할 때, Fig. 2의 A의 경우에는 패널 1개당 수평 방향 629.7 N, 수직 방향 1184.2 N의 풍하중이 작용하는 것으로 계산하였으며, Fig. 2의 B의 경우에는 A의 경우와 크기는 같으나 반대 방향으로 풍하중이 작용하는 것으로 계산하였다. 패널에 작용하는 풍하중 도해 및 도출계산식은 Fig. 5에 나타내었다. Fig. 5에서 ρ는 -20oC일 때의 공기의 밀도이고, CD는 항력 계수이다. 또한, 면적 A는 바람이 부는 방향에 수직한 평면에 투영한 패널의 면적이다.
Definition of incidence angle of wind load
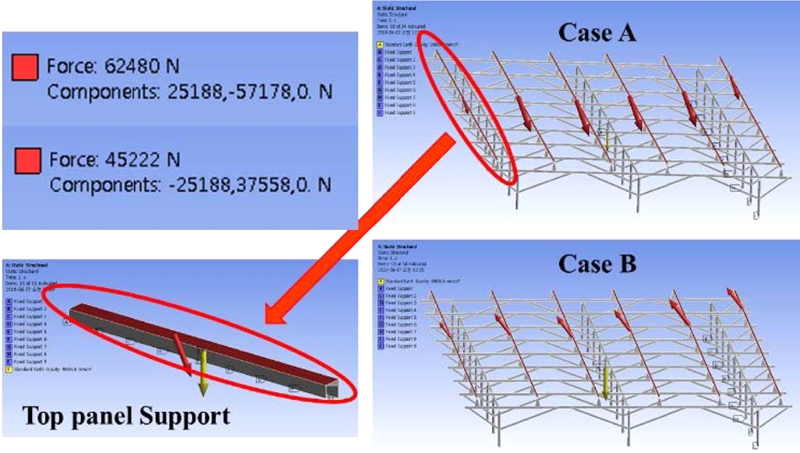
패널이 거치되는 각 패널 지지대에 Fig. 2의 A의 경우에는 수평 방향 25,188 N, 수직 방향 47,368 N의 풍하중을 적용하였으며, Fig. 2의 B의 경우에는 크기는 같으나 반대 방향의 하중을 적용하였다. 최종적으로 패널의 자중, 표준 중력가속도(약 9,810 N) 및 풍하중을 조합한 결과, 각 상단 패널 지지대에는 Fig. 2의 A의 경우 총 62,480 N(수평 방향 25,188 N, 수직 방향 -57,178 N), Fig. 2의 B의 경우 총 45,222 N(수평 방향 -25,188 N, 수직 방향 37,558 N)의 하중을 부여하였다. 상단 패널 지지대 및 구조물에 부여된 중력 및 풍하중은 Fig. 6에 나타내었다.
Load condition
3. 해석 결과 및 고찰
풍하중이 태양광 발전 설비 지지구조물 및 패널의 측면 방향보다 정방향(Forward Direction) 및 역방향(Reverse Direction)으로 작용할 때 패널에 대하여 가장 큰 항력이 작용하고, 구조물에 큰 응력이 발생할 것으로 예상된다. 이는 바람이 불어오는 방향에 수직한 패널의 투영면적이 가장 넓기 때문이다. 이에 대하여 구조물에 정, 역방향으로 풍하중이 작용할 때 발생하는 응력분포를 확인 및 분석하기 위하여 2가지 방향, 3가지 구간, 2가지 응력 등에 대해 총 12가지 응력해석 결과를 확인하였다. 이는 Figs. 7부터 10에 나타내었다.
Stress measurement position
Von-mises stress distribution of case A
Maximum principal stress distribution of case A
Von-mises stress distribution of case B
응력해석의 결과로써 Von-Mises Stress와 Maximum Principal Stress 2가지 응력을 측정하였으며, 이를 정량적으로 비교하기 위하여 응력 측정 위치를 결정하였다. 또한, 결과로부터 일관성있는 데이터를 획득하기 위하여 Top, Middle, Bottom에서 인접한 3곳의 데이터를 측정하여 평균값을 산출하였다. 응력 측정 위치는 프로그램 내 구조물에 고정 구속 조건을 부여한 지점으로 정하였다. 자세한 측정 위치는 Fig. 7에 나타내었으며, 응력분포를 육안으로도 확인하여 비교분석할 수 있도록 0-90 MPa 범위를 11단계로 구분하여 응력분포의 Scale을 동일하게 설정하였다. 이를 통하여 동일색은 동일응력을 나타내는 것으로 해석 결과를 보기 쉽게 하였다.
3.1 Case A의 해석 결과
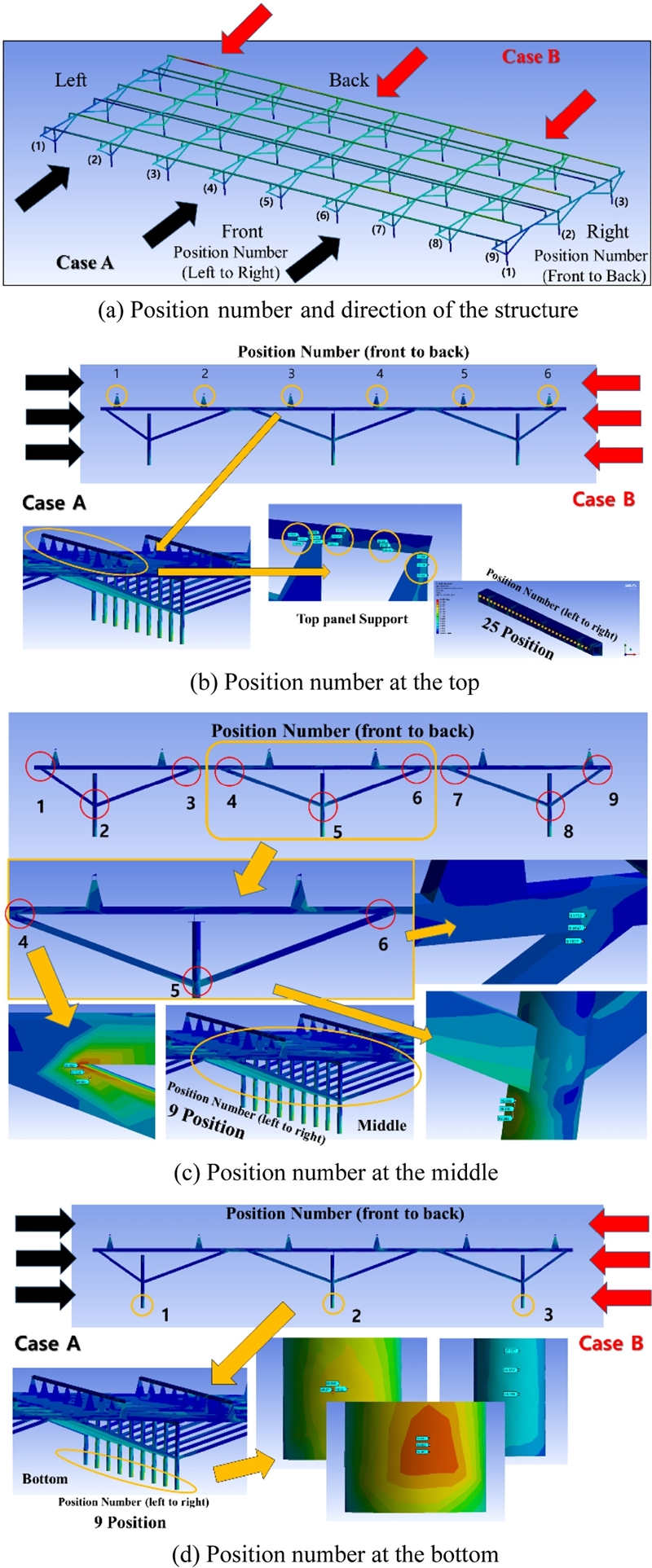
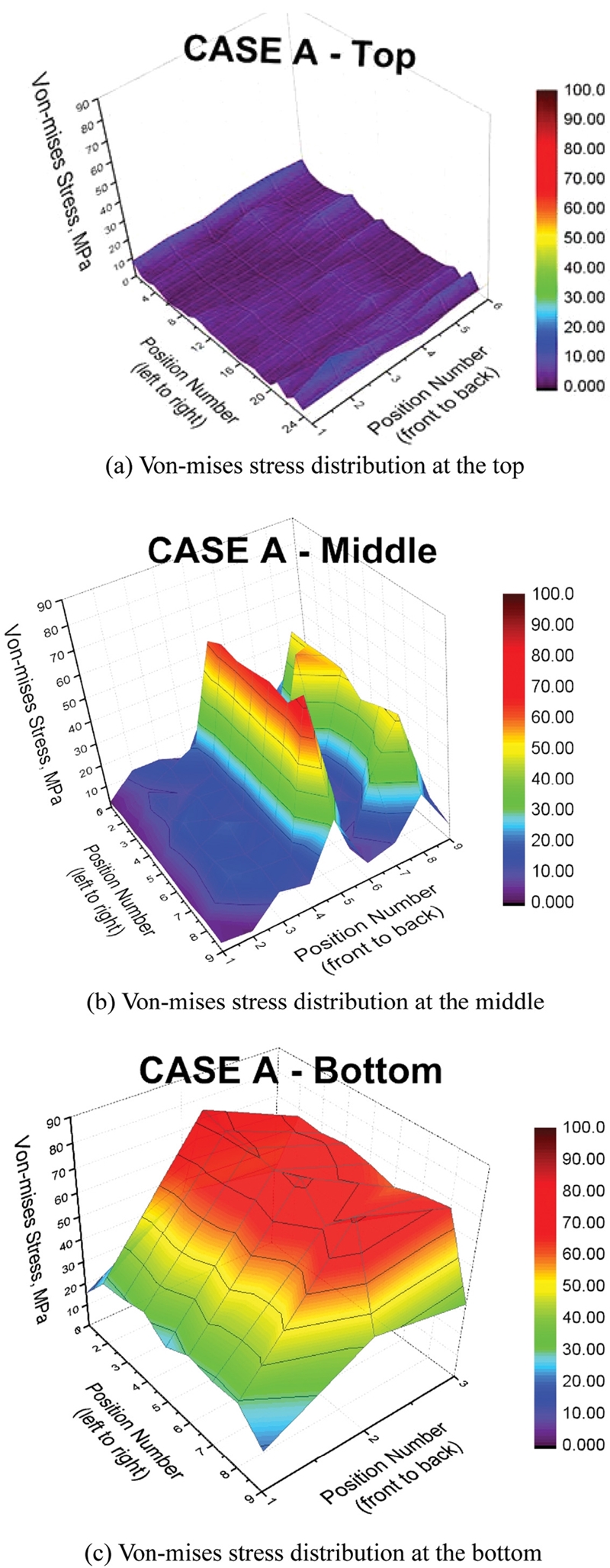
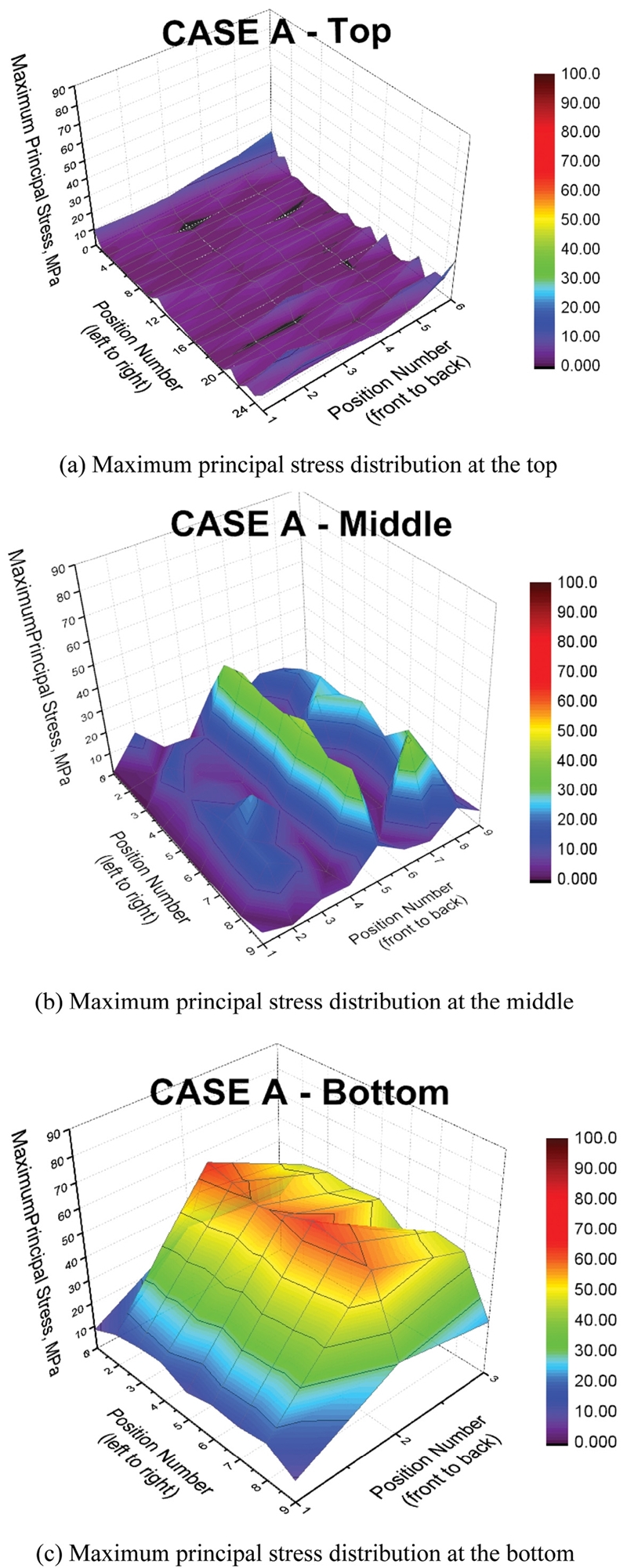
Fig. 8은 Case A의 Top, Middle, Bottom 구간별 Von-Mises Stress 응력분포를 나타낸 것이고, Fig. 9 는 Maximum Principal Stress 응력분포를 나타낸 것이다. 이때 Figs. 8과 9의 구간별 Position Number는 Figs. 7(b)부터 7(d)에서 나타낸 바와 같이 Position Number (Left to Right)-(Front to Back) 각각 25 Position-6 Position, 9 Position-9 Position, 9 Position-3 Position으로 다르게 지정하였다.
Case A Top의 Von-Mises Stress, Maximum Principal Stress 응력분포 확인 결과, Figs. 8(a) 및 9(a)에 나타낸 것과 같이 응력범위는 0-20 MPa이었으며, 발생한 응력이 구조물 Top에서 평균적으로 약 10 MPa이 발생하였고, 모든 응력 측정 위치에서 큰 차이가 없는 것으로 해석되었다.
Case A Middle의 Von-Mises Stress 응력분포 확인 결과, Fig. 8(b)에 나타낸 것과 같이 응력 범위는 0-70 MPa이었으며, Fig. 8(b)의 Position Number (Front to Back) 중 5와 8에서 응력이 크게 발생할 것으로 해석되었다. 이를 통해 Fig. 7(a)에 나타낸 Position Number (Front to Back)의 (1), (2), (3)에 해당하는 3곳의 수직 기둥 중 (2), (3)과 같고, 이는 구조물 기준 Front보다 Back에서 응력이 크게 발생할 것임을 의미한다. 또한, 이는 상대적으로 높은 하중이 구조물의 수직 기둥과 Y자 형태의 지지대 연결 부위에 작용할 것으로 생각된다.
Case A Bottom의 Von-Mises Stress 응력분포 확인 결과, Fig. 8(c)에 나타낸 것과 같이 응력 범위는 20-85 MPa이었으며, Case A Middle과 마찬가지로 구조물 기준 Front보다 Back에서 응력이 다소 크게 발생할 것으로 생각된다. 또한, 토지에 묻혀있는 수직 기둥에 대하여 지표면과 접하는 부분에 집중적으로 응력이 발생할 것으로 해석되었다. 이때 응력 범위가 최소 0 MPa 수준인 Top, Middle과 다르게 최소 20 MPa으로 측정되었는데, 이것은 상대적으로 높은 하중이 구조물 Bottom에 작용할 뿐만 아니라 풍하중이 작용하는 경우 항상 응력이 발생될 것으로 판단된다.
Case A Middle의 Maximum Principal Stress 응력분포 확인 결과, Fig. 9(b)에 나타낸 것과 같이 응력 범위는 0-45 MPa이며, Fig. 8(b)의 Position Number (Front to Back) 중 5와 8에서 상대적으로 큰 응력이 발생할 것으로 해석되었다. 이는 Fig. 7(a)에 나타낸 Position Number (Front to Back)의 (1), (2), (3)에 해당하는 3곳의 수직 기둥 중 (2), (3)과 같고, 이는 Case A Middle의 Von-Mises Stress 응력분포 확인 결과와 마찬가지로 구조물 기준 Front보다 Back에서 높은 응력이 발생할 것임을 의미한다.
Case A Bottom의 Maximum Principal Stress 응력분포 확인 결과, Fig. 9(c)에 나타낸 것과 같이 응력 범위는 10-85 MPa이며, Case A Bottom의 Von-Mises Stress 해석 결과와 마찬가지로 구조물 기준 Front보다 Back에서 응력이 다소 크게 발생할 것으로 생각된다. FEA 해석 결과에 의하면, 발생한 최대 응력값은 약 84 MPa으로 Bottom에서 가장 높게 나타났고, Top에서 가장 낮은 응력이 발생하였다.
전체적인 Case A 응력분포 확인 결과, Von-Mises Stress와 Maximum Principal Stress 응력 범위는 모두 약 0-85 MPa 이내의 수준이었으며, Von-Mises Stress와 Maximum Principal Stress의 응력분포가 유사한 것으로 확인되었다. 이때 Von-Mises Stress 및 Maximum Principal Stress 최소, 최댓값이 각각 Top 및 Bottom에서 확인되었다. 또한, 지지구조물의 Top 및 Front(바람을 앞서 맞는 부분)에서 낮은 응력이 발생할 것이며, 구조물 기준 Front와 Back 사이 Position Number (Front to Back) (2) 중앙 기둥에서 가장 큰 응력이 발생함을 알 수 있었다.
하지만 Fig. 7(a)에서 나타낸 Position Number (Left to Right)에 해당하는 구조물 기준 Left와 Right 사이의 응력분포는 응력 측정 위치에 따른 큰 차이를 보이지 않았다. 이는 풍하중이 작용하는 패널의 면적에 따른 결과로 보여진다.
이러한 응력 발생 원인은 패널에 작용하는 풍하중이 경사진 각도에 의하여 수평 및 수직 방향 하중으로 나누어지기 때문이라고 생각된다. 수평 방향의 경우, 수평 방향 풍하중 Fx가 작용하여 구조물이 Back 방향으로 밀리게 되어 Position Number (Front to Back) (2), (3)에 해당하는 수직 기둥에 높은 하중이 작용하여 구조물 기준 Front보다 Back에 높은 응력이 발생하게 될 것이다.
수직 방향의 경우, 풍하중에 의한 중력 방향 수직 하중 Fz와 구조물의 자중에 의한 고정 하중이 더해져 구조물의 Top보다 Bottom에 큰 하중이 작용 큰 응력이 발생할 것으로 판단된다.
3.2 Case B의 해석 결과
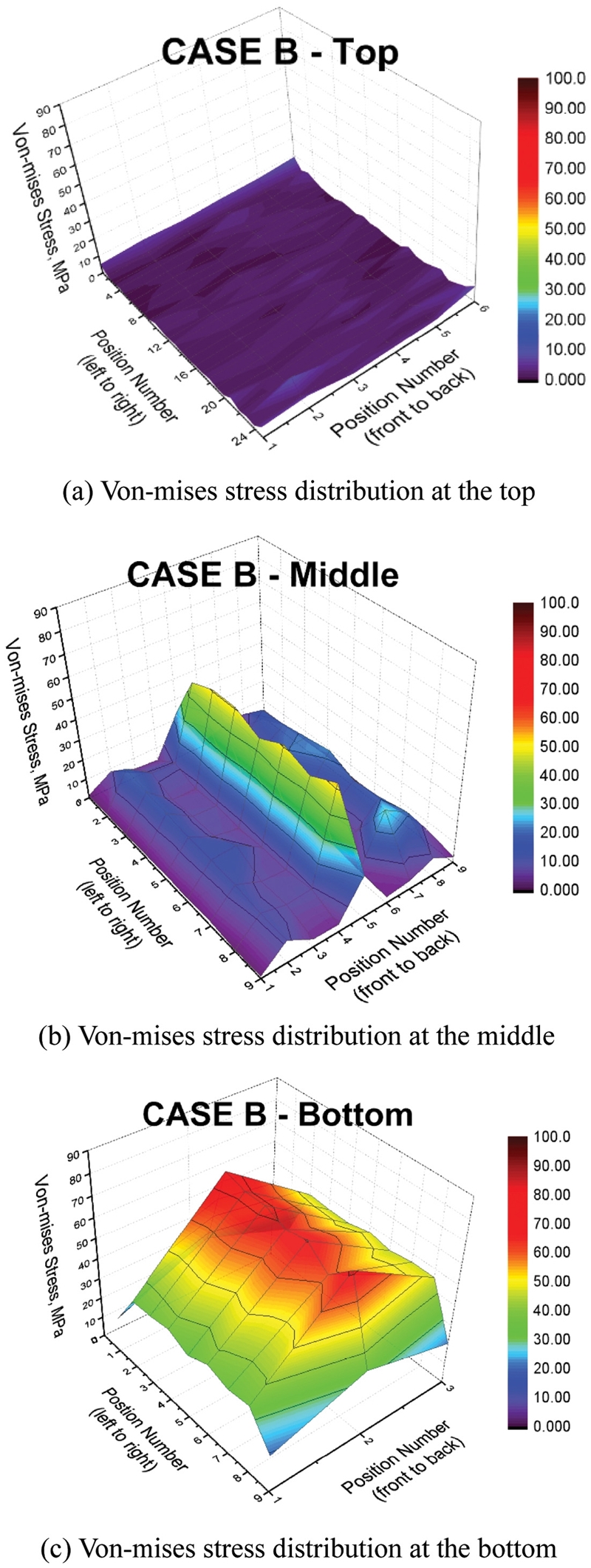
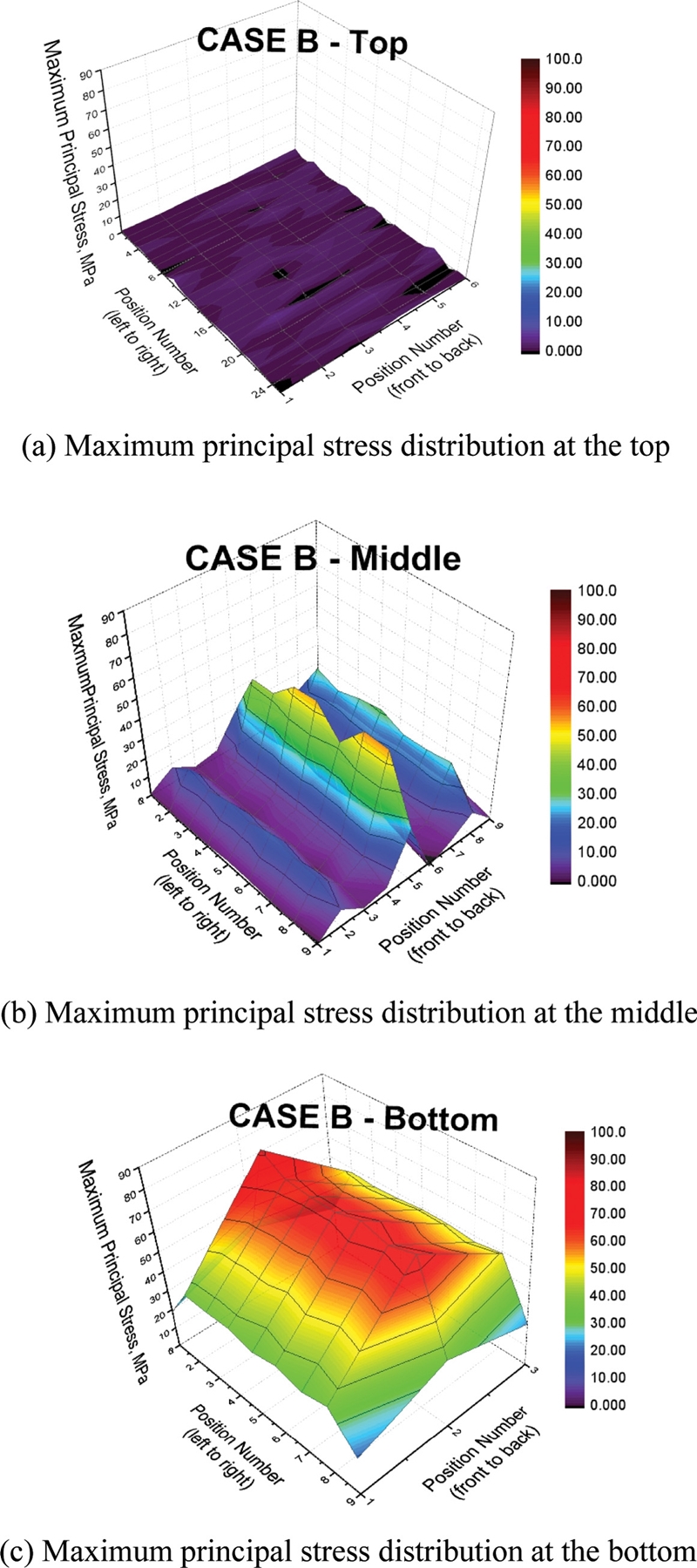
Fig. 10은 Case B의 Top, Middle, Bottom 구간별 Von-Mises Stress 응력분포를 나타낸 것이고, Fig. 11은 Maximum Principal Stress 응력분포를 나타낸 것이다. 이때 Figs. 10과 11의 구간별 Position Number는 Figs. 7(b)부터 7(d)에서 나타낸 바와 같이 각각 25 Position-6 Position, 9 Position-9 Position, 9 Position-3 Position으로 다르게 지정하였다.
Maximum principal stress distribution of case B
Case B Top Von-Mises Stress, Maximum Principal Stress 응력분포 확인 결과, Fig. 10(a)에 나타낸 것과 같이 응력 범위는 0-10 MPa이며, 발생한 응력이 구조물 Top에서 평균적으로 약 5 MPa이 발생하였고, 모든 응력 측정 위치에서 큰 차이가 없는 것으로 해석되었다.
Case B Middle Von-Mises Stress, Maximum Principal Stress 응력분포 확인 결과, Fig. 10(b)에 나타낸 것과 같이 응력 범위는 0-53 MPa이며, Fig. 10(b)의 Position Number (Front to Back) 중 5에서 응력이 크게 발생할 것으로 해석되었다. 이는 Fig. 7(a)에 나타낸 Position Number (Front to Back)의 (1), (2), (3)에 해당하는 3곳의 수직 기둥 중 (2), (3)과 같고 이는 구조물 기준 Front와 Back 사이 중앙 기둥에서 응력이 집중적으로 크게 발생할 것임을 의미한다.
Case B Bottom Von-Mises Stress, Maximum Principal Stress 응력분포 확인 결과, Fig. 10(c)에 나타낸 것과 같이 응력 범위는 20-82 MPa이며, Case 2의 B와 마찬가지로 구조물 기준 Front와 Back 사이 중앙 기둥에서 응력이 다소 크게 발생할 것으로 해석되었다. FEA 해석 결과에 의하면, 발생한 최대 응력 값은 약 82 MPa으로 Bottom에서 가장 높게 나타났고, Top에서 가장 낮게 나타났다.
전체적인 Case B 응력분포 확인 결과, Von-Mises Stress와 Maximum Principal Stress 2가지 응력 범위는 약 0-82 MPa 수준이었으며, Von-Mises Stress 및 Maximum Principal Stress 모두 최소, 최댓값이 각각 Top 및 Bottom에서 확인되었다. 또한, Case A와 마찬가지로 Von-Mises Stress와 Maximum Principal Stress의 응력분포가 유사한 것으로 확인되었다. 지지구조물의 Top에서는 낮은 응력이 발생할 것으로 생각되고, 구조물 기준 Front와 Back 사이 중앙 기둥에서 가장 큰 응력이 발생할 것으로 해석되었다.
이러한 응력 발생 원인은 수평 방향의 경우, 구조물 기준 Front와 Back 사이 중앙 기둥에서 풍하중에 의한 수평 하중 -Fx와 중력 반대 방향 수직 하중 -Fz이 구조물의 자중에 의한 고정 하중과 일부 상쇄되어 Front와 Back 사이 중앙 기둥에 상대적으로 집중 작용하여 발생한 것으로 판단된다.
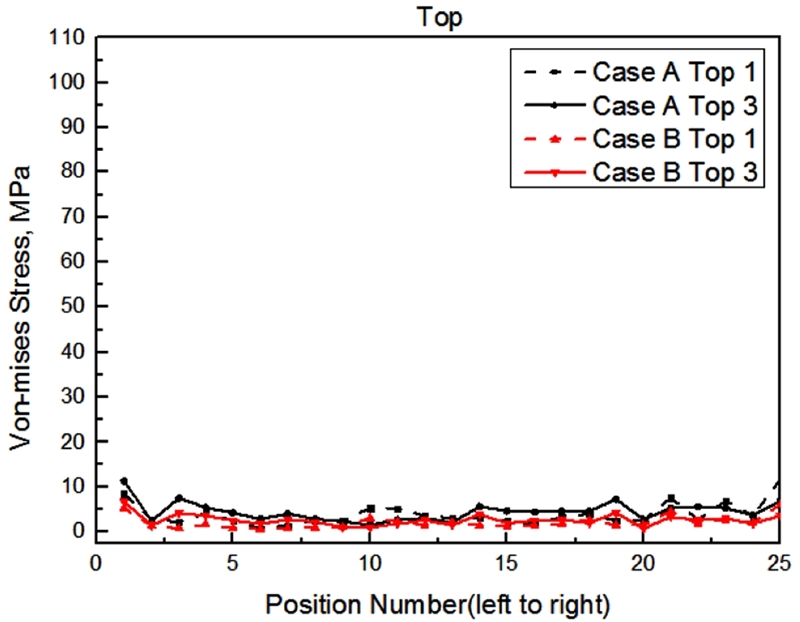
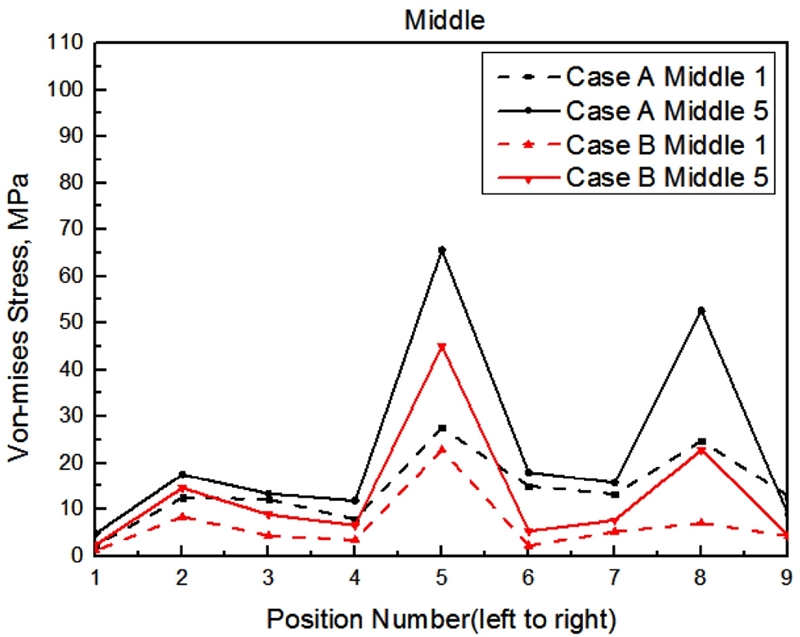
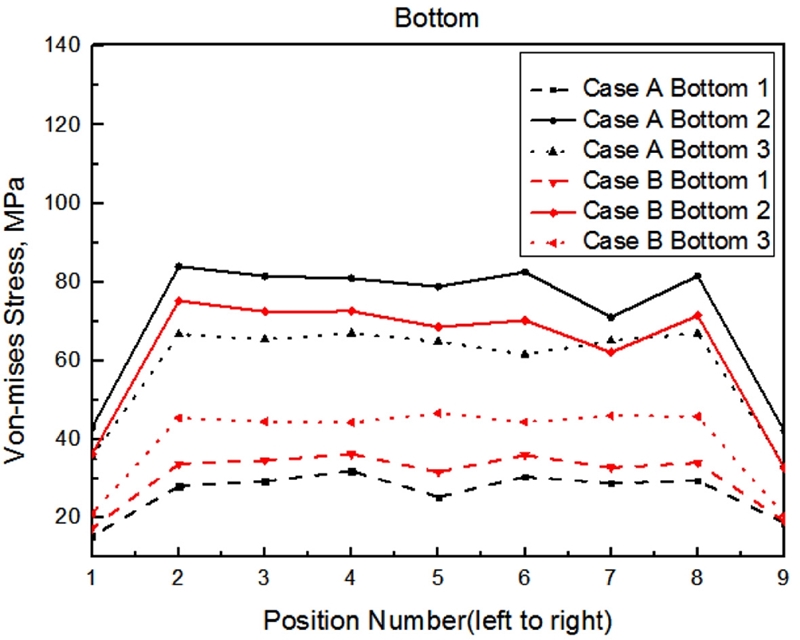
Fig. 11에서는 Fig. 7(b)에 나타낸 태양광 패널이 장착되는 Top의 Front측 1과 Back측 3에 대한 Cases A 및 B의 Von-Mises Stress 응력값을 비교한 해석 결과이다. 해석 결과, 구조물의 Top은 Cases A와 B 2가지 경우 모두 최대 약 10 MPa이 발생하였고, 평균적으로 약 5 MPa의 낮은 응력이 균일하게 발생하는 것을 확인하였다. 이는 Top에 상대적으로 적은 하중이 작용하며 낮은 응력이 발생한다는 것을 의미한다. Figs. 12와 13은 각각 Fig. 7(c)에 나타낸 Middle의 Front측 1번과 Back측 5번의 Cases A 및 B에 대한 Von-Mises Stress 응력 값과 Fig. 7(d)에 나타낸 Bottom의 Cases A 및 B에 대한 Von-Mises Stress 응력값을 나타낸 해석 결과이다.
Von-mises stress comparison of cases A and B top
Von-mises stress comparison of cases A and B middle
Von-mises stress comparison of cases A and B bottom
Fig. 12 해석 결과에서 나타낸 바와 같이 Case A의 경우 최대 약 65 MPa이 발생하였고, Case B의 경우 Case A에 비해 30.8% 낮은 45 MPa이 발생하였다. 또한, Middle과 Top을 비교했을 때 약 6배 높은 응력이 발생했으므로, 이는 수직 기둥을 포함한 수직 기둥을 지지하는 Y자 형태의 지지대에 상대적으로 높은 안전성 설계 및 고내구성 설계가 요구된다는 것을 의미한다. 또한, Fig. 13 해석 결과에서 볼 수 있듯이 Case A의 경우 최대 약 85 MPa이 발생하였고, Case B의 경우 11.8% 낮은 약 75 MPa이 발생하였다. Top과 비교했을 때 약 9배, Middle과 비교했을 때 약 1.5배 높은 응력이 발생했으므로, 이는 지지구조물 설계 중 지반에 묻혀있는 수직 기둥이 지표면과 접하는 부분에 대하여 가장 높은 내구성과 안전성이 고려되어야 할 것임을 의미한다.
4. 결론
본 논문에서는 경사진 패널 및 구조물에 작용하는 풍하중에 대한 패널 1 개체의 셀 단위 응력해석이 아닌, 클러스터 단위의 태양광 발전 설비 지지구조물 전체에 대하여 응력해석을 수행하였다. 이를 통해 전체구조물에 발생하는 응력분포를 6개의 Case에 대하여 확인하였으며, 높은 응력이 발생하는 부분을 확인할 수 있었다. 본 논문의 구체적인 결론은 4가지로 추려지며 아래와 같다.
(1) 태양광 발전 설비 지지구조물의 전체 구간 Top, Middle, Bottom 중 Bottom에 가장 높은 응력이 발생하는 것으로 해석되었으며, Bottom에서 Top으로 갈수록 상대적으로 적은 하중이 작용하며 낮은 응력이 발생하는 것으로 해석되었다.
(2) Case A의 경우, 구조물의 Front보다 Back에 작용하는 응력이 더 높게 나타났다. 이는 구조물에 작용하는 풍하중이 패널의 경사진 각도에 의하여 수평 방향 풍하중이 작용하여 구조물의 Back과 구조물을 지탱하는 수직 기둥에 높은 하중이 작용하여 높은 응력이 발생하는 것으로 판단된다.
(3) 풍하중이 태양광 발전 설비 지지구조물에 작용할 때, Case B보다 Case A의 경우에 더 높은 응력이 발생하는 것으로 해석되었으며, 이는 구조물이 풍하중의 중력 방향 수직 하중 뿐만 아니라 중력 및 구조물의 자중에 의한 고정하중에도 큰 영향을 받는 것으로 판단되었다.
(4) 태양광 발전 설비 지지구조물의 단일 셀에 작용하는 응력 값을 전체구조물 설비에 확대 적용하는 것은 안정성에 문제가 생길 가능성이 있다. 그러므로 클러스터 단위의 전체 구조물에 대하여 해석을 수행하여 높은 응력이 발생하는 부분에 대한 설계를 진행하는 것이 태양광 발전 설비 지지구조물의 전체 안정성을 높일 것으로 예상된다.
Acknowledgments
본 연구는 2019년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(No. NRF-2019R1I1A3A01062764)에 의해 지원되었음. 또한 2020년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(No. P0012769, 2020년 산업혁신인재성장지원사업).
References
- Kang, K. K., “A Study on the Status of New and Renewable Energy Convergence and Consolidation,” M.Sc. Thesis, Korea University, 2019.
- Ministry of Culture, Sports and Tourism, “Weekly No. 504,” http://gonggam.korea.kr/archView.do?newsId=01JEgkEugDGJM000§Id=gg_cover&pageIndex=4&srchType=&srchKeyword=, (Accessed 4 JUNE 2020)
- Park, Gi. Tae., “A Study on Structural Safety as per Installation Height of a Solar Tracker,” M.Sc. Thesis, Kyungpook National University, 2012.
- Ministry of Trade, Industry and Energy, “Announcement of Renewable Energy 3020 Plan,” http://www.motie.go.kr/motie/ne/presse/press2/bbs/bbsView.do?bbs_cd_n=81&bbs_seq_n=159996, (Accessed 4 JUNE 2020)
- Kim, W. S., Park, S. J., and An, S. R., “Analysis of the Status of Safety Management of Photovoltaic Power Generation Facilities,” Current Photovoltaic Research, Vol. 7, No. 2, pp. 38-45, 2019.
- Choi, Y. M. and Lim, J. Y., “A Study on Optimal Design of Photovoltaic System for Efficiency Progress,” Journal of IKEEE, Vol. 13, No. 2, pp. 175-180, 2009.
- Lee, J. H., “Current Status and Future Prospects of Solar Cells,” Journal of the Korean Society for Precision Engineering, Vol. 25, No. 10, pp. 7-22, 2008.
- Han, C. H., “Structural Performance Evaluation of Solar Photovoltaic Installation Structure,” M.Sc. Thesis, Cheongju University, 2011.
- Han, C. H., Lee, J. Y., Park, Y. S., Kim, H. S., Lim, J. S., et al., “Structural Modeling and Evaluation of Solar Photovoltaic Installation Structure,” Proc. of the Academic Presentation Contest on the Regional Association of Architectural Institute of Korea, 2011.
-
Kim, Y. W. and Lee, S. Y., “Stability Analysis on Solar Tracker due to Wind,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 22, No. 2, pp. 216-222, 2013.
[https://doi.org/10.7735/ksmte.2013.22.2.216]
-
Kim, Y. W. and Kim, W. B., “Stress Analysis on a Structure of Solar Tracker Subjected to Wind Load,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 21, No. 5, pp. 747-754, 2012.
[https://doi.org/10.7735/ksmte.2012.21.5.747]
-
Eswaran, M., Verma, R., and Reddy, G., “Wind-Induced Loads and Integrity Assessment of Hyperboloid Reflector of Solar Power Plants,” Alexandria Engineering Journal, Vol. 55, No. 2, pp. 837-850, 2016.
[https://doi.org/10.1016/j.aej.2016.02.005]
-
Aly, A. M., “On the Evaluation of Wind Loads on Solar Panels: the Scale Issue,” Solar Energy, Vol. 135, pp. 423-434, 2016.
[https://doi.org/10.1016/j.solener.2016.06.018]
-
Li, Y., Xie, L., Zhang, T., Wu, Y., Sun, Y., et al., “Mechanical Analysis of Photovoltaic Panels with Various Boundary Condition,” Renewable Energy, Vol. 145, pp. 242-260, 2020.
[https://doi.org/10.1016/j.renene.2019.05.121]
- Lee, S. W., Shim, J. J., Han, D. S., Park, J. S., Han, G. J., et al., “The Effect of Wind Load on the Stability of a Container Crane,” Journal of the Korean Society for Precision Engineering, Vol. 22, No. 2, pp. 148-155, 2005.
-
Ellingwood, B. R. and Tekie, P. B., “Wind Load Statistics for Probability-Based Structural Design,” Journal of Structural Engineering, Vol. 125, No. 4, pp. 453-463, 1999.
[https://doi.org/10.1061/(ASCE)0733-9445(1999)125:4(453)]
- Dyrbye, C. and Hansen, S. O., “Wind Loads on Structures,” John Wiley & Sons, pp. 19-48, 1996.
- Simiu, E. and Scanlan, R. H., “Wind Effects on Structure,” John Wiley & Sons, pp. 327-382, 1996.
Bs. in the School of Mechanical Convergence System Engineering, Kunsan University. His research interest is Mechanics.
E-mail: gwanyongjeong@kunsan.ac.kr
Professor in the School of Mechanical Convergence System Engineering, Kunsan University. Prof. Kim’s research interest are in the Material, Fatigue and Fracture Mechanics
E-mail: sangyoungkim@kunsan.ac.kr