주름식 굽힘 팽창 구동기 개발을 위한 모델링

1. 서론

최근 외골격 로봇(Exoskeleton)의 개발을 통해 인간의 근력을 증강하거나 환자들의 재활을 도와주는 연구가 활발히 진행 중이다.^1,2 특히, 소프트 웨어러블 로봇(Soft Wearable Robot) 개발을 통해 인간 로봇 상호작용에서 안전성을 도모하는 연구가 활발히 진행 중이다.^3,4 착용형 로봇의 많은 구동 전달 방식 중에서 공압을 이용한 방식의 유연 공압 구동기는 컴플라이언트(Compliant)한 특성을 이용해 안정성을 보장할 수 있다.⁵ 유연 공압 구동기는 인공 근육 구조체, 탄성중합체, 팽창형 구조체 등의 다양한 매개체를 이용해 동력을 전달할 수 있다.⁵ 인공 근육 구조체를 이용할 경우 큰 힘을 전달할 수 있다는 장점이 있으나, 스트로크(Stroke) 길이에 제한이 생겨 다양한 관절에 적용할 수 없고,^6,7 탄성 중합체를 이용하면 소재 자체의 특성으로 인해 공기의 배기가 용이하다는 장점이 있으나 이론적 모델링을 통해 원하는 출력 힘이나 토크(Torque)와 같은 설계 조건을 만족시키기 어렵고 최대 허용 압력이 낮아 발생시킬 힘이 다른 구동 방식에 비해 작다.^8,9 팽창형 구조체를 이용할 경우, 제작이 쉽고 다양한 형태의 구조물을 제작할 수 있다는 장점이 있고 이론적 모델링에 기반해 원하는 토크 또는 반응 속도를 만족시키는 구동기 개발이 가능하다.^10,11 선행 연구들의 결과를 보았을 때, 다양한 관절에 적용할 수 있는 유연 공압 구동기를 제작하기 위해서 팽창형 구조체가 필요하다. 뇌졸중 환자들의 보행을 교정해줄 수 있는 능동형 발목 보조기, 보행 시 무릎의 스윙 동작을 보조하는 소프트 웨어러블 로봇처럼 팽창형 구동기는 다양한 관절에 적용되고 있다.^12,13 그러나, 해당 연구들에서 제안된 모델링 기법에 기반한 구동기는 원하는 실험값과 이론값의 차이가 상대적으로 크기 때문에 설계 조건을 만족시키기 어렵다는 단점이 있다.

본 연구에서는 기존의 주름식 팽창형 구동기 설계를 위한 이론적 모델링 기법을 제안한다. 특정 관절에 한정하는 것이 아닌 다양한 관절의 조건에 맞추어 구동기 설계 조건을 도출할 수 있다. 본 논문에서는 무릎을 보조하는 구동기 설계를 위한 설계 조건을 도출하고 이를 만족하는 구동기를 개발하고자 한다. 또한, 고안한 모델링 기법을 통해 계산한 발생 토크와 실험을 통해 측정한 토크를 비교해 오차를 분석하고 이를 기존의 연구와 비교하고자 한다.

2. 구동기 설계 및 고찰

2.1 구조 및 특성

주름식 팽창형 구동기는 Fig. 1과 같이 개발했다. 구동기는 두께 0.3 mm, 경도 85Hs 열가소성 폴리우레탄(Thermal Polyurethane, TPU) 필름(Film)을 고주파 융착기(JTC1003, Jinheung Industry Co., Ltd, 대한민국)를 통해 레이어(Layer)를 만들고, 바닥과 레이어들을 금속 몰드를 사용하여 입체적으로 결합할 수 있다. 레이어가 밀어내는 힘을 다리로 전달하는 PU 큐브(Polyurethane Cube)를 구동기 양 끝에 부착한다. TPU로 제작된 TPU는 부드럽고 유연하며, PU 큐브는 최대 2 mm까지 수축하고 형상을 복원할 정도로 유연하다. 이런 특성은 일상생활에서 구동기를 사용할 때 불편함을 줄여줄 수 있다. 구동기 설계 변수는 Fig. 1 (a)와 같이 정의된다. 구동기 길이는 L이며, w는 너비, d는 레이어 사이의 거리다. 무릎을 보조하는 공압 구동기에 대한 기존의 연구를 참고하여 길이는 200 mm,¹² 너비는 사람의 무릎 두께에 맞추어 100 mm로 결정했다.¹⁴ Fig. 1(b)는 구동기를 제어하기 위한 공기의 주입 경로를 나타낸다. 각 레이어는 직경 6 mm 호스로 공압이 조절된다. 개발된 구동기는 사람의 보행 주기 중 유각기(Swing Phase)에 100% 보조하는 것을 목표로 한다. 1.25 m/s로 걸을 때 유각기 초기 무릎 각도는 120^o이며, 최대 발생시킨다.¹⁵ 성인 남성 평균 몸무게 70 kg에 근거하여 유각기에 무릎은 14 Nm만큼 필요하다. 다음 장에서 이론적 모델을 통해서 설계 조건에 따른 무릎에 제공할 수 있는 토크의 크기를 구하고, 원하는 토크를 제공할 수 있는 설계 조건 레이어 높이(h)와 레이어 개수(n)를 결정한다.

Fig. 1

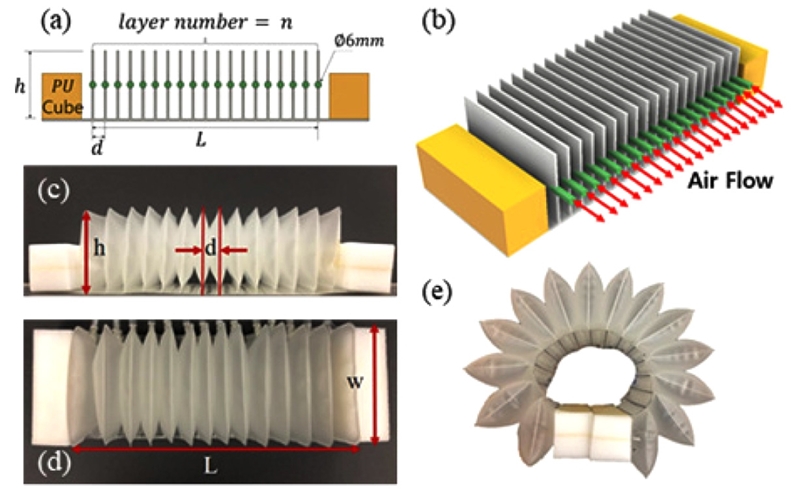
(a) Side view of wrinkle inflatable actuator: the height of the layers (h), the distance between each layer (d), the length of the actuator (L), the number of the layers (n), the width o f the actuator (w), and radius of hose which connected with each layer (ϕ 6 mm). At the end of the actuator, polyurethane cubes are combined on the floor, and (b) Wrinkle inflatable actuator graphical illustration (c, d, e). Deflated state and inflated state of wrinkle inflatable actuator

2.2 이론적 모델

레이어들에 공기를 주입하여 팽창하면 서로 밀어내면서 구동기는 구부러진다. 이때 인접한 레이어가 밀어내는 힘은 사용자 다리로 전달되어 무릎을 보조한다. Fig. 2는 구동기가 팽창하면서 인접한 레이어와 생긴 접촉면의 수직 방향으로 힘을 가하는 것을 보여준다. Fig. 2에서 곡률(α)은 무릎 각도(θ)에 의해 α = π-θ으로 결정된다. 또한, 팽창한 구동기는 곡률 반경 C는 L/α로 결정된다.

Fig. 2

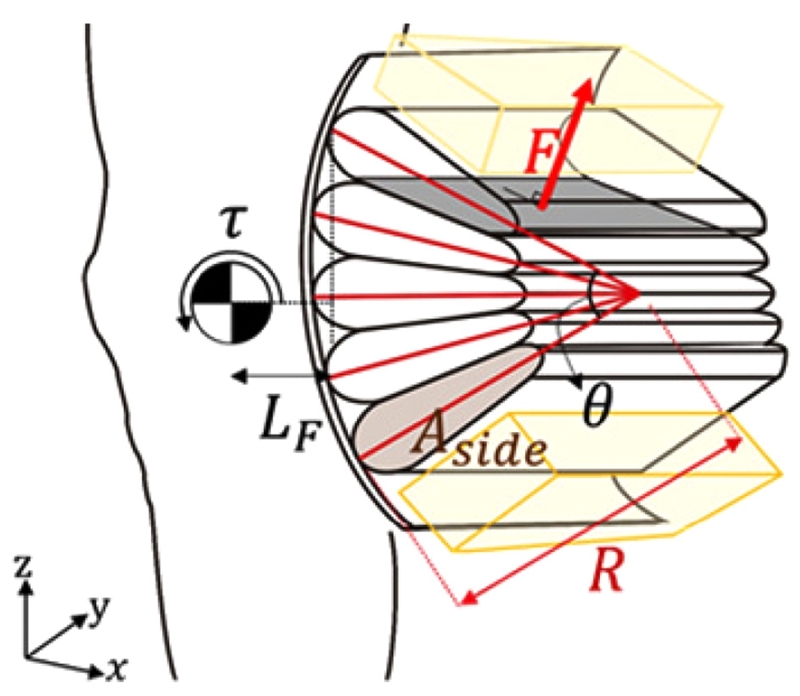
Graphic illustration of wrinkle actuator inflated state: Each layer is pushed against each other by the force (F). The torque assisted by actuator (τ). The radius of the actuator curvature (C), the bending angle (α), the moment arm (MA), cross-area of each layer (Sside) and the torque assisted by actuator (τ)

Fig. 3은 팽창한 레이어에 대한 자유 물체도이며, 대칭 구조인 레이어 위쪽만 고려했다. 레이어는 2δ 만큼의 각도를 갖고 팽창한다. 구동기의 레이어가 n개 일 때 식(1)로 정의된다. 팽창한 레이어들은 서로 밀어내면서 평평한 접촉면을 만든다.

$\[ \mathrm{\delta }=\frac{\mathrm{\alpha }}{2\left(n-1\right)} \]$

(1)

Fig. 3

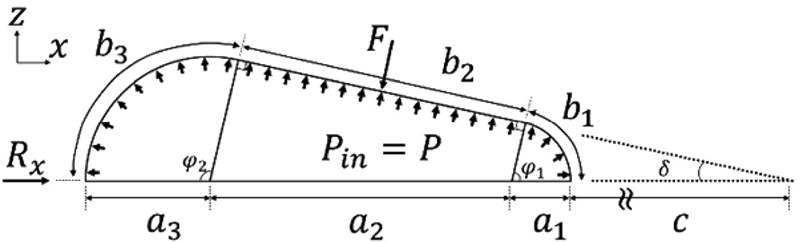
Geometric representation of the inflated layer's cross-section. The contact areas with each layer are flat, and the other areas expand in an arc

TPU 레이어의 내부 응력 모두 동일하다고 가정함에 따라서 접촉면을 제외한 다른 부분은 원호로 팽창한다.

각 원호의 반지름은 a₁, a₃이다. a₂는 레이어의 중심 길이에서 각 원호의 반지름을 제외한 길이다. c는 곡률 중심에서 레이어의 가장 가까운 점과의 거리다. 곡률 반경 C는 c, a₁, a₂, a₃의 합이며, 이를 통해 a₁, a₂, a₃을 C과 c로 표현할 수 있다.

$\[ \begin{array}{l}{a}_1=c{s}_1\sin \delta \\ a_2=C{s}_2-c{s}_1\\ a_3=C{s}_2\sin \delta \end{array} \]$

(2)

식(2)에서 s₁, s₂는 s₁= (1 -sinδ)^-1, s₂= (1 +sinδ)^-1로 정의한다. b₁, b₃는 각 원호의 길이, b₂는 인접한 레이어와 생긴 접촉면의 길이다. b₁, b₂, b₃는 a₁, a₂, a₃와 원호의 각도 φ₁, φ₂로 표현할 수 있고 식(2)를 통해서 C, c, δ로 표현할 수 있다.

$\[ \begin{array}{l}{b}_1=\left(\frac{\mathrm{\pi }}{2}-\delta \right)c{s}_1\sin \delta \\ b_2=C{s}_2\cos \delta -c{s}_1\cos \delta \\ b_3=\left(\frac{\mathrm{\pi }}{2}+\delta \right)C{s}_2\sin \delta \end{array} \]$

(3)

수축 상태의 구동기 레이어 겉넓이는 S_Def, 팽창 상태에서 겉넓이는 S_Inf일 때 다음 식(4)와 같다.

$\[ \begin{array}{l}{S}_{Def}=2w\mathrm{h}\\ S_{Inf}=2w\left(b_1+b_2+b_3\right)+S_{side}\end{array} \]$

(4)

이때 w는 100 mm이며, S_side는 팽창한 레이어의 단면의 넓이다.

$\[ S_{side}=2\left(a_1^2{\phi }_1+a_3^2{\phi }_2+\left(a_1+a_3\right)b_2\right) \]$

(5)

TPU로 제작된 레이어들은 팽창되더라도 인장되지 않기 때문에 겉넓이는 일정하다. 즉, S_Def = S_Inf이다. 이는 식(2)와 식(3)을 통해서 c에 대한 2차 방정식으로 식(6)과 같다. P₂, P₁는 c², c에 대한 계수이며 P₀는 상수항으로 다음 식(7)과 같다.

$\[ P_2{c}^2+P_{1}c+P_0=0 \]$

(6)

$\[ \begin{array}{l}{P}_2=\left(s_1-1\right)\left(\left(s_1-1\right)\left(\frac{\mathrm{\pi }}{2}-\delta \right)-s_1\mathit{cos}\delta \right)\\ P_1=\left(\left(s_1-1\right)\left(\frac{\mathrm{\pi }}{2}-\delta \right)-s_1\mathit{cos}\delta \right)w+\left(2s_1{s}_2-s_1-s_2\right)C\mathit{cos}\delta \\ P_0=\left(1-s_2\right)\left(\left(1-s_2\right)\left(\frac{\mathrm{\pi }}{2}+\delta \right)+s_2\mathit{cos}\delta \right)C^2\\ +\left(\left(1-s_2\right)\left(\frac{\mathrm{\pi }}{2}+\delta \right)+s_2\mathit{cos}\delta \right)wC-wh\end{array} \]$

(7)

보조하는 다리 각도와 레이어의 개수가 결정되면 인접한 레이어 사이의 접촉 면적을 Fig. 4(a)와 같이 구할 수 있다. 이때 일정 길이보다 작은 높이로 레이어를 제작하면 서로 접촉하지 않고 힘을 전달할 수 없는 것을 알 수 있다. 인접한 레이어들이 서로 접촉할 수 있는 최소 레이어 높이만 고려하여 레이어 높이와 개수에 따른 c를 구하면 Fig. 4(b)와 같다. 곡률 중심에서 레이어까지 최단 거리 c를 알면, 식(2)와 식(3)을 통해서 a₁, a₂, a₃, b₁, b₂, b₃을 구할 수 있고, 레이어가 서로 밀어내는 힘을 구할 수 있다.

Fig. 4

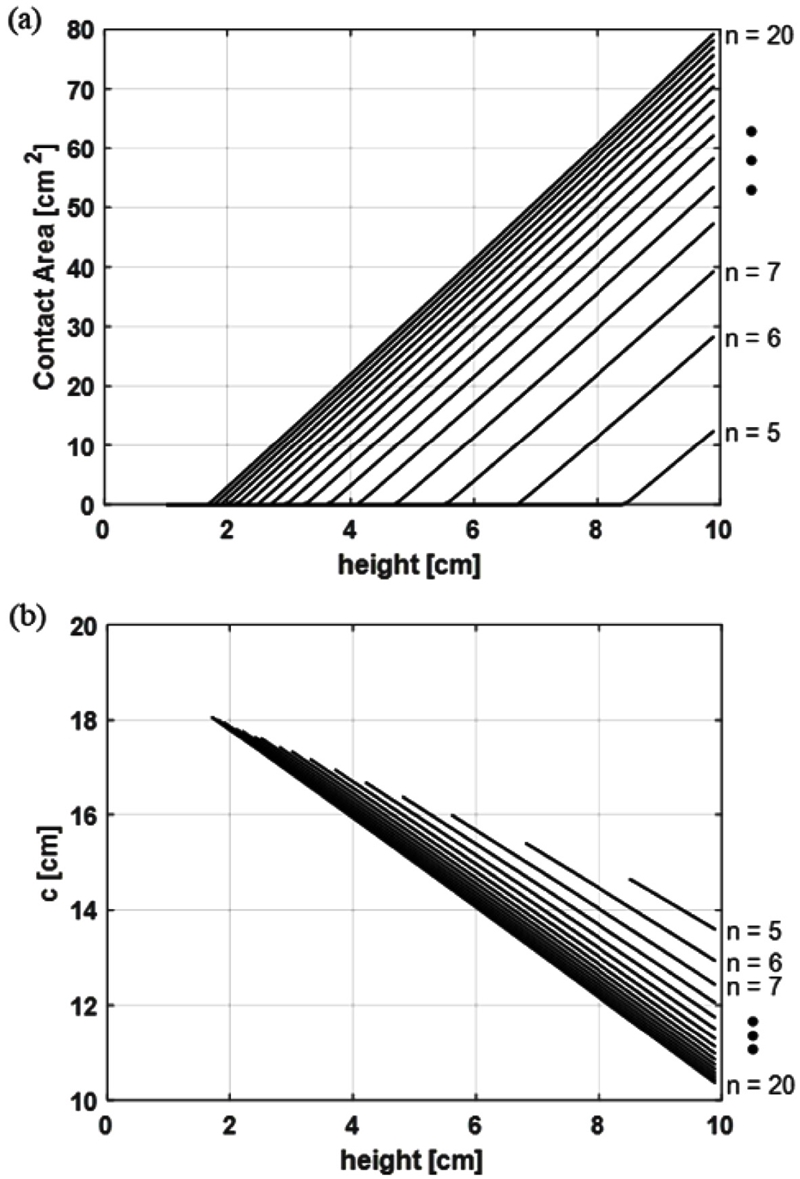
(a) Estimated contact area for the layer height (h) with layer number (n) from theoretical model, and (b) Estimated a1 for the layer height (h) with layer number (n) from theoretical model: when layers are not contacted c = inf

레이어들은 구동기 바닥과 결합되어 있기 때문에 x축 방향으로는 힘 평형 상태를 이루게 된다. 인접한 레이어는 서로 힘 F으로 밀어내고 내부 공기 압력과 평형 상태를 이룬다. 이에 대한 z 축 방향 운동 방정식은 다음 식(8)과 같다.

$\[ \sum F_z=\begin{array}{l}0=Pw{b}_2\sin {\phi }_1+{\int }_0^{{\mathrm{\phi }}_1}Pw{a}_1\sin \mathrm{\gamma }d\mathrm{\gamma }\\ +{\int }_{\mathrm{\pi }-{\phi }_2}^{\mathrm{\pi }}Pw{a}_3\sin \mathrm{\gamma }d\mathrm{\gamma }-F\mathrm{s}\mathrm{i}\mathrm{n} {\phi }_1\end{array} \]$

(8)

따라서 인접한 레이어가 밀어내는 힘은

$\[ F=Pw\left(b_2+\left(a_3+a_1\right)\sec \delta +\left(a_3-a_1\right)\tan \delta \right) \]$

(9)

식(9)와 같고 구동기가 무릎에 제공하는 토크는

$\[ \tau =M{A}^{\mathrm{*}}F\cos \frac{\alpha }{2} \]$

(10)

식(10)과 같다. MA는 구동기가 제공하는 힘의 작용선에서 무릎 회전축까지 거리이다. MA는 각도에 따라서

$\[ MA=C\tan \frac{\alpha }{2}\sin \frac{\alpha }{2}+t_{leg} \]$

(11)

식(11)로 구해진다. t_leg는 구동기 부착면에서 무릎 중심까지 수직 거리이다. 실험에서는 구동기의 부착면과 회전 중심까지의 수직 거리를 측정하여 t_leg = 1 cm로 설정했다.

구동기가 제공하는 토크를 레이어 개수와 레이어 높이에 대해서 구할 수 있다. Fig. 5는 50 kPa, 무릎 각도 120^o에서 레이어 개수별로 높이 h에 대한 제공할 수 있는 토크의 그래프다. 사용자의 보행을 보조하기 위해서 120^o에서 최대 14 Nm의 크기가 필요하다. 이를 통해서 레이어 높이별로 필요한 최소 개수를 구할 수 있다.

Fig. 5

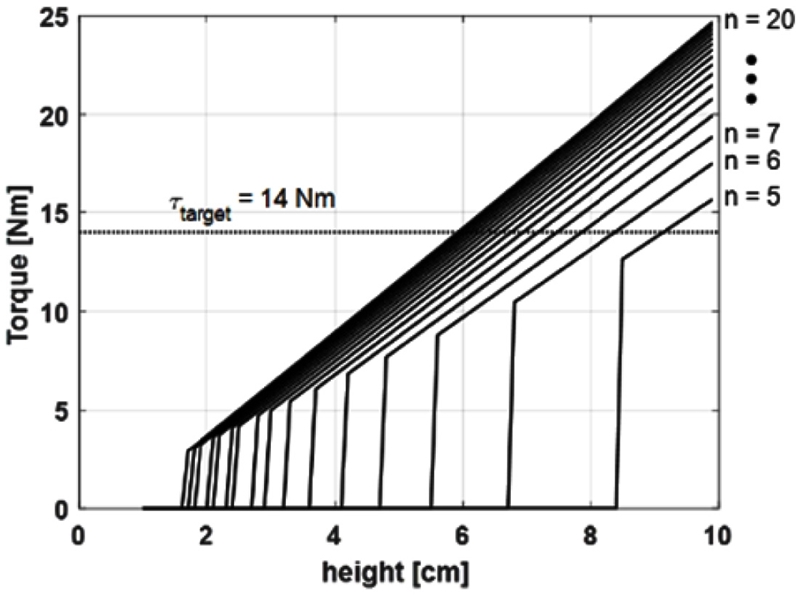
Estimated torque for the layer height (h) with layer number (n) from the theoretical model. The dotted line represents the target torque at 120o, 14 Nm

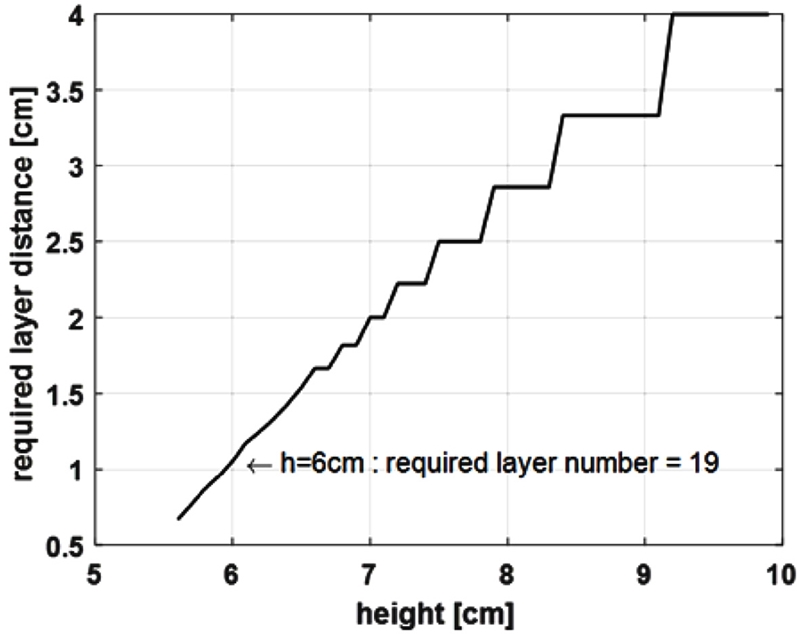
Fig. 6은 구동기가 14 Nm를 제공하기 위해서 높이에 따라 필요한 레이어 사이의 최대 간격을 보여준다. Fig. 6을 통해서 다리 각도가 120^o일 때 무릎 토크를 최대로 도와주기 위한 설계 조건을 정할 수 있다. 레이어 높이가 크면 구동기 부피가 커지면서 불편함을 야기할 수 있다. 레이어의 개수가 많을수록 레이어 사이의 거리가 줄어들어 제작이 어려워진다. 따라서 적절한 개수와 높이를 결정해야 한다. 본 논문에서는 적절히 레이어의 높이를 6 cm로 결정했다. 이에 해당하는 필요한 레이어의 최소 개수는 19개다.

Fig. 6

The minimum number of layers to satisfy target torque (14 Nm) for each height (h). If the height of the layer is 6 cm, the actuator requires a minimum of 19 layers

3. 이론적 모델 검증

3.1 실험 설계

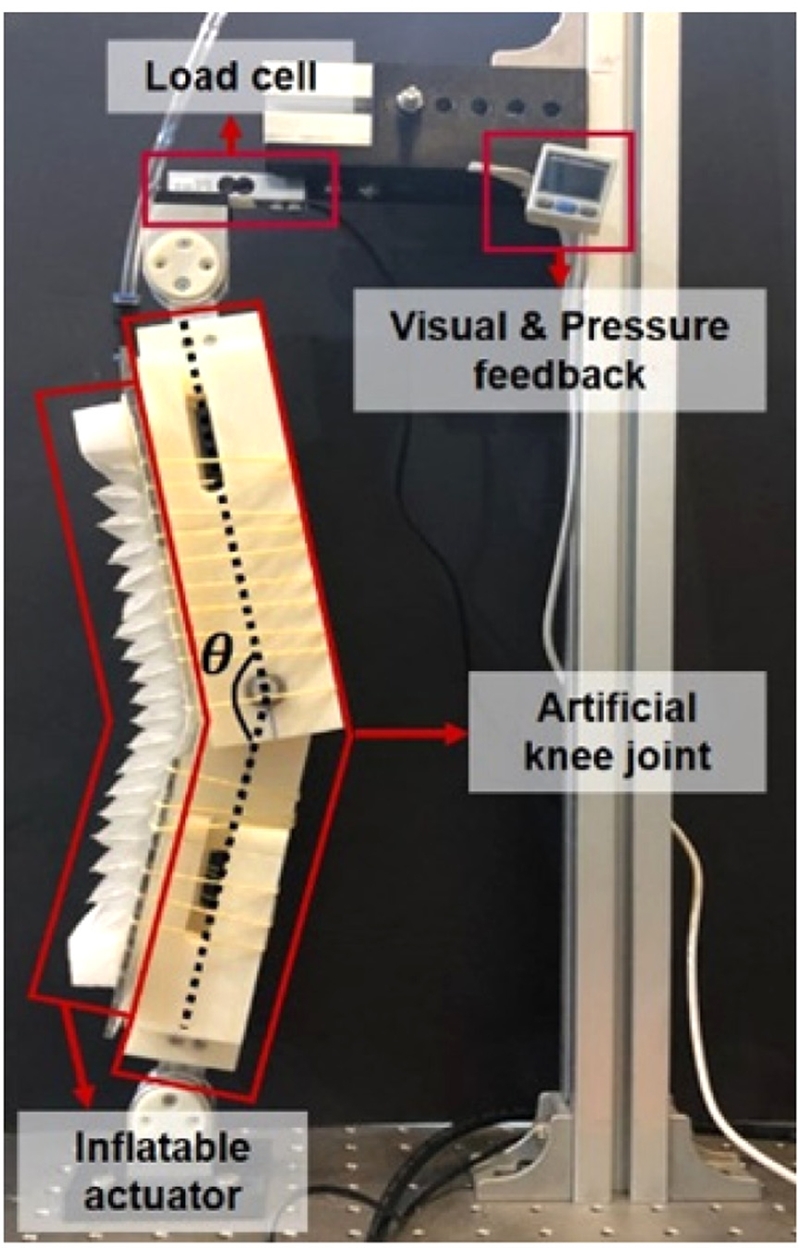
구동기가 제공하는 실제 토크와 이론적 모델로 구한 토크를 비교하여 이론적 모델을 검증해야 한다. Fig. 7은 구동기가 제공하는 토크의 크기를 측정하기 위한 실험 환경이다. 사람의 무릎 관절을 모방하여 각도 조절이 가능한 다리 모델을 3D 프린터로 제작하고, 모델 뒤에 구동기를 고정시킨다. 다리 모델은 전체 길이 42, 두께 4.8, 너비 10 cm로 실제 다리를 약 50% 축소하여 제작했다. 각 레이어에 연결된 호스를 통해서 공기를 주입하여 압력을 조절하며, 팽창한 구동기가 다리를 밀어내는 힘을 로드 셀(Load Cell) (BCA-50L, CASKOEA Co., Ltd, 대한민국)으로 측정한다. 구동기 양끝의 PU 큐브는 힘에 의해 쉽게 수축하기 때문에 힘의 방향이 명확하지 않기 때문에 PU 큐브 대신 아크릴(Acryl) 큐브로 교체하여 힘의 방향을 명확하게 한다.

Fig. 7

Experiment setup to measure torque generated by the actuator. The load cell measures perpendicular force of actuator and the torque can be calculated by multiplying the force and the moment arm of the leg model

3.2 결과

실험에서는 3개의 동일한 구동기에 대해서 무릎 각도별로 압력을 0에서 50 kPa까지 높이면서 힘을 측정하고, 모멘트의 팔(Arm of Moment)(0.247 cos 60^o)을 곱하여 구동기가 제공하는 토크를 구할 수 있다. Fig. 8은 각도에 따른 구동기가 제공하는 토크의 크기를 각 압력에 대해서 보여준다. 이론적 모델과 실제 제공하는 토크의 오차는 10 kPa에서 8.6%, 20 kPa에서 9.2%, 30 kPa에서 9.3%, 40 kPa에서 6.5%, 50 kPa에서는 5.0%로 나타났다. 120^o에서 구동기는 12.93 Nm를 제공하며, 목표하는 토크 값 14 Nm에 근접하게 제공할 수 있었고, 평균 오차 8.3%를 보인다. 각 압력과 무릎 각도에서 실험값과 이론값의 오차는 Table 1과 같으며, 모든 각도, 압력에 대한 평균 오차는 7.8%로 나타난다.

Fig. 8

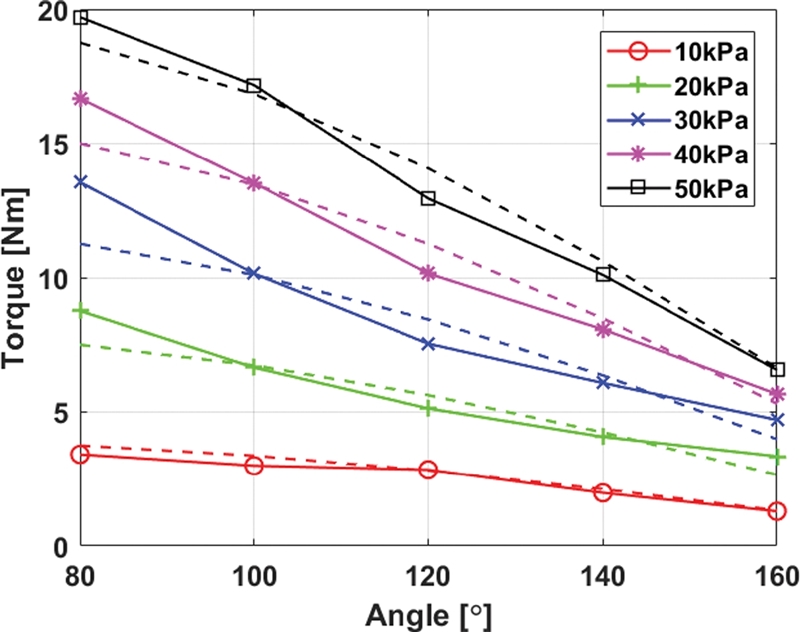
Graph of torque provided by the actuator according to the angle from 0 to 50 kPa. The solid line is the amount of torque measured through the experiment, and the dashed line is the amount of torque estimated by the theoretical model

Table 1

Mean error (SD) for each leg model angle (o) and the actuator pressure (kPa)

4. 결론

본 연구에서 주름식 팽창형 구동기를 제작하기 위한 이론적 모델을 제안했다. 유각기에서 사용자의 무릎을 100% 보조하기 위해 필요한 14 Nm을 제공할 수 있는 구동기의 설계 조건을 이론적 모델을 통해서 구하였다. 레이어 높이를 6 cm로 결정하였고 이에 따라 레이어의 최소 개수는 19개로 결정되었다. 이론적으로 구한 설계 조건에 따라 제작된 구동기는 12.93 Nm을 제공할 수 있었다. 이론적 모델의 검증을 위해 다리 모델의 각도와 구동기의 압력을 변화시키면서 제공하는 토크의 크기를 측정하여 검증했다. 구동기가 제공하는 토크와 이론값은 < 10%의 오차를 보이며, 기존의 제안되었던 모델들에 비해 높은 정확도를 보여준다. 구동기의 각 레이어가 서로를 누르면서 의도하는 유량보다 적은 양이 주입되면서 실제로 팽창되는 정도가 이론적 모델과 다르게 팽창해서 오차가 발생했다. 또한 이론적 모델에서는 모든 레이어를 균일하게 팽창했다고 가정했으나, 실제 실험에서는 하나의 호스에서 공압을 제어하기 때문에 각 레이어의 팽창 정도가 다르다. 이론적 모델을 통해서 무릎 외의 다른 관절을 위한 구동기의 설계 조건을 결정할 수 있다. 관절의 크기를 고려하여 구동기 크기를 결정하고 목표하는 토크에 따라 레이어의 높이와 개수를 구할 수 있다. 다음 작업으로 다양한 관절에 대한 주름식 팽창형 구동기를 제작하여 검증해야 한다. 또한 제작한 구동기를 착용한 사용자의 보조 정도에 대한 고찰을 해야 한다.

References

• Yan, T., Cempini, M., Oddo, C. M., and Vitiello, N., “Review of Assistive Strategies in Powered Lower-Limb Orthoses and Exoskeletons,” Robotics and Autonomous Systems, Vol. 64, pp. 120-136, 2015. [https://doi.org/10.1016/j.robot.2014.09.032]
• Gopura, R., Bandara, D., Kiguchi, K., and Mann, G. K., “Developments in Hardware Systems of Active Upper-Limb Exoskeleton Robots: A Review,” Robotics and Autonomous Systems, Vol. 75, pp. 203-220, 2016. [https://doi.org/10.1016/j.robot.2015.10.001]
• Asbeck, A. T., De Rossi, S. M., Galiana, I., Ding, Y., and Walsh, C. J., “Stronger, Smarter, Softer: Next-Generation Wearable Robots,” IEEE Robotics & Automation Magazine, Vol. 21, No. 4, pp. 22-33, 2014. [https://doi.org/10.1109/MRA.2014.2360283]
• Yap, H. K., Khin, P. M., Koh, T. H., Sun, Y., Liang, X., et al., “A Fully Fabric-Based Bidirectional Soft Robotic Glove for Assistance and Rehabilitation of Hand Impaired Patients,” IEEE Robotics and Automation Letters, Vol. 2, No. 3, pp. 1383-1390, 2017. [https://doi.org/10.1109/LRA.2017.2669366]
• Felt, W., “Folded-Tube Soft Pneumatic Actuators for Bending,” Soft Robotics, Vol. 6, No. 2, pp. 174-183, 2019. [https://doi.org/10.1089/soro.2018.0075]
• Chou, C. P. and Hannaford, B., “Measurement and Modeling of Mckibben Pneumatic Artificial Muscles,” IEEE Transactions on Robotics and Automation, Vol. 12, No. 1, pp. 90-102, 1996. [https://doi.org/10.1109/70.481753]
• Andrikopoulos, G., Nikolakopoulos, G., and Manesis, S., “A Survey on Applications of Pneumatic Artificial Muscles,” Proc. of the 19th Mediterranean Conference on Control & Automation, pp. 1439-1446, 2011. [https://doi.org/10.1109/MED.2011.5982983]
• Park, Y. L., Chen, B. R., Majidi, C., Wood, R. J., Nagpal, R., et al., “Active Modular Elastomer Sleeve for Soft Wearable Assistance Robots,” Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 1595-1602, 2012. [https://doi.org/10.1109/IROS.2012.6386158]
• Agarwal, G., Besuchet, N., Audergon, B., and Paik, J., “Stretchable Materials for Robust Soft Actuators towards Assistive Wearable Devices,” Scientific Reports, Vol. 6, No. 1, pp. 1-8, 2016. [https://doi.org/10.1038/srep34224]
• Thalm an, C. M ., L am, Q. P., Nguyen, P. H ., S ridar, S ., a nd Polygerinos, P., “A Novel Soft Elbow Exosuit to Supplement Bicep Lifting Capacity,” Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 6965-6971, 2018. [https://doi.org/10.1109/IROS.2018.8594403]
• Natividad, R. F., Del Rosario, M. R., Chen, P. C., and Yeow, C. H., “A Hybrid Plastic-Fabric Soft Bending Actuator with Reconfigurable Bending Profiles,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 6700-6705, 2017. [https://doi.org/10.1109/ICRA.2017.7989792]
• Sridar, S., Qiao, Z., Muthukrishnan, N., Zhang, W., and Polygerinos, P., “A Soft-Inflatable Exosuit for Knee Rehabilitation: Assisting Swing Phase during Walking,” Frontiers in Robotics and AI, Vol. 5, p. 44, 2018. [https://doi.org/10.3389/frobt.2018.00044]
• Chung, J., Heimgartner, R., O'Neill, C. T., Phipps, N. S., and Walsh, C. J., “ExoBoot, a Soft Inflatable Robotic Boot to Assist Ankle during Walking: Design, Characterization and Preliminary Tests,” Proc. of the 7th IEEE International Conference on Biomedical Robotics and Biomechatronics, pp. 509-516, 2018. [https://doi.org/10.1109/BIOROB.2018.8487903]
• Wilke, H. J., Neef, P., Hinz, B., Seidel, H., and Claes, L., “Intradiscal Pressure Together with Anthropometric Data-A Data Set for the Validation of Models,” Clinical Biomechanics, Vol. 16, pp. S111-S126, 2001. [https://doi.org/10.1016/S0268-0033(00)00103-0]
• Zelik, K. E. and Kuo, A. D., “Human Walking Isn’t All Hard Work: Evidence of Soft Tissue Contributions to Energy Dissipation and Return,” Journal of Experimental Biology, Vol. 213, No. 24, pp. 4257-4264, 2010. [https://doi.org/10.1242/jeb.044297]