전기자동차 2차 전지에서의 Carbon 소재를 활용한 수냉식 냉각 성능 향상 및 최적 설계 연구

1. 서론

최근 자동차 시장은 지구 온난화와 각종 대기 오염 문제에 영향을 끼치는 것을 막기 위해 배기가스 규제가 강화되면서 신재생 에너지와 연계한 에너지 저장 시스템(Energy Storage System, ESS) 및 전력 구동용 전기자동차의 연구개발 필요성을 더욱 가속시켰다. 이처럼 ESS 시장이 최근 급성장하고 있고 화재 및 폭발 위험성이 있는 ESS 및 배터리의 안정성을 강화하기 위한 기술 개발이 지속적으로 이루어지고 있다.^1,2 이러한 기술 트렌드 하에서 전기자동차의 핵심 요소인 인버터, 배터리, 모터, 3가지 요소 중 전기를 저장하는 배터리 연구의 필요성은 더욱 중요시 해지고 있다. 대부분의 전기자동차의 배터리로는 리튬 이온(Li-Ion) 배터리가 주로 사용되고 있다. 그 이유는 리튬 이온은 가벼운 무게, 높은 에너지 밀도, 고전압, 긴 수명, 낮은 자기 방전율 등 장점이 있기 때문이다. 이러한 배터리는 충·방전 시 산화·환원 반응과 전류의 흐름으로 인해 발열이 발생하여 전반적으로 열이 발생하는 특징을 갖는다.³ 리튬 이온이 배터리 에너지원으로 가장 적합하지만, 리튬 이온 전지는 특성상 충격과 고온에 약하기 때문에 높은 온도에 장시간으로 노출되면 배터리의 전극 손상이 가속화되어 수명이 짧아지고 심하면(80-90^oC 이상)열 폭주 현상으로 폭발 사고로 이어지는 문제점을 가지고 있다.⁴ 따라서 배터리와 같이 고전압 핵심 부품들의 효율적인 열관리 기술은 전기구동 자동차에서 해결해야 할 중요한 과제이고 열관리를 위해 기존 공냉식과 최근 발전하고 있는 수냉식 냉각 시스템으로 열관리가 이뤄지고 있다. 이에 관한 기존 연구들은 발열 집중 배터리에 대하여 효과적인 이유로 설계의 영향을 파악하기 위한 전기자동차용 배터리 팩 주위의 유동장 해석,⁵ 전기 자동차용 배터리 팩의 효율적인 냉각을 위하여 냉각팬을 이용하여 강제 송풍 시의 송풍량에 따른 냉각 성능을 배터리 모듈 입구 형상에 따라 수치 해석 연구,⁶ 공기 냉각팬을 이용한 강제 대류 방열 시스템에서 셀 레이아웃에 따라 냉각 성능을 비교하는 연구⁷ 등의 공냉식 연구가 있고 수냉식 연구로는 배터리 열관리 시스템에서 수냉식을 이용하여 배터리에 신소재의 재질 적용 가능성을 확인한 연구,⁸ 냉각을 위한 소모 전력을 최소화하기 위한 냉각판의 구조, 유동 경로 내부에 벽의 수를 변화하며 각각의 냉각 특성을 예측하는 연구,⁹ U형 냉각판의 냉각 유로를 이용하여 유동 방향과 유량이 냉각 특성에 미치는 영향을 확인하는 연구,¹⁰ 하이브리드 배터리 시스템을 구성하여 차량용 배터리 팩의 성능 향상을 제안하고 배터리 시스템의 열관리를 위한 간접 수냉식 배터리 팩의 설계 및 검증을 수행하는 연구,¹¹ 수냉식 배터리 냉각 관리의 구조적 매개변수로 최적의 상태를 채택하는 연구¹² 등이 있었지만 실제 운행을 가정한 수냉식과 공냉식 비교 및 냉각수 유로 입구 단면에 따른 배터리 냉각 성능 연구는 거의 수행되지 않았다.

본 연구는 수냉식을 이용한 냉각 시스템에서 실제 운행 상태를 고려하여 저속 공냉 방식과 수냉식 냉각수 유로 입구 단면을 원, 정사각형, 복합 단면, 3가지로 분류하여 속도와 온도를 수치적으로 해석하여 대류 열전달을 통해 냉각 성능을 비교할 것이며, 그 중 냉각 성능이 가장 우수한 최적의 유로 입구 단면을 선택하여 공냉식 냉각 시스템과 냉각 성능의 차이를 열전달 계수로 비교하고 또한 최적의 유로 입구 단면에서 냉각수 유량을 5가지로 변화시켜 냉각 성능을 비교하고 이를 통해 최적의 유량을 선정하여 수냉식 냉각 성능을 향상시키기 위한 최적 설계가 이번 연구 목표이다.

2. VFD 해석 모델 및 설계 조건

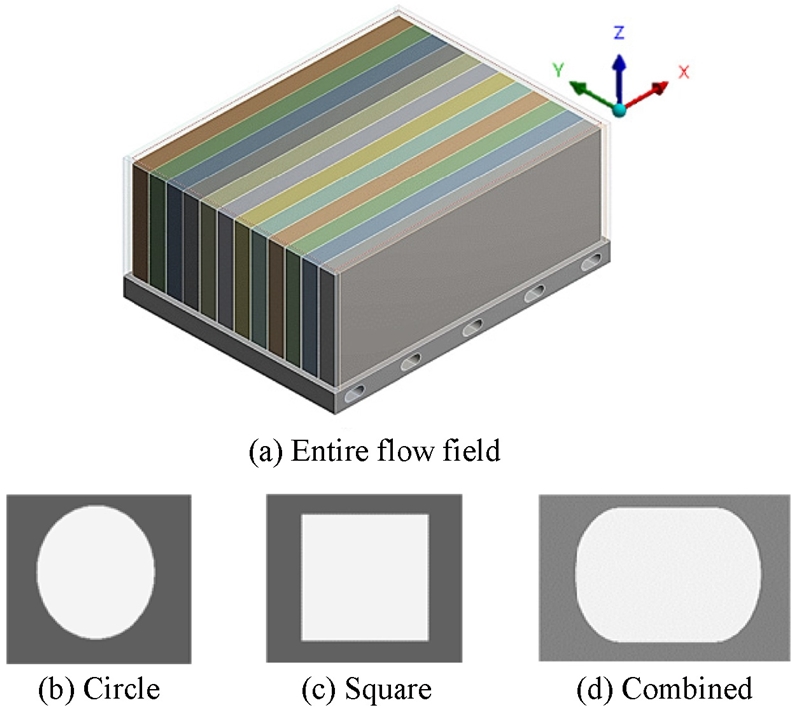
글로벌 완성차 업체 ㈜T사 전기자동차에 사용되는 Fig. 1(a)는 실제 배터리 팩의 사진이고, Fig. 1(b)는 실제 배터리 셀의 사진이다. CAD 형상은 실제 차량의 배터리를 분해 및 실측하여 모델링을 하였다. Fig. 2는 CATIA V5R21을 사용하여 모델링한 후 ANSYS V19.1로 형상을 임포트(Import)한 전체 유동장과 냉각수 유로 입구의 단면이다. 배터리 셀은 유동해석에 필요 없는 부분(결합부, 플래쉬, 굴곡진 부분)을 제외하고 단순화시켰다.⁷ Fig. 2(a)는 단순화한 셀 12개와 셀의 간격을 국내 ㈜S사 실제 설계 간격인 0.5 mm(최근 연구에서 타당성이 검증된 배터리 셀 간격이다.⁷)로 하였고 셀 주위의 공기 유동장도 실제 형상처럼 나타내고 셀 하반부에 냉각수 유로 채널을 나타냈다. Figs. 2(b)부터 2(d)는 각각의 냉각수 유로 입구 단면이 원, 정사각형, 복합 단면, 3가지로 나눈 단면이다. 이렇게 분류한 이유는 동일한 규격의 배터리 팩에서 유로 입구 면적이 증가함에 따라 유량도 증가하므로 이에 따른 냉각 성능을 비교하기 위함이다. 좌표 방향으로는 12개 셀 두께 방향(Y축, 냉각수 유동 방향), 셀 높이(수직) 방향(Z축), 셀 폭(수평) 방향(X축, 공기 유동 방향)으로 3가지 유로 입구 모두 동일하게 설정하였다. 냉각수의 입·출구는 Y축을 기준으로 동일한 수평선으로 설정하였고 공기의 입·출구는 X축을 기준으로 하여 동일한 수평선으로 설정하였다. Table 1은 CATIA V5R21을 활용하여 배터리 셀과 공기 유동장, 유로 채널을 모델링한 형상을 ANSYS V19.1로 임포트한 Fig. 2의 제원 및 크기를 표로 나열한 것이다.

Fig. 1

Actual geometry of battery pack and cell

Fig. 2

Imported geometries of battery module and three different inlet sections of water-cooling channel

Table 1

Physical dimensions of battery module

2.1 유동 및 경계 조건

설계 조건은 유체 유동 및 열전달 해석을 위해서 질량 보존 법칙, Navier-Stokes Equation, Energy Equation 기반으로 ANSYS FLUENT V19.1로 비압축성 유동해석을 하였다. 유로의 수력 직경을 기준 길이로 설정하여 내부 유동의 최대 레이놀즈 수가 42,238로 계산되어 난류 해석을 진행하였으며, 경계층 흐름에 대해 더 많은 계산을 수행하고 해석 결과의 정확도를 향상시키기 위해 Standard k-ω 모델을 사용하였다.

초기 조건으로 유체(냉각수, 공기) 온도는 상온을 기준으로 하여 298.15 K를 부여하였고, 유체의 물성치는 Table 2와 같이 상수를 적용하였다. 냉각수 입구 유량은 완성차 업체에서 사용하는 냉각수 유량 실험값인 10 Lpm (Liter per Minute)을 활용하여 유로 단면의 기준을 원 모양으로 하였을 때 0.166 kg/s를 도출하였다. 정사각형 및 복합 단면은 원 모양의 단면적에 비례하여 각각 0.212, 0.378 kg/s를 부여하였다. 공기 입구 유량은 실제 운행 중 냉각팬을 작동시키지 않는 상태에서의 저속의 공기가 유입되는 것을 가정하기 위하여 0.00001 kg/s를 부여하였고 자연 대류로 부력을 고려하기 위하여 중력 반대 방향인 Z축에 -9.81 m/s²를 적용했다. 출구는 대기압으로 가정하여 계기압력 0Pa을 부여하였다. 유로 채널의 재질은 알루미늄이고 셀의 재질은 알루미늄이 아닌 카본 소재인 그래파이트를 선정하였다. 그래파이트는 자연에서 쉽게 구할 수 있기 때문에 가격이 저렴하고, 탄소 물질의 높은 열전도성과 균일한 열전도, 낮은 밀도로 배터리, 에너지 저장, 복합소재 산업에 많은 응용이 되고 냉각 성능이 우수하다.¹³ 또한 그래파이트의 경우 밀봉성이 우수하여 배터리 셀이 누수로 인해 냉각수를 흡수하는 것을 완화할 수 있기 때문에 선정하였다. 배터리 셀 표면에는 점착 조건(No Slip Condition)을 주며 일정 열유속(Heat Flux) 조건을 열 경계 조건으로 사용하였다. 배터리 셀 주위 공기 유동장의 표면에는 Wall 조건, 점착 조건을 설정하였다. 또한 유체의 영역과 고체의 영역의 접촉면을 통해 열전달이 일어날 수 있도록 커플링을 하여 유체 유동과 고체가 상호 연계되는 FSI (Fluid-Structure Interaction) 기법을 활용하여 대류 및 전도 열전달 해석을 진행하였다.

Table 2

Boundary conditions of numerical simulation

Table 2는 열 및 유동해석을 위한 경계 조건들을 표로 나타낸 것이다.

2.2 Grid 생성

배터리 전체 형상의 격자 생성은 ANSYS MESH를 사용하여 고체(배터리 셀 및 유로 채널)와 유체 영역을 분류하여 생성하였다. Body Sizing을 셀에는 1.5 mm, 셀 주위의 공기 유동장과 냉각수 유로에는 1 mm를 주었다. 유로 벽면에서의 유동 영역에는 벽면에 Inflation을 적용하여 해석의 정확성을 높이도록 격자를 생성하였다.

Method에서 셀과 셀 간격은 Hexa 격자로 설정하고 유로와 셀 주위의 공기 유동장은 Tetra로 설정하였다. 유로 채널은 Tetra로 설정하고 주위로 인해 자동으로 격자 모양이 생성되도록 하였다. 격자 의존도 테스트를 약 1,900만 개 이상 격자수와 진행하였을 때, 해석 오차율(온도 약 0.215%)이 나타났고 1,100-1,200만 개 격자 수와 진행하였을 때, 해석 오차율(온도 약 3.95%)이 나타나 해석 시간과 수렴성을 고려하여 배터리 전체 형상에 대한 격자의 수는 냉각수 유로 입구 단면이 원 모양일 경우 총 1,451만 개, 정사각형 모양일 경우 총 1,483만 개, 복합 단면 모양일 경우 총 1,508만 개로 격자를 생성하였다. Y Plus (Y+) 값은 연구대상인 배터리 셀 표면을 기준으로 0-23.06 값을 유지하였다.

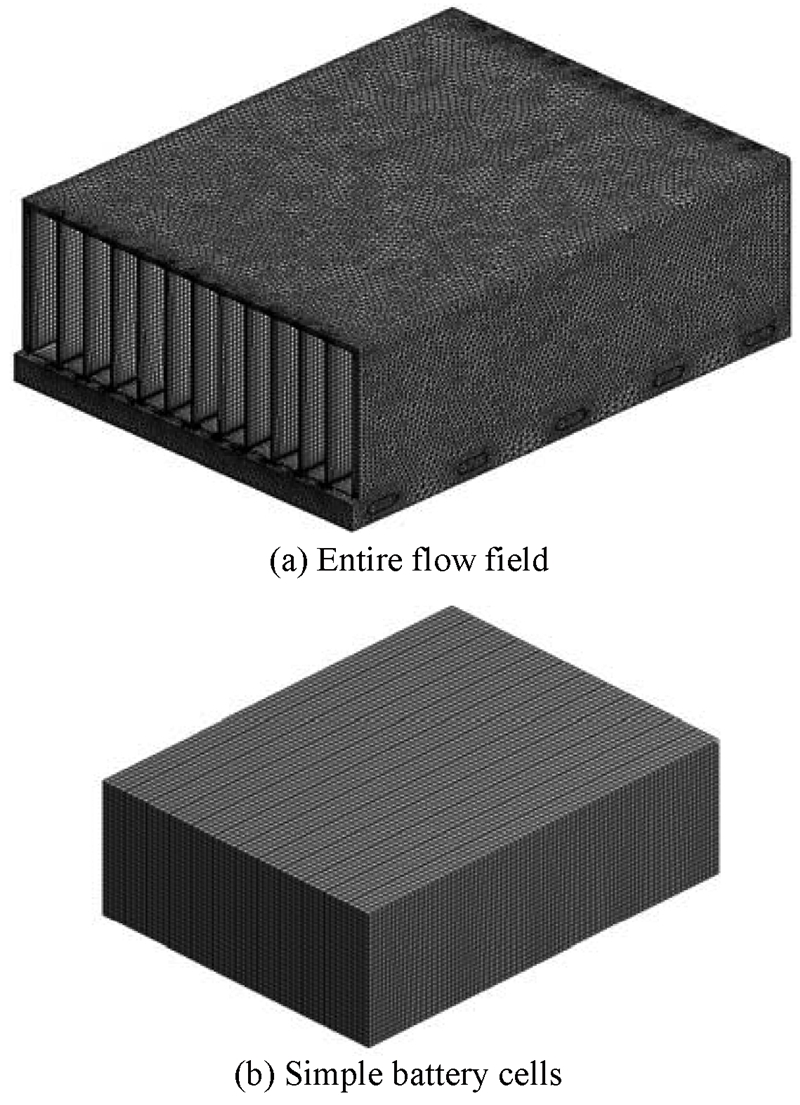
Fig. 3(a)는 배터리 팩 전체 형상(셀, 유로 채널, 공기 유동장)에 해당되는 격자의 형상이고, Fig. 3(b)는 배터리 셀에 해당되는 격자의 형상이다.

Fig. 3

Grid of flow field and battery cells at entire battery module

3. 결과 및 고찰

본 연구는 ANSYS FLUENT V19.1을 활용하여 실제 ㈜S사의 배터리 셀의 실제 간격 0.5 mm인 배터리 팩을 실제 운행 상태를 고려해 수냉식과 저속 공냉식을 채택하여 냉각수 유로 입구 단면을 3가지(원, 정사각형, 복합 단면)로 분류하여 유동해석을 진행하였다. 해석 이후 유동해석의 경향과 신뢰성을 확인하기 위해 속도, 온도 분포를 확인하고 냉각 성능이 취약한 국소적 위치(셀 높이)에서의 열전달 계수 해석을 진행하여 수냉식 유로 입구 단면에 따른 냉각 성능을 비교하였다. 그 중 냉각 성능이 가장 우수한 최적의 냉각수 유로 입구 단면을 선택하여 기존의 단순 공냉식 시스템과 냉각 성능을 비교하고 5가지 유로 입구의 냉각수 유량을 변화시켜 냉각 성능을 비교하였다. 정밀한 계산과 해석의 신뢰성을 높이기 위해 KISTI에서 제공하는 Intel Xeon Phi 7250(KNL) 모델 68코어 16GB*6, 6Ch per CPU의 성능을 가진 슈퍼컴퓨터를 사용하였다.

3.1 속도 분포

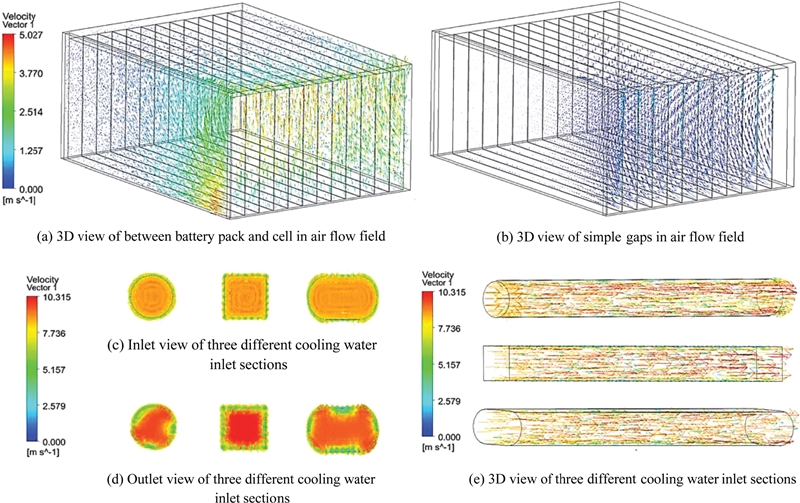
Fig. 4는 냉각수 유로 입구 단면에 따른 속도벡터를 나타낸 그림이다. Fig. 4(a)는 셀 간격 내의 공기 유동장을 제외한 셀 주위 공기 유동장의 속도벡터를 3차원으로 본 모습이고, Fig. 4(b)는 셀 간격 내의 공기 유동장의 속도벡터를 3차원으로 본 모습이다. Figs. 4(a)와 4(b)는 유로 입구 단면 3가지의 속도 분포가 거의 동일하여 하나의 형태로 나타냈다. 냉각수 유로 입구 단면 3가지의 속도 분포를 Fig. 4(c)는 입구에서, Fig. 4(d)는 출구에서 본 모습을 2차원으로 나타냈고 Fig. 4(e)는 3차원으로 나타낸 모습이다.

Fig. 4

Velocity vectors at three different cooling water inlet sections of battery module

속도벡터는 냉각수 유로 입구 단면에 따라 3가지(원, 정사각형, 복합 단면)로 분류하였다. 공기 유동장을 3차원으로 파악하였을 때, 공기 유동장에서의 속도벡터는 밀도차에 의한 부력에 의해 가열된 공기의 밀도가 낮아져 올라가는 것을 볼 수 있었다. 공기의 속도가 입구에서는 냉각팬을 작동시키지 않는 상태에서의 저속의 공냉식이므로 0 m/s에 가깝지만 셀과 만났을 때 면적이 급격하게 줄어들어 배터리 팩과 셀 사이의 공기 속도가 증가하는 것을 볼 수 있었고, 냉각팬과 셀 간격 입구 사이에 수많은 유동 저항이 발생하여 셀 간격의 공기 유속은 거의 0 m/s에 가까웠다. 냉각수의 속도는 유로 벽면에서 점착이 되어 속도가 0 m/s이고 유동 저항의 큰 영향이 없는 유로 중심부에서 최고속도가 유로 입구 단면이 원 모양일 때 10.3 m/s(10 Lpm), 정사각형일 때 10.2 m/s(10 Lpm), 복합 단면일 때 10.3 m/s(10 Lpm)로 나타났다. 냉각수의 유량을 입구 단면적에 비례하여 주었기 때문에 최고속도가 거의 동일하게 나타나는 것을 확인할 수 있었다.

3.2 온도 분포

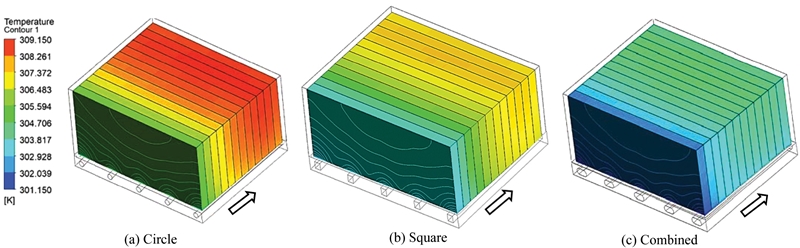
Fig. 5는 냉각수 유로 입구 단면 3가지(원, 정사각형, 복합 단면) 타입으로 냉각한 배터리 셀의 표면 온도 분포를 나타낸 그림이고 화살표는 냉각수 유동 방향이다. 전체적인 경향으로는 3가지 입구 단면 모두 냉각수가 입구에서 출구로 흐르면서 가열되어 유로 입구에서 거리가 가까운 1번째 배터리 셀이 가장 낮은 온도 분포가 띄고 유로 입구에서 11번째 떨어진 배터리 셀이 가장 높은 온도 분포가 띄는 것을 볼 수 있었다. 속도벡터를 통해 분석해보면 저속 공냉식 공기의 유량이 셀 간격 사이로는 좁아서 거의 유입되지 못하고 Fig. 4(a)와 같이 배터리 팩과 셀 사이로 유동하므로 배터리 팩과 가까운 1번째 셀과 12번째 셀이 공기의 영향을 받아 유로 입구에서 가장 멀고 공기의 영향을 덜 받은 11번째 셀이 높은 온도 분포가 나타났다. 3가지 유로 단면 모두 최고온도는 11번째 셀, 최저온도는 1번째 셀에서 나타났고 유로 입구 단면이 복합 단면, 정사각형, 원 모양 순으로 배터리 셀 표면 온도가 낮게 나타났다. 냉각수 유로 입구 단면 3가지의 최고온도와 최저온도는 각각 원 모양(308.7/304.1 K), 정사각형 모양(307.5/302.4 K), 복합 단면(304.3/301.2 K)이 나타나는 것을 확인할 수 있었다.

Fig. 5

Cell surface temperature at three different cooling water inlet sections of battery module

유로 입구 단면 3가지의 냉각 성능을 비교하기 위하여 냉각이 취약한 국소적인 위치를 정하여 위치별로 냉각의 정도를 확인하였다. 위치를 나타낸 지점은 유로 입구에서 11번째 셀이 높은 온도 분포를 나타내어 선정하였고, Fig. 6과 같이 수직 방향(Z축, 셀의 높이)을 흑색 실선으로 표시하여 한눈에 파악할 수 있게 나타냈다. 수직선으로 나타낸 이유는 수평 방향보다 다양한 온도 변화가 존재하기 때문이다.

Fig. 6

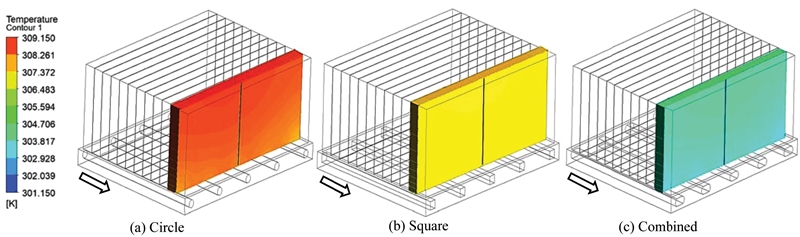
Cell surface temperature with vertical axis at three different cooling water inlet sections of battery module

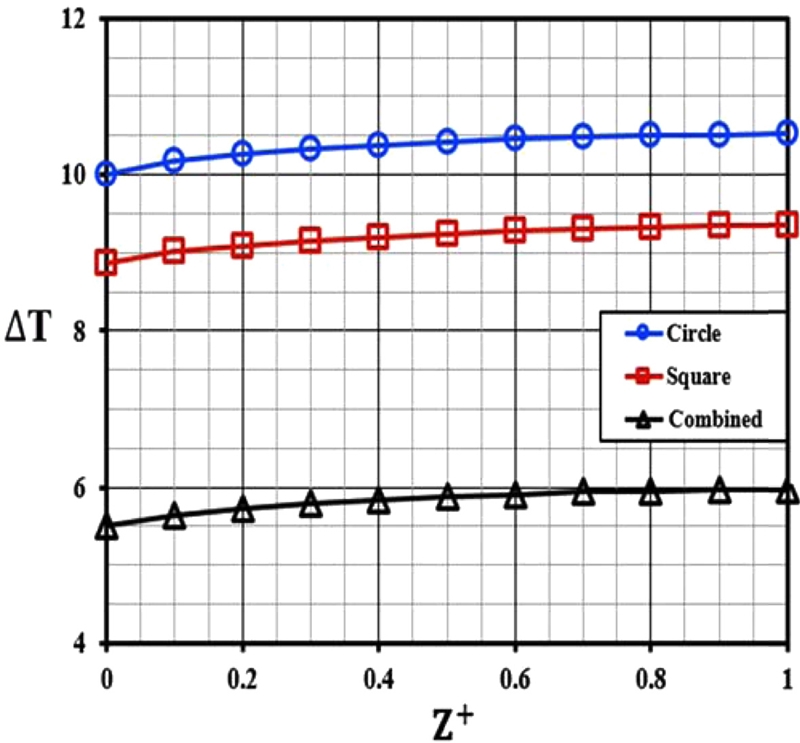
냉각수 유로 입구 단면 3가지에 따른 냉각 성능을 정량적으로 비교하기 위해 열전달 성능을 무차원 Nusselt 수를 사용하여 강제 대류 열전달에 의한 셀 표면의 냉각 정도를 나타냈다. Nusselt 수를 확인하기에 앞서 3가지의 유로 입구 단면에서 무차원 기준 길이(Z⁺)를 유로 채널에서 가장 가까운 곳(Z⁺ = 0), 유로 채널에서 가장 먼 곳(Z⁺ = 1)으로 설정하여 각 위치의 온도 차이를 Fig. 7과 같이 하나의 그래프로 비교하여 나타냈다. 온도 차이(ΔT)는 아래 식(1)로 계산할 수 있다.

$\[ ∆\mathrm{T}={\mathrm{T}}_{\mathrm{s}}-{\mathrm{T}}_{\mathrm{\infty }}\left[\mathrm{K}\right] \]$

(1)

Fig. 7

Temperature difference vs. Vertical position (Z) at three different cooling water inlet sections

여기서 T_s는 배터리 셀의 표면 온도이고, T_∞는 자유 흐름 상태의 유체의 온도(298.15 K)를 나타낸다. 이와 같이 계산하였을 때, 전반적인 경향으로는 냉각수 유로 입구 단면이 복합 단면일 때 온도 차이(ΔT)가 가장 낮은 분포로 나타났다. 각각 유로 입구 단면에서의 최고온도 차이는 원 모양일 때 10.52 K, 정사각형 모양일 때 9.34 K, 복합 단면일 때 5.97 K이며 모두 유로 채널에서 가장 먼 곳(Z⁺ = 1)에서 나타났다. 최저온도 차이는 원 모양일 때 10.01 K, 정사각형 모양일 때 8.87 K, 복합 단면일 때 5.51 K이며 모두 유로 채널에서 가장 가까운 곳(Z⁺ = 0)에서 나타났다. 평균적으로 복합 단면이 원 및 정사각형 모양에 비해 각각 77.87, 57.57% 낮은 온도 차이가 나타났다.

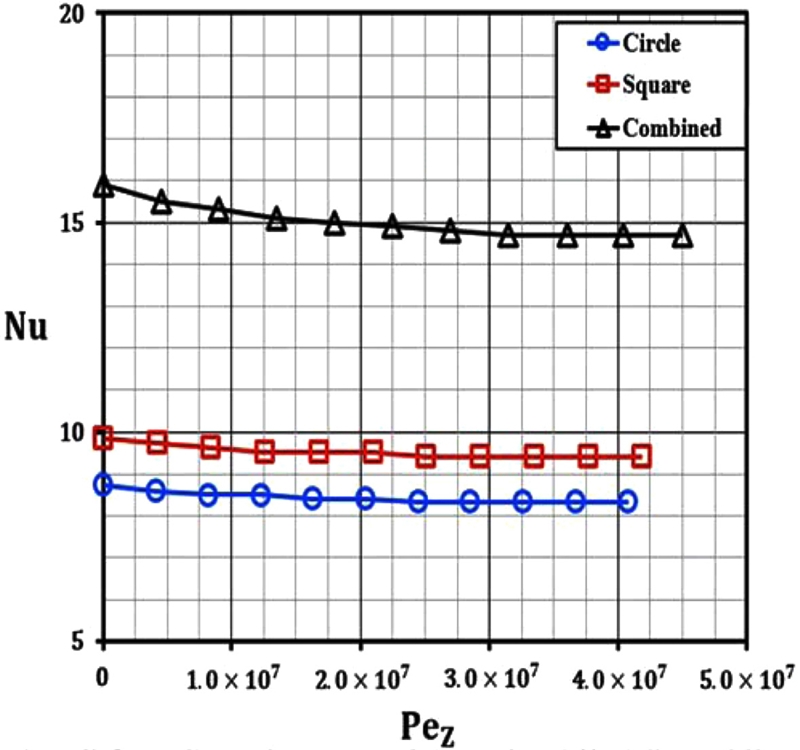
앞에서 나타난 온도 분포와 온도 차이를 통해 열전달 성능을 파악하기 위하여 Nusselt 수를 사용하여 Peclet 수와 함께 냉각 정도를 나타냈다. Nusselt 수는 순수 유체의 전도 열전달에 의한 냉각 성능과 대류 열전달에 의한 냉각 성능을 비교하는 척도이다. Peclet 수는 유체 전도 열전달률에 대한 유동 대류 열전달률의 비를 나타내며 식(2)로 계산할 수 있다.

$\[ \mathrm{P}{\mathrm{e}}_{\mathrm{L}}=\mathrm{R}{\mathrm{e}}_{\mathrm{L}}\cdot \mathrm{P}\mathrm{r}=\frac{\mathrm{V}\mathrm{L}}{\mathrm{\alpha }} \]$

(2)

여기서 α는 열확산 계수, V는 평균속도, L은 기준 길이, Re는 레이놀즈 수, Pr은 Prandtl 수이다. Prandtl 수는 운동량 확산 계수와 열확산 계수의 비이며 속도 경계층과 온도 경계층에서 확산에 의한 운동량 전달과 에너지 전달의 상대적인 유효도의 척도를 의미한다. Nusselt 수와 Peclet 수의 기준 길이는 Z⁺을 적용하였다.

Fig. 8은 11번째 셀의 Z⁺ 위치별로 Nusselt 수와 Peclet 수(Z)에 대한 냉각 성능 비교를 더욱 쉽게 나타낸 그래프이다. 전반적으로 그래파이트의 장점인 균일하고 우수한 열전도성으로 인해 냉각 정도가 균일한 것을 볼 수 있었다. 우수한 냉각 성능은 유로 채널에서 가장 가까운 곳(Z⁺ = 0)에서 나타났고 낮은 냉각 성능은 유로 채널에서 가장 먼 곳(Z⁺ = 1)에서 나타났다. 냉각 성능이 유로 입구 복합 단면이 원 및 정사각형 모양에 비해 유로 채널에서 가장 가까운 곳(Z⁺ = 0)에서 81.71, 61.98% 각각 높게 나타났고, 유로 채널에서 가장 먼 곳(Z⁺ = 1)에서 76.18, 55.91% 높게 나타났다. 평균 냉각 성능은 복합 단면이 원 및 정사각형 모양에 비해 77.95, 58.33%만큼 각각 높게 나타나 냉각 성능이 우수한 것을 볼 수 있었다.

Fig. 8

Nusselt number vs. Peclet number (Z) at three different cooling water inlet sections

냉각수 유로 입구 단면 3가지 중 냉각 성능이 우수한 복합 단면을 선정하여 기존의 단순 공냉식과 비교하였다. 기존의 유일 공냉식의 해석 조건은 배터리 셀 재질과 공기의 입구 유량을 제외하고 수냉식과 동일한 조건을 적용하였다. 공냉식의 배터리 셀 재질은 알루미늄으로 하였고 입구 공기의 질량 유량은 배터리 냉각팬 제원에서 확인한 200 CMH (Cubic Meter per Hour)을 활용하여 도출한 0.067 kg/s를 적용하였다.

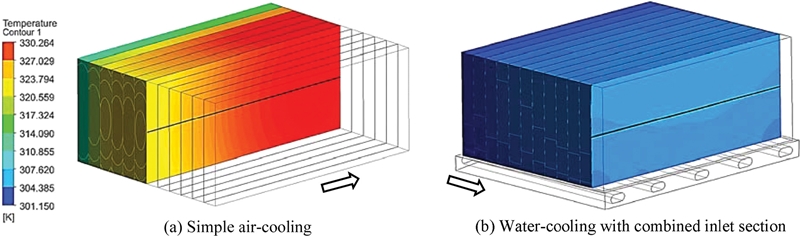
Fig. 9는 공냉식과 수냉식의 냉각 성능을 정량적으로 비교하기 위해 가장 높은 온도 분포를 가진 셀(왼쪽에서 공냉식 6번째 셀, 수냉식 11번째 셀)을 선정하여 수평 방향(X축, 셀의 폭)을 흑색 실선으로 표시하여 한눈에 파악할 수 있게 나타냈고 화살표는 공기 및 냉각수 유동 방향이다. 수평 방향(X축)을 선정한 이유는 공냉식인 경우 셀 간격 입구에서 유입된 공기가 가열되어 흐르기 때문에 수평 방향(X축)이 다양한 온도 분포가 나타나서 선정하였고 수냉식도 공냉식과 비교하기 위하여 동일한 위치의 수평 방향(X축)에 나타냈다. 온도 분포를 통해 공냉식의 경우 최고온도는 6번째 배터리 셀에서 330.15 K가 나타나는 것을 확인할 수 있었다. 수평 방향(X축)에서 배터리 셀 표면 온도 차이(ΔT)는 공냉식에서 25.9-31.4 K, 수냉식에서 5.8-5.9 K가 나타났다. 이를 통해 수냉식이 공냉식에 비해 셀 온도 편차가 균일한 것을 확인할 수 있었다.

Fig. 9

Cell surface temperature with horizontal axis at between air and water-cooling

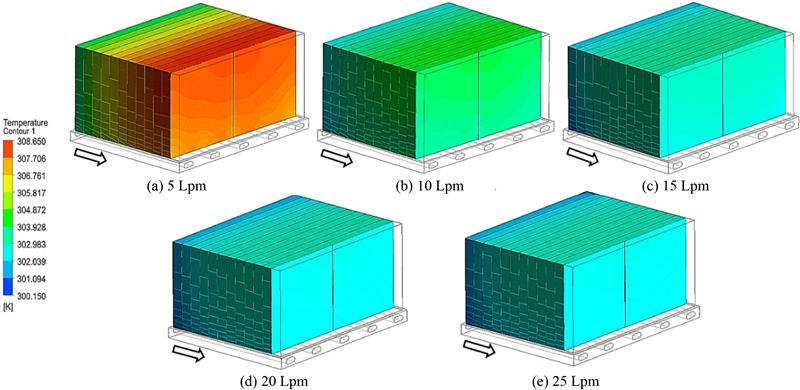
Fig. 10은 냉각수 유로 입구 단면이 복합 단면을 기준으로 하여 최적의 유량을 정하기 위하여 실제 주행 차량의 기준 유량인 10 Lpm(0.378 kg/s)과 타 5 Lpm(0.189 kg/s), 15 Lpm(0.576 kg/s), 20 Lpm(0.756 kg/s), 25 Lpm(0.945 kg/s) 5가지로 분류하고 냉각 성능을 비교하기 위해 높은 온도 분포가 나타난 11번째 셀을 선정하여 수직 방향(Z축, 셀의 높이)을 흑색 실선으로 표시하여 한눈에 파악할 수 있게 나타낸 그림이고 화살표는 냉각수 유동 방향이다. 11번째 셀에서 5가지 유량의 최고온도와 최저온도는 5 Lpm(308.15/307.75 K), 10 Lpm(304.15/303.65 K), 15 Lpm(303.25/302.85 K), 20 Lpm(302.84/302.37 K), 25 Lpm(302.57/302.09 K)가 나타났다.

Fig. 10

Cell surface temperature with vertical axis at five different flow rates of cooling water

먼저 공냉식과 수냉식의 냉각 성능을 정량적으로 비교하기 위하여 열전달 계수를 해석하였다. Fig. 11은 무차원 기준 길이(X⁺)를 셀 간격 입구(X⁺= 0, 가장 왼쪽), 셀 간격 출구(X⁺= 1, 가장 오른쪽)로 설정하여 각 위치의 열전달 계수를 h⁺로 무차원화하여 나타낸 그래프이다. h⁺는 아래 식(3)으로 계산하였다.

$\[ {\text{h}}^{\text{+}}\text{=}\frac{{\text{h}}_{\text{w}}}{{\text{h}}_{\text{a}}} \]$

(3)

Fig. 11

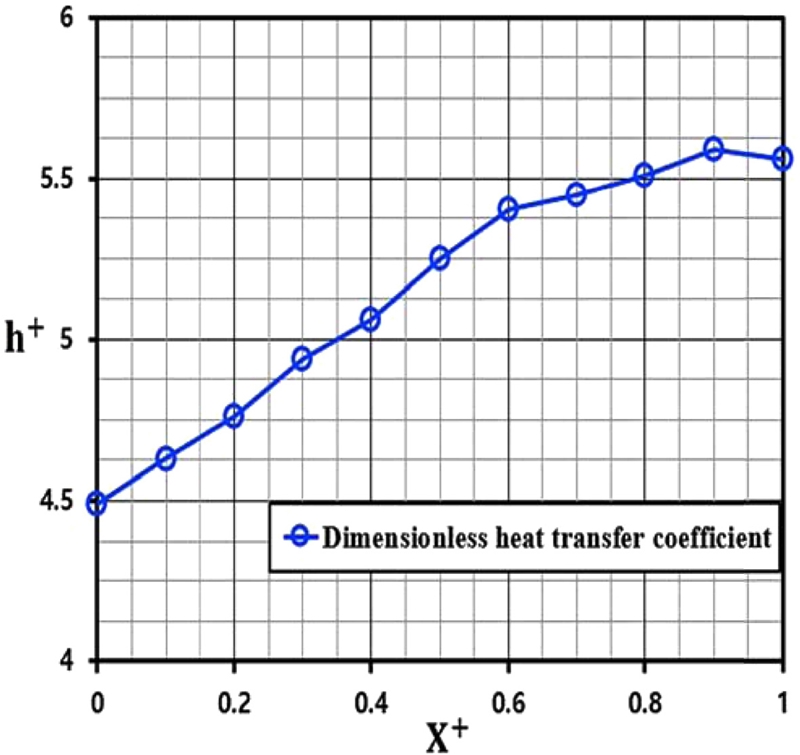
Heat transfer coefficient vs. Horizontal position (X) at relative heat transfer coefficient of water-cooling to air-cooling

여기서 h_a는 공냉식일 때 X⁺ 위치의 열전달 계수이고 h_w는 수냉식일 때 X⁺ 위치의 열전달 계수이다. 무차원화하여 나타낸 이유는 수냉식이 공냉식에 비해 상대적으로 냉각 성능이 어느정도 우수한지 정량적 수치로 비교하기 위함이다.

공냉식의 열전달 계수는 셀 간격 입구(X⁺= 0)에서 가장 높았고 셀 간격 출구 부근(X⁺ = 0.9)에서 가장 낮았다. 무차원화한 h⁺로 냉각 성능을 비교해보면 셀 간격 입구(X⁺ = 0)와 셀 간격 출구 부근(X⁺ = 0.9)에서 수냉식이 공냉식에 비해 각각 4.49배, 5.59배 높게 나타났다. 평균 냉각 성능은 수냉식이 공냉식에 비해 5.15배 높은 것을 볼 수 있었다.

다음 5가지의 유량에 따른 냉각수 성능을 정량적으로 비교하기 위하여 무차원 Nusselt 수와 Peclet 수를 사용하였고 기준 길이는 Nusselt 수 경우 열전달 계수만 고려하기 위하여 온도 편차가 큰 Z축(11번째 셀의 전체 높이)을 적용하였으며 Peclet 수는 유량만 고려하기 위하여 Nusselt 수와 동일한 Z축(11번째 셀의 전체 높이)을 적용하였다. Table 3은 무차원 기준 길이(Z⁺)의 위치에 대한 온도 차이(ΔT = T_s-T_∞)와 T_max를 수치적으로 계산한 표이다. T_max는 온도 분포가 다양한 셀 높이(Z축)의 가장 냉각이 취약한 부분을 찾기 위하여 셀의 폭(X), 두께(Y)와 상관없이 셀 높이(Z)를 고정하여 무차원 기준 길이(Z⁺)에서 나타난 가장 높은 온도이다. 최대온도는 냉각수 유로 입구에서 11번째 떨어진 셀에서 나타났고 5가지 유량 모두 유로 채널에서 가장 먼 곳(Z⁺ = 1)에서 가장 높은 온도가 나타났다.

Table 3

Numerical data of temperature difference and maximum temperature for vertical position (Z) on the battery cell surface at five different flow rates of cooling water

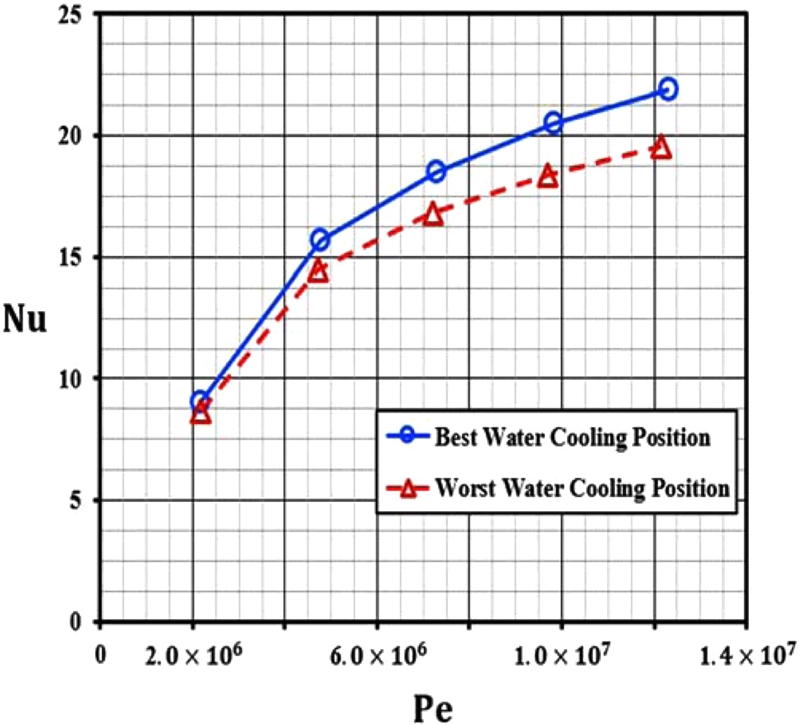
5가지 유량의 냉각 성능을 비교하였을 때, 전체적으로 5가지의 유량 모두 유로 채널에서 가장 가까운 곳(Z⁺ = 0)에서 냉각 성능이 우수하였고 유로 채널에서 가장 먼 곳(Z⁺ = 1)에서 냉각 성능이 떨어졌다. Fig. 12는 5가지의 유량에 대한 냉각 성능을 한눈에 비교하기 위하여 냉각 성능이 우수한 지점(Z⁺ = 0)과 냉각 성능이 낮은 지점(Z⁺ = 1)의 위치에 대한 Nusselt 수와 Peclet 수로 냉각 정도를 정량적으로 나타낸 그래프이다. 파란색 실선과 원 모양은 냉각이 우수한 지점(Z⁺ = 0)의 기호이고 빨간색 점선과 삼각형 모양은 냉각이 낮은 지점(Z⁺ = 1)의 기호이다. 전반적인 경향은 냉각수 유량이 증가할수록 열전달 계수가 증가하여 냉각 성능도 증가하였다. 또한 냉각 성능이 우수한 지점(Z⁺ = 0)과 냉각 성능이 낮은 지점(Z⁺ = 1)의 냉각 성능의 차이는 5 Lpm: 4.4%, 10 Lpm: 8.28%, 15 Lpm: 8.63%, 20 Lpm: 11.41%, 25 Lpm: 11.73%가 나타났다.

Fig. 12

Nusselt number vs. Peclet number at five different flow rates of cooling water

냉각 성능이 우수한 지점(Z⁺ = 0)과 냉각 성능이 낮은 지점(Z⁺ = 1)에서 10Lpm이 5Lpm보다 냉각 성능이 각각 74.25, 68.02% 높게 나타났다. 15 Lpm이 10Lpm보다 각각 17.83, 15.86% 높게 나타났고 20 Lpm이 10 Lpm보다 각각 30.57, 26.9% 높게 나타났고 25 Lpm이 10 Lpm보다 각각 39.49, 35.17% 높게 나타났다. 냉각 성능이 우수한 지점(Z⁺ = 0)과 냉각 성능이 낮은 지점(Z⁺ = 1)에서 25 Lpm과 20 Lpm의 온도 차이가 0.28, 0.27 K로 작기 때문에 30 Lpm은 진행하지 않았다. 5가지의 유량에 따라 냉각 성능을 비교하였을 때, 10 Lpm이 5 Lpm에 비해 68-74% 냉각 성능이 우수하였다. 25 Lpm이 10 Lpm보다 냉각 성능은 우수하지만 큰 온도 차이(ΔT = 1.57 K)가 나타나지 않았다. 따라서 온도 차이(ΔT = 1.57 K)와 펌프의 동력 소모(차압)를 고려할 때 최적의 냉각수 유량은 10 Lpm이라고 판단된다.

4. 결론

이번 연구는 수냉식을 이용한 냉각 시스템에서 속도 및 온도 분포를 수치적으로 해석하여 냉각 성능 향상 및 최적 설계를 초점을 두고 연구를 하였다. 배터리 셀 재질을 균일하고 높은 열전도율과 밀봉성의 장점이 있는 그래파이트로 적용하여 진행하였다. 냉각수 유로 입구 단면을 3 가지(원, 정사각형, 복합 단면)로 분류하여 냉각 성능을 비교하였다. 그 중 우수한 냉각 성능을 가진 복합 유로 입구 단면을 기준으로 기존의 단순 공냉식과 냉각 성능을 비교하였으며, 냉각수 입구 유량을 5가지(5, 10, 15, 20, 25 Lpm)로 분류하여 냉각 성능을 비교한 뒤 최적의 냉각수 유량을 선정하였다. 냉각 성능을 손쉽게 비교하기 위하여 기준 길이를 무차원화한 X⁺, Z⁺(셀 폭, 셀 높이) 각각의 위치에 따른 열전달 계수와 Nusselt 수를 계산하여 무차원 기준 길이, Peclet 수와 함께 그래프로 나타냈다. 이에 따른 결과를 다음과 같이 정리하였다.

(1) 3가지 냉각수 유로 입구(원, 정사각형, 복합 단면)의 속도 벡터는 유로에서 유동 저항의 큰 영향이 없는 유로 중심부에서 나타났고 입구 단면적에 비례하여 유량을 주었기 때문에 최고 속도가 거의 동일했다. 공기 유동장에서는 밀도차에 의한 부력에 의해 가열된 공기가 밀도가 낮아져 올라가는 것을 볼 수 있었다.

(2) 냉각팬을 작동시키지 않는 상태에서의 저속 공냉식의 공기 유량이 입구에서는 속도가 0 m/s에 가깝지만 셀과 만났을 때 면적이 급격하게 줄어 속도가 증가했다. 냉각팬과 셀 간격 사이에는 수많은 유동 저항이 발생하여 거의 공기가 유입되지 못하고 배터리 팩과 셀 사이로 유동하므로 1번째 셀과 12번째 셀이 공기의 영향을 받았다. 따라서 공기의 영향을 덜 받고 냉각수 유로 입구에서 가장 먼 11번째 셀이 높은 온도 분포가 나타났다.

(3) 냉각수 유로 입구 단면 3가지(원, 정사각형, 복합 단면)를 온도 분포가 가장 높은 11번째 셀에서 무차원 기준 길이(Z⁺, 셀의 높이)를 설정하여 각각의 위치에 Nusselt 수로 나타낸 결과 복합 단면이 원 및 정사각형 모양보다 열전달 계수가 증가하여 평균 냉각 성능이 복합 단면이 원 및 정사각형 모양에 비해 각각 77.95, 58.33% 높게 나타났다.

(4) 3가지 유로 입구 단면 중 냉각 성능이 우수한 복합 단면과 기존의 단순 공냉식 냉각 시스템과 냉각 성능을 각각의 가장 높은 온도 분포를 가진 셀(공냉식 6 번째 셀, 수냉식 11번째 셀)의 열전달 계수를 계산하고 무차원화한 h⁺로 비교하였다. 무차원 기준 길이(X⁺, 셀의 폭)를 설정하여 각각의 위치에 무차원화한 h⁺로 나타낸 결과 평균 냉각 성능은 수냉식이 공냉식에 비해 5.15배 높은 것을 볼 수 있었다.

(5) 냉각수 유로 입구 단면을 복합 단면으로 하여 5가지 냉각수 유량(5, 10, 15, 20, 25 Lpm)으로 분류하여 냉각 성능을 비교하였다. 온도에 따른 Peclet 수를 고려하여 무차원 기준 길이(Z⁺, 셀 높이)에 냉각 성능이 우수한 지점(유로 채널에서 가장 가까운 곳(Z⁺ = 0)), 냉각 성능이 낮은 지점(유로 채널에서 가장 먼 곳(Z⁺ = 1))의 위치에 대한 Nusselt 수와 Peclet 수로 나타낸 결과 10 Lpm이 5 Lpm에 비해 68-74% 냉각 성능이 우수하였다. 25 Lpm이 10 Lpm에 비해 35-40% 냉각 성능이 우수하였지만 큰 온도 차이(ΔT=1.57K)는 나지 않았다. 온도 차이(ΔT=1.57K)와 펌프의 동력 소모(차압)를 고려할 때 최적의 냉각수 유량은 10 Lpm이라고 판단된다.

(6) 배터리 셀의 온도 편차가 커지면 성능과 수명을 관리하는 BMS (Battery Management System) 측면에서도 효율성이 떨어지고 배터리 성능도 떨어지게 된다. 공냉식 배터리의 셀 표면 재질인 알루미늄에 비해 수냉식 배터리의 셀 표면 재질을 그래파이트로 적용하였을 때 배터리 셀 온도 편차가 균일하였다. 그래파이트와 같은 카본 소재를 배터리 셀 표면에 사용하면 온도를 균일하게 냉각할 수 있다. 또한 그래파이트의 밀봉성을 이용해 배터리 셀이 누수로 인해 냉각수를 흡수하는 것을 완화하고 더불어 가볍고 얇기 때문에 배터리 팩의 경량화를 통해 주행 효율도 증가시킬 수도 있고, 냉각수 유로 입구 단면적이 증가할수록 동일한 펌프의 동력 소모(차압)로 많은 유량을 투입하여 배터리 냉각 성능을 증가시켜 배터리 셀의 수명, 성능의 효율을 높여주므로 차량 주행 효율을 증가시킬 수 있다고 판단된다.

(7) 최종적으로 내리는 연구 결과는 냉각수 유로 입구 단면이 복합 단면일 때 냉각 성능이 가장 우수하였고 유량은 10 Lpm이 최적의 냉각수 유량으로 나타났다. 냉각수 입구 단면을 복합 단면으로 하였을 때, 단순 공냉식보다 냉각 성능이 약 5배 우수하였다. 또한 배터리 셀 표면 재질을 그래파이트로 적용함으로써 밀봉성, 균일하고 우수한 열전도, 경량화 등 장점을 얻을 수 있다. 냉각 성능이 저조한 11번째 셀 중 유로 채널에서 가장 먼 곳(Z⁺ = 1)을 고려하였을 때, 셀 간격에 유로 채널을 삽입하거나 다양한 유로 채널의 형상을 통해 유로 채널의 공간 점유율을 감소시키고 그래핀이나 탄소 나노튜브 등 다른 첨단 소재를 배터리 셀 재질로 사용하여 냉각 성능이 저조한 부분을 보완하여 냉각 성능의 효율성을 더욱 향상시킬 것이다.

References

• Kim, J. H., “Battery and BMS Research Trends in Mobile Vehicles,” Magazine of the Korean Korean Institute of Power Electronics, Vol. 24, No. 1, pp.35-39, 2019.
• Song, H. S., “Latest Trends in ESS and Battery Safety Technologies,” The Magazine of the Korean Institute of Power Electronics, Vol. 24, No. 6, pp. 66-71, 2019.
• Kim, M. S., “The Importance of Integrated Thermal Management System for Electric Vehicle,” Auto Journal, Journal of the Korean Society of Automotive Engineers, Vol. 41, No. 6, pp.62-64, 2019.
• Jeon, W. H., “Integrated Thermal Management with Thermal Mapping and Heat Dissipation,” M.Sc. Thesis, Seoul National University, 2016.
• Kim, H. S., Han, B. Y., and Park, H. K., “Flow Analyses Around the Battery Pack for a NEV,” Journal of Computational Fluids Engineering, Vol. 16, No. 3, pp. 82-87, 2011. [https://doi.org/10.6112/kscfe.2011.16.3.082]
• Suh, H. K., “Effect of Inlet Geometry on the Cooling Performance of Battery Pack for an Electric Vehicle,” Journal of Korean Society of Mechanical Technology, Vol. 15, No. 5, pp. 679-684, 2013. [https://doi.org/10.17958/ksmt.15.5.201310.679]
• Hyun, S. B., Kim, B. Y., Song, J. H., and Lee, D. R., “A Study on the Convective Cooling Performance of the Secondary Battery in Electric Vehicle,” Journal of the Korean Society for Precision Engineering, Vol. 37, No. 4, pp.271-282, 2020.
• Kang, M. W., “Analysis of the Thermal Management System Using the New Material and Analysis of the Effectiveness at the System Level,” M.Sc. Thesis, Kookmin University, 2018.
• Kwon, H. B. and Park, H. S., “Numerical Investigation of Cooling Performance of Liquid-Cooled Battery in Electric Vehicles,” Transactions of the Korean Society of Mechanical Engineers-B, Vol. 40, No. 6, pp.403-408, 2016. [https://doi.org/10.3795/KSME-B.2016.40.6.403]
• Oh, H. J. and Park, S. G., “Effect of Coolant Flow Characteristics in Cooling Plates on the Performance of HEV/EV Battery Cooling Systems,” Transaction of the Korean Society of Automotive Engineers, Vol. 22, No. 3, pp.179-185, 2014. [https://doi.org/10.7467/KSAE.2014.22.3.179]
• Kim, H. S., “Study of the Power Characteristics and Cooling Performance of Externally Hybridized Battery Pack for Automotive Applications,” M.Sc. Thesis, Chonnam National University, 2018.
• Jiaqiang, E., Han, D., Qiu, A., Zhu, H., Deng, Y., et al., “Orthogonal Experimental Design of Liquid-Cooling Structure on the Cooling Effect of a Liquid-Cooled Battery Thermal Management System,” Applied Thermal Engineering, Vol. 132, pp. 508-520, 2018. [https://doi.org/10.1016/j.applthermaleng.2017.12.115]
• Lee, S. T., “Thermal and Mechanical Properties Improvement of Epoxy Composites Including Expanded Graphite and Multi-Walled Carbon Nanotubes Hybrid Fillers,” M.Sc. Thesis, Sejong University, 2016.