파편형 탄두의 표적무력화거리 예측을 위한 확률식 기반 해석 방법과 시험기반 해석 방법
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper addresses two methods to estimate the target incapacitation distance and probability of the arbitrary fragmentation warhead under the static detonation test condition. One is based on the probability equation suggested by Sperrazza and Kokinakis. The other is originated from the stationary detonation test concept to measure the performance of the fragmentation warhead. In the arbitrary fragmentation warhead, the target incapacitation probabilities obtained from the two methods were compared with each other. We found that the size of the fragment with cubic shape should be more than 3.5 mm to maximize the target incapacitation distance in the test method. And we also realized that the difference between the target incapacitation distance of the analysis method based on the test (AMBT) and that of the analysis method based on the probability equation (AMBPE) is decreased according to the increase of the fragment size. In conclusion, this paper can be useful for the estimation of the fragmentation warhead performance at the design stage.
Keywords:
Static detonation test, Live fragment, Effective fragment, Target incapacitation distance, Fragmentation warhead키워드:
정치기폭시험, 활성파편, 유효파편, 표적무력화거리, 파편형 탄두1. 서론
각국의 국방기술 보안 정책에 의해 유도탄 개발기술의 경우 기술자료 확보가 용이하지 않으며, 특히 유도탄 내 탑재되는 탄두(Warhead)의 경우 유도탄의 종말 성능 발휘에 중요한 구성품으로 유도탄 종말 단계 위력을 고려한 탄두 설계 방법에 관한 기술자료 확보는 더욱 제한적이다.
제한된 기술자료 내에서 이와 관련된 기존 연구로 Solomos 외 4인은 탄두 기폭 시 발생하는 파편, 폭풍파 등에 의한 표적 피해를 계산하는 여러 가지 모델을 정리하였으며,1 Chang 외 2인은 조절형 파편이 적용된 탄두의 표적무력화 효과를 분석하는 방법을 다루었다.2 또한, Baek 외 3인은 미래병사용 초소형 자연형 파편탄두의 표적무력화거리를 최대로 하는 설계 방법을 제안하였다.3
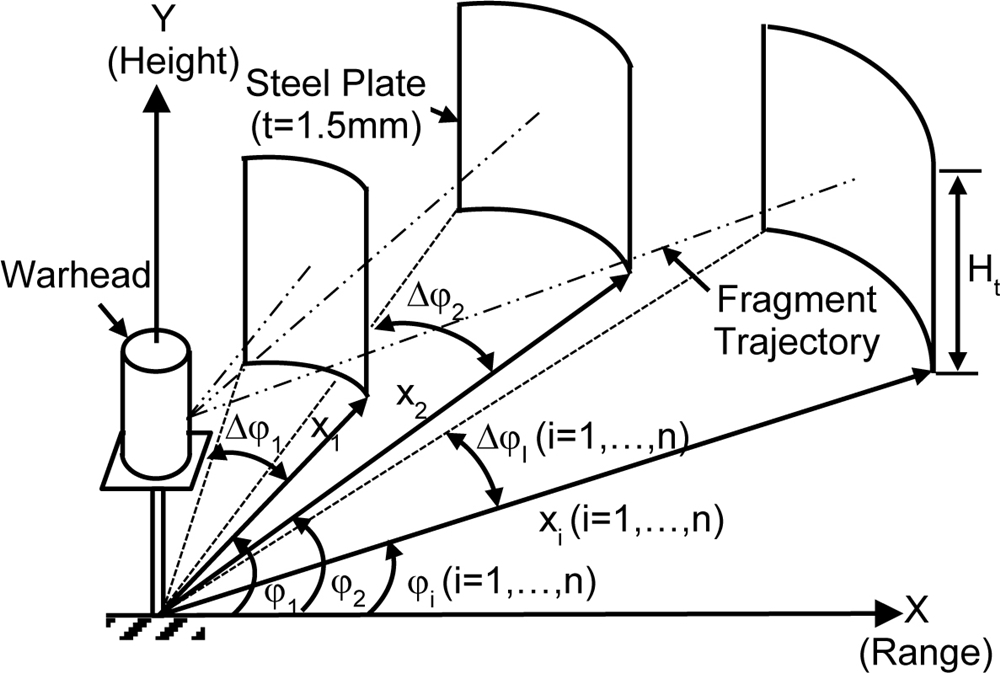
그러나, 이들 연구들은 확률론에 근거한 해석적 방법에 의해 탄두 성능을 판단하므로 실제 제작된 탄두 위력 확인을 위해 수행되는 정치기폭시험에서 나타나는 성능을 예측하기 용이하지 않다. 정치기폭시험이란 Fig. 1에 나타낸 바와 같이 탄두를 임의 높이에 수직으로 세워 고정한 후 기폭 시 발생하는 파편들이 거리별로 설치된 표적판을 관통하는 단위 면적당 관통 파편 수를 측정하여 표적무력화거리를 측정하는 시험을 말한다.2
따라서 본 연구는 확률론에 근거하여 추정하는 기존 해석적 방법의 표적무력화성능과 정치기폭시험 수행을 통해 표적무력화성능을 추정하는 방법을 서로 비교하여 각 방법의 차이를 비교하는데 연구 목적이 있다.
본 연구에서는 확률론에 근거하여 표적무력화성능을 추정하는 방법을 확률식 기반 해석 방법(Analysis Method based on Probability Equation, AMBPE)이라 정의하였으며, 정치기폭시험을 모사하여 표적무력화성능을 예측하는 방법을 시험기반 해석 방법(Analysis Method based on Test, AMBT)이라 정의하였다.
또한, 탄두의 표적무력화성능은 표적무력화거리(Target Incapacitation Distance)로 정의하였으며 표적무력화거리는 50% 확률로 표적을 무력화할 수 있는 거리를 의미한다.4
유도탄 무기 효과(Weapon Effectiveness) 분석 시 사용되는 병사 표적무력화성능분석에는 스페라자와 코키나키스(Sperrazza and Kokinakis)가 제안한 표적무력확률식(Target Incapacitation Probability Equation)이 널리 사용되고 있으며, 병사 표적 충돌 시 1개 파편이 갖는 파편 질량, 파편 속도 및 표적 자세 등에 따라 표적무력화확률을 구할 수 있다.5
이에 반해 실제 탄두 성능시험에서는 Fig. 1에 나타낸 정치기폭시험 하에서 탄두 기폭 시 발생하는 파편이 거리별로 설치된 모의표적판(Simulated Target Plate)을 관통하는 단위 면적당 파편 수인 파편밀도(Fragment Density) 계측을 통해 탄두 성능을 측정하고 있다. 이때 모의 표적판은 두께 1.5mm인 연강판(Mild Steel Plat)이 사용되며 시험적 방법은 50% 확률로 표적을 무력화할 수 있는 거리를 표적무력화거리라 정의하고 탄두 성능지표(Performance Index)로 사용하고 있다.2,6
본 연구에서는 파편형 탄두의 표적무력화거리와 확률을 구하기 위해 무기효과분석(Weapon Effectiveness Analysis)에서 사용되는 스페라자와 코키나키스 표적무력화 확률식을 Fig. 1의 정치기폭시험에 적용하여 표적무력화거리와 확률을 구하는 확률식 기반 해석 방법을 제시하고, 실제 정치기폭시험을 수식화하여 표적무력화거리와 확률을 구하는 시험기반 해석 방법도 함께 제시하고자 한다. 또한 제시된 두 해석 방법으로부터 얻어진 표적무력화거리와 확률값을 서로 비교하고자 한다.
해석의 편이를 위해 원통형 형상(Cylindrical Shape)을 갖는 파편형 탄두(Fragmentation Warhead)를 고려하였으며 탄체 두께를 한 변의 길이로 갖는 정육면체(Cubic) 파편이 탄두 기폭 시 발생하도록 탄두가 설계되어 있다고 가정하였다.
참고로 파편형 탄두 종류에는 자연형 파편탄두(Natural Fragmentation Warhead), 조절형 파편탄두(Controlled Fragmentation Warhead)와 성형파편탄두(Preformed Fragmentation Warhead)가 있으며 성형파편탄두나 조절형 파편탄두의 경우 파편 크기를 여러 가지 방법을 통해 원하는 크기로 조절할 수 있다.7
2. 본론
2.1 확률식 기반 해석 방법의 표적무력화확률과 표적무력화거리
임의거리 x에 위치한 병사 표적이 파편에 충돌할 때 무력화(Incapatation)되는 확률은 스페라자와 코키나키스에 의해 다음 식(1)과 같다.5
| (1) |
여기서, PI/H는 1개 파편을 맞았을 경우 병사 표적이 무력화되는 확률, mf는 파편 질량(kg), Vf는 파편의 충돌 속도(m/sec), a1, a2, a3은 무력화 기준(Casualty Criterion), 표적 충돌 위치 및 표적 자세 등에 따라 결정된 실험 계수(Coefficient)로 a1 = 7.47 × 10-3, a2 = 2.12 × 104, a3 = 3.629 × 10-1이다.
또한 임의거리 x에 위치한 병사 표적에 n개의 파편이 충돌할 때 표적무력화확률은 다음 식(2)와 같다.5
| (2) |
앞에 식(1)과 식(2)로부터 표적에 충돌하는 파편 수 n, 파편 질량 mf 및 파편 충돌 속도 Vf 등을 안다면 임의거리 x에 위치한 병사 표적에 n개 파편이 충돌할 때 거리별 표적무력화확률과 표적무력화거리를 구할 수 있다.
2.2 시험기반 해석 방법의 표적무력화확률과 표적무력화거리
시험기반 해석 방법은 Fig. 1에 나타낸 바와 같이 탄두 기폭 시 발생하는 파편의 거리별 유효파편밀도(Effective Fragment Density)로부터 표적무력화거리를 구할 수 있다.2,4,6 여기서 유효파편(Effective Fragment)이란 표적판에 충돌한 활성파편(Live Fragment) 중 표적판을 관통한 파편을 말한다.
시험기반 해석 방법에서 유효파편밀도는 다음 식(3)과 같다.
| (3) |
여기서, ρtrial,i는 i번째 철판이 설치된 거리에서 파편밀도(fragment#/m2), Neffect_f,i는 i번째 철판을 관통한 파편 수, Apanel,i는 i번째 철판 면적(m2), Δφi는 i번째 철판의 원주각(Rad), xi는 폭심(Detonation Center)에서 i번째 철판까지 거리(m)이고, Ht는 표적 높이 등을 고려한 철판 높이(m)이다.
시험기반 해석 방법에서 표적무력화확률은 병사 표적의 전신투영면적 0.5m2(≅0.5572 m2)에 1.5 mm 철판을 관통한 파편이 1개일 때 100%로 정의되며(1 fragment/0.5 m2), 1 m2 면적에 1개의 유효파편이 관통한 경우 표적 무력화확률은 50% 이다.2,4,6
따라서, 본 연구에서도 시험기반 해석 방법의 단위 면적당 파편 밀도, ρtrial가 50%가 되는 거리를 무력화거리로 정의하였으며, 시험기반 해석 방법에 의한 표적무력화확률 계산식은 다음 식(4)와 같다.
| (4) |
여기서, PI,trial는 시험기반 해석 방법으로 구한 표적무력화확률, ρtrial는 1.5 mm 두께를 갖는 철판을 1 m2 면적당 관통한 파편 수로 유효파편밀도(fragment#/m2)이다.
파편이 임의 거리에서 모사표적판을 관통하는지 판단하기 위해 THOR 관통식(THOR Formula)이 사용되었으며 다음 식(5)와 같다.7
| (5) |
여기서, Vf_r는 표적판 관통 후 파편 속도(m/sec), Vf_s는 파편 충돌 속도(Striking Velocity) (m/sec), tp는 표적판 두께(m), As는 파편이 표적판 충돌 시 접촉면적(Contact Area) (m2), mf,s는 표적판 충돌 전 파편 질량(kg), θs는 입사각(Incidence Angle)으로 파편 진행 방향과 표적판에 수직한 방향과 이루는 사잇각이고, c1-c5는 표적판 재질에 따라 실험적에 의해 결정된 계수로 표적판 재질이 연강(Mild Steel)인 경우 c1= 4.356, c2= 0.674, c3= -0.791, c4= 0.989, c5 = 0.434이다.7
표적판에 충돌한 파편 중에서 표적무력화확률 계산에 유효한 파편(Effective Fragment)은 식(5)에서 계산된 표적판 관통 후 파편 속도 Vf_r가 0 m/sec을 초과한 파편이며, 표적판 관통 후 파편 속도, Vf_r가 0 이하인 파편은 표적판을 관통하지 못함을 의미한다.
이와 같이 식(3)부터 식(5)를 통해 표적판에 충돌하는 파편 질량, 파편 충돌 속도 등을 안다면 시험기반 해석 방법의 표적무력화거리와 거리별 표적무력화확률을 구할 수 있다.
2.3 파편 비산각과 거리에 따른 활성파편 수
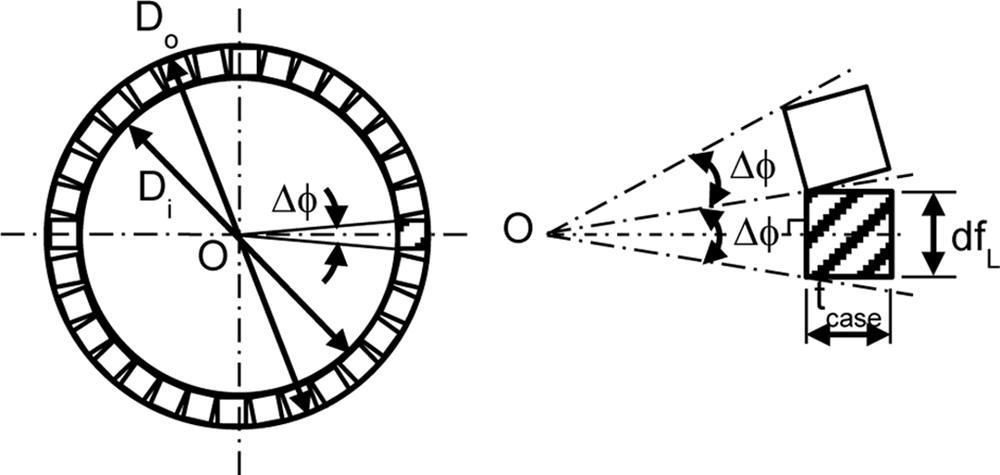
본 연구에서 고려된 탄두는 탄체 두께를 한 변의 길이로 갖는 정육면체 파편이 고르게 생성되도록 설계되었다고 가정하였으므로 Figs. 2와 3과 같이 탄두는 여러 개의 파편층(Fragment Layer)으로 구성되며 각 파편층에는 동일한 크기의 파편이 일정한 방위각 간격마다 존재한다고 가정할 수 있다.
따라서, 탄체 두께와 탄두 길이 제원이 주어진다면 탄두 내 존재하는 파편층의 총 층수(Totla Layer Number), nL는 다음 식(6)과 같다.
| (6) |
여기서, nL는 탄두 내 존재하는 파편층의 총 층수, Lwh는 파편이 형성되는 유효탄체길이(Effective Body Case Length) (m), dfL는 정육면체 파편의 한 변 길이(m), tcase는 탄체 두께(m)이고, Floor( )는 바닥함수(Floor Function)로 ( )안에 값보다 작은 정수값 중 가장 큰 값을 출력하는 수학연산자이다.
일반적으로 Fig. 1과 같은 정치기폭조건에서 탄두가 기폭될 경우 파편은 Fig. 2와 같이 임의 비산각을 갖고 비산하며 표적 거리가 먼 경우 파편은 표적에 도달하기 전에 지면에 충돌하여 소실하게 된다.
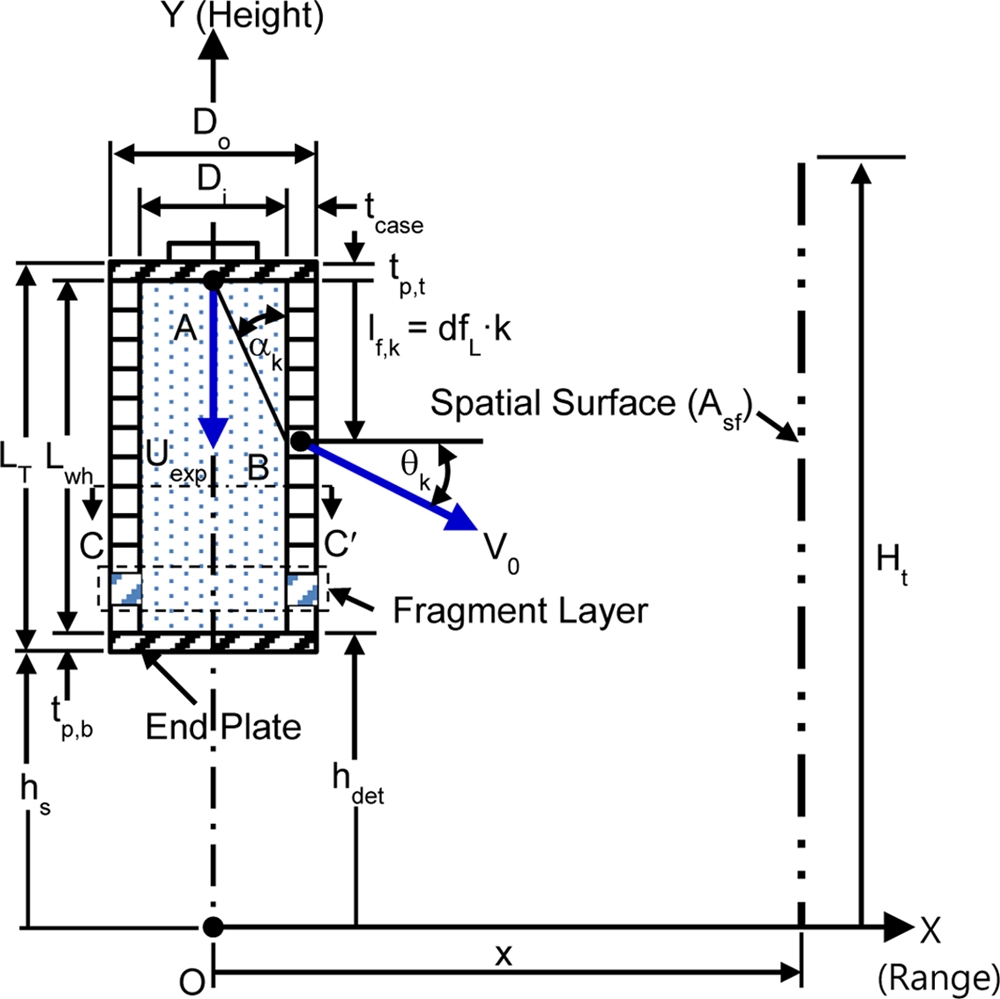
Fig. 2의 B점에 위치한 파편 역시 비산각을 갖고 비산하며 비산각, θk를 테일러 각(Taylor Angle)이라 부르며 다음 식(7)과 같다.7
| (7) |
여기서, Vo는 파편초기속도(m/sec), Uexp는 충진된 화약의 폭속(Detonation Velocity) (m/sec), αk는 탄체 내부 벽면과 기폭시작점(A점)과 파편입자(B점)를 연결한 선분 AB 사잇각, Di는 탄체내경(m)이고, k는 k번째 파편층 지수(Index)이다.
Fig. 3은 Fig. 2에 나타낸 탄두 단면도(C-C')로 일정한 크기의 정육면체 파편이 방위각 방향으로 고르게 분포된 형상을 보여준다. Fig. 3으로부터 1개 파편입자의 미소방위각(Infinitesimal Azimuth Angle), Δϕ는 근사적으로 다음 식(8)과 같다.
| (8) |
여기서, Δϕ는 파편입자 1개의 미소방위각, Di는 탄체 내경(m)이다.
또한, Fig. 3과 같이 파편은 방위각 방향으로 일정하게 분포하므로 각 파편층 내 파편 수, nf/L는 다음 식(9)와 같다.
| (9) |
Fig. 2에서 k번째 파편층의 파편은 임의 비산각을 갖고 비산하므로 임의거리 x에서 파편 높이는 감소하게 되며 실제 파편 높이는 탄두 기폭 높이와 표적 거리에 따라 달라지게 된다.
따라서, 임의거리 x에서 k번째 파편층의 파편 높이는 다음 식(10)과 같이 구할 수 있다. 이때 파편은 높은 속도를 갖는 반면 비행 시간이 짧아 중력의 영향은 무시하였으며 파편은 비산각 방향으로만 직선비행한다고 가정하였다.
| (10) |
여기서, Yf,k(x)는 거리 x에서 k번째 파편층 내 파편의 비산 높이(m), hdet는 Fig. 2에 나타낸 기폭 높이로 지면에서 유효탄체 하단부까지 높이(m)이다.
Fig. 3에서 거리 x에서의 파편밀도(Fragment Density)는 미소방위각 Δϕ이 형성하는 미소공간표면적(Infinitesimal Spatial Surface Area) 내 존재하는 활성파편 파편 수 nf_live로부터 다음 식(11)과 같으며, 파편 입자가 미소방위각 Δϕ를 갖고 전방위에 걸쳐 동일한 간격으로 존재하므로 전체 방위각 공간표면적에 존재하는 파편밀도 역시 식(11)과 같다.
| (11) |
여기서, nf_live(x)는 미소방위각 Δϕ 내 존재하는 거리 x에서 활성파편 수, Ht는 표적 높이이다.
미소방위각 Δϕ에 존재하는 nL개의 파편 중 k번째 파편층에서 비산된 파편 높이가 0이 된다면 표적 거리 x에서 방위각 공간표면적(Azimuth Spatial Surface Area)상에 존재하는 활성파편(Live Fragment) 개수, nf_live(x)는 다음 식(12)와 같다. 이때, 활성파편이란 파편의 비산 높이가 0m 이상으로 표적과 충돌이 가능한 파편을 말한다. 활성파편과 유효파편의 차이는 활성파편은 표적과 충돌이 가능한 파편을 의미하며 유효파편은 활성파편 중 표적 충돌 후 표적을 관통할 수 있는 파편을 말한다.
| (12) |
여기서, k|Yf,k(x)≤0는 거리 x에서 파편 높이 Yf,k(x)가 0m 이하가 되는 파편층의 지수(Index), k이다.
최종적으로 임의거리 x에서는 전체 방위각 공간표면적에 존재하는 활성파편 총 개수는 다음 식(13)과 같다.
| (13) |
여기서, nf_total_live(x)는 거리 x에서 전체 방위각 공간표면적에 존재하는 표적과 충돌 가능한 활성파편 총 개수이다.
2.4 등가표적크기 및 탄두 기폭 높이
무기효과분석에서 일반적으로 고려하여 서 있는 병사의 전신 투영면적은 0.5572 m2, 병사 평균 키 높이는 1.75 m, 직사각형 표적으로 병사 표적을 등가화한다.5
그러나 Fig. 1에 나타낸 정치기폭시험의 경우는 등가표적크기(Equivalent Target Size)를 0.5m2, 파편포집 높이를 고려하여 표적 높이 2.4 m를 사용하고 있다.2,4,6
확률식 기반 해석 방법과 시험기반 해석 방법에서 얻은 표적무력화거리 및 확률을 비교하기 위해 등가표적크기, 표적 높이 및 탄두기폭높이를 동일하게 적용해야 하므로 본 연구에서는 병사 표적의 등가표적크기는 0.5m2, 표적 높이는 1.75 m, 탄두기폭 높이는 1.5m로 동일하게 적용하였다. 이 경우 단일 병사 표적의 가로 폭은 0.285 m로 설정하였다.
2.5 파편 질량 및 파편 충돌 속도
탄두 기폭 시 생성되는 파편 질량은 탄체 두께를 한 변의 길이로 갖는 정육면체 파편이라는 가정에 의해 다음 식(14)와 같다.
| (14) |
여기서, mf는 파편 질량(kg), ρm는 탄체 재질밀도(kg/m3), dfL는 정육면체 파편의 한변 길이(m), tcase는 탄체 두께(m)이다.
표적에 충돌하는 파편 충돌 속도를 구하기 전에 탄두 기폭 시 생성되는 파편의 초기 속도를 구하면 다음 식(15)와 같다.7
| (15) |
여기서, V0는 탄두 기폭 시 비산하는 파편의 초기속도(m/sec), 는 화약 종류에 따라 실험적으로 결정된 거니(Gurney), 상수(m/sec), E는 화약의 단위 질량당 에너지를 에너지 변환 손실을 고려하여 실험적으로 구한 단위 질량당 운동에너지(0.5 ) (m/sec),2 Cexp는 탄두 내 화약의 질량(kg), Mcase은 파편이 되는 탄체질량(kg), Cexp/Mcase은 탄두의 단위 길이 단위 면적당 금속케이스 질량과 화약량의 비율이다.
파편의 초기속도, V0는 비행하는 동안 공기저항에 의해 감소하게 되며 임의거리 l에 도달하는 파편 속도는 다음 식(16)과 같다.7
| (16) |
여기서, l는 파편의 비행거리(m), Vf,_s(l)는 비행거리 l에서 파편속도(m/sec), V0는 탄두 기폭 시 파편 초기속도(m/sec), ρair는 공기밀도(kg/m3), CD는 파편 형상에 따른 항력계수, Afrag는 파편 진행 방향에 수직한 면에 투영된 파편의 단면적(m2), mf는 파편 질량(kg)이다.
파편은 비행 중 공기 유동에 의해 회전할 수 있으므로 파편의 투영단면적, Afrag는 변하게 된다. 그러나 본 연구에서는 보수적인 탄두위력 분석을 위해 파편은 비행 중 가장 큰 투영단면적을 갖고 비행한다고 가정하였으며, 파편이 정육면체 형상을 갖는다는 가정에 따라 식(16)은 정육면체 파편의 단면형상계수(m2/kg2/3)를 갖는 식(17)로 표현될 수 있다.3
| (17) |
여기서, Sf는 로 정육면체 파편의 단면형상계수이다.
그리고, 파편은 비산각 방향으로 비산하므로 지면에서 수직하게 위치한 표적 공간표면적에 도달하는 파편의 속도는 다음 식(18)과 식(19)와 같다.
| (18) |
| (19) |
여기서, Vf_s,x(x)는 비산각 방향의 파편 속도인 Vf,_s(l)의 X축(수평) 방향 속도성분(m/sec)이고, Vf_s,y(x)는 Y축(수직) 방향 속도성분(m/sec)이다.
2.6 확률식 기반 해석 방법과 시험기반 해석 방법의 표적무력화확률
확률식 기반 해석 방법의 표적무력화확률을 구하기 위해서는 식(2)와 같이 1개의 표적에 충돌하는 파편 수를 알아야 한다.
임의거리 x에서 방위각 방향으로 서 있는 병사 표적의 수는 자연수(Natural Number)이므로 다음 식(20)과 같다.
| (20) |
여기서, Nsoldier(x)는 거리 x에 원주 방향으로 서 있는 병사 표적의 총 수(Nsoldier(x)∈N),Wt는 등가화된 병사 표적 폭(m)이다.
임의거리 x에 서 있는 병사 표적들에게 활성파편이 고르게 충돌한다고 가정하면 1명의 병사 표적에 충돌 가능한 평균 활성파편 수(The Number of Averaged Live Fragment)는 다음 식(21)과 같으며 실수(Real Number)가 된다.
| (21) |
여기서, nhit,Real(x)는 거리 x에 원주 방향으로 서 있는 1명의 병사 표적에 충돌할 수 있는 평균 활성파편 수(nhit,Real(x)∈R)이다.
그러나, 식(21)의 단위 병사당 충돌 가능한 평균 활성파편 수, nhit,Real(x)는 실수(Real Number)이나 실제론 Nsoldier(x)명의 병사 중 일부는 nhit,Real(x)보다 많은 자연수(Natural Number)개의 파편에 충돌되고 또 일부 병사는 nhit,Real(x)보다 작은 자연수개의 파편에 충돌하게 된다. 또한, 식(2)를 이용하여 다수개의 파편을 맞는 병사 표적의 무력화확률을 구하기 위해서는 파편 수는 자연수가 되어야 하므로, 병사 표적에 자연수 개수만큼 충돌한다고 가정함으로써 임의거리 x에 위치한 병사 표적에 충돌한 파편 수는 다음 식(22)부터 식(24)와 같이 구할 수 있다.
| (22) |
| (23) |
| (24) |
여기서, Ns_n_hit_natural(x)는 거리 x에 서 있는 병사 표적 중 Nhit_natural(x)개 파편에 충돌하는 병사 표적 수(Ns_n_hit_natural(x)∈N), Ns_(n+1)_hit_natural(x)는 거리 x에 서 있는 병사 표적 중 Nhit_natural(x)+1개 파편에 충돌되는 병사 표적 수(Ns_(n+1)_hit_natural(x)∈N), Nhit_natural(x)는 거리 x에 병사 표적 중 Ns_n_hit_natural(x)명의 병사 1명에게 충돌하는 활성파편 수(Nhit_natural(x)∈N)이다.
식(22)부터 식(24)에 의해 임의거리 x에 존재하는 병사 표적 중 일부는 충돌하는 파편에 1개 차이가 있게 되며 다른 표적무력화확률을 갖게 된다. 따라서, 임의거리 x의 전체 병사 표적에 대한 평균적인 표적무력화확률을 구하기 위해 산출평균무력화확률을 구해보면 다음 식(25)와 같다.
| (25) |
여기서, PI/H,N_f_total_live(x)는 거리 x에 서 있는 Nsoldier(x) 명의 병사 표적에 Nf_total_live(x)개의 활성파편이 충돌할 때 산술평균무력화확률, PI/H,n_hit_natiral는 거리 x에 병사 표적 중 nhit_natiral(x) 파편에 충돌되는 병사 표적의 무력화확률, PI/H,(n+1)_hit_natiral는 거리 x에 병사 표적 중 nhit_natiral(x)+1개 파편에 충돌되는 병사 표적의 무력화확률이다.
시험기반 해석 방법의 표적무력화확률은 확률식 기반 해석 방법의 표적무력화확률 계산식과 달리 2.2절에서 언급한 바와 같이 표적에 충돌한 파편들 중 표적 관통에 성공한 관통유효파편 수에 따라 결정되므로 단위 표적당 관통유효파편밀도를 구해보면 다음 식(26)과 같다.
| (26) |
여기서, ρtrial(x)는 단위 표적당 유효파편밀도(Effective Fragments#/m2), Neffect_f (x)는 거리 x에 위치한 방위각 공간표면적 내 존재하는 활성파편들 중 표적판 관통이 가능한 유효파편 수이다.
3. 시뮬레이션
Fig. 1에 나타낸 정치기폭시험 조건에서 확률식 기반 해석 방법과 시험기반 해석 방법으로 얻어진 표적무력화거리 및 거리별 무력화확률을 비교하기 위해 Table 1에 나타낸 임의 탄두 제원 및 시뮬레이션 조건을 사용하였다.
거리별 표적무력화확률을 구하기 위해서는 두 방법 모두 표적과 충돌하는 파편 수, 파편 질량 및 파편 충돌 속도를 구해야한다.
확률식 기반 해석 방법의 표적무력화확률 계산은 거리별 공간표면적상에 존재하는 모든 파편에 대해서 파편 질량 식(14), 파편충돌속도 식(18)을 스페라자와 코키나키스 무력화확률식 식(1)에 대입하여 1개 파편의 무력화확률을 구한 후 식(20)부터 식(24)에서 계산한 병사표적에 충돌하는 파편 수를 식(2)에 대입하여 다수개 파편에 충돌되는 표적의 무력화확률을 구한다.
이후 최종적으로 식(25)를 이용하여 임의거리 x에 존재하는 전체 표적의 산술평균무력화확률을 구한다
또한, 시험기반 해석 방법의 표적무력확확률 계산은 파편 질량 식(14)와 파편 충돌 속도 식(17)을 거리별 공간표면적상에 존재하는 모든 활성파편에 대해 THOR 관통식인 식(5)를 통해 철판 관통 후 파편 속도, Vf_r이 0 이상인 관통유효파편을 골라낸 후 유효파편밀도를 나타내는 식(26)과 시험기반 해석 방법의 표적무력화확률 계산식인 식(4)로부터 거리별 표적무력화확률을 구한다.
3.1 파편 비산각과 거리에 따른 활성파편 수
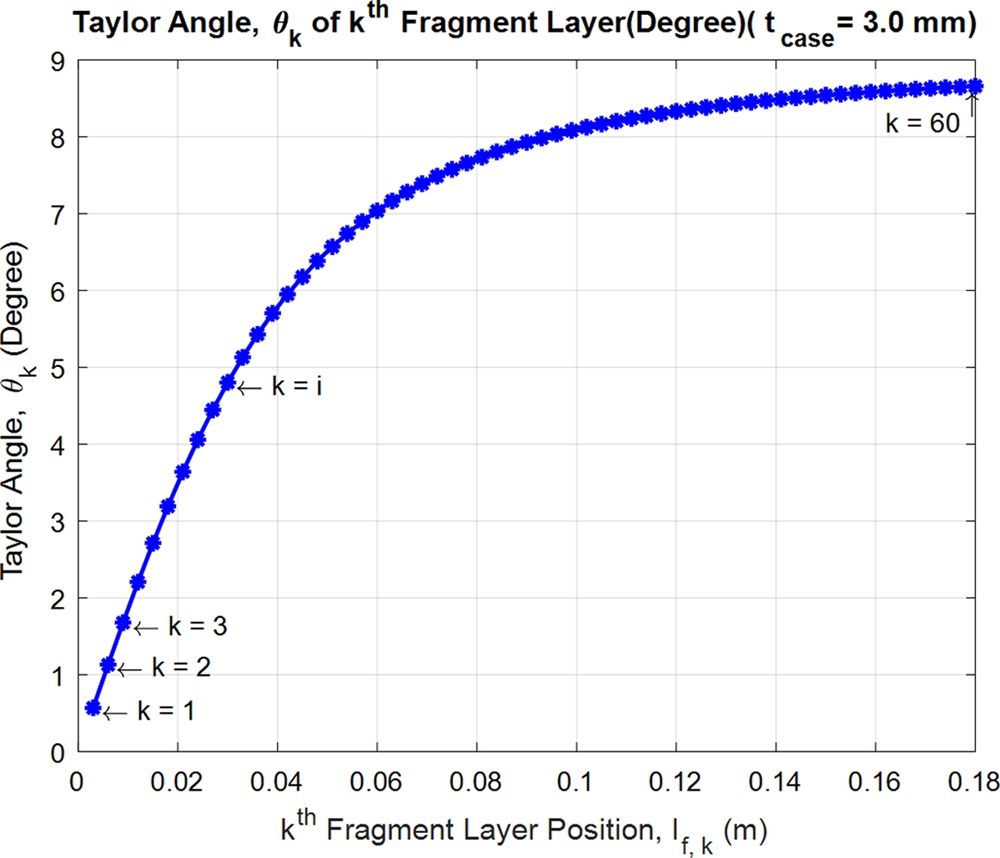
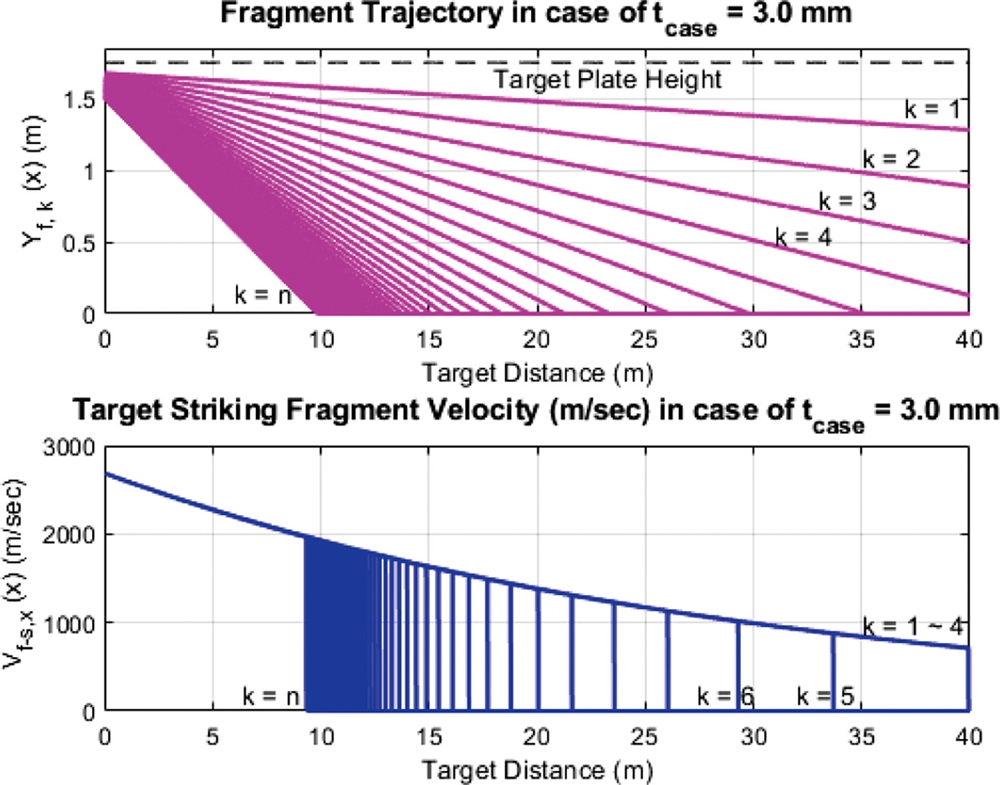
식(7)을 이용하여 Table 1의 제원을 갖는 임의탄두의 파편 비산각을 구하면 다음 Fig. 4와 같다. 이때 탄체 두께는 3.0mm로 하였으며 가정에 의해 파편 크기는 3.0mm를 한 변의 길이로 갖는 정육면체 파편이라 가정하였다.
파편층 지수 k가 증가할수록 다시 말해 탄두 하단에 위치한 파편일수록 파편 비산각은 증가하며 최상단 파편층(k = 1)은 약 0.6°의 비산각을 갖는 반면 최하단 파편층(k = 60)은 약 8.7°의 상대적으로 큰 비산각을 갖음을 Fig. 4를 통해 알 수 있다.
식(10)과 식(18)를 이용하여 Fig. 4의 비산각을 갖는 파편의 거리별 궤적(높이)과 표적 충돌 전 속도를 X-Y축 단면상에 대해 구해보면 다음 Fig. 5와 같다.
표적 거리가 길어짐에 따라 탄두 하부 파편층의 파편들은 비산각에 의해 지면과 충돌하여 소실되는 모습을 Fig. 5 상단에서 볼 수 있으며, 초기비산속도 2,680 m/sec 이상을 갖는 파편들이 공기저항에 의해 속도가 감소하다 지면 충돌로 인해 속도가 0이 되는 것을 Fig. 5의 하단 그림을 통해 볼 수 있다.
결론적으로 표적 거리가 길어짐에 따라 파편 비산각에 의해 많은 파편이 지면과 충돌에 의해 소실되어 표적과 충돌이 가능한 활성파편 수는 감소하게 된다.
임의거리 x에 존재하는 활성파편 수를 X-Y축에 대해 나타내면 Fig. 6의 상단과 같으며, 전체 방위각 공간표면적 내 존재하는 활성파편 수를 표적 거리 x에 대해 나타내면 Fig. 6의 하단과 같다. 다시 말해 Fig. 6의 상단 그림은 미소방위각 Δϕ내 존재하는 거리별 활성파편 수를 나타내며, Fig. 6의 하단 그림은 전체 방위각에 걸쳐 존재하는 거리별 활성파편 수이다.
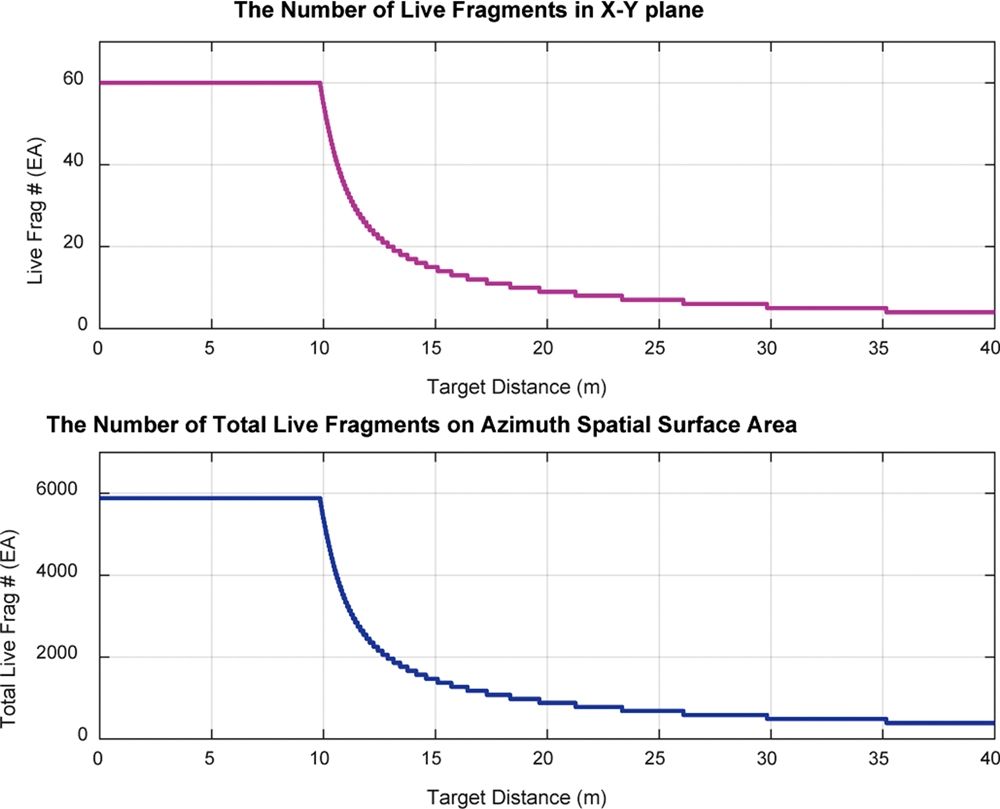
The number of live fragments in X-Y plane and azimuth spatial surface area in case of tcase = 3.0 mm
미소방위각 Δϕ내 존재하는 활성파편 수를 나타내는 Fig. 6의 상단 그림의 경우 9.8 m 이내 거리에서는 60개의 활성파편 수를 가지나 거리 증가에 따라 활성파편 수는 점차 감소하다가 표적 거리 40m에서 활성파편 수는 4개로 감소함을 보여주며, Fig. 6의 하단 그림 역시 반경(Radius) 9.8 m 이내에서는 방위각 공간 표면적상에 5,880개의 활성파편이 존재하다가 표적 거리 40m에서는 활성파편 수가 392개로 감소함을 보여준다.
3.2 시험기반 해석 방법에 따른 표적무력화거리
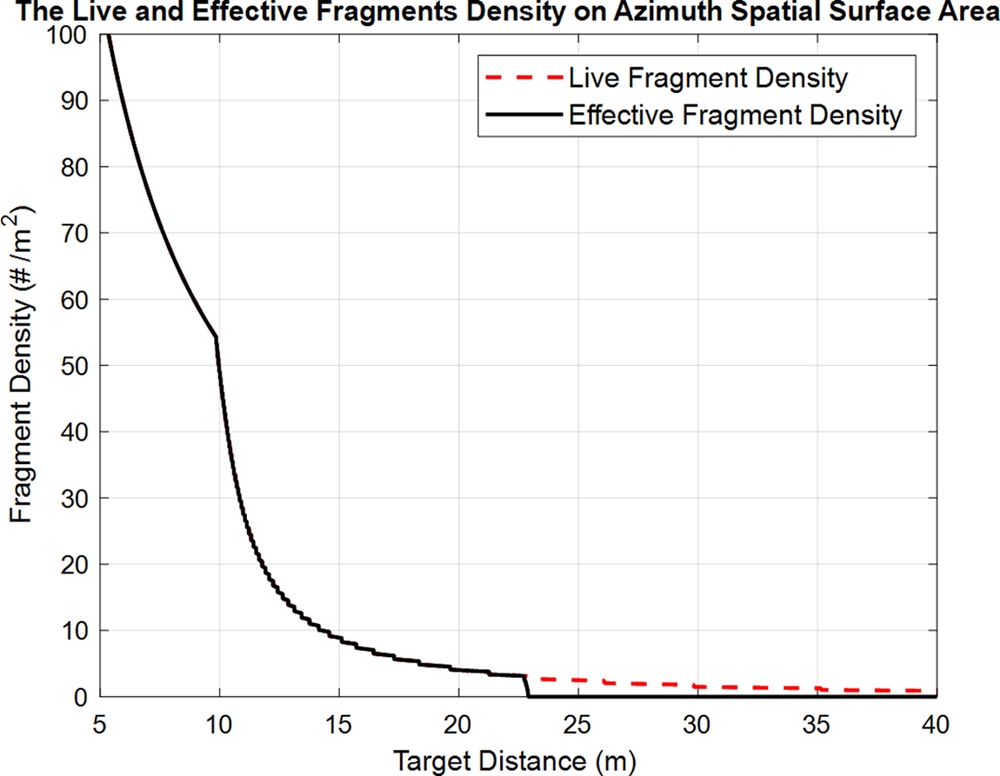
거리 x에 따라 존재하는 활성파편 중 1.5 mm 연강표적판을 관통할 수 있는 관통유효파편 수를 식(5)를 이용하여 구한 후 활성파편밀도(Live Fragment Density)와 유효파편밀도(Effective Fragment Density)를 구해보면 Fig. 7과 같다.
Fig. 7의 경우 표적 거리 9.8m까지는 거리 증가에 따라 공간표면적 증가로 파편밀도가 감소하다가 9.8m 이상 거리부터는 파편 중 일부가 지면 충돌로 소실되어 파편밀도가 급격히 감소하는 모습을 보여준다.
또한, 표적 거리 22.9m부터는 활성파편 일부가 표적판에 충돌하나 관통하지 못해 관통유효파편밀도가 0이 됨을 보여준다.
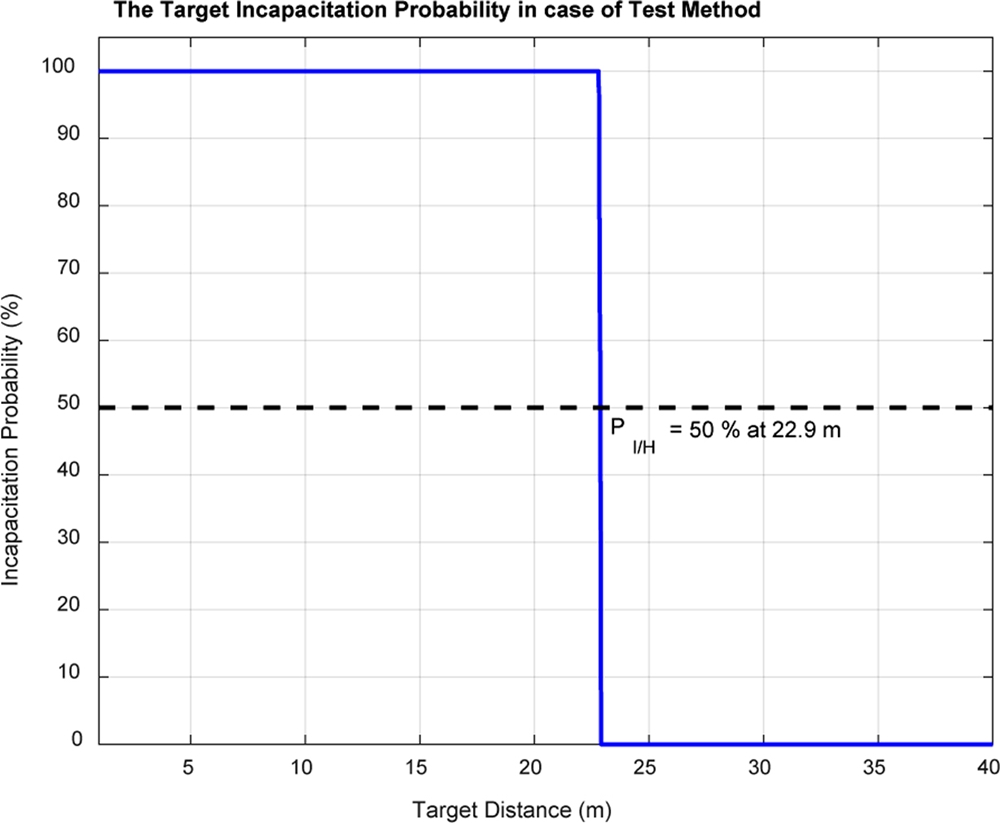
Fig. 7의 유효파편밀도를 갖는 탄두에 대한 시험기반 해석 방법에 의한 거리별 표적무력화확률을 식(4)를 이용하여 구해보면 다음 Fig. 8과 같으며 표적무력화확률이 50%인 표적무력화거리는 22.9 m임을 알 수 있다.
3.3 확률식 기반 해석 방법에 따른 표적무력화거리
식(1), 식(2)와 식(20)부터 식(25)를 이용하여 확률식 기반 해석 방법에 의한 거리별 표적무력화확률을 구해보면 다음 Fig. 9와 같다. 확률식 기반 해석 방법으로 얻어진 표적무력화확률은 13.7 m 이상부터 무력화확률이 감소하다가 29.8 m에서 50% 무력화확률을 가짐을 볼 수 있으며, 40 m에서도 20% 이상의 표적무력화확률을 가짐을 볼 수 있다.
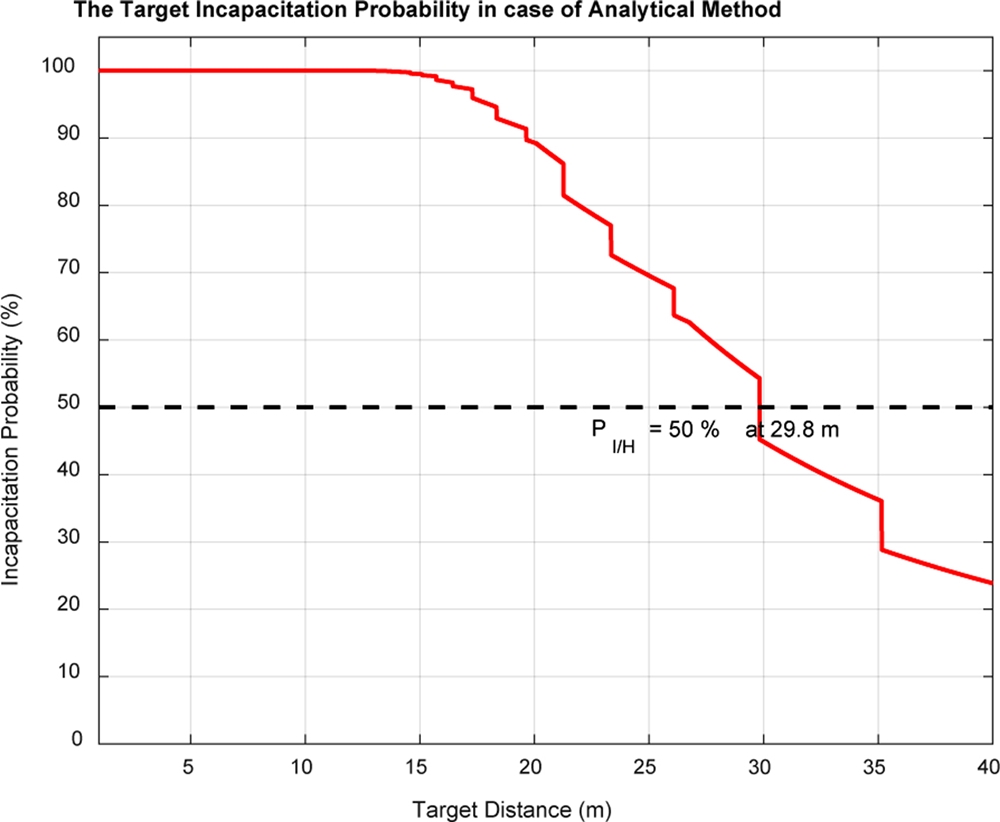
Target incapacitation probability obtained from analysis method based on probability equation (AMBPE) in case of tcase = 3.0 mm
탄체 두께 3.0mm를 갖는 탄두의 경우 스페라자와 코키나키스 무력화확률식에 근거한 확률식 기반 해석 방법의 표적무력화거리가 시험기반 해석 방법에 의해 얻어진 표적무력화거리보다 더 크게 계산됨을 알 수 있다.
이 원인으론 시험기반 해석 방법의 경우 파편이 일정 수준 이상의 질량을 갖는 크기를 가져야 공기저항을 극복하고 1.5mm 두께 표적판을 관통할 수 있으므로 확률식 기반 해석 방법의 표적무력화거리보다 작은 표적무력화거리를 갖는 것으로 판단된다.
3.4 시험기반 해석 방법과 확률식 기반 해석 방법에 따른 표적무력화거리 비교
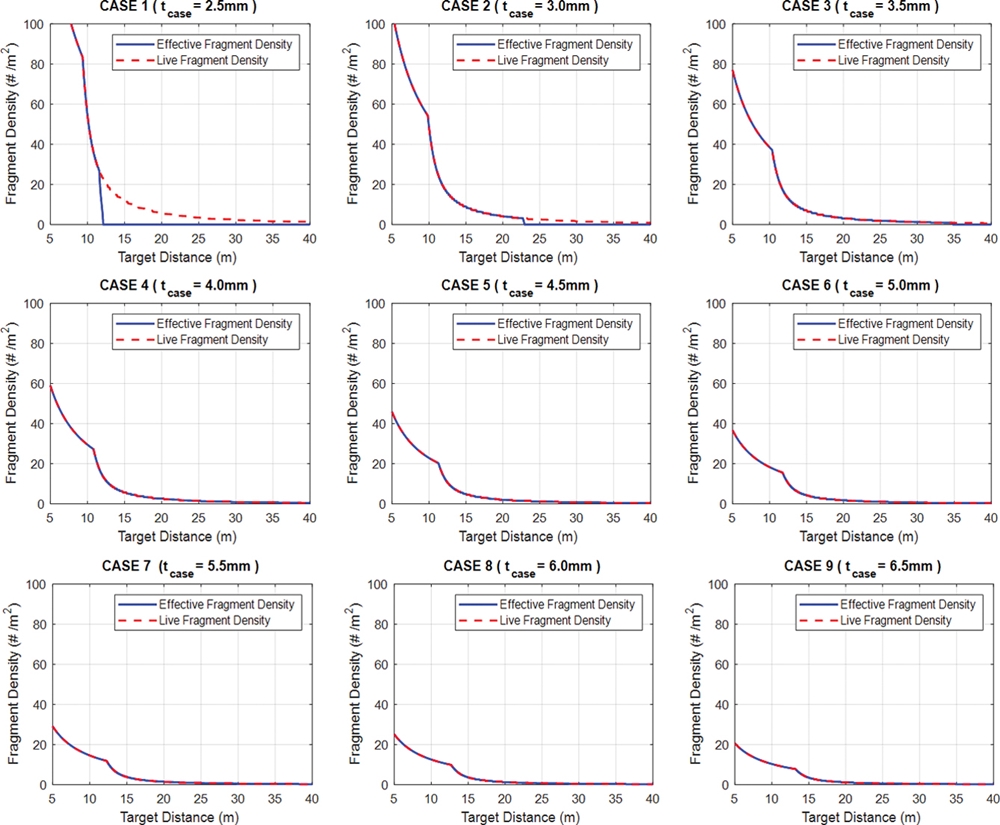
파편 크기에 따른 시험기반 해석 방법과 확률식 기반 해석 방법에 의한 표적무력화거리 변화를 관찰하기 위해 탄체 두께 조정을 통해 정육면체 파편 길이를 2.5에서 6.5 mm까지 0.5 mm씩 증가시켜 설계된 탄두들에 대한 거리별 파편밀도와 거리별 표적무력화확률을 Figs. 10과 11에 각각 나타내었다.
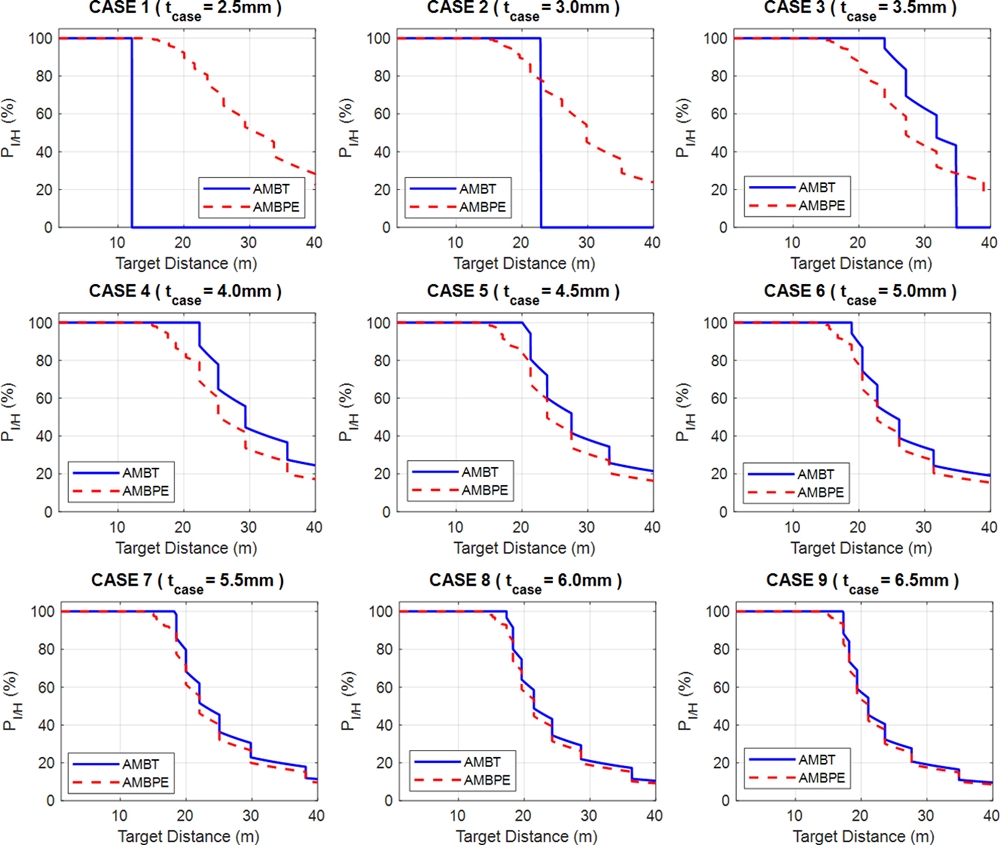
Comparison between the target incapacitation probability of analysis method based on test (AMBT) and that of analysis method based on probability equation (AMBPE)
Fig. 10을 살펴보면 파편 크기(길이)가 3.0 mm 이하의 경우 표적 거리 증가에 따라 임의거리에서 표적판 관통이 가능한 유효파편밀도가 0이 됨을 알 수 있다.
3.0 mm 이하의 경우 파편 크기가 작아 파편 질량이 갖는 관성력 대비 공기저항에 의한 속도감소가 상대적으로 커 표적 거리가 증가함에 따라 표적판 관통에 필요한 운동에너지가 부족하기 때문이다.
또한, 파편 크기(길이)가 3.5mm 이상의 경우 유효파편밀도와 활성파편밀도는 같으나 파편 크기가 커짐에 따라 탄두 기폭 시 발생하는 파편 총 개수가 감소하여 거리 증가에 따라 파편 밀도가 감소하는 경향을 보여준다.
Fig. 11은 각 파편 크기(길이)별 거리에 따른 표적무력화확률을 나타내며 유효파편밀도에 근거한 시험기반 해석 방법의 경우 Fig. 10에 나타낸 바와 같이 파편 크기(길이)가 3.0 mm 이하에서 유효파편밀도가 0이 되는 거리가 존재하여 해당 거리에서 표적무력화확률은 0%가 됨을 보여준다. 또한, 파편 크기(길이)가 3.5 mm 이상인 경우 시험기반 해석 방법의 표적무력화확률은 전반적으로 확률식 기반 해석 방법의 표적무력화확률보다 큰 값을 가지다가 파편 크기(길이) 6.0 mm 이상에서 확률식 기반 해석 방법의 표적무력화확률과 유사한 값을 가짐을 보여준다.
Fig. 12는 파편 크기(길이) 증가에 따른 두 해석 방법의 표적무력화거리 변화를 보여주며, 확률식 기반 해석 방법의 경우 파편 크기(길이) 증가에 따라 표적무력화거리가 점진적으로 줄어드는 경향을 보여주는 반면 시험기반 해석 방법의 경우 파편 크기(길이) 3.5 mm까지는 표적무력화거리가 증가하다 3.5mm에서 최대가 됨을 보여준다. 이 이유는 파편 크기(길이)가 증가함에 따라 전체 파편 수는 감소하나 파편 질량 증가에 따라 표적판 관통이 가능한 유효파편 수가 증가하기 때문이다.
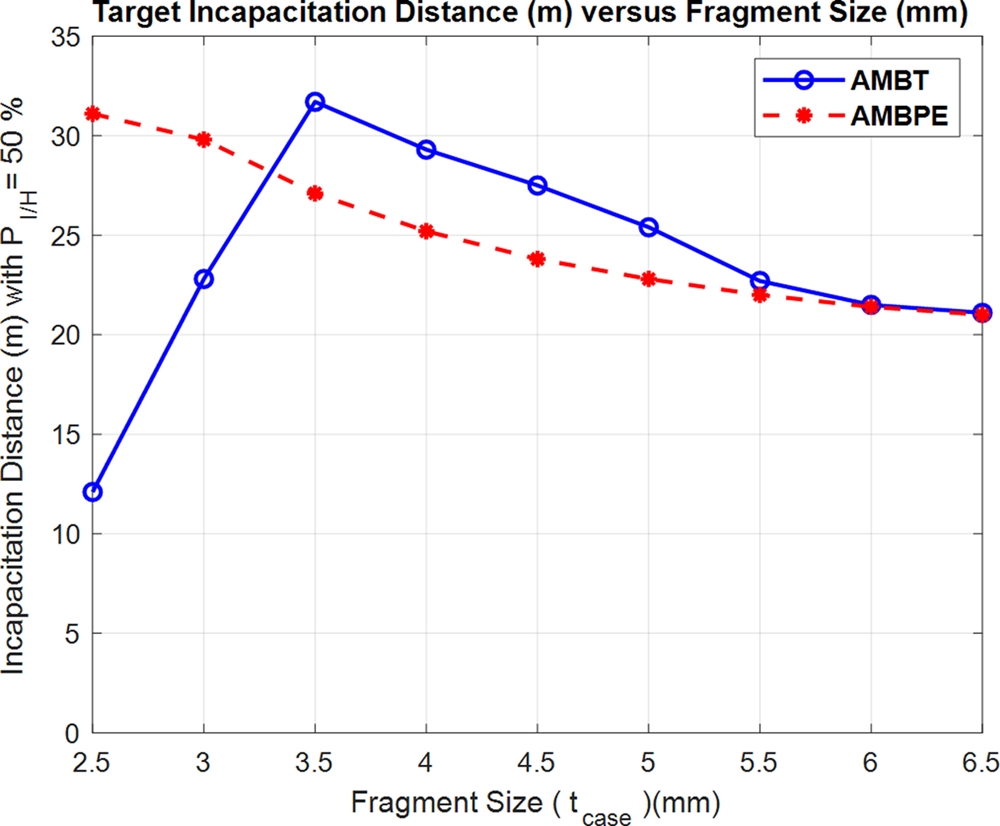
Comparison between the target incapacitation distance of analysis method based on test (AMBT) and that of analysis method based on probability equation (AMBPE)
또한, 시험기반 해석 방법의 경우 3.5 mm 이상의 파편 크기에서 확률식 기반 해석 방법과 마찬가지로 파편밀도 감소에 따라 표적무력화거리가 점차 감소하다가 6.0 mm 이상에서는 확률식 기반 해석 방법과 유사한 표적무력화거리를 가짐을 볼 수 있다.
따라서 Table 1에 주어진 탄두의 경우 정치기폭시험에서 측정되는 표적무력화거리를 최대화하기 위해 탄체 두께는 최소 3.5 mm 이상이 되어야 하며 탄체 두께 6.0 mm 이상에서 확률식 기반 해석 방법과 시험기반 해석 방법은 유사한 표적무력화거리를 가짐을 알 수 있다.
4. 결론
본 연구에서는 정치기폭시험에서 탄두가 갖는 표적무력화거리를 탄두 개념 설계 단계에서 산출하기 위해 스페라자와 코키나키스 표적무력화확률식을 이용한 확률식 기반 해석 방법을 제시하였으며, 표적판 관통유효파편밀도에 근거한 시험기반 해석 방법도 제시하고 두 방법을 통해 얻어진 표적무력화거리와 확률을 비교하였다. 비교한 결과 본 연구에서 고려한 제원의 탄두 경우 파편 크기(길이)를 3.5 mm로 할 때 시험기반 해석 방법에 의한 표적무력화거리가 최대가 됨을 알 수 있었으며, 파편 크기(길이)가 커질수록 확률식 기반 해석 방법과 시험기반 해석 방법은 유사한 표적무력화거리와 확률값을 갖게 됨을 알 수 있었다. 그리고 본 연구에서도 선행연구자 연구 결과와 마찬가지로 정치기폭시험 시 파편형 탄두의 파편은 하방향 비산각에 의해 표적 거리 증가에 따라 지면과 다수의 파편이 충돌하게 되어 많은 수의 활성파편이 소실되며, 파편 크기가 작을수록 공기저항 대비 관성력이 작아 표적 거리가 증가할수록 표적판 관통이 가능한 유효파편 수 역시 크게 감소함을 확인할 수 있었다. 본 연구를 통해 향후 파편형 탄두 설계 시 설계 단계부터 정치기폭 시험 시 탄두가 가질 표적무력화거리 성능을 고려한 탄두 설계가 가능해지리라 판단된다.
REFERENCES
- Solomos, G., Larcher, M, Valsamos, G., Karlos, V, and Casadei, F, “A Survey of Computational Models for Blast Induced Human Injuries for Security and Defence Applications,” Publications Office of the European Union, https://publications.jrc.ec.europa.eu/repository/bitstream/JRC119310/00surveyprobits_final-1.pdf, (Accessed 8 September 2020)
- Chang, K., Lee, M., and Ahn, B., “Anti-Personnel Fragment Effects of High Explosive Ammunition with Controlled Fragmentation,” Proc. of the Korea Institute of Military Science and Technology, pp. 835-836, 2015.
-
Baek, J. H., Lee, S. P., Lee, Y. J., and Kim, S. U., “Design of Subminiaturized Natural Fragment Warhead based on the Analysis of Warhead Effectiveness,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 10, pp. 933-941, 2018.
[https://doi.org/10.7736/KSPE.2018.35.10.933]

- Tanapornraweekit, G. and Kulsirikasem, W., “FEM Simulation of HE Blast-Fragmentation Warhead and the Calculation of Lethal Range,” International Journal of Mechanical and Mechatronics Engineering, Vol. 6, No. 6, pp. 1070-1074, 2012.
- Driels, M. R., “Weaponeering: Conventional Weapon System Effectiveness,” American Institute of Aeronautics and Astronautics Reston, 2nd Ed., pp. 703-734, 2004.
-
Hirsch, E., Shapiro, R., and Raz, A., “Layered Pre-Fragmentation Warhead Reveals Strong Shock Wave Effect,” Proc. of the 30th International Symposium on Shock Waves 2, pp. 897-898, 2017.
[https://doi.org/10.1007/978-3-319-44866-4_18]

-
Lloyd, R. M., “Conventional Warhead Systems Physics and Engineering Design,” Progress in Astronautics and Aeronautics, Vol. 179, pp. 19-77, 1998.
[https://doi.org/10.2514/4.472558]


Ph.D. Chief research engineer in LIG Nex1 Co., Ltd. His research interest is nonlinear system dynamics, fault diagnostics, and biomimetic robot.
E-mail: drbaek100@naver.com

Chief research engineer in LIG Nex1 Co., Ltd. His research interest is the system design of a missile and a guided bomb.
E-mail: yhjo1202@gmail.com

Research fellow in LIG Nex1 Co., Ltd. His research interest is the system design of shaped charge warhead.
E-mail: lbu1258@naver.com

Research Director in LIG Nex1 Co., Ltd. His research interest is mechanical system design and management
E-mail: guhyunyu@lignex1.com