다단 딥 드로잉 공정 두께 및 변형률 예측을 위한 심층 신경망 개발
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Deep drawing is one of the most crucial processes in sheet metal forming. As for the multi-stage deep drawing process, because of many design parameters it comprises, predicting process results is a difficult and time-consuming task. In this study, to predict process results, the deep neural network was proposed. Seven design parameters were set and their range was determined with references to empirical formulas. Then, we determined prediction outputs, comprising maximum effective strain, minimum thickness, and bottom mean thickness. Five-hundred sampling points were determined using latin-hypercube sampling method. According to the sampling points, finite element analysis was conducted to achieve process results. From the data rendered by the finite element analysis, the deep neural network was trained. Then, the deep neural network was tested with an additional 80 test samples to evaluate performance, and its performance was compared with radial basis function kernel support vector regression. The results showed that the relative performance of the deep neural network was superior to support vector regression.
Keywords:
Multi-stage deep drawing, Finite element analysis, Deep neural network키워드:
다단 딥 드로잉, 유한요소해석, 심층 신경망1. 서론
딥 드로잉 공정은 이음매가 없는 금속 판재의 중간 부분을 펀치를 이용하여 다이로 밀어 넣어, 깊이가 깊은 원통형 제품이나 각형 제품을 생산하는 공정이다. 딥 드로잉 공정을 통해 제작된 제품은 생산 비용이 저렴하고 생산 속도가 빠르기 때문에, 딥 드로잉 공정은 자동차 산업이나 포장 산업 등에 널리 활용되고 있다. 딥 드로잉 공정은 블랭크 물성, 마찰 조건, 펀치 및 다이 형상과 같은 다양한 설계 변수들에 의해서 복합적으로 영향을 받으며 복잡한 변형 양상을 보인다. 딥 드로잉 공정의 설계 변수 선택에 대한 성형 결과를 파악하기 위해 오랜 기간 연구가 진행되어 왔다.1-3 원형 딥 드로잉 공정의 경우 오랜 기간 동안 연구가 진행되어 왔기 때문에 경험식이 존재한다. 하지만 경험식에서 설계 변수들은 특정값으로 정해지기보다, 상한값과 하한값을 갖는 범위로 표현되기 때문에 해당 범위 내에 포함된 설계 변수들의 선택에 대한 결과를 정량적으로 비교할 수 없다. 또한 공정을 개발할 때, 마찰 계수나 블랭크 물성 등의 조건이 경험식의 환경과 다를 가능성이 존재한다. 따라서 공정을 개발할 경우 실험을 반복적으로 수행하는 경우가 일반적이다. 실험에 드는 비용을 줄이기 위해서, 유한요소해석을 통해 공정 결과를 예측하고 이를 활용하기 위한 연구들이 진행되었다. Manoochehri4 등은 유한요소해석 데이터를 이용하여 성형된 블랭크의 최소 두께를 예측하는 인공신경망(Artificial Neural Network)을 학습시키고, 담금질 기법(Simulated Annealing)을 활용하여 최소 두께를 갖는 설계 변수를 찾는 최적화에 관한 연구를 진행하였다. Kim5 등은 유한요소해석을 기반으로 다단 딥드로잉의 공정 최적화에 관한 연구를 수행하였다. 각 공정마다 담글질 기법과 패턴 검색 기법을 이용하여 최대 유효 변형률(Effective Strain)을 최소화하는 설계 변수들을 결정하였다. Park6 등은 각형 딥 드로잉의 유한요소해석 데이터를 이용하여 블랭크 두께 변화율을 예측하는 심층 신경망(Deep Neural Network)을 개발하였고, 예측 성능을 방사형 기저 함수와 비교하였다.
다단 딥 드로잉 공정의 경우 단일 딥 드로잉 공정과 달리, 실험 계획법(Design of Experiment)을 이용하여 설계 변수를 고려한 공정 결과를 예측하기 어려운데, 이는 고려해야할 설계 변수가 단일 공정에 비해 많기 때문이다. 최근에는 심층 신경망 관련 이론이 발달함에 따라, 다단 공정에서도 심층 신경망을 적용하여 설계 변수의 선택에 대한 공정 결과를 예측하는 것이 가능할 것이라 판단된다. 심층 신경망을 활용한 예측 모델은 연산 속도가 유한요소해석에 비해 월등히 빠르다는 장점이 있다. 다단 딥 드로잉 공정의 결과를 예측하는 신뢰성 있는 심층 신경망이 개발된다면, 설계 공간을 전역적으로 탐색하여 예측된 결과 값을 얻을 수 있기 때문에, 산업적으로 의미 있게 활용될 수 있을 것이다. 하지만, 심층 신경망이 다단 딥 드로잉 공정에 적용된 사례가 없기 때문에 성능에 대한 정량적 평가가 필요하다.
본 연구에서는 해석적 연구를 통해 심층 신경망을 다단 딥드로잉 공정 결과 예측에 적용하였으며, 개발된 모델의 성능을 평가하는 것을 목표로 하였다. 목적 형상을 선정한 후 블랭크 사이즈, 드로잉 비(Drawing Ratio), 설계 공간을 경험식을 참고하여 결정하였다. 이후 설계 변수로 각 공정의 펀치 및 다이 곡률 반경, 마찰 계수 등 7개의 변수를 설정하였고, 공정 결과를 판단할 지표로는 최대 유효 변형률, 최소 두께, 바닥 부분 평균 두께를 고려하였다. 라틴 하이퍼 큐브 샘플링 방법을 이용하여 500개의 샘플링 포인트를 선정하고, 유한요소해석을 수행하였으며, 유한요소해석의 데이터를 활용하여 심층 신경망을 학습시켰다. 다음으로, 심층 신경망의 성능을 대표적인 머신러닝 알고리즘 중 하나인 서포트 벡터 회귀(Support Vector Regression)와 비교하여 평가하였다.
2. 다단 딥 드로잉 공정
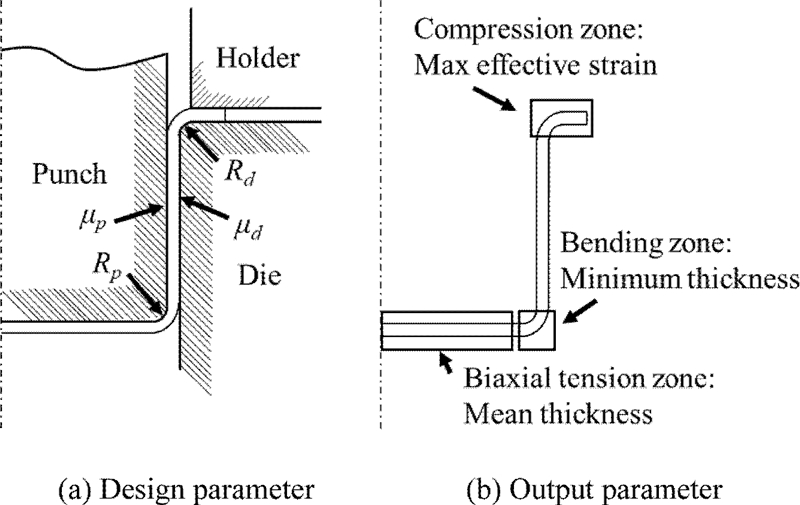
원형 드로잉 공정은 Fig. 1(a)와 같이 펀치, 다이, 블랭크로 구 성되며 최초 드로잉 시에는 주름을 방지하기 위한 목적으로 블 랭크 홀더가 존재한다. 딥 드로잉 공정의 주요 설계 변수는 Fig. 1(a)에 표현되어 있으며, 여기서 Rp는 펀치 곡률 반경, Rd는 다 이 곡률 반경, μp는 펀치와 블랭크 간의 마찰 계수, μd는 다이와 블랭크 간의 마찰 계수이다. 설계 변수들은 복잡하게 상호작용 하여 재료 유입량을 결정한다. 적절하지 않게 결정된 설계 변수 들은 블랭크의 파단이나, 주름(Wrinkle)과 같은 결함을 유발한 다. 따라서, 결함을 유발하지 않도록 설계 변수들을 적절하게 선 택하는 것이 중요하다.
딥 드로잉 공정의 블랭크의 변형은 3가지 지역으로 구분지어 평가할 수 있다. 최초의 블랭크 직경은 성형된 컵의 직경과 같 아져야 하기 때문에, 플랜지 부근에서 블랭크 직경이 줄어들면서 원주 방향으로 압축력을 받는다. Rp 부근에서는 블랭크가 Rp 형 상에 맞게 굽혀지는 동시에 인장력을 받는다. 블랭크 두께는 Rp 부근에서 가장 작은 값을 갖는다. 컵의 바닥 부분에는 펀치의 움직임에 따라 이축 인장력을 받으며, 일반적으로 변형이 거의 발생하지 않는다. 하지만 다단 공정이나, 스테인리스강과 같이 가공 경화(Work Hardening)가 큰 소재의 경우 바닥 부분 두께 감소가 문제가 될 수 있다.7 위와 같은 3가지 변형 지역 모두를 고려하여, 공정의 결과를 평가하기 위한 지표로 Fig. 1(b)와 같 이 최대 유효 변형률, 최소 두께, 바닥 부분 평균 두께를 선정하 였다. 최대 유효 변형률은 블랭크가 받는 압축력에 비례하여 증 가한다. 따라서 다른 조건이 같을 경우에, 최대 유효 변형률이 크면 다이의 마모가 촉진된다. 최소 두께는 블랭크의 파단과 밀 접한 관계가 있으며, 바닥 부분 평균 두께는 파단과 직접적인 관련 없지만 바닥 부분 평균 두께가 감소하는 것은 바람직하지 않은 현상이다.
드로잉 가능성은 드로잉 비를 기준으로 판단할 수 있다. 드로잉 비는 블랭크 직경을 펀치의 직경으로 나눈 값이다. 따라서 드로잉 비가 큰 값을 가질수록 블랭크 직경에 비해 드로잉 깊이가 깊다. 임의의 펀치 직경에 대해 드로잉 가능한 최대 블랭크 직경을 구할 수 있는데, 이때의 드로잉 비를 한계 드로잉 비(Limit Drawing Ratio)라고 한다. 한계 드로잉 비는 블랭크의 물성과 성형 조건에 따라서 차이가 날 수 있으며, 주로 실험을 통해서 값이 결정된다. 드로잉 비가 한계 드로잉 비 이상인 제품의 경우, 다단 드로잉 가공이 필요하게 된다. 다단 공정에서 각단의 드로잉 비는 주로 실험에서 구한 한계 드로잉 비보다 더 작은 값이 선택되어 사용되고 있다. 경험적으로 블랭크 두께와 직경을 고려하여, 각 공정별 드로잉 비를 Table 1과 같이 결정할 수 있다.
3. 유한요소해석 및 샘플링
3.1 목적 형상 및 설계 변수 선정
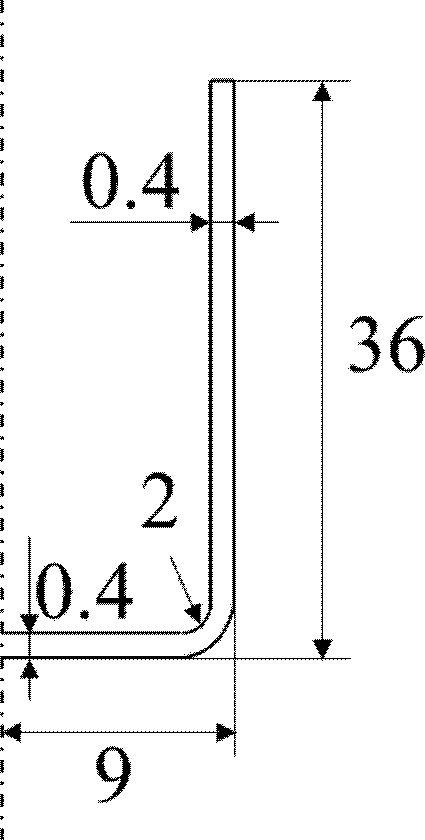
원형 컵의 목적 형상은 Fig. 2와 같으며 재질은 STS304이다. 스테인리스 강재는 크롬 원소를 함유하고 있기 때문에 부식에 대한 저항성이 높아, 배터리 케이스 소재로 자주 사용되고 있다. 블랭크의 가공 경화 모델은 식(1)과 같이 표현되는 Swift 경화 모델을 선택하였고, 식(1)에 사용된 물성값은 Table 2와 같다.
| (1) |
금속의 소성변형은 원자 간의 거리 변화가 아닌 슬립 변형에 의해 일어나기 때문에 소성변형 중에는 체적 일정 법칙이 성립한다. 따라서 Fig. 2의 목적 형상을 바탕으로 체적 일정 법칙을 적용하여, 블랭크 초기 사이즈를 결정할 수 있다. 계산된 블랭크의 직경은 51.26 mm이며 두께는 0.4 mm이다. 다음으로, 드로잉 비를 Table 1을 참고하여 0.58, 0.78, 0.82로 결정하였다.
설계 변수 및 범위는 Table 3과 같다. 설계 변수는 총 7개이며 1, 2 공정의 펀치 곡률 반경 Rp1, Rp2 와 1, 2, 3 공정의 다이곡률 반경 Rd1, Rd2, Rd3와 펀치 블랭크 간의 마찰 계수 μp와 다이 블랭크간 마찰 계수 μd로 구성되어 있다. Table 3에서 마지막 공정인 3번 공정의 펀치의 곡률 반경은 목적 형상에 의해 결정되어지기 때문에 설계 변수로 고려하지 않았다. 또한 펀치와 블랭크 간의 마찰 계수 μp와 블랭크와 다이간 마찰 계수 μd를 각각 다르게 설정하였는데, 이는 Manoochehri4 등의 선행 연구를 참고한 결과이다. 다이 반경 및 펀치 반경은 경험적으로 직전 공정에 비해 같거나 작은 값을 설정하는 것이 일반적이다. 하지만 본 연구에서는 모든 공정에 대해 다이 곡률 반경 및 펀치 곡률 반경의 범위를 같게 설정했는데, 최적의 결과가 항상 경험식의 범위 내에 있다는 보장이 없기 때문에, 경험식의 범위를 약간 벗어난 값도 고려하고자 하였기 때문이다.
3.2 딥 드로잉 공정 모델링
심층 신경망의 예측 성능은 데이터의 양에 의존적이기 때문에, 적정 수준의 데이터의 양을 획득하는 것이 중요하다. 데이터의 양이 적정 수준보다 적을 경우 테스트에서 심층 신경망의 예측 성능이 크게 감소하는 과적합(Overfitting) 현상이 발생한다. 따라서 심층 신경망의 과적합을 방지하기 위해, 500개의 데이터를 사용할 것을 고려하였다. 공정이 3번의 다단 공정으로 이루어져 있기 때문에, 500개의 유한요소해석 결과 데이터를 얻기 위해서는 총 1,500번의 유한요소해석을 수행하여야 한다. 일반적인 경우보다 많은 양의 유한요소해석을 수행하여야 하기 때문에, 해석 시간이 큰 문제점으로 작용할 수 있다. 본 연구에서는 해석에 사용된 요소 수를 줄여 해석 시간을 단축할 목적으로, 2차원 축 대칭 모델을 이용하여 해석을 수행하였다. 2차원 축대칭 모델은 3차원 모델에 비해 시간 비용이 크게 감소하지만, 이방성(Anisotropic)을 고려할 수 없다는 단점이 있다. 이방성으로 인해 귀 생김(Earing)이 발생할 수 있는데, 이는 결과로 고려하지 않았다.
딥 드로잉 공정 모델링 및 해석에는 범용 유한요소해석 소프트웨어 ABAQUS EXPLICT를 이용하였다. 블랭크에는 이중 선형 사변형 저감적분 요소인 CAX4R를 사용하였으며, 두께 방향 5개의 요소를 포함하여 총 3,200개의 요소가 사용되었다. 펀치, 블랭크 홀더, 다이는 강체로 설정하였으며, 모든 접촉 조건에는 면대면(Surface to Surface) 접촉이 사용되었다.
3.3 유한요소해석
샘플링 방법은 모집단인 선정된 설계 공간 내에서 표본을 추출하는 방법을 의미하며, 실험 계획법으로 불리기도 한다. 샘플링 방법은 심층 신경망의 성능에 영향을 끼치기 때문에 적절한 방법을 선택하는 것이 중요하다. 본 연구에서는 샘플링 방법 중 가장 널리 활용되고 있는 라틴 하이퍼큐브(Latin Hypercube) 방법을 이용하였다. 라틴 하이퍼큐브 방법은 무작위성을 유지하면서 샘플링 포인트가 전 범위에서 고르게 추출되기 때문에 효율적인 방법으로 평가받고 있다.9 라틴 하이퍼큐브 방법을 통해 500개의 샘플링 포인트를 결정한 후, 샘플링 포인트에 대한 유한요소해석을 수행하였다. 유한요소해석을 통해 블랭크의 각 노드에서 유효 변형률과 각 노드의 2차원상의 좌표를 획득할 수 있다.
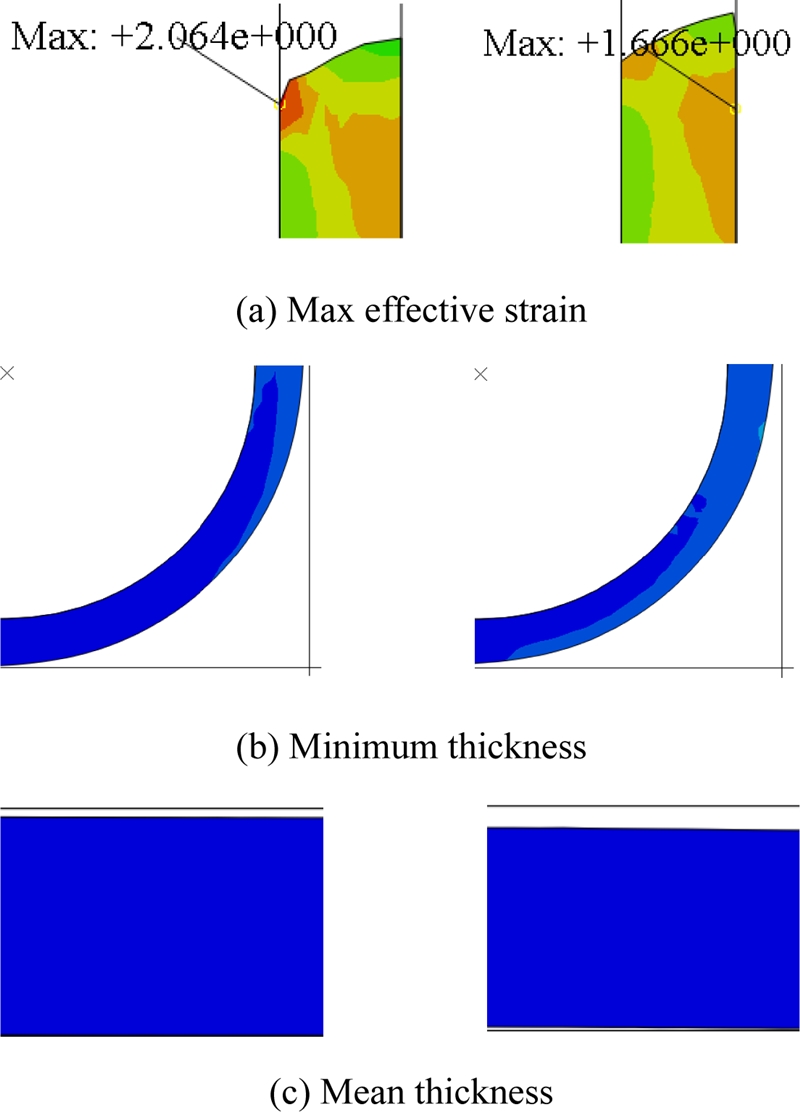
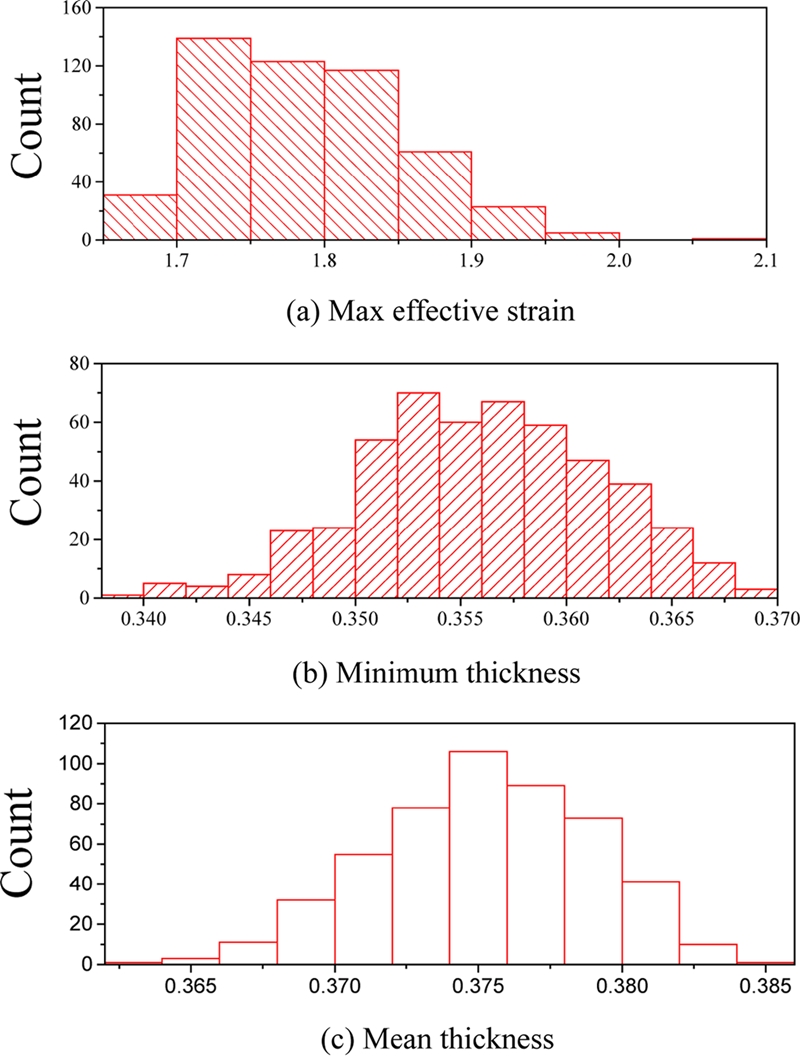
획득한 노드의 좌표를 연산하여 바닥 부분 평균 두께 및 최소 두께를 구할 수 있다. 500번의 유한요소해석에서 설정한 3가지 결과의 최대와 최소의 경우는 Fig. 3과 같고, 500가지 데이터 결과 분포를 Fig. 4와 같이 히스토그램으로(Histogram)으로 나타내었다. Fig. 3에서 최대 유효 변형률의 최솟값과 최댓값은 각각 1.660, 2.064이다. 플랜지 부근에서 소재의 압축이 크게 일어났기 때문에, 일반적인 판재 성형 공정에 비해 큰 값을 가졌다. 최소 두께의 경우 최솟값과 최댓값은 각각 0.340, 0.3685 mm이며 평균 두께의 경우 0.363, 0.384 mm이다. 설계 변수들의 범위는 경험식을 바탕으로 결정됐기 때문에, 두께 감소율이 20%가 넘는 과도한 시닝(Thinning) 현상은 발생하지 않았다. Fig. 4에서 유한요소해석 결과 데이터의 분포를 시각적으로 확인할 수 있다. 설정한 3가지 결과에 모두에서, 평균에 비해 지나치게 높거나 낮은 이상값(Outlier)을 확인할 수 없었다. 따라서 데이터를 별도로 수정하지 않았다.
4. 심층 신경망 예측 모델 개발
4.1 심층 신경망
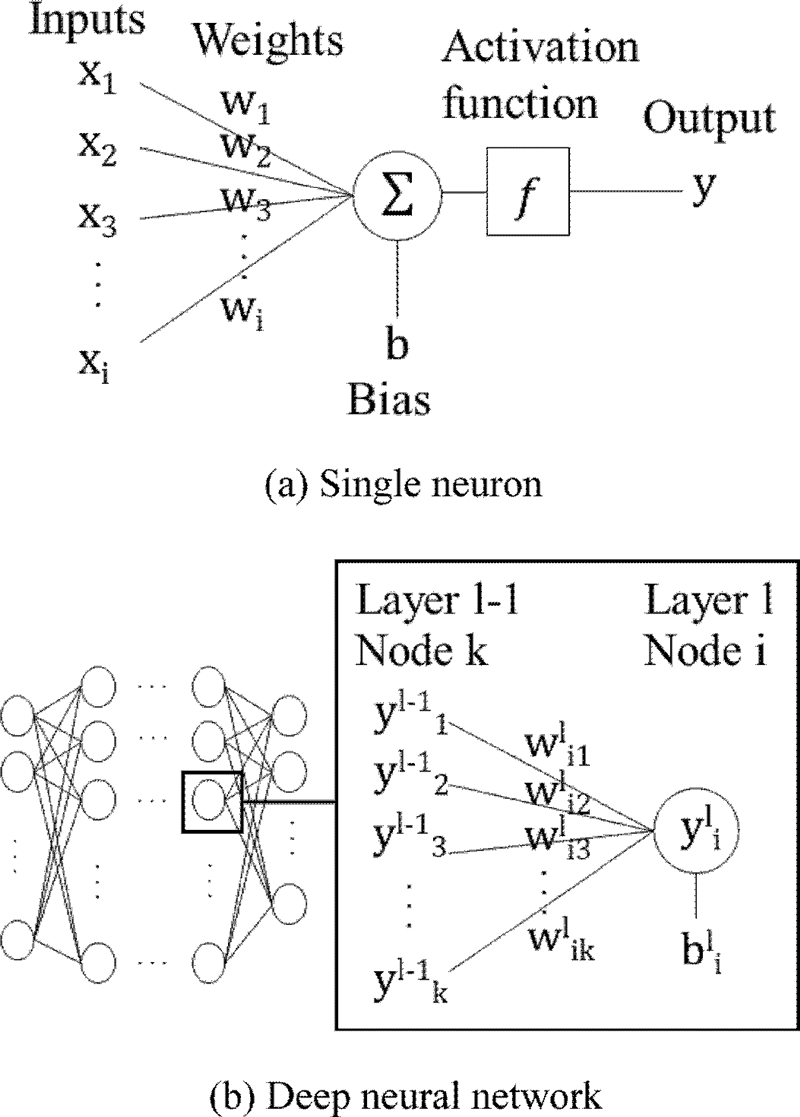
심층 신경망은 2개 이상의 은닉층(Hidden Layer)을 갖는 인공신경망을 의미한다. 인공신경망은 회귀(Regression) 및 분류(Classification) 목적으로 사용되며, 본 연구의 경우 회귀 모델에 해당한다. 심층 신경망은 퍼셉트론(Perceptron)이라고 불리기도하는 단일 신경망을 중첩시킨 것이다. 단일 신경망과 심층 신경망의 구조는 Fig. 5와 같다. 단일 신경망의 연산은 아래 식(2)와 같이 표현할 수 있으며 식(2)에서 xj는 j번 입력값, wj는 j번 가중치, b는 편향, f는 활성 함수, y는 출력값을 의미한다.
| (2) |
심층 신경망에서 직전 레이어에서의 노드들의 출력값은 다음 레이어의 입력값이 되며, 각각 레이어와 노드에서 아래 식(3)과 같은 연산을 수행한다.
| (3) |
식(3)에서 yli는 l번 레이어 i번 노드에서의 출력값을 의미하며, wlij는 l번 레이어 i번 노드와 l-1번 레이어에서 j번 노드 사이의 가중치를 의미하며, bli는 l번 레이어의 i번 노드에서의 편향을 의미한다. 심층 신경망에서 가중치와 편향의 값은 지도 학습(Supervised Learning)이 진행됨에 따라 업데이트된다. 학습이 끝나면, 심층 신경망에서 결정된 가중치와 편향값을 통해, 학습 데이터 외의 입력값에 대한 예측값을 얻을 수 있다.
지도 학습은 학습 데이터의 입력값을 심층 신경망에 연산한 출력값과 정답으로 설정된 학습 데이터의 출력값의 차이인 손실 함수를 최소화하는 방향으로 가중치와 편향의 값을 업데이트하는 것을 의미한다. 손실 함수로는 일반적으로 평균 제곱 오차(Mean Squared Error) 또는 평균 절대 오차(Mean Absolute Error)가 사용된다. 심층 신경망에서 가중치를 업데이트하는 방법 중 가장 널리 쓰이고 있는 알고리즘은 오류 역전파(Backpropagation)이다. 오류 역전파 알고리즘은 복잡한 문제에서 효율적이라고 알려져 있다.10 오류 역전파 알고리즘은 순전파를 통해 오류를 계산하고, 역 방향으로 연쇄 법칙(Chain Rule)을 적용하여 기울기 값을 구하고, 기울기값을 바탕으로 가중치를 업데이트한다. 비선형 활성 함수는 중첩되어 사용될 경우, 기울기값이 빠르게 0으로 수렴하는 기울기 소실(Vanishing Gradient) 현상이 발생하여 가중치를 업데이트할 수 없다. 활성 함수로 Relu (Rectified Linear Unit)와 같은 선형 함수를 선택하면, 중첩되어 사용하여도 기울기 소실 문제가 발생하지 않는다. 따라서 깊은 구조의 신경망의 경우 활성 함수로 선형 함수를 사용한다.
심층 신경망 구현에는 오픈소스 라이브러리 Keras가 사용되었다. 학습 방법은 오류 역전파, 손실 함수는 평균 제곱 오차, 활성 함수는 Relu, 최적화 방법은 Adam, 가중치 초기화 방법은 Glorot이 사용되었다.
4.2 데이터 변환 및 신경망 학습
유한요소해석을 통해 얻은 데이터값을 심층 신경망에 사용하기 위해서, 입력 변수와 출력값에 대해 최소 최대 변환(Min-Max Scaling)을 적용하였다. 최소 최대 변환은 아래 식(4)와 같은 식으로 표현할 수 있다.
| (4) |
식(4)에서 x는 변환 전, x*는 변환 후의 데이터를 의미하며 i와 j는 각각 데이터의 행과 열을 의미한다. 최소 최대 변환 후에는 데이터의 각각의 열에 대해서 0과 1 사이 값으로 변환된다. 이때 0은 최솟값이며, 1이 최댓값이다. 본 연구의 경우 데이터의 열은 설계 변수 7개와 3개의 결과값의 합인 10개로 구성되며, 행은 전체 샘플링 수와 동일한 500개로 구성되어 있다.
데이터의 크기를 변환시키는 이유는 학습의 효율성을 높이기 위함이다. 입력 또는 출력 변수간의 크기 차이가 심하게 난다면, 크기가 큰 변수가 학습의 목적 함수에 끼치는 영향력이 지배적이기 때문에, 수렴 속도가 느려지고 지역적인 최적점(Local Optimum Point)에 수렴할 가능성이 높아진다.
변환된 데이터를 이용하여 심층 신경망의 학습을 진행하기 앞서 하이퍼 파라미터(Hyper Parameter)를 설정해주어야 한다. 하이퍼 파라미터는 사용자가 직접 설정해야 하는 값이며 모델 성능에 영향을 끼친다. 하이퍼 파라미터의 종류로는 신경망 노드 및 레이어 수, 전체 데이터가 학습에 사용된 수를 의미하는 에폭(Epoch), 학습의 보폭(Step Size)을 결정하는 학습률(Learning Rate) 등이 있다. 하이퍼 파라미터는 히든 레이어 3개, 레이어별 노드수 400개, 에폭 500, 학습률은 0.01로 시행착오(Trial and Error)를 통해 결정하였다.
4.3 심층 신경망 성능 평가
심층 신경망의 성능을 평가하기 위해 회귀 모델에서 자주 사용되고 있는 성능 평가 지표인 RMSE (Root Mean Square Error), MAE (Mean Absolute Error), R2 (Coefficient of Determination)을 고려하였다. 각각의 성능 지표에 대해 식(5)부터 식(7)과 같이 표현할 수 있다. 이때 yj는 실제 값, ŷj는 회귀 모델의 예측값, ȳj는 실제 값의 평균이다.
| (5) |
| (6) |
| (7) |
RMSE, MAE는 낮은 값일수록, R2는 높은 값일수록 회귀 모델의 예측 성능이 우수하다고 평가할 수 있다. RMSE는 오차값이 평균으로 나누어지기 전에 제곱해지기 때문에, MAE에 비해 큰 오차에 가중치를 주게 된다. R2는 모델의 설명력을 의미하며 0과 1 사이 값을 갖는다. 평균값의 오차에 비해 예측값의 오차가 작을수록, R2값은 1에 근접하게 된다. 또한 실제값 대 예측값 그래프(Actual vs Predicted Plot)를 고려하였다. 실제값 대 예측값 그래프는 실제값과 예측값의 산점도(Scattering Plot)이며, 점들이 직선상에 가까운 정도를 기준으로 회귀 모델의 예측 성능을 시각적으로 판단할 수 있다.
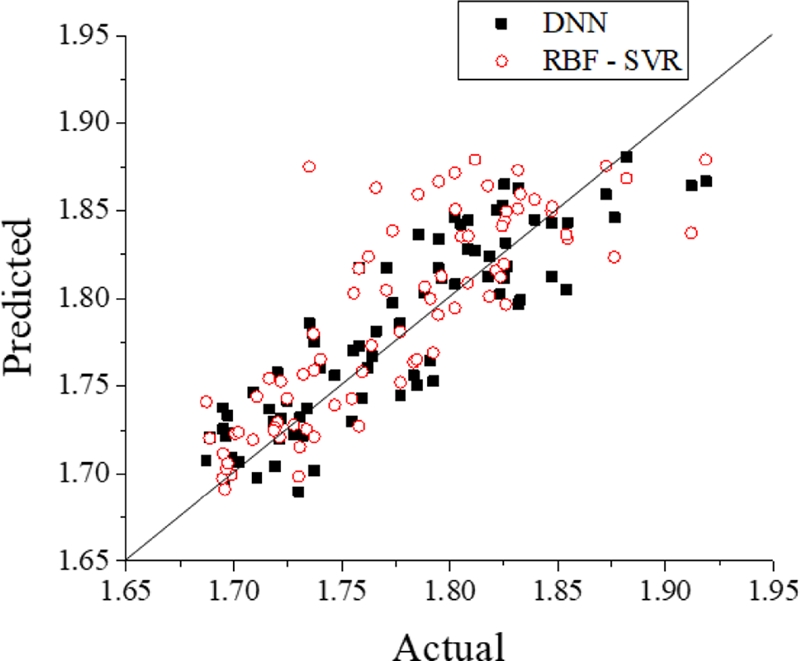
80개의 랜덤 샘플 포인트에 대해 유한요소해석을 추가적으로 수행하여, 테스트를 위해 사용하였다. 심층 신경망의 상대적인 성능을 평가를 위해 대표적인 머신러닝 알고리즘인 방사형 기저 함수 커널 서포트 벡터 회귀(Radial Basis Function Kernel Support Vector Regression)을 고려하였다. 서포트 벡터 회귀의 하이퍼 파라미터는 그리드 서치(Grid Search)를 이용하여 결정했다. 최대 유효 변형률의 테스트 결과를 Fig. 6의 그래프 및 Table 4에 나타내었다. Fig. 6에서 심층 신경망의 점들이 직선에 더 가까운 경향을 확인할 수 있다. Table 4에서 심층 신경망의 경우 RMSE 0.0280, MAE 0.0235, R2 0.7478를 나타냈으며, 서포트 벡터 회귀의 경우 RMSE 0.0362, MAE 0.0264, R2 0.5794로 나타났다. 심층 신경망은 서포트 벡터 회귀에 비해 RMSE, MAE가 더 낮고 R2가 높기 때문에 더 우수한 모델이라고 평가할 수 있다.
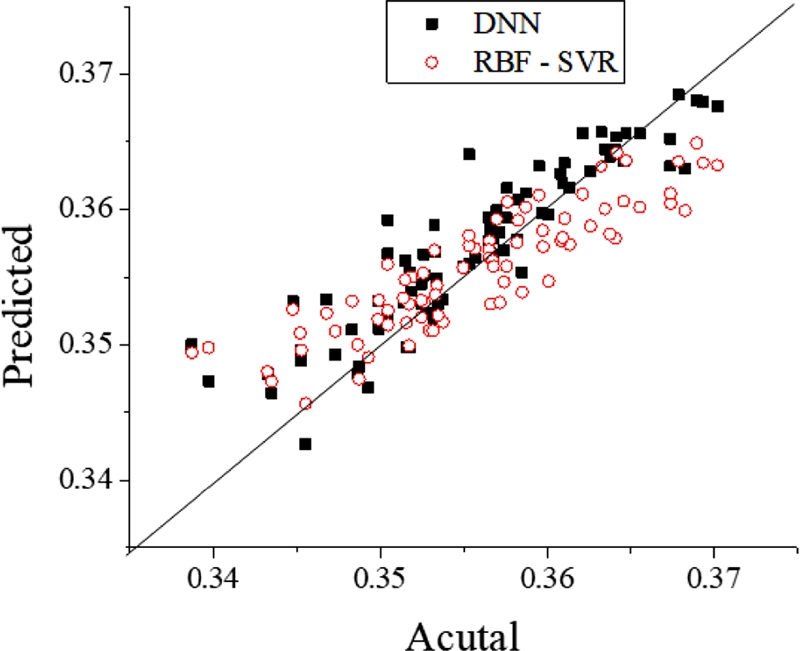
최소 두께 테스트 결과는 Fig. 7과 Table 5에 나타나 있다. Fig. 7은 Fig. 6과 달리 심층 신경망과 서포트 벡터 회귀와 비슷한 경향을 보여 시각적으로 상대적 성능을 파악하기 어려웠다. Table 5에서 심층 신경망의 성능은 RMSE 0.0033, MAE 0.0024, R2 0.7780를 나타냈으며, 서포트 벡터 회귀의 경우 RMSE 0.0038, MAE 0.0030, R2 0.7136를 나타냈다. 따라서 최소 두께 역시 심층 신경망의 예측 성능이 우수하다고 평가할 수 있다.
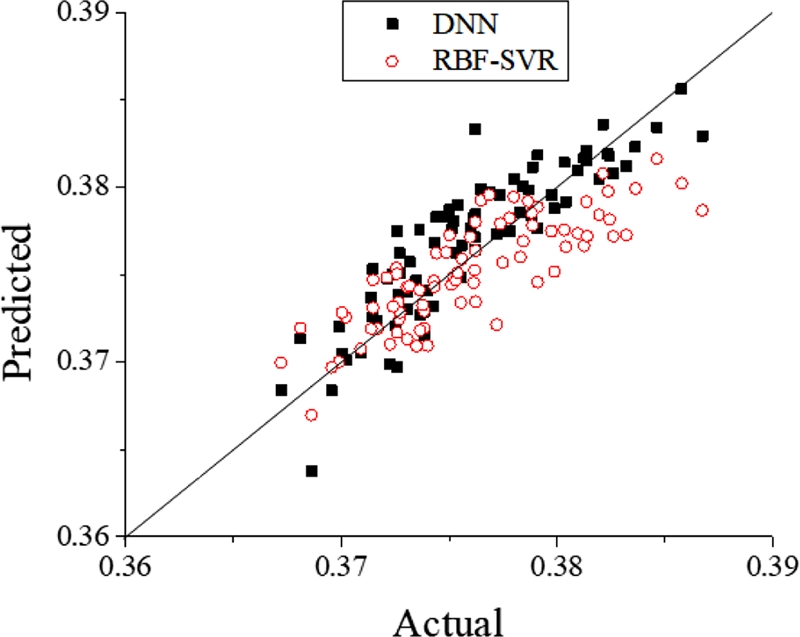
바닥 부분 평균 두께 테스트 결과는 Fig. 8과 Table 6에 나타나 있다. Fig. 8은 Fig. 7과 비슷하게, 시각적으로 심층 신경망과 상대적 성능을 파악하기 어려웠다. Table 6에서 심층 신경망의 성능은 RMSE 0.0022, MAE 0.0017, R2 0.7344를 나타냈으며, 서포트 벡터 회귀의 경우 RMSE 0.0026, MAE 0.0020, R2 0.6285를 나타냈다. 따라서 바닥 부분 평균 두께 테스트에서 역시 심층 신경망의 예측 성능이 우수하다고 평가할 수 있다.
Table 7은 3가지 테스트 결과 각각에서 최대 상대 오차의 값과 설계 변수 조건을 나타낸다. 설계 변수 조건은 각각 달랐지만, 3가지 테스트의 경우 공통적으로 Rd3가 Rd2에 비해 증가하였으며 μp와 μd의 차이가 0.09보다 크게 나타났다. 해당 설계 변수 부근에서 각각의 결과값이 민감하게 변했기 때문에 최대 상대 오차를 가진 것으로 판단된다. 3가지 테스트 경우 모두에서, 심층 신경망이 서포트 벡터 회귀에 비해 더 우수한 예측 성능을 가진 것을 확인할 수 있었다. 결론적으로 심층 신경망은 다단딥 드로잉 공정 결과 예측에 적합한 모델이라고 판단할 수 있다. 하지만 3가지 테스트 모두에서 R2값이 0.8 이하였고, Table 7에서 최대 상대 오차가 각각 3.36, 3.33, 1.89%였기 때문에 심층 신경망의 예측 결과는 실제 유한요소해석 데이터와 다소 차이가 있다고 판단된다. 심층 신경망은 유한요소해석 데이터를 기반으로 하고 있고, 유한요소해석은 실험과 달리 외부 환경 요인이 개입할 수 없기 때문에, 심층 신경망의 성능은 더 좋아질 여지가 있다. 심층 신경망은 데이터의 양이 많아질수록 성능이 좋아진다고 알려져 있다. 따라서, 설계 공간에 해당하는 유한요소해석 데이터를 추가한다면, 성능이 더 높아질 것이라 판단할 수 있다. 개발된 심층 신경망의 예측값은 유한요소해석과 다소 차이가 존재하지만, 심층 신경망의 연산 속도는 유한요소해석에 비해 월등히 빠르다는 장점이 있다. 따라서 심층 신경망의 예측값을 통해 설계 공간을 전역적 탐색하는 것이 가능하기 때문에 개발된 심층 신경망은 대체 모델 기반 최적화(Surrogate Based Optimization) 등에 활용될 수 있을 것이다.
5. 결론
본 연구에서는 다단 딥 드로잉 공정의 결과인 블랭크의 최대 유효 변형률, 최소 두께, 바닥 부분 평균 두께 예측을 위한 심층 신경망을 제안하였으며 이를 구현하였다. 선정된 설계 공간에서, 라틴 하이퍼 큐브 방법을 이용한 500개의 샘플링 포인트에 대해 유한요소해석을 수행하였고, 유한요소해석 데이터를 이용하여 심층 신경망을 학습시켰다. 추가적으로, 80개의 랜덤 샘플링 포인트에 대한 유한요소해석을 통해 테스트 데이터를 획득하였으며, 해당 테스트 데이터를 활용하여 심층 신경망의 상대적 성능을 서포트 벡터 회귀와 비교하여 정량적으로 평가하였다. 테스트 결과 RMSE, MAE, R2 지표에서, 심층 신경망의 성능이 서포트 벡터 회귀에 비해 더 우수함을 확인하였다. 개발된 심층 신경망의 예측 결과는 유한요소해석 데이터와 다소 차이가 존재하지만, 대체 모델 기반 최적화 등에 활용할 수 있을 것이다. 추가적인 연구로, 드로잉 비 및 아이어닝(Ironing) 률을 변수로 고려한 심층 신경망에 관한 연구를 수행할 계획이다.
Acknowledgments
이 논문은 정부(미래창조과학부)의 재원으로 한국연구재단의 선도연구센터지원사업(No. 2019R1A5A6099595)의 지원을 받아 수행된 연구임. 이에 관계자 여러분께 감사드립니다.
REFERENCES
-
Yossifon, S., Sweeney, K., Ahmetoglu, M., and Altan, T., “On the Acceptable Blank-Holder Force Range in the Deep-Drawing Process,” Journal of Materials Processing Technology, Vol. 33, No. 1-2, pp. 175-194, 1992.
[https://doi.org/10.1016/0924-0136(92)90318-M]

-
Browne, M. and Hillery, M., “Optimising the Variables When Deep-Drawing C.R.1 Cups,” Journal of Materials Processing Technology, Vol. 136, Nos. 1-3, pp. 64-71, 2003.
[https://doi.org/10.1016/S0924-0136(02)00934-2]

-
Colgan, M. and Monaghan, J., “Deep Drawing Process: Analysis and Experiment,” Journal of Materials Processing Technology, Vol. 132, Nos. 1-3, pp. 35-41, 2003.
[https://doi.org/10.1016/S0924-0136(02)00253-4]

-
Manoochehri, M. and Kolahan, F., “Integration of Artificial Neural Network and Simulated Annealing Algorithm to Optimize Deep Drawing Process,” The International Journal of Advanced Manufacturing Technology, Vol. 73, Nos. 1-4, pp. 241-249, 2014.
[https://doi.org/10.1007/s00170-014-5788-5]

-
Kim, H. K. and Hong, S. K., “FEM-Based Optimum Design of Multi-Stage Deep Drawing Process of Molybdenum Sheet,” Journal of Materials Processing Technology, Vol. 184, Nos. 1-3, pp. 354-362, 2007.
[https://doi.org/10.1016/j.jmatprotec.2006.12.001]

- Park, K., Park, J., Kwak, M., and Kang, B., “Prediction of Blank Thickness Variation in a Deep Drawing Process Using Deep Neural Network,” Transactions of Materials Processing, Vol. 29, No. 2, pp. 89-96, 2020.
-
Lee, J., Kim, J., and Won, S., “Influence of Process Design Scheme on Product Qualities in Cylindrical Cup Drawing,” Transactions of Materials Process, Vol. 11, No. 8, pp. 716-723, 2002.
[https://doi.org/10.5228/KSPP.2002.11.8.716]

-
Belali-Owsia, M., Bakhshi-Jooybari, M., Hosseinipour, S., and Gorji, A., “A New Process of Forming Metallic Bipolar Plates for PEM Fuel Cell with Pin-Type Pattern,” The International Journal of Advanced Manufacturing Technology, Vol. 77, Nos. 5-8, pp. 1281-1293, 2015.
[https://doi.org/10.1007/s00170-014-6563-3]

-
Stein, M., “Large Sample Properties of Simulations Using Latin Hypercube Sampling,” Technometrics, Vol. 29, No. 2, pp. 143-151, 1987.
[https://doi.org/10.1080/00401706.1987.10488205]

-
Montavon, G., Orr, G., and Müller, K. R., “Neural Networks: Tricks of the Trade,” Springer, 2nd Ed., pp. 9-48, 2012.
[https://doi.org/10.1007/978-3-642-35289-8]


M.Sc. candidate in the Department of Aerospace Engineering, Pusan National University. His research interest is CAE and machine learning.
E-mail: ktshd_@naver.com

Associated research engineer in the Industrial Liaison Innovation Center, His research interest is CAE, sheet metal forming, and machine learning.
E-mail: lgslgsl@naver.com

M.Sc. candidate in the Department of Aerospace Engineering, Pusan National University. His research interest is CAE.
E-mail: kwoak0987@naver.com

Professor in the Department of Aerospace Engineering, Pusan National University. His research interest include materials processing, FEM, and flexibly-reconfigurable roll forming technology.
E-mail: bskang@pusan.ac.kr