초고속 터보기계의 회전 속도에 대한 공력-소음 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study is to numerically investigate the Aero-Acoustics of Turbocharger compressor. The turbocharger compressor is high-speed turbomachinery that rotates faster than 200,000 RPM. The Aero-Acoustics with five different rotational speeds (120,000, 150,000, 180,000, 200,000, and 220,000 RPM) is used herein. The fluid domain is designed by CATIA V5R21 and analyzed by ANSYS FLUENT V19.1 with compressible momentum equation. The Pressure-velocity coupling method of the solver is the coupled algorithm and calculated by a pressure-based method. Numerical analysis of the aero-acoustics by broadband noise sources model provides calculated sound-source and acoustic-level based on steady RANS. At the industrial site, it is important to quickly analyze the noise source. APL (Acoustic Power Level) with five different rotational speeds and sound characteristics based on flow factor at the compressor wheel was numerically calculated for the noise-based design. The maximum APL is located at blade tips in case of 120,000, 150,000 and 180,000 RPM. In the case of 200,000 RPM, the maximum APL is located at splitter tips. At more than 220,000 RPM, the maximum APL is located at the balancing cutting section of the wheel. In order to optimally design the high-speed turbomachinery, cutting sections and side locations of the wheel are essential factors to reduce physical noise.
Keywords:
High-speed turbomachinery, Centrifugal compressor, Virtual fluid dynamics, Virtual aero-acoustics, Flow noise, Broadband noise source model키워드:
초고속 터보기계, 원심 압축기, 가상유체역학, 가상 공력음향학, 유동소음, 광대역 소음원 모델1. 서론
항공기 기술에서 유래한 터보차저는 최대 200,000 RPM 이상으로 회전하는 초고속 터보기계이다. 최근 전산 유체 역학(Computational Fluid Dynamics, CFD)의 급격한 발전과 더불어 터보기계의 성능은 기하급수적으로 성장하였다. 이전 연구인 Song1의 연구를 통해 터보기계 유동해석의 타당성은 검증하였다. Gwak2과 Han3 등의 연구에서는 적절한 유동해석 모델링을 검증하였고, 형상 및 구조를 변경하여 터보차저 성능 향상을 위해 노력하였다.
터보기계의 일종인 터보차저 압축기에서는 압축비가 가장 중요한 설계인자로 평가되어왔다. 하지만 최근 도심 항공기(Urban Air Mobility, UAM)와 개인 항공기(Personal Air Vehicle, PAV) 시장이 도래함에 따라 운송기계의 고성능화, 경량화 및 승차감은 더욱 중요시 여겨지고 있다. 따라서 이러한 요소들에 직접적으로 영향을 미치는 소음 및 진동 연구는 주요 연구분야로 새롭게 각광받고 있다. 그동안 터보기계의 유동소음을 개선하기 위해 다양한 연구가 수행되었다. Lee4는 본 연구에서 사용된 터보차저와 유사한 모델을 활용하여 유동소음에 대한 시험을 진행하였고, 소음의 특성을 파악하였다. Park5은 압축기 휠의 다양한 컷팅 형상을 기반으로 연구를 진행하였고, Park6은 노이즈맵을 작성하여 적정 운전 영역을 분석하였다. Park7은 축의 회전수와 압축기 휠의 날개수의 곱에 해당하는 주파수 성분을 갖는 BPF (Blade Passing Frequency) 소음에 대한 연구를 진행하였다. 터보차저 회전수가 증가함에 따라 증가하는 기류음(Flow-Induced Noise) 연구는 Kang8에 의해 수행되었으며, 이와 유사한 입구 덕트의 형상이나 호스 길이9 및 단면 그루브 형상10에 따른 소음 연구도 진행되었다.
하지만 대부분의 터보차저 유동소음 연구는 시험에 의해 수행되었다. 개발업체에서도 터보차저의 성능연구는 해석과 시험을 병행하고 있지만, 소음연구는 전적으로 시험에 의존하는 실정이다. 일반적으로 유동소음 예측은 Lighthill11의 음향상사법에 기초하여 유도된 Ffowcs Williams and Hawkings Equation12 (이하 FW-H식)으로 계산된다. Lighthill의 음향상사법을 임의의 속도로 운동하는 강체의 경계조건을 포함할 수 있도록 발전시킨 FW-H식은 도플러 효과를 고려할 수 있어서 유동소음 연구에 다양하게 활용된다. FW-H식은 중심축을 기준으로 회전하는 터보기계에도 적용이 가능하도록 Williams13에 의해 연구되었다. 실제로 FW-H식은 Kim14과 Mo15의 연구와 같이 소음의 종류 및 강도 등을 파악하는데 널리 활용되지만 대부분은 수천 RPM 이하의 저속 터보기계 연구에 활용된다. Broatch16는 소음 특성에 대해 상용 소프트웨어인 STAR-CCM+을 활용하여 계산하였으나, 소음 연구의 특성상 비정상 해석을 전제로 계산되기 때문에 200,000 RPM(3,666 RPS) 이상으로 고속 회전하는 터보차저 압축기에는 많은 시간이 요구된다. 따라서 개발 및 생산 업체에서도 큰 비용 소모를 감수하고 전적으로 시험에 의존하고 있다. 하지만 실제 산업 현장에서는 소음 특성을 연구하는 일보다 신속하게 소음 발생을 파악하여, 저소음 후보군을 선택하는 것이 중요할 수 있다. 특히 적절한 저소음 후보군을 선택하여 다양한 설계 인자에 대한 소음 분포를 연구하는 일은 신속한 제품 개발에 더욱 의미 있는 과정으로 보인다.
따라서 본 연구에서는 시험적 상관관계를 사용한 Steady RANS (Reynolds Averaged Navier-Stoke식)의 평균적 유동해에 기초하여 음향방사(Acoustic Radiation)를 평가하는 ANSYS FLUENT사의 Broadband Noise Source Model을 사용하여 Acoustic Power Level(이하 APL)을 수치적으로 계산하였다. 터보차저 압축기의 5가지 실제 설계 회전수에 대한 APL 분석을 통해 광대역 소음원의 위치 및 크기를 분석하였다. 본 연구에서 사용된 5가지 회전수는 터보차저 제작사에서 실제 시험 및 해석 연구를 수행할 때 사용되는 회전수를 활용하였다.
2. 공력소음 수치해석 및 설계조건
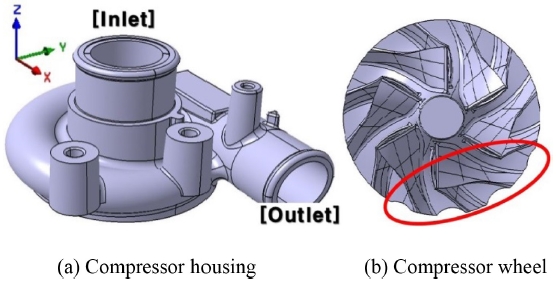
본 연구는 글로벌 완성차 업체인 ㈜H사의 S모델에 적용되는 2.0 L급 터보차저 압축기를 활용하였다. Fig. 1은 국내 터보차저 선도기업인 ㈜K사에서 개발한 터보차저 압축기의 형상이다. Fig. 1(a)는 터보차저 압축기 하우징의 형상이며, Fig. 1(b)는 하우징 내부의 압축기 휠의 형상이다. 압축기 휠의 직경은 40, 높이는 18.2 mm이며, 주날개(Main Blade)와 보조날개(Split Vane)가 각각 6개씩 총 12개의 날개로 구성되어 있다. 압축기 휠의 형상에서 컷팅부(Fig. 1(b)의 적색)를 확인할 수 있는데, 이는 밸런싱 컷팅의 형상이다. 밸런싱 컷팅은 주조(Casting)로 제작되는 압축기 휠의 특성상 질량 불균형 현상이 발생할 수 있기 때문에, 고속에서의 파손 및 진동을 고려하여 균형을 맞춰주기 위해 필수적인 작업이다. 본 연구에서는 컷팅부가 소음에 미치는 영향을 고려하기 위해 컷팅부를 포함한 실제 압축기의 형상을 3D 스캐닝하여 사용하였다.
안정화된 대기 유입의 표현과 압축 이후 유출 공기를 전 데이터(Total Data)로 표현하기 위해 실제 형상으로부터 출구를 0.5 m, 입구를 0.8 m로 연장하였다. 입구의 경우 0.8 m 이하에서도 안정적인 전 데이터 형태로 계산되지만, 기존연구4와 비교 및 ㈜K사의 소음 측정장비4를 이용할 수 있도록 0.8m로 위치 설정하였다. 유동장 입·출구 길이와 형상 수정에는 CATIA V5R21을 활용하였다. 압축기의 입구 방향(Fig. 1(a)의 상부)을 Z축, 출구 방향을 X축으로 좌표를 설정하여 ANSYS Design Modeler V19.1 Geometry로 유동장을 나타내었다.
2.1 격자 생성
터보기계는 축대칭 구조로 해석연구를 진행할 경우 회전대칭기법을 활용한다. 하지만 본 연구 대상인 터보차저 압축기 휠은 컷팅부가 존재하며, 하우징 형상이 비대칭 구조로 회전대칭 기법을 사용할 수 없다. 또한 매질을 통한 전파(Propagation)를 고려하기 위해서 공간 해상도를 높이는 일은 필수적이다. 따라서 본 연구는 전체 유동장에 대한 격자를 직접 생성하였다.
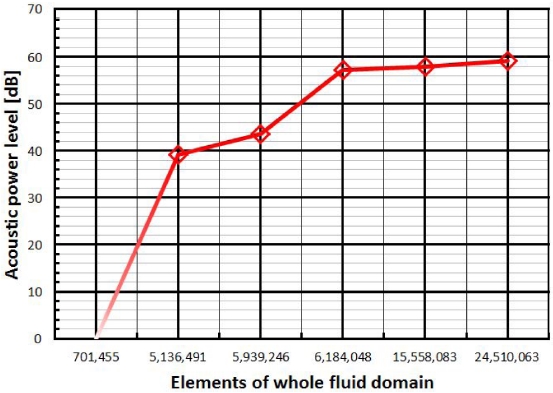
격자생성은 ANSYS MESH V19.1을 사용하였다. SST 난류 모델 특성상 별도의 벽함수 모델을 사용하지 않았기 때문에 Y+는 압축기 휠의 성능에 가장 큰 영향을 미치는 블레이드 팁(Blade Tip)을 기준으로 6.423 이하의 값을 유지하며, 하우징과 휠의 형상을 고려하여 사각격자와 삼각격자를 적절히 혼합하여 사용하였다. 생성된 격자에 대해 출구 음압의 변화를 살피며 격자 의존도 검사를 진행하였다. 70만개 이하의 격자를 생성하였을 때는 유동이 발산하며 계산이 제대로 수렴되지 않았으며, 600만개 미만의 격자에서는 격자에 대한 의존도가 매우 높았다. 1,500만개와 2,400만개의 격자는 수퍼 컴퓨터를 활용하여 계산하였으며, 각각 1.2, 3.25%의 APL 오차가 발생하였다. 해석 시간 및 효율성을 고려하여 610만개의 격자가 적절하다고 판단해 해당 격자를 활용하였다. 격자 의존도 검사의 결과는 Fig. 2에서 차트로 도시하였다.
2.2 VFD 수치해석
터보차저 압축기의 작동유체(공기)는 최저속도인 120,000 RPM 에서도 0.72의 마하수(Mach No)를 보임으로 압축성 유동으로 고려하였다. 밀도 변화는 이상기체의 거동을 따르도록 설정하였고, 중력항을 제외한 압축성 운동량 방정식에 이상기체식을 적용하여 아래 식(1)과 식(2)를 유도하였다.
| (1) |
| (2) |
여기서, Pij: Stress Tensor [Pa], u: Velocity Vector [m/s], T: Temperature [K], R: Gas Constant [kJ kg-1K-1]
식(1)은 각 요소에서 계산된 밀도를 반영하는 질량 보존 방정식이며, 식(2)는 운동량 방정식이다. 두 방정식을 결합하여 유도한 방정식은 압력 기반 방법(Pressure-Based Method)으로 처리했다. Pressure-velocity Coupling 기법으로 Coupled Algorithm을 적용하여 운동량 방정식의 속도와 압력 변동(Pressure Fluctuation)을 연립하여 동시에 계산하였다. 압력 변동에 대한 셀 미분 값은 Least Squares Cell Based 방식으로 처리하였다. 대류항의 이산화 기법은 2차 상류 차분화(Second Order Upwind) 기법으로 계산하였다.
실제 터보차저 압축기의 운전 상황을 구현하기 위해 초기 경계조건으로 입구와 출구 모두 대기압으로 설계하였다. 5가지 회전수에 대한 유동해석을 수행하였고, 해석의 수렴성을 위해 출구 질량 유량을 추가적으로 고려하여 연속 방정식을 만족시켰다. 질량유량은 개발 및 제작사인 ㈜K사의 시험 데이터를 활용하였으며, 휠의 회전 운동을 표현하기 위해 MRF (Multiple Reference Frame) 기법을 사용하여 유체가 회전하는 효과를 부여하였다.
난류 모델은 벽면 근처에서 발생하는 복잡한 유동 현상과 완전 발달된(Fully-Developed) 유동장에서도 뛰어난 정확성을 보일 수 있도록 고안된, k-ω SST (Shear Stress Transport) 난류 모델을 사용하였다. SST 난류 모델은 k-ω 모델을 개선한 모델로 난류 점성으로 정의된 난류 전단응력 수송방정식을 처리하는 모델이다.17 k-ω SST 난류 모델은 터보기계 연구에 주로 사용되며, 국소 와류를 예측에 강점이 있다. 유동해석에서 활용된 경계조건과 유체의 물성치 정보는 Table 1로 정리하였다.
2.3 Broadband Noise Source 수치해석
소음 해석은 관심 주파수 영역인 20 Hz-20 kHZ 범위에 대한 분석이 중요하다. 이는 실제로 인간이 들을 수 있는 소음의 범위인 가청주파수 범위이다. 따라서 유동소음은 근본적으로 비정상(Unsteady) 유동을 다루며, CFD를 활용하여 음원 영역의 유동장에 대한 계산을 마친 후 해석적 해를 활용하여 소음 전파과정을 계산하는 FW-H Model12 등의 음원·전파 분리 계산법(Segregated Source-Propagation Methods, SSPM)을 활용한다.
하지만 산업 현장에서는 정량적인 소음의 종류 및 강도 분석보다는 효율적으로 소음원(Noise Source)을 파악하여, 형상 및 작동조건에 따른 대략적인 소음의 크기와 특징을 빠르게 분석하는 것이 중요할 때가 있다. 따라서 본 연구에서는 시험적 상관관계를 사용하여 Steady RANS의 평균적 유동해에 기초하여 음향방사(Acoustic Radiation)를 평가하는 ANSYS FLUENT사의 Broadband Noise Source Model을 사용하여 Acoustic Power Level(이하 APL)을 계산하였다.
APL은 소리의 강도를 나타내는 물리량인 음향출력을 로그 규모로 표현한 것이다. APL은 식(3)과 같이 나타낼 수 있으며, 음향출력은 식(4)와 같이 음향강도의 면적분으로 정의한다.
| (3) |
| (4) |
여기서, P: Sound Power (Acoustic Power) [W], P0: Reference Sound Power [W], A: Area [m2], I: Sound Intensity [W/m2]
Song1에서 살펴본 터보차저 압축기 휠의 5가지 회전수에 따른 소음 특성을 분석하기 위하여 각 회전수의 APL을 계산하였다. 정밀한 계산으로 해석의 신뢰성을 높이기 위해 KISTI에서 제공하는 Intel Xeon Phi 7250(KNL) 모델 68코어 16 GB*6, 6Ch per CPU의 성능을 가진 수퍼 컴퓨터를 사용하였다. 상용 CFD-Code인 ANSYS FLUENT V19.1로 유동해석을 진행 후 FLUENT의 Broadband Noise Source Model을 사용하여 APL을 계산하였다.
3. 결과 및 고찰
본 연구에서는 시험적 상관관계를 통해 Steady RANS의 평균적 유동해에 기초하여 음향방사를 평가하는 BNS Model을 사용하여, APL을 계산 하였다. Sharland18의 연구에 의하면 축류팬의 소음은 특정 주파수에서 최곳값을 나타내는 이산소음(Discrete Noise)과 저주파에서 고주파에 걸쳐진 소음으로 나타내는 광역소음(Broadband Noise)로 구분된다. 산업 현장에서 불필요한 비용을 낭비하지 않고, 설계 단계별 적절한 소음해석 방법을 선택하는 것이 중요하다. 개념설계 단계에서 단순한 수식과 축척 데이터 베이스를 사용하여 적절한 저소음 후보군을 선택하고, 예비설계 단계에서 Steady RANS 방법을 통해 후보별 소음원 분포를 고려하는 것이 좋다. 이후 상세설계 단계에서 음향상사법을 사용한 과도해석 및 음향시험을 통한 검증을 병행하여 최종으로 제품 성능을 확인하는 것이 요구됨19으로 BNS Model을 활용한 연구는 효율성과 활용도가 높다. 따라서 본 연구에서는 BNS Model을 활용하여 압축기 휠의 5가지의 설계 회전수(120,000, 150,000, 180,000, 200,000 및 220,000 RPM)에 대한 소음을 분석하였다.
3.1 압축기 휠의 Broadband 소음 특성
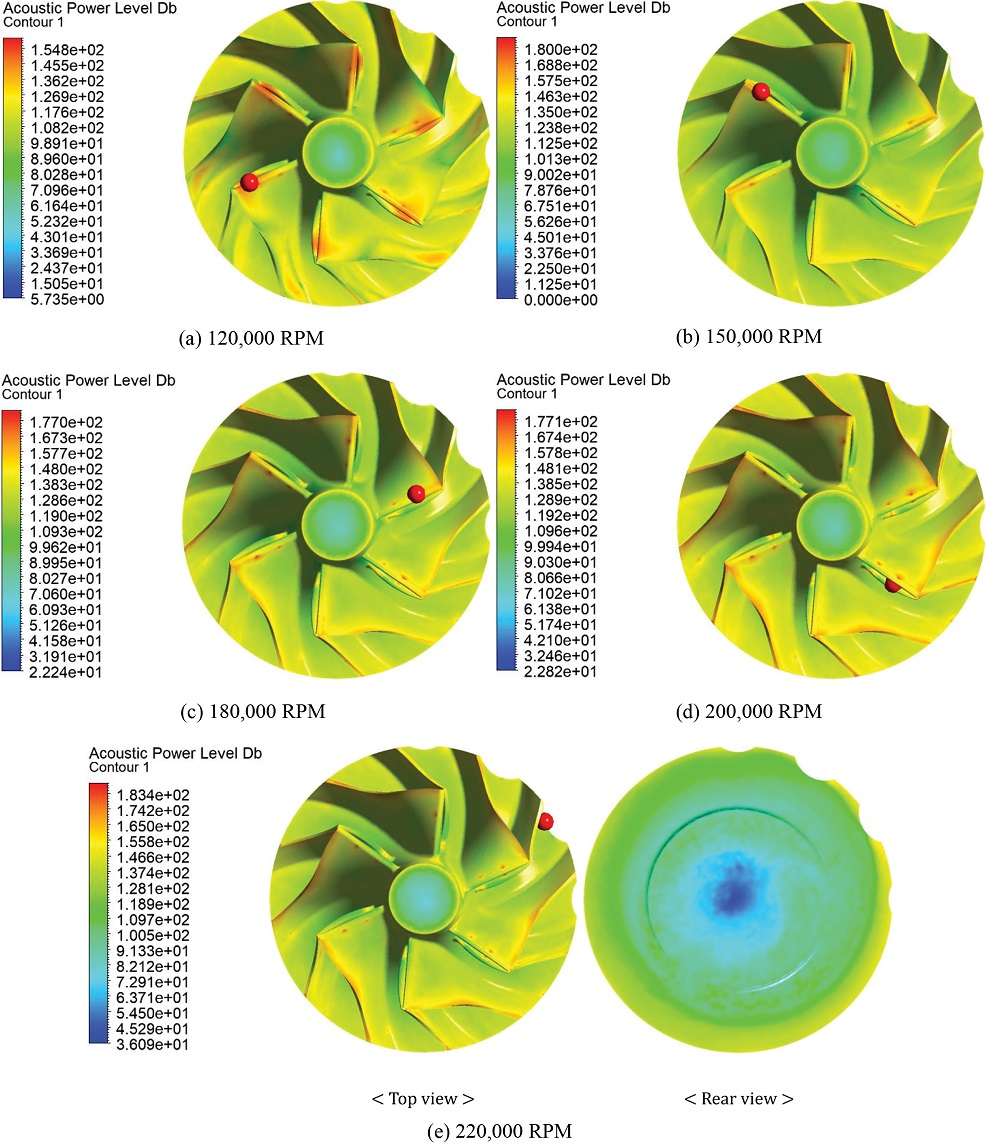
Figs. 3(a) 부터 3(e)는 터보차저 압축기 휠의 5가지 설계 회전수에 대한 APL을 도식하였다. 압축기의 각 형상은 압축기 휠을 입구(위쪽)에서 본 형상이며, 220,000 RPM인 Fig. 3(e)의 경우 압축기 휠의 컷팅부가 소음에 미치는 영향을 분석하기 위하여 배면에 대한 APL도 나타내었다.
최저회전수인 120,000 RPM은 Fig. 3(a)로 도식하였고, 블레이드의 상부에서 154.06 dB로 최대 APL이 계산되었다. 150,000 RPM과 180,000 RPM 모두 120,000 RPM과 동일한 주날개의 끝단부에서 각각 158.77, 183.45 dB로 최대 APL이 계산되었으며, Figs. 3(b)와 3(c)에서 도식하였다. 200,000 RPM은 Fig. 3(d)로 도식하였으며, 이전 회전수와 다르게 보조날개 끝단부에서 183.49 dB로 최대 APL이 계산되었다. 최대회전속도인 220,000 RPM과 그 이상의 속도에서는 주날개와 보조날개가 아닌 컷팅부에서 189.52 dB로 최대 APL이 계산되었고, 그 위치를 Fig. 3(e)로 나타내었다. 각 회전수에 대한 최대 APL을 적색으로 표시하였다. 180,000 RPM 이하에서는 주날개의 끝단에서 최대 APL이 발생하며, 200,000 RPM에서는 보조날개의 끝단에서 220,000 RPM 이상의 회전속도에서는 밸런싱 컷팅 의한 소음이 가장 크게 발생하는 것을 확인할 수 있었다. 전반적으로 회전수가 증가함에 따라 압축기 휠의 최대 소음은 Blade Tip에서부터 Splitter Tip을 거쳐, 밸런싱 컷팅부까지 휠의 하부 방향인 –Z 방향으로 향하는 경향을 확인할 수 있다. 따라서 소음이 증가함에 따라 밸런싱 컷팅부에 대한 엄격한 설계가 진행되어야 함을 알 수 있다. 또한 Z 방향으로부터 –Z 방향까지 최대 APL의 위치가 달라짐에 따라 유체의 유입보다 유출과 관련된 압축기 휠의 축 방향 국소적 위치에서 소음의 영향이 커져, 높은 소음이 발생하는 것을 확인할 수 있다. 터보차저 압축기 휠의 배면(Rear)에서 밸런싱 컷팅에 따른 소음 분포를 확인하였고, 밸런싱 컷팅에 의해 압축기 배면에서 비원형 형태의 소음장이 발생하는 것을 확인하였다. 소음장의 비원형도는 휠의 회전속도와 비례하는 것을 알 수 있었다. 따라서 높은 회전속도의 경향을 보일수록, 낮은 회전속도와는 다르게 소음원이 압축기 출구의 볼류트 주위에서 높아지는 것을 확인할 수 있었다. 이는 초고속 터보기계에서 밸런싱 컷팅의 소음에 대한 연구가 필수적으로 요구됨을 의미한다. 이를 Fig. 3(e)로 도식하였다.
3.2 블레이드 형상에 의한 소음 특성
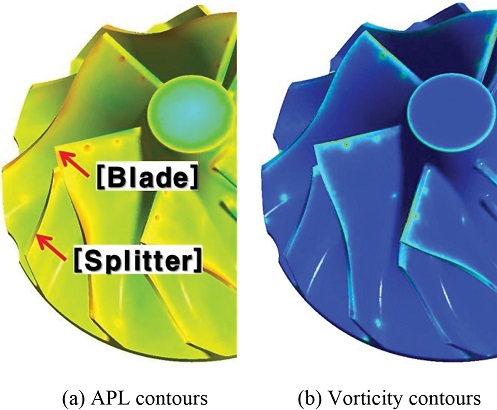
Figs. 3(a)부터 3(e)에서 압축기 휠의 5가지 설계 회전수 모두 블레이드 상부의 국소적 위치에서 2개의 원형 소음 분포를 확인할 수 있다. 원형소음 경향이 가장 뚜렷한 220,000 RPM 압축기 휠의 APL을 Fig. 4(a)에 도식하였고, 이는 Fig. 4(b)에서 나타낸 와도분포와 거의 일치하는 비슷한 분포를 보인다. 와도는 Song1의 연구에서 확인한 소음에 영향을 미치는 주요 인자 중 하나이다. 소음과 비슷한 분포 경향을 보이는 와도는 5가지의 모든 회전수에서 블레이드 상부에 국소적으로 높은 현상을 보인다. 압축기 휠이 회전할 때 블레이드 끝단부에서 가장 빠른 유체의 속도가 발생하지만, 블레이드 상부에서는 압축기 입구로 유입되는 유입기류가 블레이드의 회전운동으로 발생하는 유동과 충돌하는 특징으로 상부 2개의 지점에서 국소적으로 높은 와도가 발생하는 현상을 확인할 수 있다. 블레이드 상부의 형상을 Fig. 5에서 와도분포와 속도벡터로 도식하였다. 두 그림에서 볼 수 있듯이 블레이드의 상부는 유체의 속도가 가장 빠른 위치는 아니지만 유동 현상으로 인해 가장 큰 와도가 발생함으로 유체의 소음에 큰 영향을 미치는 것을 확인할 수 있었다. 따라서 상부 유입기류와 직접적으로 충돌하여 소음에 큰 영향을 미치는 와도 발생을 줄일 수 있는 블레이드의 끝단부에 대한 세부설계가 요구된다.
3.3 터보차저 압축기의 Broadband 소음 분석
Fig. 3에서 압축기 휠의 5가지 설계 회전수에 대한 소음분포와 밸런싱 컷팅 영향에 따른 배면의 소음분포를 확인하였다. 또한 Figs. 4와 5를 통해 소음에 영향을 미치는 인자와 블레이드 형상에 의한 소음 분포를 확인하였다. 하지만 이는 터보차저 압축기와 압축기 휠의 형상에 대한 소음원을 확인한 것이며, 실제 가청 소음의 스케일과는 큰 차이가 있다. 가청 소음은 소음원과 청취자의 거리와 매질의 밀도 등의 영향을 크게 받음으로 별도의 계산이 필요하다. 따라서 청취자가 듣는 대략적인 소음의 크기를 계산하고, 제작사 시험데이터4와 비교를 위해 입구를 0.8, 출구를 0.5 m 확장하였다. 입구와 출구, 휠의 3가지 국소적 위치에 대한 소음을 측정하였으며 세부 위치를 Table 2에서 표시하였다.
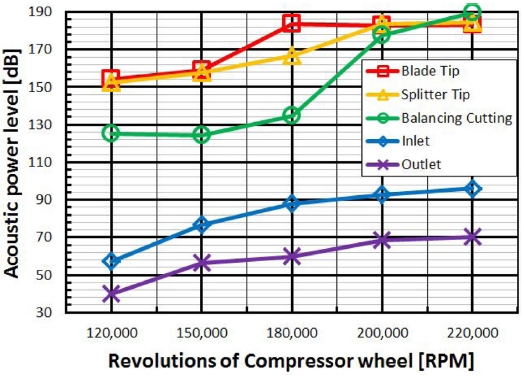
Fig. 6에서 Table 2의 각 위치에 대한 APL을 계산하여 차트로 도식하였다. 5가지 회전수에서 입구와 출구의 소음보다 휠 자체의 소음이 지배적이며, 압축기 휠의 회전 속도와 소음이 비례하는 경향을 확인할 수 있었다.
하지만 180,000 RPM의 경우 블레이드의 끝단, 200,000과 220,000 RPM의 경우 보조날개의 끝단과 입구, 출구 모두에서 소음 증가가 휠의 회전수 증가에 비교적 큰 영향을 받지 않는다는 것을 확인할 수 있었다.
반면 높은 회전수를 보일수록 밸런싱 컷팅에 의한 소음이 급격히 증가하는 경향을 확인할 수 있는데, 이는 특정 반경 이상에서 높은 회전수에 따른 급격한 압력 변화로 유동 마찰에 의한 소음이 커지는 것을 Song1의 연구를 통해 알 수 있다. 따라서 초고속 터보기계에서는 밸런싱 컷팅이 소음에 미치는 영향을 고려하여 개선 연구의 필요성이 요구된다.
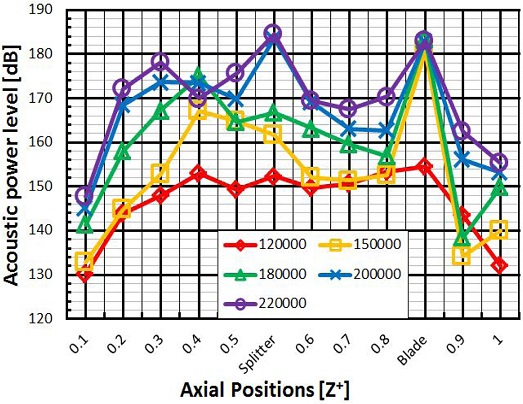
각 회전수에 해당하는 압축기 휠 근처 유동장의 최대 APL을 계산하여 Fig. 7의 차트로 도식하였다. 압축기 휠의 실제 높이(Z위치, 18.2 mm)를 1로 두고, 무차원화(Z+)하여 해당 높이에 대한 APL을 계산하였다. Z+의 국소적 위치인 0.5-0.6과 0.8-0.9 사이에 위치하는 보조날개와 주날개에 해당하는 높이에 대한 APL도 포함하여 계산을 수행하였고, 5가지 실제 회전수에 따른 소음분포를 확인하였다.
Fig. 7에서 확인할 수 있듯이 터보차저 압축기 휠의 국소적 위치에 따른 회전수 증가의 의한 소음 증가 폭은 다양한 경향을 보인다. 저속으로 회전하는 경우에는 주날개 인근에서 가장 큰 소음을 파악할 수 있으며, 압축기 휠의 회전속도가 증가할수록 보조날개가 소음에 미치는 영향이 커지는 것을 알 수 있다. 따라서 동일한 형상의 압축기 휠이지만, 압축기 휠의 회전속도에 따라 높은 소음이 발생하는 위치가 달라짐으로, 실제 운전 상황에 적합한 회전수의 소음 기반 설계가 이루어져야 함을 알 수 있다.
4. 결론
최근 개인 항공기 시장이 도래함에 따라 운송기계의 고성능화 및 경량화가 더욱 중요시 여겨지고 있다. 또한 도심에서 운용됨으로, 수직 이착륙에 적합하도록 초고속 터보기계를 사용하는 도심형 항공기 개발에 따라 도심에서 문제가 되고 있는 소음은 가장 중요한 설계인자 중 하나로 주목되고 있다. 하지만 특성상 많은 시간과 비용이 소요되는 기존의 소음연구는 초고속 터보기계 등에 적용하기 어려울 뿐만 아니라 대략적인 소음원을 파악하고, 개선설계가 목표인 산업 현장에서는 비효율적인 작업이 될 수 있다. 따라서 Song1의 후속 연구로 진행된 본 연구에서는 5가지 실제 설계 회전수에 대한 APL을 계산하여 소음원과 국소적인 소음의 특성을 분석하였으며, 그 결과를 다음과 같이 정리하였다.
(1) Steady RANS 유동해에 기초한 BNS Model은 소음원의 크기와 위치를 효율적으로 파악하는데 효과적이다. 따라서 산업 현장에서 불필요한 비용 소모를 줄이고, 효과적으로 사용할 수 있는 설계 데이터를 제공한다. 특히 터보차저와 같이 수천 RPM 이상으로 회전하는 초고속 터보기계의 공력소음 해석에서 효과적인 소음 분석법의 활용은 더욱 요구되고 있으며, 전적으로 시험에 의존하던 기존 연구법을 대체할 수 있는 새로운 방안을 제시한다.
(2) 120,000, 150,000, 180,000, 200,000, 220,000 RPM의 5가지 회전수에 대한 유동해석 데이터를 활용하여 유동소음을 계산하였다. 유동해석의 타당성은 이전 연구인 Song1의 연구를 통해 검증하였고, 유동소음 연구에서 수퍼 컴퓨터 활용을 통해 격자의 공간해상도에 따른 수렴성 여부도 검증하였다. 본 연구에서 계산된 APL을 활용하여 소음원의 분포와 크기를 파악할 수 있도록 하였다.
(3) 5가지 회전수에 대한 압축기 휠은 120,000 RPM과 150,000, 180,000 RPM에서 주날개의 상부에 각각 154.6, 158.77, 183.45 dB로 최대 APL이 계산되었다. 200,000 RPM에서는 보조날개의 상부에 183.49 dB로 최대 APL이 계산되었으며, 최대속도인 220,000 RPM에서는 질량 균형을 맞추기 위해 가공된 밸런싱 컷팅부에서 189.52 dB로 최대 APL이 계산되었다. 따라서 초고속 회전기계 설계에 있어서는 휠의 중심과 가장 먼 위치의 소음연구가 중요하며, 기존의 밸런싱 컷팅을 휠의 안쪽으로 이동하는 연구의 필요성도 요구된다는 것을 알 수 있었다. 또한 밸런싱 컷팅으로 인해 배면은 비원형 형태의 소음분포 특성을 보였다.
(4) 5가지 회전수에 대한 블레이드 상부에서 2개의 소음 지점을 확인할 수 있다. 이는 이전 연구1에서 분석한 와도(Vorticity)와 거의 동일한 분포를 보이는데, 압축기 입구로 유입되는 유입기류와 블레이드 회전 운동으로 유체의 충돌로 발생하는 블레이드 형상에 의한 특징으로 유체의 큰 속도벡터가 발생하는 것을 확인할 수 있다. 따라서 블레이드 상부의 소음을 저감하기 위해 블레이드 상부의 형상 수정이 요구된다.
(5) 5가지 실제 회전수에 대한 터보차저 압축기 입구와 출구의 소음을 분석하였다. 전반적으로 입구의 소음이 출구 소음보다 높은 경향을 보이면서, 회전수의 증가에 비례하여 증가하는 모습을 확인할 수 있었다. 이는 입구와 출구 길이에도 큰 영향을 받으며, 실제 운전자의 운행 조건에서의 소음을 분석하기 위해서는 공간에 대한 격자 생성 및 별도의 수신자 모델 설정이 요구된다.
(6) 압축기 휠의 회전속도가 증가함에 따라 압축기 휠의 모든 부분에서 소음이 증가하였다. 180,000 RPM 이하의 비교적 저속에서는 주날개와 보조날개 소음이 지배적이며, 큰 폭으로 증가한다. 하지만 180,000 RPM 이하의 고속에서는 밸런싱 컷팅 형상에 의한 소음이 급격히 증가하고, 220,000 RPM 이상의 회전수에서는 소음에 가장 큰 영향을 미치는 인자로 나타난다. 따라서 초고속 터보기계 설계에서는 밸런싱 컷팅 형상에 대한 연구가 필수적이며, 가공 정밀도를 높여 터보기계의 질량 균형을 고려한 설계가 진행되거나 소음의 영향을 고려한 밸런싱 컷팅 작업이 진행되어야 함을 알 수 있다.
(7) 터보기계의 소음은 회전수 증가에 비례하여 모든 국소적 위치에서 동일한 경향으로 증가하지 않으며, 회전수에 따라 다양한 곳에서 최대 소음 및 특이음이 발생한다. 따라서 설계 대상인 터보기계에 적합한 운전조건을 파악 후 해당 운전조건에 적합한 소음 설계가 필수적으로 이루어져야 함을 알 수 있다.
(8) 본 연구는 자동차의 터보차저 압축기 외에도 소형 항공기와 터빈 블레이드 등의 다양한 기술에 응용할 수 있는 공력음향(Aero-Acoustics) 해석법을 제공함으로써, 실제 산업 현장에서 효율적으로 적용하여 공력 소음기기를 최적으로 개선 설계할 수 있는 방안을 제시하였다.
(9) 본 연구의 결과는 추후 진행될 후속 연구의 기반 자료로 활용할 예정이며, 후속 연구는 터보기계의 소음을 직접적으로 계산하여 해당 주파수에 해당하는 청취음을 분석 후 관련 제작사의 시험 및 계측 장비를 활용하여 검증할 예정이다. 추후 연구를 통해 초고속 터보기계에 적용 가능한 효율적인 공력-소음예측법을 개발하고, 미래 소형항공기, 가스터빈, 유체기계 등 광범위한 분야에 적용하여 터보기계 산업 발전에 기여할 수 있으리라 기대한다.
REFERENCES
-
Song, J. H., Hwang, J. Y., Ryu, S. W., and Lee, D. R., “A Study on Flow Characteristics in Turbocharger Compressor,” Journal of the Korean Society for Computational Fluids Engineering, Vol. 24, No. 1, pp. 96-104, 2019.
[https://doi.org/10.6112/kscfe.2019.24.1.096]

- Gwak, W. G. and Kim, Y. J., “Effects of the Grooved Casing on the Performance of a Turbocharger,” Proc. of the KSFM Annual Summer Conference, pp. 305-305, 2016.
-
Han, M. and Cho, J., “A Study on the Configuration of Turbo Charger through Flow Analysis,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 17, No. 3, pp. 34-38, 2018.
[https://doi.org/10.14775/ksmpe.2018.17.3.034]

- Lee, Y. W. and Lee, D. J., “Airbone Noise Measurement and Analysis for Automobile Turbocharger,” Proc. of the Korean Society for Noise and Vibration Engineering Conference, pp. 51-52, 2010.
-
Park, H. I., Hong, S., Seo, J., and Lee, H., “Experimental Investigation of the Pulsation Noise Induced by Automotive Turbocharger Compressors,” Proc. of the FISITA World Automotive Congress, pp. 305-316, 2013.
[https://doi.org/10.1007/978-3-642-33832-8_24]

- Park, H., Kim, H., Kang, S., and Eom, S., “Investigation on Engine Operation Area based on Turbocharger Noise Map,” Proc. of the KSAE Conference and Exposition, pp. 462-467, 2010.
- Park, H. I., Eom, S. B., Seo, J. B., and Lee, S. H., “Compressor BPF Noise Reduction for an Automotive Turbocharger,” Proc. of the Korean Society for Noise and Vibration Engineering Conference, pp. 851-856, 2012.
- Kang, W., Kim, H. J., and Sung, H. J., “A Study on the Reduction of the Flow-Induced Noise in Turbo-Charger Diesel Engines,” Proc. of the KSME Conference, pp. 2913-2917, 2007.
- Kim, B., Hong, S., and Song, J., “A Study on Turbocharger Noise for Passenger Powertrains,” Proc. of the KSNVE Annual Spring Conference, pp. 1707-1712, 2006.
-
Park, H., Choi, S., Jang, S., and Hwang, J., “Optimization of an Intake Flow Noise Induced from an Automotive Turbocharger,” Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 8, pp. 546-552, 2015.
[https://doi.org/10.5050/KSNVE.2015.25.8.546]

-
Lighthill, M. J., “On Sound Generated Aerodynamically I. General theory,” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, Vol. 211, No. 1107, pp. 564-587, 1952.
[https://doi.org/10.1098/rspa.1952.0060]

-
Williams, J. F. and Hawkings, D. L., “Sound Generation by Turbulence and Surfaces in Arbitrary Motion,” Philosophical Transactions for the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 264, No. 1151, pp. 321-342, 1969.
[https://doi.org/10.1098/rsta.1969.0031]

-
Williams, J. F. and Hawkings, D., “Theory Relating to the Noise of Rotating Machinery,” Journal of Sound and Vibration, Vol. 10, No. 1, pp. 10-21, 1969.
[https://doi.org/10.1016/0022-460X(69)90125-4]

- Kim, S., Lee, G., and Cheong, C., “Numerical Analysis on the Flow Noise Characteristics of 300 W Savonius-Type Vertical-Axis Wind Turbines,” Proc. of the Korean Society for Noise and Vibration Engineering Conference, pp. 725-730, 2012.
-
Mo, J. O. and Lee, Y. H., “A Study on the Flow Characteristics and Noise Predictions around the Shroud Fan Using the Aero-Acoustic Noise Model,” The KSFM Journal of Fluid Machinery, Vol. 12, No. 3, pp. 19-25, 2009.
[https://doi.org/10.5293/KFMA.2009.12.3.019]

-
Broatch, A., Galindo, J., Navarro, R., and García-Tíscar, J., “Numerical and Experimental Analysis of Automotive Turbocharger Compressor Aeroacoustics at Different Operating Conditions,” International Journal of Heat and Fluid Flow, Vol. 61, pp. 245-255, 2016.
[https://doi.org/10.1016/j.ijheatfluidflow.2016.04.003]

- Fluent, A., “ANSYS Fluent 12.0 Theory Guide,” ANSYS Inc., 2009.
-
Sharland, I. J., “Sources of Noise in Axial Flow Fans,” Journal of Sound and Vibration, Vol. 1, No. 3, pp. 302-322, 1964.
[https://doi.org/10.1016/0022-460X(64)90068-9]

- Kim, Y. T., “Aeroacoustics Analysis by ANSYS Fluent,” ANZINE, Vol. 33, pp. 96-99, 2015.

M.S. candidate in the Graduate School of Mechanical Engineering, Sungkyunkwan University. His research interest is turbo machinery, future alternative energy, and aerospace engineering.
E-mail: wayinuni@cu.ac.kr

Professor in the School of Mechanical and Automotive Engineering, Catholic University of Daegu. His research interest is heat transfer, fluid engineering, and electric vehicle.
E-mail: dlee@cu.ac.kr