자동차 혼 시스템 코킹 공정 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The automobile horn system is an essential part that produces sound for safety reasons. Production of horn system is classified based on two main processes. One of them is the caulking process which makes body assembly and forms the lower part of the horn system. The control dimension of body assembly is a crucial factor for quality control as the sound of the horn is largely determined by the control dimension. In this paper it has been found that plastic deformation of body and its restoration after caulking process is the main reason for the change in control dimension. Typically, 100 specimens of the body assembly were employed and the results were compared (Restore the Length of the Body) with another data set that had the same body but different parts in the assembly. Monte carlo simulation was used for tolerance analysis of control dimension for the body assembly including the deformation of the body in the caulking process. The simulation was identified as a good model to predict the satisfaction ratio of the control dimension with high accuracy and was observed to be useful in designing parts of the assembly and equipment used in the caulking process.
Keywords:
Horn system, Caulking process, Control dimension, Tolerance analysis, Air gap, Monte carlo simulation키워드:
혼 시스템, 코킹 공정, 관리 치수, 공차 해석, 에어갭, 몬테카를로 시뮬레이션1. 서론
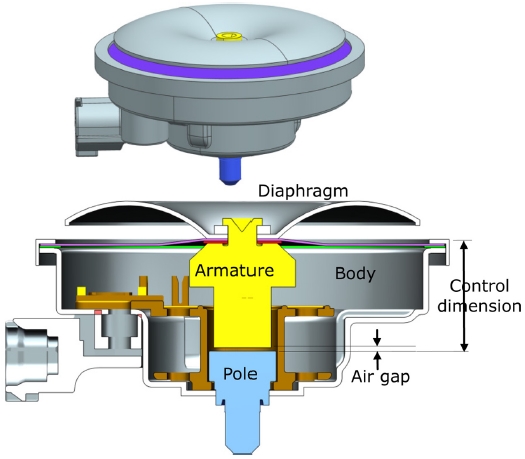
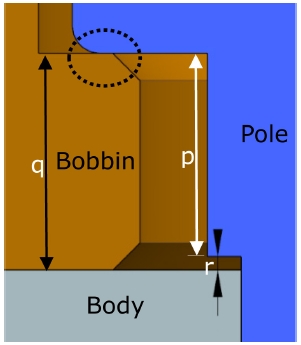
자동차용 혼 시스템(Horn System)은 모든 차량에 필수적으로 장착되어야 하는 안전 관련 부품으로서 운전자가 보행자나 다른 차량의 운전자 등을 대상으로 소리를 발생시키는 장치이다. 혼 시스템의 여러 조립 공정 중에서 성능에 중대한 영향을 미치는 2개의 공정은 코킹 공정(Caulking)과 리벳팅 공정이다. 이 중에서 코킹 공정은 혼 시스템 몸체(Body)에 보빈(Bobbin)과 폴(Pole)을 결합하여 혼 시스템 아랫부분의 바디(Body) 어셈블리를 구성한다. 본 논문의 대상인 전기식 혼은 7개의 부품으로 구성되며 보빈을 제외한 모든 부품의 재질이 금속이다. 혼 시스템의 전체 형상과 단면을 Fig. 1에 도시하였다. Fig. 1에 표시된 관리 치수(Control Dimension)는 코킹 공정으로 제작되는 바디 어셈블리에서 폴과 몸체 상단 사이의 거리를 가리키며 에어갭(Air Gap)은 폴과 아마추어(Armature) 사이의 간격을 나타낸다.
에어갭은 혼 시스템의 소리에 가장 큰 영향을 주기 때문에 품질 평가의 핵심적인 항목이다. 그리고 바디 어셈블리에서는 에어갭과 직접 연관된 관리 치수의 규정 구간(Satisfying Zone) 만족 여부가 품질 평가의 기준이 되며 규정된 규정 구간의 범위는 0.5 mm 정도로 매우 작다. 현재까지 바디 어셈블리 개발과 생산은 설계데이터가 부족한 상태에서 실험과 경험에 의존하여 이루어졌다. 본 논문에서는 코킹 공정이 바디 어셈블리의 관리 치수에 미치는 영향에 대한 연구를 수행하였으며 이 연구 결과는 바디 어셈블리 부품들과 공정에 사용되는 장비 개발에 활용된다.
제조 현장에서 이루어지고 있는 혼 시스템의 조립 공정에 대해 기술하면 다음과 같다. 리벳팅 공정에서는 진동에 의해 소리를 만들어내는 아마추어를 다이어프램(Diaphragm)에 리벳팅 방식으로 결합하여 에어갭 상위 부분의 어셈블리를 조립한다. 그런데 리벳팅 과정의 압축력에 의하여 다이어프램의 형상이 변화하고 어셈블리 부품 사이의 접촉 위치가 달라진다. 이러한 결과로 에어갭이 영향을 받게 되는데 상기한 두 경우 모두 변형에 대한 정밀한 분석이 어려워서 실험을 통하여 어셈블리 관리 치수의 변형량을 확보하는 것이 현실적인 방안이다.
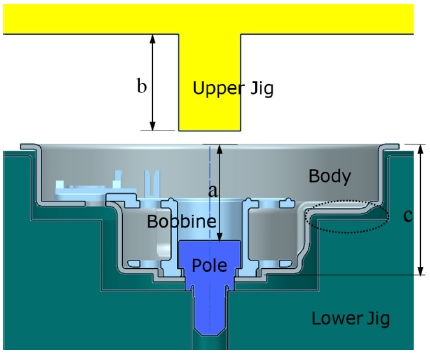
코킹 공정에서는 상부 지그(Upper Jig)에 의한 압축력으로 폴이 몸체 및 보빈에 압축력을 가하면서 세 부품이 결합하여 바디 어셈블리가 조립된다. 코킹 공정이 시작되는 상황에서 지그와 바디 어셈블리 단면을 Fig. 2에 표현하였다. 공정 과정에서 관리 치수(Fig. 2(a))는 상부 지그의 돌출 부위 길이(지그 길이, Fig. 2(b))만큼 일정하게 확장된다고 가정할 수 있으며, 이 부분이 리벳팅 공정과 다른 코킹 공정의 특징이다. 본 논문에서는 이 현상에 주목하여 코킹 공정의 관리 치수 변화에 대한 이론을 제시하였다.
2. 코킹 공정
2.1 코킹 공정의 순서
바디 어셈블리를 결합하는 코킹 공정에서는 폴이 몸체와 보빈에 압입되고, 폴의 일부분이 좌굴되어 몸체의 외곽을 감싸게 됨으로써 세 부품이 서로 결합된다. 제조 현장에서 공정이 이루어지는 과정을 저자가 관찰한 순서대로 정리하면 다음과 같다.
(1) 코킹 공정이 시작되면 보빈은 몸체 내부에 놓이며 이때 몸체의 리브(Rib) 부분이 하부 지그(Lower Jig)에 닿게 된다(Fig. 2의 점선부분).
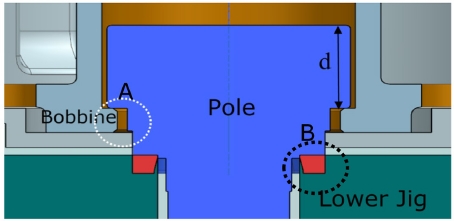
(2) 공정 과정에서 상부 지그가 폴의 상단에 압력을 가하면 폴의 단차 부분 중 윗부분이(Fig. 3의 타원 A 내부) 보빈의 구경을 확장, 관통하면서 아래 방향으로 이동하고 이후 단차 아랫 부분이 몸체를 밀게 되는데 이 과정에서 관리 치수가 확장된다. 이때 반대쪽에 있는 하부 지그와 접촉한 폴의 돌기 부분(Fig. 3의 타원 B)이 좌굴되어 넓게 퍼지며 몸체를 감싸면서 서로 결합된다.
(3) 상부 지그와 하부 지그가 맞닿게 되어 공정이 완료되면 관리 치수는 지그 길이와 초기 관리 치수의 차이(B-A)만큼 증가하게 된다. 코킹 공정 전(前)과 후(後)의 폴과 몸체의 결합 형태를 Figs. 4(a)와 4(b)에 각각 수록하였다(타원형 점선 부위). 폴의 돌기 부분이 좌굴에 의해 넓게 퍼져서 몸체 외부를 봉합하는 형태를 그림에서 볼 수 있다.
2.2 코킹 공정에 의한 관리 치수 변화
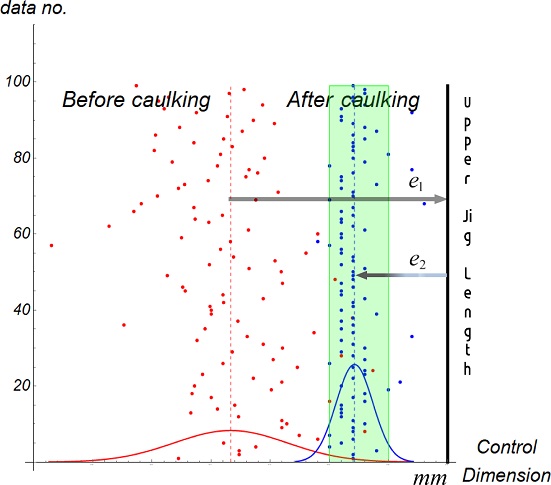
코킹 공정 전, 후의 관리 치수 측정 결과를 Fig. 5에 나타냈는데 100개의 바디 어셈블리 시편(1차 데이터)의 관리 치수가 각각의 점으로 표현되었다. Fig. 5에 나타낸 직사각형이 관리 치수가 만족되는 범위를 나타내는 규정 구간(Satisfying Zone)이며 공정 전, 후의 관리 치수 평균값이 점선의 연직선으로 표시되었다. 공정 전에는 관리 치수가 대부분 규정 구간에 미치지 못하다가 공정 후에 만족률이 높아지는 것을 Fig. 5에서 볼 수 있다. 공정 과정에서 관리 치수는 지그 길이(Upper Jig Length)로 표시된 지점까지 확장되며 이때 관리 치수(Fig. 2(a))가 지그 길이(Fig. 2(b))와 같아지게 된다. 확장된 관리 치수의 크기를 평균값에 대해 나타내면 화살표로 표시된 Fig. 5에 표시된 e1과 같다. 특이한 점은 공정이 완료된 이후에 관리 치수 평균값이 e2만큼 줄어드는 현상이 나타나는데 이것에 대한 분석은 다음 장에 수록한다. Fig. 5에 나타낸 실험 결과에서 관리 치수의 규정 범위 만족률이 코킹 공정 전에 약 6%이며 공정 후에는 94%로 높아진다.
코킹 공정에서 한 가지 주목할 점은 관리 치수의 표준편차가 공정 전에 비해 약 32% 줄어든다. 관리 치수의 평균과 표준편차로 만든 정규분포 곡선을 Fig. 5의 아랫부분에 표시하였다. Fig. 5에서 공정 후의 곡선 폭이 훨씬 좁다. 이러한 이유는 공정 과정에서 시편들의 관리 치수 분포가 지그 길이에 의해 한 지점에 모이게 되며(Fig. 5의 Upper Jig Length) 이후에 몸체가 복원되는 길이의 편차가 상대적으로 작기 때문이다. 관리 치수 구간이 매우 작게 규정된 코킹 공정에서 이런 현상은 만족률을 높이는데 유리하다.
3. 코킹 공정 관리 치수 및 시뮬레이션
3.1 코킹 공정 분석
코킹 공정 과정에서 확장된 관리 치수가 복원되는 현상은 상부 지그에 의해 늘어난 몸체가 자체의 탄성에 의해 복원되기 때문인 것으로 추정된다. 재질이 플라스틱인 보빈은 공정 과정에서 관리 치수에 영향을 주는 변형이 발생하지 않는다. 폴의 경우도 하부 지그와 맞닿은 돌기 부분의 좌굴(Fig. 3 참고)이 발생하여 전체 길이의 변형이 거의 없다. 따라서 관리 치수의 확장 및 복원이 모두 몸체의 변형에 의해 발생한다고 가정할 수 있다.
코킹 공정이 진행되기 전의 바디 어셈블리 결합 상태를 Fig. 6에 상세히 표현하였다(Fig. 3의 타원 A부분을 확대). Fig. 6에서 폴의 단차가 보빈의 단차보다 작은 경우(p < q) 몸체와는 거리 r만큼 떨어져 있게 된다. 공정이 시작되면 상부 지그가 폴을 밀게 되며 이때 폴과 보빈의 접촉면적(Fig. 6의 타원 부분)이 매우 작아서 폴이 보빈의 구경을 확장하여 거리 r만큼 이동한 후에 몸체와 접촉하게 된다. 관리 치수를 결정하는 몸체와 폴, 보빈의 치수를 그림으로 표현하면 각각 Fig. 2에 표시된 c와 Fig. 3에 표시된 d 그리고 Fig. 6에 표시된 p와 q가 된다. 혼 시스템 구성 부품들의 길이 차이가 크지 않아서 Fig. 6에 표시된 p와 q의 크기가 두 부품의 공차에 따라 역전되는 경우가 발생하며, 두 경우의 관리 치수를 수식으로 표현하면 다음 식(1)과 같다.
| (1) |
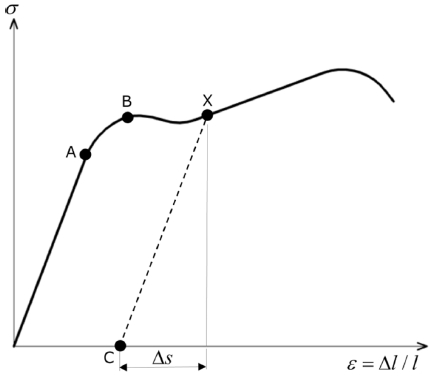
몸체의 두께는 1 mm 내외이며 재질은 냉간압연강판(SPCC)으로 연신율이 해당 두께에서 36%이므로 연성재료에 속한다.1-3 일반적인 연성재료의 응력-변형도 선도를 Fig. 7에 나타내었다.4,5 Fig. 7에 비례한계(점A), 탄성한계(점A), 하중해제 지점(점 X), 복원 지점(점C) 등을 각각 표시하였고, Δs는 응력이 제거된 뒤에 변형률이 복원되는 양을 의미하며 점 C는 하중 해제 뒤에 영구 변형이 발생하여 변형률이 증가된 상태를 나타낸다.
코킹 공정에서 폴에 의해 힘이 가해지는 몸체의 원주 부위에는 외팔보 형태의 변형이 발생하는데 본 논문에서는 관리 치수가 측정되는 방향(Fig. 1의 y축)으로만 몸체의 변형과 복원을 정의한다. 그리고 몸체의 변형률은 Fig. 7의 곡선 형태를 갖는다고 가정한다. 몸체의 형상이 응력-변형도 실험을 위해 규정된 시편 형상과 다르지만 실험에서 나타나는 관리 치수의 변화를 고려하면 이러한 가정이 가능하다.
결과적으로 몸체는 코킹 공정 과정에서 탄성한계를 지나 소성 영역까지 늘어난 후에 영구 변형을 남기고 일정거리만큼 복원된다. 따라서 공정이 끝난 뒤에 관리 치수는 몸체가 복원되는 길이(복원 길이)만큼 줄어들게 되며(Fig. 5의 e2 참고) 초기값에 비해서는 평균 e1-e2만큼 늘어나게 된다.
바디 어셈블리를 구성하는 각각의 부품들은 공차 범위에서 무작위적인 치수를 갖게 되고 어셈블리 구성을 위한 부품들의 조합도 무작위적으로 발생하므로 초기의 관리 치수는 제품마다 일정 범위에서 각각 다르게 된다. 이에 따라 코킹 공정이 완료된 시점에서 몸체의 소성변형이 진행된 상태(Fig. 7의 점X의 위치)와 이후 복원되는 변형률도(Fig. 7의 Δs) 서로 다르다. 본 논문에서는 이전술한 1차 데이터에 대한 실험에 의해 통계적으로 몸체의 복원 길이를 구하였고, 해당 결과를 부품의 치수가 다른 시편(2차 데이터: 40개)의 실험 결과와 비교하여 Table 1에 수록하였다.
상기한 두 데이터는 몸체의 형상은 같으나 관리 치수 계산에 사용되는 폴의 치수가 다르다. 그래서 1차 데이터는 지그 길이까지의 평균 변화량 e1이 0.18mm인거에 비하여 2차 데이터는 0.26 mm로서 규정된 관리 치수 구간(0.05 mm)을 고려할 때 큰 차이가 난다. 이에 상응하여 코킹 공정에서 두 데이터의 관리 치수 변화량은 평균 39%의 많은 차이가 나는거에 비해 복원 길이 평균(e2)의 차이는 3% 내외로 차이가 거의 없다. 또한 복원 길이의 표준편차도 두 데이터가 서로 비슷하다. 결과적으로 어셈블리를 구성하는 부품들의 치수에 관계없이(몸체는 제외) 코킹 공정 후의 몸체의 복원 길이는 일정한 값을 갖는다고 가정할 수 있다.
3.2 코킹 공정 시뮬레이션
코킹 공정 후에 만족되어야 할 관리 치수 범위가 매우 작아서 관련된 부품들의 공차에 의해서도 규정 범위가 큰 영향을 받는다. 그래서 바디 어셈블리 설계를 위해서는 공정에서의 몸체 변형과 더불어 부품들의 누적 공차가 관리 치수에 미치는 영향을 산정할 수 있어야 한다. 공차 해석 기법들8-10 중에서 산술적 방법은 본 논문의 경우처럼 누적 공차에 대한 허용 범위가 엄밀한 경우에는 적합하지 않다.6-8 왜냐하면 관리 치수 계산을 위한(식(1) 참고) 기존 부품들의 산술적인 누적 공차가 이미 약 0.3 mm가 되어 규정된 범위보다 6배가 크다. 이 경우에 해당 공차 해석 결과에 따라 규정 범위를 만족시키려면 공차를 1/1000 mm 단위 이하까지 지정해야 하는데 이것은 제품의 생산성 측면에서 적합하지 않다.
몬테카를로 시뮬레이션은 공차 범위에서 각 부품들의 치수를 정규분포 형태로 산출하여 조립품에 대한 누적 공차의 산포를 분석하는데 1만회 이상의 시뮬레이션이 수행되면 실제 상황과 99% 일치하는 것으로 알려져 있다.9,10 이 방법은 규정 범위의 만족률에 대한 설계자의 선택이 가능하기 때문에 주어진 상황에 맞는 것보다 유연한 공차 선정이 가능하다. 다만 어셈블리를 구성하는 부품들의 치수가 공차 범위에서 정규분포를 이룬다고 전제가 필요하며 이것은 대량 생산을 위한 생산시스템이 안정되면 가능하다. 본 논문에서는 몬테카를로 시뮬레이션을 이용하여 몸체의 변형을 포함한 공차 해석을 수행하였다.
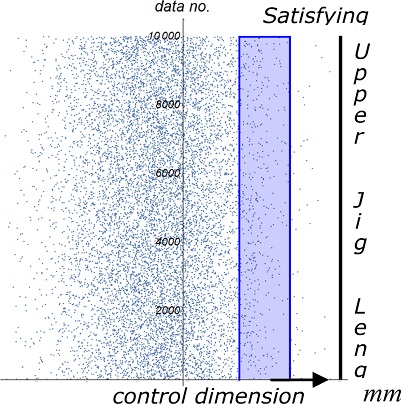
1차 데이터에 대하여 실험에서 얻은 평균값과 표준편차를 기반으로 코킹 공정 전의 관리 치수에 대한 몬테카를로 시뮬레이션 결과를 Fig. 8에 나타내었다. 시뮬레이션에서는 각 부품의 치수에 대해 공차 범위 내 정규분포 형태로 1만개의 난수를 만들었다. 그리고 식(1)에 따라 관리 치수를 계산한 결과를 1만개의 점으로 그림에 표시하였는데 대부분이 Fig. 5의 실험 결과처럼 규정 구간에서 왼쪽으로 벗어나 있다.
코킹 공정 후의 관리 치수 시뮬레이션은 공정 전의 1만개 관리 치수(Fig. 8 참고)가 지그 길이까지 이동(지그 이동거리: Fig. 5의 e1)하고 다시 몸체의 복원 길이만큼 축소되는(Fig. 5의 e2) 과정을 모사하였다(3.1장 내용 참고). 몸체의 복원 길이는 실험에서 얻은 값(평균, 표준편차)에 기반하여 정규분포 형태의 난수를 발생하여 구하였다. 시뮬레이션 과정에서 복원 길이보다 지그 이동거리가 작은 경우가 발생하면 관리 치수는 원래의 상태로 축소되게 프로그램하였고, 결국 공정 전과 후의 관리 치수가 서로 같게 된다.
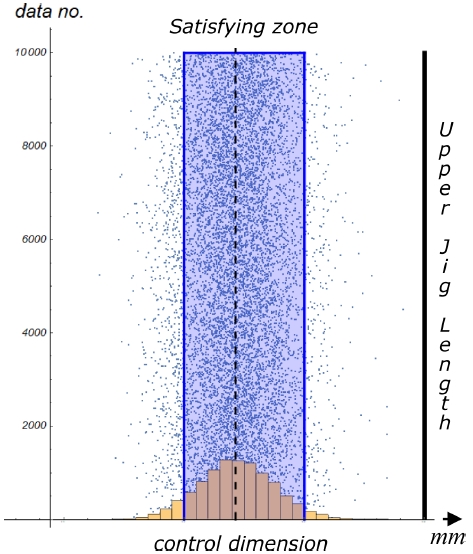
코킹 공정 후, 관리 치수 시뮬레이션 결과(1차 데이터)를 히스토그램과 함께 Fig. 9에 도시하였다. Fig. 9에서 규정 구간 내부의 점선은 공정 후 관리 치수의 평균을 나타내며 실험에서 얻은 값에 기반하여 시뮬레이션이 이루어졌으므로 실험 결과와 같게 된다.
상기와 같은 방법으로 몬테카를로 시뮬레이션을 2차 데이터에 적용하여 공정 후 관리 치수를 예측한 결과를 1차 데이터의 결과와 함께 Table 2에 수록하였다. 관리 치수의 초기값이 1, 2차 데이터가 서로 다르지만 2차 데이터의 시뮬레이션 결과는 실험 결과와 매우 근접한데 그 이유는 두 데이터 모두 코킹 공정 과정에서 같은 지그 길이만큼 관리 치수가 늘어나고 이후 복원되는 거리가 3% 차이로 서로 비슷하기 때문이다(Table 1 참고). 표준편차의 경우 1, 2차 데이터 모두 코킹 공정 후의 값이 약 1/3정도 줄어들어서 상대적으로 평균값을 중심으로 밀집된 형태를 나타낸다.
본 논문의 시뮬레이션은 1차 데이터에 기반하여 이를 모사하였기 때문에 그 결과가 1차 데이터의 실험 결과와 비슷하다. 관리 치수 만족률이 약간의 차이가 나는 이유는 100개의 시편을 사용한 1차 데이터의 경우 부품들의 치수 및 복원 길이가 정확하게 정규분포를 형성하지 않는다. 그러나 시뮬레이션에서는 정규분포를 가정한 1만개의 난수에 기반하여 관리 치수를 계산하였다. 따라서 시뮬레이션은 반복적으로 수행해도 결과의 차이가 거의 없는데 반해 실험에서는 몇 개의 시편에 대한 측정값이 달라져도 결과에 큰 영향을 미치게 된다. 공정 후 2차 데이터의 관리 치수 표준편차의 실험값이 시뮬레이션 대비 약 19% 차이가 나는데 이것은 전술한 것처럼 실험값이 정규분포에서 벗어나 있기 때문이며 보다 많은 수의 시편으로 실험이 이루어지면 정규분포에 근접하면서 두 값의 차이가 줄어들 것이다.
4. 결론
자동차 혼 시스템 코킹 공정의 관리 치수에 대한 분석이 부품들의 공차에 대한 고려와 함께 본 논문에서 수행되었다. 그 결과 코킹 공정 과정에서 관리 치수가 모든 제품에 대해 지그 길이만큼 동일하게 확장되는 특성을 파악하였다. 그리고 공정 후에 관리 치수의 복원 길이가 어셈블리 부품의 치수에 관계없이 3%의 오차 범위 내에서 일정하다는 것을 실험을 통해 확인하였다. 이러한 사실에 기반하여 몸체의 소성 변형 및 복원에 의한 관리 치수 변형 이론을 제시하여 코킹 공정 과정의 관리 치수 변화 요인을 명확히 밝혔다. 이에 따라 몸체를 포함한 어셈블리 구성 부품들의 형상과 지그 길이가 바뀐 경우에도 몸체의 복원 길이에 대한 정보에 근거하여 공정 후의 관리 치수를 계산할 수 있게 되었다.
코킹 공정의 경우처럼 목표로 하는 정밀도가 매우 엄밀한 경우에는 부품들 누적 공차가 관리 치수에 미치는 영향도 계산해야 한다. 이를 위해 몸체의 변형과 함께 공차에 의한 관리 치수 변화량을 몬테카를로 시뮬레이션을 통해 확률적으로 분석하였다. 1차 데이터를 기반으로 수행한 시뮬레이션 모델을 2차 데이터에 적용한 결과 공정 후 관리 치수의 만족 여부를 높은 정확도로 예측하였다. 본 논문의 시뮬레이션 방법을 어셈블리 부품들과 코킹 공정에서 사용되는 지그 및 금형 개발을 위해 활용하면 기존의 경험에 근거한 설계에서 비롯되는 과도하게 조밀한 공차를 피할 수 있다.
본 논문의 실험은 제한된 시편 수에 대해 수행되었으나 보다 많은 수의 부품으로 실험이 이루어져서 부품 치수가 기준 치수에 대해 정규분포에 근접하게 되면, 시뮬레이션 결과와 보다 가깝게 될 것이다. 향후에는 본 논문의 성과를 바탕으로 코킹 공정에 사용되는 부품의 치수 및 공차의 최적 설계를 통해 관리 치수의 만족률을 최대화하기 위한 연구가 필요하다.
Acknowledgments
이 논문은 한국생산기술연구원에서 수요대응형 공동기술지원사업으로 시행한 “자동차 혼 시스템 설계기술지원” 과제(2017)의 기술 개발 결과임(주관기관: 한국생산기술연구원, 참여 기업: 인팩혼시스템㈜).
REFERENCES
-
Lin, C. H. and Lee, J. R., “Characterization of SPCC Steel Stress Behaviour in Brine Water Environment,” International Journal of Electrochemical Science, Vol. 14, No. 1, pp. 2321-2332, 2019.
[https://doi.org/10.20964/2019.03.26]

- HANKUM, “Cold Rolled Low Carbaon-Elongation Test,” http://hankum.deacon.co.kr/korean/products/pd01.php?tep=03, (Accessed 11 NOVEMBER 2020)
- ASTM A1008, “Grade CS Type B,” 2020.
- Beer, F., Johnston, E., DeWolf, J., and Mazurek, D., “Mechanics of Materials,” Mcgraw-Hill Education, 5th Ed., 2009.
- Budynas, R. G. and Nisbett, J. K., “Shigley’s Mechanical Engineering Design,” McGraw-Hill New York, 10th Ed., 2015.
- Krulikowski, A., “Fundamentals of Geometric Dimensioning and Tolerancing,” Cengage Learning, 2nd Ed., 2007.
- Cogorno, G. R., “Geometric Dimensioning and Tolerancing for Mechanical Design,” McGraw-Hill, 2017.
- Lee, J. Y., “Tolerance Analysis of Automobile Steering System,” Journal of the Korean Society for Precision Engineering, Vol. 28, No. 12, pp. 1397-1402, 2011.
- Lee, J. Y., “Tolerance Analysis of Spline Shaft Assembly,” Journal of the Korean Society for Precision Engineering, Vol. 27, No. 12, pp. 75-83, 2010.
- Lee, J., “Tolerance Analysis of Universal Joint,” Proc. of the KSPE Fall Conference, pp. 633-634, 2010.

Principal Researcher in Korea Institute of Industrial Technology. His research interest is product design & development, machine and mechanism design.
E-mail: caravan@kitech.re.kr

Executive Director in R&D Center of INFAC Horn System Co., Ltd.. His research interest is product design & development of smart actuator systems for autonomous vehicle.
E-mail: taesung.kwon@infac.com