열전발전 시스템의 열교환 핀 성능 향상을 위한 치수최적설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
As global warming is rapidly emerging as one of the inherently global issues, one of the renewable energies, i.e. thermoelectric generation, has received attention. In order to increase the efficiency of thermo-electric generation, a maximum temperature difference in plain fins in a heat exchanger is needed, and an appropriate pressure drop is required to ensure stable flow of high temperature fluid. In the present study, the characteristics of the temperature difference and pressure difference for the 2 kW-class thermo-electric generator installed in exhaust pipes of a cogeneration plant were investigated numerically via thermal fluid analysis using ANSYS CFX. Then, size optimization for plain fins of a heat exchanger was carried out using SAS JMP, in which the temperature difference was maximized while meeting the requirement of a given pressure drop condition. A meta-model was generated by using the response surface model, and individual desirability functions were defined to derive the optimal solution that provided the maximal overall desirability function. The result obtained by size optimization showed that the temperature difference of the optimized plain fins of a heat exchanger increased by approximately 27% in comparison with the original model under the given pressure drop condition.
Keywords:
Design of experiments, Desirability function, Plain fin of heat exchanger, Response surface model, Size optimization, Thermo-electric power system키워드:
실험계획법, 만족도 함수, 열교환 핀, 반응표면모델, 치수최적설계, 열전발전 시스템1. 서론
최근 고유가와 지구 온난화 문제가 대두됨에 따라 정부에서는 2030년 온실가스 배출량 대비 37% 감축을 목표로 하여 환경규제를 강화하고 있다.1 이에 따라 화력 발전과 같은 화석연료 에너지원의 의존도를 낮추고, 신재생 에너지원의 활용을 늘리는 추세다. 그러나 신재생 에너지로 주목받았던 태양광, 풍력 및 수력 발전 등은 공급이 일정하지 않고, 발전량이 기존의 화력 발전을 대체하기에 충분하지 않아, 발전 중 버려지는 에너지를 재활용하여 전력을 생산하는 열전발전 기술이 대안으로 주목받고 있다.2
에너지 하베스팅의 일종으로 불리는 열전발전은 미사용 산업에너지에서 전기를 얻을 수 있는 방법으로 열에너지를 전기에너지로 직접 변환하는 발전 방법이다.2,3 열전발전 기술의 핵심은 열전 효과이며 이는 크게 제백 효과(Seebeck Effect)와 펠티어 효과(Peltier Effect) 두 가지로 분류된다. 제백 효과는 서로 다른 두 종류의 도체 양끝에 일정한 온도차를 주었을 때 이에 비례하는 기전력이 발생하는 현상이며, 열전발전에 이용되는 기본원리이다. 펠티어 효과는 반대로 전류를 흘렸을 경우 도체의 한쪽은 열이 발생하고, 다른 한쪽은 열을 흡수하는 현상이다.4 본 연구에서 주목하는 열전발전 시스템은 제백 효과를 이용하는 방식으로 폐열원, 냉각 장치 및 열전발전 스택으로 구성되며, 사용 환경에 따라 단위소자를 여러 형태 및 크기로 배열한 모듈을 제작하여 사용할 수 있어 다양한 산업에서 사용이 용이하다.
현재 열전발전 기술 적용을 위해 활발히 진행되는 연구는 자동차 배기열 및 공장 폐열을 이용한 분야이다.5 그러나 열전발전시스템은 기전력 출력 밀도와 에너지 변환 효율이 낮기 때문에 다양한 기술 적용 분야로의 확장이 어려운 실정이다. 이를 해결하기 위해 국내·외에서 다양한 방법으로 열전발전 시스템에 대한 연구가 진행되어 왔다. Kushch 등6은 대형 디젤엔진의 폐열을 이용하여 엔진 배기가스의 열적 조건 변화에 따른 열전소자의 발전 특성을 고려하여 1 kW급 열전발전 시스템을 개발한 바 있다. n형과 p형 접합 소재로 구성된 네 가지의 열전소자를 대상으로 실험을 수행하였고, 연비의 개선 정도를 비교하였다. Nagao 등7은 스포츠형 다목적 차량과 압축천연가스 차량의 배기가스를 이용하여 열전소자 QW와 Bi₂Te를 실험적으로 비교 하였고, QW를 사용하였을 때 스포츠형 다목적 차량의 경우 2.3%, 압축천연가스 차량의 경우 3%의 연료 절감 효과를 확인한 바 있다. Jang 등8은 열전모듈에 부착되는 절연기판이 발전 효율에 미치는 영향을 실험을 통해 평가하였다. 높은 효율을 갖는 열전발전 모듈을 설계하기 위해서는 열전소자에 부착되는 절연기판의 두께를 얇고 열전도성이 좋은 재료를 선택하는 것을 제안하였다. Moon 등9은 열전소자의 발전효율에 대한 저해 인자를 찾아 그 대안을 제시하였다. 흡열원과 접촉면의 불균일함과 공급열량의 편차에 의해 발전량이 차이를 보이기 때문에 열원의 크기와 발전소자의 위치 배열을 조절하여 발전량을 증가시키는 열전발전 시스템 장치를 제안하였다.
상기한 대부분의 연구에서는 열전발전 출력 여부나 열전소자와 관련된 내용이 주로 다루어졌으며, 고온부 배관 내부의 열교환기 형상이나 열교환기 핀의 형상 최적화를 통한 발전효율에 대한 연구는 부족한 상황이다. 본 연구에서는 배기가스 폐열을 이용하는 열전발전 장치에 적용된 열교환 핀을 대상으로, 이의 치수최적화를 통해 열전발전 효율의 정도를 검토하였다. 치수최적화는 만족도 함수(Desirability Function)를 이용하여 이루어졌으며, 열·유동해석을 통하여 최대 온도차가 발생하는 열교환기핀 두께와 폭의 최적해를 결정하였다.
2. 대상체
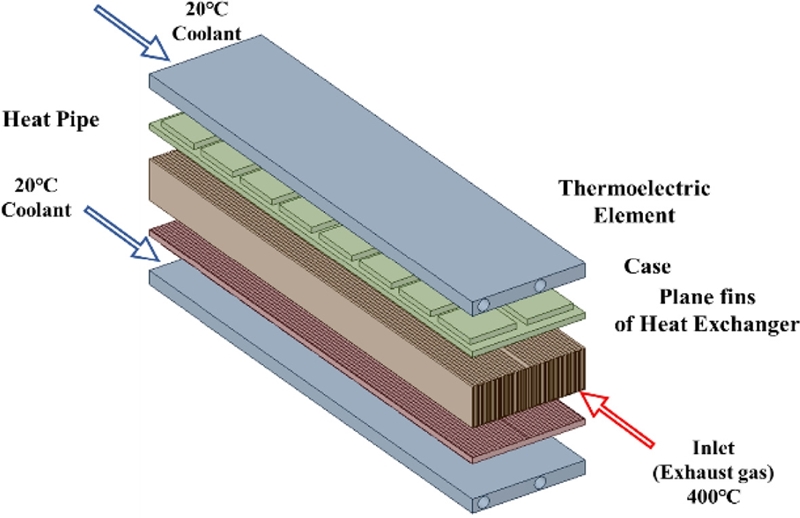
Fig. 1(a)는 열병합 발전소의 고온 배기가스 폐열을 이용하는 열전발전 장치의 전체적인 모식도로서, 배기가스가 지나가는 배기구에 2 kW급 열전발전 장치의 열교환기가 설치되어 있다. 열병합 발전소는 4층으로 구성되며 2층 소음기 후단에서 3층의 배기구를 통해 열전발전 시스템으로 배기가스가 유입된다. 열전발전 장치는 Fig. 1(b)와 같이 100 W급 열교환기 단위 스택 10개가 병렬로 연결되어 있는 구조이며, 이를 상·하로 설치하여 총 발전 용량은 2 kW급이고, 크기는 길이 2,143, 폭 1,903 및 높이 1,489 mm이다. 400°C 고온의 배기가스가 우측의 입구단으로 유입되고 열교환기 단위 스택을 지나면서 열전소자와 냉각수에서 발생하는 온도차를 이용하여 제백 효과가 발행하여 전력생산이 이루어진다.
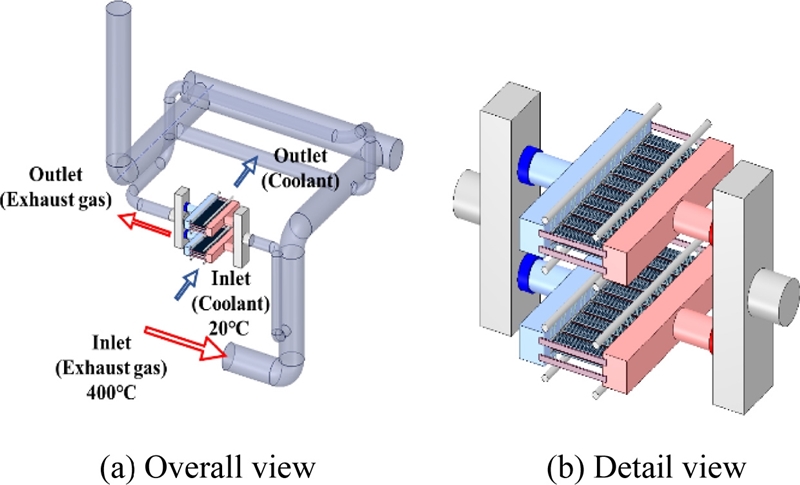
Schematic illustration of 2 kW-class thermo-electric generator installed in exhaust pipes of cogeneration plant
Fig. 2는 열교환기 단위 스택의 형상으로, 중앙에 고온의 배기가스가 지나가는 열교환 핀이 있으며, 상·하로 열전소자가 설치되어있고, 가장 바깥면에 20°C의 냉각수가 흐르는 냉각 장치가 위치한다. 열전소자는 PGM-TK-1 모델10로 상·하부에 각각 16개씩 총 32개가 사용되었다. 열교환 핀은 폭 100, 높이 35 및 길이 410 mm로 폭과 높이에 비하여 길이가 크므로 압력 손실이 작게 나타나는 Plain 타입11으로 선정하였다.
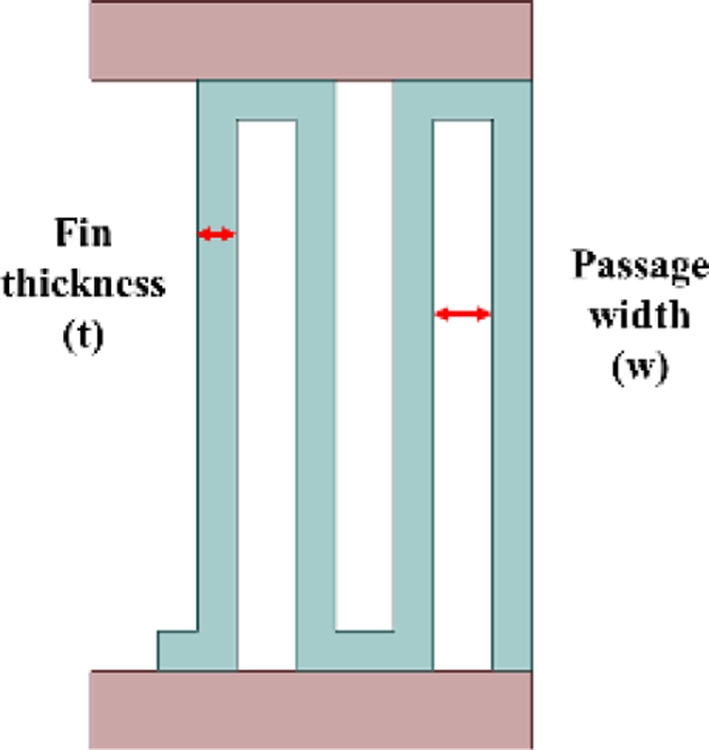
Fig. 3은 열교환기의 단면도로서, 총 68개의 열교환 핀이 설치 되어있으며, 유로 폭(w)과 핀 두께(t)가 각각 2 및 0.5 mm이다. 열교환 핀은 열변형과 부식에 강한 스테인리스 스틸인 STS316L12로 제작되었다.
열전발전에서 열전소자 양측의 온도차가 클수록 발전량이 증가하기 때문에 열교환기의 성능은 발전량과 밀접하게 연관되어 있고,13 열교환 핀의 w 및 t에 따라 차압 및 온도차가 변화하므로,11 이는 설계에 중요한 인자가 된다. 따라서 400°C 배기가스의 유속 조건에서 w와 t의 변화에 따른 차압과 온도차를 열·유동해석을 통해 계산하였으며, 온도차를 최대로 하고 차압 조건을 만족하는 w와 t의 치수최적설계를 수행하였다.
3. 열·유동해석
3.1 해석 방법
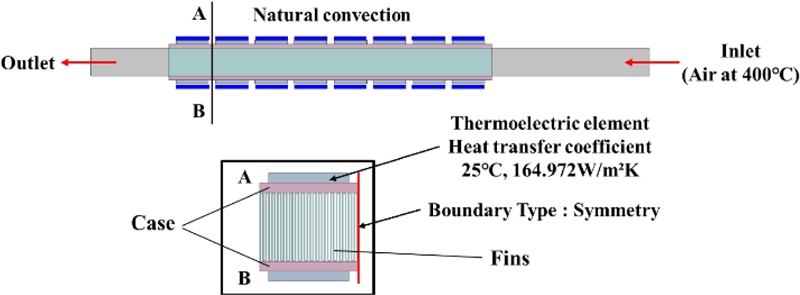
열·유동해석은 고온부 배관 내 열교환기 단위 스택에서 대칭 경계 조건을 고려한 1/2 형상에 대하여 이루어졌으며, 상용해석소프트웨어인 ANSYS CFX14를 이용하였다. 열전발전 스택의 입구 및 출구의 온도차와 차압을 확인하기 위해 냉각 장치는 해석에서 고려하지 않았으며, 완전 발달 유동이 이루어지도록 단위 스택 입구단에서 300, 출구단에서 100 mm의 거리를 두고 고온부 배관을 모델링하였다. 고온부 배관 크기에 비해 열교환핀의 두께와 유로 폭이 작아 효율적으로 격자를 생성하기 위해 해석의 정확도가 높은 육면체를 우선적으로 생성하는 Hex-Dominant Meshing을 적용하였다. 열교환 핀의 격자수는 사례연구에 따라 52만개-120만개 사이이며, 고온부 배관 전체 격자수는 100만개-360만개 수준이다. 해석에는 배기가스 대신 공기를 사용하였으며, 온도 변화에 따라 변하는 상태량인 열전도도(Thermal Conductivity)와 동점성계수(Dynamic Viscosity)는 400과 270°C의 평균값을 적용하였다. 또한, 400°C의 배기가스가 고온부 배관에 지날 때 열전소자 PGM-TK-1 모델10이 상온공기(25°C)에 노출되었을 경우 사용되는 총괄 열전달 계수(Heat Transfer Coefficient, 164.972 W/m2K)와 자연대류 조건(h = 5W/m2K)을 적용하였다. 이때, 총괄 열전달 계수는 열전소자의 전도 열저항에 의해 구해졌다. 열·유동해석의 경계 조건을 모식도로 나타내면 Fig. 4와 같고, 각 해석 대상체에 적용된 물성치를 Table 1에 정리하였다.
3.2 지배방정식
열·유동해석은 유체 연속방정식, 운동방정식 및 난류유동 에너지방정식을 통해서 수행된다. 유체는 3차원 정상상태, 비압축성 유체로 가정하였고, 이때 비압축성 유체에 대한 연속방정식은 다음 식(1)과 같다. 여기서, i와 j는 직교좌표계의 방향으로 1, 2 그리고 3으로 구성되며, 이는 각각 x, y, z 방향을 나타낸다.
| (1) |
운동방정식은 Reynolds Average Navier-Stroke (RANS) 모델을 기반으로 계산되었고, 식은 다음 식(2)와 같다.
| (2) |
열교환기 내부 고온 가스의 난류 유동 에너지방정식은 계산 속도가 빠르고 해석의 수렴성을 확보하기에 가장 적합한 k-ε 모델15을 사용하였다.
| (3) |
이때, 레이놀즈 응력은 식(4)의 부씨네스크 근사(Boussinesq Approximation)에 의해 계산되고, k-ε 모델의 난류점성 계수(Turbulent Eddy Viscosity)는 식(5)와 같이 나타난다.
| (4) |
| (5) |
난류 열유속(Turbulence Heat Flux)은 식(6)으로 계산된다.
| (6) |
고온부 배관의 열교환 핀에 고온의 배기가스가 유입될 때 유체와 고체 간의 복합열전달이 발생한다. 이는 식(7)의 복합열전달 방정식에 의해 계산된다.
| (7) |
고온부 배관과 열전소자 간의 열전도는 3차원 열전달 방정식을 통해서 계산되며 식은 다음 식(8)과 같다.
| (8) |
열전소자와 고온부 배관의 자연대류가 적용되었다. 상온 공기(25°C)의 자연대류 조건(h = 5W/m2K)이 적용되었고, 아래와 같은 식(9)로 계산된다.
| (9) |
단위 스택 입구단에서 주어진 공기의 온도와 유속 조건에서 유로 폭(w)과 핀 두께(t)의 변화에 따른 공기의 차압과 온도차는 단위 스택 출구단에서의 계산된 압력과 온도의 결과로 구해진다. 이때, 공기의 유속은 5에서 30m/s 범위로 하였고, w는 1에서 4 mm로 그리고 t는 0.3에서 0.7mm로 변화시키는 사례연구를 수행하였다.
3.3 해석 결과
사례연구에 앞서 공기의 유속이 10 m/s일 때, 유로 폭(w)과 핀 두께(t)는 각각 2 및 0.5 mm인 열교환기 단위 스택의 초기 모델에 대하여 열·유동해석을 수행하였다. Fig. 5는 이의 결과로서, 열교환 핀에서 열전소자로 열전달이 발생하여 Fig. 5(a)와 같이 출구단으로 갈수록 온도가 감소하여 약 130°C의 온도차가 발생하였다. 압력의 변화는 Fig. 5(b)와 같으며, 37 mmH2O 수준의 차압이 발생하였다.
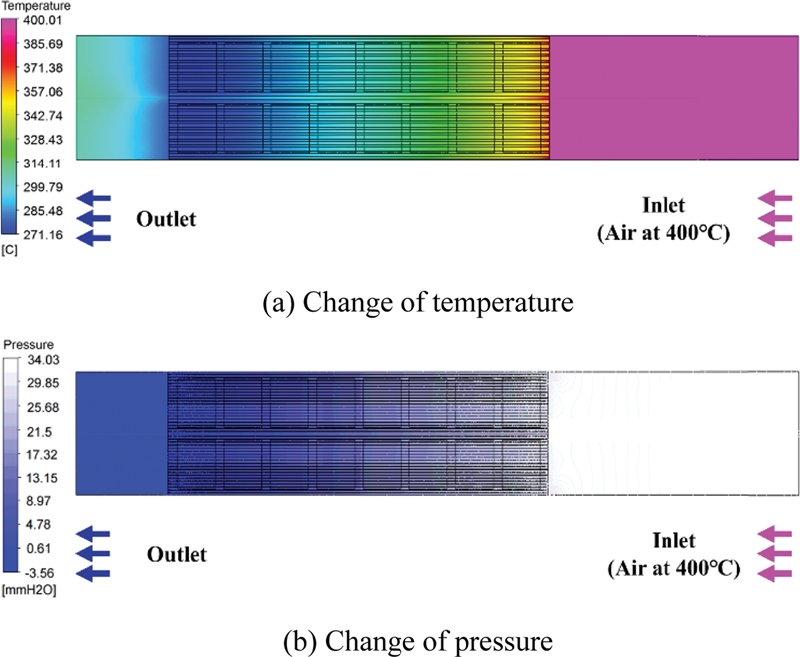
Results of thermal fluid analysis in stack of heat exchanger (w = 2, w = 0.5 mm) for velocity of exhaust gas with 10 m/s
공기 유속의 변화에 대한 차압과 온도차를 살펴보기 위하여, 초기 설계안인 열교환 핀의 t가 0.5 mm에 대한 w의 영향을 살펴보았다. Fig. 6은 이의 결과이다. 차압의 경우 Fig. 6(a)와 같이 공기 유속이 증가함에 따라 차압은 증가하였다. 이때, w가 커질수록 차압 증가의 경향이 대폭 감소하였는데, 차압 감소는 배기가스의 유동에 대한 저항을 낮추고 원활한 열교환을 유발하여 열전모듈 흡열량의 증가로 이어진다.16 Park 등17 은 배기가스 배출용으로 사용되는 송풍기의 사용 적정 차압을 100 mmH2O 이하로 제시하였는데, 이를 만족하는 열교환기 단위 스택의 조건은 공기 유속 10m/s에서 w가 2 및 4mm임을 알 수 있다. Fig. 6(b)는 온도차의 결과로서 공기 유속이 증가함에 따라 온도차는 감소하였다. 여기서 w에 대한 영향을 살펴보면, w가 커짐에 따라 온도차의 감소폭도 커지게 된다. w가 가장 작은 1mm의 경우 온도차가 가장 크게 나타나 열전발전에 유리하지만, Fig. 6(a)와 같이 차압이 크게 발생하여 서로 상충되는 관계가 나타남을 알 수 있다.
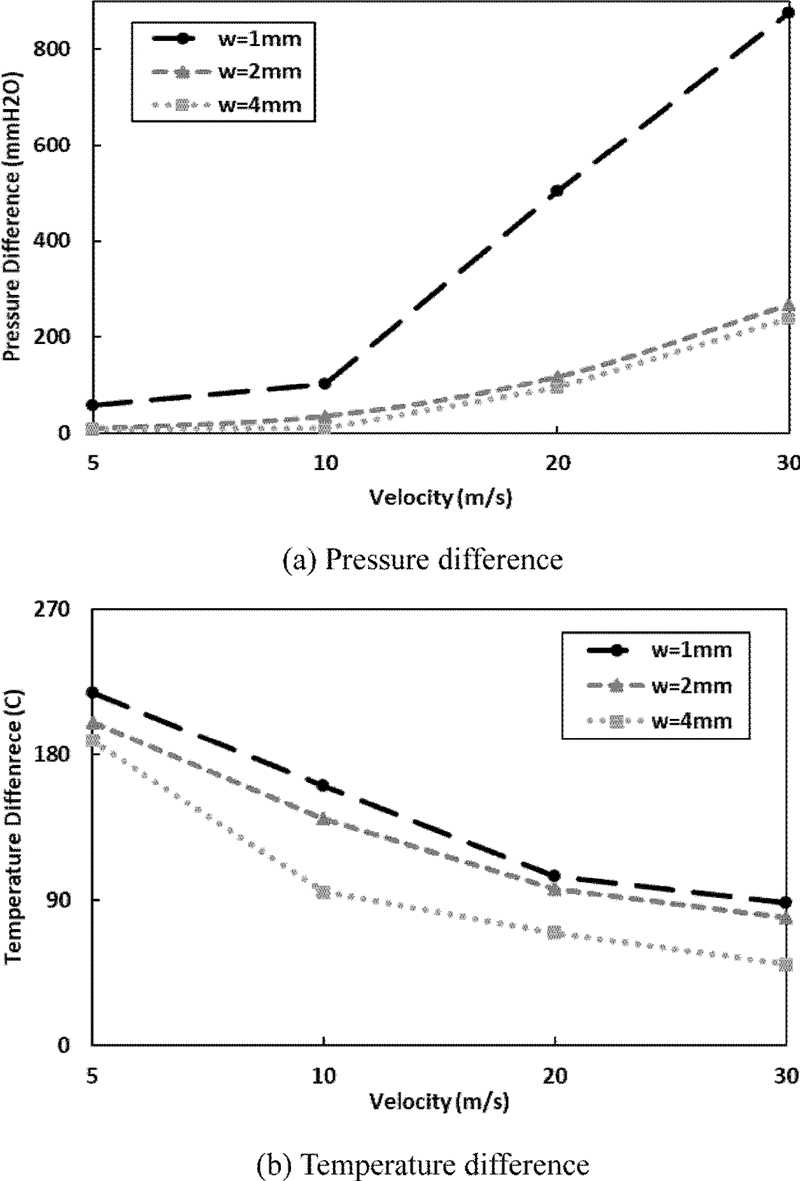
Pressure and temperature differences at t = 0.5 mm in relation with velocity of exhaust gas due to change of w
한편, Fig. 7은 초기 설계안인 열교환 핀의 유로 폭 w = 2mm에 대하여 공기 유속의 변화에 따른 차압과 온도차의 해석 결과로서 t의 변화에 따라 미치는 영향을 보여준다. Fig. 7(a)는 차압의 경우로서 공기의 유속이 느린 영역에서는 t의 영향이 적으나, 유속이 30 m/s 이상인 경우 t가 커짐에 따라 차압이 증가하는 경향이 보인다. 이에 반해 온도차는 Fig. 7(b)와 같이 공기의 유속이 빨라짐에 따라 열전모듈의 흡열량이 감소하여 줄어든다.16 이때 t에 의한 영향이 뚜렷하게 나타나는데, t가 커짐에 따라 열전모듈과 열교환 핀의 접촉 면적이 증가하여 온도차가 크게 발생하였다.
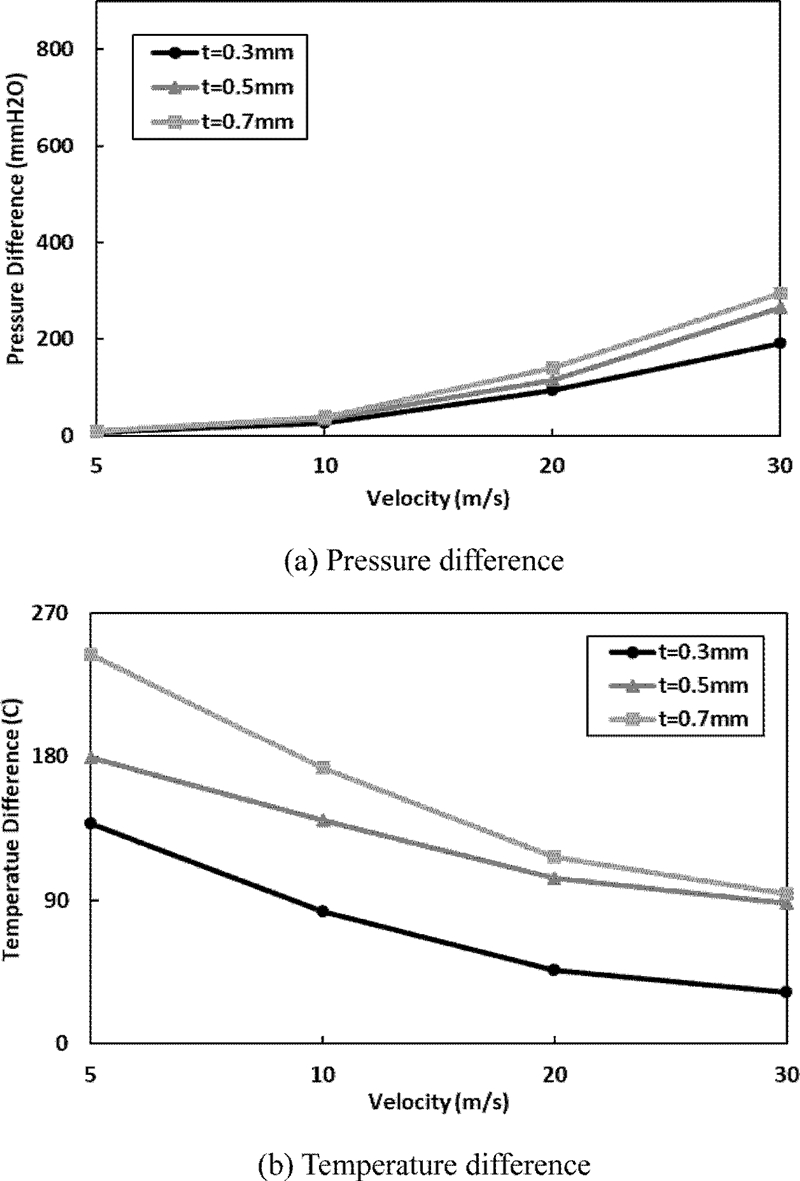
Pressure and temperature differences w = 2 mm in relation with velocity of exhaust gas due to change of t
이상의 결과로부터 적정 차압인 100 mmH2O 이하의 조건을 만족하며, 온도차가 최대가 되기 위해서 공기의 속도가 10m/s이하이어야 한다는 것을 확인하였다. 그리고 열교환 핀의 w와 t는 차압과 온도차에 대하여 서로 상충되는 영향을 주고 있으므로, 열전발전의 발전량과 밀접한 관련이 있는 열교환기의 성능을 높이기 위하여 두 값을 설계변수로 치환하고 최적해를 찾기 위한 치수최적설계의 수행이 필요하다.
4. 치수최적설계
4.1 최적설계 정식화
열전발전 시스템의 열교환기 효율을 높이기 위해서는 열전소자로 온도전달이 잘 이루어져야하며, 고온의 유체가 안정적으로 흐를 수 있도록 적절한 압력차가 필요하다. 따라서 열교환기의 효율과 고온 배기가스의 원활한 유동을 위하여 열교환 핀의 유로 폭(w)과 핀 두께(t)에 대한 치수최적설계가 수행되었다.
열교환기 단위 스택 입구 및 출구단에서 공기의 온도차인 ΔT(w, t)를 최대화하기 위한 최적설계 정식화가 이루어졌다. 이때, 공기의 입구속도가 10m/s인 조건에서 입구 및 출구단에서 차압 ΔP(w, t)는 100mmH2O 이하가 되어야 한다. 치수최적설계를 위한 목적함수 그리고 설계변수 및 제약 조건은 다음과 같다.
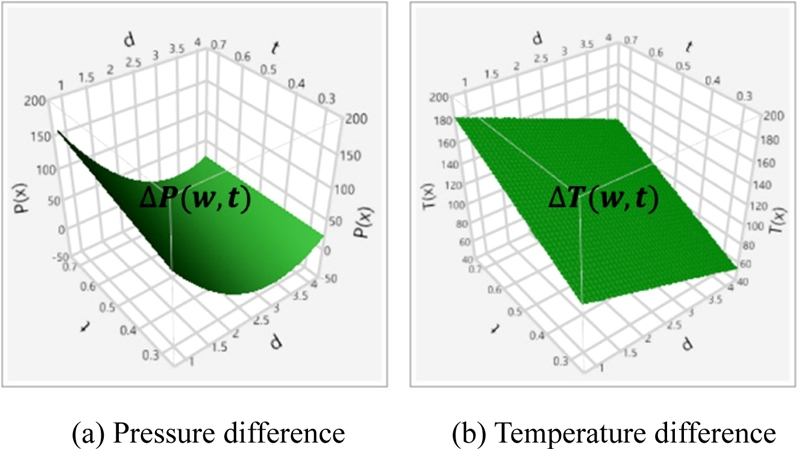
설계영역 탐색에 필요한 근사식 도출을 위해 실험계획법(Design of Experiments, DOE)이 수행되었다. 완전요인배치법을 사용하여 3수준 2인자로 32회의 실험 조건이 적용되었고, Table 2와 같이 w와 t에 대하여 각각 9개의 실험점이 생성되었다. 실험계획법으로 얻어진 각 실험점에서의 목적함수 ΔT(w, t)와 제약 조건인 ΔP(w, t)를 대상으로 단계적 회귀분석(Stepwise Regression Analysis)을 이용한 반응표면법(Response Surface Method, RSM)으로 근사식이 도출되었다. 이때 SAS사의 상용통계해석 프로그램인 JMP18가 이용되었고, Table 3에 도출된 근사식을 수식으로 나타내었다. Fig. 8은 근사식으로 얻어진 ΔT(w, t)와 ΔP(w, t)의 등고선도(Contour Plot)이다.
단계적 회귀분석을 사용하여 생성된 근사식의 적합도를 확인하기 위해 0에서 1 사이의 값을 가지는 결정계수 R2 (RSquare)19와 조정결정계수 (Adjusted RSquare)20가 사용되었다. Table 4는 이의 결과로서 R2와 모두 1에 가깝게 나타나 근사식의 적합도가 높음을 알 수 있다.
4.2 만족도 함수를 적용한 최적설계
목적함수와 제한 조건을 만족하는 최적해를 도출하기 위하여 만족도 함수(Desirability Function)21를 적용하였다. 만족도 함수는 RSM으로 생성된 근사식이 설계변수의 조합에 따른 목적함수에 만족하는 정도를 평가하는 함수로서, 0에서 1까지의 범위 내에서 1일 때 가장 이상적인 최적해라고 평가한다. 전체 만족도 함수 D는 목적함수와 제한 조건에 대한 개별 만족도 dn에 대한 기하평균을 적용하여 아래 식(10)과 같이 계산할 수 있다.
| (10) |
설계변수에 개별 만족도를 정의하기 위하여 예측분석도(Prediction Profiler)를 이용하여 설계변수인 w와 t가 ΔP(w, t) 및 ΔT(w, t)에 미치는 영향을 확인하였다. Fig. 9는 이의 결과로서, ΔP(w, t)는 w에 대하여 최솟값이 존재하는 비선형적인 특성을 보인다. 이에 비해 ΔT(w, t)의 경우, w와 t는 모두 선형적으로 영향을 미치지만, 서로 상충되는 효과가 나타남을 알 수 있다. 따라서 ΔP(w, t)가 100 mmH2O 이하가 되는 범위 내에서 w는 줄이고 t는 늘리는 설계가 필요하다. 전체 만족도 함수 D의 최댓값은 ΔP(w, t)와 ΔT(w, t)의 개별 만족도 d1과 d2에 대하여 w = 1.4, t = 0.7mm에서 0.924로 얻어졌다. 이때, ΔP(w, t)는 94.4 mmH2O 그리고 ΔT(w, t)는 164.3°C이다. Table 5는 초기 모델과 비교한 결과로서, ΔP(w, t)가 100 mmH2O 이하를 만족하는 조건에서 ΔT(w, t)는 약 27% 증가하였다.
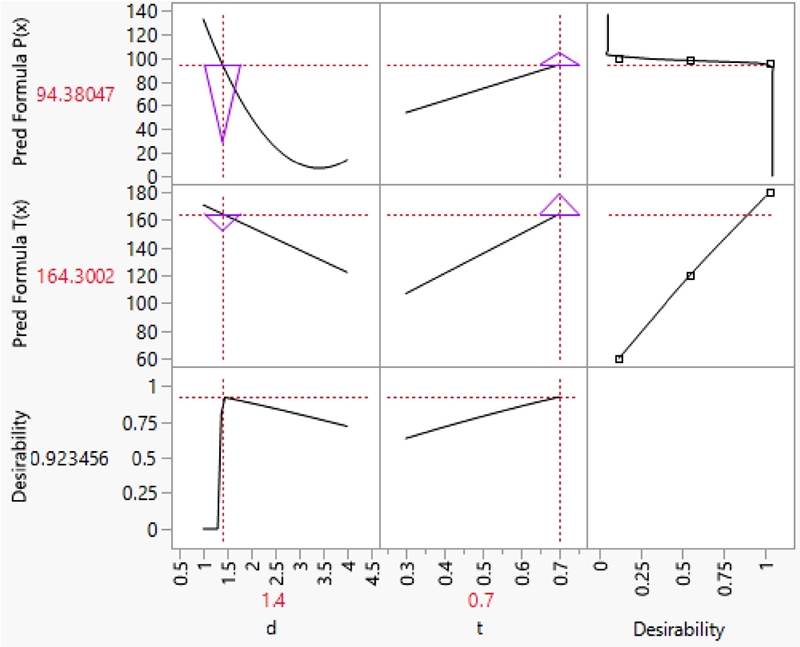
Prediction profilers of ΔP(w, t), ΔT(w, t) and desirability functions with regarding to design variables
만족도 함수로 얻어진 최적해를 검증하기 위하여, 설계변수의 최적해 w = 1.4, t = 0.7mm로 생성된 열교환 핀의 유한요소 모델을 이용한 열·유동해석을 수행하였다. 해석은 앞서 수행된열·유동해석 조건과 동일하게 진행되었으며, Table 6은 이의 결과로서 목적함수 ΔT(w, t)와 제약 조건 ΔP(w, t) 모두 예측값과 검증값이 유사함을 확인하였다.
5. 결론
본 연구에서는 배기가스 폐열을 이용하는 열전발전 장치에 적용된 열교환 핀을 대상으로, 이의 치수최적화를 통해 열교환기의 차압 성능과 온도차의 변화를 고찰하였다. 얻어진 결과는 다음과 같다.
(1) 열교환기에서 발생하는 차압은 공기 유속이 증가함에 따라 증가하였고, t = 0.5mm인 경우 w가 커질수록 차압 증가의 경향이 대폭 감소하였다. 사용 적정 차압인 100 mmH2O 이하를 만족하는 열교환기 단위 스택의 조건은 공기 유속 10 m/s에서 w가 2 및 4 mm로 나타났다.
(2) 온도차는 공기 유속이 증가함에 따라 감소하였는데, t = 0.5mm인 경우 w가 커짐에 따라 온도차의 감소폭도 커지게 된다. w = 1 mm의 경우 온도차가 가장 크게 나타나 열전발전에 유리하지만, 차압이 크게 발생하여 서로 상충되는 관계가 나타났다.
(3) 공기의 입구속도가 10m/s인 조건에서 차압이 100 mmH2O 이하가 되어야 하는 치수최적설계 정식화가 이루어졌으며, 실험 계획법과 단계적 회귀분석을 사용하여 근사식을 생성하였다.
(4) 만족도 함수를 적용하여 얻어진 치수최적설계로부터 각 설계변수인 w와 t의 최적해는 각각 1.4 및 0.7 mm이며, 이때 차압과 온도차는 각각 94.4 mmH2O 및 164.3°C로 얻어졌다.
(5) 차압 성능 100 mmH2O 이하를 만족하는 조건에서 얻어진 온도차의 최적해는 초기 모델 대비 약 27% 증가하여 열전발전의 발전효율이 증가할 것이라고 예상된다.
NOMENCLATURE
| ρ : | Density |
| p : | Pressure |
| μ : | Viscocity |
| T : | Temperature |
| t : | Time |
| λ : | Thermal Conductivity |
| CP : | Specific Heat Capacity |
| gi : | Acceleration due to Gravity |
| β : | Coefficient of Thermal Expansion |
| T0 : | Initial Temperature |
| μt : | Turbulent Eddy Viscosity |
| ke : | Turbulent Kinetic Energy |
| δi,j : | Kronecker Delta |
| Cμ : | Constant in the k-ε Models |
| σT : | Turbulent Prandtl Number |
| k : | Coefficient of Thermal Conductivity |
| : | Heat Generation |
| q : | Thermal Conductance |
| h : | Convective Heat Transfer Coefficient |
| A : | Cross Sectional Area |
| T∞ : | Ambience Temperature |
| Ts : | Temperature of Pipe Surface |
Acknowledgments
본 연구는 중소벤처기업부 ‘기업연계형 연구개발 인력양성사업’(다학제기반 고성능 자동차·기계부품 설계인력양성 사업단, No. N0001592)의 재원으로 한국산업기술진흥원(KIAT)의 지원을 받아 수행되었으며, 대상품에 대한 기술정보를 제공해 주신 ㈜스페이스센싱에 감사드립니다.
References
- Seo, J. G., Park, J. H., Oh, Y. J., and Park, S. W., “Prediction of Greenhouse Gas Emission from Heavy Duty Vehicle Using Simulation Method,” Transactions of the Korean Society of Mechanical Engineers B, Vol. 26, No. 10, pp. 1824-1827, 2016.
- Kim, K. H., “Thermal Power Generation Technology for Converting Waste Heat into Electricity,” Convergence Research Review, Vol. 4, No. 8, pp. 35-70, 2018.
-
Chung, J. H., Kim, W. C., Lee, J. H., and Yu, T. U., “Experimental Study of Power Generation Performance of Small-Scale Thermoelectric System,” Transactions of the Korean Society of Mechanical Engineers B, Vol. 34, No. 4, pp. 383-390, 2010.
[https://doi.org/10.3795/KSME-B.2010.34.4.383]

-
Woo, B. C., Lee, H. W., and Suh, C. M., “Characteristic of Electric Generation for the Water Flow Rate in Thermoelctric Generator Using Hot Water,” Transactions of the Korean Society of Mechanical Engineers B, Vol. 26, No. 10, pp. 1333-1340, 2002.
[https://doi.org/10.3795/KSME-B.2002.26.10.1333]

- Han, H. S., Kim, M. K., Um, S. K., and Kim, S. Y., “Performance of Thermoelectric Power Generator with Various Thermal Conditions,” Korean Journal of Air-Conditioning and Refrigeration Engineering, Vol. 22, No. 3, pp. 165-170, 2010.
- Kushch, A. S., Bass, J. C., Ghamaty, S., and Eisner, N., “Thermoelectric Development at Hi-Z Technology,” Proc. of the 20th International Conference on Thermoelectrics, pp. 422-430, 2001.
- Nagao, K., Nagai, A., Fujii, I., Sakurai, T., Fujimoto, M., et al., “Design of Thermoelectric Generation System Utilizing the Exhaust Gas of Internal-Combustion Power Plant,” Proc of the 17th International Conference on Thermoelectrics, pp. 468-472, 1998.
- Jang, B., Han, S., and Kim, J., “Simulation of Thermoelectric Performance for Thermoelectric Generation Module Design,” Proc. of the Korean Society of Precision Engineering Conference, pp. 445-446, 2009.
- Moon, C. J., Cheang, E. H., Lim, J. M., Park, S. J., Kim, T. G., et al., “A Study for Thermoelectric Generator System and Caused Low Thermoelectric Power,” Proc. of the KSES Spring Annual Conference, pp. 68-74, 2008.
- HTRD-Korea Inc., “TE Module,” http://www.htrdkorea.com/tem.htm, (Accessed 16 DECEMBER 2020)
- Jung, Y. K., Kim, H. J., Lee, H. S., and Yoon, J. I., “A Numerical Study of Plate Fin Heat Exchanger with Variation in Fin Configuration,” Journal of the Korean Solar Energy Society, Vol. 23, No. 1, pp. 2444-2447, 2014.
- Kwak, J. S., An, W. G., Yang, I. Y., Park, Y. I., and Yang, S. S., “Development of the Plate-Fin Type Heat Exchanger for High Temperature Application-Part 1: Design and Manufacture,” Proc. of the KSME Spring Conference, pp. 2137-2142, 2005.
- Han, H. S., Kim, M. K., Kim, S. Y., and Um, S. K., “Characteristics of Power Generation Using a Thermoelectric Cooler,” Transactions of the Korean Society of Mechanical Engineers B, Vol. 25, No. 4, pp. 130-133, 2009.
- ANSYS, “Computational Fluid Dynamics (CFD) Simulation,” https://www.ansys.com/products/fluids, / (Accessed 29 DECEMBER 2020)
-
Launder, B. E. and Spalding, D. B., “The Numerical Computation of Turbulent Flows,” Computer Methods in Applied Mechanics and Engineering, Vol. 3, No. 2, pp. 269-289, 1974.
[https://doi.org/10.1016/0045-7825(74)90029-2]

- Shin, J. H., Han, H. S., Kim, Y. H., Kim, S. Y., and Hyun, J. M., “Cooling Performance of Thermoelectric Module with Air-Cooled Heat Exchanger Fins,” Korean Journal of Air-Conditioning and Refrigeration Engineering, Vol. 22, No. 3, pp. 171-179, 2010.
-
Park, Y. Y., Song, H. C., Ahn, G. J., and Shim, C. S., “Preliminary Study on Factor Technology of Selective Catalytic Reduction System in Marine Diesel Engine,” Journal of Navigation and Port Research, Vol. 40, No. 4, pp. 173-181, 2016.
[https://doi.org/10.5394/KINPR.2016.40.4.173]

- SAS Institute Inc., “2020, JMP Pro 15,” https://www.jmp.com/en_us/software/new-release/new-in-jmp-and-jmp-pro.html, (Accessed 29 DECEMBER 2020)
- Jeon, J. H., Kim, H. J., Kim, Y. J., and Huh, S. C., “A Study on Shape Optimization of in-Lin Type Subsea Separator,” Proc. of the KSME Spring Conference, pp. 273-277, 2018.
- Kim, D. S. and Lee, J. S., “Optimization of the Stress and Displacement of Valve by Using RSM and NSGA-Ⅱ,” Proc. of the KSME Spring Conference, pp. 43-50, 2012.
-
Lee, K. K. and Han, S. H., “Optimization of Wind Turbine Pitch Controller by Neural Network Model based on Latin Hypercube,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 36, No. 9, pp. 1065-1071, 2012.
[https://doi.org/10.3795/KSME-A.2012.36.9.1065]


M.S. candidate in the Department of Mechanical Engineering, Dong-A University. Her research interest is numerical simulation and design optimization.
E-mail: 1970701@donga.ac.kr

Ph.D. candidate in the Department of Mechanical Engineering, Dong-A University. His research interest is numerical simulation.
E-mail: gudwns3481@gmail.com

Professor in the Department of Mechanical Engineering, Dong-A University. His research interest is structural analysis and reliability based design.
E-mail: shhan85@dau.ac.kr