초정밀 직선 스테이지의 6자유도 운동 오차 보정을 위한 미세 구동 스테이지 개발 및 성능 평가

1. 서론

우주항공 부품, 초정밀 금형, 미세 절삭 가공(Micro-Cutting) 등 초정밀 가공에 대한 수요는 꾸준히 증가하고 있고, 독일, 일본 등의 가공 선진국의 경우 전략 기술로 초정밀급 가공기술이 관리되고 있다.^1-3 초정밀의 가공 품질은 가공시스템 자체의 정확도 및 정밀도 성능이 확보되어야 한다. 가공시스템의 이송 성능은 구동계의 기하학적 오차, 절삭력 기인 오차, 열 변위 오차 등에 의해 악화된다. 따라서, 형상 정밀도 향상을 위해 다자유도 오차에 대한 실시간 측정 및 보정 기술이 연구되고 있다.^4-8

이중서보 스테이지(Dual-Servo Stage)는 초정밀급의 위치 정확도와 넓은 이송 범위를 위해 제안된 이송시스템 개념으로 다자유도 오차를 실시간으로 측정 및 보정을 할 수 있다.^4-11 넓은 이송 범위를 가진 조동 스테이지(Coarse Stage)에 높은 제어분해능과 응답 속도를 가진 미세 구동 스테이지(Fine Stage)가 직렬로 연결된 형태가 일반적인 이중서보 스테이지의 구조이다. 조동 스테이지가 미세 구동 스테이지를 목표 위치로 이송하고, 미세 구동 스테이지는 이동 및 가공 중에 발생한 다자유도 오차를 실시간으로 측정 및 보정함으로써 위치 오차를 감소시킨다.^4-8

이러한 이중서보 스테이지에 대한 다양한 연구들이 있어 왔고, 대부분은 6자유도 운동 오차 중 일부만을 측정 및 보정하였다. 이에, Choi와 Kim은 Halbach 자석 배열과 보이스코일 모터를 이용하여 6자유도 운동이 가능한 미세 구동 스테이지를 개발하였고, 이를 평면 스테이지에 부착하여 이중서보 스테이지를 제작하였다.^7,8 한편, Lee는 압전 구동기와 유연 힌지로 구성된 스튜어트 플랫폼(Stewart Platform)과 5개의 정전용량 센서를 이용하여 직선 스테이지의 5자유도 운동 오차(선형 변위 오차 제외)를 실시간 측정 및 보정하고, 레이저 간섭계를 이용하여 나머지 선형 변위 오차에 대한 오프라인 보정을 수행하였다.^12,13

본 논문은 초정밀 가공에 활용할 수 있도록 초정밀 보정시스템의 구조적 강성을 보완하는 3-RPS + 3-RPR 유연 힌지 기반 미세 구동 스테이지 구조 및 보정 방법을 제안한다. 제안한 미세 구동 스테이지는 콤팩트하고 6자유도의 초정밀 이송이 가능하여 이중서보 시스템의 보정 스테이지로서 효과적으로 활용가능하다. 2장에는 미세 구동 스테이지의 설계 및 기구학 분석에 대하여 설명하고, 3장에는 개발된 미세 구동 스테이지를 활용한 이중서보 스테이지의 구축과 이에 대한 성능 평가 및 검증 실험 결과에 대하여 기술한다.

2. 미세 구동 스테이지 구조 및 기구학 분석

2.1 미세 구동 스테이지 구조 설계

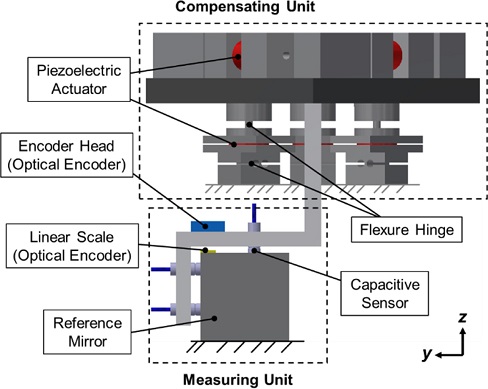
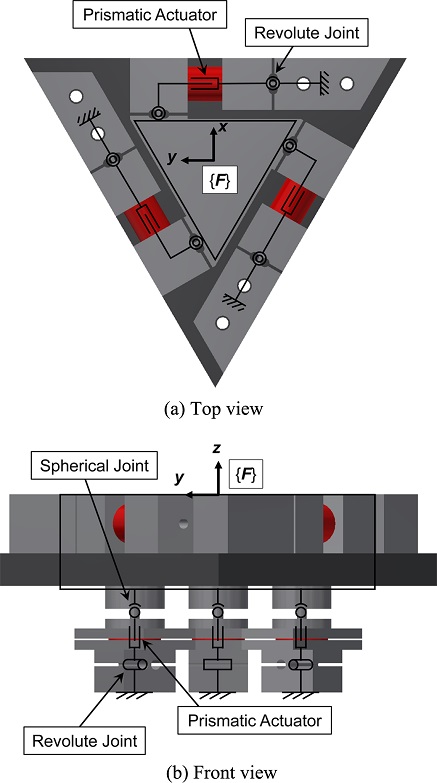
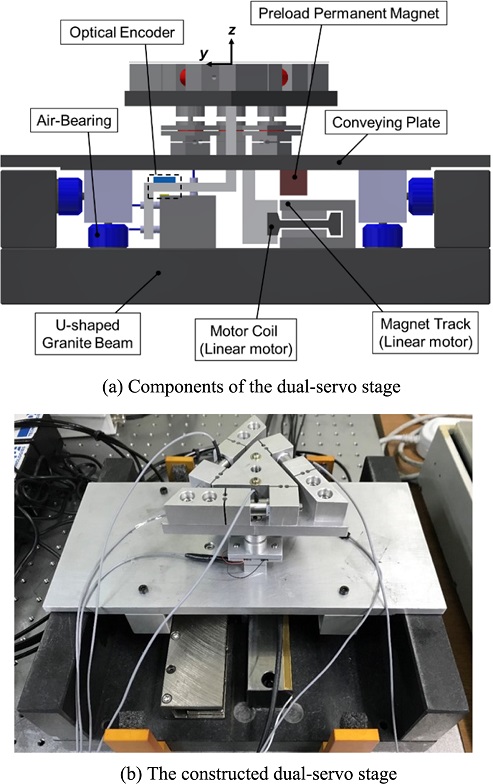
미세 구동 스테이지는 Fig. 1과 같이 보정 유닛(Compensating Unit)과 측정 유닛(Measuring Unit)으로 구성된다. 보정 유닛은 Fig. 2와 같이 3-RPS (Revolute-Prismatic-Spherical) 병렬 기구와 3-RPR (Revolute-Prismatic-Revolute) 병렬 기구가 직렬로 연결된 구조를 가지며, 이는 6자유도 운동 구현이 가능하다. 그리고, 두 병렬 기구의 선형 구동기(Prismatic Actuator)와 회전/구면 조인트(Revolute/Spherical Joint)에는 압전 구동기(Piezoelectric Actuator)와 유연 힌지(Flexure Hinge)가 사용된다. 유연 힌지는 기계적 조인트의 한계인 스틱 슬립(Stick-Slip)과 마모의 문제점을 최소화한다는 장점 때문에, 압전 구동기는 높은 응답 속도와 제어분해능을 가지기 때문에 각각 활용되었다.¹²

Fig. 1

Structure of the fine stage

Fig. 2

Structure of the compensating unit

측정 유닛은 Lee가 제안한 초정밀 측정 시스템을 활용하였으며, 기준 미러(Reference Mirror)와 5개의 정전용량 센서(Capacitive Sensor)를 이용하여 스테이지의 5자유도 운동 오차를 측정하고, 광학 인코더(Optical Encoder)를 이용하여 나머지 선형 운동 오차(Linear Motion Error)를 측정한다.^14,15 기준 미러와 광학 인코더의 리니어 스케일(Linear Scale)은 스테이지의 베이스에 고정되고, 인코더 헤드와 정전용량 센서는 이동하는 보정 유닛에 연결되므로 센서의 측정값은 스테이지에 오차가 발생함에 따라 변하게 된다.

2.2 측정 유닛의 오차 계산식

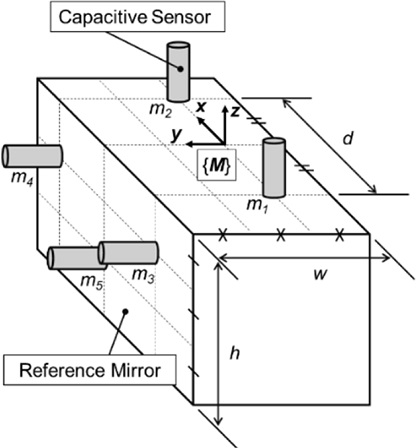
6자유도 운동 오차를 도출하기 위해 측정 유닛의 오차 계산식은 5개의 정전용량 센서와 광학 인코더의 측정값을 변수로하여 유도되었다. 측정 유닛의 좌표계는 1번과 2번 정전용량 센서 중간 지점에 설정한다. 이때의 측정 유닛의 좌표계에서 정의된 5자유도 운동 오차와 정전용량 센서의 거리 측정값 사이의 관계는 식(1)과 같다.^14,15

$\[ \begin{array}{c}{\delta }_{yx,M}=m_3+m_4-m_5\hfill \\ {\delta }_{zx,M}=\left(m_1+m_2\right)/2\hfill \\ {\epsilon }_{xx,M}=\left({2m}_5-m_3-m_4\right)/\left(2h/3\right)\hfill \\ {\epsilon }_{yx,M}=\left(m_1-m_2\right)/d\hfill \\ {\epsilon }_{zx,M}=\left(m_4-m_3\right)/d\hfill \end{array} \]$

(1)

여기서, δ_yx,M는 측정 유닛의 좌표계({M})에서 정의된 수평 진직도(Horizontal Straightness Error), δ_zx,M는 수직 진직도(Vertical Straightness Error), ε_xx,M는 롤 오차(Roll Error), ε_yx,M는 피치 오차(Pitch Error), ε_zx,M는 요 오차(Yaw Error), d는 1번과 2번 센서 프로브 사이의 거리, w와 h는 기준 미러의 폭과 높이, m_i (i = 1, 2, …, 5)는 정전용량 센서의 거리 측정값이다.

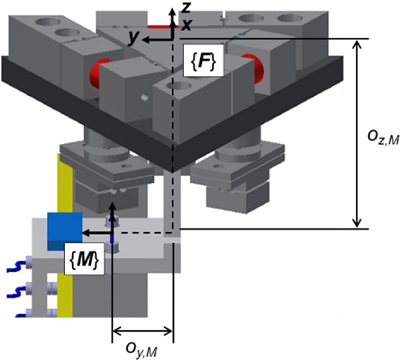
하지만, 구조적인 한계로 인해 측정 유닛의 좌표계와 기준 좌표계 사이에는 Fig. 3과 같이 아베 오프셋(Abbe’s Offset)이 존재하게 된다. 이 아베 오프셋을 고려하면, 기준 좌표계에서 정의된 5자유도 운동 오차는 다음 식(2)와 같이 계산된다.¹²

$\[ \begin{array}{c}{\delta }_{yx}={\delta }_{yx,M}-o_{z,M}{\epsilon }_{xx,M}\hfill \\ {\delta }_{zx}={\delta }_{zx,M}+o_{y,M}{\epsilon }_{xx,M}\hfill \\ {\epsilon }_{xx}={\epsilon }_{xx,M}\hfill \\ {\epsilon }_{yx}={\epsilon }_{yx,M}\hfill \\ {\epsilon }_{zx}={\epsilon }_{zx,M}\hfill \end{array} \]$

(2)

Fig. 3

Positions of sensor probes on a reference mirror

Fig. 4

Abbe’s offset between the measuring unit and the compensating unit

여기서, δ_yx는 기준 좌표계({F})에서 정의된 수평 진직도, δ_zx는 수직 진직도, ε_xx는 롤 오차, ε_yx는 피치 오차, ε_zx는 요 오차, 그리고 o_y,M와 o_z,M는 기준 좌표계({F})와 측정 유닛의 좌표계({M}) 사이의 y, z축 방향의 아베 오프셋이다.

나머지 광학 인코더를 이용한 선형 변위 오차 측정에서도 이러한 아베 오프셋이 존재한다. 따라서, 기준 좌표계에서 정의된 선형 변위 오차는 인코더에서 측정된 선형 변위 오차를 식(3)에 대입하여 계산된다.

$\[ {\delta }_{xx}={\delta }_{xx,E}+o_{z,E}{\epsilon }_{yx}-o_{y,E}{\epsilon }_{zx} \]$

(3)

여기서, δ_xx는 기준 좌표계({F})에서 정의된 선형 변위 오차, δ_xx,E은 광학 인코더의 좌표계({E})에서 정의된 선형 변위 오차, o_y,E와 o_z,E는 기준 좌표계({F})와 센서의 좌표계 ({E}) 사이의 y, z축 방향의 아베 오프셋이다.

2.3 보정 유닛의 기구학 분석

보정 유닛의 위치와 회전 각도에 대한 압전 구동기의 구동거리를 계산하기 위해 보정 유닛의 역기구학 방정식이 요구된다. 따라서, 식(4)와 같은 형태의 방정식을 유도한다.

$\[ a_j=f_{inv,j}\left(p_x,p_y,p_z,{\theta }_x,{\theta }_y,{\theta }_z\right) \]$

(4)

여기서, a_j (j = 1, 2, …, 6)는 j번째 압전 구동기의 구동 길이, f_inv,j (j = 1, 2, …, 6)는 j번째 압전 구동기에 대한 보정 유닛의 역기구학 함수, p_k (k = x, y, z)는 보정 유닛의 k축 위치, θ_k (k = x, y, z)는 보정 유닛의 k축 회전 각도이다.

보정 유닛의 6자유도 운동은 기준 좌표계에서 정의된 두 병렬 기구의 위치와 회전 각도의 변화량이 미소하다면 두 병렬 기구의 위치와 회전 각도의 중첩으로 근사된다. 따라서, 보정 유닛의 운동은 식(5)와 같이 표현된다.

$\[ \begin{array}{c}{p}_k=p_{k,RPS}+p_{k,RPR}\hfill \\ {\theta }_k={\theta }_{k,RPS}+{\theta }_{k,RPR}\hfill \end{array} \]$

(5)

여기서, p_k,RPS와 p_k,RPR (k = x, y, z)은 각각 기준 좌표계({F})에서 정의된 3-RPS와 3-RPR 병렬 기구의 k축 위치, θ_k,RPS와 θ_k,RPR (k = x, y, z)는 3-RPS와 3-RPR 병렬 기구의 k축 회전 각도이다.

3-RPR 병렬 기구는 x, y축 방향의 회전과 z축 방향 이동을 하지 않으므로 이에 관한 항은 소거된다. 또한, 3-RPS 병렬 기구의 z축 방향의 회전 각도와 x, y축 방향의 이동 거리는 회전/구면 조인트의 구속 조건으로 인해 x, y축 방향의 회전 각도의 함수로 표현된다.¹⁴ 따라서, 식(5)는 식(6)과 식(7)로 정리된다. 식(6)과 식(7)을 3-RPS 병렬 기구와 3-RPR병렬 기구의 역기구학 방정식에 대입하고 정리하면 식(4)와 같은 보정 유닛의 역기구학 방정식이 유도된다.^12,16

$\[ \begin{array}{c}{p}_{z,RPS}=p_z\hfill \\ {\theta }_{z,RPS}={\theta }_x\hfill \\ {\theta }_{y,RPS}={\theta }_y\hfill \end{array} \]$

(6)

$\[ \begin{array}{c}{p}_{x,RPR}=p_x-p_{x,RPS}\left({\theta }_x,{\theta }_y\right)\hfill \\ p_{y,RPR}=p_y-p_{y,RPS}\left({\theta }_x,{\theta }_y\right)\hfill \\ {\theta }_{z,RPR}={\theta }_z-{\theta }_{z,RPS}\left({\theta }_x,{\theta }_y\right)\hfill \end{array} \]$

(7)

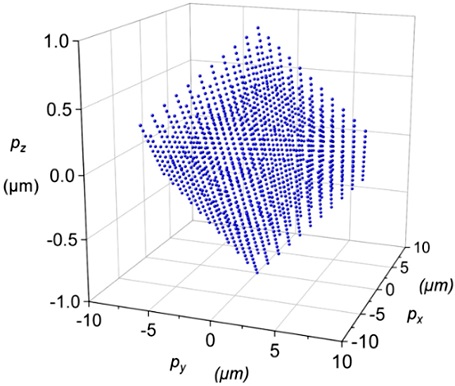
유도한 역기구학 모델과 가우스-뉴턴 방법을 활용하여 미세 구동 스테이지의 이송 영역이 Fig. 5와 같이 계산되었다. 3-RPS와 3-RPR 병렬 기구에 사용된 압전 구동기가 각각 ± 1, ± 7.5 μm의 구동 범위를 가질 때, 보정 유닛의 각 이송 자유도의 최대 범위는 Table 1과 같이 계산된다.

Fig. 5

Workspace of the compensating unit

Table 1

Maximum drive ranges of the compensating unit

3. 이중서보 스테이지 제작 및 성능평가

3.1 이중서보 스테이지의 제작

이중서보 스테이지는 개발된 미세 구동 스테이지를 조동 스테이지와 결합하여 Fig. 6과 같이 제작되었다. 조동 스테이지는 U자 석정반(U-Shaped Granite Beam)을 이송안내면으로 하는 공기 베어링(Air-Bearing) 스테이지의 형태를 가지며, 리니어 모터(Linear Motor)와 광학 인코더(Optical Encoder)를 활용한 피드백 제어를 통해 구동된다. 또한 수직 방향의 강성 확보를 위해 예압용 영구 자석(Preload Permanent Magnet)이 이송 플레이트(Moving Plate) 밑면에 장착된다. 제작된 이중서보 스테이지는 실험 환경에서 발생하는 진동의 영향을 최소화하기 위해 방진대(Vibration Isolator) 상에 설치되었다.

Fig. 6

The dual-servo stage equipped with developed fine stage

3.2 미세 구동 스테이지의 성능평가 실험

미세 구동 스테이지의 성능평가는 제작된 이중서보 스테이지를 활용하여 수행되었다. 이 실험에 사용된 측정 센서는 정전용량 센서(4810 Module, 2812 Probe, ADE Tech.), 기준 미러(Nitto Optical), 그리고 광학 인코더(RGH25F Encoder System)이며, 성능은 Table 2와 같다.

Table 2

Specification of the measuring instrument in experiments

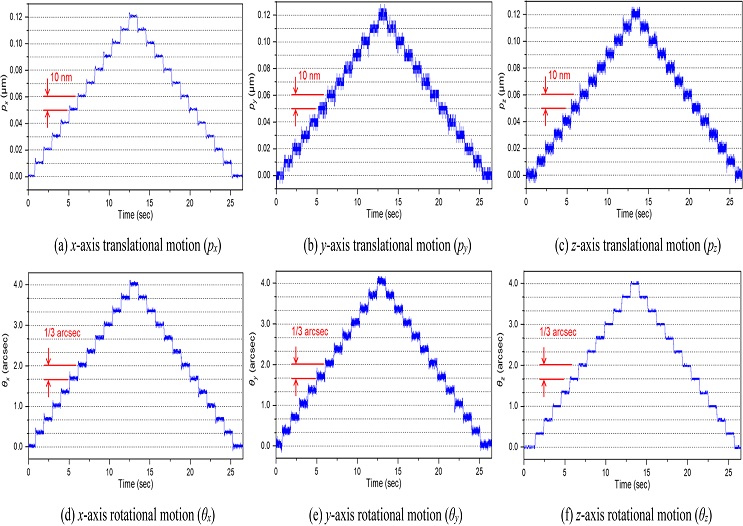
개발된 미세 구동 스테이지의 제어분해능을 확인하기 위해 1초 간격으로 10 nm 혹은 1/3 arcsec만큼의 스텝으로 이동과 회전을 지령하고, x축 방향 위치는 광학 인코더를 활용하여 측정하였고, y, z축 방향 위치 및 회전 각도는 5개의 정전용량 센서 및 레퍼런스 미러를 활용하여 Fig. 7과 같이 측정하였다. 미세 구동 스테이지가 10 nm와 1/3 arcsec 이하의 분해능으로 구동 가능함을 확인하였다.

Fig. 7

Consecutive step motion of developed fine stage

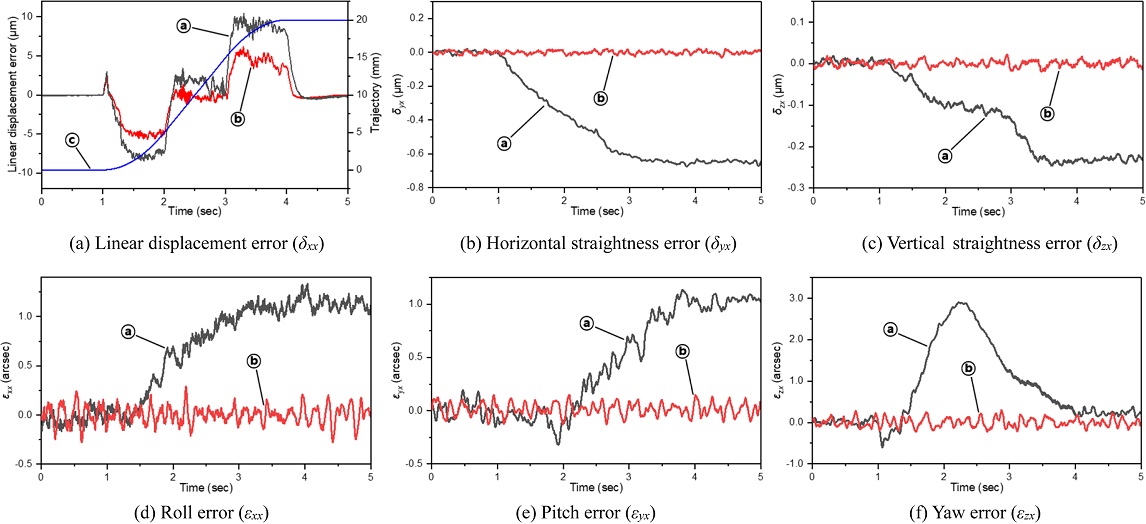
미세 구동 스테이지의 보정 성능은 조동 스테이지에 20 mm의 계단 이동을 명령하고, 이때 발생되는 6자유도 오차를 측정 및 보정하여 검증하였다. 오차 측정은 앞선 실험과 마찬가지로 측정 유닛을 통해 이루어졌다. Fig. 8의 ⓐ와 ⓑ는 각각 보정 전과 후의 6자유도 운동 오차를 의미하며, Fig. 8(a)의 ⓒ는 조동 스테이지의 기준 궤적을 나타낸다. 보정 후의 선형 운동 오차는 보정 전에 비해 8.2 μm 감소하였으며, 나머지 5자유도 운동 오차는 측정 유닛의 측정 안정성 수준으로 보정되었다. 즉, 보정 전과 후의 6자유도 운동 오차(PV-Value)는 Table 3과 같이 미세 구동 스테이지 구동 범위 내에서 보정되었고, 평균적으로 73% 감소함을 확인하였다.

Fig. 8

The 6-DOF motion errors during 20 mm step motion

Table 3

PV-Value of the 6-DOF error

4. 결론

본 연구에서는 초정밀 직선 스테이지의 6자유도 운동 오차를 실시간으로 보정하기 위한 미세 구동 스테이지 모델을 제안하였다. 제안된 미세 구동 스테이지는 5개의 정전용량 센서와 1개의 광학 인코더를 활용하여 오차를 측정하고, 압전 구동기를 활용한 유연 힌지 메커니즘을 이용해 구동한다. 초정밀 가공 보정용으로 활용 가능하도록 6자유도 보정 유닛을 10 nm와 1/3 arcsec 이하의 분해능을 가지도록 설계하였으며, 이중서보 스테이지를 구성하여 조동 스테이지 이송 범위 내에서 6자유도 운동 오차가 효과적으로 보정되는 것을 확인하였다. 제안한 보정 시스템은 모듈화를 통해 다축 초정밀 가공시스템 및 정렬 장치 등에 적용 가능하다. 또한, 이송 시스템의 개별축 오차를 최소화하고 오차 누적을 방지하여 초정밀 공정의 정확도 향상 및 안정성 확보에 기여할 것으로 기대한다.

Acknowledgments

이 논문은 2020년도 과학기술정보통신부의 재원으로 한국연구재단(No. NRF-2019R1A2C2088683)의 지원을 받아 수행된 연구임.

REFERENCES

• Son, S. M., Lim, H. S., and Ahn, J. H., “Effects of the Fiction Coefficient on the Minimum Cutting Thickness in Micro Cutting,” International Journal of Machine Tools and Manufacture, Vol. 45, Nos. 4-5, pp. 529-535, 2005. [https://doi.org/10.1016/j.ijmachtools.2004.09.001]
• Egashira, K., Hosono, S., Takemoto, S., and Masao, Y., “Fabrication and Cutting Performance of Cemented Tungsten Carbide Micro-Cutting Tools,” Precision Engineering, Vol. 35, No. 4, pp. 547-553, 2011. [https://doi.org/10.1016/j.precisioneng.2011.06.002]
• Chae, J., Park, S., and Freiheit, T., “Investigation of micro-cutting operations,” International Journal of Machine Tools and Manufacture, Vol. 46, Nos. 3-4, pp. 313-332, 2006. [https://doi.org/10.1016/j.ijmachtools.2005.05.015]
• Park, J. S. and Jeong, K. W., “A Study on the Design and Control of an Ultra-Precision Stage,” Transactions of the Korean Society of Machine Tool Engineers, Vol. 15, No. 3, pp. 111-119, 2006.
• Nam, B. U., Kim, K. H., Choi, Y. M., Kim, J. J., Lee, S. W., et al., “Control of Decoupled Type High Precision Dual-Servo,” Journal of the Korean Society of Precision Engineering, Vol. 23, No. 2, pp. 43-50, 2006.
• Kim, K. H., Choi, Y. M., Nam, B. U., and Lee, M. G., “Dual Servo Stage without Mechanical Coupling for Process of Manufacture and Inspection of Flat Panel Displays via Modular Design Approach,” International Journal of Precision Engineering and Manufacturing, Vol. 13, No. 3, pp. 407-412, 2012. [https://doi.org/10.1007/s12541-012-0052-0]
• Choi, Y. M. and Gweon, D. G., “A High-Precision Dual-Servo Stage Using Halbach Linear Active Magnetic Bearing,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 5, pp. 925-931, 2011. [https://doi.org/10.1109/TMECH.2010.2056694]
• Kim, M. H., Jeong, J. H., Kim, H. Y., and Gweon, D. G., “A Six-DOF Magnetic Levitation Fine Stage for a High-Precision and High-Acceleration Dual-Servo Stage,” Smart Materials and Structures, Vol. 24, No. 10, Paper No. 105022, 2015. [https://doi.org/10.1088/0964-1726/24/10/105022]
• Lee, J. C., Lee, K. I., and Yang, S. H., “Development of Compact Three-Degrees-of-Freedom Compensation System for Geometric Errors of an Ultra-Precision,” Mechanism and Machine Theory, Vol. 99, pp. 72-82, 2016. [https://doi.org/10.1016/j.mechmachtheory.2015.12.015]
• Polit, S. and Dong, J., “Development of a High-Bandwidth XY Nanopositioning Stage for High-Rate Micro/Nanomanufacturing,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 4, pp. 724-733, 2011. [https://doi.org/10.1109/TMECH.2010.2052107]
• Zhang, H., Kou, B., Zhang, H., and Jin Y., “A Three-Degree-of-Freedom Short-Stroke Lorentz-Force-Driven Planar Motor Using a Halbach Permanent-Magnet Array with Unequal Thickness,” IEEE Transactions on Industrial Electronics, Vol. 62, No. 6, pp. 3640-3650, 2015.
• Lee, J. C., Lee, M. J., and Yang, S. H., “Development and Performance Evaluation of Fine Stage for 3-DOF Error compensation of a Linear Axis,” Journal of the Korean Society of Precision Engineering, Vol. 34, No. 1, pp. 53-58, 2017. [https://doi.org/10.7736/KSPE.2017.34.1.53]
• Lee, J. C. and Yang S. H., “Development of Nanopositioning Mechanism with Real-time Compensation Algorithm to Improve the Positional Accuracy of a Linear Stage,” Precision Engineering, Vol. 50, pp. 328-336, 2017. [https://doi.org/10.1016/j.precisioneng.2017.06.006]
• Lee, K. I., Lee, J. C., and Yang S. H., “The Optimal Design of a Measurement System to Measure the Geometric Errors of Linear Axes,” International Journal of Advanced Manufacturing Technology, Vol. 66, Nos. 1-4, pp. 141-149, 2013. [https://doi.org/10.1007/s00170-012-4312-z]
• Lee, K. I., Lee, J. C., and Yang, S. H., “Performance Evaluation of Five-DOF Motion in Ultra-Precision Linear Stage,” International Journal of Precision Engineering and Manufacturing, Vol. 15, No. 1, pp. 129-134, 2014. [https://doi.org/10.1007/s12541-013-0315-4]
• Rao, P. S. and Rao, N. M., “Position Analysis of Spatial 3-RPS Parallel Manipulator,” International Journal of Mechanical Engineering and Robotics Research, Vol. 2, No. 2, pp. 80-90, 2013.