상용 CFD 프로그램을 이용한 풍력터빈 축소 모델 해석 및 실험적 검증
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, both mechanical power and the wind speed distribution in the wake of a wind turbine scaled model were analyzed using a commercial CFD program (Ansys CFX) along with experimental validation. For the simulation, two different turbulence models including the SST model and the k-ε model were used. The scaled model was originally designed and manufactured by the researchers at the Technical University of Munich and was slightly modified for this research. To experimentally verify the CFD results, tests were performed with the scaled model under the turbulent wind in a wind tunnel. From the experimental validation, it was found that the k-ε turbulence model gives a better prediction than the SST model in the wake results. However, the SST turbulence model showed better prediction than the k-ε turbulence model in the power prediction. The discrepancy between the CFD results and the experimental validation is partially due to the fact that the blades are deformed at all times and control of pitch in the rated power region but these aspects are not considered in the simulation. If a transient analysis is performed using LES models, it will more accurately predict the change of wake with high turbulence intensity.
Keywords:
Scaled wind turbine, Computational fluid dynamics, Wake, Wind tunnel test키워드:
풍력터빈 축소 모델, 전산유체역학, 후류, 풍동 실험1. 서론
정부는 2017년말 재생에너지 3020 이행계획안을 발표함에 따라 2030년까지 재생에너지 발전량 비중을 20%까지 확대하겠다는 목표를 제시하였다.1 재생에너지발전원 중 풍력은 이행계획안 목표 달성을 위해 2030년까지 17.7 GW의 신규 풍력발전단지의 건설이 요구되며, 이 중 13GW 이상은 해상에 건설될 것으로 예상되고 있다.
대규모 풍력발전단지 개발은 MW당 수십억원 내외의 많은 비용이 소요되는 사업으로서, 풍력발전단지 개발 전 해당 풍력발전단지의 발전량 예측에 기반한 경제성 분석은 사업 진행을 위해 매우 중요한 부분이다. 이에 대한 연구로 유동해석 및 단지 내 후류 예측을 통해 풍력발전단지 유망 후보지 선정, 단지 내 풍력터빈 최적 배치, 단지 연간 발전량 예측 및 검증 등의 연구가 그동안 많이 수행되어왔다. 이와 같은 단지 배치에 의한 수동적인 단지 발전량 향상뿐만 아니라, 풍력터빈 제어알고리즘 또는 단지 차원에서의 개별 풍력터빈의 출력량 또는 요잉에 대한 제어를 통해 단지 발전량 향상 및 풍력터빈의 하중 저감을 통한 O&M 비용 저감에 대한 연구들이 진행되고 있다.2-5
이 중 단지 제어에 관한 연구는 단지발전량 향상을 위한 매우 중요한 연구 중 하나로서, 전 세계적으로 많은 연구가 진행되고 있지만, 실제 풍력발전단지에서 검증된 사례는 미미한 상황이다.6,7 이러한 단지 개발 제어 알고리즘은 상류 풍력터빈에 의해 발생하는 후류로 인한 하류 풍력터빈의 발전량 손실을 줄이기 위한 제어 알고리즘이며, 실제 단지에 적용하기 이전에, 시뮬레이션을 통한 검증이 반드시 필요하다. 이를 위해 시뮬레이션을 통한 풍력터빈 후류에 대한 예측 연구가 많이 이루어져 왔다.
일반적으로 풍력발전단지에서는 상류에 위치한 풍력터빈이로터 블레이드를 이용하여 바람으로부터 에너지를 최대한 추출하게 되며, 에너지가 추출된 바람은 상류 바람에 비해 풍속이 저감되고, 난류 강도가 높아지게 된다. 이러한 후류로 인해 하류에 위치한 풍력터빈의 발전량은 감소되고, 피로하중이 증가하여 풍력터빈 수명에 영향을 주게 된다. 이러한 풍력터빈 후류 모델에 관한 연구는 몇몇 연구와 논문을 통해 제시되어 왔다.
먼저, 수치해석법으로 간단하게 몇 개의 파라미터로 후류를 예측할 수 있는 단순화된 난류 모델들이 제시되어 왔다.8 이런 단순화된 후류 모델의 경우 계산 시간이 짧고 다양한 범위에서 활용이 가능하다는 장점이 있지만, 정확한 후류를 예측하는 것에 한계가 존재한다. 따라서 이런 단순화된 후류 모델이 아닌 CFD(전산유체해석법)를 통해 실제 후류를 더 정확하게 예측하려는 연구들이 추가로 진행되어오고 있다. CFD 프로그램을 통해 1기 이상의 풍력터빈을 모델링하여 발전단지 차원에서 후류를 예측하거나 후류로 인한 하류쪽 풍력발전기의 발전량을 예측하는 결과들이 문헌에서 제시되고 있다.9,10 하지만 이러한 연구들은 대부분 실험적 검증이 이루어지지 않아, 실제 예측이 어떤 정확도를 갖고 있는지를 파악하는 것은 매우 어렵다. 또한, 풍력터빈의 제원 및 실험 결과가 문헌상에 제시되어 있는 NREL Phase VI 풍력터빈을 이용하여 CFD 해석 결과와 비교한 연구들이 제시되고 있다.11,12 이외에도 수직축 풍력터빈 모델을 Axial Momentum 이론과 CFD를 통한 보정을 바탕으로 후류를 예측하는 연구 결과도 제시되었다.13 하지만 실제 풍력발전단지에 설치되는 대형 풍력터빈은 일반적으로 3개의 블레이드를 갖는 수평축 양력식 풍력터빈으로 NREL Phase VI와 같이 2개의 블레이드를 갖는 풍력터빈이나 수직축 풍력터빈의 경우와 공력 성능에서 차이를 보이게 된다. 또한, 선행연구에서는 대형 풍력터빈과 유사한 출력제어 특성을 갖는 풍력터빈을 이용하여 풍동실험을 통해 후류를 직접 측정하고 이를 CFD 결과와 비교한 연구는 매우 제한적이다.
따라서 본 연구에서는 상용 CFD 프로그램(CFX)을 이용하여 대형 풍력터빈과 유사한 출력제어 특성을 갖는 풍력터빈 축소 모델을 해석하고 이를 실제 풍동에서 실험을 통해 측정한 후류 및 발전량 결과와 비교함으로 CFD 프로그램의 해석 결과를 실험적으로 검증해보고자 하였다. CFD 해석의 경우 2가지 난류 모델을 사용하여 풍동 실험 결과와 비교하였으며 해석을 위해 축소 모델을 적절한 전처리 과정을 통해 모델링하였다. 또한, 풍동 실험에서와 동일한 경계 조건(Boundary Condition)을 적용하여 해석을 진행하였으며, 격자 독립성 검정을 통해 시뮬레이션의 타당성을 확보하였다. 그리고 풍력 분야에서 많이 사용되는 다물체 동역학 공탄성 프로그램인 Bladed를 이용하여 날개요소 운동량 이론에 기반하여 대상 풍력터빈의 로터 성능을 예측하였고, 이를 CFD에서의 성능예측과 비교하여 제시하였다.
2. 대상 풍력터빈
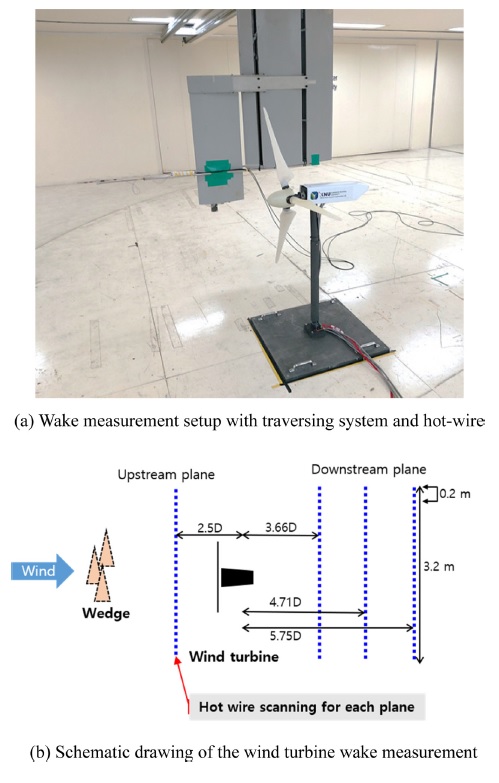
본 연구에서 사용된 대상 풍력터빈 축소 모델의 원형은 뮌헨 공대에서 설계 제작한 모델로서 최대출력계수를 갖는 선단속도비가 대형 풍력터빈과 유사한 값을 갖게 하기 위해 약 7.1이 되도록 설계되었다.14,15 본 연구에서는 해당 모델의 블레이드와 연결 부위를 별도로 제작하고, 풍력터빈 출력제어 알고리즘을 새로 적용하여 활용하였다. 대상 풍력터빈 모델은 대형 풍력과 마찬가지로 가변속 피치(Variable-Speed Variable-Pitch)제어, 개별 피치제어(Individual Pitch Control, IPC)가 가능하며 풍속에 따라 블레이드의 개별 피칭이 가능하다. Table 1에 제시된 것처럼 모델의 제원은 로터 직경 1.1 m, 우수 피치각(Fine Pitch Angle)은 0.5°이다. 또한 정격 회전속도는 678 RPM이며, 정격 발전용량은 39.8W이다. Fig. 1은 풍동 실험 당시 설치가 완료된 대상 풍력터빈 사진을 나타낸다.
3. 블레이드 해석
3.1 블레이드 및 로터 모델링
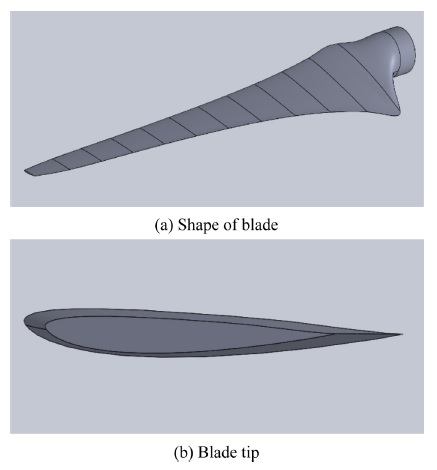
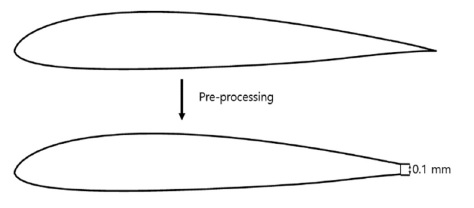
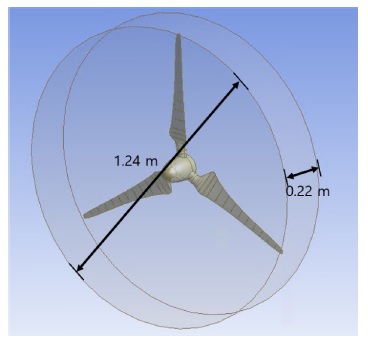
본 연구에서 대상 풍력터빈의 블레이드의 경우 3D 프린팅을 이용하여 제작하였으며, 재질은 ABS (Acrylonitrile Butadiene Styrene)이고, 길이는 0.48 m이다. Fig. 2(a)는 CAD 프로그램을 통해 모델링한 블레이드의 전체적인 형상을 보여주며 Fig. 2(b)는 블레이드 팁 부분만을 확대하여 제시하였고 이 모델링된 블레이드로 대상 풍력터빈의 블레이드가 제작되었다. 블레이드는 Fig. 3과 같이 저 레이놀즈 수에서 우수한 공력 성능을 갖는 RG14가 단일 익형으로 적용되어 있다.16 Fig. 2(b)에서 보이는 것과 같이 블레이드 익형의 뒷전(Trailing Edge) 부분이 예리한 형상으로 돼 있는 것을 확인할 수 있다. 해당 부분은 격자 생성 시 문제가 될 수 있기 때문에 Fig. 3과 같이 0.1mm의 폭을 갖도록 전처리를 하여 모델링하였다. 전처리가 된 블레이드 뒷전의 폭은 블레이드 팁에서 익형의 코드 길이의 1% 미만이다. 실제 제작된 블레이드의 경우 뒷전의 폭은 블레이드의 경우 약 0.25 mm이며 블레이드 팁에서 익형 코드 길이의 1.9% 정도이기 때문에 CFD에서의 모델과 실제 실험에 사용한 블레이드의 공력 성능이 큰 차이를 보이지 않을 것으로 판단하였다.17-19 또한, Fig. 4와 같이 CFD 해석을 위한 회전 도메인은 전처리가 완료된 블레이드와 콘을 넣어 모델링하였고 직경은 1.24, 높이는 0.22 m의 원통형으로 설정하였다.
3.2 블레이드 격자
본 연구에서는 시간 평균된 Navier-Stokes식인 RANS (Reynolds Averaged Navier-Stokes Simulation)식을 이용하여 CFD를 수행하였고, 난류 모델은 Shear Stress Transport (SST) 모델과 k - ε 모델을 각각 적용하였다.
SST 난류 모델을 사용하여 CFD 해석을 수행할 경우 y+의 값이 5 이하가 되도록 격자를 생성해야 한다. y+란 무차원 연직 거리로 식(1)로 계산할 수 있다.20
| (1) |
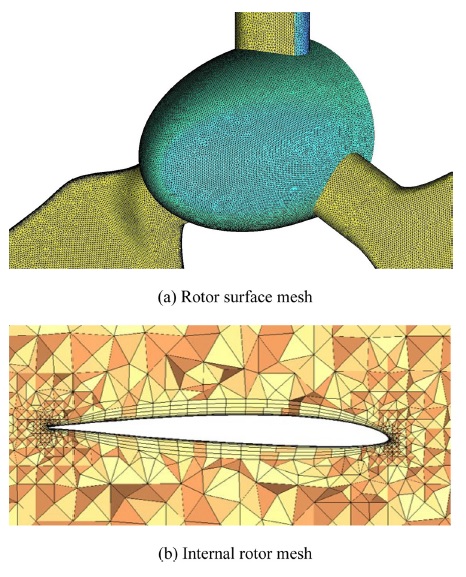
본 연구에서의 모든 격자 생성은 격자 전용 프로그램인 ICEM-CFD를 이용하였고 사면체 형상인 Tetra로 격자를 생성하였다. 대상 풍력터빈의 로터 부분의 격자는 y+를 고려하여 8개의 층과 Exponential 1.1의 생장률을 갖도록 하였다.21Fig. 5(a)는 로터 표면의 격자, Fig. 5(b)는 로터의 안쪽 격자를 보여준다.
3.3 블레이드 해석
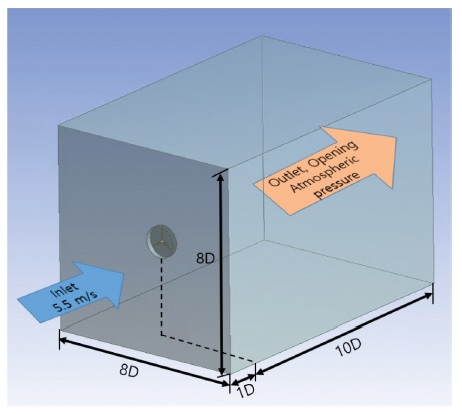
본 연구에서는 풍력발전기 로터의 격자에 따른 y+의 값을 확인하기 위하여 CFD 해석을 진행하였다. 경계 조건은 Table 2와 같으며 풍력터빈의 정격 풍속과 정격 회전속도를 기준으로 해석하였다. 시뮬레이션은 정상 상태(Steady-State) 해석으로 진행하였고 전체 유동 영역은 Fig. 6과 같이 모델링하였다. Fig. 6에서와 같이 직육면체 모양인 전체 유동장에서 I n let면을 제외한 나머지 5개의 면(Opening, Outlet)은 대기압으로 경계 조건을 설정하였다.
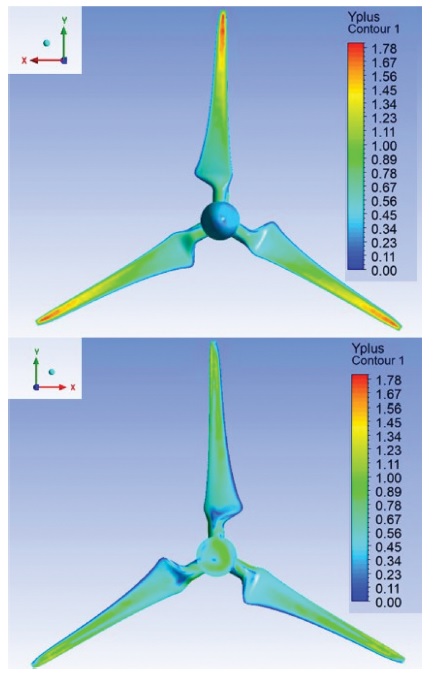
Fig. 7은 y+값을 확인하기 위한 해석 결과를 나타낸다. Fig. 7에서 살펴보면, y+의 값은 최대 1.78로 계산되었고, 5 이하임을 알수 있다. 이로써 SST 난류 모델에 적합한 격자임을 확인하였다.
4. CFD 해석
4.1 유동장 모델링 및 격자 생성
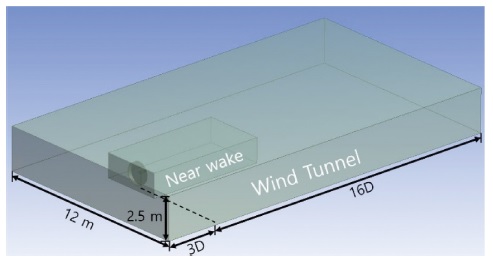
위해 Fig. 8과 같이 전체 유동장을 모델링하였고, Fig. 6에서의 유동장과는 다르게 대상 풍력터빈의 나셀과 타워가 포함되어 있다. 격자를 효율적으로 생성하기 위해 풍력터빈으로부터 약 6 D 정도까지의 하류 영역(Near Wake)에 대해서는 조밀한 격자를 생성하였고, 그 이후 영역에 대해서는 격자를 성기게 생성하였다. 격자 생성 결과는 Fig. 9에 제시하였다.
Fig. 9는 전체 유동장의 격자 결과를 보여주며, 로터 격자와 마찬가지로 풍력터빈의 타워와 낫셀 부분은 8개의 층과 Exponential 1.1의 생장률을 갖도록 격자를 생성하였다. 또한 회전하는 로터의 피치각은 풍동 실험에서 측정된 피치각의 평균으로 정격풍속 이하일 경우 0.5°, 이상일 경우에는 5.37°로 설정되었다.
4.2 경계 조건
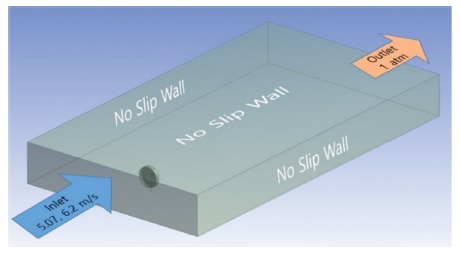
본 연구에서 CFD 해석의 경계 조건은 풍동 실험과 동일하게 부여하였고, Table 3에서와 같이 정격 이하와 정격 이상의 풍속으로 나누어서 진행하였다. Fig. 10은 CFD 해석의 전체적인 경계 조건을 보여주며 유동장의 입구 출구를 제외한 영역은 No Slip Wall로 설정하였고 블레이드, 나셀, 타워 등과 같은 구조물의 표면 거칠기(Roughness)는 해석 비용을 고려하여 Smooth Wall로 처리하였다. 또한, 회전체 해석에 많이 사용되며 상대적으로 적은 계산 비용을 요구하며 강건하다는 장점이 있는 Frozen Rotor 기법을 이용하여 정상 상태 해석을 수행하였다.22
5. 풍동 실험
5.1 풍동 실험 제원
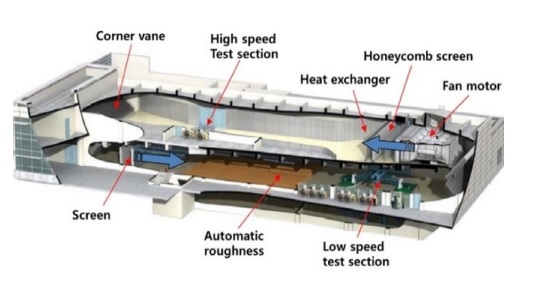
본 연구에서 풍동 실험은 국내 대형풍동실험센터에서 진행되었으며, 실험장의 구조를 Fig. 11에 제시하였다. Table 4는 풍동 실험센터의 제원을 보여주며, 본 연구의 실험은 저속시험부(Low Speed Test Section)에서 진행되었다.
5.2 후류 및 발전량 측정
Fig. 12(a)는 풍동 내에서 열선풍속계를 이용한 후류 측정 셋업을 보여준다. 먼저 풍동 최상류에 웨지(Wedge)를 설치하여 난류 강도를 약 12%가 될 수 있도록 구성하였다. 그리고 후류 측정 이전에 풍력터빈의 타워를 중심으로 2.5 D (D: Rotor Diameter) 상류에서, 풍력터빈에 입력되는 풍속을 먼저 측정하였다. 모든 풍속이 측정되는 높이는 대상 풍력터빈의 허브 높이인 0.91m로 고정되었다. 그 뒤 풍력터빈으로부터 하류로 3.66, 4.71, 5.75 D만큼 이격된 P lan e에서 후류를 측정하였다. 그리고 후류를 측정한 포인트는 Fig. 12(b)와 같이 로터회전축을 중심으로 ±1.6 m에서 각 포인트별로 0.2m의 간격을 갖도록 설정하여 총 45개의 포인트를 측정하였다. 이때 후류는 열선(Hot-Wire) 풍속계를 이용하여 샘플링 주파수 6,000 Hz로 약 1분간 시계열로 측정하였다.
풍력터빈의 출력의 경우 풍력터빈과 연결된 PLC에서 데이터를 받아 계산하였으며, 전기적인 에너지 변환 손실을 고려하지 않기 위해 발전기 회전속도와 토크의 곱으로 출력을 계산하였다.
6. CFD 결과 및 풍동 실험 검증
6.1 후류 검증
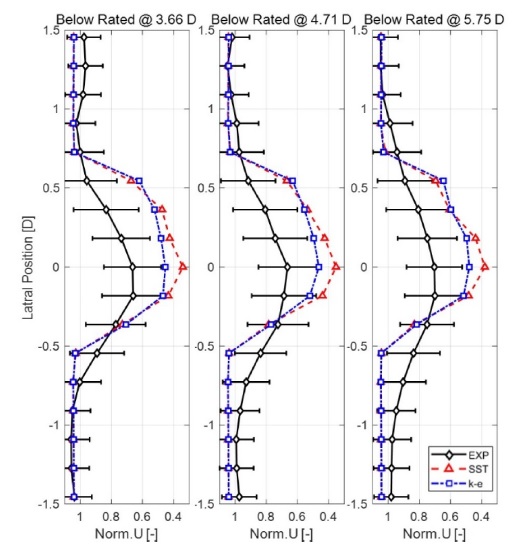
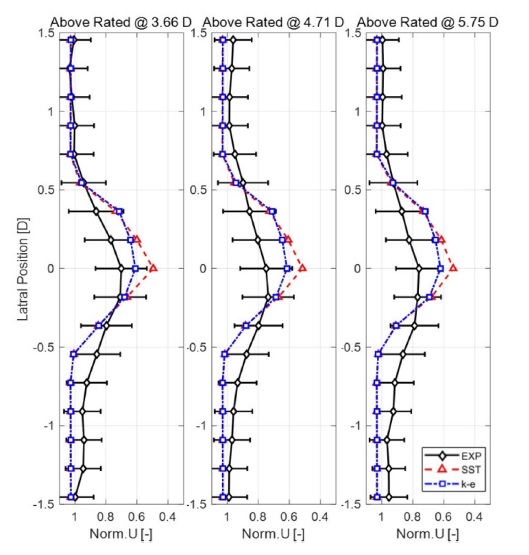
정격 풍속 이하와 이상의 두 경우에 대해 CFD에서 해석한 후류 데이터와 풍동 실험에서 측정한 후류 데이터를 Figs. 12와 13에 그래프로 제시하였다. CFD의 경우 SST 난류 모델과 k - ε 난류 모델 등 두 가지 난류 모델을 적용한 결과를 함께 비교하였다. 그래프의 x축은 무차원화된 풍속으로 각 포인트에서 측정한 후류 풍속 V를 입력된 풍속 V∞(정격 풍속 이하: 5.07 m/s, 정격 풍속 이상: 6.2 m/s)로 나누어 무차원화하였다.
y축의 데이터는 로터 회전중심축(기준점)에서 후류를 측정하는 포인트까지의 거리를 로터 직경으로 나누어 무차원화하였다. 또한, 실험 데이터의 경우 측정하는 포인트별로 1분간 측정된 후류의 평균값에 표준편차를 +/-하여 에러바로 함께 나타내었다. Figs. 13과 14를 살펴보면, 실험 결과와 CFD 해석 결과 모두 유사한 풍속 저감의 경향성을 보이고 k - ε 모델의 경우 대부분의 결과가 실험값의 에러바 범위 안에 있지만 평균값에서는 다소 차이가 있는 것을 확인할 수 있다. 또한 풍속 저감이 발생하는 후류폭의 경우에도 풍동 심험 결과가 시뮬레이션보다는 후류폭이 넓게 측정된 것을 확인할 수 있다. 또한, CFD를 통해 계산된 로터 회전 영역에서 벗어난 영역(0.55≤ |y|≤ 1.45)의 후류 풍속은 1보다 조금 큰 1.02의 값을 갖는다. 이는 차단 효과(Blockage Effect)로 인해 후류의 속도가 조금 증가한 것으로 판단된다. 차단비(BR)는 식(2)와 같으며 S는 풍동의 단면적, A는 풍력터빈의 투영면적을 나타낸다.
| (2) |
본 연구에서의 풍동의 단면적은 30m2이며, 풍력터빈의 투영면적은 약 0.1m2로서 BR은 약 3.3%이다. 또한, 선행 연구에서 BR이 2% 이상일 때 유사한 영역에서 무차원화된 후류 풍속이 1보다 크게 나오는 것을 확인하였다.24 또한, 후류를 면밀히 비교하기 위해 로터 직경에 해당하는 영역(-0.54≤ y≤ 0.54)에서의 후류 무차원 풍속을 평균을 낸 뒤 Tables 5와 6에 나타내었고, 실험값과의 오차를 함께 제시하였다. Table 5를 통해 정격 풍속 이하에서는 SST 모델과 k - ε 모델 모두 풍력터빈과 멀어질수록 오차가 줄어드는 것을 확인할 수 있다. 또한, k - ε 모델이 SST 모델보다 실험값과의 오차가 적은 것을 확인할 수 있다. 또한, Table 6을 통해 정격 풍속 이상에서는 오차가 6.5% 미만인 것을 확인할 수 있었으며 k - ε 모델의 경우 실험값과의 오차가 4.0% 미만으로 실제 측정한 값과 유사한 것을 확인하였다.
전반적으로 실험데이터와 비교해볼 때, SST보다 k - ε 모델이 조금 더 오차율이 적을 것을 확인할 수 있다. k - ε 모델의 경우에는 일반적으로 점성층 유동보다 자유경계의 영역을 잘 모사한다고 알려져 있으며, 난류 강도가 강한 바람에서는 후류 복원이 더 빨리 이루어진다는 연구 결과가 문헌에 제시되어 있다.25 따라서 이러한 원인으로 k - ε 모델을 사용한 결과가 SST 모델을 사용한 결과보다 후류의 복원이 더 잘 이루어진 것으로 판단된다.
또한, RANS 모델은 해석 시 시간평균기법을 사용하여 모든 비정상성을 평균화하고 근사적으로 해를 구하게 된다.26 따라서, 풍동 실험에서 측정된 후류와 같이 난류 강도가 크고 이에 따라 시간에 따른 후류의 변화폭을 정확히 모사하기에는 어느 정도 한계가 있음을 확인할 수 있다.
6.2 출력 검증
CFD에서 회전하는 도메인의 토크를 계산하고 회전속도와 함께 식(3)에 대입하면 풍력터빈의 기계적인 출력을 예측할 수 있다. 이때 P는 발전량, T는 토크, w는 회전속도를 나타낸다.
| (3) |
위 식(3)을 바탕으로 CFD에서 계산된 기계적 출력과 실제 풍동실험에서 얻어진 대상 풍력터빈의 기계적 출력을 비교하여 Tables 7과 8에 나타내었다.
Tables 7과 8을 보면 알 수 있듯이 SST 난류 모델이 k - ε 난류 모델의 경우 보다 출력을 더 정확하게 예측하는 것을 알 수 있다. 그 이유는SST 모델은 점성층 영역의 유동을 잘 모사할 수 있는 장점이 있기 때문에 블레이드의 표면 유동을 잘 모사하여 블레이드에 작용하는 양력과 항력을 k - ε 난류 모델의 경우보다 더 잘 예측하기 때문인 것으로 판단된다.27
또한 Tables 7과 8에서 살펴보면 정격 이하의 풍속일 때가 정격 이상에서의 풍속보다 출력을 더 잘 예측하는 것으로 확인할 수 있다. 이는 정격 풍속 이상에서의 대상 풍력터빈의 블레이드 피치제어를 CFD에서는 구현하지 못하고, 고정된 블레이드 피치각으로 해석하기 때문에 발생한 것으로 판단된다. 정격 이하의 풍속에서는 피치제어가 빈번히 일어나지 않고, 우수 피치각으로 블레이드 피치각이 고정되어 회전하게 된다. 하지만 정격 이상의 경우 정격 회전속도를 유지하기 위해 블레이드 피치제어를 사용하게 된다. 따라서 풍동 실험에서는 정격 이상에서 후류를 측정하는 동안 블레이드의 피치각이 계속하여 변하게 된다.
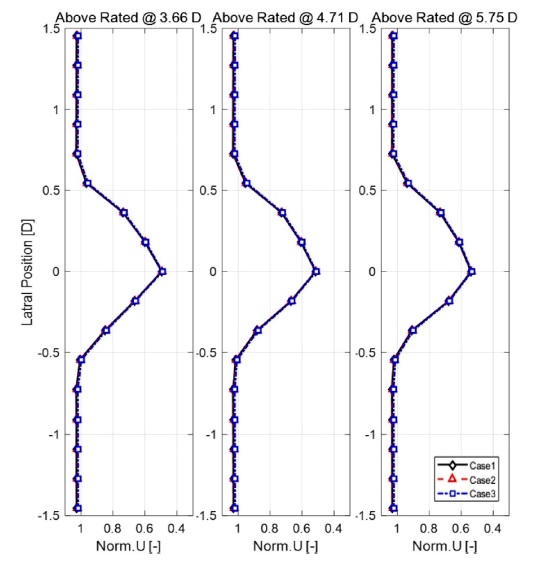
6.3 격자 독립성 검정
격자 독립성 검정(Grid Independence Test)은 SST 난류 모델의 정격 풍속 이상인 경우를 해석으로 진행하였다. Case 1의 경우가 기존 결과이고, Cases 2, 3의 경우 격자를 더 성하게 설정하여 발전량과 후류를 확인하였다. 후류는 Fig. 15를 통해 나타내었으며 오차는 1% 미만임을 확인하였다. Table 9에서는 발전량을 비교하여 나타내었으며, Table 10에서는 Case별 격자의 수를 확인할 수 있다. 다음과 같이 결과를 통해 격자의 정확성을 확인할 수 있었다.
7. BEM과 CFD를 이용한 출력계수 비교
7.1 BEMT를 이용한 출력계수 계산
BEMT (Blade Element Momentum Theory, 날개요소 운동량 이론)를 이용한 대상 풍력터빈의 로터 성능을 예측하기 위해 BEMT 및 다물체 동역학 기반 상용 풍력터빈 성능해석 프로그램인 Bladed를 이용하였다. 입력된 제원을 바탕으로 Bladed에서 풍동 실험과 동일한 조건으로 정격 풍속 이하일 때 피치각이 0.5°와 정격 풍속 이상일 때 피치각이 5.37°를 사용할 경우, 선단 속도비 변화(λ)에 대한 로터의 출력계수(Cp) 변화를 계산하였다. 선단속도비의 정의는 식(4)와 같으며 이때 V는 풍속, R은 로터의 반경, w는 로터회전속도를 나타낸다.
| (4) |
7.2 CFD 해석을 이용한 출력계수 계산
출력계수(Cp)는 식(5)와 같이 나타낼 수 있다. 식(5)에서 P는 기계적인 출력, ρ는 공기 밀도, A는 로터 단면적, V는 풍속을 의미한다.
| (5) |
CFD 해석에서 로터의 회전속도와 입력되는 풍속을 설정하고, 해석 결과로 발생하는 토크를 계산하여 풍력터빈의 기계적인 출력을 계산할 수 있다. 또한 식(5)를 이용하여, 출력계수를 계산할 수 있게 된다. 따라서, Figs. 13과 14에 제시된 후류 해석에서의 정격 풍속 이하와 정격 풍속 이상에서의 풍력터빈의 출력계수를 계산하였다.
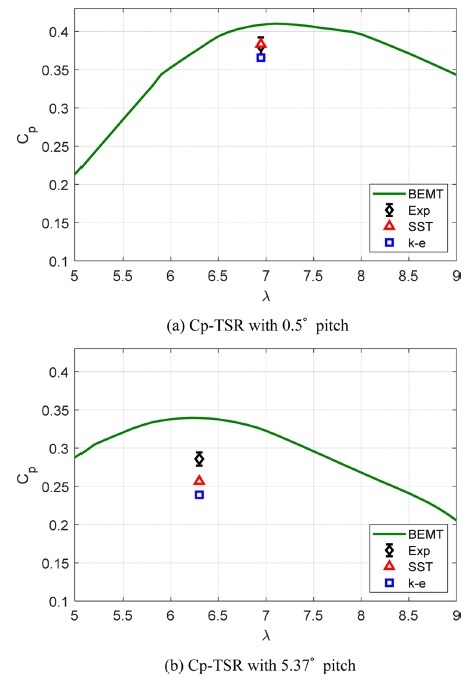
7.3 출력계수 비교
Figs. 16(a)와 16(b)는 각각 0.5, 5.37o의 피치각을 사용할 때 선단속도비에 따른 출력계수를 보여준다. Fig. 16에서 BEMT는 Bladed 프로그램을 이용하여 얻은 선단속도비 변화에 따른 출력계수 변화를 나타내며, Exp는 실험 결과에서 얻은 출력계수, SST는 SST 난류 모델을 적용한 경우의 CFD 해석 결과로 계산한 출력계수, k-e는 k - ε 난류 모델을 적용한 경우의 CFD 해석 결과로 계산한 출력계수를 각각 나타낸다. Fig. 16에서 실험 결과의 경우 난류 바람(난류 강도: 약 12%)에서 측정된 결과이기 때문에, 후류 측정을 위해 2시간 동안 250 Hz로 측정된 풍력터빈 성능데이터를 평균치를 낸 뒤, 출력계수를 계산하여 그림에 나타내고, 표준편차를 +/-하여 에러바로 나타내었다. 또한 이를 수치적으로 확인할 수 있도록 Tables 11과 12에 제시하였다. 정격 이하 풍속과 정격 이상 풍속일 때 모두 SST 모델이 가장 오차가 적은 것으로 확인되었다. 또한 CFD에서 정격 풍속 이상일때가 오차가 더 큰 것으로 나타났는데, 이는 이전의 출력 예측과 마찬가지로 블레이드의 피치제어를 시뮬레이션에서 이를 구현하지 못한 것이 원인으로 판단된다. 따라서 정격 풍속 이상일 때 CFD의 출력 예측은 제한적인 것으로 판단된다.
8. 결론
본 논문에서는 CFD (Ansys CFX)를 이용한 풍력터빈 해석정확도를 알아보기 위하여, 풍력터빈 축소 모델의 출력 성능 및 후류를 예측하고, 이를 풍동 실험을 이용하여, 실험적으로 검증하였다. CFD 시뮬레이션을 위해 대상 풍력터빈을 모델링하였으며, 2가지의 상이한 난류모델을 적용하여 후류와 출력을 예측하고 풍동 실험값과 비교하였다.
해석 및 검증 결과, 후류에서는 k - ε 난류 모델을 사용하였을 때 오차가 더 적었으며 전반적으로 CFD에서의 후류 풍속이 실제 풍동 실험을 통해 관측한 후류 풍속값보다 낮고, 풍속이 저감되는 후류 영역도 작은 것을 알 수 있었다. 이는 부분적으로는 풍동 실험에서는 대상 풍력터빈의 블레이드가 ABS 재질이고 풍압으로 인한 변위가 발생하게 되는데 이것을 CFD에서는 구현하지 못하였기 때문에 발생하였을 것으로 판단된다. 또한 실험에서 측정된 후류의 난류 강도가 크기 때문에 시간에 따른 후류의 변화폭을 RANS 모델에서는 정확히 구현하지 못한다는 한계가 있다.
풍력터빈의 출력의 경우 k - ε 난류 모델보다 SST 난류 모델이 더 정확한 예측 결과를 보여주었다. 정격 풍속 이하의 경우 SST 모델과 실제 풍력터빈의 출력 오차율은 0.7%로 매우 작았지만, 정격 이상의 경우 9.3%의 오차율을 보였다. 이는 정격 풍속 이상에서는 풍력터빈은 블레이드 피치제어에 의해 피치각 변화가 발생하지만, 이와 같은 피치각 변화를 CFD 해석에서는 구현하기 어렵기 때문에 발생한 것으로 판단된다.
결론적으로 CFD와 풍동 실험을 비교할 경우, Bladed와 같은 BEMT 기반 프로그램이나 CFD를 이용하여 블레이드가 받는 하중을 먼저 계산하고 이를 FEM (Finite Element Method) 기반 구조 해석에 적용하여 블레이드의 변형을 계산하며, 그 결과를 다시 CFD에 입력하여 유동해석을 수행한다면, 보다 정확한 시뮬레이션이 될 것으로 판단된다. 또한, RANS 모델이 아닌 LES 해석으로 시간에 대한 과도 영역을 해석한다면 후류를 보다 정확하게 구현할 수 있을 것으로 판단된다. 또한, 난류 바람에 따라 풍력터빈의 피치제어를 CFD에서 구현하게 된다면 정격 풍속 이상에서도 보다 정확한 발전량 예측이 가능할 것으로 예상된다.
NOMENCLATURE
| D : | Rotor Diameter |
| R : | Rotor Radius |
| P : | Electrical Power |
| V : | Wind Speed |
| A : | Swept Area |
| CP : | Power Coefficient |
| λ : | Tip Speed Ratio |
Acknowledgments
본 연구는 2018년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20183010025440).
REFERENCES
- Ministry of Trade, Industry and Energy, “Renewable Energy 3020 Implementation Plan,” http://www.motie.go.kr/motiee/presse/press2/bbs/bbsView.do?bbs_seq_n=159996&bbs_cd_n=81, (Accessed 5 FEBRUARY 2021)
-
Woo, J. K., Kim, H. G., Kim, B. M., Paek, I. S., and Yoo, N. S., “Prediction of Annual Energy Production of Gangwon Wind Farm Using AWS Wind Data,” Journal of the Korean Solar Energy Society, Vol. 31, No. 2, pp. 72-81, 2011.
[https://doi.org/10.7836/kses.2011.31.2.072]

-
Kim, K., Paek, I., Kim, C. J., Kim, H. G., and Kim, H. G., “Design of Power and Load Reduction Controller for a Medium-Capacity Wind Turbine,” Journal of the Korean Solar Energy Society, Vol. 36, No. 6, pp. 1-12, 2016.
[https://doi.org/10.7836/kses.2016.36.6.001]

-
Kim, K., Kim, H. G., Kim, C. J., Paek, I., Bottasso, C. L., et al., “Design and Validation of Demanded Power Point Tracking Control Algorithm of Wind Turbine,” International Journal of Precision Engineering and Manufacturing-Green Technology, Vol. 5, No. 3, pp. 387-400, 2018.
[https://doi.org/10.1007/s40684-018-0041-6]

-
Song, Y., Kim, H., Byeon, J., Paek, I., and Yoo, N., “A Feasibility Study on Annual Energy Production of the Offshore Wind Farm Using MERRA Reanalysis Data,” Journal of the Korean Solar Energy Society, Vol. 35, No. 2, pp. 33-41, 2015.
[https://doi.org/10.7836/kses.2015.35.2.033]

-
Kim, H., Kim, K., and Paek, I., “Power Regulation of Upstream Wind Turbines for Power Increase in a Wind Farm,” International Journal of Precision Engineering and Manufacturing, Vol. 17, No. 5, pp. 665-670, 2016.
[https://doi.org/10.1007/s12541-016-0081-1]

-
Kim, H., Kim, K., and Paek, I., “Model Based Open-Loop Wind Farm Control Using Active Power for Power Increase and Load Reduction,” Applied Sciences, Vol. 7, No. 10, p. 1068, 2017.
[https://doi.org/10.3390/app7101068]

-
Peña, A., Réthoré, P. E., and Van Der Laan, M. P., “On the Application of the Jensen Wake Model Using a Turbulence‐Dependent Wake Decay Coefficient: The Sexbierum Case,” Wind Energy, Vol. 19, No. 4, pp. 763-776, 2016.
[https://doi.org/10.1002/we.1863]

-
Rodrigues, R. V. and Lengsfeld, C., “Development of a Computational System to Improve Wind Farm Layout, Part II: Wind Turbine Wakes Interaction,” Energies, Vol. 12, No. 7, p. 1328, 2019.
[https://doi.org/10.3390/en12071328]

-
Sanderse, B., Van der Pijl, S., and Koren, B., “Review of Computational Fluid Dynamics for Wind Turbine Wake Aerodynamics,” Wind Energy, Vol. 14, No. 7, pp. 799-819, 2011.
[https://doi.org/10.1002/we.458]

- Kim, B., Eum, H., and Won, J., “Flow Simulation and Power Prediction of a HAWT Based upon a Change of Turbulence Models,” The Korean Society of Mechanical Engineers, Vol. 5, pp. 27-32, 2008.
-
Mo, J. O., Choudhry, A., Arjomandi, M., and Lee, Y. H., “Large Eddy Simulation of the Wind Turbine Wake Characteristics in the Numerical Wind Tunnel Model,” Journal of Wind Engineering and Industrial Aerodynamics, Vol. 112, pp. 11-24, 2013.
[https://doi.org/10.1016/j.jweia.2012.09.002]

-
Ma, Y., Lam, W. H., Cui, Y., Zhang, T., Jiang, J., et al., “Theoretical Vertical-Axis Tidal-Current-Turbine Wake Model Using Axial Momentum Theory with CFD Corrections,” Applied Ocean Research, Vol. 79, pp. 113-122, 2018.
[https://doi.org/10.1016/j.apor.2018.07.016]

- Campagnolo, F., Petrovic, V., Nanos, E. M., Tan, C. W., Bottasso, C. L., et al., “Wind Tunnel Testing of Power Maximization Control Strategies Applied to a Multi-Turbine Floating Wind Power Platform,” Proc. of the 26th International Ocean and Polar Engineering Conference, 2016.
-
Schreiber, J., Bottasso, C. L., Salbert, B., and Campagnolo, F., “Improving Wind Farm Flow Models by Learning from Operational Data,” Wind Energy Science, Vol. 5, No. 2, pp. 647-673, 2020.
[https://doi.org/10.5194/wes-5-647-2020]

-
Kim, D., Paek, I., Won, B., and Jeon, T., “Performance Test of 3D Printed Blades for a Scaled Wind Turbine in a Wind Tunnel,” Journal of the Korean Society for Precision Engineering, Vol. 37, No. 9, pp. 707-715, 2020.
[https://doi.org/10.7736/JKSPE.020.057]

-
Almohammadi, K. M., Ingham, D. B., Ma, L., and Pourkashanian, M., “2-D-CFD Analysis of the Effect of Trailing Edge Shape on the Performance of a Straight-Blade Vertical Axis Wind Turbine,” IEEE Transactions on Sustainable Energy, Vol. 6, No. 1, pp. 228-235, 2014.
[https://doi.org/10.1109/TSTE.2014.2365474]

-
Lee, S. G., Park, S. J., Lee, K. S., and Chung, C., “Performance Prediction of NREL (National Renewable Energy Laboratory) Phase VI Blade Adopting Blunt Trailing Edge Airfoil,” Energy, Vol. 47, No. 1, pp. 47-61, 2012.
[https://doi.org/10.1016/j.energy.2012.08.007]

- Zhang, X., Li, W., and Kong, C., “Effect of Relative Thickness on Improving Airfoil Aerodynamic Performance by Blunt Trailing-Edge Modification,” Advances in Mechanical Engineering, 2014.
- ANSYS, Inc., “ANSYS Fluent Theory Guide,” http://www.pmt.usp.br/ACADEMIC/martoran/NotasModelosGrad/ANSYS%20Fluent%20Theory%20Guide%2015.pdf, (Accessed 5 FEBRUARY 2021.
- ANSYS, Inc., “ANSYS ICEM CFD Tutorial Manual,” https://engineering.purdue.edu/~scalo/menu/teaching/me608/tutorial.pdf, (Accessed 5 FEBRUARY 2021)
-
Lanzafame, R., Mauro, S., and Messina, M., “Wind Turbine CFD Modeling Using a Correlation-Based Transitional Model,” Renewable Energy, Vol. 52, pp. 31-39, 2013.
[https://doi.org/10.1016/j.renene.2012.10.007]

- KOCED, “Wind Tunnel Center,” https://www.koced.or.kr/facility/sub52, (Accessed 23 FEBRUARY 2021)
-
Sarlak, H., Nishino, T., Martínez-Tossas, L., Meneveau, C., and Sørensen, J. N., “Assessment of Blockage Effects on the Wake Characteristics and Power of Wind Turbines,” Renewable Energy, Vol. 93, pp. 340-352, 2016.
[https://doi.org/10.1016/j.renene.2016.01.101]

-
Van Der Laan, M. and Andersen, S., “The Turbulence Scales of a Wind Turbine Wake: A Revisit of Extended K-Epsilon Models,” Journal of Physics: Conference Series, Vol. 1037, No. 7, Paper No. 072001, 2018.
[https://doi.org/10.1088/1742-6596/1037/7/072001]

-
Chen, H., Patel, V., and Ju, S., “Solutions of Reynolds-Averaged Navier-Stokes Equations for Three-Dimensional Incompressible Flows,” Journal of Computational Physics, Vol. 88, No. 2, pp. 305-336, 1990.
[https://doi.org/10.1016/0021-9991(90)90182-Z]

-
Rezaeiha, A., Montazeri, H., and Blocken, B., “On the Accuracy of Turbulence Models for CFD Simulations of Vertical Axis Wind Turbines,” Energy, Vol. 180, pp. 838-857, 2019.
[https://doi.org/10.1016/j.energy.2019.05.053]


Ph.D. Candidate in the Department of Integrated Energy and Infra System, Graduate School, Kangwon National University. His research interests are computational fluid dynamics (CFD) and fluid-structure interface (FSI) analysis.
E-mail: yc0630@kangwon.ac.kr

Professor in the Department of Mechatronics Engineering, Kangwon National University. His research interests are various topics of wind energy including wind turbine and farm simulation and control, wind resource assessment and wind farm design, and power performance testing of small wind turbines.
E-mail: paek@kangwon.ac.kr