열분석 시험 및 삭마 해석을 통한 극초음속 유도탄의 열분해 특성 및 표면 침식량 확인
1LIG넥스원 기계융합연구소2LIG넥스원 해외사업개발단
2PGM R&D Lab, LIG Nex1 Co., Ltd.
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, the DSC and TGA for phenol and silica/phenolic composite were carried out by increasing temperature up to 950oC with variable heating rate, to figure out basic thermal and pyrolysis characteristics of the composite. Also, the aim was to obtain the activation energy and the frequency factor which are the main parameters of the Arrhenius equation based on the Kissinger theory. The activation energy and frequency factor were used for the ablation model as material property. To confirm surface temperature distribution and recession of missiles, the CFD analysis using ANSYS Fluent R18.2 was performed to examine the thermal fluid characteristics of the hypersonic flight environment. Subsequently, the analysis results were applied as boundary conditions to a 2D axisymmetric pyrolysis and ablation model. Finally, pyrolysis and ablation analysis were performed using the ablation analysis code SAMCEF AMARYLLIS V.17, which uses the specific ablation module based on finite element code by applying carbon/phenolic and cork materials up to t = 10 s.
Keywords:
Hypersonic missile, Pyrolysis, Ablation analysis, Thermogravimetric analysis, Differential scanning calorimeter, Silica/Phenolic키워드:
극초음속 유도탄, 열분해, 삭마 해석, 열중량 분석, 시차주사열량법, 실리카/페놀릭1. 서론
유도무기 체계개발에서 기체 구조는 유도무기의 비행 및 운용 환경에 적합한 동체 및 날개 등의 비행 구조물을 설계하고, 개발하는 업무를 수행하는 분야이다. 최근, 유도무기의 비행 속도가 극초음속 영역으로 확장됨에 따라 공력가열 환경에서 발생하는 고온 열에너지로부터 유도무기 탐색기 및 내부 탑재구 성품을 보호할 수 있는 열보호시스템(Thermal Protection System, TPS)설계가 요구되고 있으며, 이러한 내열 설계는 구조 안전성 측면에서 유도무기 성능에 영향을 주는 매우 중요한 요소이다.1-3 열보호시스템설계는 열에너지를 소산하는 방법에 따라 다양한 방법으로 적용이 가능하나 내열소재로서 유도탄 중량 설계가 용이하고, 비행 시간 동안 유도무기의 외부 형상을 유지할 수 있는 삭마 복합재료(Ablative Composite)가 주로 적용되고 있으며, 일반적으로 잘 알려진 탄소/페놀릭(Carbon/Phenolic) 복합재뿐만 아니라 실리카(Silica) 및 코르크(Cork) 등을 적용한 삭마 복합재로 점차 그 영역이 확대되고 있다.4-8
극초음속 환경에서 유도무기 내열 설계를 위해서는 적용하고자하는 삭마 복합재료의 정확한 물성을 기반으로 열분해 및 삭마 수치 모델에 대한 온도 및 밀도 변화와 함께 표면 삭마량을 예측할 수 있어야 한다. 지상에서 극초음속 유동 환경을 모사하여 재료 표면 온도, 숯층 두께 및 삭마량 등의 열구조 성능을 확인하는 슬레드 시험(Sled Test) 및 고온 플라즈마 풍동 시험(High Enthalpy Plasma Wind Tunnel Test)이 수행되고 있으나,9,10 이들 시험은 열전도계수와 같은 제한된 열 물성만을 계측할 수 있으며, 고온에너지 유입에 따라 초기 삭마 복합재의 열분해 거동을 예측하는데 필요한 빈도 인자(Reaction Rate Constant) 및 활성화 에너지(Activation Energy)와 같은 열화학적 물성을 얻는 데에는 한계가 있다. 따라서, 시차주사열량 분석(Differential Scanning Calorimeter, DSC) 및 열중량 분석(Thermogravimetric Analysis, TGA)와 같은 열분석(Thermal Analysis) 시험을 통해 삭마 복합 재료의 열분해 특성과 열화학적 분해 반응에 영향을 주는 인자를 확인하고, 이를 열분해 모델에 적용함으로써 극초음속 비행 환경에서 발생하는 유도무기의 열분해 및 삭마 현상을 보다 정밀하게 예측할 수 있다.
시료(Sample)와 기준(Reference) 가열로(Furnace)에 공급된 에너지로부터 온도 및 열에너지 변화를 측정하는 시차주사열량 분석을 통해 시료의 유리전이 온도(Glass Transition Temperature), 냉결정화 온도(Cold Crystallization Temperature), 용융 온도(Melting Temperature) 및 결정화 온도(Crystallization Temperature)와 같은 고분자 수지의 기본적인 열적 특성을 확인할 수 있다. 한편, 열분해 과정에서 재료의 흡열 또는 발열 반응에 따라 중량 변화가 발생하기 때문에 TGA 시험으로 구한 중량-온도 곡선으로부터 열분해 온도 구간을 알 수 있으며 승온 속도(Heating Rate, q)에 따른 중량-온도 곡선을 미분한 DTG (Derivative Thermogravimetry) 곡선상 최대 변곡점 온도는 열분해에 가장 크게 기여하는 최대 분해 반응 온도라고 가정하는 Kissinger 이론을 적용하면 아레니우스(Arrhenius) 기반의 열분해 모델링에 필요한 재료의 활성화에너지 및 빈도 인자를 구할 수 있다.11,12
따라서, 본 논문에서는 공력가열 현상이 발생하는 유도무기의 열분해 특성 및 표면 침식량을 확인하기 위하여 열분석 시험 및 삭마 해석을 수행하였다. 순수 페놀 및 실리카/페놀릭 복합 재료를 950oC까지 가열하는 열분석 시험을 통해 기본적인 열 특성을 파악하였으며 Kissinger 이론을 기반으로 아레니우스 열분해 모델의 주요 인자인 활성화에너지 Ea, 빈도 인자 A를 구하여 수치 모델에 적용하였다. ANSYS Fluent R18.2를 이용하여 극초음속 비행 환경에 대한 열-유동 특성 변화를 검토하였고, 그 결과를 수치 모델의 경계 조건으로 적용하였으며 SAMCEF AMARYLLIS V.17를 이용하여 탄소/페놀릭 및 코르크 재료를 적용한 열분해 및 삭마 모델에 대한 해석을 수행하였다.
2. 열분석 시험
2.1 시차주사열량 분석(DSC)
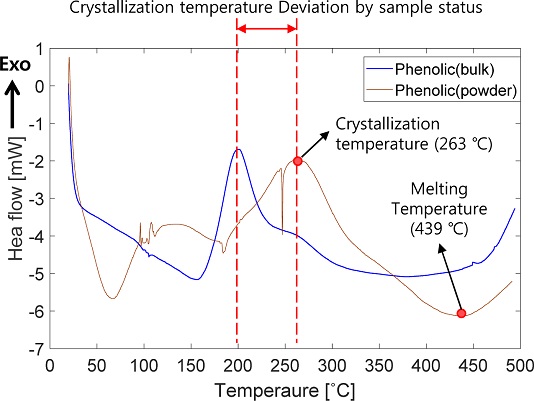
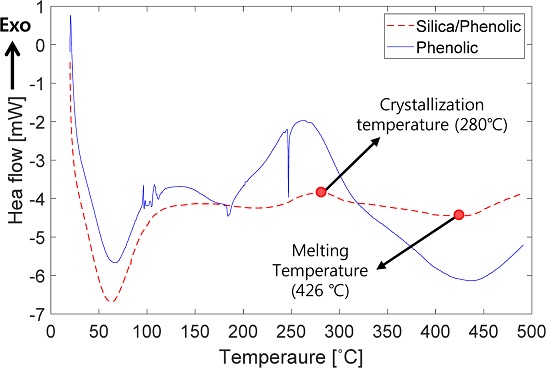
순수 페놀 고분자수지의 기본적인 열적 특성과 고체 결정(Bulk) 또는 분말(Powder) 형태의 시료 상태에 따른 열적 특성 변화를 확인하기 위하여 최대 온도 600oC까지 가열이 가능한 TA Instruments사의 Q2000 장비를 이용하여 Fig. 1과 같이 시험 가능한 크기가 10 mm3 이하이고, 중량이 100 mg 이내인 시료에 대하여 DSC 시험을 진행하였다. Table 1의 시험 조건과 같이 열분해 과정에서 섬유에 의한 열적 영향성을 살펴보고자 경화된 페놀릭 및 실리카/페놀릭(Silica/Phenolic, S/P) 복합재를 기계 가공한 분말 시료에 대한 시험을 수행하였으며, 재료의 온도에 따른 열량 변화 결과는 Figs. 2 및 3과 같다.
DSC 분석 결과 Fig. 2에서와 같이 고체 결정 또는 분말의 시료 상태에 따라 상이한 경향을 나타내었다. 결정화 및 용융과 같은 재료의 상변화 현상이 고체 결정에 비해 분말 시료에서 비교적 뚜렷하게 나타나는 것을 알 수 있으며 시료 상태에 따라 결정화는 200-263oC 온도에서 발생하였다. 분말 형태의 페놀 및 실리카/페놀릭 재료의 열적 특성은 Fig. 3에 비교하여 나타내었다. 페놀 및 실리카/페놀릭 재료는 온도에 따른 열에너지 변화에 다소 차이가 있으나 결정화 및 용융과 같은 재료 상변화 온도는 대체적으로 일치하는 경향을 나타내었다. 이를 통해 고온 증가에 따라 복합재료의 물리적 상변화는 섬유보다 고분자 수지에 더 지배적인 영향을 받는 것을 알 수 있으며 실리카/페놀릭 재료의 결정화 및 용융은 각각 280, 426oC에서 발생하는 것으로 나타났다.
2.2 열중량 분석(TGA)
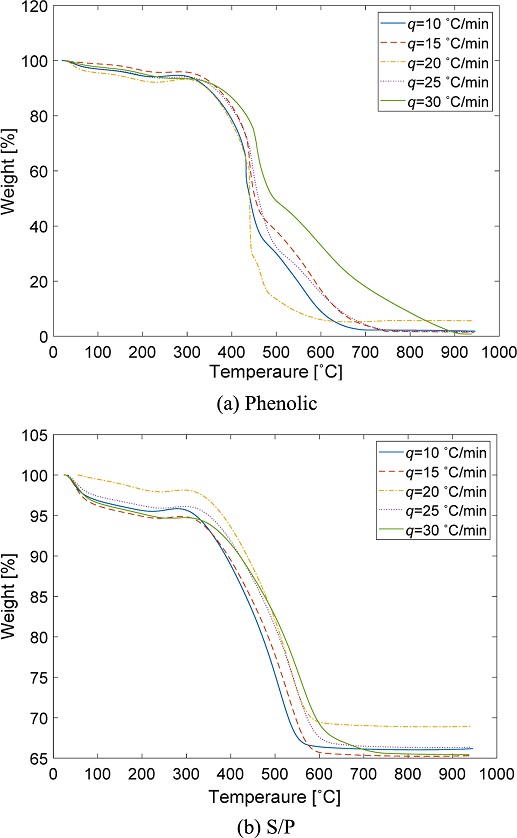
열중량 분석은 정밀도 높은 저울(Thermobalance), 가열로(Furnance) 및 시간에 따라 승온 속도를 일정하게 유지시켜주는 장치를 통해 중량-온도 곡선으로부터 열 안정성(Thermal Stability)과 재료의 열분해 과정에서 발생하는 중량 변화를 확인하는 시험이다. 본 연구에서는 Fig. 4와 같이 최대 온도 1,000oC까지 가열할 수 있는 TA Instruments사의 Q50 장비를 이용하여 순수 페놀 및 실리카/페놀릭 재료를 950oC까지 10, 15, 20, 25, 30oC/min 승온 속도를 달리한 TGA 시험을 통해 재료의 기본적인 열 특성과 분해 반응 속도와의 영향성을 확인하였다. 이와 함께 빈도 인자 및 활성화에너지와 같은 열분해 물성을 산출하였으며 각 시험 조건은 Table 2에 나타내었다.
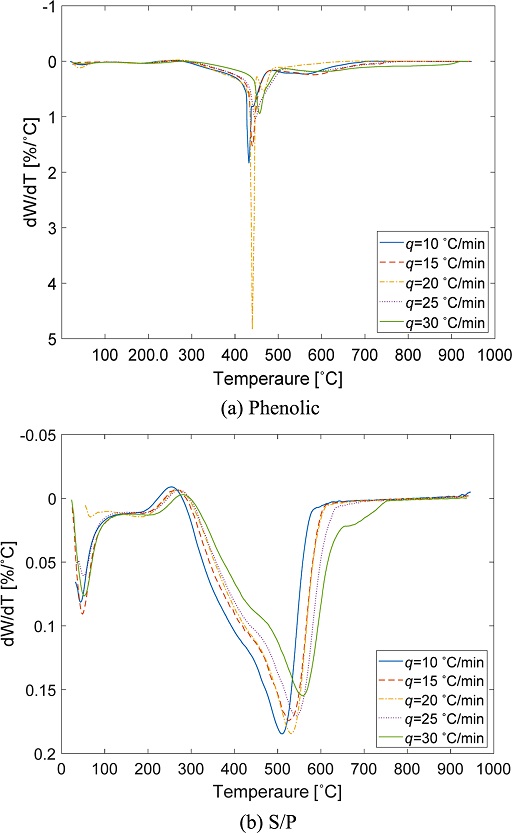
시험 조건 Cases 1 및 2와 같이 20oC/min 일정한 승온 속도로 시험한 TGA 결과, 고체 결정보다 분말 시료가 열분해 과정에서 열적 안정성이 더 우수한 것으로 나타났으며 고체 결정의 경우 열전달 특성이 달라지면서 재료 분해가 잘 진행되지 않아 중량이 51.3% 감소하는데 그친 것으로 확인하였다. Figs. 5 및 6은 분말 형태의 페놀 및 실리카/페놀릭 재료에 대하여 승온 속도를 달리한 시험 조건 Cases 2-11까지의 TGA 및 DTG 결과를 나타낸다. 페놀릭 재료의 경우 열분해 온도 구간 중 443.2oC일 때, 재료 분해 반응 속도가 가장 빠른 것으로 나타났으며, 승온 속도 q가 증가함에 따라 페놀릭 재료의 열분해 온도 및 최대 분해 반응 온도 θpx도 증가하는 경향을 나타내었다. 시험을 통하여 페놀릭 재료는 평균적으로 280-731oC 온도 구간에서 열분해가 진행되는 것을 확인하였으며, 10, 15, 20, 25, 30oC/min 승온 속도에 따라 최대 분해 반응 온도 θpx는 각각 432.22, 439.97, 440.10, 447.06, 457.06oC임을 알 수 있다. 또한, 실리카/페놀릭 재료는 TGA에서 950oC까지 가열하여도 재료가 완전히 분해되지 않는 것을 확인하였으며, 이를 통해 복합재료의 섬유층이 열분해 과정에 기여하지 않음을 알 수 있다.
페놀 및 실리카/페놀릭 재료의 열분해 물성을 산출하기 위하여 TGA 시험 데이터를 이용하였으며 재료의 열화학적 분해반응 속도는 식(1)과 같이 아레니우스식(Arrhenius’s Equation)의 주요 인자로서 빈도 인자 A, 활성화에너지 Ea 및 반응차수 n으로 결정된다.16
| ˙ζ=AeEa/Rθ(1-ζ)n | (1) |
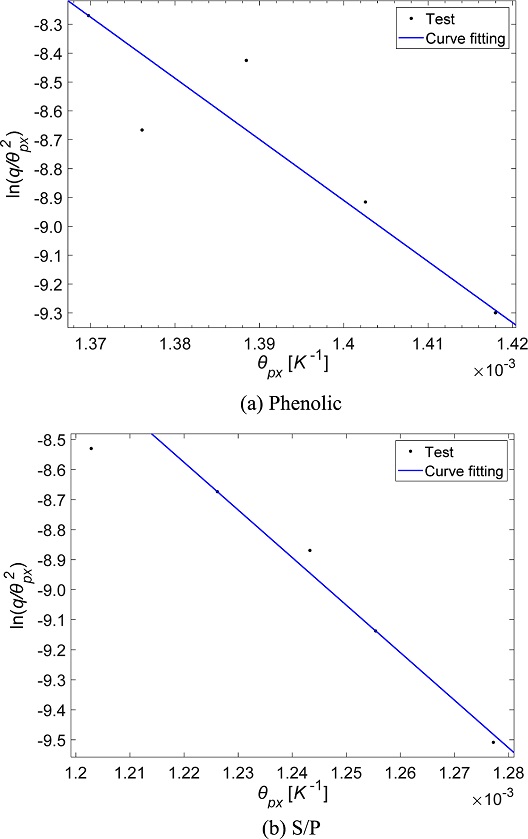
여기서 Ea, A, n은 Kissinger 이론 또는 Flynn-Wall-Owaza 이론으로 계산할 수 있으며 본 연구에서는 승온 속도에 따른 중량-온도 곡선을 미분한 DTG 곡선의 최대 변곡점 온도는 열분해에 가장 크게 기여하는 최대 분해 반응 온도(θpx)라고 가정하는 Kissinger 이론을 적용하였다. 분해 반응이 초기부터 종료 시점까지 일정하고, 열분해 과정에서의 복합 반응을 평균값으로 고려하면 식(2)와 같이 표현된다.
| ln(qθpx)=-EaR(1θpx)+ln(RAEa) | (2) |
식(2)를 이용하여 Fig. 7과 같이 각 승온 속도에서 ln(q/θpx2) 값을 나타내는 Kissinger 곡선의 기울기를 통해 활성화에너지를 산출할 수 있으며 이렇게 구한 활성화에너지를 식(2)에 대입하면 빈도 인자 A값을 얻을 수 있다. 페놀 및 실리카/페놀릭 재료의 활성화에너지는 Kissinger 곡선을 피팅하여 구한 175.19, 131.77 kJ/mol이며, TGA 시험 중 시료에 첨가된 휘발성 저분자 물질 및 미반응 수지 등이 열분해 과정에 영향을 주면서 일부 시험값이 기울기에서 벗어난 것으로 판단된다. 페놀 및 실리카/페놀릭 재료의 빈도 인자는 21,161, 15,851 /s이다.
3. 삭마 해석 및 결과
3.1 열화학적 분해 모델
열분해 및 삭마 해석을 위해서는 재료 외부 및 내부에서의 열에너지 평형과 함께 열화학적 분해에 따른 재료 밀도 감소, 기공 가스 생성 및 확산 등이 고려된 아레니우스 및 다시(Darcy) 구성 방정식을 연계해서 다루어야 하며 열분해 과정 동안 부피가 일정할 경우, 재료 밀도 감소는 열분해층에서 생성되는 기공 가스 질량에 비례한다고 가정하면 다음 식(3)과 같이 표현할 수 있다.
| -˙ρs=˙mgi,i | (3) |
재료 분해 속도는 식(4)와 같이 밀도 변화를 고려한 아레니우스 방정식으로 정의된다.
| ˙ρs=-A(ρν)(1-n)(ρ-ρc)ne-Ea/Rθ | (4) |
재료의 복합 분해 반응은 식(5)와 같이 0에서 1사이 값을 갖는 밀도 변화비로 표현할 수 있으며
| ζ=ρν-ρρν-ρc | (5) |
식(5)의 양변을 미분 형태로 나타내면 식(4)는 다음과 같이 식(6)으로 표현된다. 따라서, 복합 분해 반응이 고려된 재료 분해 속도를 최종적으로 정리하면 식(8)과 같다.
| ˙ζ=A(ρν)(1-n)(ρν-ρc)n-1(1+ζ)e-Ea/Rθ | (6) |
| ρ=ρν-∑iΔρiζi | (7) |
| ˙ρ=-∑iΔρiAi(ρν)(1-ni)(ρν-ρc)ni-1(1+ζi)nie-Eai/Rθ | (8) |
열분해 과정에서 생성된 분해 가스를 이상 기체로 가정하면 가스질량 플럭스는 식(9)로 표현된다.
여기서, ρg는 가스 밀도, μg는 가스점성계수, pg는 기공 압력, β는 침투성을 의미하며, 가스질량 플럭스를 가스확산계수(Gas Diffusion Coefficient)의 함수로 나타내면 식(10)으로 표현할 수 있다.
| ˙mgi=-ρgpgμgβij,j | (9) |
| ˙mgi=-γgijpg,j | (10) |
3.2 극초음속 유도탄 열분해/삭마 해석
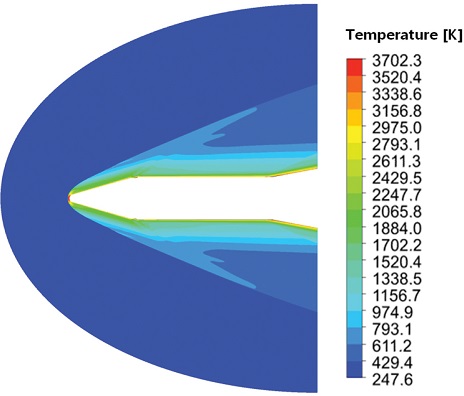
극초음속 유도탄의 열분해 특성과 표면 침식량을 확인하기 위하여 비행 속도 마하 M > 6, 비행고도 h > 20 km 이상의 비행 조건에 대한 열-유동 변화를 먼저 검토하였으며, Fig. 8과 같이 ANSYS Fluent R18.2를 이용하여 유도탄 전방부 형상에 대한 CFD 해석을 수행하였으며 2차원 압축성 RANS (Reynolds-Averaged Navier-Stokes) 방정식을 지배방정식으로 사용하였다. 또한 RANS 기반의 난류 유동을 해석하기 위해 SST (Shear-Stress Transport) 및 Sparlart-Allmaras 난류 모델을 적용하였으며 공간 차분법으로는 격자 중심의 유한 체적법과 고속 비행 조건에 적합한 Roe-FDS를 적용하였다. 유동 해석 모델은 약 80만 개 혼합 격자계 기반의 공간 격자로 구성하였다. Fig. 8은 열-유동 모델의 온도해석 결과를 나타낸다. 노즈 및 동체 후방 확대부에서 많은 양의 열에너지가 유입되면서 최고 표면온도는 3,702.3 K까지 상승하는 것으로 나타났으며, 이렇게 구한 온도, 압력 및 대류 열전달계수를 기반으로 하여 유도탄 고온 표면의 열하중 및 경계 조건으로 적용하였다.
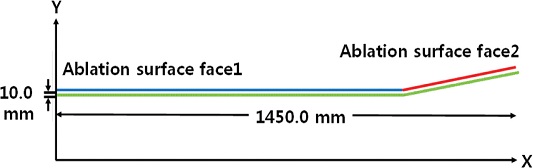
비행 중 유도탄 동체에서 발생하는 표면 침식과 온도 분포를 확인하기 위하여 온도, 압력 및 밀도 자유도를 연계하여 대류, 복사, 전도에 의한 열전달 현상과 재료 내부 에너지 변화 따른 열분해 반응 및 표면 침식에 대한 삭마 해석이 가능한 SAMCEF AMARYLLIS V.17를 이용하였으며 Fig. 9와 같이 유도탄 동체의 일부 영역에 대해 서로 다른 경계 및 삭마면을 갖는 축대칭 수치 모델을 생성하였다. 해석에 사용된 재료는 33.8%의 페놀릭 수지를 함유한 직교 이방성 탄소/페놀릭 복합재료와 P45 코르크 재료를 두께 방향으로 동일하게 5.0mm를 적용하였으며 재료의 축 방향 물성이 동일한 균질화 물성으로 고려하였다. 초기재료, 열분해 가스, 숯 층에서 복합재료의 열구조 및 재료분해 물성치는 NASA의 물성 시험 데이터를 이용하였으며,13-15 탄소/페놀릭의 열분해 물성치는 본 연구의 TGA 시험을 통해 구한 값을 적용하였다.
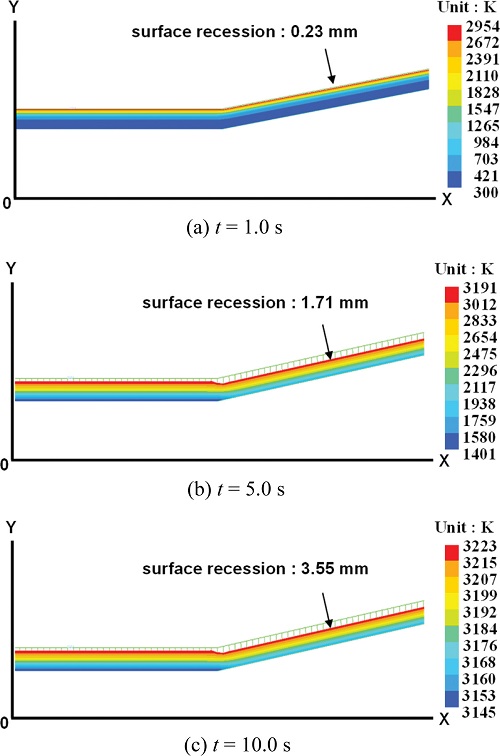
극초음속 유도탄의 비행 속도, 고도 및 비행 자세를 고려하여 극고온의 공력가열 현상이 짧은 시간에 발생하는 것으로 가정하여 t = 10 s까지 2차원 유도탄 축 대칭 모델에 대하여 열분해 및 삭마 해석을 수행하였다. t = 1, 5, 10 s에서 표면 침식량 및 온도 분포 결과를 Fig. 10에 나타내었다. 유도탄 진행 방향으로 열 유동 접촉 면적이 증가함에 따라 열 하중이 커지기 때문에 전체적으로 동체 확대부에서 동체 전방부에 비해 표면 침식이 더 크게 나타났으나 동일한 탄소/페놀릭 영역을 갖는 표면 온도 분포는 비슷한 경향을 나타내었다. t = 1 s일 때, 최대 표면 침식량 0.23 mm이며 초기부터 극고온 환경에 노출되는 해석 조건에 따라 표면 최고 온도는 2,954 K까지 상승하였다. t = 5 s일 때, 최대 표면 침식량은 1.71mm이고, 표면 최고 온도는 3,191 K까지 상승하였다. 지속적인 열하중 유입에 따라 재료 내부로까지 열에너지가 전달되면서 코르크 재료층을 포함한 TPS 재료 전체 영역에서 열분해 및 삭마 현상이 발생하였음을 알 수 있다. t = 10 s일 때, 최대 표면 침식량은 3.55mm로 나타났으며, 표면 최고온도는 3,323K까지 상승하였다. 재료의 열분해가 진행됨에 따라 숯층과 열분해층이 발달하여 재료 표면에서 최고 온도 도달 이후 일정하게 유지되는 경향을 나타내었다.
4. 결론
본 논문에서는 극초음속 유도탄의 열분해 특성 및 표면 침식량을 확인하기 위하여 DSC 및 TGA 통한 열분석 시험과 2차원 축 대칭 모델에 대한 열분해 및 삭마 해석을 수행하였다. 페놀 및 실리카/페놀릭 복합재료를 950oC까지 가열하는 열분석 시험을 통해 실리카 섬유가 열분해 과정에 크게 기여하지 않으며 섬유보다 고분자 수지에 더 지배적인 영향을 받아 페놀 및 실리카/페놀릭 재료는 온도에 따른 열량 변화에 다소 차이가 발생하였으나 결정화 및 용융과 같은 재료 상변화 온도는 대체적으로 일치하는 경향을 나타내었으며 평균적으로 280-731oC 온도 구간에서 열분해가 진행되는 것을 확인하였다. 또한, TGA 시험과 DTG 분석을 통해 10, 15, 20, 25, 30oC/min 승온 속도에 따른 최대 분해 반응 온도 θpx를 이용하여 Kissinger 이론을 기반으로 아레니우스 열분해 모델의 주요 인자인 활성화에너지 Ea, 빈도 인자 A를 구하여 열분해 및 삭마 해석 모델의 재료 물성으로 적용하였다.
극초음속 유도탄 비행 환경에 대한 열-유동 특성 변화를 검토하기 위하여 마하 M > 6, 비행고도 h > 20 km 이상의 비행 조건에서 ANSYS Fluent R18.2를 이용한 CFD 해석을 수행하였으며 해석 결과를 탄소/페놀릭 및 코르크 재료를 적용한 유도탄 2차원 축 대칭 모델에 경계 조건으로 적용하였다. t = 10까지 표면 침식량 및 온도 분포를 확인하기 위하여 상용 삭마 해석 코드 SAMCEF AMARYLLIS V.17를 이용한 열분해 및 삭마 해석을 수행하였다. 동체 전방부보다 동체 확대부에서 표면 침식이 더 크게 발생하였으며 표면 온도 분포는 비슷한 경향을 나타내었다. 지속적인 열하중 유입에 따라 재료 내부까지 열에너지가 전달되면서 코르크 재료층을 포함한 TPS 재료 전체 영역에서 열분해 및 삭마 현상이 발생하였으며 재료의 열분해가 진행됨에 따라 숯층과 열분해층이 발달하여 최고 온도 도달 이후 일정하게 유지되는 경향을 나타내었다. 따라서, 내부로 침투되는 열에너지를 효과적으로 차단하기 위해서는 적절한 표면 삭마와 단열을 통해 표면에서 고온 다량의 열에너지를 소산하고 차단할 수 있는 TPS 설계가 이루어져야 할 것으로 판단된다.
NOMENCLATURE
| A : | Frequency Factor of the Arrhenius Law [/s] |
| Ea : | Activation Energy [J/mol] |
| ˙m : | Gas Mass Flux [kg/ m2s] |
| n : | Order of Reaction [-] |
| q : | Hating Rate [oC/min] |
| β : | Permeability [m2] |
| γ : | Gas Diffusion Coefficient [kg·m/N·s] |
| ζ : | Generalized Density [-] |
REFERENCES
-
Choi, Y. G., Noh, K. H., Park, J. Y., and Jo, Y. H., “Pyrolysis and Chemical Ablation Analysis of Hypersonic Missile for Thermal Protection Design Applying Charring Phenol Resin Composites,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 10, pp. 987-993, 2018.
[https://doi.org/10.7736/KSPE.2018.35.10.987]

-
Choi, Y. G., Kim, S. J., and Shin, E. S., “Thermomechanical Analysis of Composite Structures in Pyrolysis and Ablation Environments,” Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 41, No. 8, pp. 597-604, 2013.
[https://doi.org/10.5139/JKSAS.2013.41.8.597]

-
Sutton, G. W., “The Initial Development of Ablation Heat Protection, an Historical Perspective,” Journal of Spacecraft and Rockets, Vol. 19, No. 1, pp. 3-11, 1982.
[https://doi.org/10.2514/3.62196]

-
Yang, B. C., Cheung, F. B., and Koo, J. H., “A Theoretical Study of Thermomechanical Erosion of High-Temperature Ablatives,” Journal of Applied Mechanics, Vol. 60, No. 4, pp. 1027-1032, 1993.
[https://doi.org/10.1115/1.2900970]

-
Dimitrienko, Y. I., “Thermal Stresses and Heat-Mass Transfer in Ablating Composite Materials,” International Journal of Heat and Mass Transfer, Vol. 38, No. 1, pp. 139-146, 1995.
[https://doi.org/10.1016/0017-9310(94)00137-K]

-
Milos, F. S. and Chen, Y. K., “Two-Dimensional Ablation, Thermal Response, and Sizing Program for Pyrolyzing Ablators,” Journal of Spacecraft and Rockets, Vol. 46, No. 6, pp. 1089-1099, 2009.
[https://doi.org/10.2514/1.36575]

-
Dec, J. A., Braun, R. D., and Laub, B., “Ablative Thermal Response Analysis Using the Finite Element Method,” Journal of Thermophysics and Heat Transfer, Vol. 26, No. 2, pp. 201-212, 2012.
[https://doi.org/10.2514/1.T3694]

-
Mcmanus, H. L. and Springer, G. S., “High Temperature Thermomechanical Behavior of Carbon-Phenolic and Carbon-Carbon Composites, II. Results,” Journal of Composite Materials, Vol. 26, No. 2, pp. 230-255, 1992.
[https://doi.org/10.1177/002199839202600205]

-
Reynolds, R., Russell, G., and Nourse, R., “Ablation Performance Characterization of Thermal Protection Materials Using a Mach 4.4 Sled Test,” Proc. of the 28th Joint Propulsion Conference and Exhibit, p. 3055, 1992.
[https://doi.org/10.2514/6.1992-3055]

-
Covington, M., Heinemann, J., Goldstein, H., Chen, Y. K., Terrazas-Salinas, I., et al., “Performance of a Low Density Ablative Heat Shield Material,” Journal of Spacecraft and Rockets, Vol. 45, No. 2, pp. 237-247, 2008.
[https://doi.org/10.2514/1.12403]

-
Kissinger, H. E., “Reaction Kinetics in Differential Thermal Analysis,” Analytical Chemistry, Vol. 29, No. 11, pp. 1702-1706, 1957.
[https://doi.org/10.1021/ac60131a045]

-
Flynn, J. H. and Wall, L. A., “A Quick, Direct Method for the Determination of Activation Energy from Thermogravimetric Data,” Journal of Polymer Science Part B: Polymer Letters, Vol. 4, No. 5, pp. 323-328, 1966.
[https://doi.org/10.1002/pol.1966.110040504]

- Sykes Jr, G. F., “Decomposition Characteristics of a Char-Forming Phenolic Polymer Used for Ablative Composites,” National Aeronautics and Space Administration Langley Research Center, 1967.
- April, G. C., “Energy Transfer in the Char Zone of a Charring Ablator,” Ph.D. Thesis, Louisiana State University, 1969.
- Williams, S., “Thermal Protection Materials: Thermophysical Property Data,” National Aeronautics and Space Administration, 1992.
-
Arrhenius, S., “Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte,” Zeitschrift für Physikalische Chemie, Vol. 4, No. 1, pp. 96-116, 188. (in German)
[https://doi.org/10.1515/zpch-1889-0408]


Research Engineer in Mechanical R&D Lab., LIG Nex1 Co., Ltd.. His research interest is composites structures mechanics and multi-physics coupling analysis.
E-mail: youngyu.choi@lignex1.com

Research Engineer in Mechanical R&D Lab., LIG Nex1 Co., Ltd.. Her research interest is composites propulsion mechanics and multi-physics coupling analysis.
E-mail: jeongeun.kim@lignex1.com

Research Engineer in PGM R&D Lab., LIG Nex1 Co., Ltd.. His research interest is aerodynamics and system engineering.
E-mail: nohkh36@lignex1.com

Research Engineer in Mechanical R&D Lab., LIG Nex1 Co., Ltd.. His research interest is missile system design and mechanical engineering.
E-mail: joyounghwan@lignex1.com

Research Engineer in Mechanical R&D Lab., LIG Nex1 Co., Ltd.. His research interest is system engineering and mechanical engineering.
E-mail: guhyunryu@lignex1.com