전자기력 보상 방식 고정밀 저울을 위한 광학식 위치 센서 개발
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The electromagnetic force compensation (EMFC) measurement principle has been widely adopted in the high-precision mass metrology system due to its sensitive compliant mechanism and nanometer level position sensor. In EMFC, an electromagnetic actuator balances the gravitational weight to maintain zero (or Null) position by feedback control using a position sensor, and the weight is calculated from the current applied to the actuator. Thus, a position sensor in the EMFC system should measure the null position accurately with high sensitivity and resolution. The position sensor commonly used in EMFC balance is an optical sensor that measures the displacement of EMFC balance from the intensity of light coming through a slit using a two-segment photodiode. This paper analyzed the characteristics of an optical position sensor for EMFC balance through parametric analysis using the Fresnel diffraction model. We also evaluated the performance of the sensor and confirmed the feasibility from weighing performance of the balance prototype. Normalized sensitivity of the sensor was 0.04237 μm-1 and measured resolution was 1.09 nm. The weighing repeatability with our optical position sensor was 4.83 mg (1σ) at 10 g measurement, which was 3 times better than the repeatability with an alternative commercial sensor.
Keywords:
Position sensor, Electromagnetic force compensation, Weighing cell, Null method키워드:
위치 센서, 전자기력 보상, 웨잉셀, 영위법1. 서론
산업기술이 발달함에 따라 의학, 반도체, 바이오 분야 등 다양한 산업분야에서 높은 분해능과 반복능을 가진 정밀 질량 측정기기의 필요성이 점차 대두되고 있다.
정밀 질량 측정기기는 크게 두 가지의 방식이 널리 사용되고 있는데, 이는 로드셀(Loadcell) 방식과 전자기력 보상(Electromagnetic Force Compensation, EMFC)의 방식이다.1 로드셀 방식의 질량측정기기는 측정 대상의 무게로 인해 변형된 탄성체의 변형량을 스트레인 게이지를 통해 측정하며, 상대적으로 가격이 저렴하고, 측정 범위가 넓다는 장점이 있지만 분해능이 낮고 온도 변화에 민감하다는 단점이 있다.2
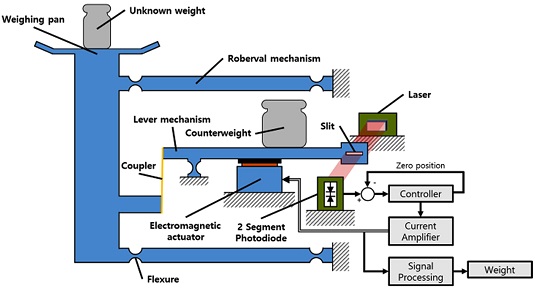
전자기력 보상 방식의 저울은 측정하고자 하는 질량과 기준량으로부터 동일한 무게로 저울을 평형상태로 위치시켜 물체의 질량을 측정하는 영위법(Null Method)을 통해 질량을 도출한다.3,4 Fig. 1과 같이 측정하고자 하는 무게가 웨잉팬에 위치하면, 중력 방향으로만 운동하기 위하여 금속 유연기구로 이루어진 Roberval 가이드 메커니즘에 의해 무게가 커플러에 전달되며, 커플러에 전달된 무게로 인해 레버 메커니즘이 기울어진다. 레버의 끝에 위치한 위치 센서는 레버가 원점에서부터 얼마나 기울어졌는지를 측정하고, 기울어진 변위만큼 전자기 구동기가 피드백 제어를 통해 평형 상태로 보상한다. 이때 보상되는 전자기력으로부터 물체의 무게를 도출한다. 전자기력 보상 방식은 유연기구 메커니즘의 높은 기계적 민감도와 위치 센서의 분해능 덕분에 로드셀 방식에 비해 분해능과 반복능이 매우 우수하다. 위치 센서의 경우 영위법을 사용하기 위해 정확한 원점(Null Position)을 측정 가능하면서 높은 분해능과 민감도를 가진 비접촉식 센서가 필요하다.
고민감도를 가진 비접촉식 위치 센서로는 레이저 간섭계, 정전 용량형 센서, 광다이오드(PD)를 이용한 광학식 센서 등이 있다. 레이저 간섭계는 가장 정밀하지만 상대적인 위치를 계산하기 때문에 재작동 시 원점을 손실하게 된다.5 정전용량 센서는 분해능은 매우 높으나 주변 기기 절연체 부근에 정전기가 축척이 될 수 있어 노이즈에 민감하며 반복성이 저하되는 단점이 있다. PD를 이용하여 광량의 변화를 통해 변위를 측정하는 광학식 센서의 경우 전자기력 보상 방식에 가장 많이 사용되는 센서이며 원점의 위치에 대한 반복능이 좋으며 경제적이라는 장점이 있다.6,7 이로 인해 정밀 질량 측정 기기 이외 정밀 스테이지 등 다른 정밀 시스템들의 위치 센서로서 사용되었다.8-11
센서의 정규화를 통해 드리프트를 저감하거나,8 Gaussian 빔과 변조를 이용해 질량측정기기를 위한 센서에 관한 연구,12 2개의 IR-LED와 1개의 PD를 이용해 센서의 민감도를 높인 연구13 등 센서의 민감도를 높이거나 센서의 안정성을 높이기 위한 선행연구 등이 있었지만, 센서의 모델링을 통해 슬릿의 크기와 슬릿과 PD 사이의 거리에 의한 성능 분석을 통해 센서의 민감도를 높인 연구는 거의 진행되지 않았다.
본 논문에서는 영위법을 통해 질량 또는 하중을 도출하는 전자기력 보상 방식 저울의 원점을 측정하는 광학식 위치 센서를 설계한다. 또한 수학적 모델링을 통해 센서 특성을 파악하고, 설계 변수에 따른 성능 변화를 예측하여 목표 측정 범위 내에서 최대 민감도를 갖는 센서를 설계하였다. 이를 바탕으로 센서 검증을 위해 제작한 저울 프로토타입에서 센서 성능을 평가하고, 모델링과의 비교 검증을 진행하였다. 마지막으로 설계한 위치 센서로 저울 프로토타입을 제어했을 때의 저울의 성능을 평가하고, 상용 위치 센서로 제어했을 때와의 성능을 비교하여 센서의 효용성을 확인하였다.
2. 원리 및 센서 모델링
2.1 Fresnel 회절 모델
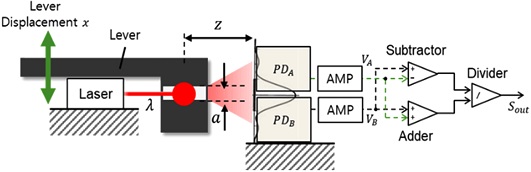
광학식 위치 센서의 구성은 Fig. 2와 같다. λ는 레이저의 파장, a는 슬릿의 크기, z는 슬릿과 PD 사이의 거리를 나타낸다. 여기에서 레이저와 PD는 고정되어 있고, 슬릿은 EMFC 저울의 레버에 고정되어 있다. 레이저에서 나온 빛은 슬릿을 통과하고, 통과된 빛의 광량은 2개의 PD 혹은 이분할 PD로 측정된다. 이때 저울의 레버가 구동 시 레버 끝에 설치된 슬릿이 같이 상하로 움직이면 PDA와 PDB에 측정되는 광량의 차가 발생하게 된다. 광량은 PD를 통해 전류로 변환된 뒤, 전류-전압 변환기(AMP)를 통해 증폭되어 전압 VA, VB로 측정되고, 이 두 전압 신호의 차등 신호를 두 신호의 합으로 나눈 값으로부터 최종적으로 슬릿의 이동 변위 x는 계산될 수 있다.
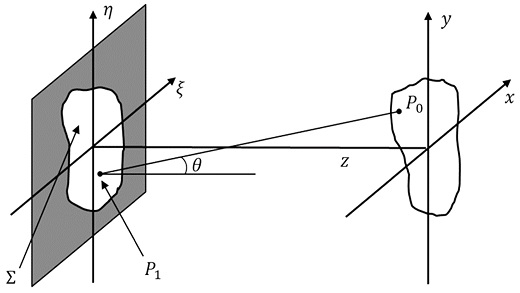
광학식 위치 센서의 특성을 파악하고, 고민감도를 가지도록 센서를 설계하기 위해서는 슬릿의 움직임에 따른 센서의 신호 변화를 구할 수 있는 해석 모델이 필요하다. 슬릿이 이동할 때 슬릿의 위치에 따라 PD에서의 광량 분포는 슬릿을 통과한 빛의 회절에 기반한다. 이때 저울에 설치된 슬릿과 PD의 거리는 수 mm 이내이기 때문에, 광원과 측정하고자 하는 위치가 가까울 때 빛의 회절을 설명한 Fresnel Diffraction14,15을 통해 모델링이 가능하다. Fig. 3에 도시된 바와 같이 임의의 Aperture를 통과한 후 회절된 빛의 세기는 Huygens-Fresnel 원리로부터 유도된다. 좌표계(ξ,η)는 Aperture의 좌표계이며 좌표계(x, y)는 회절 후 빛이 투영되는 스크린의 좌표이다. λ는 빛의 파장이며 r01은 P0과 P1의 거리이다. k는 입사파의 파수(Wavenumber)이며 정의는 k = 2π/λ와 같다. 이때 회절된 후의 빛의 세기 U는 다음 식(1)과 같이 유도될 수 있다.
| (1) |
식(1)에서 cos θ항을 삼각법을 통하여 다음 식(2)와 같이 표현될 수 있다.
| (2) |
| (3) |
| (4) |
식(4)를 식(2)에 대입하면 다음 식(5)와 같이 표현된다.
| (5) |
최종적으로 exp(ik(x2+y2)/2z)이 적분항 밖으로 나오면 다음 식(6)과 같다.
| (6) |
본 논문의 센서의 경우 y 방향으로 슬릿의 움직임은 x 방향 움직임에 비해 무시할 만한 수준이기 때문에 식(6)을 간소화하여 다음 식(7)과 같이 표현하였다.
| (7) |
식(7)에서 도출된 식에서 U(x)는 빛의 Intensity이기 때문에 PD의 크기를 고려한 적분을 통해 식(8)과 같이 각 PD의 출력값인 VA, VB을 알 수 있다. 다음으로 식(9)와 같이 정규화 과정을 통해 시간에 따른 광원의 세기가 달라져도 Sout의 오차를 최소화한다. 최종적으로 식(10)에서 출력값 Sout을 민감도 상수인 K로 나누게 되면 슬릿이 원점으로부터 움직인 거리(ΔD)를 계산할 수 있다.
| (8) |
| (9) |
| (10) |
2.2 파라미터 분석
광학식 위치 센서의 설계 파라미터는 슬릿의 크기 a와 슬릿과 PD 사이의 거리 z로 설정하였다. 상용 제품의 제원을 통해 두 PD 간의 간격은 0.02 mm, PD 하나의 크기는 1 × 0.9 mm로 계산하였다. 레이저 광원은 Beam Diameter가 2 mm인 Collimate된 Beam이라고 가정하고, 광원과 슬릿 사이의 거리는 고려하지 않았다.
민감도 상수 K는 ±5 μm 범위 내의 센서 출력값을 이용해 선형 보간하여 도출하였다. 초기 파라미터는 λ = 635 nm, a = 50 μm, z = 4 mm로 설정하였다.
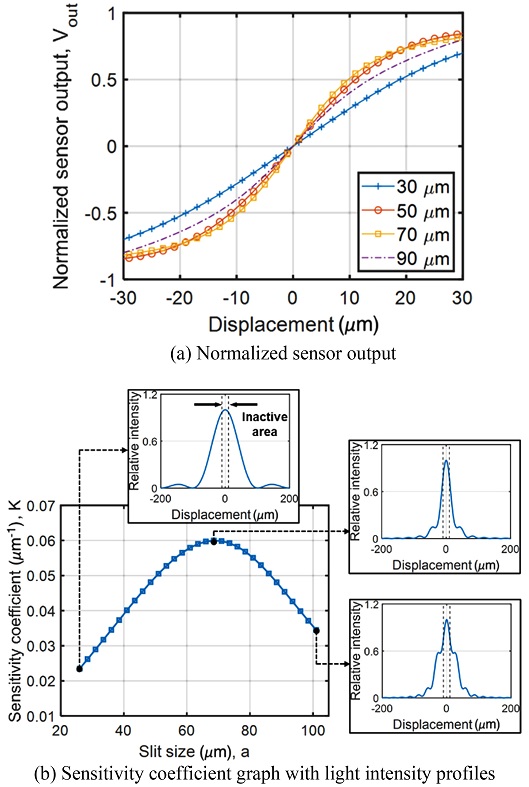
Fig. 4(a)는 광학식 위치 센서에서 출력값을 슬릿의 크기를 30에서 90 μm까지 20 μm 간격으로 증가시키며 센서의 출력을 비교한 결과로서 슬릿 크기 70 μm에서 민감도가 최대가 되었음을 알 수 있다. Fig. 4(b)와 같이 각 슬릿의 크기에서 광량의 분포를 도시하여 보면, 슬릿의 크기가 70 μm일 때 최대 민감도를 가졌다. 70 μm보다 매우 작을 때에는 Fraunhofer Diffraction의 효과가 지배적이며 슬릿의 크기가 커질수록 Fresnel Diffraction에 의해 분포 폭은 좁아지고, 기울기가 급격하게 증가한다. 반면 슬릿 크기가 70 μm보다 커지게 되면 First Maxima 값이 커지면서 오히려 민감도가 감소하게 된다.
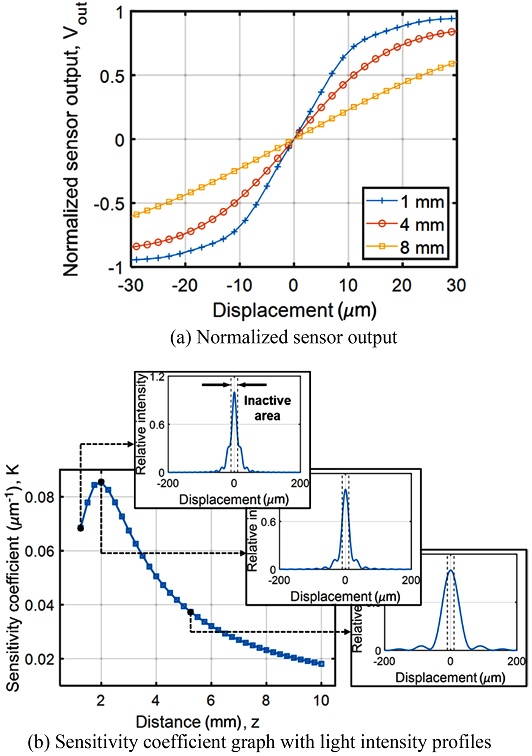
Fig. 5(a)는 슬릿의 크기는 50 μm로 하고, 슬릿과 PD 사이의 거리를 1, 4, 8 mm로 변화시키면서 센서의 출력을 비교한 결과이며, 슬릿과 PD 사이의 거리가 2 mm에서 민감도가 최대가 되었다. Fig. 4와 동일한 방법으로 광량의 분포를 보았을 때, Fresnel Diffraction 영역에서 First Maxima가 Central Maxima보다 충분히 작을 때 최대 민감도를 얻을 수 있었다(Fig. 5(b)).
민감도가 최대가 될 때 회절된 빛의 광량 분포는 두 가지 케이스에서 모두 비슷한 형상을 가지는데, 이때 슬릿 크기에 비해 슬릿과 PD 간의 거리가 얼마나 가까운지 나타내는 무차원 수인 Fresnel Number(식(11))과 같으며 대략 Fresnel Number가 대략 2일 때 민감도가 최대가 되었다.
| (11) |
또한, 민감도값은 이분할 PD 사이의 물리적 간격으로 인해 광량이 측정되지 않는 구간인 Inactive Area의 크기에 의해 달라진다. Figs. 4(b)와 5(b)의 민감도가 최대가 될 때 빛의 세기를 확인한 결과, 현재 설계에서는 Central Maxima의 반치전폭(Full Width at Half Maximum)의 크기가 대략 Inactive Area의 크기인 20 μm와 같을 때 민감도가 최대가 되었다.
3. 실험 결과
3.1 실험 셋업
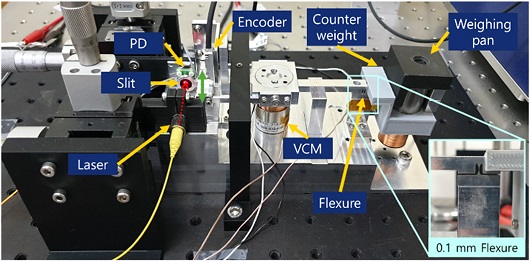
본 연구에서는 광학식 위치 센서와 함께 저울 성능 평가를 통해 센서 효용성을 확인하기 위하여 Fig. 6과 같이 EMFC 방식의 저울 프로토타입을 제작하였다.
광원은 635 nm 파장의 레이저(LPS-635-FC, Thorlabs)를 사용하였으며 Thermoelectric Cooler 회로가 장착된 레이저 컨트롤러(CLD1010LP, Thorlabs)로 레이저 광량을 컨트롤하였다. 각 PD가 1 × 0.9 mm의 크기에 0.65 A/W의 광민감도를 가진 이분할 PD (S4204, Hamamatsu Photonics)를 사용하였으며 증폭 게인 10 kV/A의 Transimpedance Amplifier (C9329, Hamamatsu Photonics)를 사용하였다. 슬릿은 상용하는 제품 중에 설계값 70 μm와 가장 가까운 50 μm 크기의 슬릿(Acktar Blackened Air Slits, Edmund Optics)을 선정하였다. 슬릿과 PD 사이의 거리는 제작 가능한 사이즈와 목표 센서의 측정 범위 ±15 μm를 고려하여 4 mm로 선정하였다. 초기 정렬은 슬릿을 제거한 후, 레이저 빔을 이분할 PD에 조사하고, 측정되는 두 전류값이 같아지도록 선형 수동 스테이지를 이용해 이분할 PD의 위치를 정렬시켰다. 이후 슬릿을 부착하여 실험을 진행하였으며 센서의 범위가 수 십 μm이므로 마이크로미터 수준의 수동 스테이지 정밀도를 고려하였을 때 충분한 초기 정렬이 가능하다.
저울 프로토타입은 단순화를 위하여 기존 EMFC 저울의 레버만 사용하였으며, 유연 힌지는 알루미늄 방전 가공을 통해 최소 두께 0.1 mm를 가진 노치 형태로 제작하였으며 변위 증폭비는 3.64이다. 저울 레버의 한 쪽에는 분동을 올려놓을 수 있는 웨잉팬과 Counter Weight를 위치시키고, 반대편에는 보이스 코일 모터(AVM 24-10, Akribis)와 광학식 위치 센서를 설치하였다. 또한 변위 센서 성능 비교를 위해 최소 분해능 1 nm의 선형 증분식 엔코더(Ti20kD, Renishaw)도 함께 설치하였다.
3.2 센서 민감도 및 분해능
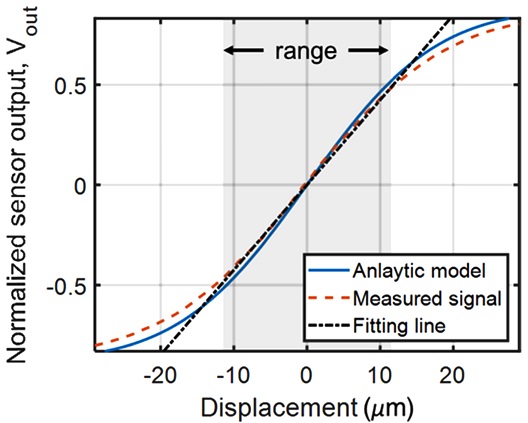
먼저 레버 이동 변위에 따른 센서의 출력 전압을 측정하여, 센서의 선형 구간과 게인값을 도출하였다. 변위는 증분형 엔코더를 통해 시스템을 위치 제어한 상태에서 0.5 μm마다 이동하며 센서의 출력을 측정하였다. Fig. 7과 같이 이론적으로 계산된 모델과 실험 결과를 비교하면 거의 일치함을 알 수 있다. 오차의 원인은 레이저 광원의 모델 오차 및 가공 및 조립 공차 때문으로 생각된다. 광학식 위치 센서의 범위는 선형성 5%를 넘지 않는 구간으로 정의하였으며, 이로 인해 센서 범위는 ±12.5 μm로 도출되었다. 그 결과 민감도 상수 K는 선형 구간에서 최소제곱법을 이용하여 도출하였으며 0.04237 μm-1으로 나타났다.
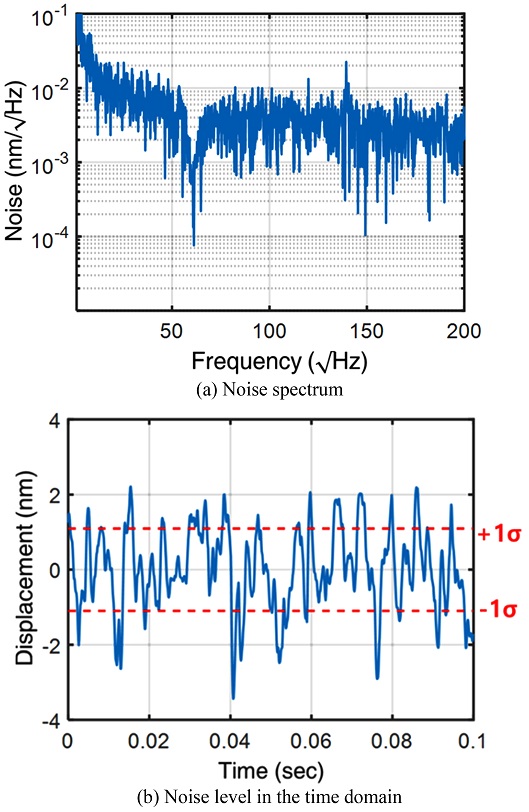
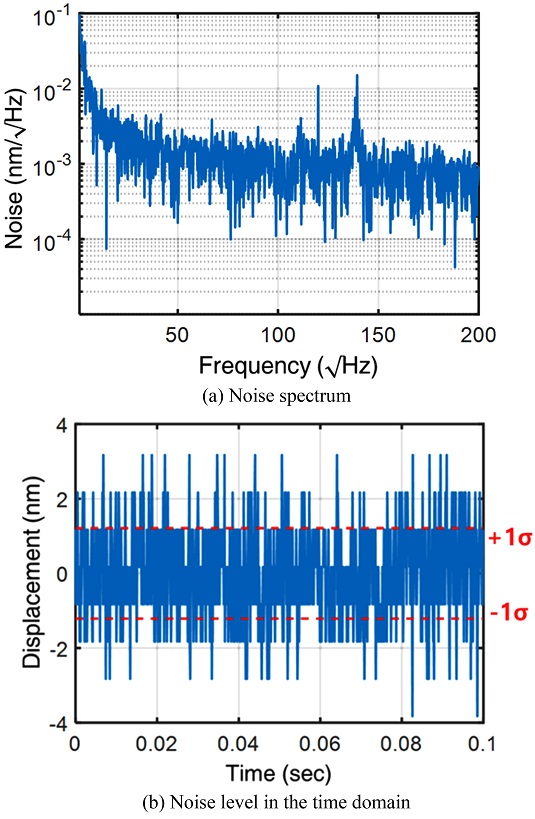
다음으로 광학식 위치 센서의 센서 노이즈 특성과 최소 분해능을 측정하였으며, 증분형 엔코더와의 성능 비교 또한 진행하였다. 데이터 샘플링 주파수는 10 kHz이며 50,000개의 데이터를 이용해 주파수 분석을 진행하였다. 광학식 위치 센서의 위치 출력값에 대한 주파수 스펙트럼을 분석한 결과 전원에 의한 60 Hz 노이즈가 주성분이었으며 해당 노이즈는 60 Hz 노치필터를 통해 제거하였고, 이는 Fig. 8(a)와 같다. 증분형 엔코더의 노이즈 스펙트럼에서는 Fig. 9(a)와 같이 저주파 영역에 특별한 주파수 성분은 없고, 전체적으로 노이즈 레벨이 광학식 위치 센서보다 좋은 특성을 보여주었다. 한편 시간 영역에서의 최소 분해능은 0.1초간 데이터의 표준편차(1σ)로 정의하였으며, 광학식 위치 센서의 분해능은 1.04 nm (Fig. 8(b))로 증분형 엔코더로 측정한 노이즈인 1.01 nm (Fig. 9(b))와 비교하였을 때 비슷한 수준임을 확인하였다.
3.3 온도에 대한 드리프트
전자기력 보상 방식의 저울의 경우 외부 온습도 등 환경 변화에 의해 시간에 따라 측정 신호가 변동하는 드리프트가 발생하는데, 이는 측정 불확도에 직접적인 영향을 미치기 때문에 드리프트에 최대한 둔감하게 시스템을 설계하고, 측정 방법을 결정해야 한다. 전자기력 보상 방식 저울에서 드리프트는 크게 구동기 자석부의 온도에 따른 잔류자속밀도의 변화, 그리고 위치 센서의 온도에 따른 전류 특성에 의해 주로 발생한다. 해당 시스템의 온도 안정성을 측정하기 위해서 상온 조건에서 센서의 출력값을 대기 온도와 함께 3시간 동안 측정하였다. 측정 결과 대기 온도 변화는 시간당 0.3oC 이내였고, 이때 증분형 엔코더의 드리프트는 8.4 nm/hour이며 광학식 위치 센서의 안정성은 -166 nm/hour이었다. 이로부터 센서의 드리프트 안정성은 증분형 엔코더가 더 우수함을 알 수 있었다.
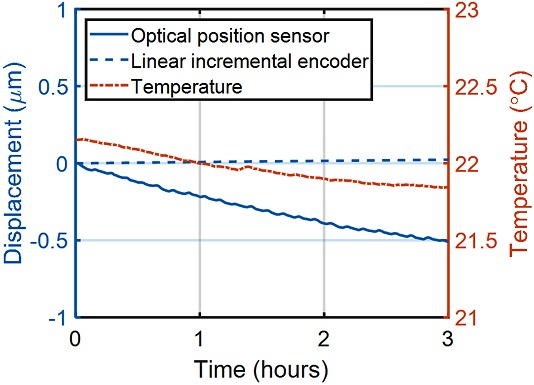
Drift in measured displacement of the optical position sensor and linear encoder according to the temperature for 3 hours
광학식 위치 센서가 온도에 대한 드리프트 특성이 저하된 이유는 레이저 광원 혹은 PD가 온도에 민감하기 때문으로 생각되며, 광원의 세기를 최적화하고, 온도에 둔감한 PD를 사용하거나 별도의 온도 보정 알고리즘을 통해 이를 보상해야 한다.16
3.4 저울 성능 실험
저울 프로토타입 및 센서의 성능 비교를 위하여 광학식 위치 센서와 증분형 엔코더를 PID 제어를 통해 비교하였다. Real-Time 컨트롤러를 통해 시스템 제어 및 계측을(Microlabox, dSPACE, Germany)하였고, 구동기에 전류를 공급하기 위한 전류원은 노이즈 수준의 고정밀 전류원(CS580, Stanford Research System, USA)을 사용하였다. 이때 전류원의 게인은 10 mA/V로 설정하였으며, 해당 고정밀 전류원의 출력 전류 한계를 고려하면 측정 가능한 최대 무게는 약 40 g이다. PID 값은 무게 측정 시 분동을 위치할 때 발생하는 외란에 대해 발산하지 않으면서 노이즈를 최소화할 수 있는 제어 게인을 Trial and Error로 결정하였으며, 광학식 위치 센서와 증분형 엔코더 모두 동일 게인으로 실험을 진행하였다.
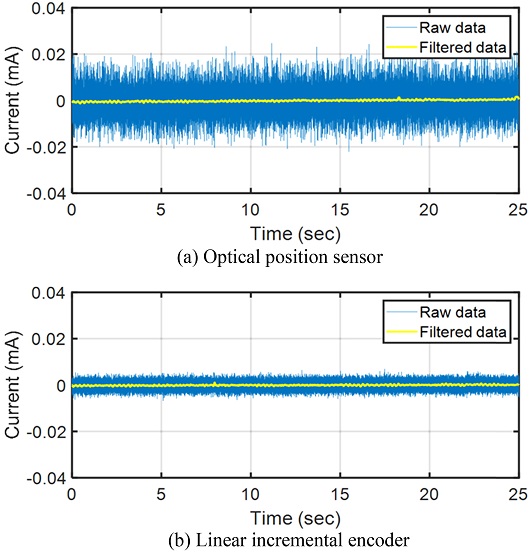
제어 결과 위치 안정성(1σ)의 경우 광학식 위치 센서가 3.41 nm, 증분형 엔코더가 1.89 nm로 도출되었다. 전류는 고주파의 노이즈 성분을 제거하고, DC 성분을 관측하기 위해 10 Hz의 컷오프 주파수를 가지는 로우패스필터를 사용하였으며 필터링 후 전류 분해능(1σ)는 광학식 위치 센서로 제어 시 0.2226 μA, 증분형 엔코더로 제어 시 0.1720 μA이다. 최종적으로 저울의 무게 분해능은 각각 0.0885, 0.0684 mg으로 도출되었다.
최종적으로 증분형 엔코더로 제어 시 앞서 살펴본 것처럼 센서 자체의 노이즈 수준이 낮기 때문에 전류 노이즈에서도 1.3배 정도 더 향상된 분해능을 나타냈지만 저울의 반복능에 영향을 줄 정도의 차이는 아니라고 판단된다.
3.5 질량 측정 실험
위치 센서에 따른 저울의 계측 성능을 평가하기 위해서 최대 허용 오차(Maximum Permissible Error) 0.05 mg인 E2급 5 g 분동과 최대 허용 오차 0.06 mg인 E2급 10 g 두 가지의 분동을 사용하여 무게를 10회 측정하였고, 측정한 결과로부터 표준편차를 통해 반복능을 도출하였다.
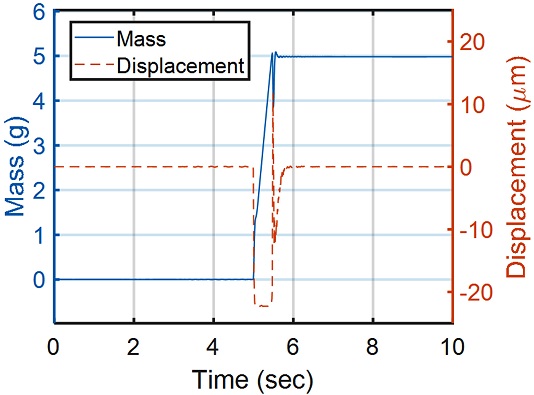
Fig. 12는 광학식 위치 센서로 제어 한 저울 프로토타입을 이용해 5 g 질량을 측정하였을 때 질량 및 광학식 위치 센서의 위치 응답 그래프이다. 질량 측정은 분동을 올려놓기 전 2초간 측정된 전류값의 평균과 원점으로 안착된 후 측정된 2초간 전류값 평균의 차로 계산되었다. 안정화 시간은 최종값에서 ±0.02% 이내로 안착하는 시간을 계산하였으며 그 결과 안정화 시간은 광학식 위치 센서로 제어 시 1.98초, 증분형 엔코더로 제어 시 1.95초로 안정화 시간은 거의 비슷하였다.
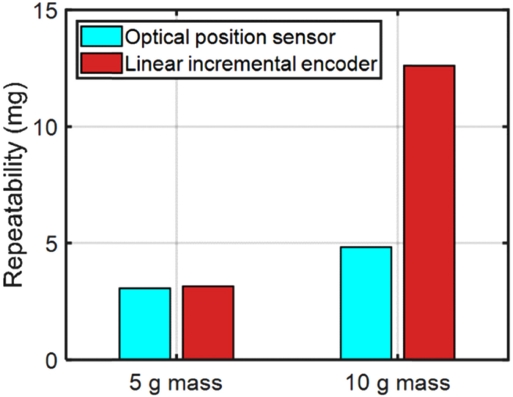
5 g을 측정한 결과 광학식 위치 센서와 증분형 엔코더로 제어 시 저울의 반복능(1σ)은 각각 3.07과 3.15 mg으로 광학식 위치 센서의 반복능이 소폭 좋게 되었지만 유의미한 차이는 아니기 때문에 5 g의 질량 측정 시에는 센서에 따라 저울의 반복능은 크게 달라지지 않는다고 볼 수 있다.
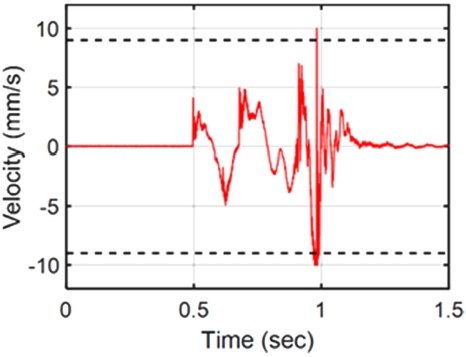
10 g 분동으로 저울을 테스트한 결과, 저울의 반복능은 광학식 위치 센서와 증분형 엔코더를 사용한 경우 각각 4.83과 12.61 mg으로 도출이 되었다. 무게가 증가함에 따라 보상을 하기 위해 VCM에 인가되는 전류의 값이 높아진다. 이로 인해 전류에 비례하는 측정 불확도가 증가되어 전체적으로 반복능이 저하되었다. 또한 증분형 엔코더로 제어 시 반복능이 약 3배 더 저하되었는데, 증분형 엔코더의 경우 컨트롤러의 클럭 주파수 한계로 인해 최대 허용 속도가 존재하며, 해당 속도를 초과할 경우 증분형 엔코더의 신호에 소실이 일어나 시스템 원점이 변하게 된다. 반복능 실험 데이터 중 평균 값에서 편차가 큰 경우에 대해 속도 응답을 확인한 결과 Fig. 14와 같이 사용된 증분형 엔코더의 최대 허용 속도인 9 mm/s를 초과하는 것을 알 수 있었다. 이러한 응답은 웨잉팬에 분동을 놓을 때 충격으로 인해 최대 허용 속도를 벗어나는 경우에 발생하였고, 최종적으로 저울의 반복능 저하로 나타났다. 반면 광학식 위치 센서의 경우 시스템 속도에 영향을 받지 않고, 정확한 영점 위치를 지시하기 때문에 증분형 엔코더에 비해 좀 더 높은 반복능으로 측정이 가능하다.
4. 결론
본 연구에서는 영위법을 사용하는 전자기력 보상 방식의 저울을 위한 광학식 위치 센서를 모델링하고 설계를 진행하였다. 그 후 제작한 저울의 프로토타입에서 센서의 성능을 평가하였고, 개발한 위치 센서로 저울을 구동 시 저울의 계측 성능을 상용 위치 센서로 제어했을 때와 비교 분석하였다. 광학식 위치 센서의 민감도에 가장 큰 영향을 미치는 요인은 PD와 슬릿 사이의 거리이며 PD의 Inactive Area에 따른 Fresnel Number 또한 설계에 있어 유의해야 한다. 최종 제작한 광학식 위치 센서의 측정 범위는 ±12.5 μm이며 민감도는 0.04237 μm-1이다. 또한 센서의 분해능은 1.09 nm이었으며 상용 위치 센서와 성능 비교 시 광학식 위치 센서가 상용 센서와 비슷한 수준의 성능을 가진 것을 확인하였다.
PID 제어를 통해 5 g 분동 무게를 측정한 결과 광학식 위치 센서를 이용한 저울의 분해능은 0.0885 mg, 반복능은 3.07 mg이었고, 측정 가능한 최대 무게는 약 40 g이다. 이는 상용 위치 센서로 제어 시와 비슷한 수준으로, 제작한 센서의 효용성을 검증하였다. 또한 중량 측정 시 충격으로 인해 발생하는 급격한 위치 변화에도 측정 위치 손실이 발생하는 증분형 엔코더 대비 제작한 광학식 위치 센서가 높은 안정성을 가지는 것을 확인하였다.
향후 과제로는 우선 온도 및 습도 등 외부 환경 변화에 의한 드리프트에 대해 강인하도록 레이저 출력 레벨을 낮추는 등 시스템 요소를 개선하고, 보정 알고리즘 적용을 진행할 계획이다. 또한 분해능 증가를 위한 노이즈 저감 회로 개발, PD 소자 변경 등을 통해 시스템 성능을 향상시키고자 한다.
Acknowledgments
본 연구는 한국표준과학연구원과 아주대학교의 지원으로 이루어졌습니다.
REFERENCES
-
Stefanescu, D. M., “Handbook of Force Transducers: Principles and Components,” Springer, pp. 41-86, 2020.
[https://doi.org/10.1007/978-3-030-35322-3_4]

-
Piskorowski, J. and Barcinski, T., “Dynamic Compensation of Load Cell Response: A Time-Varying Approach,” Mechanical Systems and Signal Processing, Vol. 22, No. 7, pp. 1694-1704, 2008.
[https://doi.org/10.1016/j.ymssp.2008.01.001]

-
Gläser, M. and Borys, M., “Precision Mass Measurements,” Reports on Progress in Physics, Vol. 72, No. 12, Paper No. 126101, 2009.
[https://doi.org/10.1088/0034-4885/72/12/126101]

- Weis, H., Hilbrunner, F., Fröhlich, T., and Jäger, G., “Parametric Mechatronic Model of a Load Cell with Electromagnetic Force Compensation,” Proc. of the IMEKO TC3, TC5 AND TC22 Conferences Metrology in Modern Context, pp. 29-32, 2010.
-
Bobroff, N., “Recent Advances in Displacement Measuring Interferometry,” Measurement Science and Technology, Vol. 4, No. 9, pp. 907-926, 1993.
[https://doi.org/10.1088/0957-0233/4/9/001]

- Maaz, G., Wedeken, U., Bierich, E., and Stadler, E., “Balance based on the Principle of the Electromagnetic Compensation of Force with Optical Position Sensor,” US Patent, 4825968, 1989.
-
Lee, C., Jeon, S., Stepanick, C. K., Zolfaghari, A., and Tarbutton, J. A., “Investigation of Optical Knife Edge Sensor for Low-Cost, Large-Range and Dual-Axis Nanopositioning Stages,” Measurement, Vol. 103, pp. 157-164, 2017.
[https://doi.org/10.1016/j.measurement.2017.02.030]

-
Choi, I. M., Choi, D. J., and Kim, S. H., “Double Force Compensation Method to Enhance the Performance of a Null Balance Force Sensor,” Japanese Journal of Applied Physics, Vol. 41, No. 6R, pp. 3987-3993, 2002.
[https://doi.org/10.1143/JJAP.41.3987]

-
Ishikawa, I., Sawada, R., Higurashi, E., Sanada, S., and Chino, D., “Integrated Micro-Displacement Sensor that Measures Tilting Angle and Linear Movement of an External Mirror,” Sensors and Actuators A: Physical, Vol. 138, No. 2, pp. 269-275, 2007.
[https://doi.org/10.1016/j.sna.2007.03.027]

- Kang, C. S., Kim, J. A., Jin, J., Eom, T. B., Suh, H. S., et al., “A Simple Optical Sensor for the Straightness Error Measurement of a Moving Stage,” Proc. of the 11th International Symposium on Measurement and Quality Control, 2013.
-
Marangoni, R. R., Schleichert, J., Rahneberg, I., Hilbrunner, F., and Fröhlich, T., “A Self-Calibrating Multicomponent Force/Torque Measuring System,” Measurement Science and Technology, Vol. 29, No. 7, Paper No. 074002, 2018.
[https://doi.org/10.1088/1361-6501/aac00f]

-
Haddad, D., Juncar, P., Geneves, G., and Wakim, M., “Gaussian Beams and Spatial Modulation in Nanopositioning,” IEEE Transactions on Instrumentation and Measurement, Vol. 58, No. 4, pp. 1003-1009, 2008.
[https://doi.org/10.1109/TIM.2008.2008475]

- Diethold, C., Fröhlich, T., Hilbrunner, F., and Jäger, G., “High Precision Optical Position Sensor for Electromagnetic Force Compensated Balances,” Proc. of the IMEKO Conference, 2010.
- Joseph W. G., “Introduction to Fourier Optics,” W. H. Freeman and Company, 4th Ed., pp. 75-85, 2017.
-
Wichtowski, M., “Simple Analytic Expressions of Fresnel Diffraction Patterns at a Straight Strip and Slit for Gaussian Wave Illumination,” American Journal of Physics, Vol. 87, No. 3, pp. 171-175, 2019.
[https://doi.org/10.1119/1.5089415]

- Schett, O. and Leemann, R., “Temperature-Corrected Weighing Apparatus Having Electromagnetic Load Compensation Means,” US Patent, 4457386, 1984.

M.S. student in the Department of Mechanical Engineering, Ajou University. His research interest is high-precision machines and optical sensors.
E-mail: dmcj421@ajou.ac.kr

Ph.D. Student in the Department of Mechanical Engineering, Ajou University. His research interest is novel instrumentation systems, actuator design, and biomechanical wearable devices.
E-mail: majesty17@ajou.ac.kr

Ph.D. Student in the Department of Mechanical Engineering, Ajou University. His research interest is compliant mechanism design and modeling.
E-mail: qwecsz@ajou.ac.kr

Associate Professor in the Department of Mechanical Engineering, Ajou University. His research interest is high-precision machines, mass metrology and wearable mechatronics.
E-mail: ymanchoi@ajou.ac.kr