유전 알고리즘을 이용한 뱀형 로봇 주행 패턴 생성

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents a novel method of designing an efficient locomotion pattern generating algorithm for snake robots by a genetic algorithm (GA). In search and rescue operations in disaster areas, a snake robot requires multiple locomotion patterns. To overcome the complexity of snake robot control, we used a central pattern generator (CPG)-based control method which mimics the motion of a biological snake. GA was used to optimize CPG parameters to maximize locomotion performance. The locomotion performance according to the CPG parameters change was analyzed using the snake robot simulator. The proposed locomotion pattern generation algorithm evolved quickly for the target performance and obtained CPG parameters for the desired locomotion.
Keywords:
Snake robot, Locomotion pattern, Genetic algorithm, Central pattern generator, Robot simulator키워드:
뱀형 로봇, 주행 패턴, 유전 알고리즘, 중앙 패턴 발생기, 로봇 시뮬레이터1. 서론
지진, 폭우, 폭설, 산사태 등으로 인한 건물붕괴 상황에서 인명을 탐지하기 위해 로봇 기술을 활용한 다양한 시도가 있으며, 특히 붕괴된 건물이나 좁은 통로에서의 수색 및 구조 작업의 경우 뱀형 로봇을 활용한 연구들이 진행되고 있다.1 뱀형 로봇은 바닥이 편평하지 않거나 장애물이 많은 지형을 극복할 수 있으며, 온몸의 무게를 분산시킬 수 있음으로 습지나 사구와 같이 지표면이 단단하지 않은 곳에서 이동이 가능하다.2
이러한 환경에서 다수의 관절로 구성된 자유도가 높은 뱀형 로봇 제어를 위해 기구학, 동역학 해석을 통한 다양한 이론적 접근이 있지만,3,4 개별 주행 패턴에 한정된 제어방식으로 다양한 환경 조건에서의 즉각적인 대응이 어려운 단점이 있다.5 재난환경에서 뱀형 로봇을 활용하기 위해서는 다양한 주행 패턴을 구현하여 장애물을 극복할 수 있는 뱀형 로봇 제어 방식이 필요하다. 이러한 뱀형 로봇의 제어 방식으로 매개변수화된 함수를 사용하는 Central Pattern Generator (CPG) 기반 제어 방법이 있으며2 몇 개의 파라미터를 조절하여 뱀형 로봇의 다양한 주행 패턴을 생성할 수 있다.6 이러한 제어 방법은 뱀형 로봇의 동역학 모델 정보를 사용하지 않고, 로봇을 제어할 수 있는 장점이 있다. CPG 기반 뱀형 로봇 제어 방법은 각 관절을 주기적으로 동작하여 이동하는 방식으로, 파형을 생성하는 파라미터의 조합에 따라 다양한 주행 패턴의 구현이 가능하다. 현재까지 연구된 뱀형 로봇의 주요 주행 패턴으로 Concertina, Lateral Undulation, Sidewinding, Inchworm, Rolling 등이 있으며,5 각 주행 패턴을 구현하기 위한 최적의 CPG 파라미터값은 뱀형 로봇의 구조 및 물성치에 따라 다르므로, 반복 실험을 통한 파라미터 튜닝이 필요하다.7
뱀형 로봇의 주행 패턴 생성을 위한 CPG 파라미터 선정 방법에 관해 다양한 연구가 진행되었다. 생물학적 뱀의 움직임을 관찰하여 이와 유사한 뱀형 로봇의 주행 패턴을 구현하거나,8,9 실제 개발한 뱀형 로봇의 실험을 통해 CPG 파라미터를 추정하여 주행 패턴을 생성하였다.16,17 그 외 대다수 연구자들은 시뮬레이션 환경을 구축하여 뱀형 로봇 주행 패턴 생성을 위한 CPG 파라미터 최적화를 수행하였다.10-15 이처럼 다양한 환경에서 반복 실험에 의한 시행착오로 얻은 뱀형 로봇 주행 패턴은 그 성능과 최적화 정도를 확인이 어려워 주행 성능을 점진적으로 최적화할 수 있는 학습 기반의 최적화 방법에 관한 연구가 필요하다.18,19
학습 기반의 뱀형 로봇 주행 패턴 최적화 방법으로는 유전 알고리즘(Genetic Algorithm, GA)을 적용한 연구가 있다.20 GA는 자연에서 종이 진화하는 과정을 모방하여 적자 생존하며 점진적으로 최적해를 찾아 문제를 해결하는 방법으로, GA를 적용하기 위해서는 뱀형 로봇 주행 패턴을 GA의 표현 방식인 유전자(CPG 파라미터)로 표현할 수 있어야 하며, 이 해가 얼마나 적합한지(주행 성능)를 평가할 수 있는 적합도 분석이 필요하다. GA를 사용한 위 연구에서는 뱀형 로봇의 관절 수에 따라 유전자의 구조 및 크기가 변경되어 관절 수가 많을수록 GA 최적화 과정에 필요한 비용이 증가하게 된다. 그리고 GA 적합도 분석을 위해 뱀형 로봇 질량 중심의 변위만을 사용하였는데, 주행 패턴의 정확도를 높이기 위해서는 적합도 분석 함수에 주행 방향 및 로봇 자세 등을 평가할 수 있는 요소를 포함할 필요가 있다.
따라서 본 연구에서 제안하는 GA를 이용한 뱀형 로봇 주행 패턴 생성 방법은 뱀형 로봇의 관절 수 변화에 따라 유전자(CPG 파라미터)의 구조가 변하지 않아 다양한 길이의 뱀형 로봇 주행 패턴 생성에 적용할 수 있다. 또한, 뱀형 로봇의 이동 속도, 방향, 자세 등을 최적화할 수 있는 적합도 분석 방법을 적용하여 정확한 측면 고속 주행 패턴을 도출할 수 있도록 하였다.
본 논문은 다음과 같이 구성된다. 2장에서는 뱀형 로봇의 구조, 주행 패턴 생성 및 제어 방식, 뱀형 로봇 주행 성능 평가를 위한 시뮬레이터에 대해 설명한다.
3장에서는 주행 패턴 생성을 위한 학습 알고리즘으로 GA를 설명하고, 목표 주행 성능을 도출하기 위한 뱀형 로봇 CPG 파라미터 결과를 얻는데 필요한 과정을 제시한다. 4장에서는 제시한 방법에 대한 시뮬레이션 환경에서의 주행 패턴 생성 실험 결과를 제시한다.
2. 뱀형 로봇 시스템
2.1 뱀형 로봇 구조
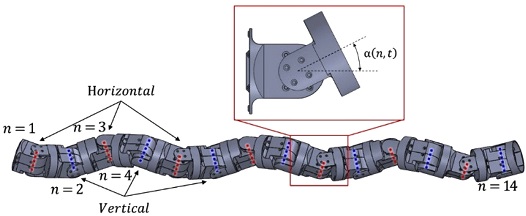
주행 패턴 생성 알고리즘을 적용하기 위한 뱀형 로봇은 Fig. 1과 같이 단일 자유도를 가지는 14개의 모듈을 수평/수직 방향 교대로 연결한 구조로 각 모듈의 회전 범위는 ±90o이다. 시뮬레이터 환경에 적용한 뱀형 로봇의 물성치는 Table 1과 같으며, 뱀형 로봇의 물성값에 따라 최적 파라미터의 조합이 달라진다.
2.2 뱀형 로봇 제어
뱀형 로봇 제어를 위한 다양한 연구가 수행되었으며, 크게 두 가지 접근 방식으로 나눌 수 있다.
첫 번째 방법은 뱀형 로봇 몸체 전체에 대한 기구학 및 동역학적 모델에 기반한 제어 방법이다. 이러한 제어 방법은 로봇 모델의 복잡성으로 인하여 평면 또는 경사면2,13 환경으로 로봇 움직임(Motion)이 제한된다. 이는 다양한 환경에 대한 뱀형 로봇의 적응성을 낮추며, 실제 뱀의 주행 패턴과도 상이한 결과를 보인다.
반면 최근 CPG를 기반으로 한 제어 방법은 뱀형 로봇과 같이 자유도가 큰 로봇의 3차원 움직임을 즉각적으로 생성할 수 있으며, 환경 적응성이 높은 모션 생성이 가능하다.20 이러한 제어 방법은 뱀형 로봇 모듈 수의 제한없이 사용할 수 있는 장점이 있다. CPG 모델은 Matsuoka21에 의해 제안되었으며, 동물과 유사한 로봇의 제어와 4족/2족 로봇의 보행 연구에 사용되었다.22-24
따라서 본 연구에서는 CPG 기반으로 뱀형 로봇의 각 관절 각도를 조절하여 로봇 움직임을 제어하는 방법을 사용한다.
2.3 뱀형 로봇 주행 패턴
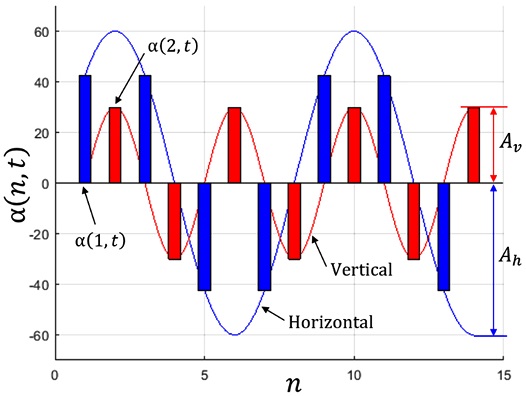
뱀형 로봇의 리드미컬한 동작 생성을 위해 Fig. 2와 같이 각 모듈의 각도는 수평과 수직 방향으로 나누어 표현하며 다음 식 (1)과 식(2)와 같다.9
| (1) |
| (2) |
여기서는 α(n,t)뱀형 로봇 n번째 관절의 t시간 에서의 각도값을 의미하며, βh,v는 Angle Offset, Ah,v는 Amplitude, θh,v는 Phase, δ는 Phase Shift, Ωh,v는 Spatial Frequency 그리고 ωh,v는 Temporal Frequency를 의미한다.
뱀형 로봇 각 관절의 파동 주파수는 θh,v에 의해 결정되며, 공간적 주파수와 시간적 주파수 성분을 모두 포함한다. 먼저 Ωh,v는 공간적 요소를 결정하며, 특정 시간 t에서 각 관절의 각도를 보면 로봇의 거시적인 모양을 확인할 수 있다. ωh,v는 시간적 요소로 파동의 속도를 나타내며, 각 관절이 얼마나 빨리 구동하는 지를 결정한다. δ는 직교한 수평/수직 관절의 교차 시점을 제어하기 위한 파라미터이다. Ah,v는 파동의 진폭을 의미하며, 그 크기가 증가할수록 로봇의 속도 및 극복 가능한 장애물의 크기가 증가하지만, 로봇의 주행 안정성은 감소하게 된다. 마지막으로 βh,v는 뱀형 로봇의 이동 방향을 조종하는데 사용된다.25
Fig. 3은 시간 t에서 수평/수직 관절의 각도값과 설정된 파라미터에 따라 반복되는 파형을 나타낸 것이다. 뱀형 로봇의 주행 패턴 파라미터는 Ah,v, δ, Ωh,v에 의해 생성되는 수평/수직 관절의 파동의 조합에 의해 결정되며, 제안하는 알고리즘을 통해 목표하는 주행 성능을 만족하는 최적 파라미터를 도출하고자 한다.
2.4 뱀형 로봇 시뮬레이터
뱀형 로봇의 주행 성능을 평가하기 위한 시뮬레이터는 Gazebo Simulator26를 기반으로 개발하였으며, 뱀형 로봇은 CPG 모델 기반으로 입력되는 각 모듈의 반복 모션에 의한 바닥 면과의 마찰 반력으로 이동한다.
시뮬레이터의 좌표계는 뱀형 로봇의 좌우 방향이 X축, 앞뒤 방향이 Y축으로, 뱀형 로봇의 초기 위치는 첫 번째 모듈이 XY 평면 원점에 위치하고, Y축과 뱀형 로봇의 길이 방향이 평행하게 배치하였다.
시뮬레이터는 GA를 통해 전달 받은 CPG 파라미터값을 기준으로 설정된 시뮬레이터 시간 동안 뱀형 로봇을 동작시킨 후 로봇의 위치 및 자세 등의 주행 성능 결과를 도출하고, GA로 전달하는 역할을 한다.
3. 주행 패턴 생성 알고리즘
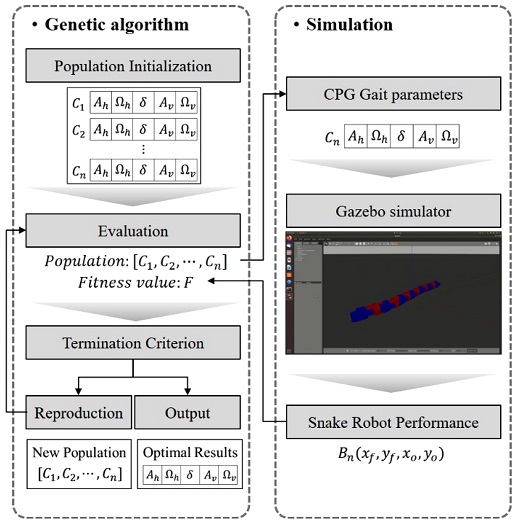
뱀형 로봇의 주행 패턴 생성 알고리즘 구조는 Fig. 4와 같이 CPG 파라미터로 구성된 염색체 데이터들을 GA 초기값으로 무작위 생성한 후, 시뮬레이션 환경으로 전달하여 주행 패턴을 생성하고, 성능을 평가한다. 그 후, 시뮬레이터를 통해 평가된 각 파라미터의 적합도 값(Fitness Value)을 기준으로 다음 세대 자손 염색체를 생성하고, GA 종료 조건을 판별하여 생성된 자손 염색체가 다음 세대로 진화 및 평가를 반복할지 GA를 종료할 것인지를 판단한다. 이러한 반복 과정에서 염색체는 진화와 퇴화를 거듭하며 최적의 주행 성능을 보이는 CPG 파라미터(주행 패턴) 결과를 도출할 수 있다.
3.1 유전 알고리즘(Genetic Algorithm, GA)
GA는 생물학적 진화를 모방한 최적화 방법으로, 수학적으로 명확하게 정의되지 않은 문제에도 적용할 수 있는 장점이 있다.27 이러한 진화적 접근 방식(GA)은 복잡한 뱀형 로봇의 해석 모델을 사용하지 않고, 로봇의 주행 패턴을 생성할 수 있다.
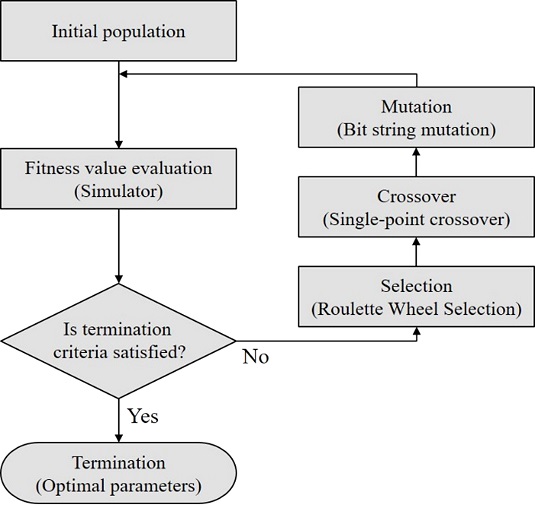
제안하는 주행 패턴 생성 알고리즘은 GA와 시뮬레이터 기반의 CPG 모델 파라미터 최적화를 통해 뱀형 로봇의 목표 성능을 만족할 수 있는 주행 패턴을 생성할 수 있다. 최적화 대상인 CPG 파라미터는 GA의 염색체로 표현하며, 염색체 구조는 CPG 파라미터를 일렬로 연결한 형태(Ah, Ωh, δ, Av, Ωv)로 구성된다. 염색체로 표현된 CPG 파라미터는 시뮬레이터를 통해 적합도를 평가하고, 염색체 집단(Population) 중에서 우수한 염색체가 선택(Selection)될 확률이 높고, 교차(Crossover) 및 변이(Mutation)에 의해 다음 세대로 번식한다. 이러한 과정을 반복하여 최종적으로 최적화된 염색체를 얻을 수 있으며, GA의 단계별 프로세스는 Fig. 5와 같은 과정으로 진행된다.
3.2 GA 실행 절차
첫 번째 단계로 새로운 염색체를 구성하는 유전자를 각 파라미터의 주어진 범위 내에서 무작위로 선정하여 염색체 집합인 첫 세대(Population 50)를 생성한다.
궁극적인 주행 패턴 생성 알고리즘은 뱀형 로봇 움직임에 구체적인 제한 사항을 지정하지 않고도 높은 주행 성능을 안정적으로 보일 수 있도록 하는 주행 패턴 도출을 목표로 하며, 이는 적절한 적합도 평가 함수를 설계하는 것에 달려 있다.28 적합도는 개발한 시뮬레이터를 통해 뱀형 로봇 동작 결과를 고려하여 평가한다.
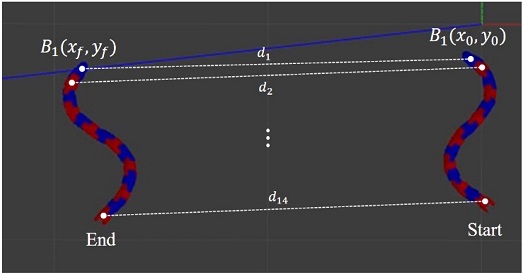
본 연구에서는 뱀형 로봇의 다양한 주행 패턴 중 측면 고속 주행을 목표로 파라미터 최적화를 진행하였으며, 최대화해야 하는 적합도는 Fig. 6과 같이 시뮬레이션 시간(t) 동안 뱀형 로봇이 측면으로 이동한 거리이다. 적합도 함수는 뱀형 로봇의 이동 방향성을 유지하기 위해 측면 방향(X) 요소는 강화(증가)하고, 방향 변화로 이어지는 앞뒤 방향(Y) 요소는 억제(감소)하는 요소로 구성되며, 식으로 표현하면 다음 식(3)과 같다.
| (3) |
여기서 F는 적합도 값으로, M개의 모듈로 구성된 뱀형 로봇의 개별 모듈(n)의 수평 이동거리 합을 의미한다. 방향계수 λ는 0-1 사이의 값을 가지며, 작을수록 로봇의 이동 속도와 클수록 로봇의 직진성에 영향을 준다.
다음 세대에 염색체를 전달하기 위한 염색체 선택 방법으로 룰렛 휠 선택(Roulette Wheel Selection) 방식을 적용하였으며, 이 방법은 적합도가 높은 부모 해의 선택 확률이 높아 다음 세대에 전달되는 확률이 증가하는 방식이다.
선택된 2개의 부모 염색체들로부터 자손 염색체를 생성하는 교차(Crossover) 방법으로, 단일 교차(Single Point Crossover) 방식을 적용하였다. 이 방법은 양쪽의 부모 염색체에서 무작위로 교차점을 지정하고, 이를 기준으로 두 부모 염색체를 교차 적용하여 2개의 자손 염색체를 생성한다. 세대를 거듭함에도 우수한 염색체를 보존/전달하기 위해 교차 연산을 확률적으로 수행한다.
돌연변이 연산은 염색체의 순서 혹은 특정 유전자 값을 임의로 변경하여 다른 염색체로 변형시키는 연산으로, Single Point Mutation 방식을 적용하였다. 돌연변이 연산은 국소 최적점에 빠지는 문제를 방지하고, 염색체를 다양화하여 진화에 도움이 된다. 학습 정확도 향상 및 학습 시간 감소를 위해 돌연변이 확률은 세대를 거듭함에 따라 변화시켰으며, 학습 시간과 적합도 결과에 미치는 영향을 고려하여 선정하였다.
GA의 진화에는 끝이 없고 항상 개선의 여지가 있기 때문에 종료 기준을 설정하지 않으면 학습 과정은 영원히 계속될 수 있다. 일반적으로 세대 수를 제한하거나 적합도 값이 목푯값을 달성할 경우 학습을 종료하게 된다.
4. 주행 패턴 생성 실험
4.1 시뮬레이션 환경
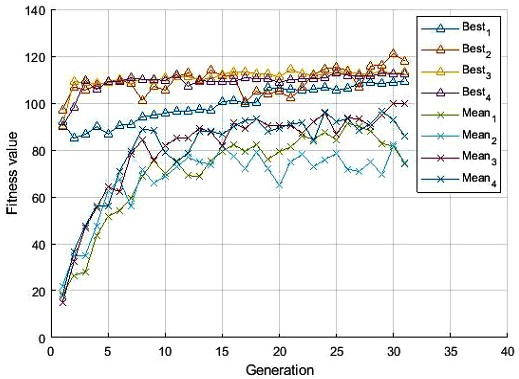
제안하는 뱀형 로봇의 주행 패턴 생성 알고리즘은 주행 패턴을 결정하는 CPG 파라미터 최적화 방법으로 GA를 사용하고, 개발한 시뮬레이터를 통해 GA 실행 중 생성되는 파라미터들의 적합도를 평가하였다. 이러한 주행 패턴 생성 알고리즘의 정밀도를 확인하기 위해 동일한 조건에서 반복 시행하여 획득한 CPG 파라미터에 해당하는 주행 패턴의 적합도 값을 비교하였다. 주행 패턴 생성 실험은 4회 반복하였으며, 각 시뮬레이션별 최대/평균 적합도 값의 세대별 변동 추세를 비교하였다. 시뮬레이션에 적용한 GA 매개변수는 Table 2와 같이 설정하였다.
4.2 시뮬레이션 결과
Fig. 7과 같이 동일한 조건에서 시뮬레이션을 4회 반복 시행한 후 적합도 분석 결과를 살펴보면, 10세대 이후부터 적합도 평균값이 안정화되는 것을 확인할 수 있으며, 20세대 이후 적합도 최댓값이 100 이상으로 수렴하는 경향을 보인다. 따라서 제안한 시뮬레이션 조건에서 20세대 이상 학습을 수행할 경우, 목표 주행 성능을 만족할 수 있는 뱀형 로봇 CPG 파라미터를 도출할 수 있다.
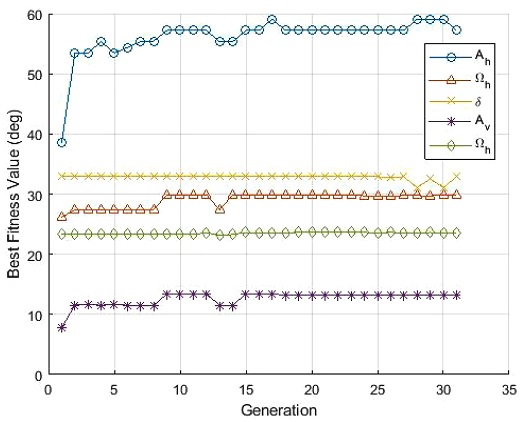
첫 번째 시뮬레이션 결과에서 세대를 거침에 따라 CPG 파라미터의 변화 과정을 Fig. 8에서 확인할 수 있으며, 마지막 세대에서의 최대 적합도 값에 해당하는 CPG 파라미터 결과는 Table 3과 같다.
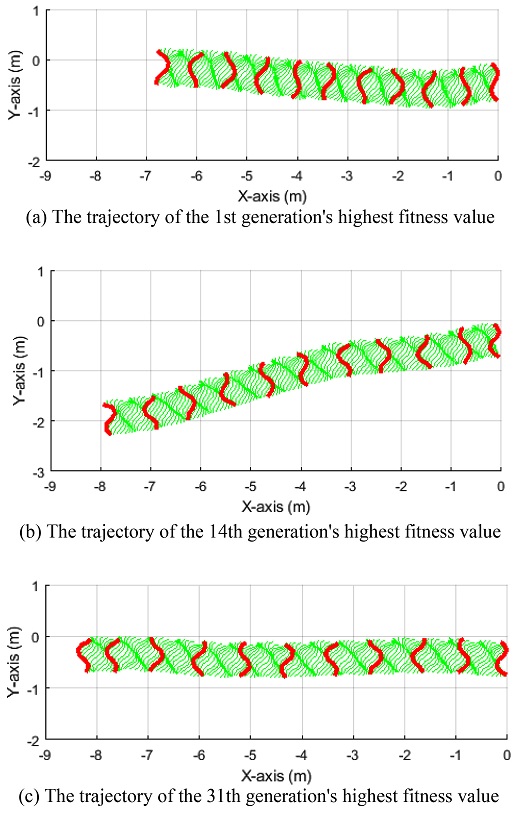
Fig. 9는 주행 패턴 생성 알고리즘 적용 전(1세대), 중(14세대), 후(31세대)의 주행 패턴 결과를 보여주고 있으며, 주행 속도 및 정확도에 있어서 점진적으로 향상되는 것을 확인할 수 있다. 모든 주행 패턴은 측면감기(Sidewinding) 궤적과 유사하며,29 최종 결과 파라미터(Table 3)의 주행 패턴 성능은 원점에서 시뮬레이션 시간(10 s) 동안 7.8 m를 이동하여, 약 0.78 m/s 속도로 횡 방향 이동하는 것을 확인할 수 있다. 학습 효과를 높이기 위해서는 초기 염색체 집합의 수를 최대화하여 가능한 한 많은 조합의 CPG 파라미터에 대한 주행 평가를 하는 것이 좋을 수 있지만, 학습시간을 기하급수적으로 늘어날 수 있으므로 적절한 GA 매개변수 설정이 중요하다.
이러한 시뮬레이션 결과들은 제안한 새로운 학습 알고리즘이 뱀형 로봇 제어를 위한 주행 패턴 생성에 활용될 수 있음을 보여준다.
5. 결론
본 논문에서는 뱀형 로봇의 주행 패턴 생성을 위해 CPG 파라미터 최적화 방법을 제안하였으며, 이를 구현하기 위한 시뮬레이션 환경을 구축하고, 반복 시행하여 알고리즘의 정밀도를 검증하였다. 또한, 시뮬레이션을 통해 최적화된 CPG 파라미터의 주행 성능을 확인하여 목표한 뱀형 로봇의 주행 패턴이 생성됨을 확인하였다.
뱀형 로봇 제어를 위해 CPG 모델 기반 제어 방법을 사용하였으며, 주행 패턴 개발을 위한 CPG 파라미터 추정 방법으로 GA를 적용하였다. 실험을 통해 생성한 주행 패턴(측면 고속 이동) 외에 종 방향 고속 이동, 협소 지형 이동, 파이프 감기, 회전(Rolling) 이동, 장애물 극복 등의 다양한 주행 패턴 생성이 가능하다. 이러한 주행 패턴 생성을 위해서는 각 주행 패턴별 로봇의 운동 특성을 정확히 반영할 수 있는 적합도 분석 함수의 설정이 필요하다. 적합도 분석 함수는 뱀형 로봇의 주행 성능(주행속도, 직진성) 뿐만 아니라 로봇의 이동중 자세를 고려하여 설정해야 더욱 더 정교한 주행 패턴을 생성할 수 있다. 예를 들어 협소 지형 이동을 위한 주행 패턴을 생성할 경우 뱀형 로봇의 각 모듈의 변위는 통과하고자 하는 협소 공간 단면 내에서 주기적인 파형을 생성하며 종 방향 이동을 해야 된다.
본 연구에서 제안한 주행 패턴 생성 알고리즘은 GA와 같은 학습 기반의 최적화 방법을 적용하여 인간의 직감으로 해결하기에 복잡한 문제를 반복 학습을 통해 CPG 파라미터를 최적화하였으며, 개발한 시뮬레이터 환경에서 각 파리미터별 주행 패턴 성능을 평가할 수 있었다. 향후, 개발한 실제 뱀형 로봇에 최적화된 파라미터를 적용하여 주행 패턴 생성 가능성을 확인하고자 한다.
Acknowledgments
본 논문은 산업통상자원부 산업기술혁신사업 지원을 받아 수행된 연구임(No. 20003739).
REFERENCES
-
Whitman, J., Zevallos, N., Travers, M., and Choset, H., “Snake Robot Urban Search after the 2017 Mexico City Earthquake,” Proc. of the IEEE International Symposium on Safety, Security, and Rescue Robotics, pp. 1-6, 2018.
[https://doi.org/10.1109/SSRR.2018.8468633]

- Hirose, S. and Mori, M., “Biologically Inspired Snake-Like Robots,” Proc. of the IEEE International Conference on Robotics and Biomimetics, pp. 1-7, 2004.
- Burdick, J. W., Radford, J., and Chirikjian, G. S., “A ‘Sidewinding’ Locomotion Gait for Hyper-Redundant Robots,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 101-106, 1993.
-
Chirikjian, G. S. and Burdick, J. W., “The Kinematics of Hyper-Redundant Robot Locomotion,” IEEE Transactions on Robotics and Automation, Vol. 11, No. 6, pp. 781-793, 1995.
[https://doi.org/10.1109/70.478426]

-
Transeth, A. A., Pettersen, K. Y., and Liljebäck, P., “A Survey on Snake Robot Modeling and Locomotion,” Robotica, Vol. 27, No. 7, pp. 999-1015, 2009.
[https://doi.org/10.1017/S0263574709005414]

-
Schmitt, J., Garcia, M., Razo, R., Holmes, P., and Full, R. J., “Dynamics and Stability of Legged Locomotion in the Horizontal Plane: A Test Case Using Insects,” Biological Cybernetics, Vol. 86, No. 5, pp. 343-353, 2002.
[https://doi.org/10.1007/s00422-001-0300-3]

- González Gómez, J., Zhang, H., and Boemo, E. I., “Locomotion Principles of 1D Topology Pitch and Pitch-Yaw-Connecting Modular Robots,” I-Tech Education and Publishing, pp. 403-428, 2007.
- Hirose, S. and Mori, M., “Biologically Inspired Snake-Like Robots,” Proc. of the IEEE International Conference on Robotics and Biomimetics, pp. 1-7, 2004.
-
Dai, J., Travers, M., Dear, T., Gong, C., Astley, H. C., et al., “Robot-Inspired Biology: The Compound-Wave Control Template,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 5879-5884, 2015.
[https://doi.org/10.1109/ICRA.2015.7140022]

- Dowling, K. J., “Limbless Locomotion: Learning to Crawl with a Snake Robot,” Carnegie Mellon University, 1997.
-
Saito, M., Fukaya, M., and Iwasaki, T., “Modeling, Analysis, and Synthesis of Serpentine Locomotion with a Multilink Robotic Snake,” IEEE Control Systems Magazine, Vol. 22, No. 1, pp. 64-81, 2002.
[https://doi.org/10.1109/37.980248]

- Ma, S., Li, W. J., and Wang, Y., “A Simulator to Analyze Creeping Locomotion of a Snake-Like Robot,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 3656-3661, 2001.
- Ma, S., Tadokoro, N., Li, B., and Inoue, K., “Analysis of Creeping Locomotion of a Snake Robot on a Slope,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 2073-2078, 2003.
- Ma, S., Ohmameuda, Y., and Inoue, K., “Dynamic Analysis of 3-Dimensional Snake Robots,” Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 767-772, 2004.
- González Gómez, J., Zhang, H., Boemo, E. I., and Zhang, J., “Locomotion Capabilities of a Modular Robot with Eight Pitch-Yaw-Connecting Modules,” Proc. of the International Conference on Climbing and Walking Robots, 2006.
- Xiao, X., Cappo, E., Zhen, W., Dai, J., Sun, K., et al., “Locomotive Reduction for Snake Robots,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 3735-3740, 2015.
- Støy, K., Shen, W., and Will, P., “Global Locomotion from Local Interaction in Self-Reconfigurable Robots,” Proc. of the 7th International Conference on Intelligent Autonomous Systems, pp. 25-27, 2002.
- Ito, K. and Matsuno, F., “Application of Reinforcement Learning to Hyper-Redundant System Acquisition of Locomotion Pattern of Snake Like Robot,” Proc. of the Korea Intelligent Information System Society Conference, pp. 65-70, 2001.
-
Hasanzadeh, S. and Tootoonchi, A. A., “Ground Adaptive and Optimized Locomotion of Snake Robot Moving with a Novel Gait,” Autonomous Robots, Vol. 28, No. 4, pp. 457-470, 2010.
[https://doi.org/10.1007/s10514-010-9179-y]

-
Hasanzadeh, S. and Tootoonchi, A. A., “Adaptive Optimal Locomotion of Snake Robot based on CPG-Network Using Fuzzy Logic Tuner,” Proc. of the IEEE Conference on Robotics, Automation and Mechatronics, pp. 187-192, 2008.
[https://doi.org/10.1109/RAMECH.2008.4681403]

-
Matsuoka, K., “Mechanisms of Frequency and Pattern Control in the Neural Rhythm Generators,” Biological Cybernetics, Vol. 56, No. 5, pp. 345-353, 1987.
[https://doi.org/10.1007/BF00319514]

-
Kimura, H., Fukuoka, Y., and Konaga, K., “Adaptive Dynamic Walking of a Quadruped Robot Using a Neural System Model,” Advanced Robotics, Vol. 15, No. 8, pp. 859-878, 2001.
[https://doi.org/10.1163/156855301317198179]

-
Fukuoka, Y., Kimura, H., and Cohen, A. H., “Adaptive Dynamic Walking of a Quadruped Robot on Irregular Terrain based on Biological Concepts,” The International Journal of Robotics Research, Vol. 22, Nos. 3-4, pp. 187-202, 2003.
[https://doi.org/10.1177/0278364903022003004]

-
Taga, G., Yamaguchi, Y., and Shimizu, H., “Self-Organized Control of Bipedal Locomotion by Neural Oscillators in Unpredictable Environment,” Biological Cybernetics, Vol. 65, No. 3, pp. 147-159, 1991.
[https://doi.org/10.1007/BF00198086]

-
Tesch, M., Lipkin, K., Brown, I., Hatton, R., Peck, A., et al., “Parameterized and Scripted Gaits for Modular Snake Robots,” Advanced Robotics, Vol. 23, No. 9, pp. 1131-1158, 2009.
[https://doi.org/10.1163/156855309X452566]

-
Agüero, C. E., Koenig, N., Chen, I., Boyer, H., Peters, S., et al., “Inside the Virtual Robotics Challenge: Simulating Real-Time Robotic Disaster Response,” IEEE Transactions on Automation Science and Engineering, Vol. 12, No. 2, pp. 494-506, 2015.
[https://doi.org/10.1109/TASE.2014.2368997]

- Aarts, E. H., Eiben, Á. E., and Van Hee, K., “A General Theory of Genetic Algorithms,” Mathematics and Computer Science, Vol. 8308, pp. 1-21, 1989.
-
Nelson, A. L., Barlow, G. J., and Doitsidis, L., “Fitness Functions in Evolutionary Robotics: A Survey and Analysis,” Robotics and Autonomous Systems, Vol. 57, No. 4, pp. 345-370, 2009.
[https://doi.org/10.1016/j.robot.2008.09.009]

-
Liljebäck, P., Pettersen, K. Y., Stavdahl, Ø., and Gravdahl, J. T., “Snake Robots: Modelling, Mechatronics, and Control,” Advances in Industrial Control, 2012.
[https://doi.org/10.1007/978-1-4471-2996-7]


Senior Researcher in Korea Institute of Robotics & Technology Convergence. His research interest is disaster/rescue robot, robot system integration, localization.
E-mail: jhpyo@kiro.re.kr

Assistant Researcher in Korea Institute of Robotics & Technology Convergence. His research interest is field robotics, robot system integration, intelligent robotics.
E-mail: meungsuklee@kiro.re.kr

Senior Researcher in Korea Institute of Robotics & Technology Convergence. His research interest is robot control, robot system integration, automation application.
E-mail: shingun@kiro.re.kr

Chief Researcher in Korea Institute of Robotics & Technology Convergence. His research interest is rescue robotics, soft wearable suit, localization.
E-mail: neoworld@kiro.re.kr

Assistant Professor in the Department of Robot and Smart System Engineering, Kyungpook National University. His research interest is field robotics, localization, underwater robotics.
E-mail: hgjoe@knu.ac.kr

Professor in the Department of Mechanical System Engineering, Pukyong National University. His research interest is field (disaster/marine) robot, robot mechanism and control.
E-mail: suhgang@pknu.ac.kr

Chief Researcher in Korea Institute of Robotics & Technology Convergence. His research interest is disaster robotics, robot motion control, electro-hydraulic actuators.
E-mail: mulimkim@kiro.re.kr