광학 기반 우주물체감시시스템의 좌표계 얼라인먼트에 관한 연구

1. 서론

최근 스페이스 X (Space Exploration Technologies Corporation)는 스타링크(Starlink) 프로젝트를 통해 수천대의 인공위성을 지구 궤도에 쏘았으며, 미국을 포함한 여러 나라에서 수만개의 인공위성을 운영하고 있다.¹ 우주물체는 이러한 인공위성들 외에도 인공위성의 부산물, 자연 우주물체의 파편 등을 포함하며, 앞으로는 현재보다 더 많은 우주물체가 지구 궤도상에 운용될 것으로 예상된다. 우주물체가 증가함에 따라 인류는 우주물체의 충돌, 추락 등에 의한 위험에 노출된다. 최근 스페이스 X의 스타 링크와 원웹(OneWeb)간 충돌 위험이 있었으며, 중국 창정-5B호의 로켓 잔해물이 지구에 추락하는 위험이 있었다. 이러한 위험에 대응하기 위해 우주물체의 정보 획득이 절실하다.

전 세계적으로 우주물체 정보 획득을 위해 많은 연구들이 수행되고 있다. 미국은 DARPA SST, MSSS 등의 광학 기반 시스템과 Haystack 전파 망원경 등의 레이더 시스템을 활용하여 우주물체 관련 정보를 획득하고 있다.² 유럽은 OGS, 일본은 BSGC 등의 광학 기반 시스템을 활용하여 연구를 수행하고 있고,³ 국내에서도 OWL 등의 시스템을 기반으로 연구에 참여하고 있다.^4,5 각 국에서 구축한 우주물체감시시스템은 인공위성을 포함한 지구 궤도상에 존재하는 우주물체를 탐지, 추적하여 해당하는 우주물체의 궤도, 분광 등의 정보를 확보하는 역할을 하며, 이렇게 획득된 정보를 바탕으로 우주물체의 추락, 충돌 등의 이상 징후를 감지하여 우주 위험에 대응할 수 있도록 한다.⁶

광학 기반의 우주물체감시시스템은 우주물체를 촬영할 수 있는 대형망원경과 망원경이 장착되어 특정 위치를 지향하도록 하는 마운트, 망원경의 촬영 영상을 데이터화하여 우주물체 정보를 획득하고, 마운트를 구동하는 제어 장치로 구성된다. 본 시스템에서는 망원경으로 지정된 방향을 정확히 지향하여 정밀하게 촬영하는 것이 중요하다. 촬영된 영상에서 우주물체의 위치를 정확하게 알지 못하면, 우주물체의 궤도가 부정확하게 산출되어 획득된 정보의 가치가 퇴색된다. 하지만, 망원경이 지향하는 천구와 이를 촬영하는 CCD간에는 대기의 산란, 망원경 등의 기계적인 처짐 등에 의해 비선형적인 관계가 존재하며 이를 해결하기 위한 방법이 필요하다.^7-11 본 연구에서는 망원경이 정확한 위치를 촬영할 수 있도록 좌표계 얼라인먼트 방법을 제안한다. 먼저, 시스템좌표계와 천구좌표계를 육안으로도 확인 가능한 항성들을 이용해 각 좌표계의 얼라인먼트 1차 모델을 완성한다. 이후 50개 이상의 항성을 촬영하여 데이터를 수집하여 제안한 2차 얼라인먼트 모델을 완성하고, 망원경이 항시 지정된 방향을 정확히 지향하도록 하였다.

본 논문은 다음과 같이 구성된다. 2장에서는 천구좌표계와 시스템좌표계의 관계 및 좌표계 얼라인먼트 모델에 대해 설명한다. 3장에서는 실제 시스템에 적용하고 제안한 모델을 검증한다. 마지막으로 4장에서는 결론을 도출한다.

2. 좌표계 얼라인먼트

2.1 좌표계 연구

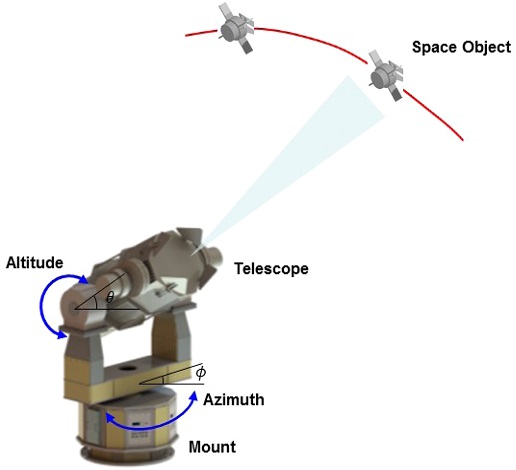
지구 어딘가에서 망원경을 이용하여 항성이나 인공위성 등 우주를 촬영하기 위해서는 RA/Dec로 표기되는 천구좌표계 기준으로 우주물체의 위치를 확인해야 한다. 한편, 지상의 망원경의 위치는 Fig. 1과 같이 고각과 방위각으로 구성되는 시스템좌표계를 사용할 수 있다. 두 좌표계 간의 상관관계를 알 수 있다면, 지상에서 우주물체를 정확히 촬영하여 우주물체의 궤도를 산출할 수 있다.

Fig. 1

System coordinate for telescope and celestial coordinate for space objects

본 연구에서 사용하고자 하는 망원경은 고각과 방위각이 구동하는 Alt-Az 형태의 마운트에 장착된다. 이에 따라 위의 상관관계를 정의하기 위해 식(1)과 식(2)와 같이 고각, 방위각에 대한 1차 모델을 정의한다.⁹ 식(1)은 고각의 오차량을 나타내며, 식(2)는 방위각의 오차량을 나타낸다.

$\[ ∆AL=L_{OFF}+C_{N}cos\varphi +C_{E}sin\varphi +C_{Me}sin\theta \]$

(1)

$\[ \begin{array}{c}∆AZ=Z_{OFF}-C_{N}sin\varphi cot\theta +C_{E}cos\varphi cot\theta +\hfill \\ C_{PZ}cot\theta +C_{pA}csc\theta \hfill \end{array} \]$

(2)

여기서, ΔAL, ΔAZ는 고각과 방위각의 오차이며, L_OFF, Z_OFF는 고각, 방위각 엔코더의 오차이다. C_N은 북쪽에 대한 오차, C_E는 동쪽에 대한 오차이며, C_ME는 망원경의 처짐으로 인한 오차이다. 또한, C_PZ는 방위각 축과 천정축 간의 수직성 오차, C_PA는 천정축과 광축간의 수직성 오차이다.

식(1)과 식(2)는 직교좌표계를 좌표 변환할 때 발생할 수 있는 오차 요소를 모두 고려한 것이다. 강체이면서 균일한 회전을 하는 모델에서 발생할 수 있는 오차 요소는 수직축이 기울어진 정도 2개 요소와 수평축과 수직축이 90^o에서 벗어난 정도 1개 요소, 수평축과 수직축의 오프셋 2개 요소 그리고 망원경과 수평축의 차이 1개 요소로 총 6개의 오차 요소가 존재하며, 여기에 기계적인 처짐까지 총 7개의 파라미터가 필요하게 된다.

식(1)과 식(2)는 망원경의 비선형적인 요소들을 반영하지만, 각 축에 대한 푸리에 급수 항을 통해 식(3)과 식(4)로 발전시킬 수 있다. 이는 이상화한 처짐이나 베어링, 광학계의 각도에 따른 비이상적인 형상학적 요소에 의한 불균일한 회전 등의 비선형성을 보상하고 본 논문에서는 이를 좌표계 얼라인먼트 2차 모델이라 한다.

$\[ \begin{array}{c}∆AL=L_{OFF}+C_{N}cos\varphi +C_{E}sin\varphi +A_{S}sin\theta +A_{C}cos\theta +\hfill \\ A_{1}sin\left(2\varphi \right)+A_{2}cos\left(2\varphi \right)+A_{3}sin\left(3\varphi \right)+A_{4}cos\left(3\varphi \right)\hfill \end{array} \]$

(3)

$\[ \begin{array}{c}∆AZ=Z_{OFF}-C_{N}sin\varphi cot\theta +C_{E}cos\varphi cot\theta +C_{PZ}cot\theta +\hfill \\ C_{PA}csc\theta +Z_{S}sin\varphi +Z_{C}cos\varphi +Z_{1}sin\left(2\varphi \right)+Z_{2}cos\left(2\varphi \right)+\hfill \\ Z_{3}sin\left(3\varphi \right)+Z_{4}cos\left(3\varphi \right)\hfill \end{array} \]$

(4)

여기서, A_S, A_C는 고각 엔코더 이심률의 sin, cos항이고, Z_S, Z_C는 방위각 엔코더 이심률의 sin, cos항이다. 또한, A₁-A₄과 Z₁-Z₄는 고각, 방위각 축에 대한 푸리에 급수항이다. 촬영한 영상에서의 오차가 선형이 아닌 비선형으로 나타나기 때문에, 위의 추가 항으로 1차 모델을 보완한다.

2.2 좌표계 얼라인먼트

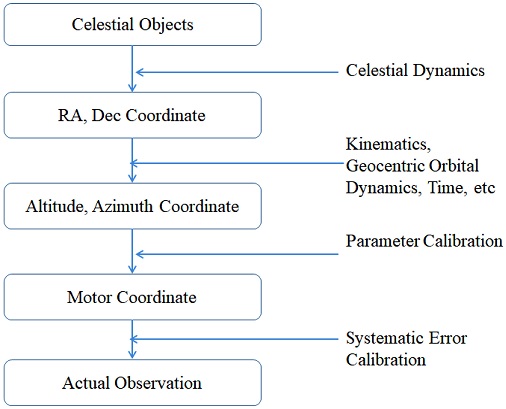
좌표계 얼라인먼트의 일반적인 절차는 Fig. 2와 같다. 천구상의 물체에 대해 망원경 좌표계로 변환하는 모델을 만들기 위해서는 6개 항성을 촬영하여 1차 모델에 대한 좌표계 얼라인먼트를 수행한다. 1차 모델이 완성되면, 다른 항성을 쉽게 촬영할 수 있게 된다. 1차 모델을 완성하기 위한 항성 후보군은 육안으로도 알 수 있는 폴라리스, 베가, 알데바란 등의 항성을 사용한다.

Fig. 2

General procedure of coordinate alignment

1차 모델을 완성한 후 더 많은 항성들을 대상으로 식(3)과 식(4)의 각 계수들을 구해야 한다. 2차 모델을 완성하기 위해서는 50개 정도의 항성을 촬영하여 진행한다. 관측이 용이한 항성을 선택하기 위해서 Bright Star Catalog의 항성 정보를 이용하였으며, 3등급 이상의 밝은 항성을 사용하였다.

항성을 촬영하는 동안 시스템은 지구 자전 반대방향으로 회전하는 기능을 가져야 한다. 지구 자전만큼을 보상하여 항성을 여러 번 촬영하고, 각 영상에서의 오차를 평균하여 계산한다.

3. 시험

본 논문에서는 광학 기반의 우주물체감시시스템으로 항성을 관측하는데 있어서 여러 항성을 지향하여 데이터를 얻고, 얻은 데이터를 통해 1차, 2차 좌표계 얼라인먼트 모델을 적용하여 모델의 오차를 검증하였다.

3.1 시험 환경

좌표계 얼라인먼트를 수행하기 위한 시험 환경으로 항성을 촬영할 수 있는 망원경이 탑재된 광학 기반의 우주물체감시시스템이 필요하다. 본 연구를 위해 제작한 시스템의 형상은 Fig. 3과 같으며, 망원경의 지향 각도를 조정하기 위해 고각, 방위각 방향으로 2축 회전 구동하는 구동장치의 말단에 망원경이 탑재되어 있는 구조이다. 망원경은 대구경 망원경과 일반 망원경이 장착되어 있어서 항성이 대구경 망원경의 시야각 밖에 있을 경우, 일반 망원경으로 항성을 찾는다.

Fig. 3

Space object surveillance system

본 감시시스템의 주요 구성품의 사양은 Table 1과 같다. 3등급 이상의 항성을 촬영할 수 있도록 망원경 및 검출기를 선정하였다. 또한, 정밀하게 항성을 추적할 수 있도록 고각, 방위각은 Kollmorgen사의 직구동 모터를 장착하였고, 각 엔코더는 Renishaw사의 RESM 엔코더를 사용하여 최대 분해능 0.0003, 정확도 0.52 arcsec를 충족하며, 본 엔코더로 피드백 신호를 받아 제어한다. 본 시스템의 구동 성능을 확인하기 위해 항성과 위성을 촬영하기 위한 속도를 산출하고 각 속도에서의 정밀도를 Table 2와 같이 확인하였다. 고각의 구동 범위는 30-80^o이고, 방위각의 구동 범위는 0-180^o로 하여 시험하였으며, 구동속도 1.2와 5^o/sec은 위성 촬영 시 필요한 속도이고, 구동속도 0.3^o/sec은 항성 촬영 시 필요한 속도이다.

Table 1

Specification of the space object surveillance system

Table 2

Driving performance of the system

시험을 수행한 장소는 대한민국 경기도 용인시에서 오후 10시 57분부터 11시 21분까지 수행하였으며, 습도 및 운량이 낮은 맑은 기상에서 수행하였다.

3.2 시험

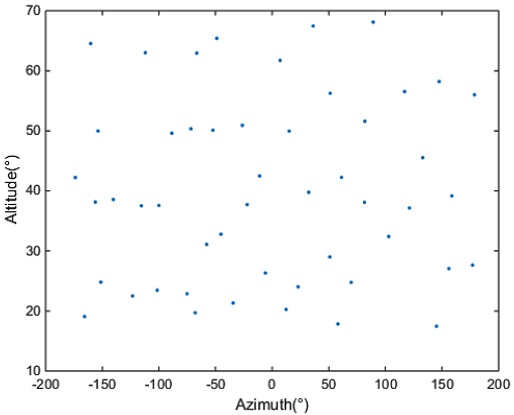
앞서 언급한 좌표계 얼라인먼트 절차에 따라 항성을 선별한다. 데이터로서 필요한 항성은 50개이며, 본 시험에서는 51개의 항성을 Fig. 4와 같이 선정하였다. 그래프에서 가로축은 항성의 방위각 방향 위치이고, 세로축은 고각 방향 위치이다.

Fig. 4

Data set of the stars for the coordinate alignment

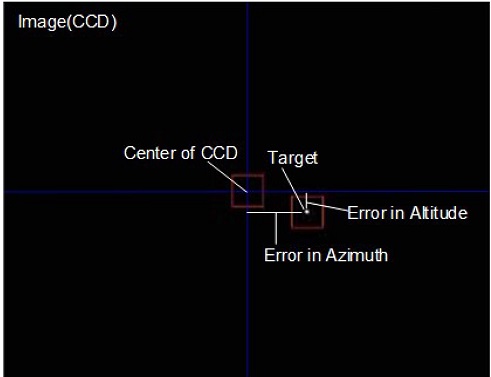
선정된 항성을 시스템으로 촬영하여 항성의 예측 위치와 실제 측정된 위치에 대한 차이를 Fig. 5와 같이 계산한다. 식(3)과 식(4)에 대입하기 위해 고각 방향 성분과 방위각 방향 성분으로 나눠서 오차를 기록한다.

Fig. 5

Data collection from the images on CCD

모델을 확인하기 위해 균일한 분포의 고도 20^o에서 고도 75^o 사이의 항성 중에서 선별된 것이며, 좌표계 얼라인먼트 절차에서와 같이 모터의 각 축은 고각, 방위각과 일치하지는 않는다. 일치하지 않는 부분에 대해서는 이론적인 모델로 보정이 어렵기 때문에 본 시험을 통해 수집한 오차를 이용하여 근사화된 모델을 찾았다.

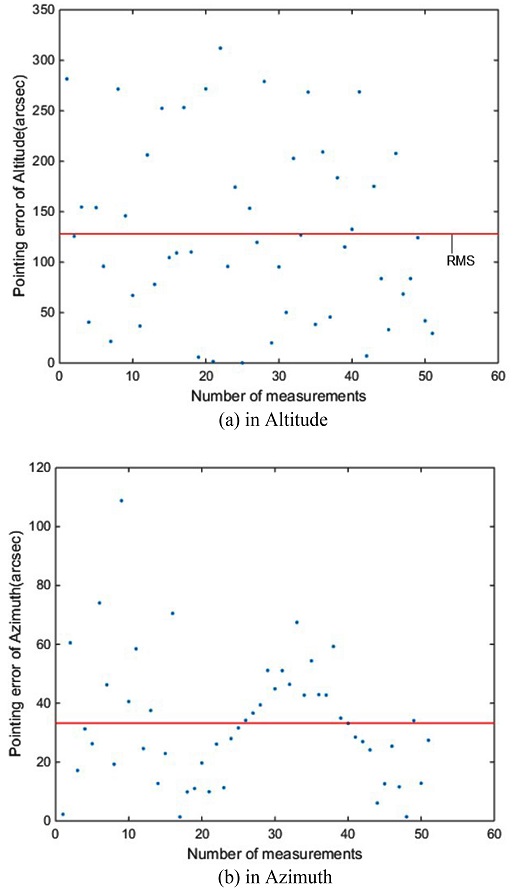
위와 같은 방법으로 항성의 예상 위치에서 영상을 촬영하게 되면, 각 항성의 고각, 방위각 오차를 기록할 수 있다. Fig. 6(a)는 각 항성의 고각 오차를 나타낸다. 고각 오차의 RMS는 128 arcsec이다. Fig. 6(b)는 각 항성의 방위 오차를 나타낸다. 방위각 오차의 RMS는 33.2 arcsec이다.

Fig. 6

Pointing errors before coordinate alignment

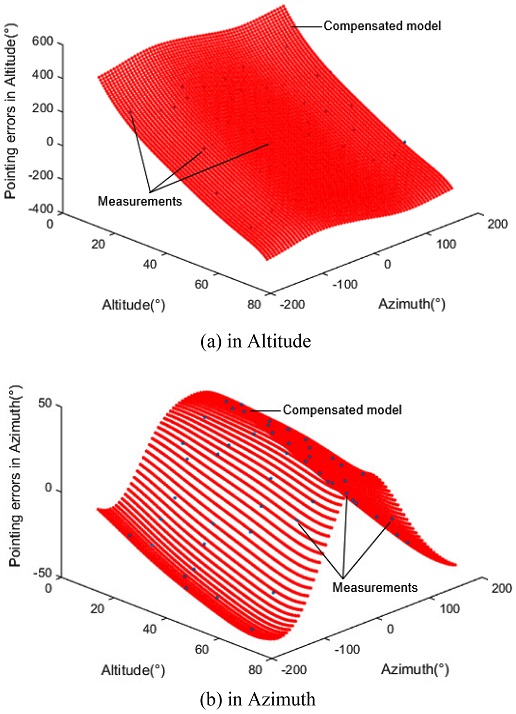
모든 항성의 오차는 최소자승법으로 식(3)과 식(4)의 각 계수들을 산출한다. Fig. 7(a)는 이렇게 산출된 계수들로 구성된 식(3)을 도식화한 것이다. 또한, Fig. 7(b)는 식(4)를 도식화한 것이다.

Fig. 7

2nd compensated model for coordinate alignment

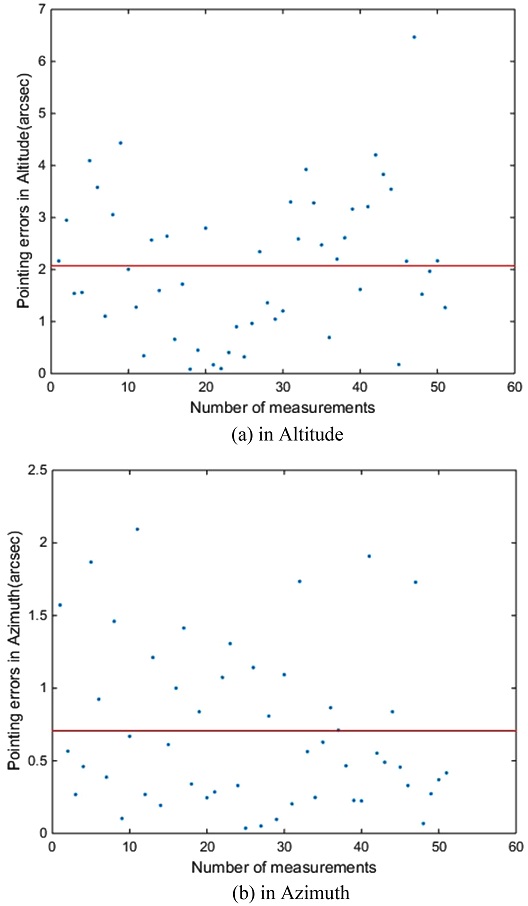
이와 같이 2차 모델에 의해 망원경이 지향하는 위치와 촬영된 영상에서의 항성 위치간 오차가 최소화 되도록 좌표계가 얼라인먼트 되면, 각 항성들을 지향했을 때 최소한의 오차로 촬영할 수 있게 된다. 좌표계 얼라인먼트 후에 각 항성을 촬영하여 고각, 방위각 방향의 오차를 Fig. 8과 같이 도시하였다. Fig. 8(a)는 각 항성의 고각 오차로 모든 항성의 고각 오차 RMS는 2.07 arcsec이다. Fig. 8(b)는 각 항성의 방위각 오차로 모든 항성의 방위각 오차 RMS는 0.71 arcsec이다.

Fig. 8

Pointing accuracy results after coordinate alignment

4. 결론

본 논문에서는 광학 기반의 우주물체감시시스템의 우주물체감시 목표 달성을 위해 망원경을 탑재한 감시시스템을 항성이 위치하는 천구좌표계 기준으로 감시장치의 좌표계 얼라인먼트 방법을 제안하였다. 이를 위해서 2축 구동이 가능한 구동장치에 광각, 협각 영상을 얻을 수 있는 2개의 망원경이 탑재된 우주물체감시시스템을 이용하였고, 비선형량을 보정할 수 있는 좌표계 얼라인먼트 방법을 활용하여 절차에 따라 시험을 수행하였다. 이로부터 다음과 같은 결론을 얻었다.

(1) 항성과 인공위성 등의 우주물체를 확인할 수 있는 우주물체 감시시스템을 개발하였다.

(2) 천구상에 존재하는 항성의 오차 수집을 통해 좌표계 얼라인먼트에 사용할 수 있는 모델을 결정하였으며, 이를 통해 시스템의 지향 오차를 3 arcsec (RMS) 미만으로 줄일 수 있었다. 이는 구동장치의 반복정밀도에 해당하는 수준이다.

본 논문에서의 연구 결과를 통해 좌표계 얼라인먼트를 수행하지 않는 상태에서 항성을 관측하게 되면 항성 영상을 획득할 수 없는 경우가 발생할 수 있다. 또한, 본 내용을 통해 광각 망원경의 요구사항과 협각 망원경의 화각에 대한 요구사항을 얻을 수 있기에 우주물체감시시스템에 관한 설계를 수행함에 있어서 좌표계 얼라인먼트에 대한 정밀도를 요구사항으로 고려해야 한다.

REFERENCES

• Liou, J., “USA Space Debris Environment, Operations, and Research Updates,” Proc. of the 55th Session of the Scientific and Technical Subcommittee Committee on the Peaceful Uses of Outer Space, 2018.
• Lee, J., Choi, E. J., Moon, H. W., Park, J., Cho, S., et al., “Design of L-Band-Phased Array Radar System for Space Situational Awareness,” The Journal of Korean Institute of Electromagnetic Engineering and Science, Vol. 29, No. 3, pp. 214-224, 2018. [https://doi.org/10.5515/KJKIEES.2018.29.3.214]
• Sans, M., Sodnik, Z., Zayer, I., and Daddato, R., “Design of the ESA Optical Ground Station for Participation in LLCD,” Proc. of the International Conference on Space Optical Systems and Applications, pp. 9-12, 2012.
• Nonaka, K., Sawabe, M., Yokota, T., Isobe, S., Hashimoto, N., et al., “Some Results of GEO Space Debris Observations and Orbit Determination under Experimental Operation,” Proc. of the 3rd European Conference on Space Debris, European Space Agency, Vol. 473, pp. 113-116, 2001.
• Park, J. H., Yim, H. S., Choi, Y. J., Jo, J. H., Moon, H. K., et al., “OWL-Net: A Global Network of Robotic Telescopes for Satellite Observation,” Advances in Space Research, Vol. 62, No. 1, pp. 152-163, 2018. [https://doi.org/10.1016/j.asr.2018.04.008]
• Liou, J. C. and Johnson, N. L., “Risks in Space from Orbiting Debris,” American Association for the Advancement of Science, Vol. 311, No. 5759, pp. 340-341, 2006. [https://doi.org/10.1126/science.1121337]
• Yan, L., Huang, Y., and Zhang, Y., “Using Allan Variance Based Semi-Parameter Model to Calibrate Pointing Errors of Alt-Az Telescopes,” Applied Sciences, Vol. 8, No. 4, pp. 164-173, 2018. [https://doi.org/10.3390/app8040614]
• Xu, C., Han, W., Wang, D., Huang, D., and Yuan, P., “Modeling and Correction for the Optical Axis Pointing Error of an Airborne Electro-Optical Platform,” Applied Optics, Vol. 58, No. 23, pp. 6455-6463, 2019. [https://doi.org/10.1364/AO.58.006455]
• Wallace, P., “Tpoint-Telescope Pointing Analysis System (v4.4),” https://sites.astro.caltech.edu/~srk/TP/Literature/Tpoint_SunWorks.pdf, (Accessed 15 SEPTEMBER 2021)
• Hempelmann, A., Gonzalezperez, J., Schmitt, J., and Hagen, H., “The Hamburg Robotic Telescope: A Test Report,” Proc. of the 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, pp. 643-646, 2005.
• Mittag, M., Hempelmann, A., Gonzalez-Perez, J., and Schmitt, J., “The Temperature Dependence of the Pointing Model of the Hamburg Robotic Telescope,” Publications of the Astronomical Society of the Pacific, Vol. 120, No. 866, pp. 425-429, 2008. [https://doi.org/10.1086/533478]