유체-구조 연성해석기법을 이용한 승하강식 드론 스테이션의 풍하중에 대한 구조안전성 평가

1. 서론

드론은 군사용으로 처음 개발되었지만 4차 산업혁명이 등장하면서 산업 및 민간용 시장으로 빠르게 확산하고 있다.¹ 하지만 드론 산업이 활성화되기 전에 비행시간, 안전, 공역 규제 등 해결되어야 할 법적·공학적 문제들이 많다. 다양한 이슈 중에서 드론의 짧은 비행시간 문제는 시급하게 해결해야 할 문제이다. 최근 드론의 비행시간을 늘리기 위하여 수소연료전지를 사용하는 드론이 개발되고 있다.² 하지만 수소 연료전지 드론을 운용하기 위해서는 수소연료전지를 외부 업체로부터 주문하거나 수소 충전소를 구축해야 하므로 에너지 수급이 전기보다 어렵다. 이와 같은 이슈를 해결하기 위하여 드론 착륙 시 무인으로 드론 배터리를 충전하는 드론 스테이션을 도입하면 주변에서 구하기 쉬운 전기에너지를 사용하더라도 드론의 임무 수행 능력을 크게 향상시킬 수 있다.³

글로벌 전자상거래 업체 아마존은 드론 배송 상용화를 위하여 물류창고 관리, 운항, 충전, 배송 등 유통망 효용성을 높일 수 있는 기술에 초점을 맞추어 혁신적인 실험을 지속적으로 추진하고 있다. 아마존의 드론 스테이션 관련 주요 특허는 복합 운송기관 유지보수, 수직 구조물을 이용한 다목적 도킹 스테이션 등이 있다.^4,5 중국 엔트워크는 식품과 의약품을 효과적으로 배송하기 위해 드론스테이션을 개발한 사례가 있으며, 그 외 여러 국가에서도 드론 스테이션에 대해 연구한 사례가 발표되고 있다.⁶

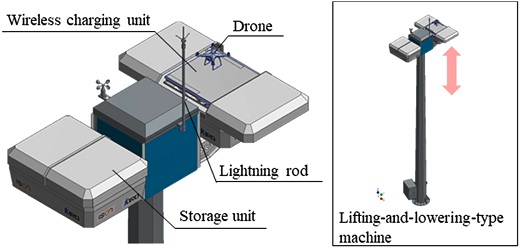
드론 스테이션을 낮은 평지에 설치했을 때 유지보수와 관리가 쉬운 장점이 있지만 산간, 오지, 산악 환경에서는 드론이 착륙하기 어려운 단점이 있다. 그러나 드론 스테이션을 높은 위치에 설치했을 때는 유지보수와 관리는 어렵지만 드론이 착륙하기 쉽다. 이러한 문제를 해결하기 위하여 Fig. 1과 같이 높이 10 m 승하강기에 드론 스테이션을 부착하여 장치의 높이를 자유롭게 조절할 수 있는 승하강식 드론 스테이션을 개발하였다.⁷ 승하강식 드론 스테이션은 높낮이 조절이 불가능한 기존 드론 스테이션의 장점과 단점을 보완하기 위해 개발되었으며, 도킹 성능 향상 및 쉬운 접근성 면에서 이점이 크다.

Fig. 1

Lifting-and-lowering-type drone station

승하강식 드론 스테이션과 유사한 가로등주의 경우 해마다 풍해로 파손되는 사례가 발생하여 내풍설계의 중요성에 대한 인식을 높이는데 크게 기여하였다.⁸ 승하강식 드론 스테이션은 가로등주와 형태가 유사한 만큼 강풍이 잦은 산간, 오지, 산악 및 해안 지역에서도 풍해가 없도록 충분히 강하게 설계되어야 한다. 다물리계 연성해석 기술의 발전으로 유체와 고체 물리계가 서로 상호작용하는 유체-구조 연성해석이 가능해지면서 제품 제작 전 단계에서 풍하중에 대한 구조물의 강도를 정확히 계산하여 설계 시행착오를 줄인 사례가 많다.^9-11 하지만 승하강식 드론 스테이션은 발표된 연구 사례가 없으며, 초기 단계여서 유체-구조 연성해석 모델 개발은 매우 중요하다. 따라서 본 논문에서는 승하강식 드론 스테이션 메커니즘을 제안하고, 제작 전 단계에서 유체-구조 연성해석 모델과 이론식으로 구조물에 대한 내풍 안정성을 검증하였다.

논문의 구성은 다음과 같다. 2장에서는 승하강식 드론 스테이션의 메커니즘, 유체-구조 연성해석 모델 및 해석 조건에 관하여 기술하였다. 3장에서는 설계안의 내풍 안정성을 검증하기 위하여 연성해석 결과와 이론적 결과값을 비교분석하여 연성해석 모델링이 잘 구현되었는지 확인하였다. 마지막 4장에서는 연구 결론 및 승하강식 드론 스테이션의 실증 시험에 관한 내용을 기술하였다.

2. 승하강식 드론 스테이션 내풍 성능 평가 모델

2.1 승하강식 드론 스테이션 메커니즘 설계

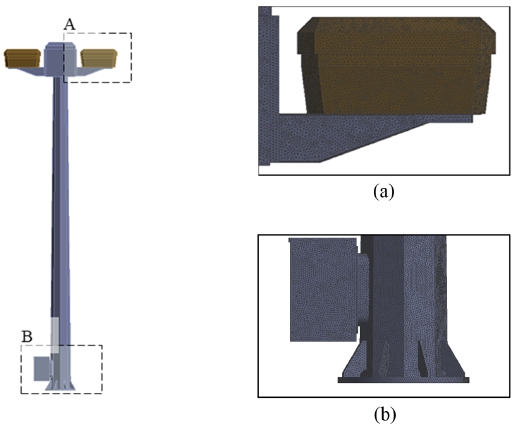
드론 스테이션은 Fig. 2와 같이 크게 승하강기(Lifting-and-Lowering-Type Machine), 무선충전소(Wireless Charging Unit), 화물보관함(Storage Unit)으로 구성된다. 승하강기는 효율적인 드론 운용과 유지보수를 위하여 무선충전소와 화물보관함을 지상으로부터 높이 10 m까지 들어 올리고 내릴 수 있도록 설계되었다. 따라서 사용자는 드론이 운반한 화물을 외부인이 접근할 수 없도록 화물보관함에서 보관하고, 필요 시 지면에서 안전하게 화물을 회수할 수 있다. 임무 수행 중 배터리가 방전될 경우 드론은 무선충전소에 착륙 후 작업자의 도움없이 무선으로 충전 가능하다. 또 악천후와 같은 자연재해로부터 피해를 최소화하기 위하여 무선충전소와 화물보관함을 하강시킬 수 있다.

Fig. 2

Schematic of the newly-developed drone station

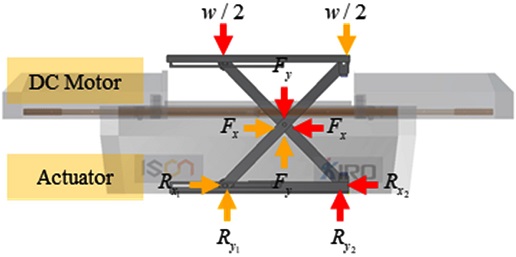
Fig. 3과 같이 무선충전소와 화물보관함의 구동 메커니즘은 크게 도어 개폐 시스템과 시저 리프트 시스템으로 구성된다. 도어 개폐 시스템은 문이 닫히고 열릴 때 풍하중의 영향을 가능한 줄이기 위하여 DC 모터로 구동되는 슬라이딩 메커니즘으로 설계하였다. 시저 리프트 시스템은 드론이 주변 구조물의 방해없이 착륙할 수 있도록 엑츄에이터로 착륙장을 들어 올리는 기능을 수행한다.

Fig. 3

Free body diagrams of Scissor lift jack

케이스 상부 슬라이드를 구동하는 모터를 선정하기 위하여 같이 운동에너지평형식을 유도하면 식(1)과 같다.

$\[ \begin{array}{c}KE=\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}I{\dot{\theta }}^2=\frac{1}{2}\left(m{R}^2+I\right){\dot{\theta }}^2\hfill \\ I_e=m{R}^2+I\hfill \\ T=I_e\ddot{\theta }\hfill \end{array} \]$

(1)

여기서, m, x, θ, R는 각각 상부 케이스 무게, 상부 케이스 위치, 구동모터 회전, 기어 반경을 나타낸다. 그리고 식(1)을 유도하여 슬라이드를 원하는 속도로 닫고 여는데 필요한 모터 용량식(2)를 유도하였다.

$\[ W_{DC}=T\dot{\theta } \]$

(2)

상부 슬라이드 시스템을 구동하는데 필요한 모터의 용량은 Table 1과 상부 도어 10 kg를 20초 동안 0.5 m 운반할 경우 최소 20.3 W 이상이 필요했고, 시스템 손실을 고려하여 80 W로 선정하였다.

Table 1

The power calculation of the sliding door mechanism

케이스 하부에 엑츄에이터가 장착되는 위치에서 반력을 계산하기 위하여 Fig. 3의 자유물체도를 이용하여 시저 리프트 평형식(3)을 정리하였다.

$\[ \begin{array}{c}{F}_x-R_{x1}=0\hfill \\ F_x-R_{x2}=0\hfill \\ -\frac{w}{2}{+F}_y+R_{y1}=0\hfill \\ -\frac{w}{2}{-F}_y+R_{y2}=0\hfill \\ L\text{*}\cos \theta \text{*}\left(\frac{w}{2}\right)+L\text{*}\cos \theta \text{*}\left(R_{y1}\right)\text{*}\sin \theta \text{*}\left(R_{x_1}\right)=0\hfill \\ L\text{*}\cos \theta \text{*}\left(\frac{w}{2}\right)+L\text{*}\cos \theta \text{*}\left(R_{y2}\right)\text{*}\sin \theta \text{*}\left(R_{x_2}\right)=0\hfill \end{array} \]$

(3)

식(3)은 총 6개의 관계식에 대한 연립방정식을 계산하여 엑츄에이터가 리프트를 들어올리는데 필요한 하중값(R_x1)을 계산하는 식(4)를 유도하였다.

$\[ R_{x_1}=\frac{w}{\tan \theta } \]$

(4)

시저 리프트 시스템을 구동하는데 필요한 엑츄에이터의 하중은 Table 2와 같이 링크의 각도가 20^o일 때를 기준으로 계산한 결과 최소 1,347.6 N 이상이 필요했으며, 시스템의 손실을 고려하여 1,500 N으로 선정하였다.

Table 2

The force calculation of the scissors mechanism

2.2 승하강식 드론 스테이션 유체-구조 연성해석

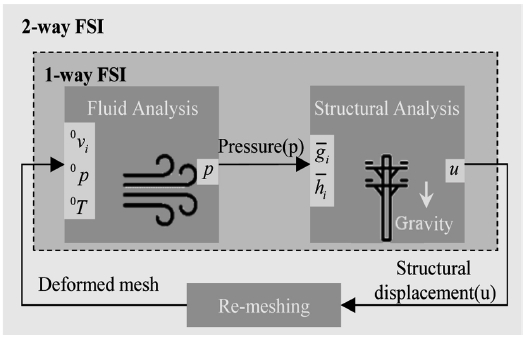
승하강식 드론 스테이션은 무선충전소, 화물보관함과 같은 여러 장치들이 폴 상부에 위치할 경우 전체 구조물의 무게 중심이 상부로 집중되게 된다. 따라서 풍하중에 대한 구조적 안전성을 검토할 필요가 있다. 유체-구조 연성해석법은 Fig. 4와 같이 크게 1-Way와 2-Way FSI로 구분되며 외력으로 변형된 구조물의 형상이 주변 유동에 영향을 미칠 경우 2-Way, 유동에 영향을 미치지 않을 경우 1-Way 유동-구조연성해석을 수행하게 된다. 본 논문에서는 유동해석 결과에서 구조물의 변형에 대한 영향이 무시 가능한 수준이라 가정하고, 상용소프트웨어 ANSYS를 이용하여 1-Way 유체-구조 연성(Fluid Structure Interaction, FSI) 해석 모델을 개발하였다. 유체해석의 경우 지배방정식은 아래 식(5)와 같이 정리할 수 있다(Zhang and Cen¹²).

$\[ \begin{array}{c}{\left.\frac{1}{B}\frac{\partial \overrightarrow{p}}{\partial t}\right|}_x+\frac{1}{B}{c}_i\frac{\partial p}{\partial x_i}+\frac{\partial v_i}{\partial x_i}=0 in {\mathrm{\Omega }}_t^f\hfill \\ {\left.\frac{1}{B}\frac{\partial \overrightarrow{v}}{\partial t}\right|}_x+\rho c_j\frac{\partial v_i}{\partial x_j}=\frac{\partial {\sigma }_{ij}}{\partial x_j}+\rho g_i+{\overleftarrow{f}}_i in {\mathrm{\Omega }}_t^f\hfill \\ {\left.\frac{\partial \left(\rho c_v\overrightarrow{T}\right)}{\partial t}\right|}_x=\frac{\partial }{\partial x_i}\left(\rho c_{v}T{v}_i-k\frac{\partial T}{\partial x_i}\right)=2\mu D^2\hfill \\ +\frac{\partial v_i}{\partial x_i}\left(-p+\lambda \frac{\partial v_i}{\partial x_i}\right)+{\overline{q}}^B in {\mathrm{\Omega }}_t^f\hfill \end{array} \]$

(5)

Fig. 4

Diagram of 1-way and 2-way FSI solution procedure

여기서, p는 압력, v는 속도, T는 온도, f는 체적하중, σ는 점성응력을 의미한다. 일반적으로 구조물 주변 유동의 임의의 위치에서 유동변수(속도, 온도, 밀도 등)의 값은 시간에 따라 변하지만 비정상 효과를 무시하더라도 해석 결과가 유효하다고 판단될 경우 정상 상태(∂( )/∂t = 0) 가정을 적용할 수 있다. 본 연구에서 정상 상태 가정을 도입하여 해석 모델을 단순화하였다. 유체해석의 초기 속도, 압력, 온도에 대한 조건은 아래 식(6)으로 나타낼 수 있다.

$\[ \begin{array}{c}{v}_i\left(0\right)={{}^{0}v}_i on {\mathrm{\Omega }}^f\hfill \\ p\left(0\right)={}^{0}p on {\mathrm{\Omega }}^f\hfill \\ T\left(0\right)={}^{0}T on {\mathrm{\Omega }}^f\hfill \end{array} \]$

(6)

유체해석에서 속도, 온도, 하중, 열유속에 대한 경계 조건은 아래 식(7)로 나타낼 수 있다.

$\[ \begin{array}{c}{v}_i={\overline{g}}_i on {\mathrm{\Gamma }}_g^f\hfill \\ {\sigma }_{ij}{n}_j={\overline{h}}_i on {\mathrm{\Gamma }}_h^f\hfill \\ T=T^s on {\mathrm{\Gamma }}_g^f\hfill \\ k\cdot n_i\frac{\partial T_i}{\partial x_i}=q^s on {\mathrm{\Gamma }}_q^f\hfill \end{array} \]$

(7)

풍하중이 부여된 구조물의 강성을 평가하기 위하여 구조해석을 수행하였다. 직교좌표계 기준 구조해석 지배방정식은 아래의 식(8)로 나타낼 수 있다(Zhang and Cen¹²).

$\[ {\left.\rho \frac{d^2{\overline{u}}_L}{d^{2}t}\right|}_X=\frac{\partial {\sigma }_{ij}}{\partial x_j}+\rho g_i+{\overline{f}}_l in {\Omega }_t^S \]$

(8)

여기서, u_i는 변위백터 성분, σ_ij는 응력텐서 성분를 의미한다. 구조해석의 강제변위, 하중 조건은 아래의 식(9)로 표현할 수 있다.

$\[ \begin{array}{c}{u}_i={\overline{g}}_i on {\mathrm{\Gamma }}_t^g\hfill \\ {\sigma }_{ji}{n}_j={\overline{h}}_i on {\mathrm{\Gamma }}_t^h\hfill \end{array} \]$

(9)

풍속은 국토교통부 ‘건축물의 구조 기준’과 경찰청 ‘교통신호기 설치·관리 매뉴얼’의 지역별 기본 풍속값을 참고하여 40, 50 m/s로 설정하였다. Table 3과 같이 풍속과 방향에 따라 총 네 가지 조건으로 유체-구조 연성해석을 수행하였다.

Table 3

The cases for FSI analysis for the drone station

2.3 승하강식 드론 스테이션 연성해석 조건

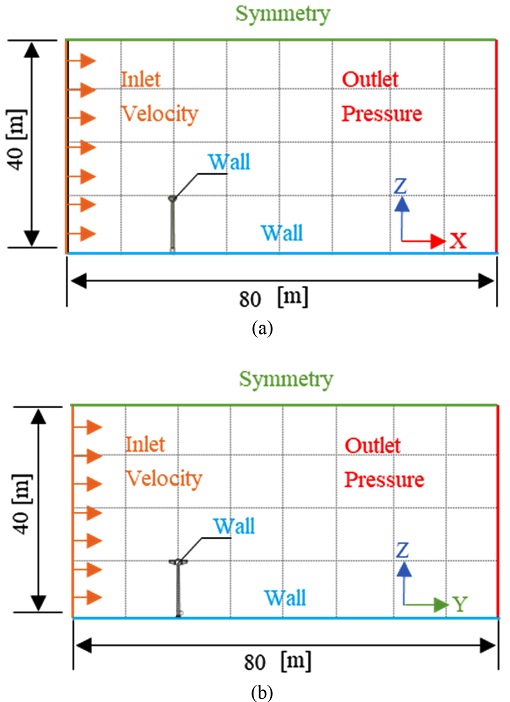
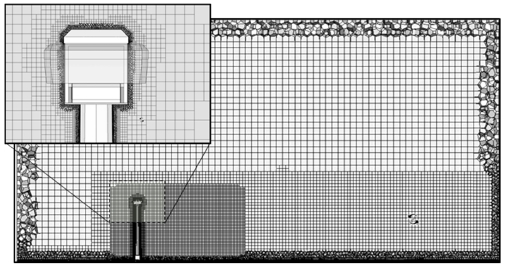
승하강식 드론 스테이션은 Fig. 5와 같이 대칭인 선이나 면이 없는 비대칭 구조이며 동일한 풍속으로 바람이 불더라도 풍속 방향에 따라 서로 다른 풍압이 구조물에 가해진다. 따라서 Fig. 5와 같이 X방향 자유 유동장(Fig. 5(a))과 Y방향 자유 유동장(Fig. 5(b))이 존재하는 경우를 구분하여 두 가지 외부 유동장 문제를 정식화하였다. 해석 영역(Domain)은 구조물 주변부의 유동장을 완전히 모사할 수 있도록 충분히 크게 모델링하였다. 경계 조건으로 입구단(Inlet)에 풍 속과 출구단(Outlet)에 압력을 부여하였다.

Fig. 5

Computational domain for fluid analysis; (a) Flow direction X, and (b) Flow direction Y

입구단과 출구단은 수렴성을 높이기 위해 대칭 조건을 부여했다. 압력 분포 결과가 해석 영역에 잘 표현될 수 있도록 Fig. 6과 같이 바람의 속도 변화가 심할 것으로 예상되는 구조물 주변부는 더욱 세밀한 계산이 가능하도록 조밀한 격자(Grid)로 이산화하였다. 구조물 내부는 무시하고, 표면만 계산되도록 벽(Wall) 조건을 구조물 표면에 부여하였다.

Fig. 6

The computational grid for the fluid analysis

유체해석으로 계산한 압력이 구조물에 미치는 영향을 검토하기 위하여 Fig. 7과 같이 유체해석 결과 압력과 중력가속도를 유한요소모델 모델에 부여하고, 구조해석을 수행하였다. 그리고 실제 구조물이 지면에 고정되는 것과 동일하게 해석 모델의 바닥부를 완전 구속(6자유도 구속)하였다. 승하강기의 모든 재료는 재료는 연강으로 제작되고, 무선 충전소와 화물보관함은 재료의 강도-무게비(Strength-Weight Ratio)를 고려하여 알루미늄으로 제작하였다. 구조해석에 사용된 재료 물성값은 Table 4와 같이 강의 탄성계수는 열처리, 탄소함량, 합금 등에 관계없는 약 200, 알루미늄은 71 GPa로 설정하였다. 응력 결과가 수렴할 수 있도록 Fig. 8과 같이 충분히 격자를 세밀하게 이산화하여 유한요소 모델링하였다.

Fig. 7

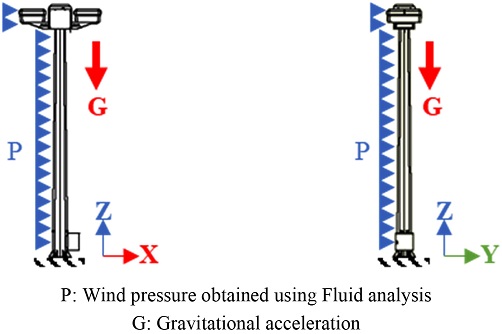
The boundary condition of the structural analysis; (a) Wind pressure obtained by applying flow direction X, and (b) Flow direction Y

Table 4

The material properties of the drone station

Fig. 8

The finite element model of the drone station; (a) Detail A, and (b) Detail B

3. 승하강식 드론 스테이션 연성해석 결과

3.1 유체해석 결과

3.1.1 압력장

유체가 평판이 아닌 드론 스테이션 주변을 흘렀기 때문에 Fig. 9와 같이 압력구배가 형성되었다. 드론 스테이션 구조물에서 멀리 떨어진 전방과 후방의 압력구배는 0(Zero)에 가깝게 계산되었지만 구조물 주변은 비교적으로 얇은 압력구배가 형성되었다.

Fig. 9

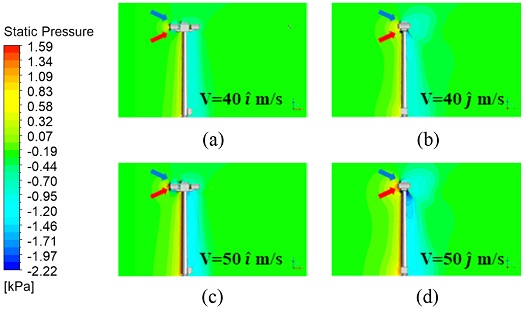
Pressure distribution of the drone station; VInlet = (a) 40i (Max = 1.032, Min = -1.230), (b) 40j (Max = 1.018, Min = -1.664), (c) 50i (Max = 1.609, Min = -1.929), and (d) 50j (Max = 1.588, Min = -2.593)

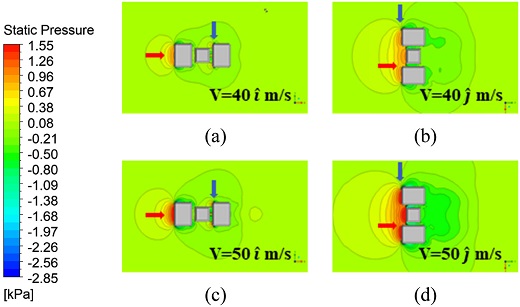
구조물 주변을 흐르는 풍속 방향의 영향을 분석한 결과에 따르면 풍속 40, 50 m/s 모두 동일하게 X방향 풍속이 존재할 때 Y방향 풍속보다 압력구배가 구조물 하류로 확장되는 정도가 19% 정도 작게 계산되었다. 구조물 주변을 흐르는 풍속의 크기의 영향을 분석한 결과 모든 해석 사례에서 동일하게 속도에 비례하여 압력구배가 더 크게 계산되었다. 구체적으로 구조물 주변을 흐르는 풍속이 10 m/s 증가할 때, 압력구배는 약 56% 정도 높게 계산되었다.

가장 큰 압력구배가 나타난 드론 스테이션의 무선충전소와 화물보관함이 위치하는 영역의 단면에 대한 결과를 추가로 검토하였다. Fig. 10과 같이 압력분포 결과에 따르면 유동이 불어오는 구조물의 전방과 후방에서 큰 압력 차이가 나타났다. 구조물 전방부에서 풍속 방향으로 압력이 증가하는 순압력구배가 나타났고, 후방부에서 풍속 방향으로 압력이 감소하는 역압력구배가 나타났다. 구조물 주변을 흐르는 풍속 방향의 영향을 분석한 결과에 따르면 풍속 40, 50 m/s 모두 동일하게 X방향 풍속이 존재할 때 Y방향 풍속보다 압력구배가 구조물 주변으로 확장되는 정도가 5.5% 작게 계산되었다. 구조물 주변을 흐르는 풍속의 크기의 영향을 분석한 결과 모든 해석 사례에서 동일하게 속도에 비례하여 압력구배가 더 크게 계산되었다. 구체적으로 구조물 주변을 흐르는 풍속이 10 m/s 증가할 때, 압력구배는 약 58% 정도 높게 계산되었다.

Fig. 10

Pressure distribution of the drone station in x-y plane at a height z = 9.5 [m]; VInlet = (a) 40i (Max = 0.981, Min = -2.60), (b) 40j (Max = 0.996, Min = -2.388), (c) 50i (Max = 1.53, Min = -4.07), and (d) 50j (Max = 1.56, Min = -3.77)

3.1.2 속도장

무선충전소와 화물보관함이 설치되는 구조물 상단에서 큰 압력구배가 나타난 원인을 분석하기 위하여 속도분포 계산 결과를 분석하였다. Fig. 11과 같이 구조물의 전류 영역에는 비교적 얇은 속도경계층이 형성되었고, 후류 영역에는 상대적으로 더 넓은 속도경계층이 형성되었다. 속도경계층 외부에서 유속은 입구단 풍속과 거의 동일했지만 속도경계층 내부에서 유속은 급격히 하강하였다. 상부에서 압력구배가 크게 나타난 원인은 유체가 이동 중 구조물 표면에서 떨어져 나가면서(박리점) 후류의 난류 변동이 형성되었기 때문이다.

Fig. 11

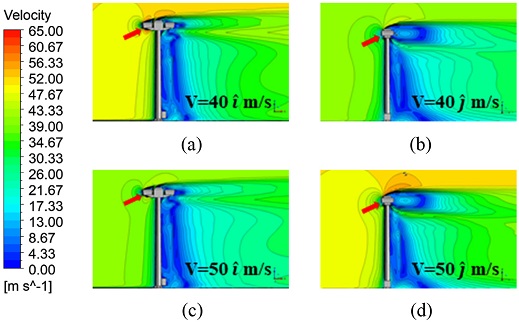
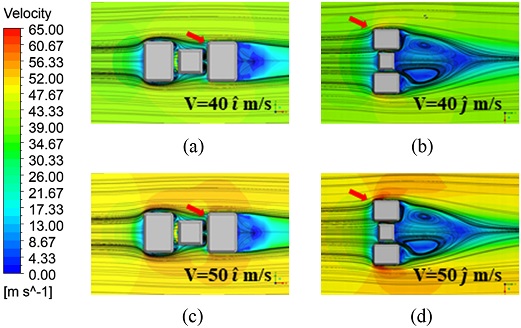
Velocity distribution of the drone station; VInlet = (a) 40i (Max = 50.54), (b) 40j (Max = 54.44), (c) 50i (Max = 63.19), and (d) 50j (Max = 69.19)

구조물 주변을 흐르는 풍속 방향의 영향을 분석한 결과에 따르면 풍속 40, 50 m/s 모두 동일하게 X방향 풍속이 존재할 때 Y방향 풍속보다 속도경계층이 구조물 주변으로 확장되는 정도가 9.5% 작게 계산되었다. 구조물 주변을 흐르는 풍속의 크기의 영향을 분석한 결과 모든 해석 사례에서 동일하게 속도에 비례하여 후방부에서 난류 변동이 더 넓게 분포하였다. 구체적으로 구조물 주변을 흐르는 풍속이 10 m/s 증가할 때, 구조물 주변부 속도분포는 최댓값은 약 27% 높게 계산되었다.

가장 큰 속도분포가 나타난 드론 스테이션의 무선충전소와 화물보관함이 위치하는 영역의 단면에 대한 결과를 추가로 검토하였다. Fig. 12와 같이 구조물 전류영역(박리점)에서 시작된 박리로 인하여 후류에는 상류유동과 반대로 흐르는 박리기포가 형성되었다. 구조물 주변을 흐르는 풍속 방향의 영향을 분석한 결과에 따르면 풍속 40, 50 m/s 모두 동일하게 X방향 풍속이 흐를 때 후류 영역은 박리기포가 완전 발달하지 못했지만 Y방향 풍속이 흐를 때 박리기포는 완전 발달하였다. 속도분포 결과는 X보다 Y방향으로 풍속을 가한 경우 구조물 주변부 속도분포는 최대 1.5% 높게 계산되었다. 구조물 주변을 흐르는 풍속의 크기의 영향을 분석한 결과 모든 해석 사례에서 동일하게 속도에 비례하여 점성의 영향을 받는 영역이 하류로 더 밀려나고(점성의 영향이 작아짐), 불규칙하고, 비정상인 유동이후류 영역이 확장되었다. 구체적으로 구조물 주변을 흐르는 풍속이 10 m/s 증가할 때, 구조물 주변 속도분포는 최댓값은 약 25% 높게 계산되었다.

Fig. 12

Velocity distribution of the drone station in x-y plane at a height z = 9.5 [m]; VInlet = (a) 40i (Max = 59.70), (b) 40j (Max = 58.89), (c) 50i (Max = 74.76), and (d) 50j (Max = 73.64)

3.2 구조해석 결과

3.2.1 강도평가

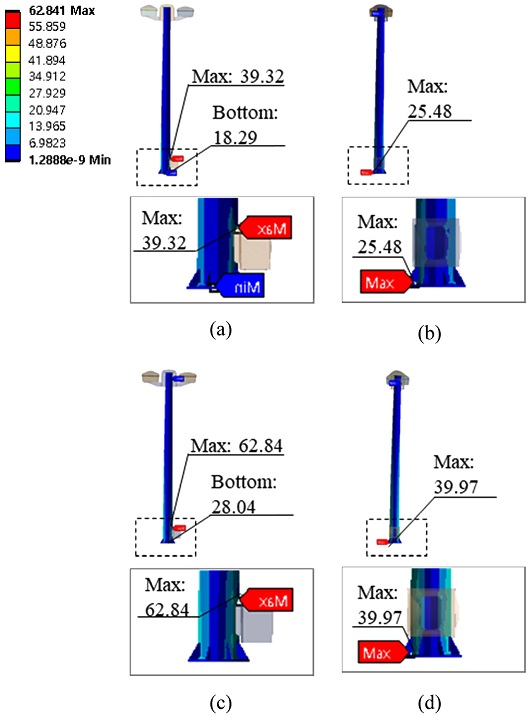
Fig. 13과 같이 구조해석을 수행한 결과 등가응력이 발생한 위치는 구조물 하부와 장치에 전원을 공급하기 위해 구조물 하부를 절삭한 부분에서 발생하였다. 구조물 주변을 흐르는 풍속 방향의 동일하게 X방향 풍속이 존재할 때 Y방향 풍속보다 응력이 최대 38% 정도 높게 계산되었다. 구조물 주변을 흐르는 풍속의 크기의 영향을 분석한 결과 모든 해석 사례에서 동일하게 속도에 비례하여 최대 응력값이 높게 계산되었다. 구체적으로 구조물 주변을 흐르는 풍속이 10 m/s 증가할 때, 구조물 주변부 최대 응력값은 약 60% 높게 계산되었다.

Fig. 13

Stress distribution of the drone station; VInlet = (a) 40i, (b) 40j, (c) 50i, and (d) 50j

구조물의 내풍 안전성을 평가하기 위한 기준은 안전계수(Factor of Safety) 식(10)과 같이 나타내며 설계기준값은 4로 설정하였다.

$\[ Factor of safety=\frac{Strength}{Stress} \]$

(10)

여기서, 강도(Strength)는 항복응력(Yield Stress), 응력은 등가응력(Working Stress)을 의미한다. Table 5와 같이 강의 항복 강도를 275 MPa로 설정할 경우 안전계수는 최대 10.8, 최소 4.38이 계산되었다. 따라서 구조물은 모든 풍속 조건에서 설계 기준을 만족하는 것을 확인하였다.

Table 5

The results of the factor of safety

3.2.2 강성평가

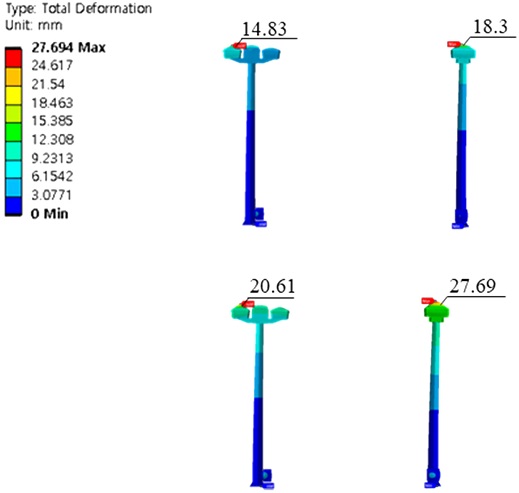
풍속에 의한 구조물의 변위 결과는 Fig. 14와 같이 입력단에서 구조물 주변에 풍속이 존재할 때 최대 변위가 발생한 위치는 모든 경우 동일하게 드론 스테이션 최상부에 위치한 화물보관함과 무선충전소였다. 구조물 주변을 흐르는 풍속 방향의 변위가 최대 34.4% 정도 높게 계산되었다. 구조물 주변을 흐르는 풍속의 크기의 영향을 분석한 결과 영향을 분석한 결과에 따르면 풍속 40, 50 m/s 모두 동일하게 X방향 풍속이 존재할 때 Y방향 풍속보다 모든 해석 사례에서 동일하게 속도에 비례하여 최대 변위값이 더 높게 계산되었다. 구체적으로 구조물 주변을 흐르는 풍속이 10 m/s 증가할 때, 구조물의 최대 변위값은 약 51.3% 높게 계산되었다.

Fig. 14

Displacement distribution of the drone station; VInlet = (a) 40, (b) 50, (c) 40, and (d) 50

3.3 계산 검증

유체-구조해석 결과를 검증하기 위하여 복합물체의 항력계산법(Composite Body)을 이용하여 구조물의 항력을 계산하고, 최종적으로 풍하중이 구조물에 가하는 응력값을 계산하였다.¹³ 구조물의 해석적 응력값을 계산하기 위하여 외팔보 응력 계산식(11)을 이용하였다.

$\[ {\sigma }_{stress}=\frac{M_{wind}c}{I_{eq}} \]$

(11)

여기서, M_wind은 구조물의 상부에서 발생한 풍하중이 가해지는 모멘트, 단면에서 응력 계산 위치 C, l_eq는 단면 관성 모멘트이다. n각형 금속 강관의 단면 관성모멘트는 아래의 식(12)로 계산된다.

$\[ I_{eq}=\frac{n}{192}\left({b_{out}}^4-{b_{in}}^4\right)\left(\frac{1}{\tan \frac{\beta }{2}}\right)\left\{3{\left(\frac{1}{\tan \frac{\beta }{2}}\right)}^2+1\right\} \]$

(12)

여기서, n은 다각형의 b는 n각형을 이루는 한 변의 길이, β는 360/n를 의미한다. 승하강기 기둥은 8각형 형상으로 한 변의 길이는 높이(z)에 따라 식(13)과 같이 선형적으로 변한다.

$\[ b_z=b_{top}+\left(b_{bottom}-b_{top}\right)\frac{z}{L} \]$

(13)

최종적으로 구조물 최하부(z = L)에서 발생하는 응력값을 계산한 결과 아래 식(14)와 같이 유도된다.

$\[ {\sigma }_1=\frac{M_{wind}c}{\frac{n}{192}\left({b_{bottom}^{out}}^4-{b_{bottom}^{in}}^4\right)\left(\text{cot}\frac{\beta }{2}\right)\left\{3{\mathrm{c}\mathrm{o}\mathrm{t}}^2\frac{\beta }{2}+1\right\}} \]$

(14)

M_wind은 아래의 식(15)로 계산할 수 있다.

$\[ M_{wind}=P_{wind}L \]$

(15)

여기서, P_wind는 풍하중이 구조물 최상단에 가하는 집중하중을 의미한다. 풍하중에 의한 집중하중은 식(16)으로 계산 가능하다.

$\[ P_{wind}=\frac{1}{2}\rho U^{2}A{C}_D \]$

(16)

여기서, 항력계수 C_D는 구, 원형 실린더 정도에 대한 실험 데이터는 넓리 사용되지만 다른 형상의 경우 실험 데이터를 구하기 힘들기 때문에 유체해석을 이용하여 계산된다.

실험 데이터는 넓리 사용되지만 다른 형상의 경우 실험 데이터를 구하기 힘들기 때문에 유체해석을 이용하여 계산된다. 본 연구에서는 Wang, Thompson, 그리고 Hu가 해석적으로 계산한 데이터를 참조하여 풍속이 X방향으로 존재할 때 상부 무선충전소와 화물보관함, 승하강기의 높이, 길이, 폭을 고려하여 항력계수를 계산하였다.¹⁴ Table 6과 같이 수치적 해와 해석적 해의 상대오차는 2.9% 정도로 계산되었다. 이러한 해석적 접근법은 유체-구조해석 결과가 물리적으로 합리적인지 검토하는 수준으로 활용하였다.

Table 6

The results of the analytic approach

4. 결론

본 연구를 통하여 승하강식 드론 스테이션을 개발하고, 유체-구조해석 모델을 이용하여 풍하중에 대한 구조 안정성을 검증하였다. 유체-구조 연성해석 결과와 해석적 해의 결과를 비교하여 해석 모델이 잘 구현되었는지 확인하였다. 이러한 과정을 통하여 승하강식 드론 스테이션의 설계에 도움이 되는 유용한 결과 및 유의점을 정리하였다.

(1) 유체해석 결과를 분석한 결과에 따르면 입력단 속도에 비례하여 구조물 주변 압력구배가 증가했다. 구조해석 결과를 분석한 결과에 따르면 입력단 풍속에 비례하여 등가응력이 증가하였다. 즉, 구조물 설치 시 강풍이 빈번한 지역에 설치하는 것을 피하는 것이 좋다.

(2) X방향 풍속이 존재할 때 Y방향 풍속보다 압력 결과가 감소했다. X방향 풍속이 존재할 때 Y방향 풍속보다 등가응력 결과가 감소했다. 즉, 구조물 설치 시 Y방향 풍속이 빈번한 장소에 설치하는 것을 피하는 것이 좋다.

(3) 풍하중에 의한 구조물의 안정성을 검토하기위해 설정한 4가지 시나리오에 대해 모든 경우 조건을 만족하였다. 즉, 유체-구조 연성해석 결과에 따르면 40, 50 m/s 풍속이 불더라도 방향에 관계없이 승하강식 드론 스테이션의 강도는 충분할 것으로 판단된다.

본 연구에서 개발한 유체-구조 연성해석 모델은 해석적 내풍 강도와 수치적 강도값을 비교하여 정확하게 계산한다는 사실을 검증하였고, 구조물의 설계 변경, 유지보수, 경량설계 등 다양한 목적으로 활용이 가능할 것으로 기대된다. 향후 연구에서는 Fig. 15와 같이 실제 제작된 승하강식 드론 스테이션을 통해 승하강 메커니즘, 도어 슬라이딩 및 시저 리프트 메커니즘을 시험하고 정량적으로 해석 모델의 유효성을 검증할 계획이다.

Fig. 15

Photo of the lifting-and-lowering-type drone station

REFERENCES

• Colomina, I. and Molina, P., “Unmanned Aerial Systems for Photogrammetry and Remote Sensing: A Review,” ISPRS Journal of Photogrammetry and Remote Sensing, Vol. 92, pp. 79-97, 2014. [https://doi.org/10.1016/j.isprsjprs.2014.02.013]
• GiantDrone Co., Ltd., “The Hydrogen Fuel Cell Drone Equipped with the Hybrid Controller,” KR Patent, 1019042250000, 2018.
• Campi, T., Cruciani, S., and Feliziani, M., “Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil,” Energies, Vol. 11, No. 2, p. 352, 2018. [https://doi.org/10.3390/en11020352]
• Beckman, B. C. and Bjone, N., “Ground-based Mobile Maintenance Facilities for Unmanned Aerial Vehicles,” US Patent, 9718564B1, 2017.
• Gentry, N. K., Hsieh, R., and Nguyen, L. K., “Multi-Use Unmanned Aerial Vehicle Docking Station,” US Patent, 9527605B1, 2014.
• Han, K. and Jung, H., “Trends in Logistics Delivery Services Using UAV,” Electronics and Telecommunications Trends, Vol. 35, No. 1, pp. 71-79, 2020.
• Aving News, “[CES 2020] ISON to Showcase Drone Charging Port and Drone Station,” http://us.aving.net/ces-2020-ison-to-showcase-drone-charging-port-and-drone-station/, (Accessed 19 OCTOBER 2021)
• Jung, S. H., Shim, J. S., and Choi, H. G., “On the Improvement for Design Methods of Luminaire Supports based on the Structural Safety,” Journal of the Korea Institute for Structural Maintenance and Inspection, Vol. 16, No. 6, pp. 45-55, 2012. [https://doi.org/10.11112/jksmi.2012.16.6.045]
• Kim, Y. W., Kim, W., Lee, S., Kim, Y. W., Kim, W., et al., “Wind Loading Analysis for Solar Tracker Structure,” Journal of the Korea Academia-Industrial Cooperation Society, Vol. 18, No. 2, pp. 672-680, 2017.
• Jeong, K. Y. and Kim, S. Y., “Stress Analysis of 100 kw Photovoltaic Plant Supporting Structure considering Wind Load,” Journal of the Korean Society for Precision Engineering, Vol. 37, No. 7, pp. 493-501, 2020. [https://doi.org/10.7736/JKSPE.019.156]
• Choi, Y. G., Kang, S. Y., and Kim, J. I., “Evaluation of Structural Stability of Small Wind Turbine Blade by Blade Test and Structural Analysis and Improvement of Blade Design,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 9, pp. 893-899, 2018. [https://doi.org/10.7736/KSPE.2018.35.9.893]
• Zhang, Q. and Cen, S., “Multiphysics Modeling: Numerical Methods and Engineering Applications,” Elsevier and Tsinghua University Press Computational Mechanics Series, pp. 6-58, 2015.
• Munson, B. R., Young, D. F., and Okiishi, T. H., “Fundamentals of Fluid Mechanics,” Oceanographic Literature Review, Vol. 10, No. 42, p. 831, 1995.
• Wang, Y., Thompson, D., and Hu, Z., “Effect of Aspect Ratios on Flow and Noise from Cuboids,” Proc. of the 25th AIAA/CEAS Aeroacoustics Conference, p. 2671, 2019. [https://doi.org/10.2514/6.2019-2671]