A Study on Ball-Race Contact in Angular Contact Ball Bearing during Rotation
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Angular contact ball bearings (ACBBs) are widely used in rotating machinery due to their heavy load-carrying capacity and excellent accuracy in high-speed operation. However, employing an ACBB requires a careful analysis because the characteristics of the ACBB significantly depend on the operating condition. The ball-race contact condition of an ACBB is one of the most important factors that can change its properties. This study deals with the ball-race contact behavior concerning several important parameters, such as rotational speed, unloaded contact angle, and external loading. Between the ball and race under loading, an elliptical contact area is formed, in which pure rolling lines may exist. In the region other than the pure rolling lines, sliding dominates due to differential slippage in the elliptical contact area. We investigated the behavior of ball-race contact in terms of the pure rolling lines. A computational procedure was presented to determine the pure rolling lines. Through simulations, it was found that rotational speed, unloaded contact angle, axial preload, and radial load significantly affected the number and locations of pure rolling lines. The presented results are useful for investigating and estimating the sliding friction torque for ACBBs.
Keywords:
Angular contact ball bearing, Centrifugal force, Elliptical contact area, Gyroscopic moment, Pure rolling line키워드:
각접촉 볼베어링, 원심력, 타원접촉면, 자이로스코픽 모멘트, 순수구름선1. Introduction
Angular contact ball bearings (ACBBs) are widely used in rotational machinery due to their low friction properties and high-speed capabilities. ACBBs can support combined radial and axial loads that are frequently found in various mechanical applications, such as electric motors, machine tool spindles, and turbofan engines.1-5 An ACBB consists of two races separated by a group of equally distributed balls that continuously roll with maintaining contact on the races. Despite the simplicity of its mechanism, modeling of an ACBB is complicated and its characteristics depend significantly on the operating condition. The ball-race contact condition of an ACBB is well known to change its characteristics. For many years, a phenomenon related to the ball-race contact in ball bearings has been the main concern of study and discussion.1,6 When a contact surface is formed between the ball and race, a simple rolling motion of a ball does not occur but sliding motion dominates.1,6 The sliding motion in the ball-race contacts is one of the main sources of friction in ACBBs that has a significant contribution to overall power loss of machinery.7-10
Many studies regarding the complex behavior of ball-race contacts were conducted. The motion of a ball in ACBBs has been experimentally observed by Hirano,11 in which he measured the change in magnetic flux induced by a magnetized ball to investigate the ball motion during operation. One of his notable contributions is the experimental investigation on predicting the occurrence of skidding. Several studies in connection with skidding were performed to help engineers prevent ACBBs from premature failure.11-17 Jones18 started an early investigation of the ball motions to analytically formulate the sliding friction force as a function of pure rolling lines (PRLs) and the associated frictional moments acting on a ball. Harris19 then utilized Jones' model to develop an analytical model of ball motions in ball bearings. However, both authors utilized a model that is simplified for the ball-race contacts in ACBBs. In 1999, Houpert20 presented a new numerical calculation in ball bearings including the estimation of friction forces and PRL locations which depend on the geometry and operating condition of ACBB. Popescu, et al.8 then extended the work by tackling the power loss of ACBBs and defining the possible existence of a single PRL in the elliptical contact area.
Under a pure thrust loading, Paleu21 analyzed the elliptical contact area of steel-steel and hybrid ball bearings with silicon nitride balls. He focused on investigating the variation of sliding velocity on ball-race contact areas which may cause the bearing to prematurely fail by scuffing at high speeds. Chen22 investigated the effects of ball motions such as rolling, gyroscopic, and spinning on the stress and fatigue life in a ball bearing through finite element modeling. Tong and Hong23,24 investigated the differential sliding friction and presented an improved formulation for spinning friction torque of ACBBs.
The literature review reveals that there were very few research results for investigating the number and locations of PRLs with regards to operating condition. In particular, the behavior of PRLs under combined loading has been rarely studied as well; in such case, PRL locations on individual balls differ from one another. In general, investigating simultaneous sliding motions in ball-race contacts requires complicated information. Ball-race contact characteristics are essential in precisely estimating ball speeds, such as ball pivotal speed and ball orbital speed.8,20 Such contact characteristics are also important to calculate bearing friction torque and power losses, which are very crucial in bearing design and application.
To address the aforementioned issues, we analyzed the sliding motions and the behavior of PRLs for ACBBs. A computational procedure was presented to determine the locations of PRLs for individual balls of the ACBBs. By the equilibrium equations along with the internal geometry of ACBBs, the locations of PRLs for individual balls were determined. A verification was performed by evaluating spinning friction torques and the sliding velocities on the races with PRLs. Extensive simulations were performed to examine the effects of the relevant parameters such as rotational speed, unloaded contact angle, axial preload, and radial load on the behavior of the number and locations of PRLs for individual balls of the ACBBs.
2. Ball Sliding Motions
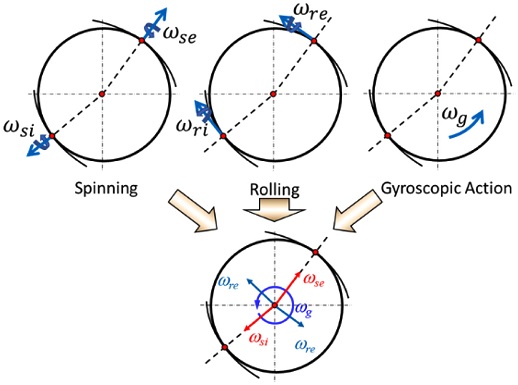
With a rotating inner ring for an ACBB, ball motions such as orbital and pivotal motions are produced in the ACBB. Then, simultaneous motions are produced in the ball-race contacts of the ACBB, such as rolling, spinning, and gyroscopic action during operation as shown in Fig. 1. These motions create sliding, which eventually becomes a source of friction.1,6,22 Motions in ball-race contacts are complicated and are needed to estimate precise orbital and pivotal speeds.8,20
One of the major sources of friction in ACBBs is induced by the sliding between the ball and races. Motions such as rolling, spinning, and gyroscopic action simultaneously occur in an ACBB that depend on the geometry, the rotational speed, and the external loadings.1,8,18-20 Then, two sources of sliding arise in the ACBB; macro-sliding caused by contact conformity due to macro-geometry features, such as ball-race contact deformation (Osculation) and spinning, and micro-sliding due to geometrical distortion from an elastic deformation.25
2.1 Sliding in Rolling Motion
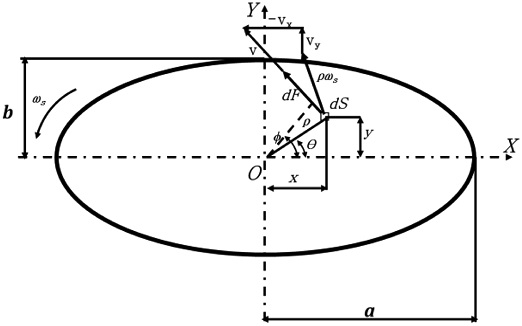
One of the major sources of sliding friction is the sliding that exists on the surface of the elliptical contact area. When a ball rotates relative to the deformed surface, combined rolling and sliding motions occur.1,12,14 Depending on bearing geometry and operation, one or two PRLs exist in the ball-race contact area.8,20 In the region other than the PRLs, sliding occurs due to the presence of differential slippage, as shown in Fig. 2. The slip velocities in the rolling directions can be determined as follows1:
For inner race,
| (1) |
For outer race,
| (2) |
where ω is the bearing rotational speed, and dm, Da are the pitch diameter and ball diameter, respectively. ai and ae are the semimajor radii of the contact ellipses on the inner and outer races, respectively. The relative speeds of the inner and outer race to the ball are given as
| (3) |
| (4) |
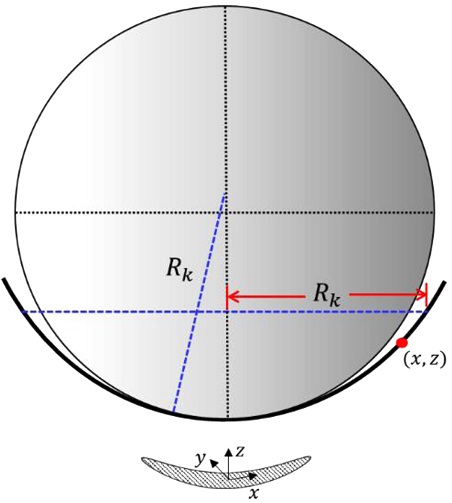
The defined ωR and ωm are the ball pivotal speed and orbital speed, respectively, and Rk is the Hertzian contact radius, or the radius caused by deformation as given by,1,8
| (5) |
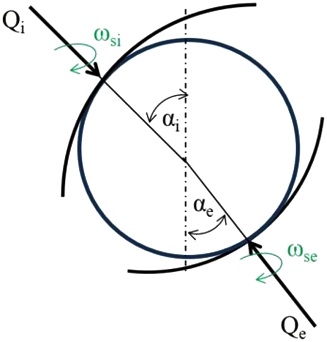
where k = i, e denote the inner and outer race, respectively, and fk is the conformity factor that is defined as the ratio of raceway radius to ball diameter. β is the pitch angle. Using the equal raceway control theory,23,24 the pitch angle is represented as
| (6) |
where αi, αe are the ball contact angles on the inner and outer races, respectively.
2.2 Sliding due to Spinning
If the rolling motion does not occur on a line exactly parallel to the raceway, a dependent motion, called spinning, occurs. Spinning is a macro-sliding that is responsible for a major portion of the total friction in an ACBB and can contribute to significant heat generation. Any ACBB experiences spinning about the transverse direction to the center of the elliptical contact area. The contact angle inevitably causes ball spinning to take place.1,6 The spinning motion in the elliptical contact area is depicted in Fig. 3. The pivotal speeds on the races are as follows:
For inner race,
| (7) |
For outer race,
| (8) |
2.3 Sliding due to Gyroscopic Action
Another factor that may complicate the ball motion in ACBBs is the existence of gyroscopic moment acting on the balls. In ball bearings with non-zero contact angles between the balls and races, a gyroscopic moment occurs in each ball. This motion creates pure sliding colinear with the major axis of the elliptical contact area.1 This implies that an additional sliding orthogonal to rolling direction will occur. At low speeds, such gyroscopic moment is negligible but becomes significant at high speeds. Gyroscopic motion may be prevented when the ACBB is sufficiently preloaded.14
On the other hand, at very high speeds, balls may experience gross sliding over the races.11-17 Such behavior is called skidding and can significantly degrade bearing endurance and performance. Skidding usually happens in ACBBs operating under a relatively light preload with rapid accelerations and decelerations.1 Then, the loading is not enough to develop sufficient friction force in ball-race contacts to overcome dragging, churning losses, and to avoid gyroscopic motion. Controlling skidding is an important issue in utilizing bearings.1,7,14,17
3. Behavior of Pure Rolling Lines
3.1 Pure Rolling Lines in the Elliptical Contact Area
Between the ball and races under loading, there forms an elliptical contact area, in which pure rolling lines (PRLs) may exist. PRLs denote “lines” in the contact area at which pure rolling motion occurs. In the region other than the location of PRLs, sliding dominates due to differential slippage.1 The elliptical contact area created by ball-race contact is shown in Fig. 4. Sliding within the elliptical contact area is significantly dependent on the PRLs.
3.2 Location of Pure Rolling Lines
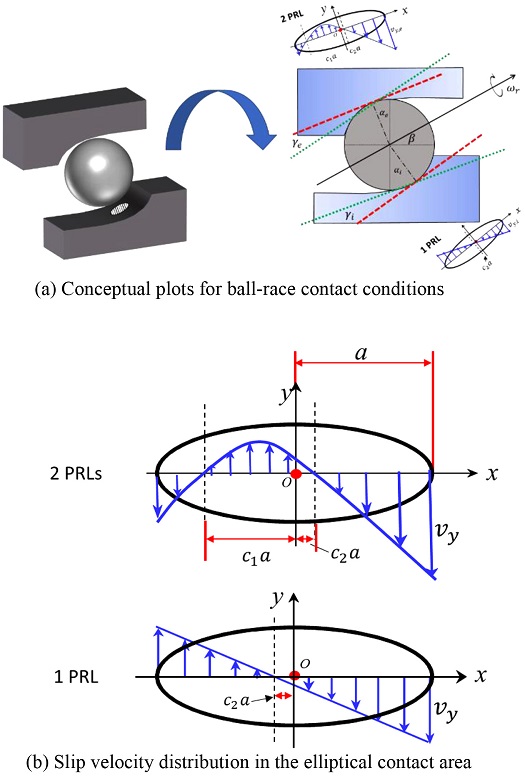
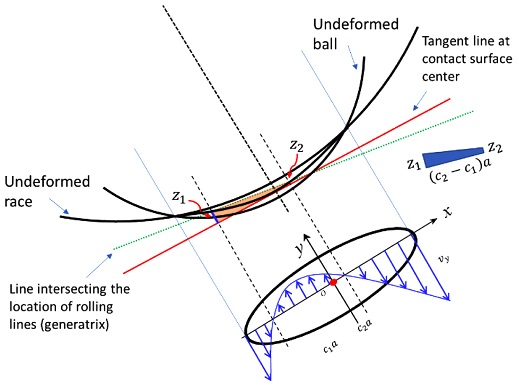
For a ball-race contact, one or two PRLs can be found inside the elliptical contact area.8,20 Fig. 5(a) shows how PRLs are formed in the elliptical contact area. If the generatrix of motion [green-dotted line] is angled with respect to the tangent plane [red-dashed line] at the center of the contact surface, the center of rolling is positioned asymmetrically in the elliptical contact area. Depending on the angle of the generatrix to the contact surface, one or two lines of intersection may occur at which pure rolling can be obtained. In other words, pure rolling may occur in one or two lines contained in the elliptical contact area as illustrated in Fig. 5(b).1,8,20
3.3 Determination of Pure Rolling Line Locations
Houpert20 has proposed an analytical calculation method for PRL locations with consideration of the effect of centrifugal force. He considered that the contact angles on the races become unequal during operation. Fig. 6 shows z1 and z2 which represent the heights of PRLs of the deformed contact surface caused by the Hertzian contact effect. The spatial shape of the contact ellipse is assumed to be parabolic as shown in Fig. 7.20 Here, the vertex and focus of the parabola are set to be at (0,0) and (0, R/2), respectively.
Then, the equation of the parabola is given by
| (9) |
Thus, the heights of the two PRLs can be obtained as
| (10) |
| (11) |
Assume here that c2kak(> 0) and c1kak(< 0) without loss of generality.
From Fig. 6, it can be seen that the two PRLs can be related to the slope of generatrix and the normal plane as follows:
| (12) |
where γk is the angle between the red and green lines in Fig. 5(a). By substituting from Eqs. (10) to (12), the following equation can be achieved:
| (13) |
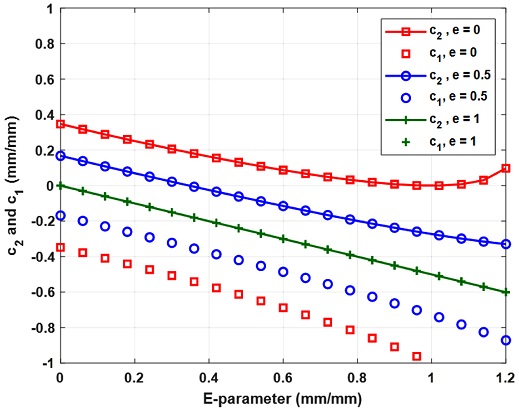
The two PRLs, associated with a geometrical E parameter, are shown in Fig. 8. Here,
| (14) |
where
| (15) |
When the sliding friction force is very small (e≈0) and E > 1 as illustrated in Fig. 8 with red squares, one PRL is present inside the elliptical contact area while its pair lies outside. On the other hand, the e parameter is defined as the ratio of sliding friction force and maximum friction force, μQk, i.e.,
| (16) |
where μ denotes the sliding friction coefficient,28 Qk being the ball contact load. The sliding friction can be expressed for the differential area of dS as
| (17) |
where bk is the semi-minor radius of the contact ellipse. Eq. (17) is used to estimate the net sliding frictional force in the rolling direction. We can utilize PRLs to determine such sliding friction force. Note here that the direction of sliding changes across PRLs. In the presence of two PRLs, the sliding direction changes twice, while the sliding direction changes once in the case of one PRL.
It should be noted here that the necessary values such as ball contact loads, contact angles, and ball speeds should be precalculated. To this end, we utilized the quasi-static model of ball bearings based on de Mul.23,24,26,27 Then we went on an iterative process associated with the equilibrium of frictional moments acting on individual balls.
3.4 PRLs for Spinning Friction Torque Estimation
Any ACBB experiences spinning motion about the normal direction to the center of the elliptical contact area (See Fig. 9).8,20,23,24,29 The friction moment with respect to the center of the elliptical contact area is calculated by10
| (18) |
which gives the integrated form as
| (19) |
where θ and φ are expressed as
| (20) |
| (21) |
The sliding velocities in the x- and y-directions are represented by vx,k and vy,k the sliding velocity in the x-direction on both races are assumed to be zero.
The PRL locations represented by c-values are very useful in estimating sliding friction force. The spinning moment is affected by the locations as well as the number of PRLs in the elliptical contact area. Houpert and Popescu8,20 suggested the spinning friction torque as a function of c-values as follows:
For 2-PRL case,
| (22) |
For 1-PRL case,
| (23) |
Then the total friction torque due to spinning is written as24,29
| (24) |
For validation of the PRL determination, we used spinning friction torque as presented here; spinning friction torque by Eqs. (22) and (23) is compared with that by Eq. (19).
4. Simulations and Discussion
This section shows the simulation results for spinning friction torque and sliding velocity using PRLs for validating the proposed formulation.
Simulations were performed with changing rotational speed. A sample bearing of ACBB 7008 was used for the simulation whose properties are listed in Table 1.
4.1 Spinning Friction Torque
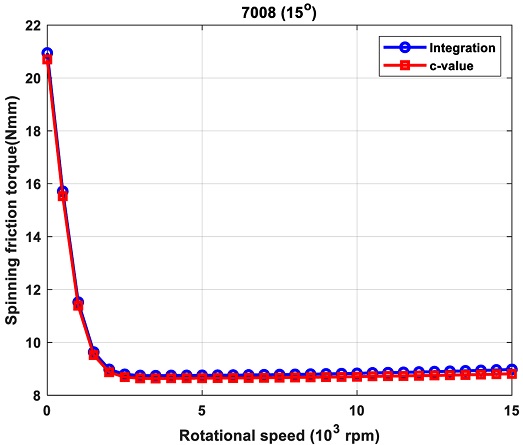
The improved spinning friction torque formulation given by Eq. (19) was used to compare the spinning friction formulas as a function of PRL locations. Fig. 11 shows the comparison of spinning friction torques by the two methods with rotational speed from 0 to 15 k rpm. Fig. 11 shows a good match between the current method and the conventional integration method, also showing that the c-value approach as presented in this study is useful in estimating spinning friction torque.
4.2 Number of PRLs
The PRL location determination was validated using spinning friction torque estimation. However, the confirmation of the existence of one or two PRLs in the elliptical contact area was not explained. Here, we will address the number of PRLs and differential sliding (Slip) velocity inside the elliptical contact area.
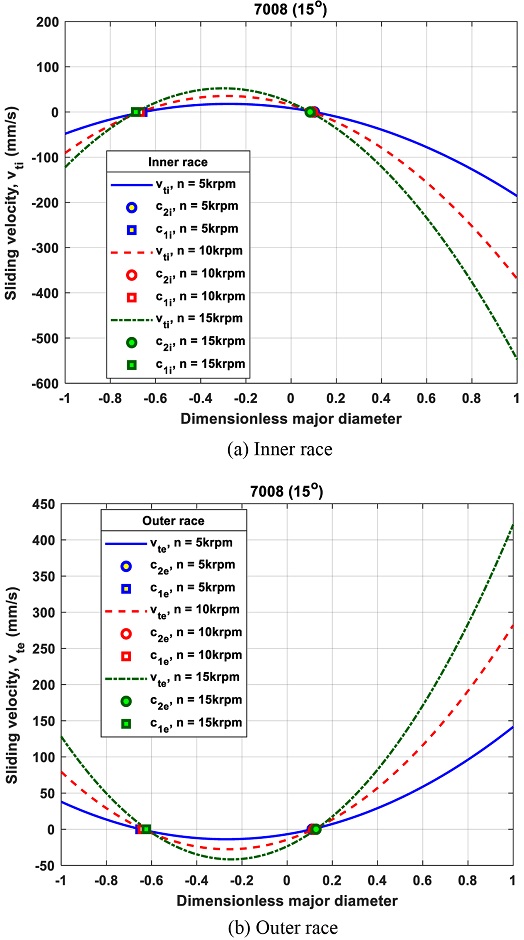
To investigate the number of PRLs and the behavior of c1 and c2, the differential sliding (Slip) velocities of the ACBB were plotted with rotational speeds of 5, 10, and 15 k rpm. Fig. 12 shows the differential sliding velocities along with the PRLs calculated using the E parameter, defined in Eqs. (14) and (15). The PRL locations calculated with the E parameter (c2-Circle, c1-Square) are well matched with those found at the points of intersection between the differential sliding velocity curves and the x-axis. In Fig. 12, it can be observed that the differential sliding velocities under Fz = 1,000 N intersect the x-axis twice in the dimensionless major diameter of the contact ellipse, showing that the direction of sliding velocity changes twice. In this case, the estimated PRLs show that there are two PRLs in the elliptical contact area as depicted in Figs. 12(a) and 12(b) both for the inner and outer races.
5. Parametric Study
This section presents a parametric study of PRLs in the elliptical contact area. Simulations using ACBB 7008 were performed with changing rotational speed, unloaded contact angle, axial preload, and radial load. Axial preload, Fz, of 500 N was used in this simulation.
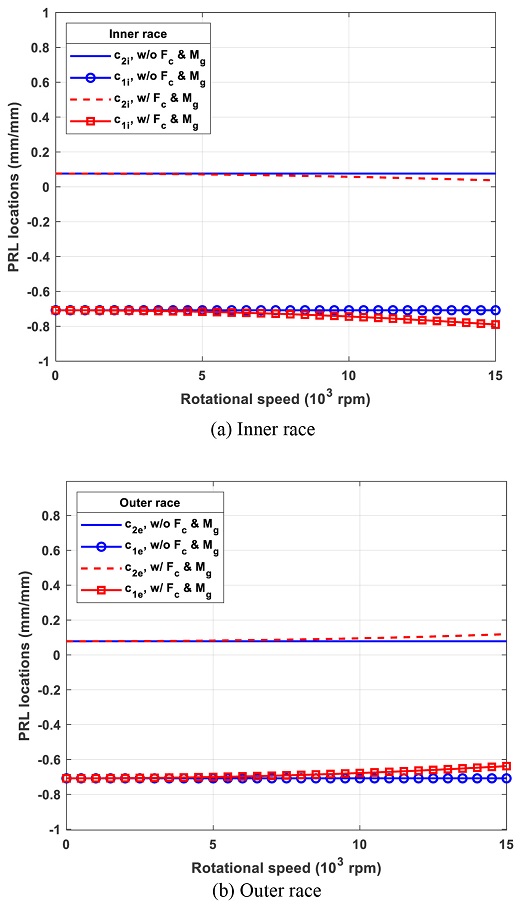
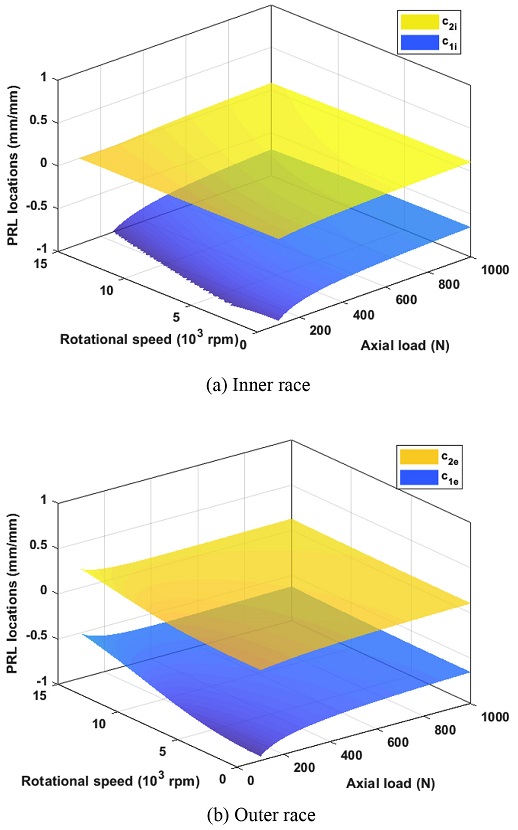
5.1 Effect of Centrifugal Force and Gyroscopic Moment
Fig. 13 shows the effects of centrifugal force and gyroscopic moments on the locations of PRLs. As rotational speed increases, the effects of centrifugal force and the gyroscopic moment become more significant. Without these effects, c1 and c2 on both races lie around -0.7 and 0.1, respectively, for the entire speed range.
The effects of centrifugal force and gyroscopic moment tend to move the two PRLs from the original position to a lower position on the inner race and a higher position on the outer race. The E parameter is a good index to correlate c1 and c2. Due to the centrifugal force and gyroscopic moment, the E parameter increases on the inner race but decreases on the outer race. Note here that the E parameter is closely tied with the contact angle on both races; the contact angle on the inner race increases while the contact angle on the outer race decreases, as the rotational speed increases.
Thus, the direction of PRL movement should be dependent on the contact angles.
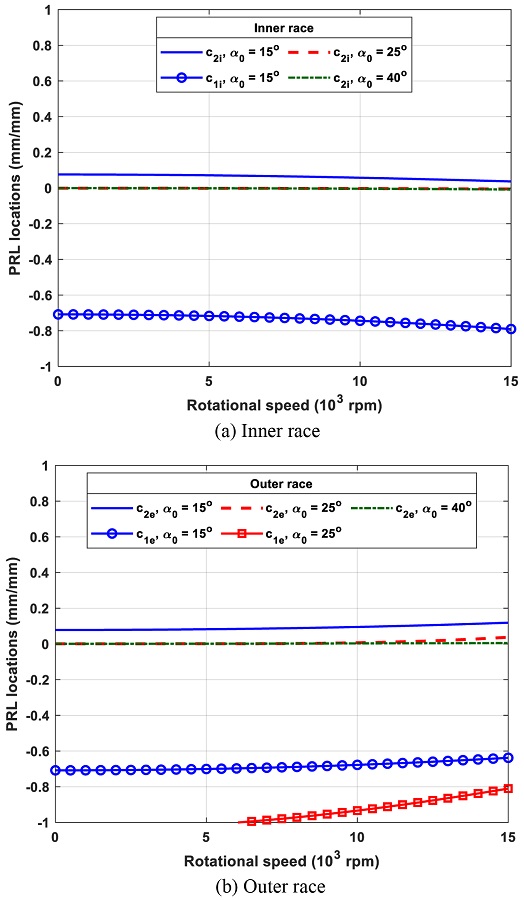
5.2 Effect of Pure Axial Load and Unloaded Contact Angle
Changing axial load also affects the location of PRLs. Fig. 14 depicts the locations of PRLs as a function of axial load and rotational speed. Fig. 14(a) shows the PRL locations on the inner race. The E parameter increases and forces c1 to approach -1. c1 approaches -1 quicker with increasing the rotational speed, when a relatively low axial load is applied.
Fig. 14(b) depicts the PRL locations on the outer race which behave oppositely to the inner race. Because the E parameter decreases, c1 tends to increase towards positive side.
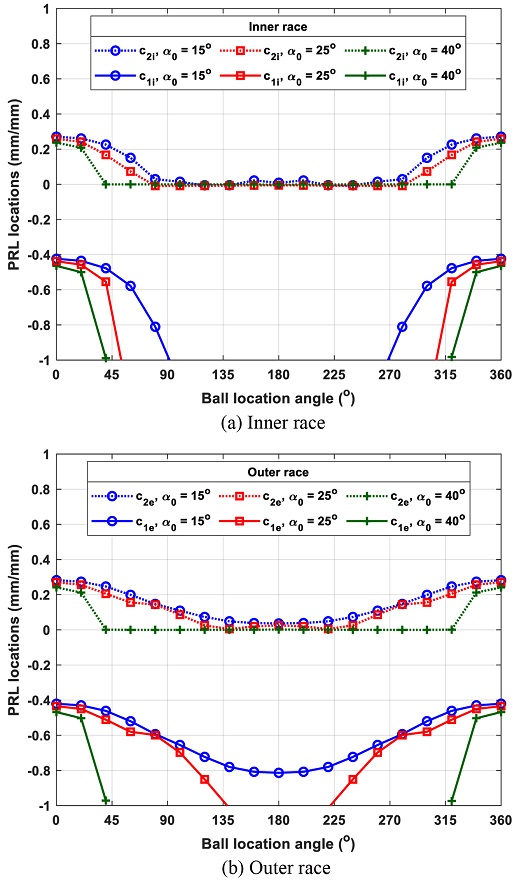
Unloaded contact angles, which inevitably affect the contact angles, change PRLs during operation. Fig. 15 shows that the unloaded contact angle gives a significant effect on the number, as well as the locations of PRLs. Figs. 15(a) and 15(b) show the PRLs on the inner and outer races, respectively. As the unloaded contact angle increases, the E parameter also increases. For α0 = 15o, two PRLs are present in both races. However, when the unloaded contact angle increases to α0 = 25o, the inner race has one PRL, while the outer race has only one PRL for low speed but two PRLs for high speed. Lastly, for the biggest unloaded contact angle, α0 = 40o, only one PRL exists for both races throughout the entire rotational speed range.
5.3 Effect of Radial Load and Unloaded Contact Angle under Combined Load
This section presents simulation results for radial load and unloaded contact angle effects subject to combined loading of axial and radial loads. In this case, axial load of 500 N is assumed.
Fig. 16 shows PRL locations on individual balls under the effect of combined load with various radial loads of 100, 500, and 1,000 N at 15 k rpm. Fig. 16(a) shows that the radial load can alter the number of PRLs on individual balls. In this case, increasing radial load can cause some balls, unlike the other balls, to operate with only one PRL on the inner race. Balls placed near 0o angle have more consistent behavior owing to sufficient contact load because the downward radial load is applied. However, balls around 180o angle are likely to experience a different condition that may lose one of the PRLs. Here, loss of c1 in a ball implies the possible occurrence of skidding at the ball.
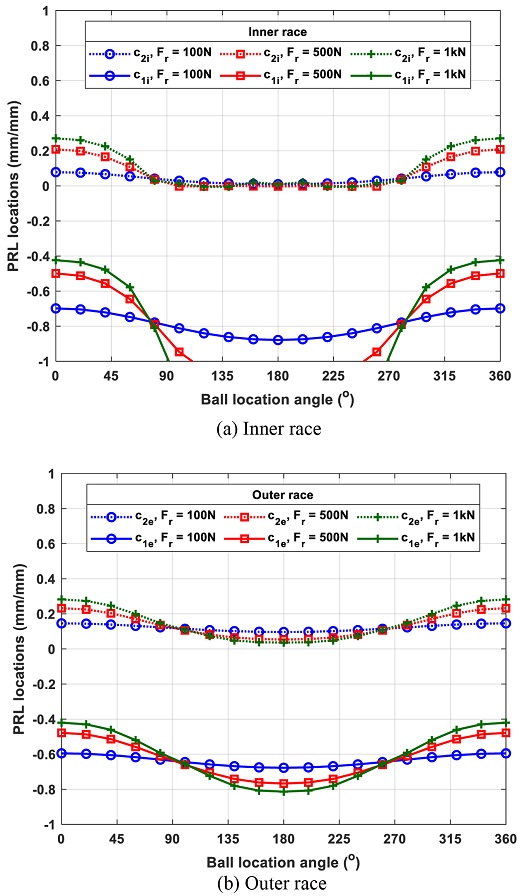
PRL locations on each ball under varying radial load; axial load Fz = 500 N, rotational speed of 15 k rpm, and unloaded contact angle of 15o
On the other hand, the PRLs on the outer race, shown in Fig. 16(b), manifest to be less sensitive to radial load. Such insensitive nature of the outer race against radial load comes from the decreased contact angle due to centrifugal force. Indeed, the balls around 180o are quite different from those on the inner race.
Fig. 17 shows the effect of unloaded contact angle on the PRL locations under the combined loading. Fig. 17 shows that a significant change occurs in the behavior of PRLs with varying unloaded contact angle. With a high unloaded contact angle, only one PRL is likely to exist both on the inner and outer races even under a small amount of radial load.
6. Concluding Remarks
This paper presented results of analysis on the behavior of the ball-race contact or more specifically PRLs to better understand sliding friction torque in ACBBs. The determination of PRLs was performed through an iterative process associated with the equilibrium of frictional moments acting on individual balls. For validation, the spinning friction torque was estimated using the PRL locations and compared with that from a conventional method. The computation results showed that one or two PRLs may exist in the elliptical contact area formed between ball and races, and that PRLs can be used to estimate spinning friction torque precisely.
A rigorous simulation study was performed for investigating the behavior of PRLs under various conditions. PRL locations were found to be functions of loading, rotational speed, and unloaded contact angle. Increasing rotational speed tends to push one of two PRLs to the outside of the elliptical contact area due to centrifugal force and gyroscopic moment. Higher axial load and lower unloaded contact angle tend to maintain two PRLs. Because of the change of contact load and contact angle at high speeds, the PRL behavior in the outer race is more insensitive than that in the inner race.
NOMENCLATURE
| a : | Semi-Major Radius [mm] |
| b : | Semi-Major Radius [mm] |
| c1, c2 : | Pure Rolling Line Locations |
| Da : | Ball Diameter [mm] |
| dm : | Pitch Diameter [mm] |
| e : | Ratio of Net and Maximum Sliding Friction Force |
| E : | Geometrical Parameter Associated with Pure Rolling Lines |
| f : | Conformity Ratio |
| F : | Sliding Friction Force [N] |
| FC : | Centrifugal Force [N] |
| Mg : | Gyroscopic Moment [Nmm] |
| ms : | Spinning Moment [Nmm] |
| Ms : | Spinning Friction Torque [Nmm] |
| n : | Rotational Speed [rpm] |
| Q : | Ball Contact Load [N] |
| R : | Hertzian Radius [mm] |
| vy : | Slip Velocity [mm/s] |
| z1, z2 : | Heights of Pure Rolling Lines [mm] |
| Z : | Number of Balls |
| α : | Contact Angle [rad] |
| β : | Pitch Angle [rad] |
| γ : | Dimensionless Parameter |
| μ : | Sliding Friction Coefficient |
| ω : | Rotational Speed [rad/s] |
| ωm : | Ball Orbital Speed [rad/s] |
| ωr : | Ball Pivotal Speed [rad/s] |
| ωs : | Spinning Speed [rad/s] |
Subscripts
| e : | Outer Raceway |
| i : | Inner Raceway |
| j : | Rolling Element Index |
| x,y,z : | Coordinate Axes |
Acknowledgments
This research is financially supported by National Research Foundation of Korea (Nos. NRF-2019R1F1A1063783, NRF-2020K2A9A1A06107195).
REFERENCES
- Harris, T. A. “Rolling Bearing Analysis,” John Wiley & Sons, 4th Ed., 2001.
-
Gupta, P. K., “Current Status of and Future Innovations in Rolling Bearing Modeling,” Tribology Transactions, Vol. 54, No. 3, pp. 394-403, 2011.
[https://doi.org/10.1080/10402004.2010.551805]

- Hamrock, B. J. and Anderson, W. J., “Rolling-Element Bearings,” http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.693.8552&rep=rep1&type=pdf, (Accessed 20 OCTOBER 2021)
-
Hong, S. W. and Tong, V. C., “Rolling-Element Bearing Modeling: A Review,” International Journal of Precision Engineering and Manufacturing, Vol. 17, No. 12, pp. 1729-1749, 2016.
[https://doi.org/10.1007/s12541-016-0200-z]

-
Tong, V. C. and Hong, S. W., “Modeling and Analysis of Double-Row Cylindrical Roller Bearings,” Journal of Mechanical Science and Technology, Vol. 31, No. 7, pp. 3379-3388, 2017.
[https://doi.org/10.1007/s12206-017-0627-x]

- Anderson, W., Parker, R., and Zaretsky, E., “A Review of Ball Motion in an Angular Contact Ball Bearing,” https://ntrs.nasa.gov/api/citations/19660018728/downloads/19660018728.pdf, (Accessed 20 OCTOBER 2021)
- Stolarski, T., “Tribology in Machine Design,” Industrial Press Inc., 1990.
-
Popescu, A., Houpert, L., and Olaru, D., “Four Approaches for Calculating Power Losses in an Angular Contact Ball Bearing,” Mechanism and Machine Theory, Vol. 144, Paper No. 103669, 2020.
[https://doi.org/10.1016/j.mechmachtheory.2019.103669]

-
Fernandes, C. M., Amaro, P. M., Martins, R. C., and Seabra, J. H., “Torque Loss in Thrust Ball Bearings Lubricated with Wind Turbine Gear Oils at Constant Temperature,” Tribology International, Vol. 66, pp. 194-202, 2013.
[https://doi.org/10.1016/j.triboint.2013.05.002]

- Fernandes, C. M. C. G., “Power Loss in Rolling Bearings and Gears Lubricated with Wind Turbine Gear Oils,” Dissertation for Faculdade de Engenharia da Universidade do Porto, Proquest Dissertations Publishing, 2015.
-
Hirano, F. and Tanoue, H., “Motion of a Ball in a Ball Bearing,” Wear, Vol. 4, No. 3, pp. 177-197, 1961.
[https://doi.org/10.1016/0043-1648(61)90121-1]

-
Hirano, F., “Motion of a Ball in Angular-Contact Ball Bearing,” Asle Transactions, Vol. 8, No. 4, pp. 425-434, 1965.
[https://doi.org/10.1080/05698196508972112]

-
Harris, T., “An Analytical Method to Predict Skidding in High Speed Roller Bearings,” Asle Transactions, Vol. 9, No. 3, pp. 229-241, 1966.
[https://doi.org/10.1080/05698196608972139]

-
Boness, R., “Minimum Load Requirements for the Prevention of Skidding in High Speed Thrust Loaded Ball Bearings,” Vol. 103, No. 1, pp. 35-39, 1981.
[https://doi.org/10.1115/1.3251611]

-
Liao, N. T. and Lin, J. F., “Ball Bearing Skidding under Radial and Axial Loads,” Mechanism and Machine Theory, Vol. 37, No. 1, pp. 91-113, 2002.
[https://doi.org/10.1016/S0094-114X(01)00066-0]

-
Xu, T., Xu, G., Zhang, Q., Hua, C., Tan, H., et al., “A Preload Analytical Method for Ball Bearings Utilising Bearing Skidding Criterion,” Tribology International, Vol. 67, pp. 44-50, 2013.
[https://doi.org/10.1016/j.triboint.2013.06.017]

-
Oktaviana, L., Tong, V. C., and Hong, S. W., “Skidding Analysis of Angular Contact Ball Bearing Subjected to Radial Load and Angular Misalignment,” Journal of Mechanical Science & Technology, Vol. 33, No. 2, pp. 837-845, 2019.
[https://doi.org/10.1007/s12206-019-0140-5]

-
Jones, A., “Ball Motion and Sliding Friction in Ball Bearings,” Journal of Basic Engineering, Vol. 81, No. 1, pp. 1-12, 1959.
[https://doi.org/10.1115/1.4008346]

-
Harris, T., “Ball Motion in Thrust-Loaded, Angular Contact Bearings with Coulomb Friction,” Vol. 93, No. 1, pp. 32-38, 1971.
[https://doi.org/10.1115/1.3451525]

- Houpert, L., “Numerical and Analytical Calculation in Ball Bearing,” Proc. of the 8th European Space Mechanisms and Tribology Symposium, 1999.
- Paleu, V., Damian, I., and Cretu, S., “Numerical Kinematics Analysis of Ball Bearings,” Vol. 51, No. 54, pp. 423-430, 2005.
-
Chen, Z. and Chen, G., “Effects of Ball’s Rolling, Gyroscopic, and Spin Slide in a Ball Bearing on Raceway’s Stress and Fatigue Life,” Journal of Tribology, Vol. 142, No. 8, Paper No. 082301, 2020.
[https://doi.org/10.1115/1.4046568]

-
Tong, V. C. and Hong, S. W., “Study on the Running Torque of Angular Contact Ball Bearings Subjected to Angular Misalignment,” Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 232, No. 7, pp. 890-909, 2018.
[https://doi.org/10.1177/1350650117732921]

-
Tong, V. C. and Hong, S. W., “Improved Formulation for Running Torque in Angular Contact Ball Bearings,” International Journal of Precision Engineering and Manufacturing, Vol. 19, No. 1, pp. 47-56, 2018.
[https://doi.org/10.1007/s12541-018-0006-2]

- Morales-Espejel, G., “Using a Friction Model as an Engineering Tool,” EVolution SKF, Vol. 6, No. 2, pp. 27-30, 2006.
-
De Mul, J., Vree, J., and Maas, D., “Equilibrium and Associated Load Distribution in Ball and Roller Bearings Loaded in Five Degrees of Freedom while Neglecting Friction-Part II: Application to Roller Bearings and Experimental Verification,” Vol. 111, No. 1, pp. 142-148, 1989.
[https://doi.org/10.1115/1.3261864]

-
Tong, V. C., Bae, G. H., and Hong, S. W., “Dynamic Analysis of Spindle Supported by Multiple Bearings of Different Types,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 2, pp. 117-125, 2015.
[https://doi.org/10.7736/KSPE.2015.32.2.117]

- SKF, “The SKF Model for Calculating the Frictional Moment,” http://www.skf.com/binary/21-299767/The0SKF0model0for0calculating0the0frictional0movement_tcm_12-299767.pdf, (Accessed 20 OCTOBER 2021)
-
Kakuta, K., “Friction Moment of Radial Ball Bearing under Thrust Load,” The Proceedings of Mechanical Engineering Congress, Japan, Vol. 27, p. 945, 1961.
[https://doi.org/10.1299/kikai1938.27.945]


He received his B.E. degree in Mechanical System Engineering from Kumoh National Institute of Technology, Korea in 2017 and a B.S. degree in Mechanical Engineering from Mapúa University, Philippines in 2019. He is currently pursuing his M.E. degree course in Mechanical Engineering from KIT, Korea.
E-mail: gibsrivera@naver.com

He received his M.S. degree in Mechanical Engineering from Hanoi University of Science and Technology, Vietnam in 2011. He earned his Ph.D. degree in Mechatronics from Kumoh National Institute of Technology, Korea in 2017. He is currently working at Samsung Display Vietnam.
E-mail: tvc785@gmail.com

He received his M.S. and Ph.D. degrees in Mechanical Engineering from KAIST, Korea, in 1985 and 1989, respectively. Currently, he is a professor in the Department of Mechanical System Engineering at Kumoh National Institute of Technology. His current research interests include spindle and bearings modeling and analysis, command shaping for positioning systems, vibration control, and structural vibration analysis for mechanical systems.
E-mail: swhong@kumoh.ac.kr