심층신경망 기반의 무릎 생체역학 변인 추정기
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Knee contact forces and knee stiffness are biomechanical factors worth considering for walking in knee osteoarthritis patients. However, it is challenging to acquire these factors in real time; thus, making it difficult to use them in robotic rehabilitation and assistive systems. This study investigated whether trained deep neural networks (DNNs) can capture the biomechanical factors only using kinematics during gait, which is possible to measure via sensors in real time. A public dataset of walking on the ground was analyzed through biomechanical analysis to train and test DNNs. Using the training dataset, several DNN topologies were explored via Bayesian optimization to tune the hyperparameters. After optimization, DNNs were trained to estimate the biomechanical factors in a supervised manner. The trained DNNs were then evaluated using two new datasets, which were not used in the training process. The trained DNNs estimated the biomechanical factors with a high level of accuracy in both types of test datasets. Results confirmed that DNNs can estimate the biomechanical factors based on only kinematics during gait.
Keywords:
Knee contact force, Muscle co-contraction ratio, Deep neural network, Knee osteoarthritis키워드:
무릎 접촉력, 근육 동시 수축 비율, 심층신경망, 무릎 퇴행성 관절염1. 서론
퇴행성 관절염(Osteoarthritis, OA)은 만성적으로 진행되는 관절 질환으로 퇴행성 관절염 환자는 관절에서 연골이 점차 마모되어 결국에는 사라지게 된다. 연골이 사라지면서 환자 관절의 뼈와 뼈가 직접 닿게 되어 고통을 포함한 강직(Stiffness), 염증(Inflammation), 종창(Swelling) 등의 다양한 증상을 유발하고 환자 삶의 질을 저하시킨다.1 OA 환자는 인구 고령화와 함께 점차 증가하고 있으나,2 OA의 이상적인 치료 방법이 아직 개발되지 않아3 환자의 증상 감소 및 관리를 돕기 위한 기구 및 로봇의 수요가 높아지고 있다.
무릎은 특히 OA가 많이 발생하는 관절로써4,5 무릎에 OA가 발생한 환자들은 보행 패턴을 바꾸어6 무릎에 가해지는 하중을 줄이려 하기 때문에 일상 생활에 지장을 받는다.7
무릎 OA 환자의 보행 보조를 위해서는 보행 중에 환자의 무릎 접촉력(Knee Contact Force, KCF)과 관절 강성(Joint Stiffness)을 관찰하여 적절한 모멘트를 제공하거나 관절 강성을 증강해야 한다. 무릎 OA 환자의 무릎 접촉력이 증가할 때, 시상(Sagittal) 평면에서 엉덩관절 굴곡/신전(Hip Flexion/Extension), 무릎 관절 굴곡/신전(Knee Flexion/Extension), 발목 관절 저측/배측 굴곡(Ankle Plantarflexion/Dorsiflexion) 방향의 모멘트 보조를 통해 무릎 접촉력을 감소시켜 환자의 보행 중 고통을 줄일 수 있다.8 또한 보행 패턴에 맞춰 관절 강성을 증가시키면 무릎 OA 환자들의 보행 안정성을 향상시킬 수 있다.9-11 특히 운동 요법을 통한 관절 강성의 증가가 환자의 보행 중 통증이나 장애 정도를 감소시킨다는 연구 결과가 보고되었다.12
다양한 하지 로봇들이 환자의 보행 재활이나 보조를 위해 개발되고 있으나, 대다수의 로봇은 환자의 운동 상태와 관계없이 사전에 계획된 경로를 따라 환자를 보조하도록 개발되고 있다.13 사전에 계획된 경로만 반복적으로 보조하는 로봇은 환자가 로봇에 전적으로 의존하여 수동적인 운동을 하게 만들며, 이는 재활 효과를 떨어트리고 환자가 로봇이 보조하는 동작에 대해 이질감과 불편함을 느끼게 한다. 이러한 문제를 해결하기 위해 실시간 측정이 가능한 환자의 근신호나 뇌전도 등의 생체신호는 추가 센서를 사용하여 로봇 제어에 이용하는 연구도 진행되고 있다.13
로봇을 이용한 무릎 OA 환자의 보행 보조에 사용할 수 있는 무릎 접촉력이나 관절 강성과 같은 생체역학적 변인은 보행 중에 측정된 동작과 지면 반발력(Ground Reaction Force)을 이용해 생체역학 해석 방법으로 계산할 수 있다. 그러나 해석에 소요되는 시간이 길기 때문에 주로 후처리 방식으로 사용되며 해석한 결과를 실시간으로 제어에 활용하기는 어렵다.
본 연구에서는 실시간 측정이 용이한 환자의 관절 각도, 각속도, 각가속도와 같은 운동학(Kinematics) 정보로부터 무릎 접촉력 및 무릎 관절 강성과 같은 생체역학적 변인을 예측할 수 있는 추정기의 개발 가능성을 확인하고자 하였다.
2. 무릎의 생체역학적 변인 추정기
무릎의 생체역학적 변인 추정기는 심층인공신경망을 활용해 개발하였다. 무릎의 생체역학적 변인 추정기는 제한적인 로봇의 연산 능력(Computation Power)을 사용해 센서에서 측정되는 운동학 정보를 생체역학적 정보로 실시간 맵핑해야 하므로 매우 깊은 구조의 심층인공신경망은 지양하고, 대표적인 합성곱 신경망(Convolution Neural Network, CNN)과 다층 퍼셉트론(Multilayer Perceptron, MLP) 알고리즘을 활용하였다.
무릎의 생체역학적 변인 추정기는 두 종류로 개발하였다. 두 종류의 추정기는 동일한 입력을 사용하지만 다른 출력을 가지며, 출력의 종류에 따라 KCF 추정기(Knee Contact Force Estimator)와 CCR 추정기(Co-Contraction Ratio Estimator)로 명명하였다. KCF 추정기는 양측 무릎 접촉력을 출력하고, CCR 추정기는 양측 무릎에서 주동근(Agonist)과 길항근(Antagonist)의 동시 수축 비율(Co-Contraction Ratio, CCR)을 출력한다. 여기서 주동근과 길항근의 동시 수축 비율(이하 동시 수축 비율)은 관절 강성에 비례하는 값으로 관절 강성을 대신하여 예측하도록 개발하였다.
2.1 실험 데이터와 입력-라벨 데이터
KCF 추정기와 CCR 추정기에 사용되는 심층인공신경망은 지도학습 방식으로 훈련시켰다. 지도학습을 위한 학습 데이터는 입력 데이터와 라벨의 쌍으로 구성된다. 입력 데이터는 훈련 과정에서 심층인공신경망에 입력되며 훈련된 심층인공신경망의 사용을 위해서는 훈련 과정에 사용된 입력 데이터와 동일한 종류와 형태의 정보를 심층인공신경망에 입력해야 한다. 따라서 입력 데이터는 센서로 측정이 용이한 무릎 관절의 각도, 각속도, 각가속도와 같은 운동학 정보를 사용하였다.
라벨은 입력 데이터를 이용해 심층인공신경망이 예측하고자하는 값으로 지도학습 과정에서 목표값으로 사용되었다. KCF 추정기에 사용한 라벨은 무릎 접촉력이었고, CCR 추정기에 사용한 라벨은 무릎 동시 수축 비율이었다. 무릎 접촉력과 동시 수축 비율은 생체역학 분석 방법을 통해 보행 실험 데이터를 해석하여 획득하였다.
보행 실험 데이터는 Fabian et al.14이 공개한 데이터를 사용하였다. 공개된 보행 실험 데이터는 9명의 건강한 피험자들이 트레드밀을 사용하지 않고, 지상에서 보행하는 동안 측정하였다. 9명의 피험자는 3명의 여성과 6명의 남성으로 구성되었으며 피험자들은 평균 27.4세였다. 피험자들은 동일한 날에 약 10 m씩 90회를 보행하였으며, 15회 보행마다 휴식을 취하였다. 공개된 보행 실험 데이터는 피험자에게 적외선 반사 마커를 부착하고, 적외선 카메라를 이용해 250 Hz로 마커의 위치를 측정한 모션 캡처(Motion Capture) 정보와 바닥의 Force Plate를 이용해 1,000 Hz로 측정한 지면 반발력 정보로 구성되어 있다.
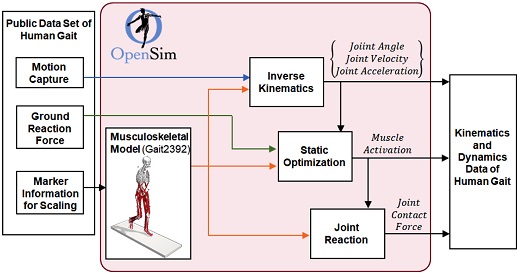
생체역학 분석 방법을 이용해 공개된 보행 실험 데이터에서 관절 각도, 근육 활성도, 관절 접촉력을 계산하였다. OpenSim 오픈소스를 이용해 Fig. 1과 같은 과정으로 공개된 보행 실험 데이터의 생체역학 분석을 수행하였다. 공개된 보행 실험 데이터에 포함된 각 피험자의 직립 자세에서의 적외선 반사 마커 추적 정보와 마커의 부착 위치 정보를 함께 이용해 OpenSim의 근골격(Musculoskeletal) 모델인 Gait2392 모델을 각 피험자의 신체 크기에 맞춰 크기 조정하였다. 크기 조정된 근골격 모델과 역운동학(Inverse Kinematics) 도구를 이용해 각 피험자의 모션 캡처 정보를 해석하고, 하체 관절의 각도, 각속도, 각가속도 정보를 획득하였다. Static Optimization 도구에 크기 조정된 근골격 모델, 해석한 하체 관절의 각도, 각속도, 각가속도 정보와 지면 반발력 정보를 이용해 각 하체 근육 힘과 근육 활성도 정보를 획득하였다. Joint Reaction 도구에 크기 조정된 근골격 모델과 Static Optimization 결과를 이용해 각 하체 관절에 작용하는 힘과 모멘트 정보를 획득하였다.
하나의 입력 데이터는 2차원 행렬로 50 × 6의 크기를 가진다. 열 방향으로 특징(Feature) 정보를 나열하였고, 특징 정보는 양측 무릎 관절의 운동학 정보를 사용하였다. 여기서 운동학 정보는 보행 실험 데이터 분석을 통해 획득한 각 관절의 각도, 각속도, 그리고 각가속도 정보이다. 각 특징 정보에 대해 4 ms 간격을 가지는 50개의 값을 행 방향으로 나열하였다.
라벨 데이터는 KCF 추정기와 CCR 추정기에 대해서 각각 양측 무릎 접촉력과 양측 무릎 동시 수축 비율로 선정하였다. 무릎 접촉력에는 OpenSim을 이용해 해석한 무릎 접촉력을 그대로 사용하였다. 동시 수축 비율은 OpenSim을 이용해 해석한 근육 활성도 정보를 식(1)에 적용해 계산하였다.
| (1) |
- Here,
- AEMGagonist: Average of normalized activation of agonist muscles
- AEMGantagonist: Average of normalized activation of antagonist muscles
- CCR: Co-contraction ratio
식(1)에서 AEMGagonist는 0-1 범위로 표준화된 무릎 주동근의 활성도 평균값이다. AEMGagonist를 계산하기 위해서 대퇴직근(Rectus Femoris), 내광근(Vastus Medialis), 중간광근(Vastus Intermedius), 외측광근(Vastus Lateralis), 대퇴근막장근(Tensor Fasciae Latae)의 표준화된 활성도를 사용하였다. AEMGantagonist는 표준화된 무릎 길항근의 활성도 평균값이며, 대퇴박근(Gracilis), 넙다리두갈래근(Biceps Femoris), 반막양근(Semimembranosus), 반힘줄근(Semitendinosus), 봉공근(Sartorius)의 표준화된 활성도를 사용해 계산하였다. CCR은 무릎 동시 수축 비율을 나타내며 AEMGagonist와 AEMGantagonist 값에 따라 [-1, 1]범위의 값을 가진다. 예를 들어, 무릎의 주동근과 길항근이 활성도가 비슷해 무릎 강성이 커질수록 CCR은 식(1)에 의해 0에 가까운 값으로 계산된다.
하나의 라벨 데이터는 1차원 배열로 2개의 값을 갖도록 구성하였다. 라벨 데이터에 사용된 2개의 값은 입력 데이터의 행 방향 50번째 데이터와 같은 시간의 양측 무릎 접촉력 또는 양측 무릎의 동시 수축 비율이었다.
입력-라벨 데이터 쌍을 구성하기 위해 분석한 Fabian et al.의 보행 실험 데이터는 9명의 피험자에게서 90회씩 측정한 810회의 보행 데이터로 구성된다.14 훈련 과정에 사용되는 입력-라벨 데이터 쌍을 구성하기 위해 8명의 피험자에게서 80회씩 측정한 640회의 보행 데이터를 참고하였다. 이렇게 구성된 입력-라벨 데이터 쌍을 9 : 1의 비율로 훈련 데이터 쌍(Training Dataset)과 검증 데이터 쌍(Validation Dataset)으로 나누어 사용하였다.
추정기의 성능을 평가하기 위해 평가 데이터 쌍(Test Dataset)을 두 가지 방법으로 구성하였다. 첫 번째 방법으로 8명 피험자의 보행 실험 데이터 중에서 훈련 데이터 쌍과 검증 데이터 쌍을 구성하기 위해 사용된 데이터 이외에 나머지 10회씩의 보행 실험 데이터(총 80회)를 입력-라벨 데이터 쌍으로 구성하였고, Unseen Data Acquired from Identical Subjects (UD-IS)로 명명하였다. 두 번째 방법으로 8명 피험자 이외에 9번째 피험자의 보행 실험 데이터를 참고하여 입력-라벨 데이터 쌍을 구성하였고, Unseen Data Acquired from a New Subject (UD-NS)로 명명하였다.
2.2 추정기의 구조 선정 및 평가 방법
KCF 추정기와 CCR 추정기를 구성하기 위해 심층인공신경망중 CNN과 MLP 구조를 고려하였다. KCF 추정기와 CCR 추정기는 같은 입력을 사용하지만 출력이 서로 다르기 때문에 각 추정기별로 서로 다른 MLP 구조와 CNN 구조를 선정해야 한다. 각 추정기의 MLP 구조와 CNN 구조 선정을 위해 Bayesian Optimization 방법을 이용해 CNN 층의 수, 각 CNN 층의 필터 수, CNN 필터 크기, 패딩 여부, Fully Connected (FC) 층의 수, 각 FC 층의 뉴런 수, 각 층의 활성화 함수, 학습율, 손실 함수와 같은 하이퍼파라미터를 바꿔가며 각 추정기별로 MLP 구조 700개와 CNN 구조 700개를 탐색하였다. 매 탐색에서 MLP 구조와 CNN 구조는 훈련 데이터 쌍을 이용해 학습되었고, 검증 데이터 쌍을 이용해 예측값과 목표값 사이의 잔차 표준 오차(Residual Standard Error, RSE)를 계산하였다. 각 추정기별로 RSE가 가장 낮은 MLP 구조와 CNN 구조 하나씩을 최적화된 구조로 선택하였다.
각 추정기의 최적화된 MLP 구조와 CNN 구조 중에서 어느 구조가 해당 추정기에 더 적합한지 판단하기 위해 평가 데이터 쌍을 이용해 예측값과 목표값 사이의 유사도를 측정하였다. 유사도는 평균 제곱근(Root Mean Square, RMS) 유사도, Peak 유사도, 그리고 벡터 사이의 코사인 각도(CA) 세 가지 방법을 이용해 측정되었다. RMS 유사도와 Peak 유사도는 식(2)와 식(3)을 이용해 계산하였으며, 계산 결과가 1에 가까울수록 두 데이터가 유사함을 의미한다.15
| (2) |
| (3) |
- Here,
- SimRMS(X, Y): Root mean square similarity
- SimPEAK(X, Y): Root mean square similarity
- X,Y: Data vector
- xi ∈ X, yi ∈ Y
CA는 식(4)와 같이 두 데이터를 마치 벡터처럼 보고, 두 데이터의 유사도를 두 벡터 사이의 각도에 대한 코사인값으로 측정한다. CA의 계산 결과가 1에 가까울수록 두 데이터가 유사함을 나타낸다.16
| (4) |
- Here,
- CA(X,Y): Cosine of the angle between two data vectors
- X,Y: Data vector
- xi ∈ X, yi ∈ Y
각 추정기에 최적화된 MLP 구조와 CNN 구조를 이용해 UD-IS와 UD-NS에 대한 예측값과 목표값 사이의 세 가지 유사도를 계산하였다. 유사도 계산 결과를 이용해 목표값을 더 유사하게 추종하는 심층인공신경망 구조를 최종 확인하였다.
3. 결과 및 논의
3.1 무릎 접촉력 예측을 위한 CNN과 MLP 구조
KCF 추정기의 구조를 최적화하기 위해 사람이 결정한 CNN과 MLP 구조를 초기값으로 하여 Bayesian Optimization 방법을 이용해 CNN과 MLP 구조를 각각 700개씩 탐색하였다. 사람이 결정한 초기 CNN 구조와 MLP 구조는 RSE가 1.564와 1.544로 계산되었으나 탐색 후에는 CNN과 MLP 구조의 RSE가 0.09847과 0.1121로 향상되었다. Figs. 2와 3은 최적화된 CNN과 MLP 구조를 나타낸다.
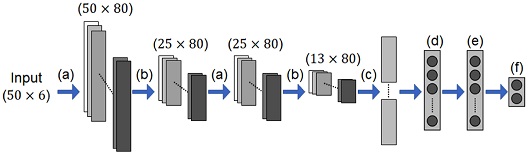
Selected CNN structure for KCF estimator: (a) 80 Filters of 1 × 3 convolution, (b) 1 × 2 Max pooling with stride two, (c) Flatten, (d) 258 Neurons in fully connected layer, (e) 129 Neurons in fully connected layer, and (f) 2 Neurons in output layer
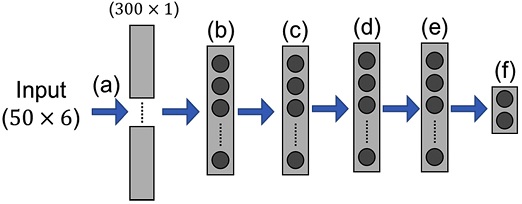
Selected MLP structure for KCF estimator: (a) Flatten, (b) 400 Neurons with a dropout of 0.4, (c) 800 Neurons with a dropout of 0.4, (d) 400 Neurons with a dropout of 0.6, (e) 200 Neurons with a dropout of 0.6 in each of fully connected layers, and (f) 2 Neurons in output layer
최적의 CNN 구조는 80개의 1 × 3 합성곱(Convolution) 필터와 1 × 2 Max Pooling을 교차로 두 번씩 가지며 합성곱 필터의 입력에 Padding을 적용하여 합성곱 필터의 입출력이 동일한 크기를 갖는다. 마지막 Max Pooling 층의 출력을 1차원으로 이어 붙이고, 각각 258개와 129개의 뉴런을 가지는 Fully Connected(FC) 층 2개를 지나 출력층에서 양측 무릎 접촉력을 출력한다. 모든 은닉층의 활성화 함수에는 ReLu가 사용되었으며 출력층의 활성화 함수에는 Tanh가 사용되었다. 학습 과정에서 가중치(Weight) 갱신을 위해 RMSprop을 사용하였으며, 이때 학습율은 0.003이었다.
최적의 MLP 구조는 총 4개의 FC 층을 은닉층으로 가지며, 각각의 FC 층은 400, 800, 400, 200개의 뉴런을 가진다. 은닉층을 지나 출력층에서는 양측 무릎 접촉력을 출력한다. 모든 은닉층의 활성화 함수에는 ReLu가 사용되었으며 출력층의 활성화 함수에는 Tanh가 사용되었다. 학습 과정에서 각 FC층에 0.4, 0.4, 0.6, 0.6 비율의 Dropout을 적용하였다. 가중치 갱신을 위해 Adam을 사용하였으며, 학습율은 0.002를 사용하였다.
3.2 무릎 동시 수축 비율 예측을 위한 CNN과 MLP 구조
CCR 추정기의 구조 최적화를 위해 사람이 결정한 CNN과 MLP 구조를 초기값으로 사용해 Bayesian Optimization 방법으로 CNN과 MLP 구조를 각각 700개씩 탐색하였다. 사람이 결정한 초기 CNN 구조와 MLP 구조는 RSE가 8.776과 6.404로 계산되었으나 탐색 후에는 CNN과 MLP 구조의 RSE가 0.1659와 0.1591로 향상되었다. Figs. 4와 5는 최적화된 CNN과 MLP 구조를 보여준다.
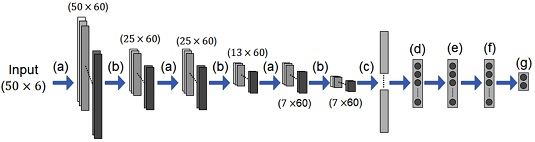
Selected CNN structure for CCR estimator: (a) 60 Filters of 1 × 5 convolution, (b) 1 × 2 Max pooling with stride two, (c) Flatten, (d) 180 Neurons in fully connected layer, (e) 90 Neurons in fully connected layer, (f) 45 Neurons in fully connected layer, and (g) 2 Neurons in output layer
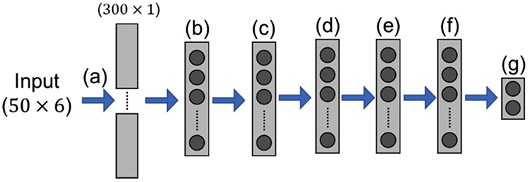
Selected MLP structure for CCR estimator: (a) Flatten, (b) 290 Neurons with a dropout of 0.2, (c) 420 Neurons with a dropout of 0.4, (d) 290 Neurons with a dropout of 0.4, (e) 200 Neurons with a dropout of 0.6, (f) 138 Neurons with a dropout of 0.6 in each of fully connected layers, and (g) 2 Neurons in output layer
최적의 CNN 구조는 세 번의 합성곱 필터와 Max Pooling이 교차로 나타난다. 먼저 110개의 1 × 3 합성곱 필터와 1 × 2 Max Pooling을 교차로 두 번씩 가지며, 이어서 165개의 1 × 3 합성곱 필터와 1 × 2 Max Pooling을 한 번씩 갖는다. 합성곱 필터의 입력에는 Padding을 적용하였다. 마지막 Max Pooling 층의 출력을 1차원으로 이어 붙이고 각각 88, 176, 88개의 뉴런을 가지는 3개의 FC층이 나타난다. 3개의 FC층 뒤에 출력층이 오며 양측 무릎의 동시수축 비율을 출력한다. 모든 은닉층의 활성화 함수에는 ReLu가 사용되었으며 출력층의 활성화 함수에는 Tanh가 사용되었다. 학습 과정에서 가중치 갱신을 위해 RMSprop을 사용하였으며 학습율은 0.001이었다.
최적의 MLP 구조는 은닉층에 총 5개의 FC층을 가지며 각각의 FC층은 290, 420, 290, 200, 138개의 뉴런을 가진다. 마지막으로 출력층은 2개의 뉴런에서 양측 무릎의 동시수축 비율을 출력한다. 모든 은닉층의 활성화 함수에는 ReLu가 사용되었으며 출력층의 활성화 함수에는 Tanh가 사용되었다. 학습 과정에서 각 FC층에 0.2, 0.4, 0.4, 0.6, 0.6 비율의 Dropout을 적용하였다. 가중치 갱신을 위해 RMSprop을 사용하였으며 학습율은 0.001이었다.
3.3 예측값과 타겟값의 유사도 측정 결과
UD-IS와 UD-NS 평가 데이터 쌍을 이용해 각 추정기에 최적화된 CNN 구조와 MLP 구조의 예측값과 목표값 사이의 유사도를 비교하였다. UD-IS와 UD-NS는 12,589개와 21,950개의 입력-라벨 데이터 쌍으로 구성되었다.
UD-IS와 UD-NS 중 일부 데이터 쌍에 대해 KCF 추정기에 최적화된 CNN 구조와 MLP 구조의 예측값과 목표값을 Fig. 6에 표시하였다. 각 그래프에서 파란 점선, 빨간 점선, 그리고 검은 실선은 동일한 입력 데이터에 대해 CNN 구조의 예측값, MLP 구조의 예측값, 그리고 목표 무릎 접촉력을 나타낸다. 그래프에서 무릎 접촉력은 각 피험자의 몸무게(Body Weight, BW)로 나누어 BW의 실수배로 표시하였다. Figs. 6(a)와 6(b)는 UD-IS를 사용한 결과이며, 6(c)와 6(d)는 UD-NS를 사용한 결과이다. CNN 구조와 MLP 구조의 UD-IS와 UD-NS에 대한 예측이 목표 무릎 접촉력의 경향을 잘 추종하였다.
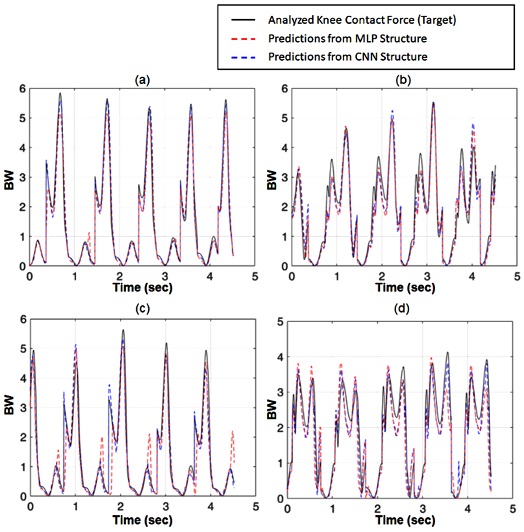
Knee contact force (KCF) expressed in body wight (BW): (a) KCF of right knee, and (b) KCF of left knee, which were acquired from identical subjects whose data were used to training deep neural networks. (c) KCF of right knee, and (d) KCF of left knee, which were acquired from a new subject
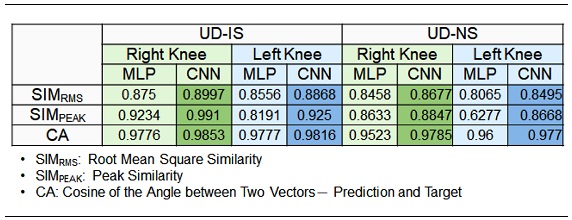
전체 평가 데이터 쌍에 대해 KCF 추정기에 최적화된 CNN 구조와 MLP 구조의 예측값과 목표값 사이의 유사도 계산 결과를 Table 1에 표시하였다. 유사도는 RMS 유사도, Peak 유사도, CA 방법으로 계산되었다. UD-IS와 UD-NS 모두에 대해 CNN 구조가 MLP 구조에 비해 세 가지 유사도 측정 방법에서 더 높은 유사도를 보였다. 특히 Peak 유사도에서 CNN 구조와 MLP 구조가 비교적 큰 차이를 보였다. KCF 추정기에 최적화된 CNN 구조가 MLP 구조에 비해 전반적인 예측 성능이 좋았으며, Peak 값에 대해 더 우수한 추종 성능을 보였다. 동일한 심층인 공신경망 구조에 대해 UD-IS와 UD-NS에 대한 유사도 계산 결과를 비교해보면, CNN 구조와 MLP 구조 모두 UD-IS를 목표값에 더 유사하게 예측했지만, UD-NS에 대해서도 예측값이 목표값과 높은 유사도를 보였다. 두 종류의 평가 데이터 쌍 모두에 대해 더 나은 예측을 수행한 CNN 구조가 KCF 추정기에 더 적합했다.
Fig. 7은 CCR 추정기에 최적화된 CNN 구조와 MLP 구조의 일부 UD-IS와 UD-NS에 대한 예측값과 목표값의 경향을 보여준다. 각 그래프에서 파란 점선, 빨간 점선, 그리고 검은 실선은 동일한 입력 데이터에 대해 CNN 구조의 예측값, MLP 구조의 예측값, 그리고 무릎의 동시 수축 비율을 나타낸다. Figs. 7(a)와 7(b)는 UD-IS를 사용한 결과이며, 7(c)와 7(d)는 UD-NS를 사용한 결과를 보여준다. CNN 구조와 MLP 구조의 예측이 목표값인 무릎 동시 수축 비율의 경향을 잘 추종한다.
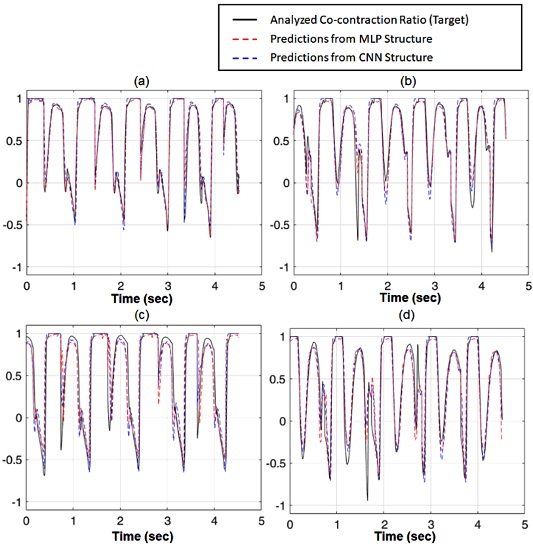
Co-contraction ratio (CCR) of antagonist-agonist activation: (a) CCR of right knee, and (b) CCR of left knee, which were acquired from identical subjects whose data were used to training deep neural networks. (c) CCR of right knee, and (d) CCR of left knee, which were acquired from a new subject
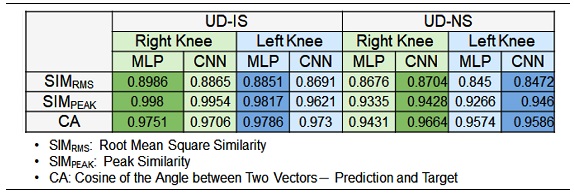
Table 2에 전체 평가 데이터 쌍에 대해 CCR 추정기에 최적화된 CNN 구조와 MLP 구조의 예측값과 목표값 사이의 유사도를 나열하였다. MLP 구조가 UD-IS에 대해 CNN 구조에 비해 세 가지 유사도 측정 방법에서 더 높은 유사도를 보였다. UD-NS에 대해서는 CNN 구조가 MLP 구조에 비해 더 높은 유사도를 보였다. 동일한 심층인공신경망 구조에 대해 UD-IS와 UD-NS에 대한 유사도 측정 결과를 비교해보면 CNN 구조와 MLP 구조 모두 UD-IS를 목표값에 더 유사하게 예측했지만, UD-NS에 대해서도 예측값이 목표값과 높은 유사도를 보였다. 실제 적용에 있어서 UD-NS에 대한 예측 결과가 목표값과 유사한 것이 더 중요하기 때문에 최적화된 CNN 구조가 MLP 구조에 비해 CCR 추정기에 더 적합하다고 판단할 수 있다.
4. 결론
로봇이 무릎 OA 환자의 보행을 보조할 때, 로봇의 제어에 무릎 접촉력이나 관절 강성과 같은 생체역학적 변인을 참고하여 환자 재활 및 보조 효과를 높이기 위해 본 연구에서는 실시간 측정이 용이한 환자 무릎의 관절 각도, 각속도, 각가속도 정보로부터 무릎 접촉력 및 무릎 동시 수축 비율을 예측할 수 있는 두 종류의 추정기를 심층인공신경망 기반으로 개발하였다. 공개된 보행 실험 데이터를 생체역학적 분석을 통해 데이터 쌍으로 구성하였으며, 구성한 데이터 쌍을 지도학습방식과 Bayesian Optimization에 적용해 두 종류의 추정기를 위한 심층인공신경망구조를 탐색하였다. 예측값과 목표값 사이의 유사도 계산 및 비교를 통해 추정기별로 최적의 CNN 구조를 확인하였다.
추정기를 학습시키기 위한 학습 데이터 쌍에 로봇을 사용할 모든 환자의 정보를 미리 포함하여 사전에 모든 환자에 대한 정보를 추정기에 학습시킬 수는 없으므로 개발한 추정기를 적용하는 단계에서는 새로운 사용자 데이터에 대한 예측 성능이 중요하다. 평가 데이터 쌍에 대해 각 추정기의 최적 CNN 구조가 예측한 값이 목표값과 높은 유사도를 보였으며, 목표값을 잘 추종하였다. 특히, 학습 데이터 쌍에 포함되지 않았던 새로운 피험자의 데이터에 대한 예측에서도 목표값과 높은 유사도를 보였다. 실험 결과를 통해 보행 실험 데이터를 이용한 생체역학적 변인 추정기의 개발 가능성을 확인하였다.
본 연구에서는 OA가 없는 일반인 9명의 데이터를 이용해 개발한 생체역학적 변인 추정기의 성능을 검증하였으나, 더 다양한 다수의 피험자를 대상으로 실험을 수행하여 생체역학적 변인 추정기 성능의 재현성 확인을 위한 추가 연구가 필요하다. 특히, OA 환자와 OA가 없는 일반인의 보행에는 차이가 있으므로 OA 환자를 대상으로 하는 추가 실험이 필요하다.
본 연구의 결과를 바탕으로 실시간으로 측정되는 관절 운동학 정보를 이용해 생체역학적 변인을 예측하고, 이를 실제 착용형 로봇 시스템에 적용하기 위한 추가 연구와 OA 환자를 대상으로 하는 추가 실험을 준비하고 있다.
Acknowledgments
본 연구는 산업통상자원부 및 한국산업기술진흥원의 혁신성장글로벌인재양성사업의 수행 결과임(No. P0008749, 로봇분야 혁신성장 글로벌 인재양성사업).
REFERENCES
-
Silverwood, V., Blagojevic-Bucknall, M., Jinks, C., Jordan, J., Protheroe, J., et al., “Current Evidence on Risk Factors for Knee Osteoarthritis in Older Adults: A Systematic Review and Meta-Analysis,” Osteoarthritis and Cartilage, Vol. 23, No. 4, pp. 507-515, 2015.
[https://doi.org/10.1016/j.joca.2014.11.019]

-
Neogi, T., “The Epidemiology and Impact of Pain in Osteoarthritis,” Osteoarthritis and Cartilage, Vol. 21, No. 9, pp. 1145-1153, 2013.
[https://doi.org/10.1016/j.joca.2013.03.018]

-
Hinman, R. S., Bowles, K. A., Metcalf, B. B., Wrigley, T. V., and Bennell, K. L., “Lateral Wedge Insoles for Medial Knee Osteoarthritis: Effects on Lower Limb Frontal Plane Biomechanics,” Clinical Biomechanics, Vol. 27, No. 1, pp. 27-33, 2012.
[https://doi.org/10.1016/j.clinbiomech.2011.07.010]

-
Felson, D. T. and Zhang, Y., “An Update on the Epidemiology of Knee and Hip Osteoarthritis with a View to Prevention,” Arthritis & Rheumatism: Official Journal of the American College of Rheumatology, Vol. 41, No. 8, pp. 1343-1355, 1998.
[https://doi.org/10.1002/1529-0131(199808)41:8<1343::AID-ART3>3.0.CO;2-9]

-
Cushnaghan, J. and Dieppe, P., “Study of 500 Patients with Limb Joint Osteoarthritis. I. Analysis by Age, Sex, and Distribution of Symptomatic Joint Sites,” Annals of the Rheumatic Diseases, Vol. 50, No. 1, pp. 8-13, 1991.
[https://doi.org/10.1136/ard.50.1.8]

-
Kaufman, K. R., Hughes, C., Morrey, B. F., Morrey, M., and An, K. N., “Gait Characteristics of Patients with Knee Osteoarthritis,” Journal of Biomechanics, Vol. 34, No. 7, pp. 907-915, 2001.
[https://doi.org/10.1016/S0021-9290(01)00036-7]

-
Brooks, K. S., “Osteoarthritic Knee Braces on the Market: A Literature Review,” Journal of Prosthetics and Orthotics, Vol. 26, No. 1, pp. 2-30, 2014.
[https://doi.org/10.1097/JPO.0000000000000013]

-
Stensgaard Stoltze, J., Rasmussen, J., and Skipper Andersen, M., “On the Biomechanical Relationship between Applied Hip, Knee and Ankle Joint Moments and the Internal Knee Compressive Forces,” International Biomechanics, Vol. 5, No. 1, pp. 63-74, 2018.
[https://doi.org/10.1080/23335432.2018.1499442]

-
Childs, J. D., Sparto, P. J., Fitzgerald, G. K., Bizzini, M., and Irrgang, J. J., “Alterations in Lower Extremity Movement and Muscle Activation Patterns in Individuals with Knee Osteoarthritis,” Clinical Biomechanics, Vol. 19, No. 1, pp. 44-49, 2004.
[https://doi.org/10.1016/j.clinbiomech.2003.08.007]

-
Hortobágyi, T., Westerkamp, L., Beam, S., Moody, J., Garry, J., et al., “Altered Hamstring-Quadriceps Muscle Balance in Patients with Knee Osteoarthritis,” Clinical Biomechanics, Vol. 20, No. 1, pp. 97-104, 2005.
[https://doi.org/10.1016/j.clinbiomech.2004.08.004]

-
Lewek, M. D., Ramsey, D. K., Snyder-Mackler, L., and Rudolph, K. S., “Knee Stabilization in Patients with Medial Compartment Knee Osteoarthritis,” Arthritis & Rheumatism, Vol. 52, No. 9, pp. 2845-2853, 2005.
[https://doi.org/10.1002/art.21237]

- Fransen, M., McConnell, S., and Bell, M., “Therapeutic Exercise for People with Osteoarthritis of the Hip or Knee. A Systematic Review,” The Journal of Rheumatology, Vol. 29, No. 8, pp. 1737-1745, 2002.
-
Shi, D., Zhang, W., Zhang, W., and Ding, X., “A Review on Lower Limb Rehabilitation Exoskeleton Robots,” Chinese Journal of Mechanical Engineering, Vol. 32, No. 1, pp. 1-11, 2019.
[https://doi.org/10.1186/s10033-019-0389-8]

- Horst, F., Eekhoff, A., Newell, K., and Schöllhorn, W., “A Public Dataset of Overground Walking Kinetics and Lower-Body Kinematics in Healthy Adult Individuals on Different Sessions within One Day,” Mendeley Data, Version. 1, 2019.
-
Fink, E. and Pratt, K. B., “Indexing of Compressed Time Series,” Data Mining in Time Series Databases, pp. 43-65, 2004.
[https://doi.org/10.1142/9789812565402_0003]

- Cassisi, C., Montalto, P., Aliotta, M., Cannata, A., and Pulvirenti, A., “Advances in Data Mining Knowledge Discovery and Applications,” IntechOpen, 71-96, 2012.

Assistant Professor at the Department of Human Intelligence Robot Engineering, Sangmyung University. His research interest is autonomous robots, human-machine interface, machine learning.
E-mail: drbong@smu.ac.kr

Professor at SDU Biorobotics, Maersk Mc-Kinney Moller Institute, University of Southern Denmark. His research interest is autonomous robots, artificial intelligence, swarm intelligence, complex systems.
E-mail: andc@mmmi.sdu.dk

Associate Professor at SDU Biorobotics, Maersk Mc-Kinney Moller Institute, University of Southern Denmark. His research interest is biomimetic/bio-inspired robotics and machine learning
E-mail: danish@mmmi.sdu.dk

Associate Professor at the Department of Human Intelligence Robot Engineering, Sangmyung University. His research interest is sensor fusion.
E-mail: skjeong@smu.ac.kr