원형 노치를 갖는 원통형 플렉셔 힌지의 해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Flexure hinges are widely used as joint linkages for precision stages applied to lithography processes. Among them, precision stages with 3 DOF (Degrees of Freedom) of x, y and θz prevail in semiconductor manufacturing and they have been adopting single directional flexure hinges as mechanical linkages without backlash and debris. However, new technologies including nano-imprinting, which replaces lithography, needs more than 3 DOF precision positioning stages that adopt cylindrical flexure hinges. In this study, the cylindrical flexure hinges with circular notches were analyzed using the Timoshenko beam theory and FEM (Finite Element Method), with focused on their directional stiffness. Based on the analysis and result comparison between theoretical equations and FEM, several practical suggestions for determining important design variables are provided in the conclusion of this study.
Keywords:
Flexure hinge, Finite element analysis, Directional stiffness키워드:
플렉셔 힌지, 유한요소해석, 방향강성1. 서론
1.1 필요성
반도체 산업이 발전함에 따라 정밀한 식각 공정 구현을 위해 플렉셔 힌지(Flexure Hinge)를 활용한 정밀 스테이지가 보편적으로 사용되고 있다. 이러한 공정에 사용되는 스테이지는 x, y, θz의 3자유도 평면 운동을 하며, 사용되는 플렉셔 힌지는 단방향(Uni-Directional) 플렉셔 힌지이다. 식각 공정은 독성 물질이 사용되어 환경 비용을 많이 지불하게 되므로 식각을 대체하는 나노 임프린팅 등과 같은 신기술이 대두되고 있다. 이러한 공정에는 평면 운동에 직각 방향 운동을 더하는 3자유도 이상의 스테이지가 요구되며 3자유도 이상의 스테이지에서는 원통형(Cylindrical) 플렉셔 힌지가 사용된다.
단방향 플렉셔 힌지는 널리 사용되기 때문에 많은 연구가 진행되어 왔지만 원통형 플렉셔 힌지에 대한 연구는 부족한 현실이다. 특히 효과적인 설계를 위한 지침이 될 만한 연구가 필요하다.
1.2 관련 연구 및 연구의 방향
플렉셔 힌지의 설계는 주로 유한요소해석에 의존하고 있다. 금속과 같은 등방성 재질의 탄성 영역에서의 응력 해석과 모달 해석은 상당히 신뢰성이 있어서, 메시(Mesh)가 충분히 잘 나누어진 경우 거의 실험 결과와 같은 수준으로 인정받고 있다.4 하지만 설계변수를 일일이 입력하여 얻은 유한요소해석 프로그램으로 계산하는 것은 많은 시간이 걸릴 뿐 아니라 설계변수에 대한 민감도나 경향을 알 수 없다.
단방향 플렉셔 힌지의 강성을 계산하는 방법으로는 티모셴코보로 근사화하여 계산하는 것이 많이 수행되어 왔다.1-3 Yong4의 논문에서는 단방향 플렉셔 힌지에 대해서 유한요소해석을 기준으로 하여 기존의 연구된 여러 방법의 결과와의 오차를 조사하였으며 주요한 내용은 다음과 같다. Paros-Weisbord1과 Wu5의 연구 결과는 모든 것이 같아서 Wu의 연구는 Paros-Weisbord 연구의 다른 표현이라 볼 수 있고, Lobontiu6의 연구 결과도 전단 유연성을 고려한 횡방향 강성을 제외하면 Paros-Weisbord의 연구와 결과가 같다. 특이한 점은 Paros-Weisbord의 간략식(Simplified Equation)이 해석적으로 유도된 전체식(Full Equation)보다 더 유한요소해석 결과와 유사한 회전 강성값을 계산한다는 점이다. Yong4의 연구 결과는 플렉셔 힌지의 해석과 연관한 우리의 연구에 방향을 제시하였으며 우리는 이 사실을 기초로 하여 연구하였다.
이렇게 단방향 플렉셔 힌지에 대해서는 신뢰할 만한 여러 가지 설계 방법이 연구되어 왔으나, 원통형 플렉셔 힌지의 효과적인 설계를 위한 해석적 방법은 부분적으로만 연구가 되었을 뿐이어서, 본 연구에서는 이론식과 유한요소해석을 활용하여 원통형 플렉셔 힌지의 실용적인 설계 방법을 제시하고자 한다. 본 연구에서는 원통형 플렉셔 힌지의 강성을 계산하는 해석적인식의 결과와 유한요소해석 결과와 실험식의 결과를 모두 비교하여 실험식의 형태와 계수의 타당성을 검증하고 실험식을 적용할 수 없는 설계변수의 범위를 도출한다는 점에서 기존의 연구와는 다른 독창성을 갖는다.
1.3 연구의 목표 및 논문의 구성
본 연구에서는 다음과 같은 목표를 성취하고자 한다. 첫째, 원통형 플렉셔 힌지의 물리적인 모델에 기초한 주요 성능지표인 축방향 강성과 굽힘 강성의 계산 방법을 유도한다. 둘째, 유도된 성능지표 계산법을 이용하여 설계변수에 따른 성능지표의 변화를 관찰하고 효과적인 설계를 제안한다. 셋째, 원형 노치가 완전한 반원이 아닌 호일 때와 완전한 반원일 때의 성능비교를 통해 효과적인 설계를 제안한다. 넷째, 개발된 해석적 방법과 유한요소해석법에 의한 수치반복적 방법의 비교를 통해 개발된 방법의 신뢰성을 점검한다.
본 논문은 다음과 같은 순서로 구성이 되어 있다. 1장에서 본 연구의 필요성과 목적을 기술한다. 2장에서 원통형 플렉셔 힌지의 구조에 관하여 설명하고, 원통형 플렉셔 힌지의 물리적인 모델에 기초한 주요 성능지표 계산법을 유도한다. 3장에서는 2장에서 개발된 방법과 유한요소해석에 의한 결과를 비교하여 개발된 방법을 평가한다. 4장에서 원형 노치가 완전한 반원의 형태가 아닐 때의 성능을 개발된 방법과 유한요소해석으로 도출하여 효과적인 설계 방법을 제안한다. 5장에서 연구의 결론을 정리한다.
2. 원통형 플렉셔 힌지의 구조와 강성
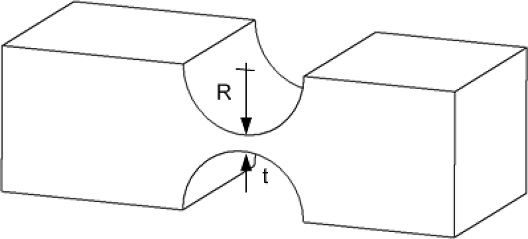
플렉셔 힌지는 서브 마이크로미터 단위의 구동을 하는 초정밀 스테이지의 필수 구성 요소이다. 현재까지 정밀 스테이지에서 주로 사용되고 있는 단방향 플렉셔 힌지는 Fig. 1에서 볼 수 있다. 이 단방향 플렉셔 힌지는 구조에서 알 수 있듯이 1개의 회전 자유도만 낮은 강성을 가지며 나머지 5개의 자유도는 높은 강성을 가지기 때문에 경첩과 같이 활용되고 있다. 이와 같은 형상의 단방향 플렉셔 힌지를 1-D Flexure Hinge,7 Single-Axis Flexure Hinge6 등으로 부른다.
Uni-directional flexure hinge
3자유도를 초과하는 자유도를 갖는 정밀 스테이지에서 원통형 플렉셔 힌지가 필요한 이유는 기존에 동작하던 회전 자유도에 직각인 방향의 회전 자유도를 더해 2개의 회전 자유도가 있어야 평면을 벗어난 자유도 구현이 가능하기 때문이다. 이와 같은 플렉셔 힌지를 2-D Flexure Hinge,7,9 2-Axis Toroidal Flexure Hinge,3 Multi-Axis Flexure Hinge6 등으로 부르며, 특히 노치의 형상이 원형일 경우에는 Circular라는 단어를 각 명칭의 앞에 넣어 부른다.3,6
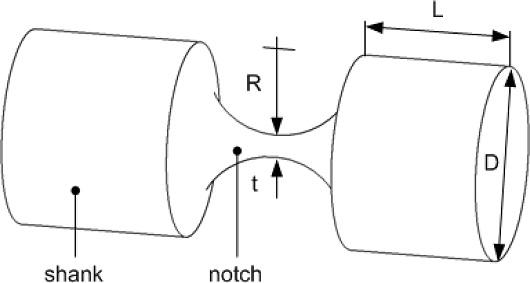
본 논문에서는 회전 자유도가 2개인 플렉셔 힌지가 원통형의 형상을 가진 것에 착안하여 원통형 플렉셔 힌지라고 부르기로 하며, 그 형상은 Fig. 2에 나타내었다. 원통형 플렉셔 힌지는 본 연구의 선행연구를 통해 반도체 공정용 정밀 스테이지에서 활용되었으며,7 이후 기업과의 공동연구를 통해 개발된 정밀 스테이지에서도 활용된 바 있다.10
Cylindrical flexure hinge (Circularly notched)
원통형 플렉셔 힌지의 설계는 허용응력 이내에서 2개의 회전 자유도의 강성은 낮게 하고 그 밖의 1개의 회전 자유도와 3개의 병진자유도의 강성은 높게 하여야 한다.
원통형 플렉셔 힌지의 경우 대칭적인 구조로 인해 경첩과 같이 사용하는 2개의 회전 자유도에 대한 강성과 응력의 식이 같으며, 그 회전축 방향의 병진자유도에 대한 강성과 응력의식이 같다. 즉, 축방향을 z축이라고 할 때 x축과 y축 방향의 회전 강성이 서로 같으며, x축과 y축 방향의 병진 강성이 있다. 그래서 강성식이 총 4개가 된다. 따라서 x축과 y축 방향의 회전 강성을 굽힘 강성 Kb라고 하고, z축 방향의 회전 강성을 비틀림 강성 Kt라고 하겠다. 또한 x축과 y축 방향의 병진 강성을 횡방향 강성 Kl이라고 하고, z축 방향의 강성을 축방향 강성 Ka라고 하겠다. 이를 식으로 나타내면 다음 식(1)과 식(2)와 같다.
| (1) |
| (2) |
| (3) |
| (4) |
위와 같은 강성은 다음의 두 식(5)와 식(6)을 기본으로 한다.
| (5) |
| (6) |
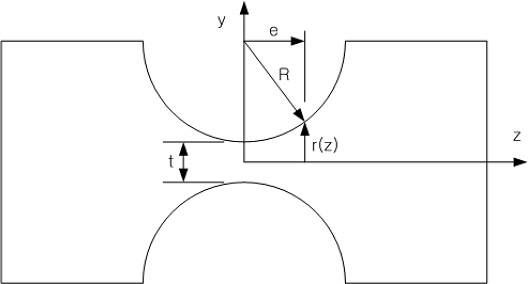
여기서 i = x, y, z이고, δ와 θ는 각각 변형길이와 변형각을 의미하며, F와 M은 각각 힘과 모멘트를 의미한다. 플렉셔 힌지의 단면 형상은 Fig. 3을 통해 나타내었다.
Cutaway view of the cylindrical flexure hinge
또한, 재료역학의 가장 기본적인 응력-변형률 공식과 인장 및 굽힘에 관한 공식들을 활용하면 플렉셔 힌지 설계에 가장 중요한 역할을 하는 축방향 강성 Ka와 굽힘 강성 Kb는 다음 식(7)과 같이 계산된다.8
| (7) |
여기서 E는 탄성계수, G는 전단탄성계수, A는 단면적, I는 관성모멘트, Iz는 극관성모멘트를 각각 의미한다.
윗 식들의 적분을 수행할 때에 원형인 단면 형상이 z축에 따라 변하는데, z축에 따른 반경 r은 다음 식(8)과 같다(Fig. 3 참조).
| (8) |
이에 따른 단면적과 관성모멘트와 극관성모멘트는 각각 다음과 같다.
| (9) |
3. 유한요소해석을 통한 검증
3.1 설계변수와 하중 조건
원통형 플렉셔 힌지의 주요한 설계변수는 가장 가는 부분의 지름(목두께) t와 원형 노치의 반지름 R이다(Fig. 2 참조). 먼저 고정한 설계변수는 t = 1 mm이다. 다음에 원형 노치의 반지름을 다음과 같이 정하였다(R = 1, 2, 5, 10, 20 mm).
하중 조건은 t가 안전계수 2에 의한 최대 허용응력에 이르도록 한 것이다. 구조용 강을 대상으로 하였기에 항복응력이 250 MPa이므로 허용응력이 125 MPa가 된다.
3.2 이론식에 의한 계산과 유한요소해석 결과의 비교
이론식은 티모셴코 보 이론(Timoshenko Beam Theory)을 적용하였다.8 유한요소해석은 힌지 부분만 하지 않고 자루(Shank)를 붙여서 했는데 그 이유는 실제로 플렉셔 힌지는 항상 자루를 붙여 사용하고 있으며, 자루를 붙여 놓으면 회전 강성을 더 잘 관찰할 수 있기 때문이다(Fig. 2참조).
유한요소해석을 수행하면서 자루 부분이 해석 결과에 영향을 주는 것을 최소화하기 위해 가장 큰 R값에 해당하는 지름 D를 고정하였다. 또 안전계수를 2로 했기 때문에 최대 응력이 125 MPa가 되어야 하는데 140-150 MPa 정도가 되었으며, 이를 통해 약간의 응력집중이 있음을 발견하였다.
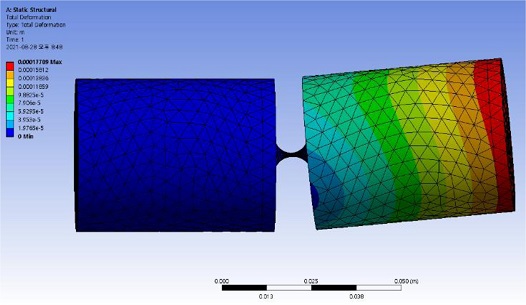
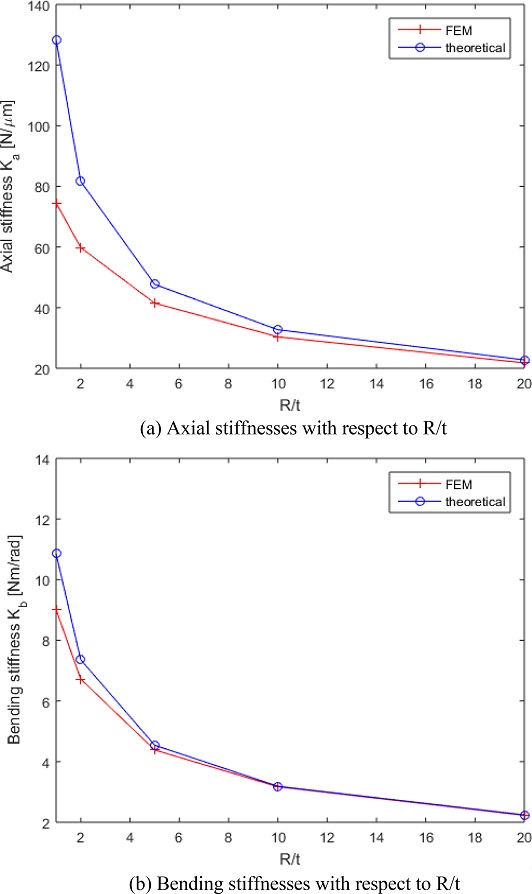
원통형 플렉셔 힌지는 주된 변수가 목두께 t와 노치반경 R이므로 이 두 설계변수만 변경하면서 축방향 강성 Ka와 굽힘 강성 Kb를 고찰하였다. 유한요소해석을 수행한 화면을 Fig. 4에 표시하였다. 또한, 이론식에 의해 계산된 강성을 Table 1에 담았고, 유한요소해석 결과를 Table 2에 담았으며, 각각을 Fig. 5에 그래프로 나타내었다.
Results of the finite element analysis
Stiffnesses resulted from theoretical calculation
Stiffnesses resulted from the finite element analysis
Stiffness comparison between FEM and theoretical calculation
결과 비교를 통해 발견된 특징은 다음과 같다. 유한요소해석 결과에서 최대 응력이 더 큰 이유는 형상 불균일이 반영된 응력 집중의 영향이라 평가된다. 결과적으로 계산된 축방향 강성 Ka와 굽힘 강성 Kb의 경우에 유한요소해석 결과가 약간 작은 이유도 유한요소해석에서 국부적으로 더 큰 응력값이 더 큰 변형을 유발했기 때문임을 유추할 수 있다. R/t의 변화에 따른 강성의 변화의 경향은 이론식이나 유한요소해석이나 비슷하다.
Yong4의 논문에서는 축방향과 횡방향 강성에 대해서 유한요소해석 결과값을 입력하여 다항식 회귀를 통해 실험식을 만들었지만 일반적인 다항식 회귀는 물리적인 의미가 없다. 오히려 Paros-Weisbord의 간략식1이 단방향 플렉셔 힌지의 굽힘 강성에서 잘 맞는 것에서 볼 수 있듯이 지수함수의 형태가 더욱 적합하다고 추론하여 Paros-Weisbord의 간략식과 비슷한 형태의 식(10)과 식(11)을 만들었다.
| (10) |
| (11) |
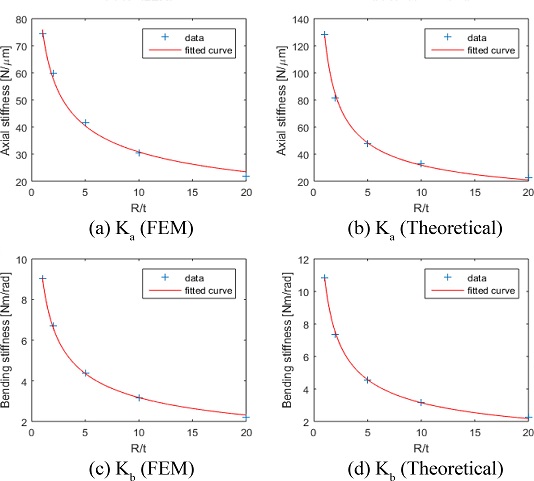
유한요소해석을 통해 얻은 축방향 강성과 굽힘 강성의 결과를 가지고 식(10)과 식(11)에 회귀를 수행하여 얻은 곡선 맞춤의 결과는 Fig. 6과 같으며 계수들의 값은 Table 3과 같다.
Curve fitting for FEM and theoretical calculation
Coefficients of the curved-fitted Eqs. (10) and (11)
Paros-Weisbord의 간략식의 계수값은 이론식과 유한요소해석에 의해 계산된 계수값들의 평균 정도의 값을 가진다. 유한요소해석에 의한 값이 실제 거동에 가장 가까우므로 실제 설계 시에는 유한요소해석에 의해 계산된 계수를 활용하는 것을 권장하며, 이를 통해 복잡한 해석 없이 효율적인 설계를 할 수 있을 것으로 기대된다.
4. 실용적 설계를 위한 고찰
4.1 노치가 완전히 원형이 아닐 때의 강성
실용적인 설계에서 노치의 원형 형태가 끝나기 전에 노치가 마무리 되도록 만드는 경우가 있는데, 그것이 강성에 미치는 영향이 어느 정도인지 파악하는 것이 필요하다. 따라서 이론식을 계산하거나 유한요소해석을 할 때, 노치의 반경에 대한 노치의 중심으로부터의 거리의 비(e/R)가 주요 설계변수가 된다.
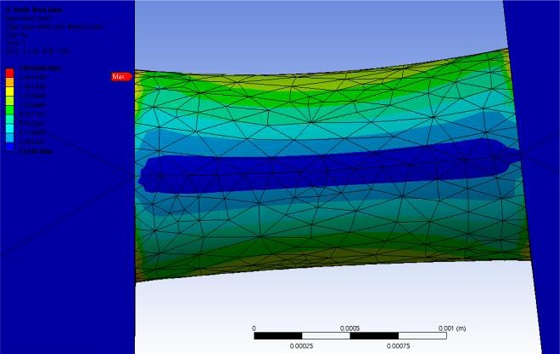
e/R = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1인 경우에 대해 (Fig. 3 참조) 유한요소해석을 실행하였으며, e/R = 0.5인 경우에 대한 유한요소해석 결과는 Fig. 7과 같다(힌지의 노치 부분이 완전히 반원이 아닌 것을 볼 수 있다).
Results of the finite element analysis with partially circular notch (e/R = 0.5)
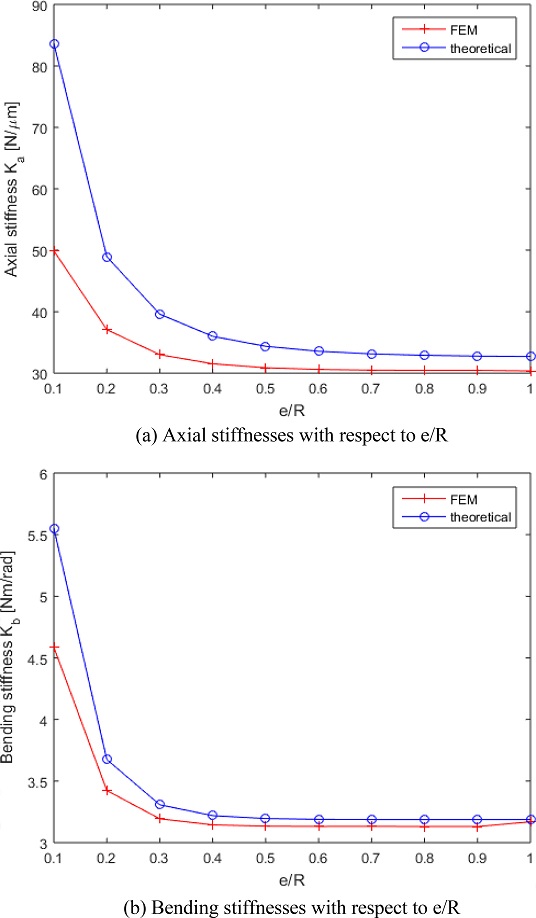
e/R의 변화에 따라 강성이 어떻게 달라지는지 이론식과 유한요소해석으로 각각 계산하였으며 그 결과를 Fig. 8에 담았다.
Stiffness comparison between FEM and theoretical calculation
4.2 이론식에 의한 계산과 유한요소해석 결과의 비교
보통 최대 응력은 플렉셔 힌지의 가장 얇은 부분에서 발생하는데, 유한요소해석을 수행해 보니 인장 하중의 경우에는 e/R = 0.1, 0.2일 때와 굽힘 하중의 경우에는 e/R = 0.1일 때, 플렉셔 힌지와 자루가 만나는 곳에서 큰 최대 응력이 발생하였다(Fig. 9 참조). 이는 그 부분의 형상 불균형이 커서 응력 집중이 발생하여 나타나는 현상이라 평가된다. 따라서 최소한 e/R = 0.3 이상이 되도록 설계하여야 한다.
Results of the finite element analysis with partially circular notch (e/R = 0.1)
4.3 강성 비교에 의한 실용적 설계 제안
e/R = 0.5, 0.6, 0.7, 0.8, 0.9에서 계산된 강성값은 e/R = 1.0에서의 값과 2% 이내의 오차 범위 내에 있다. 그래서 e/R = 0.5-1.0에서는 실용적으로 e/R = 1.0(완전한 반원 모양의 노치)일 때와 동일하다고 보고 설계를 해도 좋다. 하지만 이어지는 자루 부분이 얇아지므로 이로 인한 강성의 저하가 일어나기 쉽다는 것을 주의해야 한다.
5. 결론
(1) 반도체 가공 공정의 고도화와 특수 정밀 공정의 발달로 원형 노치를 갖는 원통형 플렉셔 힌지의 활용이 많아졌는데 실질적인 가이드라인이 부족하여 티모셴코 보 이론과 유한요소해석 각각에 대해 축방향 강성 Ka과 굽힘 강성 Kb를 해석하였다.
(2) 원형 노치를 갖는 원통형 플렉셔 힌지는 목두께 t와 노치 반경 R이라는 2개의 설계변수를 가지므로 t를 고정하고 R을 변화시킨 형상의 3차원 모델을 이용하여 축방향 강성 Ka과 굽힘 강성 Kb를 계산하였다.
(3) Ka와 Kb를 t와 R/t의 함수로 고찰하였으며 이론과 유한요소해석에 의한 값이 큰 차이를 보이지는 않았고, 유한요소해석에 의한 강성이 이론에 의한 값보다 항상 약간 적게 나오는 것을 확인하였다.
(4) 힌지의 목두께에 대한 노치반경의 비(R/t)에 의한 강성값의 변화는 일정한 경향을 보여주고 있어서 곡선 맞춤을 통해 실험식을 유도하였으며, 이는 향후 복잡한 계산이나 번거로운 유한요소해석 없이도 원통형 플렉셔 힌지의 강성 예측에 유용하게 사용될 것으로 전망된다.
(5) 노치의 반경에 대한 노치의 중심으로부터의 거리의 비(e/R)가 0.5-1.0의 범위에서는 강성값의 변화가 2% 이하이므로 실험식을 유도하기보다는 그 범위 안에서 활용하도록 하는 것을 권장한다.
(6) 본 연구의 결과를 디딤돌로 삼아서 향후 다양한 노치에 대한 해석과 실험식 도출을 발전시켜 플렉셔 힌지의 실용적인 설계에 더욱 기여하고자 한다.
NOMENCLATURE
| t : | Thickness of the Neck of Flexure Hinge |
| R : | Radius of the Notch of Flexure Hinge |
| L : | Length of the Shank |
| e : | Distance from the Center of the Neck to the Shank |
| z : | Axial Coordinate |
| Ka : | Axial Stiffness of the Flexure Hinge |
| Kl : | Lateral Stiffness of the Flexure Hinge |
| Kb : | Bending Stiffness of the Flexure Hinge |
| Kt : | Torsional Stiffness of the Flexure Hinge |
Acknowledgments
본 논문을 세심하게 읽고 수정해준 동양미래대학교 신현표교수에게 깊은 감사를 드립니다.
REFERENCES
- Paros, J. M. and Weisbord, L., “How to Design Flexure Hinges,” Machine Design, Vol. 37, No. 8, pp. 151-156, 1965.
-
Lobontiu, N., Paine, J. S., Garcia, E., and Goldfarb, M., “Corner-Filleted Flexure Hinges," Journal of Mechanical Design, Vol. 123, No. 3, pp. 346-352, 2001.
[https://doi.org/10.1115/1.1372190]
-
Smith, S. T., “Flexures: Elements of Elastic Mechanisms,” CRC Press, pp. 153-219, 2000.
[https://doi.org/10.1201/9781482282962]
-
Yong, Y. K., Lu, T.-F., and Handley, D. C., “Review of Circular Flexure Hinge Design Equations and Derivation of Empirical Formulations,” Precision Engineering, Vol. 32, No. 2, pp. 63-70, 2008.
[https://doi.org/10.1016/j.precisioneng.2007.05.002]
-
Wu, Y. and Zhou, Z., “Design Calculations for Flexure Hinges,” Review of Scientific Instruments, Vol. 73, No. 8, pp. 3101-3106, 2002.
[https://doi.org/10.1063/1.1494855]
-
Lobontiu, N., “Compliant Mechanisms: Design of Flexure Hinges,” CRC Press, pp. 110-133, 2002.
[https://doi.org/10.1201/9781420040272]
-
Moon, J.-H., Pahk, H. J., and Lee, B.-G., “Design, Modeling, and Testing of a Novel 6-DOF Micropositioning Stage with Low Profile and Low Parasitic Motion,” The International Journal of Advanced Manufacturing Technology, Vol. 55, Nos. 1-4, pp. 163-176, 2011.
[https://doi.org/10.1007/s00170-010-3033-4]
- Crandall, S. H. and Dahl, N. C., “Introduction to the Mechanics of Solids,” McGraw-Hill, 2nd Ed., 1979.
-
Shin, H.-P. and Moon, J.-H., “Kinematic Analysis of a 6-DOF Ultra-Precision Positioning Stage based on Flexure Hinge,” Journal of the Korean Society for Precision Engineering, Vol. 33, No. 7, pp. 579-586, 2016.
[https://doi.org/10.7736/KSPE.2016.33.7.579]
-
Shin, H. and Moon, J.-H., “Design of a Double Triangular Parallel Mechanism for Precision Positioning and Large Force Generation,” IEEE/ASME Transactions on Mechatronics, Vol. 19, No. 3, pp. 862-871, 2013.
[https://doi.org/10.1109/TMECH.2013.2261822]
Appendix
APPENDIX
A1. 축방향 강성 (r0 = t/2, β = sin-1(e/R))
A2. 굽힘 강성 (r0 = t/2, β = sin-1(e/R))
Associate Professor in the Department of Mechatronics Engineering, Yuhan University. His research interests include the design and control of flexure linkages and micro-positioning stages.
E-mail: jhmoon@yuhan.ac.kr