공기압축기의 이상 진단을 위한 딥러닝 기반 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Due to recent development of sensor technology and IoT, research is being actively conducted on PHM (Prognostics and Health Management), a methodology that collects equipment or system status information and determines maintenance using diagnosis and prediction techniques. Among various research studies, research on anomaly detection technology that detects abnormalities in assets through data is becoming more important due to the nature of industrial sites where it is difficult to obtain failure data. Conventional machine learning-based and statistical-based models such as PCA, KNN, MD, and iForest involve human intervention in the data preprocessing process. Thus, they are not suitable for time series data. Recently, deep learning-based anomaly detection models with better performances than conventional machine learning models are being developed. In particular, several models with improved performance by fusing time series data with LSTM, AE (Autoencoder), VAE (Variational Auto Encoder), and GAN (Generative Adversarial Network) are attracting attention as anomaly detection models for time series data. In the present study, we present a method that uses Likelihood to improve the evaluation method of existing models.
Keywords:
Air compressor, Deep learning, Anomaly detection, Prognostics and health management, Mahalanobis distance, Multivariate data키워드:
공기압축기, 딥러닝, 이상 탐지, 건전성 예측 및 관리, 마할라노비스 거리, 다변수 데이터1. 서론
기존 산업현장은 자산을 유지, 보수하는 방법으로 자산의 수리 주기를 미리 결정하고, 해당 주기로 보전을 수행하는 방식으로 진행해왔다. 해당 보전 방식은 부품의 열화 상태를 고려하지 않기 때문에 정상상태의 부품이더라도 수리 및 교체를 진행하여 불필요한 비용을 발생시킨다. 또한 자산의 상태를 실시간으로 진단하지 못하기 때문에 예상치 못한 고장이 발생했을 때 대응이 쉽지 않다[1]. 그래서 최근 자산에 대한 상태 정보를 수집하고, 해당 정보를 기반으로 유지보수를 결정하는 방법론인 PHM (Prognostics and Health Management)에 대한 연구가 활발히 진행되고 있다[2-4]. 본 연구에서는 PHM의 일환으로 철도차량에 쓰이는 공기압축기에 딥러닝 기법을 활용한 이상 진단 방법론을 제안한다. 철도차량의 공기압축기는 제동장치, 서스펜션 등에서 압축공기를 만들어내는 차량의 핵심적인 주요 장치이다[5]. 만일 공기압축기의 이상을 감지하지 못한다면 큰 인명피해를 불러올 수 있고, 해당 장치가 고장나면 운행 자체가 불가능하기 때문에 큰 비용 손실을 피할 수 없다. 또한 공기압축기는 철도차량뿐만 아니라 여러 산업현장에서 주요 기계장치로서 활용된다. 때문에 해당 장치에 PHM이 접목된 CBM (Condition Based Monitoring) 기법을 적용하여 장치의 상태 정보를 실시간으로 모니터링하고, 데이터를 분석해 이상 상태를 감지하려는 연구가 활발히 진행되고 있다[5-7]. 기존에 이상 감지 모델로서 각광받던 머신러닝 기반의 PCA (Principal Component Analysis), KNN (K-Nearest Neighbor Algorithm), MD (Mahalnobis Distance), iForest (Isolation Forest) 등은 정상 데이터가 이루는 군집과 일정 범위 이상 떨어진 데이터를 이상으로 판단하는 알고리즘이다[8]. 이러한 방법론들은 데이터 전처리 과정에서 사람의 개입이 필요하고, 시계열의 데이터에는 적합하지 않기 때문에 이러한 단점을 극복하고 더 좋은 성능을 보이는 딥러닝에 대한 연구가 더욱 활발히 진행되고 있다[9]. 특히 시계열의 데이터에 주로 쓰이는 LSTM (Long Short Term Memory)을 활용한 연구가 주를 이룬다[10]. Malhotra, et al. [11]은 처음으로 LSTM을 PHM의 이상 감지 모델로서 활용하였다. Malhotra, et al. [11]은 AE (Auto Encoder)를 LSTM과 융합한 LSTM-AE 모델을 제안했다. 해당 모델은 주변 환경의 변화나 노이즈가 있어도 이상을 잘 감지하는 결과를 보였다[11,12]. Li, et al. [13]은 주로 이미지 분야에서 이미지 창조 모델로 자주 활용되던 GAN (Generative Adversarial Network) 모델에 LSTM을 활용하는 새로운 모델을 제안하였다. GAN은 데이터의 연속적인 확률 분포 특성을 학습하기 때문에 다변수 데이터에 대해 더 심도 있는 학습이 가능했고, 기존 방법론의 성능을 앞서는 결과를 보였다. 다음으로 Niu, et al. [14]은 앞선 GAN-LSTM 모델에서 문제가 되었던 학습속도 및 수렴성에 대한 문제를 보완하는 모델을 제안하였다. 해당 모델은 VAE (Variational Auto Encoder)를 GAN 이전에 추가함으로써 랜덤 공간을 입력 데이터로 활용할 수 있는 학습을 추가했다. 해당 모델은 기존 모델에 비해 학습 시간을 단축시키고, 향상된 성능을 보였다[14]. 하지만 GAN 모델은 알고리즘의 특성상 최소 3번의 학습이 불가피하고, 학습의 수렴성이 여전히 불안정하여 학습 결과의 기복이 매우 심하다. 그러므로 GAN 모델은 산업현장에서 활용하기에는 다소 무리가 있다고 판단된다. 따라서 본 연구에서는 LSTM-AE를 활용한다. 또한 이상 데이터가 부재한 상황을 극복하기 위해 공기압축기의 고장 유형을 토대로 이상 데이터를 임의로 제작하는 방법을 제안한다. 마지막으로 본 연구에서는 평가의 기준이 되는 이상점수를 계산하는 방법에 대해 새로운 방법을 제안한다. 기존에는 다변수 데이터에 대해 모델이 예측한 데이터와 실제 데이터의 절대 차이를 구하고, 절대 차이의 MD를 계산한 후 각 윈도우 내부의 MD값들 중 가장 큰 값을 해당 윈도우의 대푯값으로 활용하였다[10]. 하지만 해당 방법론을 공기압축기에 적용하였을 때 이상 데이터와 정상 데이터를 제대로 구분하지 못하였고, 본 연구에서는 각 윈도우의 MD값들에 로그 최대우도를 적용하여 이상점수를 계산하는 방법론을 제안한다.
2. 데이터
2.1 공기압축기의 구조 및 데이터 종류
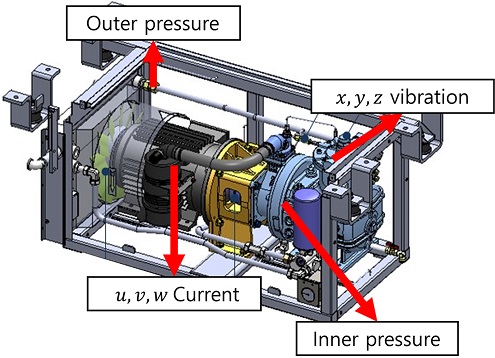
본 연구에서 대상이 되는 스크류 공기압축기는 크게 전동기, 에어앤드 유니트, 공기여과기, 기름여과기, 냉각팬, 흡입밸브, 배기밸브 등으로 이루어져 있다. 압축기는 전동기에 의해 구동되며 에어앤드 유니트의 케이싱 안에서 스크류 암/수 로터가 일정 간격으로 서로 맞물려 회전하면서 공기를 연속적으로 압축하는 구조이다. 데이터는 Fig. 1에 표시되어 있는 각 부위에서 진동, 내부 압력, 외부 압력, 모터 전류를 측정하여 얻었다. 또한 해당 데이터는 0.1초 단위로 총 8일 동안 실제 차량 운전 중 측정되었으며 6일 동안의 데이터는 각 일 수마다 학습, 검증 데이터 비율을 7 : 3으로 나누어 학습하여 Early Stop을 적용하였다. 1일 분량의 데이터에 데이터 크기의 10%에 해당하는 분량만큼 임의의 이상 데이터를 생성하여 실험 데이터로 활용하였다. 마지막 1일 분량의 데이터는 검증 데이터로서 정상 데이터의 공분산과 확률분포 정보를 얻기 위해 활용되었다.
2.2 고장 유형 및 이상 데이터 생성
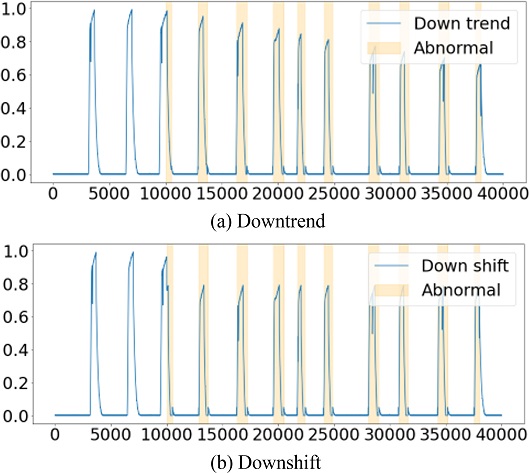
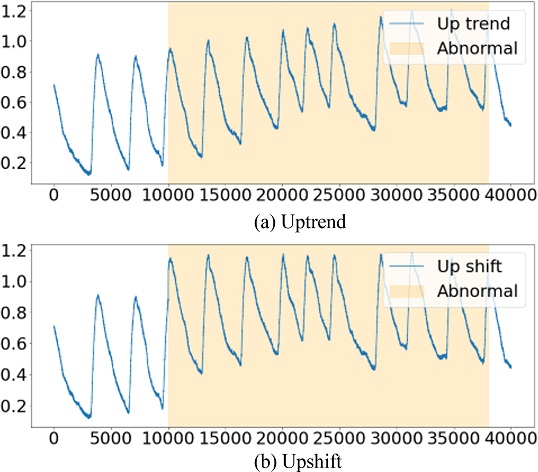
공기압축기에서 주로 발생하는 고장 상태는 공기압축기 기동 불능, 전동기 회전속도 상승 불능, 압축기 차단 설정 압력에 도달전 기동이 정지, 안전밸브 작동, 압축기 과온 현상, 윤활유 소모과다, 압축공기 생산 불충분 등 총 7가지로 이루어진다. 이상 데이터를 얻기 어려운 현실적인 한계를 극복하기 위해 상단에서 언급한 고장 상태의 유형을 토대로 이상 데이터를 시뮬레이션하여 임의로 이상 데이터를 생성하고자 한다. 실제로 여러 논문에서 모델의 성능 검증을 위해 부족한 이상 데이터를 시뮬레이션 데이터로 대체하거나 모델의 성능 향상을 위해 시뮬레이션 데이터를 활용하는 경우가 있다. El-Midany, et al. [15]은 이상 데이터의 주요 원인변수를 찾기 위해 인공신경망을 활용했고, 이 과정에서 시뮬레이션 데이터를 이용하여 인공신경망을 학습했다. 해당 모델은 시뮬레이션된 또다른 데이터와 압축기의 크랭크실에서 얻은 실제 이상 데이터를 이용하여 검증되었다[15]. 또 Ünlü [16]는 이상 탐지 모델이 이상 징후를 조기에 발견할 수 있도록 시뮬레이션 데이터를 활용하였다. Ünlü [16]는 정상 데이터에 여러 가지 패턴으로 제작된 이상 데이터를 섞어서 모델의 학습 데이터로 활용하는 것과 동시에 모델을 검증하는데 이용하였다. 본 연구에서는 공기압축기의 고장 유형과 앞선 데이터 시뮬레이션의 정형적 패턴 방식을 참고하여 이상 데이터를 생성하고, 이를 모델 검증 데이터로서 활용한다. 현재 주어진 데이터를 활용해 만들어낼 수 있는 이상 데이터는 두 가지로서 첫째는 압축기의 압력이 목표치에 도달하지 못하는 상황을 가정한 내부 압력의 Downshift, Downtrend, 두 번째는 압축기의 과온 상황을 가정한 오일 온도의 Upshift, Uptrend이다. 내부 압력의 경우는 압축기가 작동하여 압력이 올라가는 순간에만 시뮬레이션 작업을 진행했고, 오일의 온도는 일정 구간 전부에 시뮬레이션 작업을 진행했다. 다음 Figs. 3과 4는 시뮬레이션된 이상 데이터를 보여준다.
3. 딥러닝 기반 이상 탐지 모델
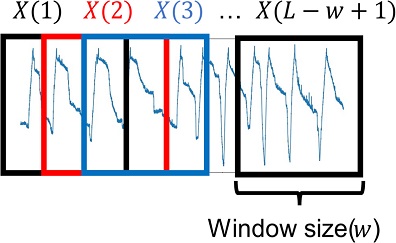
앞으로 소개할 LSTM-AE 모델에 입력으로 쓰이는 시계열 데이터 X = x1, x2,..., xL는 L개의 m차원을 지닌 벡터의 집합이다. L은 데이터의 총 개수를, m은 변수의 개수를 의미한다. 본 연구에서는 이 데이터를 윈도우 크기(w)의 단위로 묶은 Xw = {X(1), X(2), ..., X(L - w + 1)}을 활용하게 되는데 이때 X(n) = {xn, xn+1, ..., xn+w-1}이다. 이렇게 윈도우 크기(w)로 데이터를 묶음 처리하게 되면 실제로 활용하게 될 데이터 Xw의 크기는 L - w + 1이다. 다음 Fig. 2는 데이터를 윈도우 크기로 묶음 처리한 예시를 그림으로 보여준다.
3.1 LSTM-AE
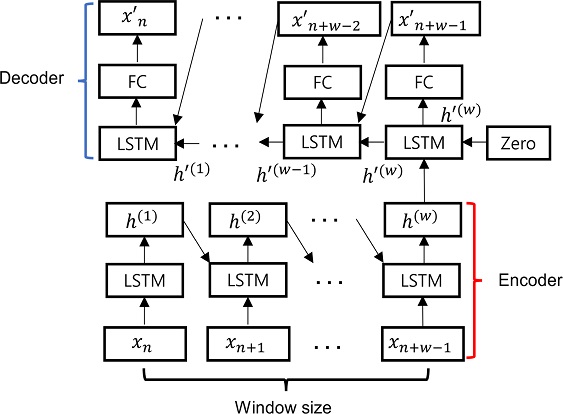
LSTM-AE는 Malhotra, et al. [10,11]이 최초로 다변수 시계열 데이터에 적용했던 모델로서 아키텍처는 Fig. 3과 같다.
LSTM-AE의 인코더는 앞서 언급한 X(n)을 입력으로 활용한다. 이때 n은 X(n)이 Xw의 n번째 행렬임을 의미한다. X(n)의 첫 번째 벡터인 xn부터 마지막 벡터인 Xn+w-1까지 차례로 LSTM-AE의 인코더에 입력으로 들어가고, 각 LSTM 층마다 은닉 상태 변수인 h(n) ∈ Rc가 출력된다. 이때 c는 지정한 은닉 상태 변수 h(n)의 차원이다. 이 h(n)은 다음 LSTM 층의 입력으로 활용되고, 마지막 Xn+w-1 벡터가 입력인 은닉 상태 변수 h(w)는 디코더의 입력으로 활용된다. 이를 ‘특징 벡터’라고 지칭한다. 디코더는 인코더와는 다르게 x(n) 의 끝 벡터 nn+w-1부터 xn까지 재생성을 시작하고 인코더와 동일한 과정을 거친다. 해당 모델의 목적함수 J는 인코더의 입력인 원래 데이터와 디코더가 재생성한 데이터의 차이인 MSE (Mean Square Error)이며 J가 최소화되는 방향으로 학습이 진행된다.
| (1) |
3.2 이상점수
딥러닝을 활용한 이상 탐지 모델은 주로 모델이 예측한 데이터와 원래(실제) 데이터의 차이를 활용한다. 이 차이(Error)가 크다면 원래의 데이터가 이상 데이터인 것이고 이 차이가 크지 않다면 이상 데이터가 아닌 정상 데이터라고 판별하는 알고리즘이다. 그래서 많은 연구에서 간단하게 MSE 또는 절대 오차를 활용한다. 하지만 다변수 데이터의 경우 여러 변수의 분산 차이를 고려한 하나의 Error(실제 데이터와 예측 데이터의 차이)값이 필요하다. 이 Error를 구하는 기본적인 방법이 MD를 활용하는 것이다[17]. 기존의 이상점수를 구하는 방법은 다음과 같다. 앞선 2장에서 언급했듯이 윈도우로 묶음 처리한 데이터를 활용한다. 먼저 원래 데이터와 예측 데이터의 절대 차이를 구한다. 그러면 원래 데이터와 크기 및 차원이 동일한 EW = {E(1), E(2), ..., E(L - w + 1)} 가 구해진다. 이때 행렬 E(n)은 식(2)와 같이 구성된다.
| (2) |
에서 n은 절대 차이 행렬 집합 Ew에서 몇 번째 행렬인지를 의미한다. m은 몇 번째 변수 및 행인지를 의미한다. k는 윈도우 크기 w의 열을 가진 행렬 E(n) 에서 몇 번째 열인지 나타낸다. 정상 데이터만으로 구성된 검증 데이터의 행렬집합 Ew의 내부행렬을 m×mㆍ(L - w + 1) 크기의 한 행렬 Em로 모두 이어붙인 후 식(3)과 같이 정상 데이터에 대한 공분산 행렬을 구한다.
| (3) |
이후 이상 데이터가 포함된 실험 데이터의 Ew의 각 E(n) 행렬의 각 벡터 e에 대해 식(5)와 같이 MD를 계산한다.
| (4) |
| (5) |
기존 이상점수 S(n) 를 계산하는 방법(Maximum Score)은 각 윈도우가 가지고 있는 MD 중 가장 큰 값을 대푯값으로 활용한다[10,11].
| (6) |
식(6)에서 MDn은 n번째 윈도우의 MD 집합을 의미한다. 하지만 이러한 기존의 방법은 윈도우 단위로 학습이 되었던 모델의 모든 은닉 상태 변수를 활용하지 못한다는 점과 윈도우 내부의 모든 벡터의 포괄적인 분포 특성을 고려하지 않기 때문에 제대로 된 이상점수를 얻기에 무리가 있다고 판단된다. 그러므로 본 연구에서는 다음의 이상점수 계산 방법(Likelihood Score)을 제안한다. 정상 데이터로 이루어진 검증 데이터의 MD를 구하고, 각 윈도우를 모두 이어 붙여 1 × (L - w + 1) 크기의 한 벡터를 구성한다. 해당 벡터에 대해 정규분포 추정을 통해 정규분포 파라미터 θ를 얻고, 식(7)과 같이 이상 데이터가 포함된 실험 데이터의 각 윈도우의 이상점수 S(n)을 로그 최대우도로 계산한다.
| (7) |
에서 n은 몇 번째 윈도우인지를, i는 해당 윈도우 내부에서 몇 번째 요소인지를 의미한다. 식(7)은 수식적으로 해당 윈도우가 정상 데이터의 확률 분포상에 포함될 확률을 의미하고, (-)가 붙음으로써 이상 데이터일수록 값이 급격히 커지게 된다.
4. 실험 및 결과
모든 데이터는 학습 진행 전에 모델의 스케일 학습에 대한 부담을 줄이고 학습의 효율성을 높이기 위해 데이터의 각 변수마다 정상 데이터의 최댓값과 최솟값을 활용해 식(8)과 같이 정규화하였다. 또 하이퍼 파라미터로 은닉층의 벡터 크기는 100, 윈도우 크기는 10 그리고 LSTM의 층은 3층으로 설정하였다.
| (8) |
이상 탐지 모델을 평가하는 방식으로 Precision, Recall, F1의 정량적인 평가를 시행하였다. 해당 평가 방식은 이상 탐지 모델을 평가하는 가장 보편적인 방법으로서 각 평가 방법에 대한 수식은 식(9)부터 식(11)과 같다. Precision은 정상 데이터를 오판하지 않는 수준, Recall은 이상 데이터를 이상 데이터로 얼마나 정확하게 판단하는지 수준, F1은 Precision과 Recall의 전체적인 평균 수준과 함께 Precision과 Recall이 얼마나 균형 있게 있는지를 볼 수 있다.
| (9) |
| (10) |
| (11) |
위의 수식에서 변수들의 의미는 다음 Table 1에 나타나 있다. 만일 Precision이 100%가 되지 못하면 정상 데이터에 대해 이상 데이터로 판별하는 경우가 많아져 해당 모델 및 시스템에 대한 신뢰도가 하락한다. 그러므로 이상 데이터와 정상 데이터를 구분하는 이상점수의 임계값은 Precision이 100%가 되는 마지막 지점으로 선정하였다. Table 2는 LSTM-AE에 기존 이상점수 계산법과 제안하는 방법론의 결과를 보여준다. 정량적으로 제안하는 방법론의 결과가 100%의 동일한 Precision에서 더 좋은 Recall 값을 보임을 알 수 있다.
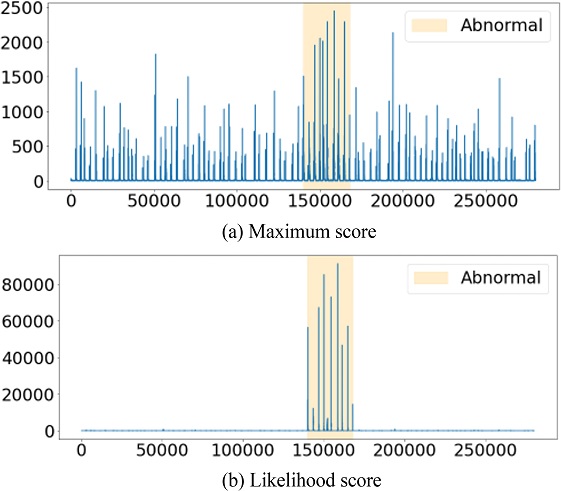
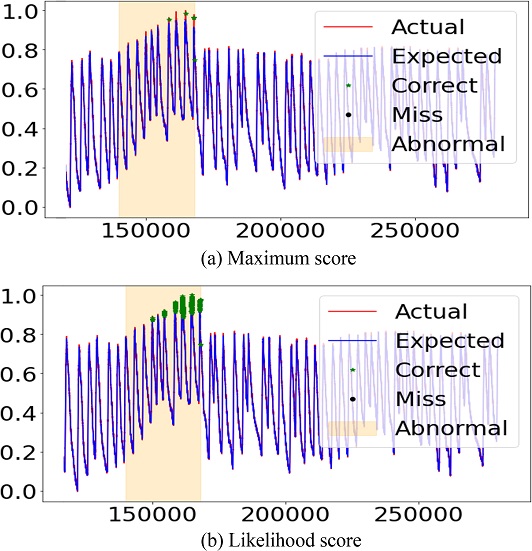
Fig. 6은 대표적으로 Oil Temperature의 Upshift 이상점수를 나타낸다. Fig. 6은 해당 결과가 왜 나올 수 있었는지를 시각적으로 보여준다. Maximum Score의 경우 정상 데이터의 이상점수와 이상 데이터의 이상점수가 잘 구분이 되지 않는다. 하지만 Likelihood Score의 경우 이상 데이터의 이상점수가 정상 데이터의 이상점수보다 훨씬 크게 나타나는 것을 알 수 있다.
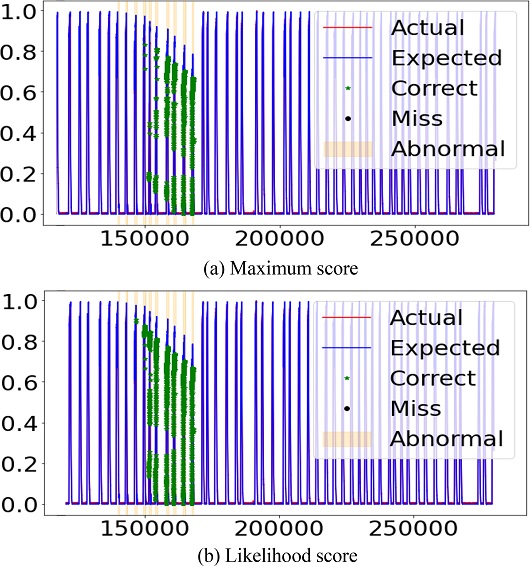
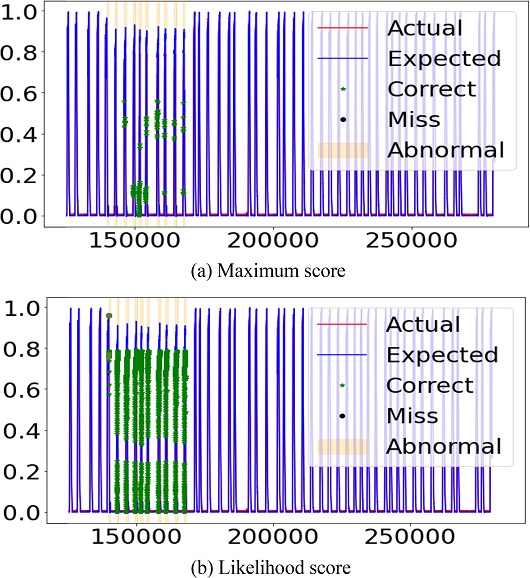
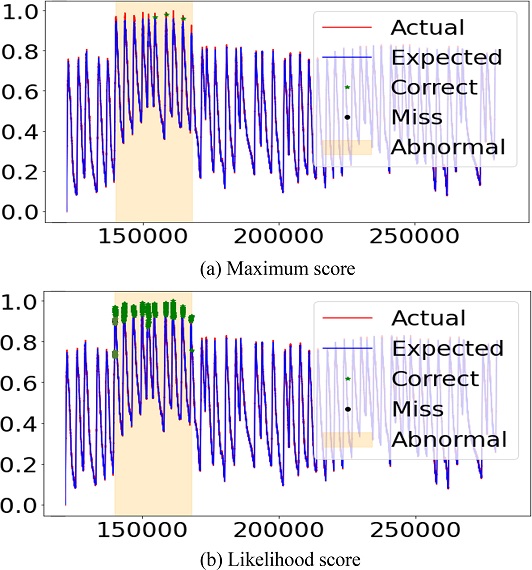
해당 결과는 앞서 언급했던 대로 윈도우 단위로 학습이 이루어지는 모델의 특성상 모델의 모든 은닉 상태 변수를 활용할 수 있는 Likelihood Score 방법이 이상점수를 계산하는 방법으로서 더 적합하다는 것을 증명한다. 다음 Figs. 7부터 10은 모델이 예측한 데이터(파란 실선), 원래 데이터(빨간 실선), 정확히 감지한 이상 데이터(초록색 별점)과 잘못 감지한 정상 데이터(검은색 점)을 보여준다. 해당 Figs. 7부터 10은 Likelihood Score 방식이 더 정확하게 이상 데이터를 감지한다는 것을 보여준다.
5. 결론
본 연구에서는 공기압축기의 다변수 데이터에 대해 딥러닝 모델인 LSTM-AE를 활용하여 이상을 감지하는 방법론에 대해 소개하였다. 이상 데이터가 부재한 상황에서 임의로 이상 데이터를 제작하여 모델을 검증하는 방법을 제시하였으며, 이상점수를 계산하는 기존의 방법론을 개선하여 모델의 모든 은닉 상태 변수를 활용하면서도 윈도우 내부의 모든 요소들의 분포 특성을 고려할 수 있는 방법론을 제시하였다. 동일한 Precision 100%의 조건에서 Recall의 정량적 수치 부분에서 제안하는 방법론이 기존 이상점수 계산 방법론보다 더 좋았으며, 이상 데이터 부분의 이상점수와 정상 데이터 부분의 이상점수를 명확하게 구분하는 것을 보여주었다. 해당 딥러닝 모델은 Precision 100%를 달성하면서도 거의 모든 패턴에서 이상을 감지할 수 있음을 보였다. 이러한 딥러닝 기반의 기계 상태 분석법은 공기압축기뿐만 아니라 여러 기계 장치에서 응용 가능할 것으로 기대된다.
Acknowledgments
이 연구는 서울과학기술대학교 교내 학술연구비 지원으로 수행되었습니다.
REFERENCES
- Shin, J., Jun, H., & Kim, D., (2014). A study on several aspects of condition based maintenance (CBM) approach and introduction of relevant case studies. Entrue Journal of Information Technology, 13(3), 123-138.
-
Baur, M., Albertelli, P., & Monno, M., (2020). A review of prognostics and health management of machine tools. The International Journal of Advanced Manufacturing Technology, 107(5), 2843-2863.
[https://doi.org/10.1007/s00170-020-05202-3]

-
Lee, J., Jin, C., Liu, Z., & Davari Ardakani, H., (2017). Introduction to data-driven methodologies for prognostics and health management. Probabilistic Prognostics and Health Management of Energy Systems, 9-32.
[https://doi.org/10.1007/978-3-319-55852-3_2]

- Chalapathy, R., & Chawla, S., (in press). Deep learning for anomaly detection: A survey. Cornell University, 1901.03407.
- Kim, S. G., Ahn, C, H., Jo, Y. S., & Park, J. H., (2017). Linkage with ICT for maintainability of main air compressor. In the Spring Conference on the Korean Society for Railway, 1175-1179.
-
Alonso, S., Pérez, D., Morán, A., Fuertes, J. J., Díaz, I., et al., (2019). A deep learning approach for fusing sensor data from screw compressors. Sensors, 19(13), 2868.
[https://doi.org/10.3390/s19132868]

-
Gribbestad, M., Hassan, M. U., Hameed, I. A., & Sundli, K., (2021). Health monitoring of air compressors using reconstruction-based deep learning for anomaly detection with increased transparency. Entropy, 23(1), 83.
[https://doi.org/10.3390/e23010083]

-
Kim, K. W., Kang, J., & Park, S. H., (2021). A machine learning-based signal analytics framework for diagnosing the anomalies of centrifugal pumps. Journal of the Korean Society for Precision Engineering, 38(4), 269-277.
[https://doi.org/10.7736/JKSPE.021.002]

-
Zhao, R., Yan, R., Chen, Z., Mao, K., Wang, P., et al., (2019). Deep learning and its applications to machine health monitoring. Mechanical Systems and Signal Processing, 115, 213-237.
[https://doi.org/10.1016/j.ymssp.2018.05.050]

- Malhotra, P., Vig, L., Shroff, G., & Agarwal, P., (2015). Long short term memory networks for anomaly detection in time series. In the 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, 89-94.
- Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., et al., (in press). LSTM-based encoder-decoder for multi-sensor anomaly detection. Cornell University, 1607.00148.
-
Lu, C., Wang, Z.-Y., Qin, W.-L., & Ma, J., (2017). Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Processing, 130, 377-388.
[https://doi.org/10.1016/j.sigpro.2016.07.028]

-
Li, D., Chen, D., Jin, B., Shi, L., Goh, J., et al., (2019). MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In the International Conference on Artificial Neural Networks, 703-716.
[https://doi.org/10.1007/978-3-030-30490-4_56]

-
Niu, Z., Yu, K., & Wu, X., (2020). LSTM-based VAE-GAN for time-series anomaly detection. Sensors, 20(13), 3738.
[https://doi.org/10.3390/s20133738]

-
El-Midany, T. T., El-Baz, M., & Abd-Elwahed, M., (2010). A proposed framework for control chart pattern recognition in multivariate process using artificial neural networks. Expert Systems with Applications, 37(2), 1035-1042.
[https://doi.org/10.1016/j.eswa.2009.05.092]

-
Ünlü, R. (2021). A robust data simulation technique to improve early detection performance of a classifier in control chart pattern recognition systems. Information Sciences, 548, 18-36.
[https://doi.org/10.1016/j.ins.2020.09.059]

-
Egan, W. J., & Morgan, S. L., (1998). Outlier detection in multivariate analytical chemical data. Analytical Chemistry, 70(11), 2372-2379.
[https://doi.org/10.1021/ac970763d]


M.Sc candidate in the Department of Mechanical Design and Robot Engineering, Seoul National University of Science & Technology. His research interest is automotive ICT engineering, PHM, AI.
E-mail: kmk8692@naver.com

Research Engineer in Smart system team, Hyundai Rotem Co., Ltd.. His research interest is railway vehicle engineering.
E-mail: yohwan@hyundai-rotem.co.kr

Associate Professor in the Department of Mechanical Systems Design Engineering, Seoul National University of Science & Technology. His research interests are analysis of dynamic control systems and application of machine learning.
E-mail: chibum@seoultech.ac.kr