GTN 모델을 이용한 Hastelloy-X의 성형성 예측을 위한 수치해석 및 실험적 파손 기준 연구

1. 서론

초내열합금은 700^oC 이상의 고온에서도 기계적 강도가 높고 크립(Creep) 저항성이 우수한 금속을 말한다. 그 중 Hastelloy-X는 니켈 기반의 합금으로 내열성, 내부식성, 내산화성이 우수하여 화학공정에서의 레토르트(Retort), 머플(Muffle), 그리드(Grid) 등에 사용되고 있으며, 가공성 및 고온 강도가 우수하여 고온에서 높은 강도를 필요로 하는 애프터버너(After Burner), 배기관(Duct), 연소기 캔(Combustor Can) 등 가스터빈 엔진의 연소기 분야 및 우주 산업에서 널리 쓰여지고 있다.

가스터빈 엔진의 연소기 부품은 형태가 복잡하고 드로우(Draw) 깊이가 깊은 편이라 성형에 어려움을 겪는 편이다. 이러한 난성형성 제품은 성형 과정에서 소재의 찢어짐 등으로 인하여 고가의 소재가 낭비되는 경우가 많으며, 이를 줄이기 위해 추가 열처리 등을 통하여 공정 최적화가 이루어지고 있다.

판재 성형공정은 공정 방법이나 절차에 따라 품질과 생산성이 좌우되므로 판재의 성형성을 사전에 확인하는 것이 중요하다. 일반적으로 판재의 성형성은 성형한계도를 통하여 예측할 수 있다. 시험을 통한 성형한계도는 비교적 많은 시간이 소요되며, 별도의 시험장비가 필요하다. 또한, 시험으로 얻은 성형한계도는 성형 이력과 변형 경로에 따라 달라지는 단점이 있다. 따라서 이러한 문제를 해결하기 위해 여러 연구가 진행되고 있다. 성형한계를 결정하기 위한 대체 모델로 GTN (Gurson-Tvergaard-Needleman) 모델이 널리 사용되고 있다.

본 연구에서는 GTN 모델을 이용하여 Hastelloy-X의 파손 기준을 제시하고자 하였다. 우선, 이를 위하여 인장시험을 이용하여 Hastelloy-X의 기계적 특성을 파악하고, RSM (Response Surface Methodology)을 통하여 최적화된 GTN 모델의 매개변수 값을 도출하였다. 도출된 GTN 모델 매개변수를 활용하여 GTN 모델 기반의 FLD를 획득하였으며, 이를 시험 기반의 FLD와 비교하였다.

2. GTN 모델

2.1 GTN 모델

Mcclitoc는 재료의 연성파괴가 재료 내부에 존재하는 공극의 성장에 의해 발생한다고 하였다. Rice와 Tracey는 이를 발전시켜 고체 내부에 구형의 단일 공극이 존재하는 것으로 가정하여 재료의 연성파괴를 기술하였다. Gurson은 재료 내부에 연속적인 공극의 분포를 가정하여 파괴과정을 기술하였다[1-3].

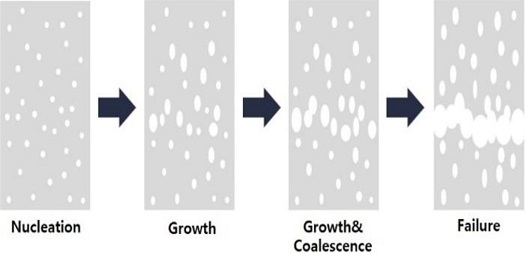
GTN 모델은 연성재료의 파괴를 기술하기 위한 수학적인 모델로 Gurson에 의해 제안되었다. 연성재료를 일종의 다공질로 기술하며, 재료의 손상 진화 과정을 Fig. 1과 같이 공극의 생성(Nucleation), 공극의 성장(Growth), 공극의 융합(Coalescence) 등으로 분류하고 있다. Gurson 모델은 고전적인 소성이론과는 달리 von Mises 항복이론에 정수압의 영향을 고려하여 항복함수를 제안하였다. Tvergaard와 Needleman은 Gurson 모델이 공극의 성장에 따른 재료의 파손을 제대로 반영하지 못하는 것으로 평가하여, 공극체적률을 유효공극체적률로 대체하였으며 다음 식(1)과 같은 항복함수를 제안하였다[4,5].

$\[ \mathrm{\Phi }={\left(\frac{{\sigma }_V}{{\sigma }_Y}\right)}^{21}+2q_1{f}^{\text{*}}\cosh \left(\frac{3}{2}{q}_2\frac{{\sigma }_H}{{\sigma }_Y}\right)-\left(1+q_3{f}^{\text{*}2}\right) \]$

(1)

Fig. 1

Schematic diagram of ductile damage process

σ_V는 von Mises 등가응력, σ_H 는 정수압응력, σ_Y 는 항복응력, q₁, q₂, q₃ 는 재료상수이다. 공극의 융합을 고려하기 위해 유효공극체적률 f* = f*(f)을 다음 식(2)와 같이 고려한다.

$\[ f^{\text{*}}=\left\{\begin{array}{ccc}f& for& f\le f_c\\ f_c+\frac{f_f^{\text{*}}-f_c}{f_f-f_c}\left(f-f_c\right)& for& f>f_c\end{array}\right. \]$

(2)

식(2)는 공극의 융합에 따른 파손을 설명하는 식으로, f_c 는 임계공극체적률, f_f는 파단공극체적률을 말한다. 여기서 식(1)에 따라 $$ f_u^{\text{*}}=f^{\text{*}}\left(f_f\right)=1/q_1$$ 일 때 응력전달 능력이 사라져 파단이 발생하게 된다. 공극체적률은 공극의 성장 속도와 공극의 생성 속도의 합으로 나타나며, 식(3)과 같이 제시하였다.

$\[ \dot{f}={\dot{f}}_{growth}+{\dot{f}}_{nucleation} \]$

(3)

공극의 성장 속도와 공극의 생성 속도는 각각 식(4)와 식(5)와 같이 나타낼 수 있으며, 공극의 생성 속도는 정규분포를 따르는 것으로 가정하였다.

$\[ {\dot{f}}_{growth}=\left(1-f\right){\dot{\epsilon }}_{kk}^p \]$

(4)

$\[ {\dot{f}}_{nucleation}=\frac{f_n}{s_n\sqrt{2\pi }}\exp \left[-\frac{1}{2}{\left(\frac{{\overline{\epsilon }}_m^{pl}-{\epsilon }_n}{s_n}\right)}^2\right]\cdot {\dot{\overline{\epsilon }}}^p \]$

(5)

식(5)에서 $$ {\dot{\overline{\epsilon }}}^p$$은 등가소성변형률속도, ε_n은 정규분포를 갖는 공극 생성 변형률의 평균값, s_n은 공극 생성 변형률의 표준편차, $$ {\overline{\epsilon }}_m^{pl}$$는 등가소성변형률이다.

GTN 모델을 활용하기 위해서는 9개의 매개변수의 값을 결정해야한다. 본 연구에서는 재료상수의 값을 q₁ =1.5, q₂ = 1.0, q₃ = q₁²의 값으로 설정하였으며[6], ε_n, s_n 의 값을 각각 0.3, 0.1로 설정하였다[7-9]. 이 값들은 연성재료의 파손을 설명하는데 일반적으로 사용하는 값들이다. 나머지 4개의 값(f₀, f_n, f_c, f_f)은 공극체적률에 해당하는 값으로 RSM과 유한요소해석을 통해 결정하였다.

3. RSM

3.1 Tensile Test

Fig. 2는 Hastelloy-X 인장시편(t1.2)을 나타낸 것으로 ASTM E08-M [10]에 따라 제작하였다. 일반적인 기계적 특성과 인장시험 결과는 Table 1과 Fig. 3에 나타내었다. 인장 시뮬레이션은 Fig. 2의 오른쪽 그림과 같이 모델링하여 상용해석 프로그램인 ABAQUS를 이용하였으며, 실제 시험 데이터를 참고하여 진행하였다. 모델링된 시편의 요소는 C3D8R(3차원 8절점 감차 적분 요소)로 모델링하였으며, 가장 작은 요소의 길이는 0.25 mm로 설정하였다.

Fig. 2

Test specimen and its simulation model (t1.2)

Table 1

Mechanical properties of Hastelloy-X sheet

Fig. 3

Responses from load-displacement curve

인장시험은 1 mm/min의 속도로 수행되었으며, 인장시험의 시편은 ASTM E08-M [10]을 따라 제작되었다. 인장시험을 통해 4개의 응답이 결정되었으며, 이는 Fig. 3에 제시되어 있다.

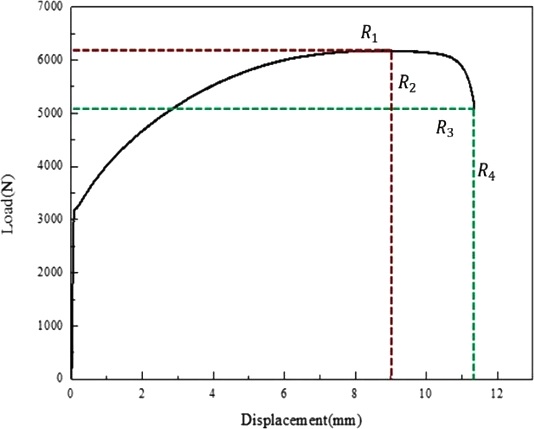
2 수준에서 4개의 요인(f₀, f_n, f_c, f_f)을 결정하기 위해 RSM-CCD를 사용하였으며 이에 따라 서로 다른 매개변수의 조합이 생성되었다. 각 매개변수의 조합을 유한요소해석에 적용하여 인장시험의 시뮬레이션을 진행하였다. 각 시뮬레이션에서 4개의 응답(Max Load (R₁), Max Load에서의 변형량(R₂), 파손 시의 Load (R₃), 파손 시의 변형량(R₄))이 도출되었다[11-13].

3.2 RSM

본 연구에서 GTN 모델의 4개의 독립변수를 구하기 위해 중심합성계획법(Central Composite Design, CCD)을 활용하였다. 중심합성계획법은 반응표면분석법의 실험계획법의 일종으로 요인배치법의 단점을 보완하기 위해 중심점과 축점을 요인실험에 추가시킨 실험계획법이다. 기본적으로 요인이 5 수준을 가지며 중심합성계획법을 사용하면 2차 회귀모형에서 제곱항의 계수를 추정할 수 있어 2차 반응 곡면을 효율적으로 추정할 수 있다. 중심점은 Miloud [8]의 연구를 참고하여 설정하였으며, RSM-CCD에 따라 31개의 인장 시험 시뮬레이션이 수행되었고, 각 시뮬레이션에서 얻은 응답은 Table 2에 나타내었다.

$\[ Y\cong a_0+\sum _{i=1}^4{a}_i{x}_i+\sum _{i,j=1}^4{a}_{ij}{x}_i{x}_j \]$

(6)

Table 2

RSM-CCD arrangement and responses

식(6)은 독립변수와 종속변수 간의 관계를 2차식으로 표현한 것으로 4개의 독립변수에 대한 회귀모형을 나타낸다. 식(6)에서 Y는 응답변수 (R)로 독립변수(GTN 모델의 매개변수)에 따라 변하는 값이다. a는 각항의 계수(선형, 제곱, 교호작용항), x는 독립변수를 나타낸다.

도출된 2차 회귀 모델의 통계적 유의성을 평가하기 위해 ANOVA 분석을 실시하였다. 응답 변수에 대한 각 변수의 영향과 선형 및 교호작용의 중요성을 판단하였다.

4. Determination of GTN Model Parameters

4.1 Regression Model

31가지 조합에 대한 반응값(R₁, R₂, R₂, R₄)들을 Table 2에 나타내었다. ANOVA 분석의 결과는 Tables 3과 4와 같다. P-value는 모델의 적합성을 나타내며 P-value가 0.1 이상인 경우 값이 유효하지 않다고 가정하였다. 유효하지 않은 항들을 제거해 나가며 최종적으로 2차 회귀 모델을 도출하였다.

$\[ R_1=\mathrm{6,778}-\mathrm{58,893}\cdot f_0-\mathrm{17,699}\cdot f_n+\mathrm{81,604}\cdot f_n{f}_n \]$

(7)

$\[ R_2=10.832-62.24\cdot f_n-111.5\cdot f_c+226.1\cdot f_n{f}_n-\mathrm{1,356}\cdot f_c{f}_c \]$

(8)

$\[ R_3=\mathrm{5,380}+\mathrm{268,731}\cdot f_0+850f_f-\mathrm{1,731,854}\cdot f_0{f}_f \]$

(9)

$\[ \begin{array}{c}{R}_4=11.380-74.48\cdot f_n+114.6f_c\cdot \\ +0.932f_0+274.6\cdot f_n{f}_n-\mathrm{1,293}\cdot f_c{f}_c\end{array} \]$

(10)

Table 3

ANOVA of the responses

Table 4

Calculated regression coefficient for responses

4.2 Optimization GTN Model Parameters

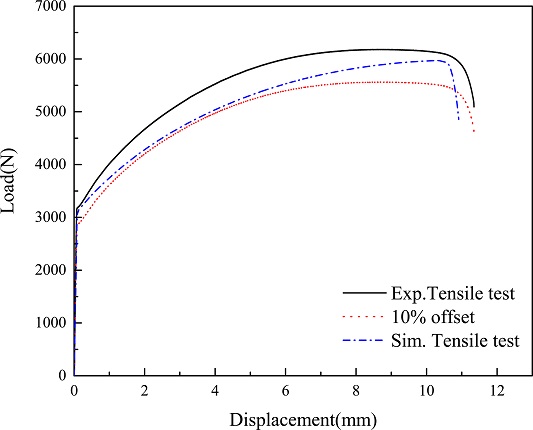
식(7)부터 식(10)에 제안된 2차 다항식을 사용하여, 회귀 모델의 해가 Fig. 3에 제시된 목표값(R)에 근사하도록 GTN 모델에 대한 최적 매개변수를 도출하였다. 회귀 모델을 통한 결과가 실제 시험과 90% 이상 일치하는 경우 활용이 가능한 것으로 볼 수 있기 때문에[12], Fig. 4와 같이 10% Offset한 그래프를 통해 나타내었다. 시뮬레이션의 결과가 Offset한 범위 내로 들어오며 Table 6과 같이 파단 시점에서는 값의 차이가 5% 이내로 나타나므로 도출된 GTN 모델의 매개변수가 적합하다고 판단하였다. Fig. 4와 같이 시뮬레이션 Load-Displacement Curve가 시험적 Load-Displacement Curve와 유사하게 나타난다.

Fig. 4

Comparison of experimental and GTN model-based load-displacement curve

Table 5

Optimized values of the GTN parameters

Table 6

Comparison of tensile test results at fracture

4.3 FLD

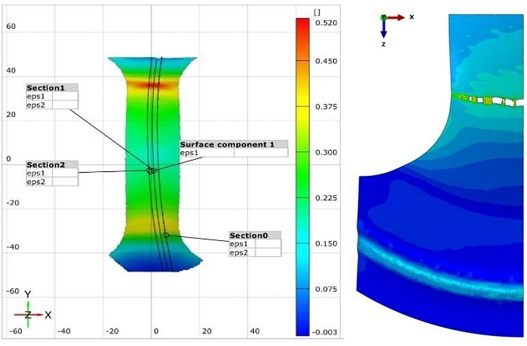
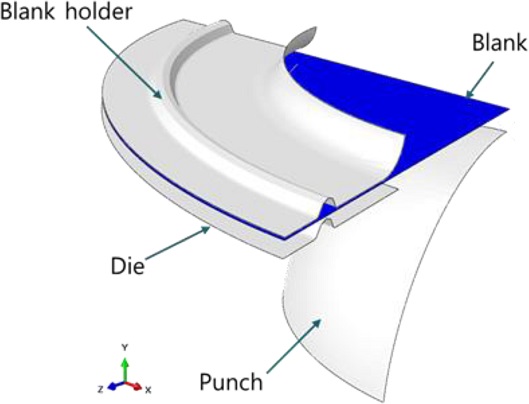
Hastelloy-X의 실험적 FLD를 작성하기 위하여 Fig. 5와 같이 폭이 25, 50, 75, 100, 125, 150, 200 mm인 총 7가지의 시편을 제작하였다. FLD 시험에서 시편의 변형률을 측정하기 위해서 시편에 불규칙적인 패턴을 칠하였다. 시험을 위해 사용한 장비는 R&B사의 200 ton 판재성형 시험기로 다이, 블랭크 홀더, 펀치로 구성되어 있다. 시험은 ISO/WD 12004 규정[14]을 참고하여 진행하였으며, 시험 시편에서 거시적으로 확인이 가능한 파단이 발생할 때까지 시험이 수행되었다. 시험 과정에서의 모든 변형 과정은 광학 측정 시스템인 Aramis를 통해 측정하였다. Aramis를 통해 측정된 결과를 바탕으로 세로축을 Major Strain, 가로축을 Minor Strain으로 하여 결정된다. Fig. 6은 Aramis를 통하여 얻은 시편의 변형률 분포도 중 하나이다.

Fig. 5

Shape of FLD test specimen

Fig. 6

One of Aramis results of FLD test

한편, GTN 모델 기반의 FLD를 얻기 위한 시뮬레이션을 수행하기 위하여 Fig. 7과 같이 시뮬레이션 모델을 모델링하였다. 블랭크 홀더와, 다이, 펀치는 Rigid Body로 간주하였고, 블랭크는 Deformable Body로 모델링하였다. 가장 작은 요소의 길이는 0.5 mm로 설정하였다. 윤활유를 칠한 금속 사이의 마찰계수는 일반적으로 0.05-0.1로 알려져 있으며, 본 연구에서는 0.1로 가정하였다.

Fig. 7

Simulation model of FLD test

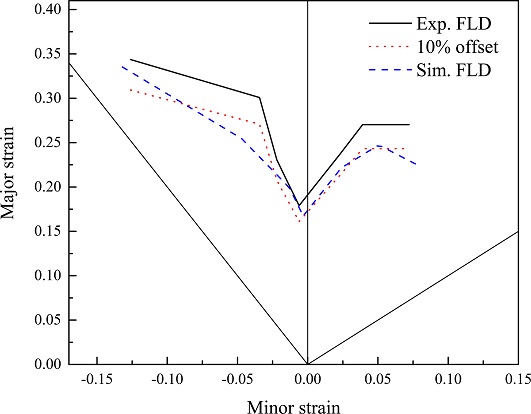
Fig. 8은 실험 기반 FLD와 GTN 모델 기반 FLD를 함께 나타내었다. 실제 FLD 시험에서 파손 부위는 시편의 상태와 실험자의 숙련도 등 외부요인에 따라 달라질 수 있다. 따라서 보다 안전한 평가를 위해 Major Strain을 10% 정도 낮춘 FLD를 사용하는 경우도 있다[15,16]. 앞선 인장시험과 같이 10% Offset한 FLD를 함께 나타내었으며, 시뮬레이션 FLD의 결과가 유사하게 나타나므로 도출한 GTN 모델의 매개변수가 적절하게 도출된 것으로 볼 수 있다.

Fig. 8

Comparison of experimental and GTN model-based FLD

5. 결론

본 연구에서는 Hastelloy-X의 성형성 예측을 위한 파손 기준을 마련하고자 하였다. 먼저 인장시험을 수행하여 Hastelloy-X의 Load-Displacement 데이터를 얻었다. RSM-CCD를 통해 시뮬레이션에 적용할 31개의 GTN 모델 매개변수의 조합들을 얻었으며, 그에 따른 응답을 시뮬레이션을 통해 구하였다. 이를 바탕으로 매개변수와 응답에 관한 회귀모형의 방정식을 도출하였다. 목표로 하는 응답(R₁, R₂, R₃, R₄)을 인장시험 데이터를 통해 설정하였고, 구해진 회귀모형의 방정식을 목표값에 대해 최적화시켜 GTN 모델의 최적 매개변수(Table 5)를 도출하였다. 도출된 GTN 모델의 매개변수를 인장시험 시뮬레이션에 적용하여 실제 시험의 결과와 비교하였다. 10% Offset한 Load-Displacement Curve를 그려 시뮬레이션 결과가 그 사이에 있을 경우에 GTN 모델의 매개변수가 적합한 것으로 가정하였으며, 그 결과 도출된 GTN 모델이 적합한 것으로 판단하였다. 이를 활용하여 GTN 모델 기반 FLD를 모사하여 실제 FLD 시험과 비교하였으며, 2개의 FLD가 유사하다고 판단하였다. 그러므로 도출된 매개변수는 Hastelloy-X 소재의 FLD를 모사하는데 적절한 것으로 보이며, 동일한 소재를 사용하는 판재성형공정에 적용하여 파손 여부를 미리 예측하는데 유용할 것으로 보인다. 또한, 이를 활용하여 형상을 수정하거나 열처리 등 추가적인 공정을 통하여 시간과 비용을 절약할 수 있다.

Acknowledgments

이 연구는 2021년도 산업통상자원부 및 한국산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(No. 20013208). 또한 2021년도 정부(과학기술정보통신)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2019R1A5A6099595). 이에 관계자 여러분께 감사드립니다.

REFERENCES

• Rice, J. R., & Tracey, D. M., (1969). On the ductile enlargement of voids in triaxial stress fields?. Journal of the Mechanics and Physics of Solids, 17(3), 201-217. [https://doi.org/10.1016/0022-5096(69)90033-7]
• Gurson, A. L. (1977). Continuum theory of ductile rupture by void nucleation and growth: Part I-Yield criteria and flow rules for porous ductile media. Journal of Engineering Materials and Technology, 99(1), 2-15. [https://doi.org/10.1115/1.3443401]
• Acharyya, S., & Dhar, S., (2008). A complete GTN model for prediction of ductile failure of pipe. Journal of Materials Science, 43(6), 1897-1909. [https://doi.org/10.1007/s10853-007-2369-0]
• Tvergaard, V., & Needleman, A., (1984). Analysis of the cup-cone fracture in a round tensile bar. Acta Metallurgica, 32(1), 157-169. [https://doi.org/10.1016/0001-6160(84)90213-X]
• Chu, C., & Needleman, A., (1980). Void nucleation effects in biaxially stretched sheets. Journal of Engineering Material and Technology, 102(3), 249-256. [https://doi.org/10.1115/1.3224807]
• Tvergaard, V. (1981). Influence of voids on shear band instabilities under plane strain conditions. International Journal of fracture, 17(4), 389-407. [https://doi.org/10.1007/BF00036191]
• Rahimidehgolan, F., Majzoobi, G., Alinejad, F., & Fathi Sola, J., (2017). Determination of the constants of GTN damage model using experiment, polynomial regression and kriging methods. Applied Sciences, 7(11), 1179. [https://doi.org/10.3390/app7111179]
• Miloud, M. H., Zidane, I., & Mendas, M., (2019). Coupled identification of the hardening behavior laws and Gurson-Tvergaard-Needleman damage parameters-validation on tear test of 12NiCr6 CT specimen. Frattura ed Integrità Strutturale, 13(49), 630-642. [https://doi.org/10.3221/IGF-ESIS.49.57]
• Springmann, M., & Kuna, M., (2006). Determination of ductile damage parameters by local deformation fields: Measurement and simulation. Archive of Applied Mechanics, 75(10), 775-797. [https://doi.org/10.1007/s00419-006-0033-9]
• ASTM E8/E8M-16A. (2020). Standard test methods for tension testing of metallic materials.
• Abbasi, M., Shafaat, M. A., Ketabchi, M., Haghshenas, D. F., & Abbasi, M., (2012). Application of the GTN model to predict the forming limit diagram of IF-Steel. Journal of Mechanical science and Technology, 26(2), 345-352. [https://doi.org/10.1007/s12206-011-1038-z]
• Abbasi, M., Ketabchi, M., Izadkhah, H., Fatmehsaria, D., & Aghbash, A., (2011). Identification of GTN model parameters by application of response surface methodology. Procedia Engineering, 10, 415-420. [https://doi.org/10.1016/j.proeng.2011.04.070]
• Ying, L., Liu, W., Wang, D., & Hu, P., (2017). Parameter calibration of GTN damage model and formability analysis of 22MnB5 in hot forming process. Journal of Materials Engineering and Performance, 26(11), 5155-5165. [https://doi.org/10.1007/s11665-017-2962-6]
• ISO 12004:1997. (2008). Metallic materials-Guidelines for the determination of forming limit diagrams.
• Hosford, W. F., & Caddell, R. M., (2011). Metal forming: Mechanics and metallurgy. Cambridge University Press. [https://doi.org/10.1017/CBO9780511976940]
• Paul, S. K. (2013). Theoretical analysis of strain-and stress-based forming limit diagrams. The Journal of Strain Analysis for Engineering Design, 48(3), 177-188. [https://doi.org/10.1177/0309324712468524]