관성센서 기반 상대위치 추정 시 연조직 변형 보상을 위한 인공신경망 적용
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Relative position estimation between body segments is one essential process for inertial sensor-based human motion analysis. Conventionally, the relative position was calculated through a constant segment to joint (S2J) vector and the orientation of the segment, assuming that the segment was rigid. However, the S2J vector is deformed by soft tissue artifact (STA) of the segment. In a previous study, in order to handle the above problem, Lee and Lee proposed the relative position estimation method using time-varying S2J vectors based on inertial sensor signals. Here, time-varying S2J vectors were determined through the joint flexion angle using regression. However, it was not appropriate to consider only the flexion angle as a deformation-related variable. In addition, regression has limitations in considering complex joint motion. This paper proposed artificial neural network models to compensate for the STA by considering all three-axis motion of the joint. A verification test was conducted for lower body segments. Experimental results showed that the proposed method was superior to the previous method. For pelvis-to-foot relative position estimation, averaged root mean squared error of the previous method was 17.38 mm, while that of the proposed method was 12.71 mm.
Keywords:
Segment-to-joint vector, Wearable inertial sensor, Relative position, Artificial neural network, Lower body segment키워드:
분절-관절 벡터, 착용형 관성센서, 상대위치, 인공신경망, 하지 분절1. 서론
최근 건강관리에 대한 사회적 관심이 증가하면서 헬스케어, 피트니스 그리고 재활 산업과 같은 분야의 시장 규모가 크게 증가하고 있다. 따라서, 공간의 제약 없이 실시간으로 신체활동 및 건강상태를 분석할 수 있는 착용형 센서의 활용성이 부각되고 있다. 그 중 착용형 관성센서(Inertial Sensor)는 신체 분절에 부착되어 신체의 움직임을 실시간으로 추정, 분석할 수 있어 많은 연구의 대상이 되고 있다[1-4]. 이때 신체 분절간 3차원 상대위치는 관성센서를 기반으로 신체를 모델링하거나 신체의 움직임을 분석하는데 있어서 필수적으로 요구되는 물리량 중 하나이다[5-8].
관성센서를 기반으로 분절간 상대위치를 실시간으로 추정하는 가장 기본적인 방법은 각 신체 분절이 강체이며, 구형 관절(Spherical Joint)로 연결되어있다는 가정으로, 분절부착좌표계의 원점에서 관절 중심까지의 벡터(Segment-to-Joint 벡터, 이하 S2J 벡터)를 미리 상수로 결정한 후 각 분절에 부착된 관성센서 신호를 통해 실시간으로 구한 분절의 자세 정보와 결합하여 분절간 상대위치를 추정하는 방법이다. 즉, 이와 같은 방법으로 추정된 분절 상대위치는 오직 추정된 분절의 자세에 따라 결정된다[9-11].
하지만 실제 신체 분절은 지방, 근육 그리고 피부와 같은 연조직으로 이루어져 있어 신체의 움직임에 따라 변형되는 비강체이다. 또한 관절은 인대에 의해 움직임이 제한되며 관절 중심이 고정되어 있지 않기 때문에 완벽한 구형 관절이 아니다[12,13]. 따라서 실제 S2J 벡터는 상수가 아닌 분절의 피부 그리고 지방 등의 연조직 변형(Soft Tissue Atrifacts, STA)에 의해 영향을 받아 변형되는 변수라 할 수 있다. 이와 같은 이유로 기존 관성센서 기반 상대위치 추정 방법에서 이러한 분절의 STA를 고려하지 않는 것은 분절 상대위치의 부정확한 추정으로 이어진다.
동작분석에서의 STA에 대한 연구는 광학식 모션캡처 시스템에서 주로 진행되어 왔다. STA는 신체에 부착된 마커와 강체로 가정되는 분절내 골조간 상대적 움직임을 발생시켜 광학식 모션 캡처를 통한 신체 모델링 또는 관절각 측정에 있어 오차를 증가시킨다. 이러한 문제를 해결하기 위해 STA로 인한 마커의 상대적 움직임을 분절 운동과 관계없는 노이즈로 처리하는 방법[14], 그리고 여러 동작에서 STA의 패턴을 통해 상대적 움직임을 보상하는 방법[15,16]으로 마커와 강체로 가정되는 분절내 골조간 상대적 움직임을 최소화시키고자 하는 연구가 진행되었다. 하지만 관성센서 기반 모션캡처 시스템에서는 STA에 대한 연구가 매우 드물게 진행되었다.
이창준과 이정근은 관성센서 기반 분절 상대위치 추정에서 신체 분절의 STA를 보상하여 추정 정확도를 향상시키는 방법을 제안하였다[17]. 여기서, S2J 벡터는 고정된 상수로 결정되는 것이 아닌 움직임에 따라 변하는 변수로 설정되어 상대위치를 추정한다. S2J 벡터는 인접한 관절의 움직임에 영향을 받아 변형된다는 가정으로 S2J 벡터와 인접한 관절의 각도에 따른 시변(Time-Varying) 벡터로 결정되었다. 이때 관절의 세 축(굴절/신전, 내전/외전, 내회전/외회전) 중 관절의 굴절각을 변형 관련 변수로 선정하였으며, 회귀법을 통해 S2J 벡터를 굴절각에 대한 함수로 시변화하였다. 예를 들어 허벅지 분절에서 무릎 관절까지의 S2J 벡터는 무릎의 굴절각에 따라 결정되며, 허벅지 분절에서 고관절까지의 S2J 벡터는 고관절의 굴절각에 따라 결정된다. 이 방법을 통해 S2J 벡터를 상수로 설정하는 기존 방법과 비교하여 상체 분절 상대위치 추정 오차를 51% 감소시켰다.
하지만 고관절, 어깨, 그리고 발목과 같은 관절은 복잡한 움직임을 갖는 다자유도 관절이므로 굴절각만을 변형 관련 변수로 선정하는 것은 적절하지 않다. 반면, 일반적인 회귀분석은 입력변수와 출력변수 간의 관계를 예측하여 적합한 모델을 직접 선정해야 한다. 따라서 모든 관절각을 입력변수로 하여 회귀함수를 도출하는 것은 그래프를 통해 확인할 수 없는 S2J 벡터와 관절각 간의 다차원 비선형관계를 알맞게 도출할 수 있는 적절한 회귀 모델(다항 회귀, 지수 회귀, 비선형 회귀 등)을 선정하기 위해 시행착오법을 통해 선정해야 하므로 많은 어려움이 따른다. 본 연구는 STA를 보다 효과적으로 보상하기 위해 모든 관절각을 S2J 벡터의 변형 관련 변수로 선정하되, 변수 간의 비선형적 관계를 학습을 통해 스스로 도출하는 인공신경망(Artificial Neural Network)을 통해 비선형 회귀 모델을 구성하여 S2J 벡터를 시변화하는 방법을 제안한다. 여기서, S2J 벡터를 시변화하는 근본적인 이유는 분절의 STA를 고려함으로써 분절간 상대위치 추정의 정확도를 향상시키기 위함이다. 즉, 본 연구에서 최종적으로 추정하고자 하는 물리량은 분절의 상대위치이다. 따라서, 관절각을 통해 분절 상대위치를 직접적으로 결정하는 인공신경망 모델을 추가적으로 구성하였다.
본 논문은 관성센서 기반의 상대위치 추정 시 STA의 보상을 위한 인공신경망 적용을 제안한다. 이때 인공신경망은 두 가지로 적용되었다. 1) S2J 벡터를 관절각에 따라 학습시켜 시변화하므로써 간접적으로 상대위치 추정 정확도를 향상시키는 방법 그리고 2) 상대위치를 관절각에 따라 학습시켜 직접적으로 상대 위치 추정 정확도를 향상시키는 방법. 제안 방법들은 기존 관절 각만을 변형 관련 변수로 설정한 방법 그리고 세 관절각을 모두 변형 관련 변수로 사용하지만 회귀법을 통해 S2J 벡터를 시변화하여 상대위치를 추정하는 방법과 성능을 비교 분석한다. 검증을 위해 하지 분절인 골반, 허벅지, 종아리, 그리고 발 분절을 대상으로 검증 실험을 진행하였다.
2. 방법
2.1 신체 분절 상대위치 결정
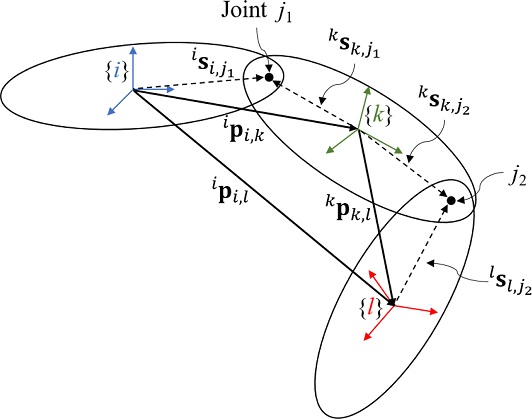
제안되는 인공신경망은 신체 골반에서 발까지의 분절 상대위치를 추정한다. 인접한 두 분절간 상대위치는 다음 식(1)과 같이 결정할 수 있다(Fig. 1 참조).
| (1) |
여기서 윗첨자 i 그리고 k는 해당 벡터가 각 분절의 분절부착좌표계에서 관찰되었음을 의미한다. ipi,k는 i분절에서 k분절까지의 상대위치 벡터, isi,j1와 ksk,j1는 각각 i와 k분절에서 두 분절 사이에 존재하는 관절 j1까지의 S2J 벡터, 는 k분절의 자세를 i분절에서 바라보는 상대자세행렬이다. 관성센서는 위치정보를 제공하지 않기 때문에 S2J 벡터는 미리 상수로 결정되며, 각 분절의 자세는 분절에 부착된 관성센서의 신호를 사용하여 자세 추정 알고리즘을 통해 실시간으로 추정된다[18-21]. k 분절을 공통된 인접 분절로 갖는 두 분절 i 그리고 l의 상대위치 ipi,l는 다음 식(2)와 같이 결정된다.
| (2) |
여기서 kpk,l은 k 분절에서 l 분절까지의 상대위치 벡터로, 각각 분절 k와 l에서 관절 j2까지의 S2J 벡터 ksk,j2, lsl,j2 그리고 k와 l의 상대자세행렬 을 활용하여 식(1)과 동일하게 결정할 수 있다. 이와 같이 식(1)과 식(2)를 활용해 다수의 관절로 이루어진 신체 분절간 상대위치를 전파하여 결정할 수 있다. 하지만이 방법을 통해 분절의 상대위치를 결정하는 것은 각 분절과 관절이 각각 강체와 기계식 관절로 이루어져 있다는 가정을 기반으로 한다. 즉, S2J 벡터의 변형이 없다고 가정하여 상수로 미리 결정된다. 하지만 실제 S2J 벡터는 분절의 피부, 지방 그리고 근육과 같은 연조직에 의해 영향을 받아 불가피하게 변형된다.
선행 연구에서는 이러한 분절의 STA를 고려하기 위해 굴절각을 S2J 벡터의 변형 관련 변수로 설정하였으며, 회귀법을 통해 굴절각에 따라 S2J 벡터를 시변화하는 함수를 도출하였다. 본 논문에서는 굴절각만을 S2J 벡터의 변형 관련 변수로 사용한 기존 방법과 달리 관절의 세 축 모두를 변형 관련 변수로 사용한다. 또한 관절각에 변화에 따른 S2J 벡터를 보다 정밀하게 고려하기 위해 회귀법이 아닌 인공신경망 모델을 구성하여 학습시킨다. S2J 벡터를 시변화하는 근본적인 이유는 STA와 연관이 있는 특정한 변수로 STA를 보상하여 상대위치를 정확히 추정하기 위함이다. 따라서 변형 관련 변수인 관절각에 따라 S2J 벡터를 시변화하는 모델이 아닌 분절 상대위치를 직접적으로 결정하는 모델을 추가적으로 구성하여 학습시킨다.
2.2 데이터 처리
모델 학습단계에서 필요한 데이터는 하지 관절의 참조 관절각, 참조 S2J 벡터 그리고 분절간 참조 상대위치 데이터이다. 하지 관절의 참조 관절각은 광학식 모션캡처 시스템으로 획득된 센서의 참조자세를 통해 결정된다. 참조 S2J 벡터의 경우 실제 관절 중심부의 계측은 어렵기 때문에 S2J 벡터의 참값을 획득하는데는 한계점이 있다. 본 연구의 목적은 분절의 STA를 보상하여 상대위치 추정 정확도를 향상시키는 것이므로 참조 상대위치와 미리 결정된 상수 S2J 벡터를 활용하여, 참조 상대위치를 만족하는 S2J 벡터를 참조 S2J 벡터로 사용하였다. 참조 상대위치를 만족하는 S2J 벡터 는 다음 식(3)과 식(4)와 같이 결정할 수 있다[17].
| (3) |
| (4) |
여기서 p와 d는 관절 j를 기준으로 각각 신체 중심부(Proximal)에 가까운 분절 그리고 말단부(Distal)에 가까운 분절이다. 예를들어 무릎관절의 경우 중심부 분절은 허벅지이며 말단부 분절은 종아리이다. 는 상수로 결정된 S2J 벡터, 는 참조 상대자세, 는 참조 상대위치 벡터 그리고 μ는 각 참조 S2J 벡터의 비율을 결정하는 가중치로 0과 1 사이의 값이다. 상수 S2J 벡터 는 광학식 모션캡처 시스템을 사용하는 최적화 기법[22]을 통해 결정하였다.
각 모델은 참조값을 통해 학습된 후 검증단계에서 관성센서를 통해 추정된 관절각과 상대자세를 사용하여 상대위치를 추정한다. 관절각과 상대자세를 실시간으로 추정하기 위해 자세추정 칼만 필터 알고리즘[18]을 사용하였다.
2.3 인공신경망 모델
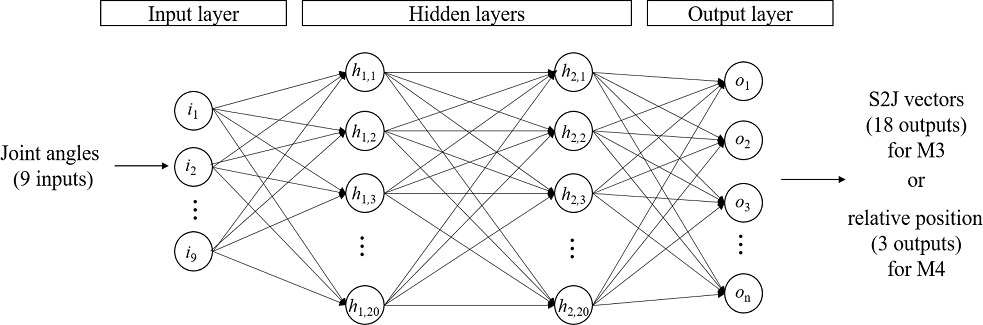
S2J 벡터를 시변으로 결정하기 위한 인공신경망 모델의 구조는 다음과 같다(Fig. 2 참조). 모델은 2개 이상의 은닉층(Hidden Layer)을 갖는 심층신경망(Deep Neural Network)에 해당한다. 첫 번째 층은 입력층으로, 입력층의 각 노드(Node)는 독립변수로 구성된다. 독립변수는 각 하지 관절(발목, 무릎, 고관절)의 3축 관절각이므로 입력층 노드의 총 개수는 9개이다. 두 번째와 세 번째 층은 은닉층이다. 은닉층은 모델 학습 과정을 통해 각 노드의 가중치가 갱신되는 층으로 각 은닉층은 20개의 노드로 구성된다. 마지막으로 네 번째 층은 출력층으로 구성된다. 출력층의 각 노드는 하지 관절의 관절각을 통해 결정되는 Foot-to-Ankle에서부터 Pelvis-to-Hip까지 총 6개, S2J 벡터의 x, y, 그리고 z축 성분으로 총 18개의 노드로 구성된다.
상대위치를 직접적으로 결정하는 인공신경망 모델의 구조는 다음과 같다. 입력층과 은닉층은 S2J 벡터를 시변으로 결정하기 위한 모델과 같다. 다만 이 모델의 경우 상대위치를 직접적으로 결정하므로, 출력층은 최종적으로 추정하고자 하는 골반에서 발까지의 상대위치 벡터의 x, y 그리고 z축 성분으로 총 3개의 노드로 구성된다.
각 은닉층 노드의 출력신호는 노드에 입력되는 입력신호를 각각의 가중치와 곱하여 더해진 후 활성화 함수를 통과해 다음 층으로 전달된다. 본 연구에서는 활성화 함수로 인공신경망에서 가장 널리 쓰이는 함수 중 하나인 ReLU 함수를 사용하였다[23].
| (5) |
여기서 f는 ReLU 활성화 함수이며, x는 노드에 입력되는 입력신호와 노드의 가중치가 곱해진 후 편향값과 더해진 결과값으로 다음 식(6)과 같다.
| (6) |
여기서 ip(p = 1, 2, , m)는 이전 층에서 전달되는 입력신호, wp 는 각 입력신호에 대응되는 가중치, b는 노드의 편향값 그리고 m은 이전 층 입력신호의 총 개수를 의미한다.
인공신경망은 역전파(Backpropagation)를 통해 손실함수를 최소화하는 방향으로 각 노드의 가중치를 갱신하여 학습된다. 본 모델 학습에 사용된 손실함수는 평균제곱오차(Mean Squared Error, MSE)로 다음 식(7)과 같다.
| (7) |
여기서, yi는 참조값이며, 는 모델을 통해 예측된 값이다. 모델 학습을 위한 최적화 함수는 모멘텀 경사하강법(Gradient Descent with Momentum)과 평균제곱근전파(Root Mean Square Propagation, RMSProp)를 동시에 사용하는 학습법 Adam을 사용하였다[24]. 학습 안정성을 향상시키고, 스케일과 관련된 입력 데이터의 편향성을 제거하기 위해 입력 데이터는 모두 0의 평균과 1의 표준편차를 갖도록 표준화하였다[25]. 또한 과적합을 방지하고 학습시간을 최소화하기 위해 설정된 에폭(Epoch) 동안 학습을 통해 검증 데이터의 손실이 더 이상 낮아지지 않으면 학습을 사전에 종료하는 Early Stopping 알고리즘을 사용하였다. 인공신경망 모델은 텐서플로우(Tensorflow, v. 2.6.0) 그리고 케라스(Keras, v. 2.6.0)를 사용해 구글 코랩(Google Colab) 환경에서 설계 및 구현되었다.
3. 결과
3.1 실험
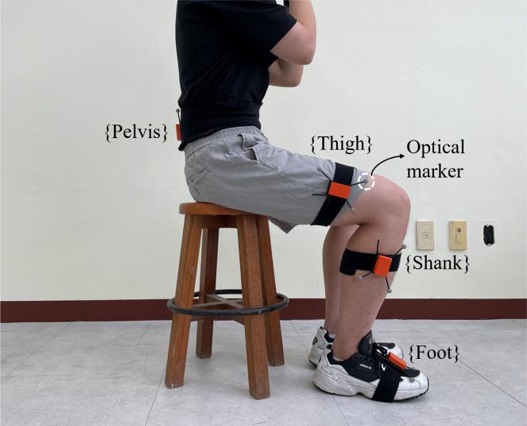
실험은 3명의 건강한 성인 남성 피실험자(나이: 27±0.5세, 키: 177±5.2 cm)를 대상으로 진행하였다. 학습 및 검증에 필요한 데이터를 얻기 위해 3축 가속도계, 3축 자이로스코프 그리고 3축 지자기 센서로 이루어진 관성센서 모듈 Mtw (Xsens Technologies B. V., Netherlands)를 사용하였다. 각 관성센서는 분절의 자세를 실시간으로 추정하기 위해 벨크로를 이용하여 발, 종아리, 허벅지 그리고 골반에 부착되었다(Fig. 3 참조). 또한 학습에 필요한 참조값을 얻기 위해 광학식 모션캡처 시스템인 Optitrack Flex 13(Natural Point, USA)을 사용하여 각 분절 간의 참조 상대위치와 센서의 참조자세를 획득하였다.
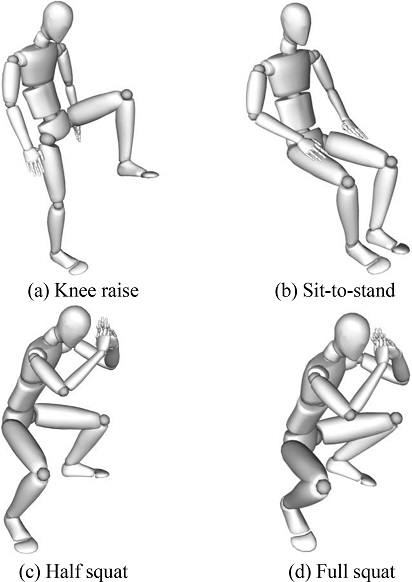
하지 분절 S2J 벡터의 변형을 다양한 하지 관절의 움직임에서 고려하기 위해 실험은 하지 분절의 S2J 벡터를 충분히 변형시킬 수 있는 네 가지 특정 동작을 반복하여 진행하였다. 각각의 실험 동작은 다음과 같다(Fig. 4 참조).
- Test 1: 제자리에서 무릎 들어올리기(Fig. 4(a))
- Test 2: 의자에서 앉았다 일어나기(Fig. 4(b))
- Test 3: 하프스쿼트(Fig. 4(c))
- Test 4: 풀스쿼트(Fig. 4(d))
각 실험은 5번씩 약 2분간 수행되었다. 데이터는 100 Hz로 샘플링되어 수집되었다. 피험자별로 각 실험의 첫 번째 시행 데이터는 인공신경망 모델의 학습과 회귀법을 통한 회귀 모델을 만들기 위해 학습 데이터로 사용되었다. 인공신경망 모델 학습을 위해 학습 데이터의 20%는 검증용 데이터로 사용하였다. 학습과 검증을 위한 데이터를 제외한 나머지 데이터는 모델의 성능 평가를 위해 활용하였다. 실험 대상자마다 센서를 부착한 위치와 분절의 길이 등이 다르기 때문에 관절각에 따른 S2J 벡터가 다르다. 따라서, 인공신경망 모델과 회귀 모델은 실험 대상자마다 개별적으로 생성되었다.
본 논문에서 제안하는 인공신경망 모델을 통한 상대위치 추정 성능을 검증하기 위해 네 가지의 추정 방법을 비교 분석하였다. 첫 번째 방법(M1)은 S2J 벡터의 변형 관련 변수로 관절의 굴절각을 사용하여 회귀법을 통해 S2J 벡터를 시변화한 방법이며, 두 번째 방법(M2)는 관절의 세 관절각을 모두 사용하여 회귀법을 통해 S2J 벡터를 시변화한 방법이며, 세 번째 방법(M3)과 네 번째 방법(M4)은 본 논문의 제안 방법으로 인공신경망 모델을 통해 S2J 벡터를 시변화한 방법 그리고 인공신경망 모델을 통해 상대위치를 직접적으로 결정하는 방법이다. 데이터를 기반으로 변수간 상관관계를 도출하기 위해 M1과 M2는 각각 커널(Kernel) 회귀와 다항(Polynomial) 회귀를 이용하였다. 네 방법 모두 학습단계에서 참조자세를 통해 계산되는 관절각을 입력변수로 사용하지만, 평가단계에서는 관성센서를 통해 실시간으로 추정된 관절각을 사용하였다. 따라서 각 방법은 실시간으로 상대위치를 추정하였다. 상대위치를 직접적으로 추정하는 M4를 제외한 다른 방법들은 식(1)과 식(2)를 통해 상대위치를 추정하기 위해 관성센서로 추정된 자세를 사용한다. 각 방법의 분절 상대위치 추정 정확도는 평균제곱근오차(Root Mean Squared Error, RMSE)를 통해 비교한다. 또한, 식(5)에서 참조 S2J 벡터의 비율을 결정하는 μ는 0.5로 설정하였다.
3.2 결과 및 고찰
Table 1은 실험에 참가한 3명의 피실험자(Subjects 1-3) 각각에 대해 Tests 1부터 4까지의 각 방법별 분절간 상대위치 추정 평균 RMSE를 보여준다. 각 실험의 RMSE는 학습데이터를 제외한 4개의 시행 데이터에 대한 평균 RMSE이다. M4의 경우 골반에서 발까지의 상대위치를 직접적으로 추정하기 때문에 부분적인 인접 분절간 상대위치에 대한 추정 결과에서는 제외되었다.
굴절각만을 고려하여 회귀법을 통해 S2J 벡터를 시변화하는 M1은 3명의 피실험자에 대해 골반에서 발까지의 상대위치 추정 평균 RMSE가 17.38 mm로 상대적으로 가장 큰 오차 수준을 나타냈다. 반면 세 관절각을 고려한 M2, M3 그리고 M4의 평균 RMSE는 각각 15.45, 12.71 그리고 14.11 mm로 M1보다 상대적으로 우세한 성능을 보였다. 따라서 S2J 벡터를 시변화함에 있어 대부분의 경우 굴절각만을 고려하는 것보다 세 관절각을 모두 고려하는 것이 STA를 적절히 보상하여 정확한 상대위치 추정을 할 수 있었다. 하지만, 허벅지에서 종아리까지의 상대위치 추정에서는 M1의 추정 정확도가 M2와 비슷하거나 더 우수한 경우가 다수 존재하였다. 허벅지에서 종아리까지의 상대위치는 무릎관절에 인접한 두 S2J 벡터를 통해 결정된다. 이때 무릎관절은 세 축 회전에 대한 움직임이 상대적으로 자유로운 발목, 고관절과 달리 굴절 축에 대한 움직임이 지배적이므로 다른 두 축을 제외한 굴절각에 밀접한 영향을 받는다. 따라서 회귀법을 통해 세 축의 관절각을 모두 고려하여 S2J 벡터를 시변화한 M2보다 굴절각만을 고려한 M1이 더 좋은 상대위치 추정 정확도를 보여주는 경우가 존재하였다.
관절각의 세 축을 모두 고려하는 방법 M2, M3 그리고 M4를 비교한다. 대부분의 분절 상대위치 추정 정확도에서 인공신경망 모델을 통해 S2J 벡터를 시변화하는 M3가 가장 우세한 성능을 보였다. 그리고 인공신경망을 통해 상대위치를 직접 추정하는 M4의 성능이 다음으로 좋았으며 M2는 관절각의 세 축을 변형 관련 변수로 사용한 방법 중 분절 상대위치 추정 정확도가 대부분의 결과에서 가장 떨어졌다. 따라서 세 관절각에 따라 S2J 벡터를 시변화 벡터로 결정하는 인공신경망 모델이 회귀법을 활용하는 방법 그리고 상대위치를 직접적으로 결정하는 인공신경망 모델보다 분절의 STA를 잘 고려하여 분절 상대위치를 잘 추정함을 확인하였다.
실험 동작별 추정 정확도를 비교한다. 제안 방법 M3을 기준으로 각 실험별 골반에서 발까지 추정 RMSE는 각각 16.3, 12.4, 11.1 그리고 11.13 mm이다. 따라서 하프스쿼트 동작에서 추정 성능이 가장 뛰어났으며, 제자리에서 무릎을 들어 올리는 동작에서 추정 성능이 가장 떨어졌다. 하프스쿼트의 경우 상대적으로 동작이 작아 STA로 인한 S2J 벡터의 변형이 심하지 않다. 반면, 무릎을 들어올리는 동작은 발이 고정되어 있는 세 동작들과 달리 발을 움직이기 때문에 동작이 상대적으로 크고, 관절각의 움직임 범위가 크다. 따라서 STA에 따른 S2J 벡터의 변형이 가장 크게 일어나 추정 성능이 떨어졌다. 반면에 풀스쿼트 동작인 Test 4보다 의자에서 앉았다 일어나는 동작인 Test 2 가 관절각의 움직임 범위가 상대적으로 작음에도 불구하고 추정 성능이 더 떨어지는 것으로 나타났다. 이는 의자에 앉아있는 경우 허벅지 분절의 연조직이 의자에 눌려, STA로 인한 S2J 벡터의 변형이 크게 일어나 생기는 현상이다.
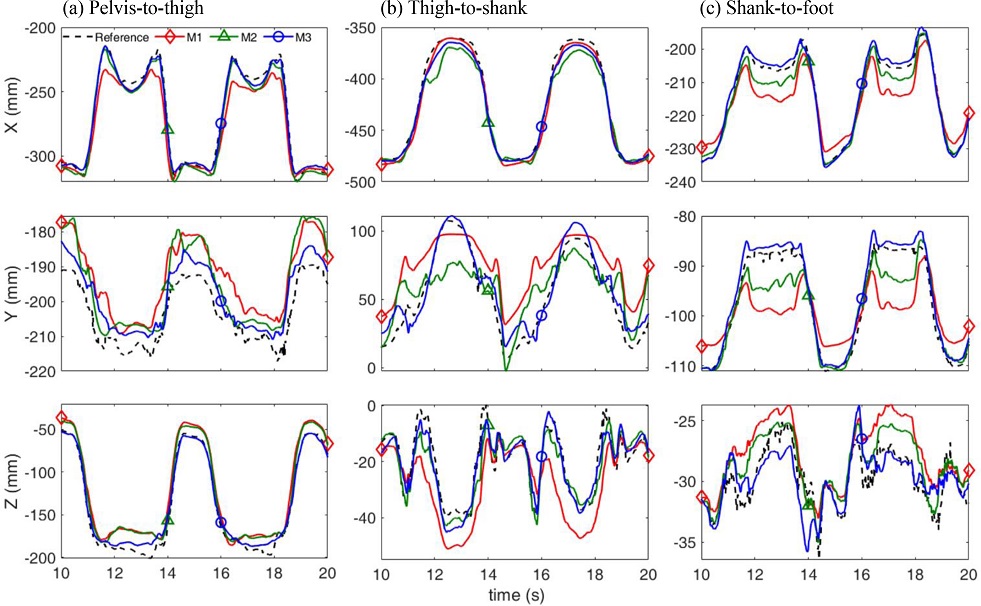
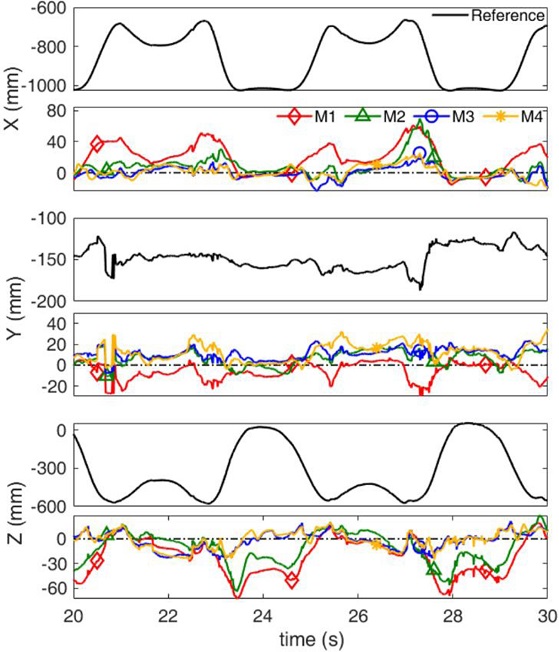
Fig. 5는 실험 대상자 2의 Test 2에서, 각 방법별 인접한 분절간 상대위치 추정 결과의 일부를 발췌한 그래프이다. 그림에서 볼 수 있다시피, 각 인접 분절 상대위치의 대부분의 축에서 M3가 참조 궤적에 가장 근접하였으며, M1은 추정 성능이 가장 낮음에 따라 참조 궤적에서도 가장 크게 벗어났다. M2의 경우 세 관절각을 모두 고려함에 따라 M1보다 좋은 성능을 보였지만, 대부분의 축에서 STA를 적절히 보상하지 못하여 참조값을 잘 추종하지 못하였다. Fig. 6은 동일 실험 대상자의 실험에 대하여 분절간 상대위치를 전파시켜 최종적으로 추정하는 골반에서 발까지의 참조 상대위치와 각 방법별 상대위치 추정 오차의 일부를 발췌한 그래프이다. 인접 분절간 상대위치 추정 결과와 마찬가지로 M1의 추정 오차가 가장 큰 것을 확인할 수 있었으며, M3의 추정 오차가 가장 0에 가까운 것을 확인하였다. 또한, M2는 x축 그리고 z축에서 M3에 비해 추정 오차가 크게 증가하였다. 상대위치를 직접적으로 결정하는 M4의 경우 M3와 비슷한 성능을 보여주었다.
골반에서 발까지의 상대위치를 추정하는 경우 관절각을 통해 상대위치를 직접적으로 구하는 인공신경망 모델 M4의 추정 정확도가 S2J 벡터 시변화를 통해 상대위치를 결정하는 인공신경망 모델 M3보다 상대적으로 낮은 이유는 다음과 같이 추정된다. M4의 경우 모델을 학습시킬 때 각 시간스텝의 참조 관절각과 그때의 참조 상대위치를 통해 학습시킨다. 하지만 상대위치의 경우 하나의 상대위치(Output)를 도출하는 하나 이상의 관절각(Input) 조합이 존재한다. 예를 들어 스쿼트 동작 시 같은 깊이로 앉아 스쿼트를 하더라도(즉, 골반에서 발까지의 상대위치가 같음) 허벅지 각도를 좁게 또는 넓게 유지하느냐에 따라 각 하지 관절의 각도가 달라질 수 있다. 따라서, 하나의 종속변수에 하나 이상의 독립변수가 존재하기 때문에 학습에 어려움을 야기시킨다. 관절각을 통해 S2J 벡터를 학습하는 M3의 경우 각 S2J 벡터에 영향을 크게 미치는 관절이 존재한다. 예를 들어 허벅지에서 무릎까지의 S2J 벡터는 무릎 각도에 큰 영향을 받으며 고관절 각도에는 상대적으로 작은 영향을 받고 발목 관절에는 전혀 영향을 받지 않을 것이다. 이와 같이 학습을 통해 각 S2J 벡터마다 관절각에 대한 가중치가 다르게 설정되기 때문에 관절의 움직임에 따른 S2J 벡터의 변화를 정밀히 고려할 수 있다.
4. 결론
본 논문은 관성센서 기반 하지 분절의 상대위치 추정에서 분절의 STA를 보상하기 위해 심층 인공신경망을 활용하는 방법을 제안하였다. 관절의 관절의 굴절/신전, 내전/외전 그리고 내회전/외회전 세 축 각도를 입력신호로 S2J 벡터를 시변화하는 모델(M3) 그리고 M3와 동일한 입력신호로 상대위치를 직접적으로 추정하는 모델(M4)을 통해 분절의 STA를 보상하였다. 제안된 모델은 참조 관절각과 참조 상대위치를 통해 학습된 후 관성센서를 통해 추정된 관절각과 분절 자세를 통해 실시간으로 상대위치를 추정할 수 있다. 제안된 방법을 검증하기 위해 하지 분절인 골반, 허벅지, 종아리 그리고 발 분절을 대상으로 검증 실험을 진행하였다. S2J 벡터를 시변화함에 있어 굴절각만을 변형 관련 변수로 설정하여 인공신경망이 아닌 일반적인 회귀법을 사용한 기존 방법(M1) 그리고 세 관절각을 모두 고려하였지만, M1과 같이 일반적인 회귀법을 사용하여 S2J 벡터를 시변화한 방법(M2)과 비교 분석하였다.
실험 결과 M1, M2, M3 그리고 M4의 골반에서 발까지의 상대위치 추정 평균 RMSE는 각각 17.38, 15.45, 12.71 그리고 14.11 mm로 제안 방법 M3의 추정 오차가 M1 그리고 M2의 오차보다 각각 27 그리고 18% 감소를 보이는 등 분절의 STA로 인한 S2J 벡터의 변형을 잘 보상하였다. 또한, 3.2절 결과 및 고찰에서 설명한 이유로 인하여 분절 상대위치를 직접적으로 결정하는 모델 M4는 S2J 벡터를 시변화하여 상대위치를 간접적으로 개선시킨 M3보다 낮은 추정 성능을 보였다.
Acknowledgments
본 연구는 2018년도 정부(교육부)의 재원으로 한국연구재단 기초연구사업(No. NRF-2018R1D1A1B07042791)의 지원을 받아 수행됨.
REFERENCES
-
Varkey, J. P., Pompili, D., & Walls, T. A., (2012). Human motion recognition using a wireless sensor-based wearable system. Personal and Ubiquitous Computing, 16(7), 897-910.
[https://doi.org/10.1007/s00779-011-0455-4]

-
Jeon, T. H., & Lee, J. K., (2018). IMU-based joint angle estimation under various walking and running conditions. Journal of the Korean Society for Precision Engineering, 35(12), 1199-1204.
[https://doi.org/10.7736/KSPE.2018.35.12.1199]

-
Cooper, G., Sheret, I., McMillian, L., Siliverdis, K., Sha, N., et al., (2009). Inertial sensor-based knee flexion/extension angle estimation. Journal of Biomechanics, 42(16), 2678-2685.
[https://doi.org/10.1016/j.jbiomech.2009.08.004]

-
Lee, J. K., Desmoulin, G. T., Khan, A. H., & Park, E. J., (2011). Comparison of 3D spinal motions during stair-climbing between individuals with and without low back pain. Gait & Posture, 34(2), 222-226.
[https://doi.org/10.1016/j.gaitpost.2011.05.002]

-
Jung, Y., Kang, D., & Kim, J., (2010). Upper body motion tracking with inertial sensors. In the IEEE International Conference on Robotics and Biomimetics, 1746-1751.
[https://doi.org/10.1109/ROBIO.2010.5723595]

-
Kok, M., Hol, J. D., & Schön, T. B., (2014). An optimization-based approach to human body motion capture using inertial sensors. IFAC Proceedings Volumes, 47(3), 79-85.
[https://doi.org/10.3182/20140824-6-ZA-1003.02252]

-
Bai, L., Pepper, M. G., Yan, Y., Spurgeon, S. K., Sakel, M., et al., (2014). Quantitative assessment of upper limb motion in neurorehabilitation utilizing inertial sensors. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 23(2), 232-243.
[https://doi.org/10.1109/TNSRE.2014.2369740]

-
Karatsidis, A., Bellusci, G., Schepers, H. M., De Zee, M., Andersen, M. S., et al., (2017). Estimation of ground reaction forces and moments during gait using only inertial motion capture. Sensors, 17(1), 75.
[https://doi.org/10.3390/s17010075]

-
Seel, T., Schauer, T., & Raisch, J., (2012). Joint axis and position estimation from inertial measurement data by exploiting kinematic constraints. In the IEEE International Conference on Control Applications, 45-49.
[https://doi.org/10.1109/CCA.2012.6402423]

-
Faber, G. S., Kingma, I., & van Dieën, J. H., (2010). Bottom-up estimation of joint moments during manual lifting using orientation sensors instead of position sensors. Journal of Biomechanics, 43(7), 1432-1436.
[https://doi.org/10.1016/j.jbiomech.2010.01.019]

-
Crabolu, M., Pani, D., Raffo, L., Conti, M., Crivelli, P., et al., (2017). In vivo estimation of the shoulder joint center of rotation using magneto-inertial sensors: MRI-based accuracy and repeatability assessment. Biomedical Engineering Online, 16(1), 1-18.
[https://doi.org/10.1186/s12938-017-0324-0]

-
Leardini, A., Chiari, L., Della Croce, U., & Cappozzo, A., (2005). Human movement analysis using stereophotogrammetry: Part 3. Soft tissue artifact assessment and compensation. Gait & Posture, 21(2), 212-225.
[https://doi.org/10.1016/j.gaitpost.2004.05.002]

-
van den Bogert, A. J., Reinschmidt, C., & Lundberg, A., (2008). Helical axes of skeletal knee joint motion during running. Journal of Biomechanics, 41(8), 1632-1638.
[https://doi.org/10.1016/j.jbiomech.2008.03.018]

-
Alexander, E. J., & Andriacchi, T. P., (2001). Correcting for deformation in skin-based marker systems. Journal of Biomechanics, 34(3), 355-361.
[https://doi.org/10.1016/S0021-9290(00)00192-5]

-
Cappello, A., Cappozzo, A., La Palombara, P. F., Lucchetti, L., & Leardini, A., (1997). Multiple anatomical landmark calibration for optimal bone pose estimation. Human Movement Science, 16(2-30, 259-274.
[https://doi.org/10.1016/S0167-9457(96)00055-3]

-
Cappello, A., Stagni, R., Fantozzi, S., & Leardini, A., (2005). Soft tissue artifact compensation in knee kinematics by double anatomical landmark calibration: Performance of a novel method during selected motor tasks. IEEE Transactions on Biomedical Engineering, 52(6), 992-998.
[https://doi.org/10.1109/TBME.2005.846728]

-
Lee, C. J., & Lee, J. K., (2021). Inertial sensor-based relative position estimation between upper body segments considering non-rigidity of human bodies. Journal of the Korean Society for Precision Engineering, 38(3), 215-222.
[https://doi.org/10.7736/JKSPE.020.108]

-
Lee, J. K. (2019). A parallel attitude-heading Kalman filter without state-augmentation of model-based disturbance components. IEEE Transactions on Instrumentation and Measurement, 68(7), 2668-2670.
[https://doi.org/10.1109/TIM.2019.2906417]

-
Suh, Y. S. (2010). Orientation estimation using a quaternion-based indirect Kalman filter with adaptive estimation of external acceleration. IEEE Transactions on Instrumentation and Measurement, 59(12), 3296-3305.
[https://doi.org/10.1109/TIM.2010.2047157]

-
Sabatini, A. M. (2006). Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Transactions on Biomedical Engineering, 53(7), 1346-1356.
[https://doi.org/10.1109/TBME.2006.875664]

-
Lee, J. K., & Park, E. J., (2009). Minimum-order Kalman filter with vector selector for accurate estimation of human body orientation. IEEE Transactions on Robotics, 25(5), 1196-1201.
[https://doi.org/10.1109/TRO.2009.2017146]

-
Cameron, J., & Lasenby, J., (2005). A real-time sequential algorithm for human joint localization. In the International Conference on Computer Graphics and Interactive Techniques, 107.
[https://doi.org/10.1145/1186954.1187076]

- Nair, V., & Hinton, G. E., (2010). Rectified linear units improve restricted boltzmann machines. In the International Conference on Machine Learning, 807-814.
- Kingma, D. P., & Ba, J., (in press). Adam: A method for stochastic optimization. 1412.6980.
- Ioffe, S., & Szegedy, C., (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. In the International Conference on Machine Learning, 448-456.

M.Sc. candidate in the School of ICT, Robotics and Mechanical Engineering, Hankyong National University. His research interests include wearable sensing and IMU-based human motion tracking.
E-mail: 2021585203@hknu.ac.kr

Professor in the School of ICT, Robotics and Mechanical Engineering, Hankyong National University. His research interests include inertial sensing-based human motion tracking, biomechatronics, wearable sensor applications, and system dynamics and control.
E-mail: jklee@hknu.ac.kr