6축 로봇의 공구중심점 교정 및 틸팅-로터리 테이블의 기하학적 오차 측정
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Tool-center-point (TCP) calibration and geometric error identification procedures are proposed to improve the accuracy of a 6-axis manipulator with a tilting rotary table. The accuracy of a 6-axis manipulator is affected by the accuracy of TCP calibration. In general, TCP calibration of the 6-axis manipulator uses a conical fixture provided by the manufacturer. However, since a TCP cannot be accurately positioned to the tip of the conical fixture repeatedly, a large positional deviation occurs at the calibration depending on the worker proficiency. Thus, accuracies of TCP calibration and the 6-axis manipulator are reduced. In this paper, a 3-DOF measuring device, consisting of a nest with three dial gauges and a precision ball, is developed to calibrate the TCP and to improve the accuracy of the 6-axis manipulator. Then, geometric errors of a tilting rotary table are identified via double ball-bar measurements according to the ISO 10791-6 with TCP initial alignment using an extension fixture. Finally, proposed TCP calibration and geometric error identification procedures are validated experimentally, and they show improvements in positional accuracy by 55 and 90%, respectively.
Keywords:
Double ball-bar, Geometric error, ISO 10791-6, Tool-center-point, 6-Axis manipulator키워드:
더블 볼바, 기하학적 오차, 국제표준 10791-6, 공구중심점, 6축 로봇1. 서론
6축 로봇은 자동차, 우주·항공 및 선박 등의 산업현장에서 사용하고 있으며, 플랜지(Flange)에 부착되는 공구의 종류에 따라 가공, 용접 및 적층 등 다양한 공정에 적용한다[1,2]. 높은 자유도로 인해 단일 셋업으로 복잡한 곡면이나 부품 작업 시 접근이용이하지만, 일부 위치에서 특이점(Singularity)이 발생하여 제한적이다. 이에 특이점을 회피하는 경로나 공구의 형상 변경 및 부가 회전축을 활용하여 극복한다[3]. 공정에 따라 플랜지에 공구를 부착하는 경우 공구중심점(Tool Center Point, TCP) 교정은 필수이며, 로봇의 정확도는 TCP의 교정 정확도에 영향을 받는다. 제조사는 6축 로봇의 TCP 교정을 위해 원추형 측정치구(Conical Measuring Fixture)를 사용한 방법을 제공하지만, 작업자의 판단을 요구하기에 TCP의 정확한 측정이 어렵고 작업자의 숙련도에 따라 큰 차이를 나타내는 문제가 있다. 비전 카메라(Vision Camera), 레이저 트래커(Laser Tracker), CMM (Coordinate Measuring Machine), 더블 볼바(Double Ball-Bar, DBB) 및 3자 유도 측정시스템 등의 측정장비를 사용한 TCP 교정방법이 개발되었지만[4-7] 복잡한 교정방법과 고가의 장비를 필요로 하여 현장 적용에 한계가 있다. 따라서 6축 로봇의 TCP를 저비용으로 정확하게 파악할 수 있는 교정방법이 필요하다.
틸팅-로터리 테이블이 추가된 6 + 2축 로봇 시스템의 정확도는 TCP 교정 후 회전축의 기하학적 오차를 측정하고 보정하여 개선한다[8]. 기하학적 오차는 이송축 사이의 오차인 위치 독립의 기하학적 오차(Position-Independent Geometric Errors, PIGEs)와 축의 위치에 따라 변하는 위치 종속의 기하학적 오차(Position-Dependent Geometric Errors, PDGEs)로 구분한다[9]. 축 사이의 관계를 나타내는 PIGEs는 작업자의 조립 숙련도에 의해 영향을 받으며, 축 자체의 오차인 PDGEs보다 상대적으로 크다[10]. 회전축의 PIGEs는 2개의 옵셋 오차(Offset Errors)와 2개의 직각도 오차(Squareness Errors)로 정의하며[11-13], ISO 10791-6에 제정된 바와 같이 3축 제어에서 DBB 또는 터치 트리거 프로브(Touch Trigger Probe)를 사용하여 측정한다[14]. 하지만 틸팅축은 일반적으로 큰 PIGEs를 나타내며, ISO 10791-6의 현장 적용 시 TCP의 초기 위치 정렬이 필요하다. 이에 DBB와 연장치구(Extension Fixture)를 사용하여 TCP의 초기 위치를 정렬하고 회전축의 PIGEs를 측정하는 방법이 보고된 바 있다[15].
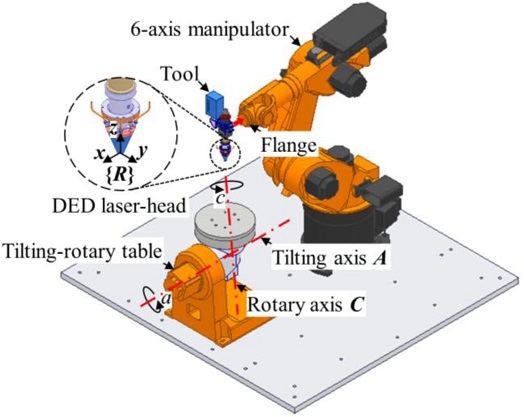
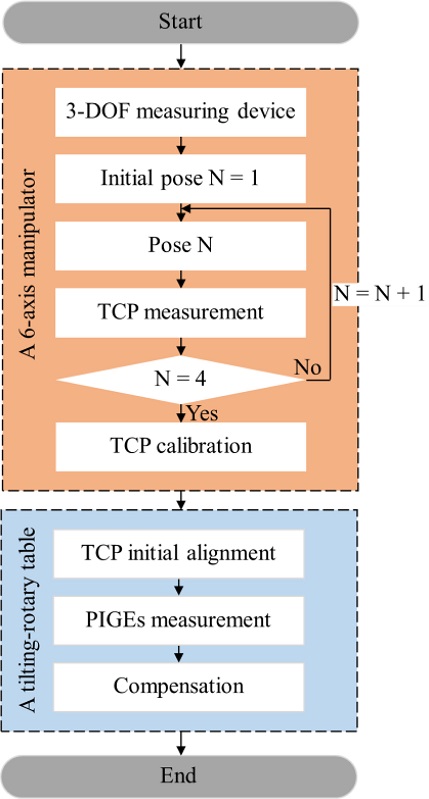
본 논문은 Figs. 1과 같이 6 + 2축 로봇 시스템의 정확도를 개선하기 위하여 3자유도 측정장치(3-DOF Measuring Device)를 사용하여 2의 순서도에 따라 TCP를 정밀 교정한다. 이후 틸팅-로터리 테이블의 기하학적 오차는 5축 공작기계의 정밀 측정 방법을 로봇 시스템에 확장 적용하고 측정 및 보정하여 검증한다[15]. TCP는 3개의 다이얼 게이지와 정밀구로 이루어진 3자 유도 측정장치를 사용하여 정밀 교정하며, 기하학적 오차는 ISO 10791-6의 DBB 방법을 적용하여 측정 및 보정한다. 2장에서는 6축 로봇의 TCP 측정장치를 나타내고, 제조사에서 제공하는 교정방법과 비교 분석하여 제안한 방법의 타당성을 검증한다. 3장에서는 6축 로봇의 틸팅-로터리 테이블의 PIGEs 측정하고 보정하여 6 + 2축 로봇 시스템의 정확도를 개선한다. 본 논문의 요약 및 결론은 4장에 나타낸다.
2. 6축 로봇의 TCP 교정
본 연구에서는 6축 로봇(KR 60HA, KUKA plc., Germany)과 틸팅-로터리 테이블(DKP-400, KUKA plc., Germany)로 구성된 DED (Directed Energy Deposition) 방식의 금속 3D 프린터(MDR-60, Maxrotec Co. Ltd., Republic of Korea)를 사용하며, 장비의 구조와 주요 사양은 각각 Fig. 1 및 Table 1과 같다.
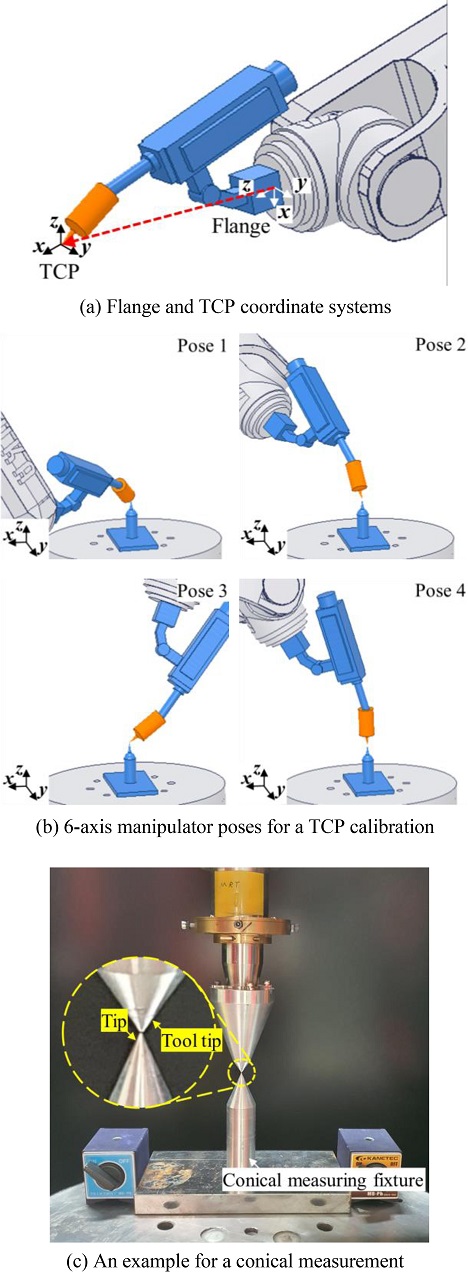
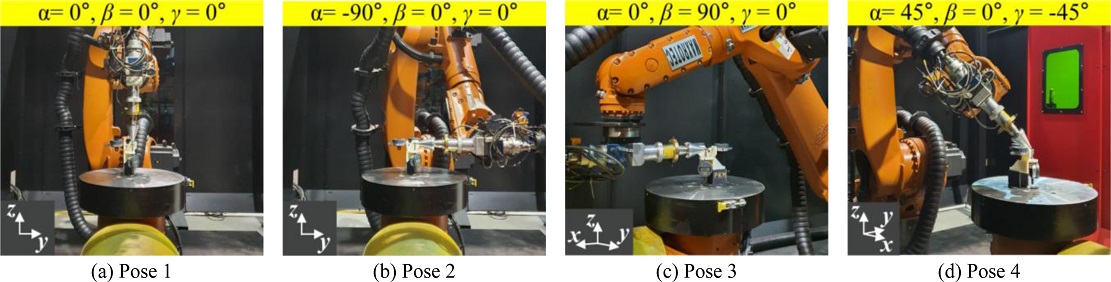
로봇 제조사에서 제공하는 끝단 좌표계(End-Effector Coordinate System)는 Fig. 3(a)와 같이 플랜지에 위치하고 있으며, 공구가 부착된 경우 TCP에 위치한 좌표계를 정확하게 교정해야 한다. 6축 로봇의 정확도는 TCP의 교정 정확도에 영향을 받는다. 제조사에서 제공하는 교정방법은 Fig. 3(b)와 같이 서로 다른 4개의 로봇 자세에서 TCP가 원추형 측정치구의 끝단에 위치하도록 정밀 이송하여 진행한다[16]. 하지만 Fig. 3(c)와 같이 원추형 측정치구를 이용한 TCP 교정은 작업자의 시야에만 의존하여 정확한 TCP의 위치를 파악할 수 없으며, 작업자의 숙련도에 따라 큰 위치 편차를 나타낸다. 따라서 작업자의 숙련도의 영향을 받지 않고, 6축 로봇의 정확도를 크게 개선하기 위한 TCP 교정방법이 필요하다.
2.1 3자유도 측정장치를 이용한 TCP 교정
본 논문에서 개발한 3자유도 측정장치는 Fig. 4와 같이 평면 형태의 측정자(Stylus)가 부착된 3개의 디지털 다이얼 게이지(Digital Dial Gauge)와 고정치구(Nest) 및 정밀구(Precision Ball)로 구성한다. 정밀구는 공구 끝단부에 고정하며, TCP 교정 시 4개의 서로 다른 로봇 자세에서 정밀구의 위치가 일정하도록 디지털 다이얼 게이지의 값을 사용하여 로봇의 위치를 제어한다. 여기서 평면 형태의 측정자는 정밀구의 위치를 직관적으로 정확하게 제어하기 위하여 사용한다.
제안한 6축 로봇의 TCP 교정방법은 Fig. 2의 순서도에 따라 서로 다른 4개의 로봇 자세(N = 1, … , 4)에서 디지털 다이얼 게이지의 값을 작업자가 확인하며 정밀구의 위치가 동일한 위치에 반복 위치하도록 제어하여 진행한다. 측정의 편의를 위해 초기 정밀구의 위치(N = 1)를 기준으로 디지털 다이얼 게이지 값은 ‘0’으로 설정하고 측정한다.
2.2 6축 로봇의 TCP 교정 및 검증
TCP 교정을 위해 제작한 3자유도 측정장치의 고정치구는 FDM (Fused Deposition Modeling) 방식의 3D 프린터(F170, Stratasys plc., USA)를 사용하여 제작하며, 장비 및 사용한 디지털 다이얼 게이지의 주요 성능은 각각 Tables 2와 3과 같다.
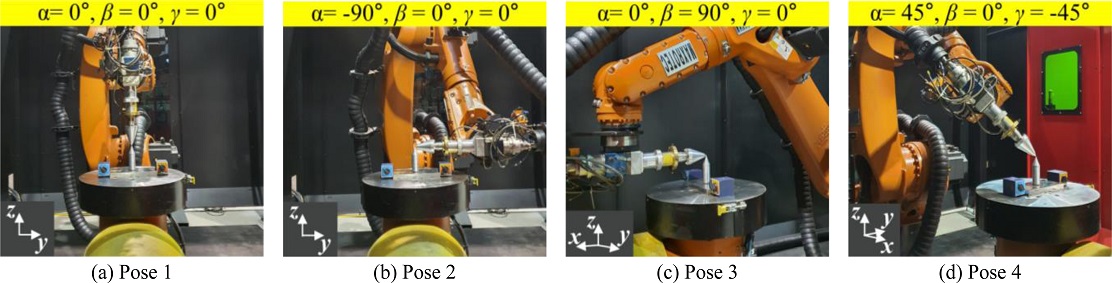
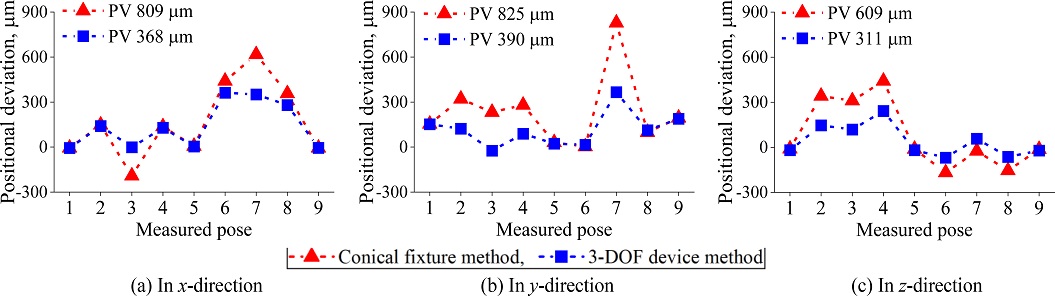
개발한 TCP 교정방법의 타당성은 로봇 제조사에서 제공하는 원추형 측정치구를 이용한 교정방법의 결과와 비교한다. TCP 교정에서 사용한 서로 다른 4개의 로봇 자세는 물리적 간섭이 없는 범위에서 최대한 서로 다른 자세를 가지도록 계획하였으며, 원추형 측정치구와 3자유도 측정장치를 사용하여 TCP를 교정하는 실험은 Figs. 5와 6과 같다. TCP 교정 결과는 Fig. 7과 같이 교정에 사용한 4개의 로봇 자세와는 다른 9개의 새로운 자세를 사용하여 검증한다. 9개의 자세에서 정밀구는 초기 정밀구의 위치(N = 1)에 가도록 지령한 후 정밀구의 x, y, z 방향의 위치 편차를 3자유도 측정장치를 사용하여 측정한다. 측정자세에 따른 정밀구의 위치 편차는 Fig. 8과 같으며, x, y, z 방향 편차의 고저값(Peak-to-Valley, PV)은 원추형 측정치구 교정방법에서는 PV 809, 825, 609 μm를 나타내고 제안한 TCP 교정방법에서는 PV 368, 390, 311 μm를 나타내어 각각 55, 53, 49%의 TCP 위치 편차가 개선된다. 제안한 TCP 교정방법에서 발생한 위치 편차는 실험에 사용한 로봇의 정확도(±160 μm), 정밀도(±50 μm) 및 환경요인에 기인한 것으로 판단한다. 제안한 TCP 교정방법을 적용하면 TCP의 교정 정확도를 크게 개선시킴을 실험적으로 나타낸다.
3. 틸팅-로터리 테이블의 PIGEs 측정 및 보정
3.1 틸팅축 A에서 기하학적 축의 초기 위치 정렬
틸팅-로터리 테이블은 연속 회전이 가능한 회전축 C와 제한된 범위에서 회전이 가능한 틸팅축 A로 구성한다. 따라서 회전축 C의 기하학적 축은 공간상에 위치하고 있어 PIGEs가 작고 측정이용이하지만, 틸팅축 A의 기하학적 축은 기계 내부에 위치하기 때문에 측정이 어렵고 측정 범위가 작아서 큰 값의 PIGEs를 나타낸다. 따라서 ISO 10791-6의 DBB 측정 시 많은 시간과 작업자의 높은 숙련도가 요구되며, 측정비용이 증가하는 문제가 있다. 이러한 문제는 5축 공작기계에서 DBB 연장치구를 사용한 TCP의 초기 위치 정렬방법을 6 + 2축의 로봇 시스템에 적용하여 해결한다[15].
TCP에 대한 틸팅축 A의 초기 위치는 DBB (QC20-W, Renishaw plc., United Kingdom)에서 제공하는 150 mm의 연장치구를 사용하며 정렬하며, 공작물 볼(Workpiece Ball, WB)의 위치는 Fig. 9(a)와 같이 틸팅축 A가 a = 0o 일 때, z 방향으로 h = 476.98 mm의 설계 위치에 설치한다. WB의 위치 편차 ΔRy, ΔRz는 틸팅축 A의 지령값 a = 90o인 경우 DBB 길이 R = 100 mm을 기준으로 Figs. 9(b)와 9(c)와 같이 측정한다. 측정한 위치 편차 ΔRy, ΔRz와 이로부터 계산한 정렬 오차 my, mz는 Table 4와 같다[15,17].
3.2 PIGEs 측정과 보정을 통한 검증
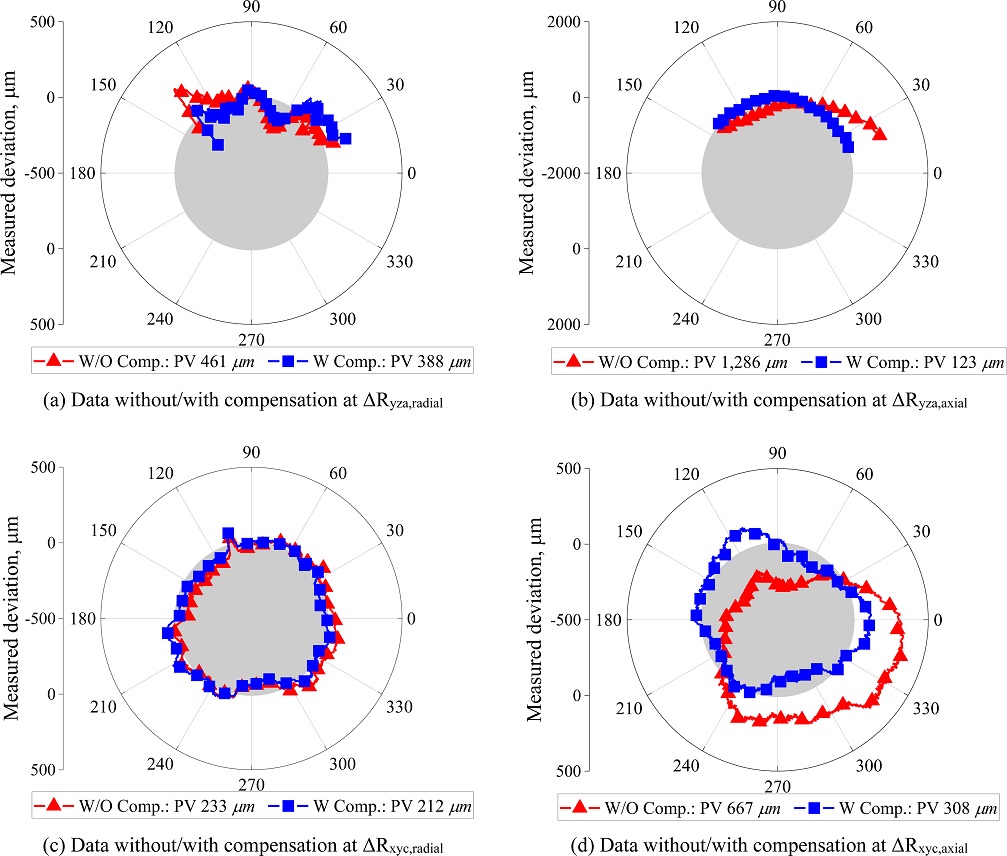
회전축 C와 틸팅축 A의 PIGEs는 Fig. 10과 같이 ISO 10791-6의 규정에 따라 측정하며, 2개의 직선축과 1개의 회전축의 동기제어에서 DBB를 사용하여 원호 경로의 반경 방향 편차(Radial Direction Deviation)와 축 방향 편차(Axial Direction Deviation)를 측정한다[14,18]. 측정데이터는 Fig. 11에 나타낸 바와 같이 큰 편차를 나타내고 있으며, 이는 PIGEs가 큰 값을 나타내기에 측정 및 보정이 필요한 것을 의미한다. 측정데이터와 PIGEs의 선형 관계는 동차변환행렬(Homogeneous Transformation Matrix)을 사용하여 결정하고, PIGEs는 최소자승법(Least Squares Method)을 적용하여 계산하며 Table 5와 같다[19].
측정한 PIGEs의 타당성을 검증하기 위해 Fig. 10의 측정 경로에서 PIGEs를 보정하는 NC-Code를 생성하고 재측정한다. 이러한 경우 틸팅축 A의 축 방향 편차는 보정 전 1,286에서 보정 후 123 μm로 90% 개선된다. 따라서 틸팅축 A의 위치를 정렬하고 PIGEs를 측정하여 보정한다면 6 + 2축 로봇 시스템의 정확도가 크게 개선되는 것을 나타낸다. PIGEs는 DBB 측정데이터에서 편심을 사용하여 계산하기에 6축 로봇의 위치 편차가 큰 영향을 미치지 않으나 보정 후 DBB 측정데이터의 반경 편차(Radial Deviation)에는 큰 영향을 가진다.
4. 결론
본 논문은 6 + 2축의 로봇 시스템 정확도를 개선하기 위해 TCP를 정확하게 교정하는 방법을 나타내고, TCP의 초기 위치를 정렬하여 틸팅-로터리 테이블의 PIGEs를 측정하는 방법을 제안한다. 제안한 방법은 실험 적용하여 6 + 2축 로봇 시스템의 정확도가 크게 개선되는 것을 확인하였으며, 결론은 다음과 같다.
(1) 6축 로봇은 플랜지 좌표계의 정밀 제어가 가능하지만, 공정에 따라 추가적인 공구가 부착되는 경우 TCP를 정확하게 교정하는 방법이 알려진 바 없으며 최종적으로 로봇의 정확도가 저하되는 문제가 있다. 따라서 TCP의 정확한 교정은 서로 다른 4개 로봇 자세에서 TCP를 동일한 위치로 제어하는 것이 필요하며, 본 논문에서 제안한 3자유도 측정장치를 사용하면 작업자가 직관적으로 정확한 교정을 수행하여 로봇 정확도를 개선한다.
(2) 틸팅-로터리 테이블의 정확도는 회전축 C와 틸팅축 A의 PIGEs 오차를 측정하고 S/W 보정하여 개선하는 것이 타당하다. 하지만 틸팅축 A의 PIGEs는 큰 값을 나타내기에 작업자의 높은 숙련도와 상당한 TCP의 초기 정렬 시간이 필요하다. 따라서 DBB 연장치구를 사용하여 TCP를 초기 정렬하고 PIGEs 측정을 진행하면 ISO 10791-6의 적용성을 높이고 보다 신속하게 6 + 2축 로봇 시스템의 정확도를 크게 향상한다.
(3) 산업용 6 + 2 로봇 시스템의 정확도는 TCP를 교정한 후 회전축 및 틸팅축의 PIGEs를 측정 및 보정하여 개선하는 것이 타당하다. 실험의 결과는 TCP를 정확하게 교정하는 경우 최대 55%의 위치 편차가 개선되며, 이후 회전축의 PIGEs를 측정 및 보정하는 경우 틸팅축 A에서 최대 90%의 축 방향 편차가 감소한다.
NOMENCLATURE
| a, c [rad] : | Rotation Angles of Rotary Axes A, C, Respectively |
| h [mm] : | Nominal Offset between Tilting Axis A and a Ball on Workpiece Table in z-Direction |
| R [mm] : | Nominal Length of a Double Ball-Bar |
| mia [mm] : | Initial Alignment Error of a TCP to Tilting Axis A along with the i-Direction, (i = y, z) |
| oij [mm] : | Offset Error of the j-Axis along with the i-Direction, (i = x, y, z; j = a, c) |
| sij [rad] : | Squareness Error of the j-Axis around the i-Direction, (i = x, y, z; j = a, c) |
| WB : | Ball Installed on a Workpiece Table |
| {A}, {C} : | Coordinate System of Rotary Axis, A, C, Respectively |
| {R} : | Reference Coordinate System |
| α, β, γ [rad] : | Rotation Angles for 6-Axis Manipulator along with x, y and z-Directions, Respectively |
| ΔRijk, m [mm] : | Measured Deviation by Control of the i-, j-, k-Axes in m-Direction, (i, j = x, y, z; k = a, c; m = Radial, Axial) |
Acknowledgments
이 성과는 2020년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(Nos. 2020R1C1C100330011 and 2019R1A2C2088683).
REFERENCES
-
Brogardh, T., (2007), Present and future robot control development-An industrial perspective, Annual Reviews in Control, 31(1), 69-79.
[https://doi.org/10.1016/j.arcontrol.2007.01.002]

-
Charalambous, G., Fletcher, S., Webb, P., (2015), Identifying the key organisational human factors for introducing human-robot collaboration in industry: An exploratory study, The International Journal of Advanced Manufacturing Technology, 81(9), 2143-2155.
[https://doi.org/10.1007/s00170-015-7335-4]

-
Huang, Y., Yong, Y. S., Chiba, R., Arai, T., Ueyama, T., Ota, J., (2015), Kinematic control with singularity avoidance for teaching-playback robot manipulator system, IEEE Transactions on Automation Science and Engineering, 13(2), 729-742.
[https://doi.org/10.1109/TASE.2015.2392095]

-
Meng, Y., Zhuang, H., (2007), Autonomous robot calibration using vision technology, Robotics and Computer-Integrated Manufacturing, 23(4), 436-446.
[https://doi.org/10.1016/j.rcim.2006.05.002]

-
Filion, A., Joubair, A., Tahan, A. S., Bonev, I. A., (2018), Robot calibration using a portable photogrammetry system, Robotics and Computer-Integrated Manufacturing, 49, 77-87.
[https://doi.org/10.1016/j.rcim.2017.05.004]

-
Nubiola, A., Bonev, I. A., (2014), Absolute robot calibration with a single telescoping ballbar, Precision Engineering, 38(3), 472-480.
[https://doi.org/10.1016/j.precisioneng.2014.01.001]

-
Gaudreault, M., Joubair, A., Bonev, I., (2018), Self-calibration of an industrial robot using a novel affordable 3D measuring device, Sensors, 18(10), 3380.
[https://doi.org/10.3390/s18103380]

-
Schwenke, H., Knapp, W., Haitjema, H., Weckenmann, A., Schmitt, R., Delbressine, F., (2008), Geometric error measurement and compensation of machines-An update, CIRP Annals, 57(2), 660-675.
[https://doi.org/10.1016/j.cirp.2008.09.008]

-
Lee, K.-I., Yang, S.-H., (2013), Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary axis using a double ball-bar, International Journal of Precision Engineering and Manufacturing, 14(2), 231-239.
[https://doi.org/10.1007/s12541-013-0032-z]

-
Lee, K.-I., Yang, S.-H., (2016), Compensation of position-independent and position-dependent geometric errors in the rotary axes of five-axis machine tools with a tilting rotary table, The International Journal of Advanced Manufacturing Technology, 85(5), 1677-1685.
[https://doi.org/10.1007/s00170-015-8080-4]

- ISO 230-7, (2015), Test code for machine tools-Part 7: Geometric accuracy of axes of rotation.
-
Jiang, X., Cripps, R. J., (2015), A method of testing position independent geometric errors in rotary axes of a five-axis machine tool using a double ball bar, International Journal of Machine Tools and Manufacture, 89, 151-158.
[https://doi.org/10.1016/j.ijmachtools.2014.10.010]

- ISO 230-1, (2012), Test code for machine tools-Part 1: Geometric accuracy of machines operating under no-load or quasi-static conditions.
- ISO 10791-6, (2014), Test code for machining centres-Part 6: Accuracy of speeds and interpolations.
-
Lee, K. I., Kim, D. H., Lee, D. M., Yang, S. H., (2021), An alignment method for a TCP position of five-axis machine tools for ISO 10791-6, Journal of the Korean Society for Precision Engineering, 38(1), 53-60.
[https://doi.org/10.7736/JKSPE.020.075]

-
Krakhmalev, O., Petreshin, D., Krakhmalev, G., (2018), Methods of calibrating the orientation of the industrial robot tool, Proceeding of the 2018 International Multi-Conference on Industrial Engineering and Modern Technologies, 1-5.
[https://doi.org/10.1109/FarEastCon.2018.8602519]

-
Yang, S.-H., Lee, K.-I., (2021), Identification of 11 position-independent geometric errors of a five-axis machine tool using 3D geometric sensitivity analysis, The International Journal of Advanced Manufacturing Technology, 113(11), 3271-3282.
[https://doi.org/10.1007/s00170-021-06844-7]

-
Tsutsumi, M., Tone, S., Kato, N., Sato, R., (2013), Enhancement of geometric accuracy of five-axis machining centers based on identification and compensation of geometric deviations, International Journal of Machine Tools and Manufacture, 68, 11-20.
[https://doi.org/10.1016/j.ijmachtools.2012.12.008]

-
Lee, D.-M., Yang, S.-H., (2010), Mathematical approach and general formulation for error synthesis modeling of multi-axis system, International Journal of Modern Physics B, 24(15-16), 2737-2742.
[https://doi.org/10.1142/S0217979210065556]


Professor in the School of Mechanical and Automotive Engineering, Kyungil University. His research interests are precision methodologies for machine tools and 3D printer.
E-mail: kilee@kiu.kr

Researcher in the School of Mechanical Engineering, Kyungpook National University. His research interests are machine tools control and CAD/CAM.
E-mail: dhk815@knu.ac.kr

Senior Researcher in the Korea Institute of Industrial Technology. His research interests are machine tool metrology and metal hybrid 3D printing.
E-mail: hhlee84@kitech.re.kr

Professor in the School of Mechanical Engineering, Kyungpook National University. His research interests are intelligent manufacturing systems and CAD/CAM.
E-mail: syang@knu.ac.kr