A Study on the Influence of Dominant Parameters Related to Brake Squeal in the Brake System with the Flexible Pad

1.1 Introduction of the Research of Brake Squeal Noise

Railway facilities play an important role as a means of transportation in our lives today since it can move passengers and cargo quickly. With research on increasing capacity and improving driving performance, reducing noise and vibration that can cause inconvenience to passengers have been actively studied since before. Brake squeal noise is known for high frequency noise above 1 kHz caused by the contact between the pad and the disk of the brake system during braking. Numerous researchers have studied the occurrence of squeal noise in the brake system. Bowden [1] proposed a “Stick-Slip Oscillation”, which shows that the model oscillation occurs through the relationship between the dynamic friction coefficient and the static friction coefficient. Ibrahim [2] published a comprehensive review paper on this phenomenon and summarized modelling the friction force between sliding bodies through factors such as material properties, geometry of sliding surface, chemical properties, temperature, speed, and normal load. Mills [3] presented the theory of “Decreasing Friction Coefficient with Increasing Velocity” to explain that a decrease in the coefficient of friction with respect to the increase in velocity is the cause of the brake squeal noise. Mills’ model has long been used as a model for people studying brake squeal noise such as Fosberry and Holubecki [4]. Spurr [5] proposed a completely new model using a pin that comes into contact with a rotating body at an angle, and presented a theory on the occurrence of brake squeal noise using pin’s buckling. Although his model showed quite an error with the behavior of the actual system, other researchers such as Jarvis [6] and Earls [7], improved Spurr’s model to fit the actual phenomenon. North [8] presented a lumped model of 8 degree-of-freedom consisting of disk, couple of brake pads, and caliper. He calculated friction in his model as follower force and confirmed that some of the eigenvalues of the entire model were in unstable areas, showing that the brake squeal noise was a phenomenon caused by the flutter instability of disk, and thus suggested directions by many researchers modelling the disk.

Research on brake squeal noise reduction in the brake system of high-speed railway is also being actively conducted. Goo [9] modeled a brake system in high-speed railway equipped with a fixed type of pad using finite element method and analyzed the effect of friction coefficient between the fixed type of pad and the disk, and elastic modulus of backplate and friction material on the unstable mode. Shin [10] applied the Rayleigh damping assumption proportional to mass and stiffness to the high-speed railway brake system model, and analyzed the change in the unstable mode of the model as the damping changed. Xiang [11] analyzed the relationship between the brake pad and the disk’s contact behavior and vibration response, and confirmed that the coefficient of friction and the contact angle give remarkable influence to vibration characteristics. This paper extended the subject of the finite element method for high-speed railway brake squeal noise to the caliper part so the effect of its behavior could be considered, and the characteristics of the flexible pad was analyzed so the effect of structural flexibility could be applied.

1.2 Introduction of Brake Squeal Noise Analysis Process

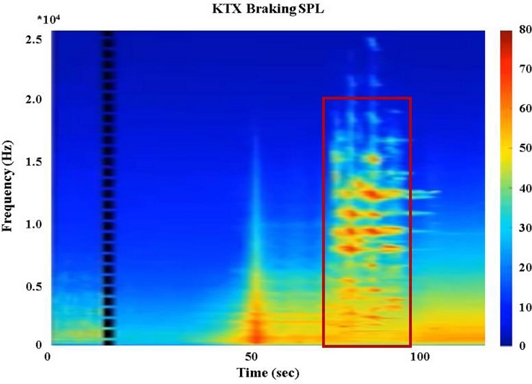
Squeal is a transient characteristic affected by the temperature change of the brake system due to braking heat generation, the instantaneous friction coefficient between the brake pad and the disk, and the driving speed. Fig. 1 shows an example of the braking squeal noise of the KTX railway. A high-frequency sound is considered to be a squeal noise occurs in a range between 70 and 100 seconds. It occurs in a wide frequency range from 100 Hz to 20 kHz. It is extremely difficult to obtain a general solution of the squeal since it has characteristics of transient and a wide frequency domain. Therefore, many studies identify the value of the transient factor in the squeal noise generation situation and analyze the cause of the occurrence of a specific squeal in the same situation. This study analyzed the cause of the occurrence of the squeal and the effect of the dominant parameters in the brake system with flexible pad.

Fig. 1

The example of measurement results of the braking squeal noise of the KTX railway

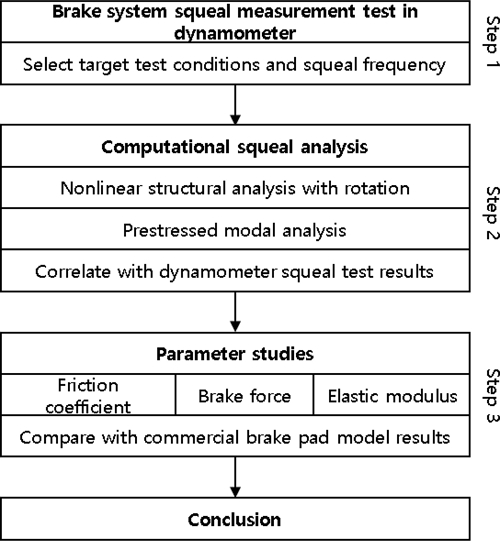
The overall process of this study is depicted in Fig. 2. In step 1, the braking situation reenacted in a dynamometer equipped with the flexible pad and the disk to be studied, and the sound pressure level (SPL) data was measured. The acquired data was examined to select the target test condition and target squeal frequency to this study. In step 2, non-linear structural analysis and pre-stressed modal analysis, which are squeal analysis processes, were performed dx. Correlation to the finite element model was performed by comparing the results with the SPL data obtained by the measurement. In step 3, the parameter study of the unstable mode was performed to three parameters i.e. friction coefficient, brake pressure force and elastic modulus. Those might cause squeal noise of the brake system. It also compared the results of the brake system with other flexible pad available on market.

Fig. 2

The flow chart of the squeal analysis process of this study

2.1 Introduction of the Flexible Structured Brake System

The brake system with the flexible pad for this paper is largely composed of three parts, i.e. caliper assembly, couple of flexible brake pads, disk and hub, as shown in Fig. 3. The stud which directly slides on the disk is connected to two plates, of which the elastic plate is connected to the backplate by three satellite rivets and the friction plate is connected by one central rivet as shown in Fig. 4. Between the elastic plate and the backplate, there is an elastic spring in the form of a cone for providing structural flexibility.

Fig. 3

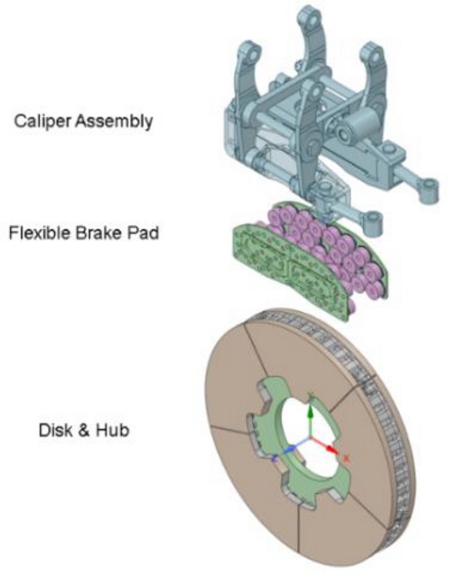
The picture of the brake system with the flexible pad which is composed of the caliper assembly, the flexible brake pad, the disk and the hub

Fig. 4

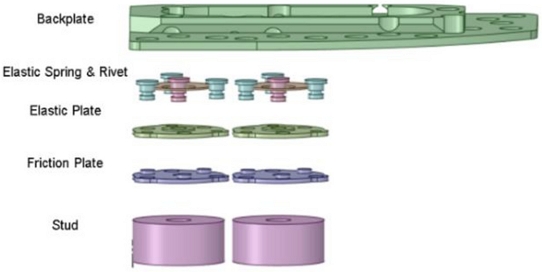
The components of the flexible brake pad. The elastic parts are the elastic spring and the elastic plate

This elastic spring alleviates the occurrence of uneven contact between the flexible brake pad and the disk depending on the contact surface between the caliper and the backplate during braking. Fig. 5 shows the contact pressure results between the rigid type of brake pad and the brake disk with a brake pressure force of 18 kN. Since it did not alleviate non-uniform contact, the shape of the contact surface between caliper and backplate was revealed in the contact pressure distribution as it was. Fig. 6 shows the contact pressure results applying 7 kN brake pressure force to the brake system equipped with the flexible pad in this paper. Although the two structural analysis conditions were not strictly the same, contact pressure was compensated for the stud located in the middle of the brake pad due to the structural flexibility, and thus the contact pressure distribution was even overall.

Fig. 5

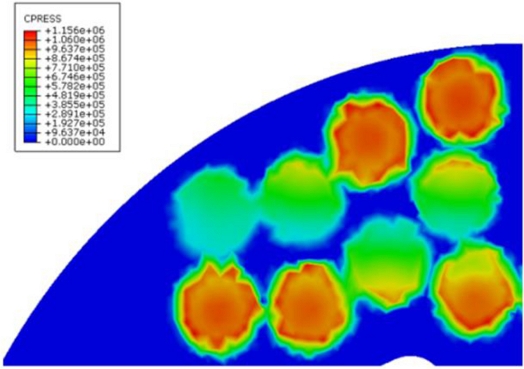
The contact pressure results of the brake system model equipped with a rigid brake pad with a brake pressure force of 18 kN

Fig. 6

The contact pressure results of the brake system model equipped with the flexible brake pad applying 7 kN brake pressure force

The brake system of the railway should pay more attention to the wear resistance of the brake pad because the brake weight and brake pressure forces are greater than that of a typical automobile brake system. The flexible pad of this study also has enough structural flexibility to ensure uniform brake pressure force transmission and wear resistance of high-weight, high-speed railway, even if the structure is somewhat complicated.

2.2 Squeal Noise Measuring Experiment Using Brake Dynamometer

Squeal noise measurement experiment were performed on the full-scale dynamometer by Dawin Friction Co., Ltd. as shown in Fig. 7 to measure the actual squeal noise of the brake system. Measurement was started while maintaining rotation at a rotational speed equivalent to the railway driving speed of 60 km/h, and squeal noise measurement experiment was performed until a brake pressure force of 10 kN was applied and completely stopped. The measurement point of the microphone is 30 cm apart from disk, 60 cm above the floor. Detailed experiment conditions are summarized in Table 1.

Fig. 7

The squeal noise measuring experiment for the railway brake system in dynamometer

Table 1

Experiment conditions on the brake dynamometer

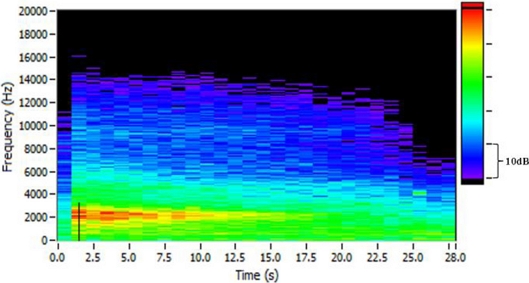
The experimental results are shown in Fig. 8. Time is shown on the x-axis, frequency on the y-axis, and SPL on the z-axis. The resolution of time is 1 second. From the moment the braking began, the high sound pressure was shown near 2 kHz, and the gradually declined as the rotational speed decreased. The SPL data at 1.5 second, which was felt the loudest, is extracted in Fig. 9 with respect to the frequency. It is difficult to find a clear peak in the graph because the shape is complicated due to the structural flexibility and the stud of the brake pad consists of 20 blocks rather than a single block. Therefore, frequencies of 75 dB_A or more were focused. The highest SPL value, 77.53 dB_A, was appeared at 1,940 Hz, and there were local peaks at 2,220, 2,320, and 2,440 Hz. 1,940 Hz was selected as the target squeal frequency to be reduced, and other frequencies as the concerned frequencies. The SPL magnitudes of every considered frequency is shown in Table 2.

Fig. 8

SPL waterfall plot applying 10 kN, 60 km/h. Brake noise is the loudest at 1.5 seconds marked as bar

Fig. 9

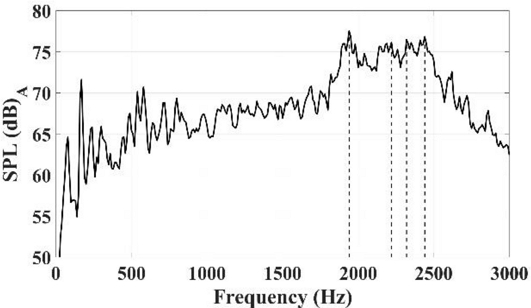
SPL at 1.5 second when applying 10 kN, 60 km/h. Considered frequencies are pointed by the dotted lines

Table 2

SPL data of the target frequency at 1,940 Hz and the concerned frequencies

3.1 Finite Element Model Setup for the Brake System with the Flexible Pad

ANSYS Mechanical R19.0 was used in this study for squeal analysis. Fig. 3 shows that high-speed railway brake system with the flexible pad is largely classified into caliper assembly, couple of flexible brake pads, disk and hub. The elastic modulus, poisson’s ratio and density of each component were listed in Table 3.

Table 3

Material properties of the brake system with the flexible pad

A complete disk is composed of five ventilated segments. Each segment is connected to other segments with two pins and is bolted to the hub. In the finite element model each piece of disk was connected using a cylindrical joint at the location of the pin, and the hub and the disk were connected using the cylindrical joint and a bonded contact.

The stud, the friction plate, the elastic plate and the rivets were set to operate in one fixed structure using bonded contact. The elastic spring was connected to the backplate and the elastic plate using a frictional contact. The friction coefficient of the frictional contact was set to 0.3. The head of each rivet was set to rub against the backplate so that the structure from stud to rivet did not fall out of the backplate.

Most of the model were consisted of TET10 elements, and only the backplate and the stud were modeled using HEX20 elements. In the size of the mesh, only brake pads with small contact areas of the parts used elements up to 4 mm in length, while others were given appropriate values so that the gap between adjacent models was not large. The total number of nodes in the model was 950,839, and the number of elements was 399,642. Fig. 10 shows the finite element model of the entire brake system in this study.

Fig. 10

The finite element model of the brake system with the flexible pad. The total number of elements was 399,642

3.2 Computational Squeal Analysis Procedure

There are three available methods for squeal analysis using ANSYS programs: Full nonlinear perturbed modal analysis, partial nonlinear perturbed modal analysis, and linear non-pre-stressed modal analysis [12]. Squeal analysis of the brake system was performed using the full nonlinear perturbed modal analysis method, which is known as the most accurate method, although it takes a long time. This method performs brake pressure force structural analysis through two load steps. In load step 1, nonlinear contact is generated by braking force, and in load step 2, frictional force is generated by setting up instantaneous rotation to the disk model. The stress in the model generated by structural analysis is replaced with an asymmetric stiffness matrix to change the model stiffness, and pre-stressed modal analysis is performed.

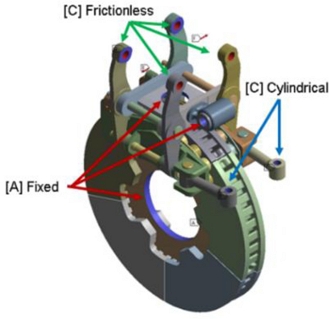
The boundary conditions of the model are shown in Fig. 11. Fixed support was applied to the hub surface in contact with the wheel shaft and the position to fix the caliper and marked as [A]. Cylindrical support was applied to the link to locate the caliper and marked as [B]. Frictionless support was applied to the link that transmits the brake pressure force and marked as [C]. 10 kN brake pressure force was assigned to the braking force that was the experimental condition of the dynamometer, and the friction coefficient between the flexible brake pad and the disk was 0.4 which was the average friction coefficient measured in the experiment.

Fig. 11

Boundary conditions of the model for the brake system with the flexible pad

Firstly, structure analysis was performed in load steps 1 and 2 as mentioned above. In load step 1, a nonlinear structural analysis of the applied brake pressure force was performed using remote force on the link of the caliper receiving the pressure of the piston. In load step 2, the axial rotation speed of 5.46 rad/s was input to the element of the disk, which was a rotating body in the model, using the “CMROTATE” command. This was the equivalent rotational speed of the high-speed railway driving speed of 60 km/h. “CMROTATE” is used to reflect the instantaneous stress change caused by rotating the target element in the stiffness matrix. Fig. 12 shows the result of the contact pressure between the stud of the flexible pad and the disk after performing load step 2. The relatively evenly distributed contact pressure distribution in Fig. 6 was tilted to one side by rotation in load step 2.

Fig. 12

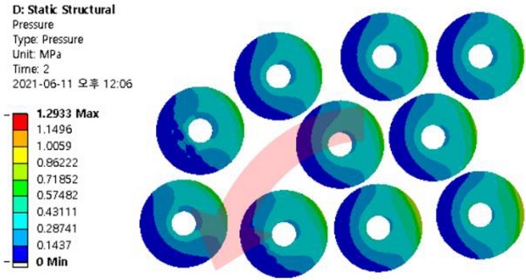
The result of the contact pressure after performing load step 2 where counterclockwise arrow shows the rotation of the disk. The “CMROTATE” command was applied under the same conditions as in Fig. 6

Second, a prestressed modal analysis was performed in which the stress results of structural analysis were reflected in the stiffness matrix. In this case, the stress caused by disk rotation and brake pressure force was replaced by an asymmetric stiffness matrix and was added to the entire model’s stiffness matrix. Asymmetric stiffness matrix was likely to make the real part value of the complex eigenvalue of this model positive, and if positive, the entire system tended to become unstable. ANSYS mechanical referred to this complex eigenvalue’s real part value as “Instability”. If instability had a positive value, the model might generate noise by self-exciting.

Lastly, the friction coefficient between stud of the flexible pad and disk, brake pressure force, and elastic modulus of the disk were changed and repeatedly analyzed to examine the result of the change in the physical properties and load conditions of the model. Table 4 shows the input values of each parameter. The tendency of instability with respect to the friction coefficient variation was studied in case 1, and that with respect to the brake pressure force variation was studied in case 2. The tendency of instability with respect to the elastic modulus of the disk was studied in case 3.

Table 4

Input values of parameters for the parameter study in this paper

3.3 Analysis Results of the Computational Squeal Analysis

3.3.1 Instability Results and Correlation

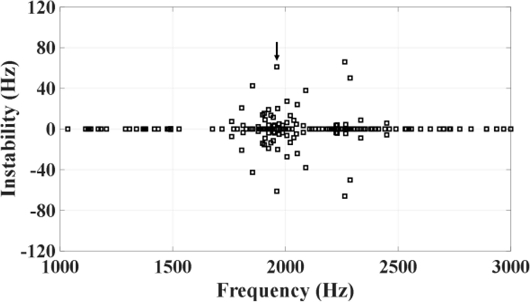
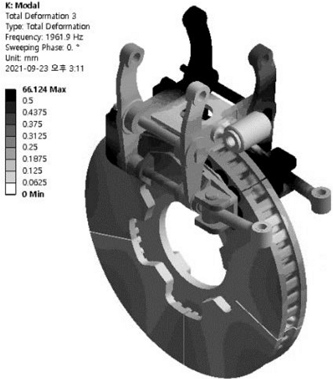
Fig. 13 shows the instability chart for the baseline case. Unstable mode with positive instability appears for the first time near 1,700, and local peaks are present at 1,961 and 2,263 Hz. Fig. 14 shows the mode shape of 1,961 Hz, which is an unstable mode with a value similar to the target squeal frequency selected in the experiment results. The nodal line shown on the disk rotates in the circumferential direction of the disk, and that is typical mode shape of an unstable mode that generates squeal noise. Unstable mode with small amount of instability can be found at 2,334 and 2,449 Hz. Table 5 compares the frequency and SPL values of target squeal frequency and concerned frequencies obtained by experiment, and the frequency and instability values of the unstable mode set obtained by squeal analysis.

Fig. 13

Instability chart for baseline case. Target squeal frequency is indicated by arrows

Fig. 14

The mode shape of the caliper and brake disk at frequency 1,961 Hz

Table 5

Comparison of frequency between test results and analysis results

The target frequency measured by the experiment was 1,940, and the frequency obtained by the squeal analysis was 1,961 Hz, with an error rate of 1.13%. Concerned frequencies have an error rate of less than 2% with the unstable mode set. It was determined that the error rate between the frequency measured by the experiment and the frequency obtained by squeal analysis was less than 2%, and that the finite element model was well correlated with the actual model.

Among the results of squeal analysis, the instability of 2,334 and 2,449 Hz shows relatively low values compared to other frequencies. It is generally known that the higher the instability, the greater the possibility of noise generation. However, in this study, the shape in the pad is complicated with structural flexibility and 20 individual studs, so the comparison of the absolute value of instability between unstable modes cannot be of great significance. So, in later studies comparing the change in the amount of instability in one unstable mode according to the parameter change was more concerned rather than comparing the amount of instability between unstable modes.

3.3.2 Instability Change with Respect to the Friction Coefficient

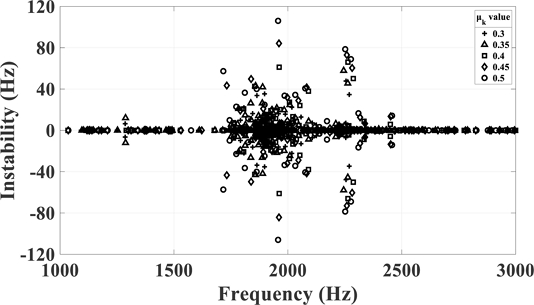
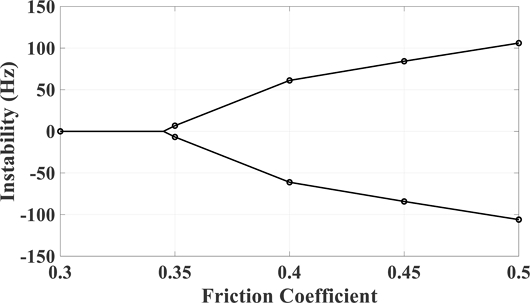
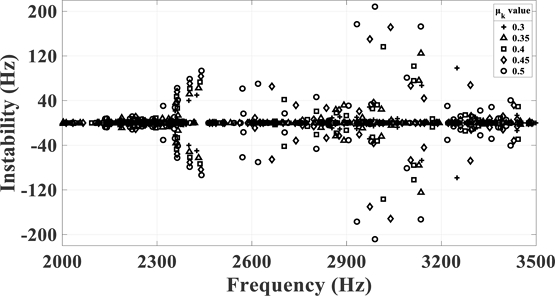
Fig. 15 shows the result of the instability value for each frequency by performing squeal analysis in conditions of case 1 in Table 4. Around 1,950 Hz, instability stands out when the coefficient of friction is 0.4 and increases as the coefficient of friction rises, so instability is the largest at 106.6 Hz when the coefficient of friction is 0.5. Around 2,250 Hz, two unstable modes are identified at similar frequencies from 0.3 friction coefficient, and the higher the friction coefficient, the higher the instability of the two modes. Around 2,450 Hz, the unstable mode appears when the coefficient of friction is 0.4 and increases as the coefficient of friction increases.

Fig. 15

Instability chart for case 1

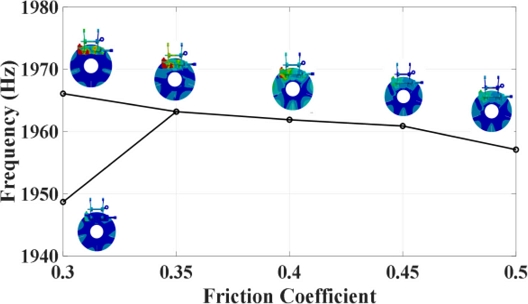
The mode shape of mode near 1,940 Hz, which is the target squeal frequency, was checked to confirm the change in frequency and instability of the unstable mode according to the friction coefficient in Figs. 16 and 17. When the friction coefficient is 0.3, there are two modes in which the frequency is similar, and the instability value is 0, because the unstable mode does not occur. When the fiction coefficient reaches 0.35, these two modes are coupled to generate an unstable mode and a stable mode in which the frequency is the same and the instability has a positive and negative value. And as the friction coefficient increases, the frequency of the two modes decreases slightly and the instability increases. Table 6 summarizes the frequency and instability values of the target squeal mode with respect to each friction coefficient.

Fig. 16

Target squeal mode’s frequency change based on friction coefficient variation, i. e. case 1

Fig. 17

Target squeal mode’s instability change based on friction coefficient variation, i. e. case 1

Table 6

Frequencies and instabilities of target squeal mode for case 1

3.3.3 Instability Change with Respect to the Brake Pressure Force

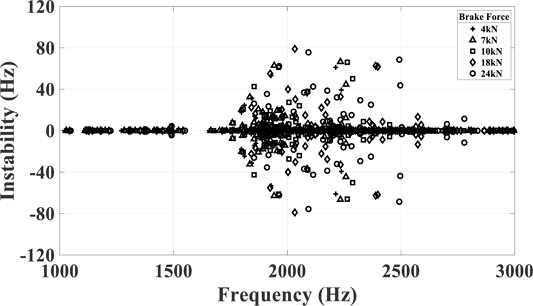
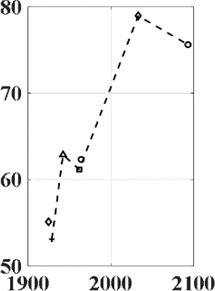
The graph in Fig. 18 is the result of the instability value for each frequency by performing squeal analysis in conditions of case 2 in Table 4. In Fig. 19, the target squeal mode change according to the brake pressure force variation was connected by a dotted line by enlarging between 1,900 and 2,100 Hz. As the brake pressure force increases, the change in instability in the unstable mode does not increase or decrease constantly. Therefore, in this model, brake pressure force variation has a nonlinear relationship with instability. Table 7 summarizes the frequency and instability values of the target squeal mode with respect to each brake pressure force.

Fig. 18

Instability chart for case 2

Fig. 19

Target squeal mode change for case 2

Table 7

The frequency and instability of target squeal mode for case 2

3.3.4 Instability Change with Respect to the Elastic Modulus of Disk

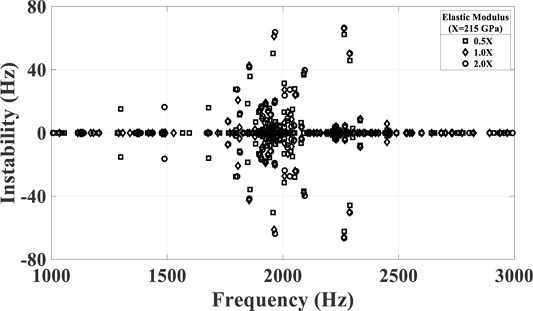
Fig. 20 shows the result of the instability value for each frequency by performing squeal analysis in conditions of case 3 in Table 4. When the elastic modulus value was half of the actual value, the instability of the target squeal frequency decreased by 10 to 50.4 Hz, and when it doubled, it increased by 2.6 to 63.8 Hz. The change in instability showed a greater change in the earlier case, although doubling to the elastic modulus of the actual disk was greater than half. Table 8 summarizes the frequency and instability values of the target squeal mode according to each elastic modulus of disk.

Fig. 20

Instability chart for case 3

Table 8

Frequency and instability of target squeal mode for case 3

3.4 Comparison with Commercial Flexible Brake Pad Model Results

The results of squeal noise analysis in this study were compared with those of the commercial flexible brake pad model. The commercial model is a flexible pad in which two stud blocks are attached to one plate and have structural flexibility. The detail expression of the model’s design is confidential, and thus further explanation of design feature is limited.

Noise measurement experiments were performed on the same dynamometer for the commercial flexible brake pad model, and when 7 kN braking force was applied, it was selected as the target squeal frequency with the largest SPL value of 94.9 dB_A at 2,720 Hz. Fig. 21 shows the results of the dynamometer noise measurement experiment equipped with a commercial flexible brake pad model in a 7 kN brake pressure force situation.

Fig. 21

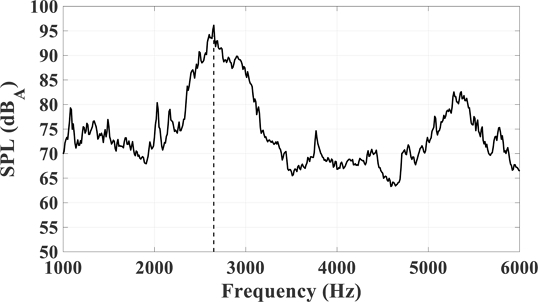
SPL graph of the benchmarking commercial model when applying 7 kN, 60 km/h. Target frequency is pointed in dotted line in the graph

Squeal analysis and parametric study were performed on the brake system including the commercial flexible brake pad model. Fig. 22 shows the instability chart of the commercial model according to the friction coefficient variation between the stud and the disk under 7 kN brake pressure force condition. Unlike the model in this study, the location of frequency with maximum instability in high friction coefficient is not near the target squeal frequency. However, there is an unstable mode with instability at 2,702 Hz, and the instability value also increases as the friction coefficient increases.

Fig. 22

The instability chart of commercial flexible brake pad with respect to the friction coefficients

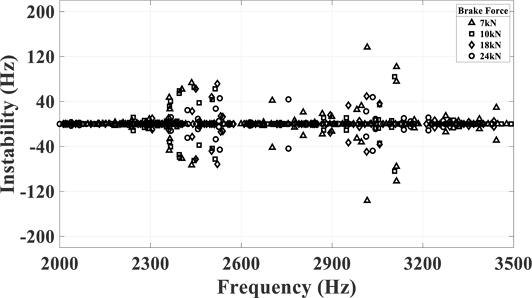
Fig. 23 shows the instability results when the brake pressure force is applied from 7 to 24 kN with the coefficient of friction fixed to 0.4. It has the largest instability value of 136.5 Hz at 3,016 Hz under 7 kN brake pressure force condition, and the instability decreases as the brake pressure force increases. The reason why the instability value tends to be nonlinear for brake pressure force changes is that the commercial flexible brake pad model is first paired with two studs on the plate to prevent individual oscillation. Second, since a force is applied to the plate spring to cause bending during assembly, internal stress is generated to secure the stiffness of the model. However, in the model of this study, each stud is connected to the backplate separately and individual behavior is possible. Therefore, compared to the commercial flexible brake pad model, the flexible pad in this study vibrates irregularly as the brake pressure force changes, so the change in the instability value of the corresponding model is not constant.

Fig. 23

The instability chart of commercial flexible brake pad with respect to the brake pressure forces