가스터빈 블레이드 막냉각 홀의 복합 형상 변화 시 열전달 특성 향상에 관한 수치해석적 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Recently, film cooling has been continuously studied to increase the efficiency of gas turbines. A turbine inlet temperature increase occurs as a way to improve the efficiency. However, it is essential to improve the cooling performance of the blade surface because of the melting point of the part. In this paper, a side hole shape wherein a general cylinder hole and two auxiliary holes are combined, is proposed to improve the film cooling efficiency, and the blowing ratio was set to 0.4, 0.8, 1.2, and 2.0. When side hole was applied, the vortex interference at the hole entrance occurred less than that of the cylinder hole. That is, the flow rate of the coolant adsorbed to the surface increased to improve the cooling performance. In conclusion, compared to the cylinder hole, the cooling efficiency of the shape to which the side hole was applied was excellent, and in particular, the average area cooling efficiency with spanwisely designed side holes improved by 83%.
Keywords:
Film cooling, Gas turbine, Side hole, Numerical analysis키워드:
막냉각, 가스터빈, 사이드 홀, 수치해석1. 서론
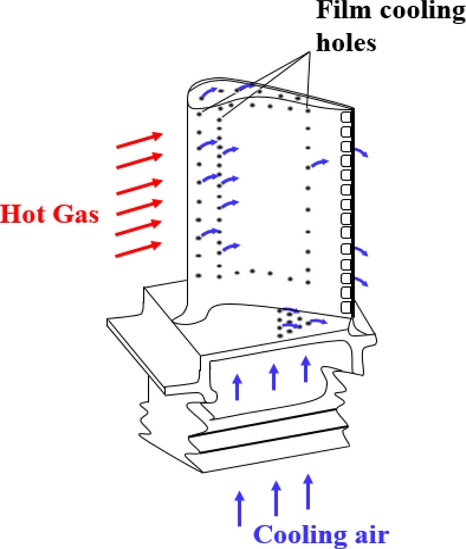
가스터빈의 효율을 높이기 위한 연구가 활발히 진행되고 있다. Zohuri는 터빈의 고압 및 고온은 열효율과 비추력을 증가시키지만 터빈 부품에 고온 가스가 지속적으로 노출될 경우 부품의 표면에 열화 현상이 생겨 수명과 효율에 영향이 있다고 주장했다[1]. 이에 따라 터빈 블레이드 표면 냉각의 중요성이 부각되었으며 Fig. 1과 같이 터빈 표면에 가공되어 있는 홀에서 냉각 유체를 흘려보내 고온의 주유동으로부터 표면을 보호하기 위한 냉각 유체막을 생성하는 기술이 제안되었다[2]. 막냉각은 터빈 익형에 적용할 수 있는 기술 중 가장 범용성 있고 효율성이 있기 때문에 현재 가장 많이 연구되고 있다.
Lee 등은 막냉각 홀에 레이드백(Laidback) 형상의 최적화에 대한 연구를 진행했으며, 분사비 0.5와 2.5가 기존 형상에 비해 30-40%의 효율 향상이 있었다고 규명했다[3]. Sajan 등은 실린더 홀 및 레이드백 형상에 변형된 복합 각도를 적용시켜 수치해석하여 실린더 홀의 결과보다 레이드백이 적용된 홀에 분사비 1.25, 복합 각도 90o에서 냉각 효율이 높다고 분석하였다[4]. Zhang 등은 막냉각 홀 전면에 모래언덕 형상(Sanddune-Shape)을 적용하여 수치적 연구를 진행하여 높은 분사비에서 효율성이 향상된다는 결론을 도출했다[5]. Liu 등은 냉각 홀의 출구에 2개의 홀을 뚫은 아령(Dumbbell) 형상과 콩(Bean) 형상을 제시하여 기존의 실린더 홀에 비해 33% 향상된 결과를 도출했다[6]. Zang 등은 냉각 효율 향상을 위해서 막냉각 홀 출구 주위에 발생하는 역방향 회전 와류(Counter Rotaing Vortex Pair, 이하 CRVP)를 제거하는 것이 핵심이라고 말하였다[7]. Khajehhasani 등은 소산 시스터 홀의 위치 변화를 통한 냉각 효율 향상에 대해 수치적 연구로 진행했다[8]. Cheng 등은 시스터 홀 형상에 대해 실험적인 연구를 진행한 결과 분사비가 0.5에서 냉각 효율이 가장 좋다고 분석되었다[9].
이와 같이 기존의 실린더 홀에서 출구 각도와 형상을 달리하는 연구가 주를 이루고 있다. 선행 연구들에서 제시하는 홀의 형상은 직선이 추가되거나 다소 복잡한 기하학적인 형상을 띄고 있다. 이로 인해 막냉각 홀을 가공하기 위해 레이저 가공, 방전 가공과 같은 복잡한 가공 공법을 이용하거나 금속 3D 프린터를 사용해 가공을 해야 한다. 하지만 위와 같은 가공 공정들은 시간 및 비용이 많이 소요되므로 현재로써는 상용화되기 어렵다. 또한 일반적인 실린더 홀의 경우 분사비가 상승함에 따라 CRVP 강도가 강해져 막냉각 효율이 급격하게 저하한다. 따라서 본 연구는 추가적인 가공 공정 없이 드릴링으로 가공할 수 있고, CRVP를 줄여 기존의 실린더 홀 형상과 비교해 막냉각 효율 및 냉각 범위를 월등히 상승시킬 수 있는 홀 형상을 설계하여 수치해석적으로 분석했다.
2. 수치해석
2.1 형상 및 구성
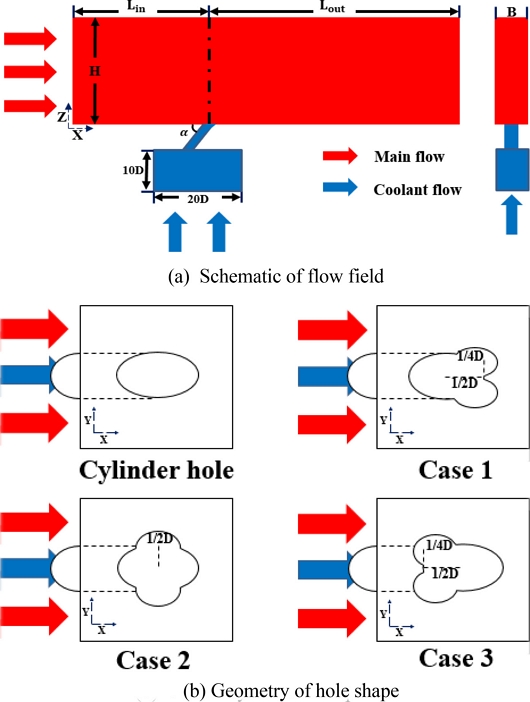
Fig. 2(a)에서 실린더의 직경은 D로 5 mm, 주유동장의 Lin은 시험 구역의 입구부터 냉각 홀 단면의 중심선까지의 거리로 35D, Lout은 냉각 홀 단면의 중심부터 시험 구역 출구까지의 거리로 55D, H는 주유동장의 높이로 30D, a는 분사각으로 35o이며 B는 유동장의 폭으로 4D이다. 냉각 유체 유동장은 길이 100, 높이 50, 폭 20 mm로 구성된다. Fig. 2(b)는 단축 직경 D인 메인 홀에 단축 직경 1/2D인 보조 홀 2개를 위치를 다르게 적용시켜 나타냈다. 보조 홀의 위치는 Cases 1과 3의 경우 메인 홀 단면의 중점으로부터 X축 방향으로 각각 1/2D와 -1/2D, y축 방향으로 1/4D와 -1/4D에 위치해 있으며, 2의 경우 y축 방향으로 ±1/2D 거리에 위치한다. 추가 공정 없이 드릴링으로만 가공할 수 있도록 하기 위해 메인 홀 및 보조 홀의 형상은 크기만 다른 타원 형상이다. 또한 냉각 공기가 실린더로 유입되는 입구가 하나로써 이에 따라 홀 출구에서 동일한 유량이 분사되도록 설계하였고, 같은 열에 위치한 다른 막냉각 홀의 영향을 최대한 줄 일 수 있는 크기로 설계하였다. Cases 1의 특징은 주유동 방향으로 2개의 보조 홀이 추가된 것이며, 이에 반해 2는 Span-Wise 방향으로 홀이 추가된 것이다. Case 3은 주유동의 역방향으로 보조 홀이 추가되었다. Cylinder Hole 및 Cases 1부터 3의 홀 출구 단면적은 각각 34.228, 44.769, 43.722, 42.735 mm2으로 설계하였다.
2.2 수치해석 방법 및 경계 조건
본 연구에서는 ANSYS FLUENT 21 버전을 사용했으며, 다양한 난류 모델을 적용했다. 해석상의 경계 조건은 비교 및 검증에 사용되는 실험 구성과 일치하도록 설정했다[10]. 경계 조건으로는 정상 상태의 흐름과 3차원 단열 벽 구조, 난류, 점성 및 비압축성 유동으로 설정하였다. 주유동의 속도는 10 m/s로 설정했으며 냉각 유체의 속도는 분사비(Blowing Ratio, 이하 M)에 따라 다르게 설정했다. 분사비의 공식은 다음 식(1)과 같다[2].
| (1) |
ρcool과 ρhot 은 각각 냉각 유체와 주유동의 밀도를 나타내며 Vhot 과 Vhot는 냉각 유체와 주유동의 속도를 나타낸다. 분사비는 냉각 유동의 속도에 따라 달라지며 0.4, 0.8, 1.2, 2.0으로 설정하였다. 난류 강도는 5%로 설정하였으며 주유동의 온도는 322.65 K, 밀도는 1.095 kg/m3, 점도는 1.95 × 10-5 kg/m·s, 열전도도는 0.02805 W/m·K로 설정했고, 냉각 유체의 온도는 295.85 K, 밀도는 1.193 kg/m3, 점도는 1.83 × 10-5 kg/m·s, 열전도도는 0.02607 W/m·K로 설정하였다. 각 유동의 물성치는 Table 2에 제시한다. 실린더 홀의 격자는 유체의 속도 및 온도 구배를 고려해 벽면 근처에 y + ≅1로 설정하고, 약 4,500,000개의 Multi Zone-Hexa로 구성했다. 본 연구에서는 가스터빈의 향상된 효율에 대해 막냉각 효율을 향상을 평가하기 위해 다음 식(2)와 같은 공식을 이용하였다[2].
| (2) |
Tadiabatic wall는 단열벽면온도를 뜻하며, Thot과 Tcool는 각각 주유동과 냉각 유체의 온도를 의미한다. 즉, 식(2)는 막냉각의 효율을 온도로부터 표현한 것이다.
2.3 수치해석 검증
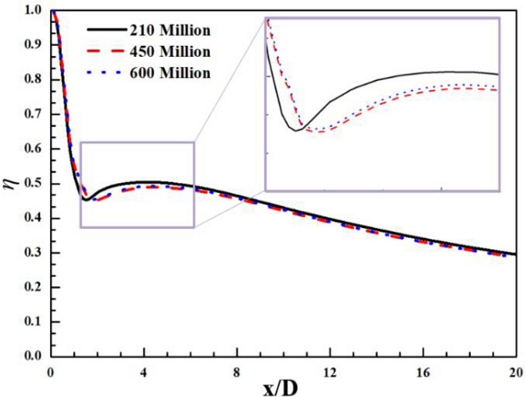
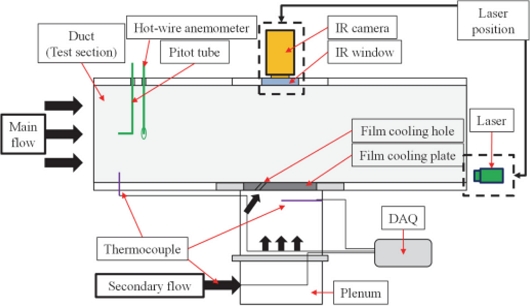
Fig. 3은 격자 의존성 검사를 수행하여 나타낸 그래프이다. 실린더 홀의 분사비 0.4를 기준으로 시행하였으며 격자수는 210만, 450만, 600만개 총 3가지로 구성하여 수행하였다. 해석 결과 격자수가 450만개부터 일정한 해석 결과를 나타내었으므로 이러한 격자 구성은 타당하다. 수치해석을 검증하기 위해 분사비가 0.4일 때 Fig. 4와 같이 시험부를 구성하였고, 측정 장비 및 시험 장비들을 설치하여 막냉각 성능 측정시험을 수행하였다[10]. 주유동은 30 마력의 사양을 갖는 블로워에 의해 20oC의 온도로 일정하게 공급된다. 냉각 유체는 11 마력 사양의 컴프레셔(Airssen Korea AS680-5H-T120W)에 의해 공급되며 3 kW 용량의 히터로 가열된다. 주유동과 냉각 유체의 온도를 측정하기 위해 T-Type 열전대를 사용하였으며, 측정 오차는 ±0.5oC이다. 막냉각 평판의 온도를 측정하기 위해 열 감도 30oC, 프레임 속도 60 Hz, 정확도 ±2oC의 사양의 IR 카메라(FLUKE TI400)를 사용하였다. IR 카메라는 T-Type 열전대로 측정된 온도 데이터를 기반으로 보정하여 신뢰성을 확보하였다. IR 카메라로 측정된 막냉각 평판의 온도를 식(2)와 같이 막냉각 효율로 변환하였다.
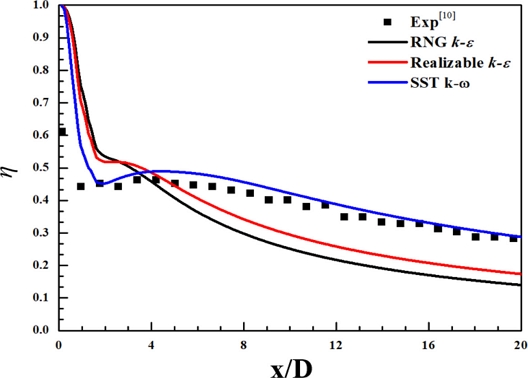
Fig. 5는 수치해석 검증을 위해 난류 모델 변경에 따른 중심선 막냉각 효율과 실험 결과를 비교하였다. 냉각 유체는 복잡한 난류인 주유동으로 침투하므로 적절한 난류 모델을 선택하는 것이 필수이다. RNG k-ε, Realizable k-ε 및 SST k-ω 난류 모델은 실험 결과와 비교 시 평균 오차는 각 56.03, 35.08 및 6.59%로 계산되었고, SST k-ω 난류 모델이 실험 결과와 가장 잘 일치하였다. SST k-ω 난류 모델은 점성 하층(Viscous Sublayer) 및 표면에 인접한 경계층에서의 유동을 해석하는데 적합하고, k-ε 계열의 난류 모델은 벽면에서 멀리 떨어진 자유 유동(Free Stream)을 해석하는데 적합하다[4,11,12]. 막냉각과 같이 경계층에서의 유동이 열전달 특성에 큰 영향을 미치는 경우 SST k-ω 모델이 난류 모델로써 가장 적합하다. 따라서 본 연구에서는 SST k-ω 난류 모델을 사용하여 계산을 수행하였다.
3. 결과 및 토의
본 연구에서는 가스터빈의 향상된 효율에 대해 막냉각 효율을 향상시키기 위해 수치해석적으로 분석하여 다음과 같은 결과를 도출하였다.
3.1 유동 특성
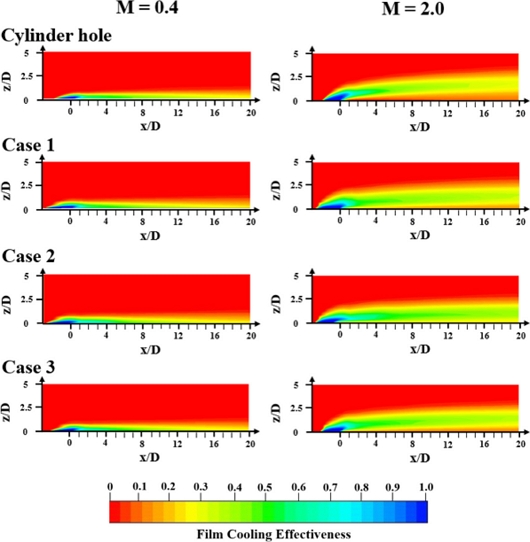
Fig. 6은 분사비가 0.4와 2.0일 경우 테스트 섹션의 옆면을 따라 유선 방향에 대한 막냉각 효과를 나타냈다. 홀 출구로부터 거리가 증가할수록 주유동과 냉각 유체의 혼합이 발생하므로 주유동의 유선 방향에 따라서 냉각 효율이 감소한다. 또한 분사비가 높을수록 냉각 효율이 감소하며, 이는 냉각 유체의 속도가 높아질수록 관성이 증가하여 바닥면에서 유동 이탈이 발생한 결과이다. 분사비가 0.4일 때 냉각수의 속도가 빠르지 않아 유동 이탈이 발생하지 않는다. 따라서 홀의 형상과는 관계없이 바닥면에 냉각 유체의 흡착이 순조롭게 이루어진다. 분사비가 2.0 일 때 모든 홀 형상에 대해 z/D 방향으로 냉각 유체가 넓게 분산된다. 특히 Case 2를 제외한 모든 형상의 경우 리프트 오프가 강하게 발생하여 바닥면에 냉각 유체가 원활하게 유동하지 않는다.
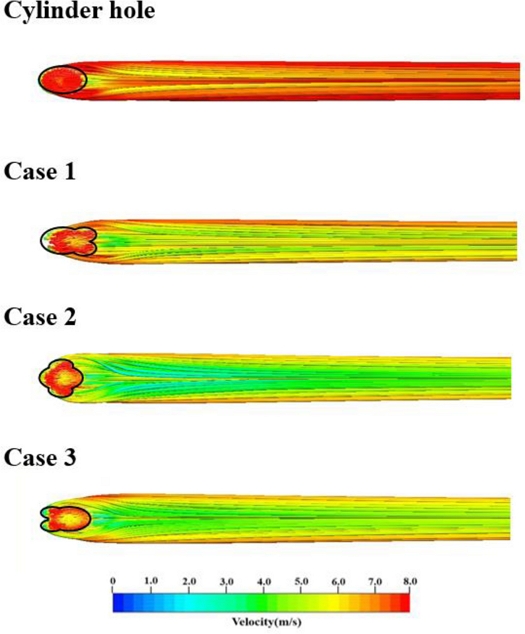
Fig. 7은 분사비가 0.8일 때 냉각 유체 속도에 대한 유선을 나타냈다. 실린더 홀 형상의 경우 홀 앞쪽에서 분사되는 냉각 유체를 제외하고 전체적으로 속도가 빠르다. 사이드 홀 형상의 경우 보조 홀에서 분사되는 냉각 유체 속도가 메인 홀에서 분사되는 냉각 유체의 속도보다 느리다. Case 1의 경우 보조 홀에서 분사되는 유체의 속도는 메인 홀 중심부에서 분사되는 유체의 영향을 받아 4-6 m/s의 속력으로 이동한다. Case 2의 경우 보조 홀에서 분사되는 냉각 유체는 메인 홀에서 분사되는 냉각 유체의 영향을 작게 받음으로 2-4 m/s의 속력으로 이동한다. Case 3의 경우 보조 홀에서 분사되는 냉각 유체가 메인 홀 주위를 지나갈 때 빠른 속도의 유체의 영향을 받아 4-6 m/s의 속력으로 이동한다. 이와 같이 홀의 유무 및 홀의 위치에 따라 냉각 유체의 유동 속도가 다른데, 냉각 유체의 속도가 느리면 바닥면에 대한 흡착성이 증가하고, 이는 곧 냉각 효율의 향상으로 이어진다[13].
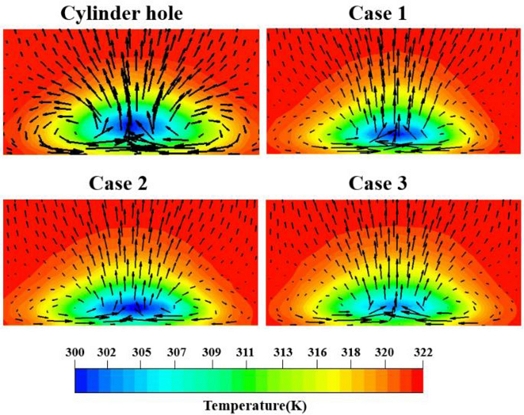
Fig. 8은 분사비가 0.8일 때 x/D = 2에서 횡단면의 속도 벡터 및 온도 분포를 나타냈다. 속도 벡터는 CRVP의 강도를 나타낸다. 속도 벡터의 크기가 크고, 홀 주위에 좁게 분포할수록 또한 한 쌍의 소용돌이 형상이 뚜렷할수록 CRVP의 강도가 강해진다. CRVP가 강해지면 고온의 주유동이 냉각 유체의 하부로 유입되는 양이 증가하여 바닥면에 대한 냉각 효율이 저하된다. 따라서 CRVP의 강도가 약할수록 냉각 효율이 증가한다. 실린더 홀의 경우 CRVP의 강도가 강하므로 보조 홀이 적용된 형상에 비해 홀 주위의 온도가 높다. 또한 사이드 홀 형상의 경우 Case 2의 CRVP가 가장 약하므로 홀 주위의 온도가 가장 낮다.
3.2 막냉각 효율
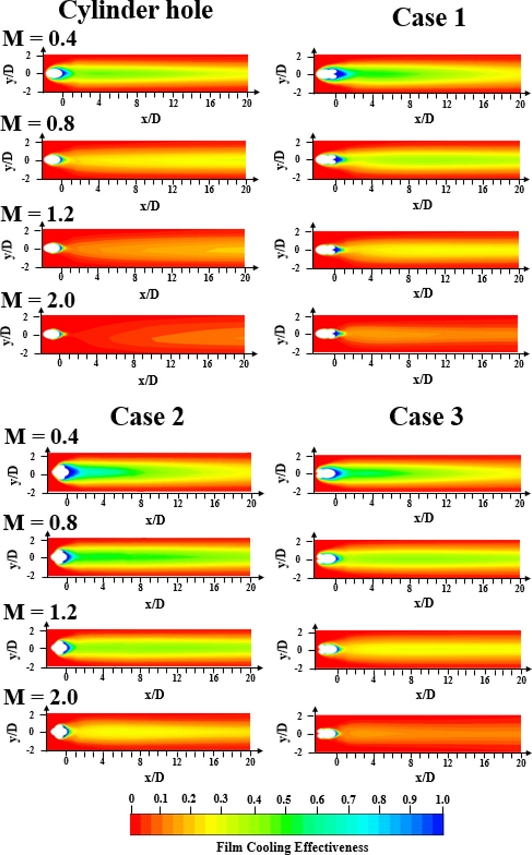
Fig. 9는 테스트 섹션 바닥 표면의 냉각 효율을 나타냈다. 분사비가 0.4일 때 모든 형상은 x/D > 8부터 유선 방향과 횡방향 양쪽에서 냉각 효율이 감소한다. 분사비가 0.8과 1.2에서의 경우 실린더 홀은 x/D의 거리가 멀어질수록 냉각 효율이 상승한다. 이는 냉각 유체가 분사된 직후 관성으로 인해 주유동을 관통하지만 거리가 멀어짐에 따라 주유동과의 압력차를 이기지 못하고 바닥면에 흡착되기 때문이다. 사이드 홀 형상에서 Cases 1과 3의 경우 x/D = 1-4에서 실린더 홀과 똑같은 이유로 냉각 효과가 상승하고 x/D > 4부터는 냉각 효율이 일정하게 유지된다. Case 2의 경우 x/D > 1부터는 냉각 효율이 일정하게 유지되며 모든 형상들 중 가장 우수한 냉각 효율을 나타낸다. 분사비가 2.0일 경우 냉각 유체의 속도가 너무 빨라서 관성으로 인해 바닥면에 흡착이 되지 않는다. 따라서 Case 2를 제외한 다른 형상들은 바닥 표면의 냉각 효과가 미미하다.
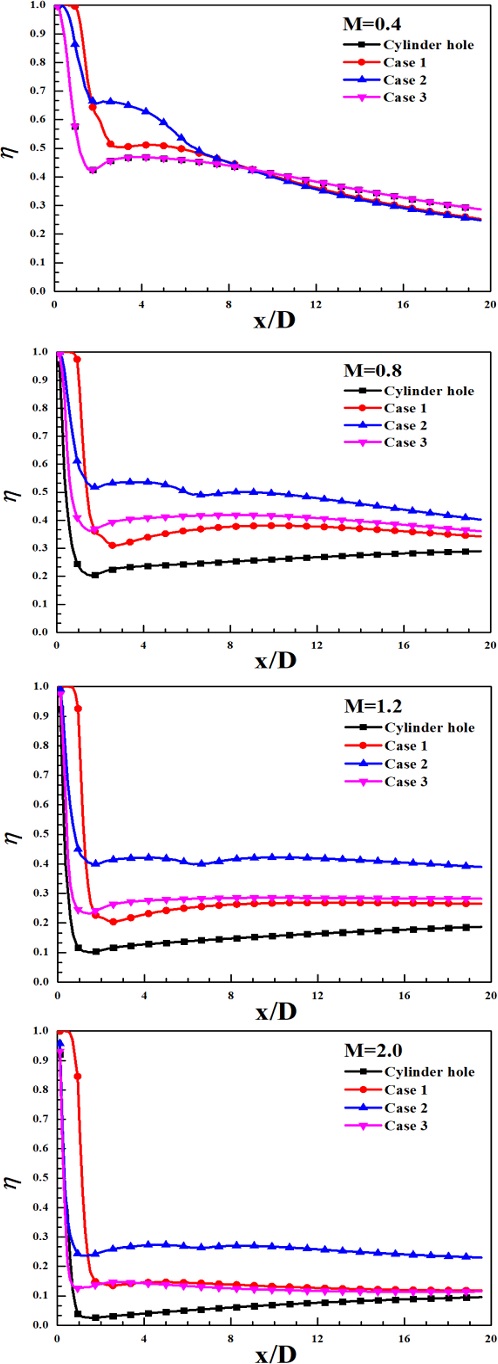
Fig. 10은 홀의 중심선에서 냉각 효율을 표현했다. 분사비 0.4에서 Case 2는 x/D = 2-8까지 가장 높았으나 x/D > 8부터는 오히려 다른 형상들보다 낮은 냉각 효율을 보였다. 분사비 0.8, 1.2, 2.0에서는 Cases 2, 3, 1 실린더 홀 순으로 냉각 효율이 우수하다. 분사비 0.8에서 실린더 홀의 경우 x/D = 1 이후로 냉각 효율이 선형적으로 증가하는 반면 사이드 홀 형상은 x/D > 8부터 점점 감소한다. 분사비 1.2에서는 사이드 홀의 형상의 경우 x/D = 2-20까지 일정한 냉각 효율을 나타냈다. 분사비 2.0에서는 실린더 홀, Cases 1, 3의 냉각 효율이 0.15 이하로 낮았다.
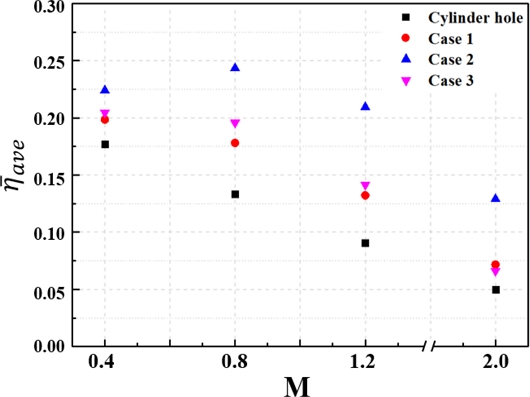
Fig. 11은 테스트 섹션에 대한 평균 면적 냉각 효율을 나타낸 그래프이다. Case 2를 제외한 다른 형상들은 분사비가 높아질수록 평균 냉각 효율이 낮아진다. Case 2의 경우 분사비 0.4에 비해 0.8일 때의 냉각 효율이 더 높다. 이는 분사비 0.4일 때 냉각 효율이 x/D > 8에서 대폭 감소하는 반면 분사비 0.8일 때는 거리에 따른 냉각 효율이 비교적 일정하게 유지되기 때문이다.
사이드 홀 형상에서 각 Case의 단면적이 큰 차이가 없음에도 Case 2의 막냉각 효율 및 면적이 우수한 이유는 Case 2의 보조홀에서 분사되는 냉각 유체의 속도가 메인 홀의 영향을 크게 받지 않아 유속이 느리고, 이에 따라 블레이드 표면에 흡착이 잘 되며, 홀 출구에서 생성되는 CRVP의 강도가 약해서 주유동이 냉각 유체의 하부로 유입되려는 성질이 저하되기 때문이다.
4. 결론
본 연구에서는 가스터빈의 막냉각 효율을 향상시키기 위해 수치해석적으로 분석하였다. 이를 위해 실린더 홀 형상과 사이드 홀 형상을 비교했으며 보조 홀의 위치에 따라 총 3가지 형상으로 구성하였다. 중심선의 냉각 효율에 대해서는 분사비가 0.4일 경우 모든 형상은 냉각 유체가 홀에서 빠져나왔을 때부터 냉각 효율이 감소하기 시작했으며 x/D > 8에서는 횡방향에서도 감소가 되었다. 분사비가 0.8 이상에서 실린더 홀의 경우 x/D = 1부터 냉각 효율이 완만하게 상승하는 양상을 띄었다. 보조 홀이 적용된 형상은 x/D가 증가함에 따른 냉각 효율의 감소폭이 작았다. 분사비가 2.0일 경우 Case 2를 제외한 다른 형상들은 CRVP 강도가 강해져 바닥 표면의 냉각 효과가 미미했다. 평균 면적 냉각 효율은 분사비 0.8일 때 Case 2 형상이 24.3%로 가장 우수했으며 동 분사비의 실린더 홀 형상과 비교하여 83% 향상된 냉각 효율을 나타냈다. 이와 같이 홀 형상과 분사비에 따라 막냉각 효율이 서로 다른 결과를 나타내므로 냉각 효율을 상승시키기 위해서는 최적의 형상과 분사비를 적용하는 방향의 수립이 필요한 것으로 사료된다.
NOMENCLATURE
| M : | Blowing Ratio |
| η : | Centerline Adiabatic Film Cooling Effectiveness |
| : | Average Area Adiabatic Film Cooling Effectiveness |
| D : | Diameter of the Film Hole |
| H : | Height of Main Flow Field |
| B : | Breadth of Flow Fields |
| α : | Blowing Angle |
| Lin : | Length of Inlet to Hole |
| Lout : | Length of Outlet to Hole |
| ρhot : | Main air Density |
| ρcool : | Coolant Air Density |
| Vhot : | Main Air Velocity |
| Vcool : | Coolant Air Velocity |
| Thot : | Main Air Temperature |
| Tcool : | Coolant Air Temperature |
| Tadiabatic wall : | Adiabatic Wall Temperature |
Acknowledgments
본 연구는 2021년도 정부(산업통상자원부) 재원 및 한국에너지기술평가원(KETEP)의 지원을 받아 수행된 연구임(Nos. 20214000000480 and 20181110100310).
REFERENCES
-
Zohuri, B., McDaniel, P., (2015), Combined cycle driven efficiency for next generation nuclear power plants: An Innovative Design Approach, 147-171.
[https://doi.org/10.1007/978-3-319-15560-9_7]

-
Goldstein, R. J., (1971), Film cooling, Advances in Heat Transfer, 321-379.
[https://doi.org/10.1016/S0065-2717(08)70020-0]

-
Lee, K.-D., Kim, K.-Y., (2011), Surrogate based optimization of a laidback fan-shaped hole for film-cooling, International Journal of Heat and Fluid Flow, 32(1), 226-238.
[https://doi.org/10.1016/j.ijheatfluidflow.2010.08.007]

-
Tamang, S., Kwon, H., Choi, J., Ligrani, P., Lee, J.-H., Jung, Y.-G., Park, H., (2020), Numerical investigation of adiabatic film cooling effectiveness through compound angle variations, Numerical Heat Transfer, Part A: Applications, 78(10), 595-618.
[https://doi.org/10.1080/10407782.2020.1803600]

-
Zhang, S., Zhang, J., Xiaoming, T., (2021), Improvement on shaped-hole film cooling effectiveness by integrating upstream sand-dune-shaped ramps, Chinese Journal of Aeronautics, 34(4), 42-55.
[https://doi.org/10.1016/j.cja.2020.10.011]

-
Liu, J. S., Malak, M. F., Tapia, L. A., Crites, D. C., Ramachandran, D., Srinivasan, B., Muthiah, G., Venkataramanan, J., (2010), Enhanced film cooling effectiveness with new shaped holes, Turbo Expo: Power for Land, Sea, and Air, 1517-1527.
[https://doi.org/10.1115/GT2010-22774]

-
Zhang, J., Zhang, S., Chunhua, W., Xiaoming, T., (2020), Recent advances in film cooling enhancement: a review, Chinese Journal of Aeronautics, 33(4), 1119-1136.
[https://doi.org/10.1016/j.cja.2019.12.023]

-
Khajehhasani, S., Jubran, B. A., (2016), A numerical investigation of film cooling performance through variations in the location of discrete sister holes, Applied Thermal Engineering, 107, 345-364.
[https://doi.org/10.1016/j.applthermaleng.2016.06.135]

-
Cheng, H., Wu, H., Li, Y., Ding, S., (2017), Effect of rotation on a downstream sister holes film cooling performance in a flat plate model, Experimental Thermal and Fluid Science, 85, 154-166.
[https://doi.org/10.1016/j.expthermflusci.2017.03.001]

-
Zhang, B.-l., Zhu, H.-R., Zhang, L., (2021), Experimental research on film cooling characteristics of multi-film-hole-rows, Case Studies in Thermal Engineering, 27, 101289.
[https://doi.org/10.1016/j.csite.2021.101289]

-
Kim, J.-H., Kim, K.-Y., (2018), Film-Cooling performance of converged-inlet hole shapes, International Journal of Thermal Sciences, 124, 196-211.
[https://doi.org/10.1016/j.ijthermalsci.2017.10.014]

-
Menter, F. R., (1994), Two-Equation eddy-viscosity turbulence models for engineering applications, AIAA Journal, 32(8), 1598-1605.
[https://doi.org/10.2514/3.12149]

-
Wang, J., Liu, C., Zhao, Z., Baleta, J., Sundén, B., (2020), Effect and optimization of backward hole parameters on film cooling performance by Taguchi method, Energy Conversion and Management, 214, 112809.
[https://doi.org/10.1016/j.enconman.2020.112809]


M.Sc. candidate in the Department of Smart Manufacturing Engineering, Changwon National University. His research interests are optimized design and performance analysis in application area of gas turbine.
E-mail: pch6311@naver.com

M.Sc. candidate in the Department of Smart Manufacturing Engineering, Changwon National University. His research interests are optimized design and performance analysis in application area of gas turbine.
E-mail: sajantamang67@gmail.com

Ph.D. candidate in the Department of Smart Manufacturing Engineering, Changwon National University. His research interests are optimized design and performance analysis in application area of gas turbine.
E-mail: hwabini90@naver.com

Graduate School of Mechanical Engineering, Smart Manufacturing Division, Changwon National University. His research interest is machine.
E-mail: jaemunchoi92@gmail.com

Professor in the Department of Industrial and Mechanical Engineering, Changwon National University. His research interest is thermos fluidic devices for sustainable energy systems.
E-mail: heesungpark@changwon.ac.kr