파라미터 중복성을 제거한 로봇 매니퓰레이터의 위치 기반 기구학 캘리브레이션

2.1 기구학 캘리브레이션 과정

먼저 DH 표현법을 사용하여 매니퓰레이터의 각 조인트에 프레임을 설정하고, 공칭 기구학 파라미터를 통해 각 프레임 사이의 변환 관계를 정의한다. 이때 기존의 DH 기구학 파라미터 α_i, a_i, d_i, θ_i에 Hayati 파라미터 β_i를 추가하여 평행한 인접 조인트 사이의 Y 방향 각도 오차를 표현한다. 따라서 최종적으로 기구학 파라미터를 통해 엔드 이펙터의 위치에 대한 수학적 모델을 정의한다. 그 후 제조상 오차, 노후화 등으로 인해 오차가 발생한 엔드 이펙터의 실제 위치 정보를 외부 센서를 통해 측정하여 공칭 파라미터로 계산한 예상 위치와의 차이를 구한다. 외부 센서의 경우 카메라, 변위 측정 센서, CMM (Coordinate Measuring Machine) 등 다양한 종류의 센서를 활용할 수 있다. 마지막 최적화 과정으로 기구학 파라미터 오차들의 결합을 통해 엔드 이펙터의 위치 오차를 표현하는 자코비안 행렬을 정의하고, 의사역행렬 형태로 변환하여 외부 센서로부터 구한 엔드 이펙터의 절대 위치 오차를 기구학 파라미터의 오차로 치환하여 반복적으로 공칭 파라미터를 보정한다.

2.2 자코비안 행렬

자코비안 행렬은 기구학 파라미터 오차들의 결합을 통해 엔드 이펙터의 위치 및 방향 오차를 표현하는 행렬이고, 최적화 과정에서는 의사역행렬 형태로 엔드 이펙터의 위치 및 방향 오차를 기구학 파라미터 오차로 치환할 때 활용한다.

자코비안 행렬을 구하기 위해서는 먼저 인접한 두 프레임 사이의 변환 행렬인 식(1)의 $$ A_{i-1}^i$$를 정의하고, 이를 통해 로봇 베이스 기준 엔드 이펙터까지의 변환 행렬인 식(2)의 $$ T_0^{EE}$$를 정의한다.

where, i = 1, ... , N, EE

따라서 식(2)의 $$ T_0^{EE}$$행렬 미소 변화를 식(3)과 같이 기구학 파라미터 오차에 대한 선형 결합 식으로 나타낸다[10].

최종적으로 식(3)을 위치 오차와 방향 오차 각각에 대해서 나누고, 이를 기구학 파라미터의 오차에 대한 행렬식으로 나타내어 자코비안 행렬을 구한다.

먼저 위치 오차의 경우 식(2)의 $$ T_0^{EE}$$행렬 내부 1-3행 4열의 $$ P_0^{EE}$$벡터가 로봇 베이스 기준 엔드 이펙터의 위치를 나타내므로 $$ {dT}_0^{EE}$$행렬 내부 1-3행 4열 위치 오차 벡터 $$ {dP}_0^{EE}$$만을 활용하여 식(4)와 같이 행렬식을 도출한다. 이때 식(4)의 J_p는 엔드 이펙터의 위치 오차에 대한 자코비안 행렬을 나타낸다.

where, K(i, j): Element in column j of row i of matrix K

또한 방향 오차의 경우 식(2)의 $$ T_0^{EE}$$행렬 내부 1-3행 1-3열 $$ R_0^{EE}$$행렬이 로봇 베이스 기준 엔드 이펙터의 방향을 나타내므로 $$ {dT}_0^{EE}$$행렬 내부 1-3행 1-3열 방향 오차 행렬 $$ {dR}_0^{EE}$$만을 활용한다. 방향 오차의 경우 위치 오차와 다르게 추가적으로 방향 오차 행렬 $$ {dR}_0^{EE}$$의 9개 원소를 3차원 방향을 나타내는 3개의 원소 dα, dβ, dγ로 나타내어 식(5)와 같이 행렬식을 도출한다. 이때 식(5)의 J_r은 엔드 이펙터의 방향 오차에 대한 자코비안 행렬을 나타낸다.

where, K_{(i, j)}: Element in column j of row i of matrix K

따라서 최종적으로 로봇 베이스 기준 엔드 이펙터의 위치 및 자세를 보정하는 전체 자코비안 행렬식은 식(6)과 같다.

본 논문에서는 기구학 위치 캘리브레이션에 대해서만 다루므로 식(4)에서 정의한 위치 오차에 대한 자코비안 행렬 J_p만을 활용하여 기구학 파라미터의 중복성을 판별 및 제거하고, 식(7)과 같이 의사역행렬 형태로 변환한 후 엔드 이펙터의 절대 위치 오차를 기구학 파라미터의 오차로 치환하여 캘리브레이션 작업을 진행한다.

where, J*: Pseudo Inverse of J

3.1 기구학 파라미터의 중복성

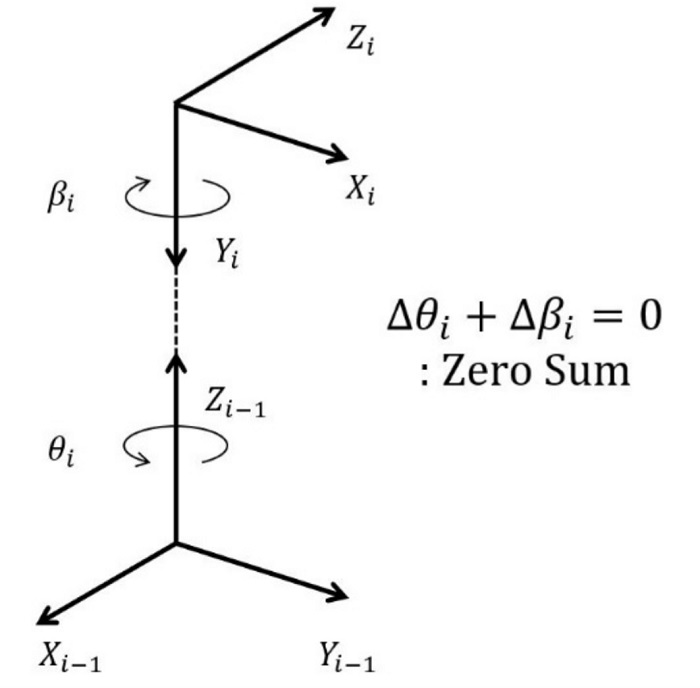
각각의 기구학 파라미터는 각 프레임의 X, Y, Z 방향 기준으로 병진 및 회전 방향의 자유도를 갖는다. 따라서 앞에서 구한 자코비안 행렬을 통해 X, Y, Z 각 방향에 대한 엔드 이펙터의 절대 위치 오차를 기구학 파라미터 오차의 선형 결합으로 치환 할 수 있고, 최종적으로 공칭 파라미터를 실제 값과 가깝게 반복적으로 보정할 수 있다. 하지만 Fig. 1과 같이 인접 조인트 사이의 특정 파라미터들은 절대적인 동일 방향에 대해 자유도가 겹칠 수 있고, 이때 동일한 변화값에 대해 제로섬(Zero-Sum)의 관계를 갖는다. 그러므로 이러한 중복성을 판별하는 과정 없이 최적화에 모든 파라미터를 사용하게 되면 하나의 자유도에 대한 보정을 위해 불필요하게 많은 파라미터를 사용하게 되고, 그 결과 비효율적인 기구학 캘리브레이션이 진행된다.

Fig. 1

Example of redundancy of kinematic parameters and zero-sum relation

앞서 구한 자코비안 행렬은 기구학 파라미터 오차의 선형 결합으로 엔드 이펙터의 절대 위치 오차를 표현할 때 활용하는데, 각 기구학 파라미터 오차의 계수를 의미한다. 그러므로 Fig. 1과 같이 중복성을 갖는 파라미터들은 동일한 자유도에 대해 제로섬의 성질을 가지므로 완전한 선형 관계를 갖게 되고, 동일하게 자코비안 행렬의 해당 계수들 또한 완전한 선형 관계를 갖게 된다. 따라서 이를 이용하여 자코비안 행렬 내부 모든 기구학 파라미터 사이의 선형 관계를 분석하여 결과적으로 기구학 파라미터의 중복성을 판별할 수 있다.

3.2 피어슨 상관 분석(Pearson Correlation Analysis)

기구학 파라미터 사이의 선형 관계 분석은 상관 분석[11]을 통해 진행하는데, 일반적으로 많이 사용하는 상관 분석 방법은 피어슨(Pearson), 스피어만(Spearman), 켄달(Kendall) 방법이다. 하지만 스피어만과 켄달 상관 분석의 경우 파라미터 값 자체가 아닌 순위 척도에 대해 상관 관계를 분석하는 방법이므로 본 논문에서 활용하기에는 적합하지 않다. 따라서 파라미터 값 자체에 대한 상관 관계를 분석하는 방법인 피어슨 상관 분석 방법을 활용하였다.

피어슨 상관 분석은 두 파라미터의 공분산과 표준 편차를 이용하여 선형 상관 관계를 수치화하는 방법이다. 식(8)과 같이 두 파라미터가 함께 변화하는 정도와 각각 변화하는 정도의 비율을 통해 피어슨 상관 계수(Pearson Correlation Coefficient)가 정의된다. 이때 A_i, B_i는 각각 두 파라미터 A, B에 대한 하나의 데이터값, $$ \overline{A},\overline{B}$$ 는 각각 두 파라미터 데이터의 평균값, r_AB는 두 파라미터 A, B에 대한 피어슨 상관 계수를 의미한다. 피어슨 상관 계수는 코시-슈바르츠(Cauchy-Schwarz) 부등식에 의해 +1과 -1 사이의 값을 갖고, 그 절댓값이 클수록 두 파라미터 사이의 선형 상관 관계가 높음을 의미한다.

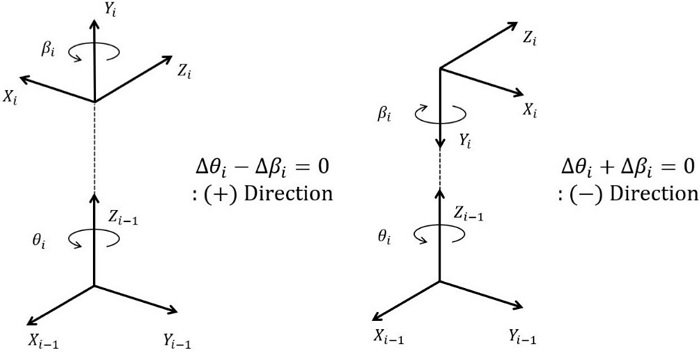
엔드 이펙터의 절대 위치 오차에 중복성을 갖는 두 기구학 파라미터들은 표현하는 오차에 대한 자유도가 중복되어 제로섬의 관계를 갖는다. 따라서 피어슨 상관 분석을 통해 두 파라미터 사이의 선형 관계를 분석하면 완전한 선형 관계의 결과가 나타나고, 피어슨 상관 계수의 경우 절댓값이 1인 +1 또는 -1의 값을 갖게 된다. 이때 상관 계수의 부호의 경우 두 파라미터가 갖는 선형 관계의 방향을 의미하므로, 이를 통해 Fig. 2와 같이 두 기구학 파라미터의 중복성이 동일한 방향 또는 반대 방향으로 발생하는지를 파악할 수 있다.

Fig. 2

Examples of direction of redundant kinematic parameters

따라서 기구학 캘리브레이션의 최적화 과정 이전에 자코비안 행렬 내 모든 두 파라미터 원소 사이의 피어슨 상관 분석을 통해 파라미터 사이의 선형 관계를 파악하고, 그 중 완전한 선형 관계를 갖는 파라미터를 중복 파라미터로 판별하여 일부를 최적화 과정에 제외시킬 수 있다. Fig. 3의 경우 θ₁ - β₁ 파라미터 사이의 피어슨 상관 계수를 계산하는 과정이다. 만약 연속된 인접 프레임에서 중복성이 발생하여 3개 이상의 중복 파라미터가 존재할 경우 하나의 파라미터만을 최적화에 참여시키고 나머지 파라미터들을 제외시킬 수 있다. 이를 통해 파라미터 사이의 중복성을 자동적으로 판별 및 제거하여 꼭 필요한 기구학 파라미터만으로 효율적인 기구학 캘리브레이션을 진행할 수 있다.

Fig. 3

Process of calculating the pearson correlation coefficient

4.1 실험 환경

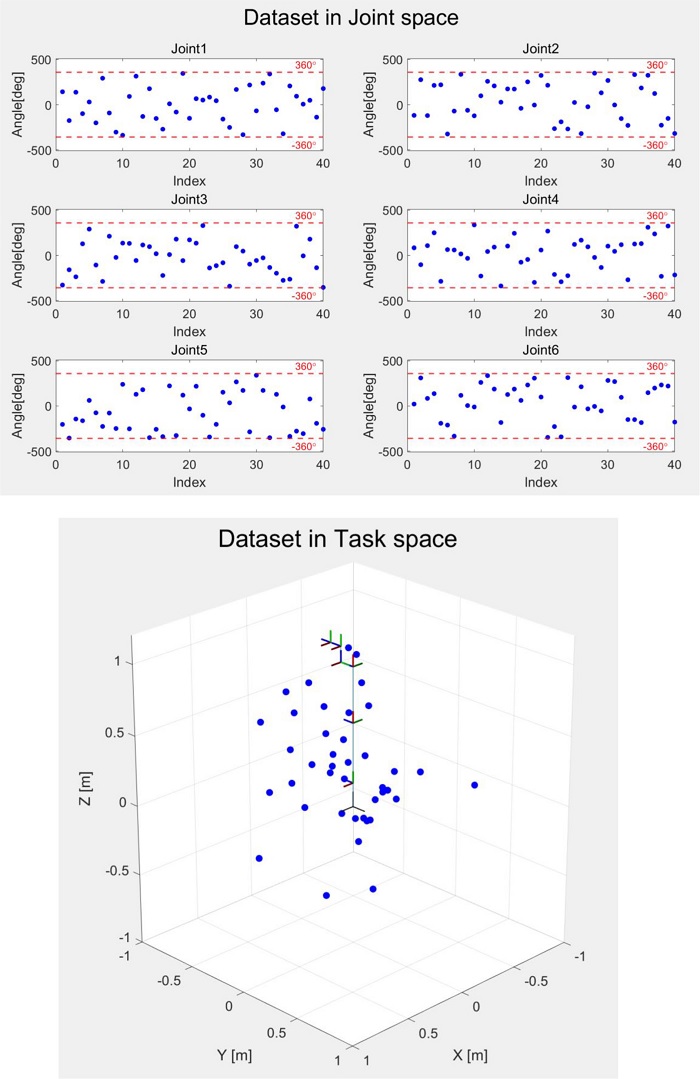
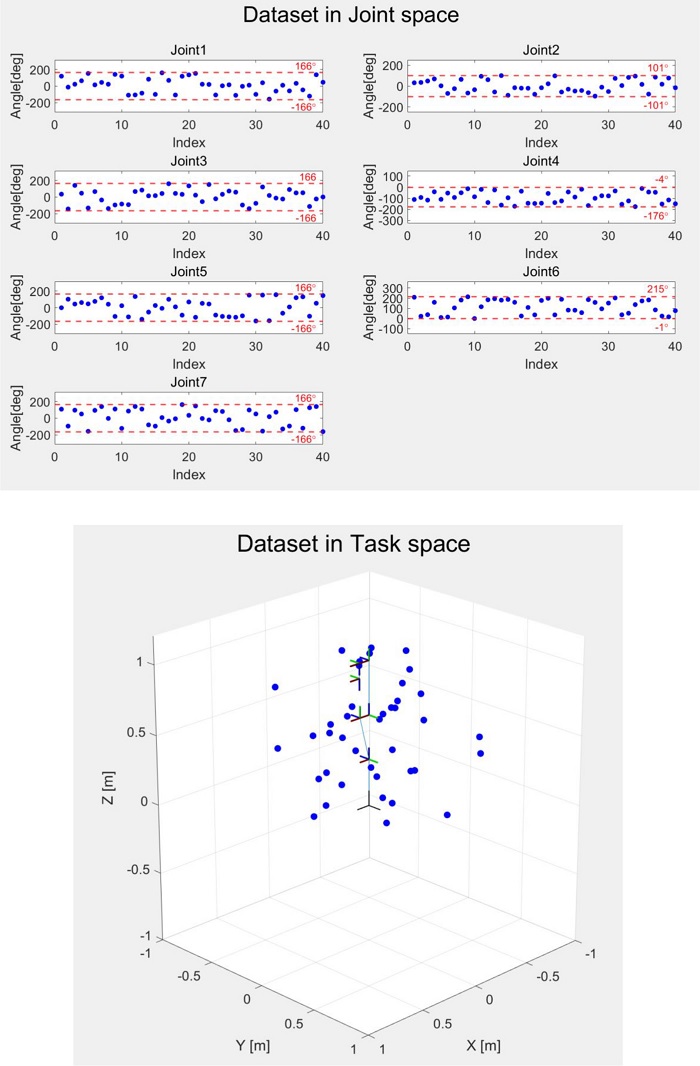
시뮬레이션을 통한 기구학 캘리브레이션은 서로 다른 형태를 가진 Rainbow Robotics 사의 6자유도 RB5 모델(Fig. 4, Table 1)과 Franka Emika 사의 7자유도 Panda 모델(Fig. 5, Table 2)에 대해 진행하였다. 각도 데이터의 경우 Figs. 6, 7과 같이 모든 조인트의 가동 범위를 포함하는 40개의 임의의 각도 조합을 생성하였고, 엔드 이펙터 프레임의 경우 마지막 조인트 프레임과 일치하도록 설정하였다. 엔드 이펙터의 실제 위치값의 경우 외부센서를 활용하지 않고 공칭 파라미터에 ±1 mm, ±1 deg 사이 임의의 오차를 부여하여 실제 파라미터 값과 실제 엔드 이펙터의 위치 값을 생성하였다. 최적화의 경우 공칭 파라미터를 반복적으로 보정하며 1,000회 동안 실시하였다.

Fig. 4

Rainbow Robotics RB5 manipulator

Table 1

DH parameters of Rainbow Robotics RB5 manipulator

Fig. 5

Franka Emika Panda manipulator [12] (Adapted from Ref. 12 on the basis of OA)

Table 2

DH parameters of Franka Emika Panda manipulator

Fig. 6

Dataset of Rainbow Robotics RB5 manipulator

Fig. 7

Dataset of Franka Emika Panda manipulator

4.2 기구학 파라미터의 중복성 판별

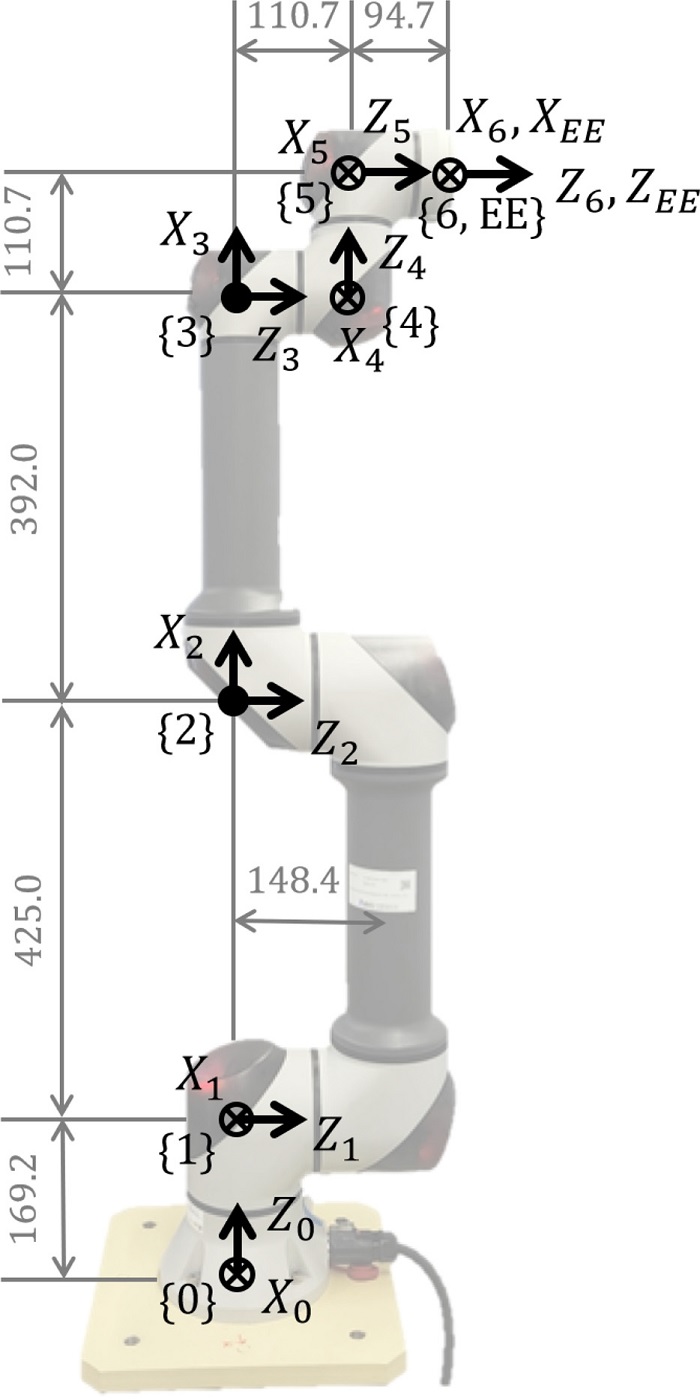
먼저 Rainbow Robotics 사의 6자유도 RB5 모델에 대해 기구학 캘리브레이션 시뮬레이션을 진행하였고, 최적화 과정에서 앞서 설명한 방법으로 자코비안 행렬을 정의하였다. 그 후 단위가 다른 병진 (a_i, d_i) 및 각도 (α_i, θ_i, β_i) 파라미터를 각각 분리하여 피어슨 상관 분석을 진행하였고, Tables 3과 5와 같이 모든 기구학 파라미터에 대해 상관 계수를 확인하였다. 피어슨 상관 계수 결과는 행렬 형태로 나타나고, 상삼각행렬과 하삼각행렬은 동일한 값을 나타낸다. 주 대각 성분의 경우 자기 자신에 대해 상관 분석을 한 결과이므로 1의 값을 갖고, α₆, α_EE, θ₆, θ_EE, β₆, β_EE와 같은 파라미터들은 엔드 이펙터 절대 위치 오차에 아무런 영향을 미치지 않으므로 자코비안 행렬 원소가 모두 0이 되어 NaN의 상관 계수값을 갖는다.

Table 3

Pearson correlation coefficients of Rainbow Robotics RB5 manipulator for prismatic parameters

Table 4

Pearson correlation coefficients of Franka Emika Panda manipulator for prismatic parameters

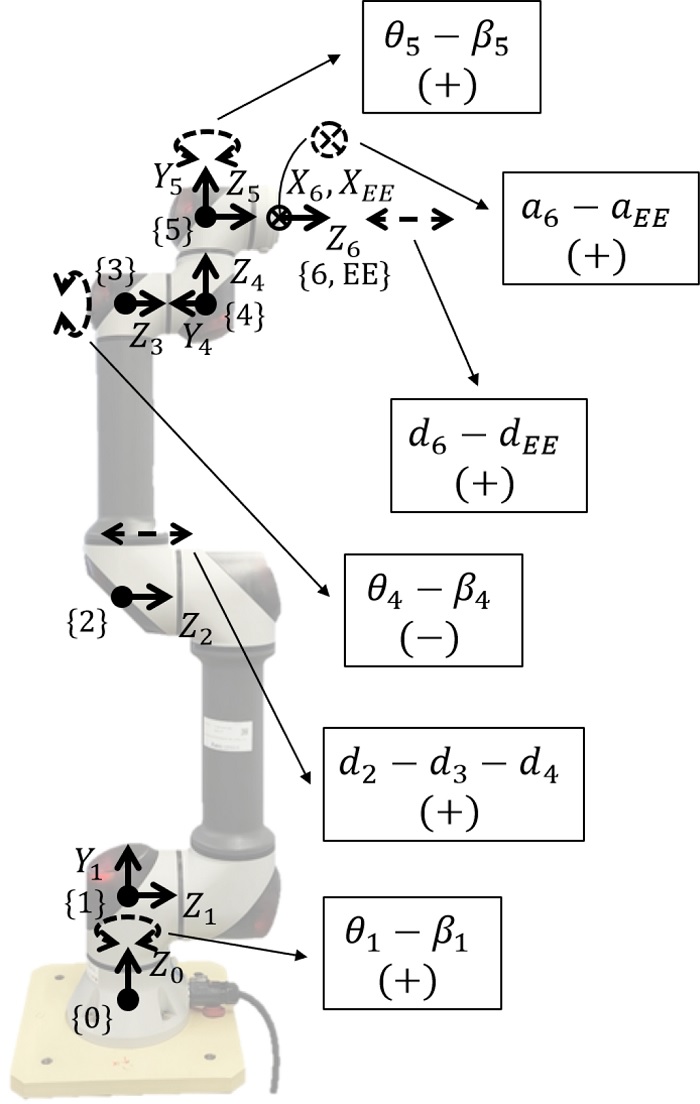
Tables 3과 5의 피어슨 상관 계수 확인 결과 절댓값이 1인 완전한 선형 관계를 갖는 a₆ - a_EE(1), d₂ - d₃ - d₄(1), d₆ - d_EE(1), θ₁ - β₁(1), θ₄ - β₄(-1), θ₅ - β₅(1)의 기구학 파라미터들이 중복성을 갖는다고 판별할 수 있다. 이때 추가적으로 d₂ - d₃ - d₄처럼 3개의 파라미터 사이의 중복성도 판별할 수 있다는 것을 확인하였다.

Table 5

Pearson correlation coefficients of Rainbow Robotics RB5 manipulator for angular parameters

따라서 해당 결과를 Fig. 8과 같이 매니퓰레이터의 기구학 분석을 통해 확인해보면 각각 X₆ - X_EE방향의 병진, Z₁ - Z₂ - Z₃ 방향의 병진, Z₅ - Z₆ 방향의 병진, Z₀ - Y₁ 방향의 회전, Z₃ - Z₄방향의 회전, Z₄ - Y₅방향의 회전에 대응되고 이들 사이에는 자유도가 중복되므로, 본 논문에서 제안한 방법을 통해 판별한 기구학 파라미터의 중복성이 정확하다고 판단할 수 있다.

Fig. 8

Kinematic analysis of Rainbow Robotics RB5 manipulator

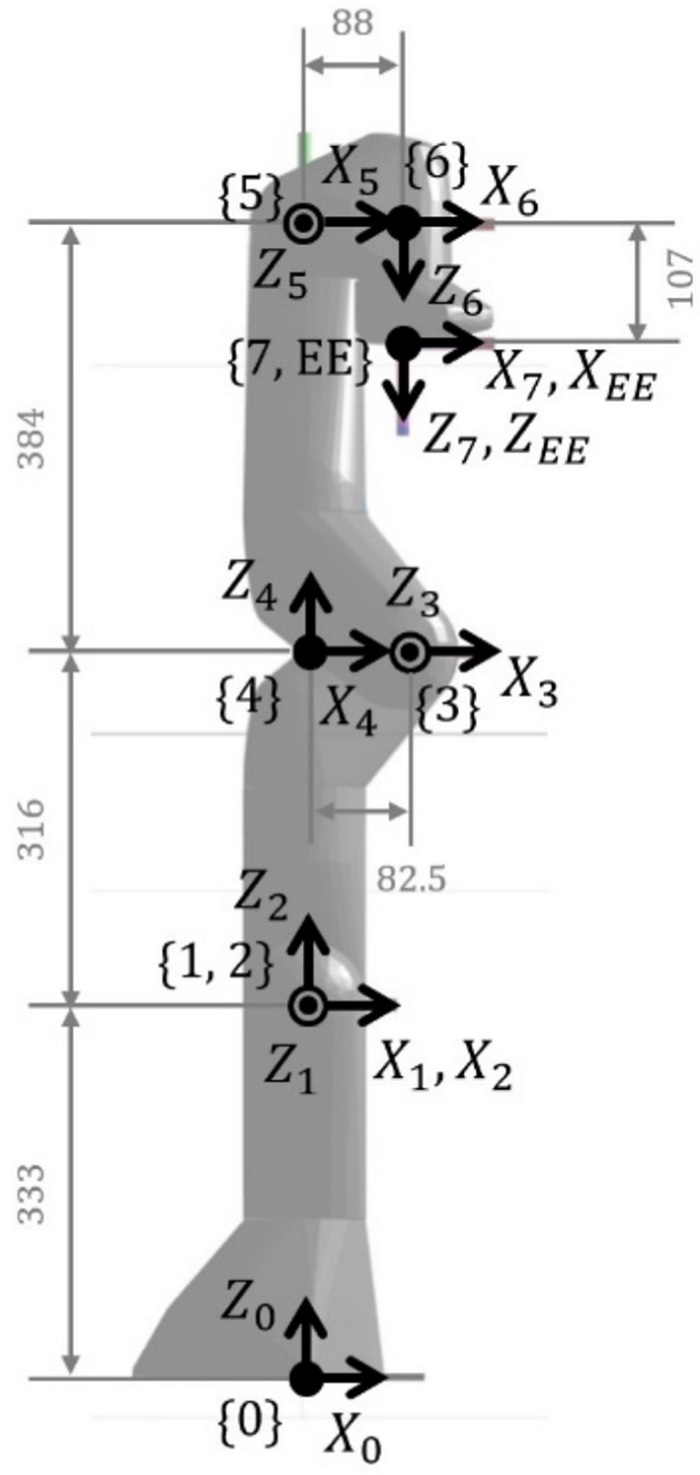
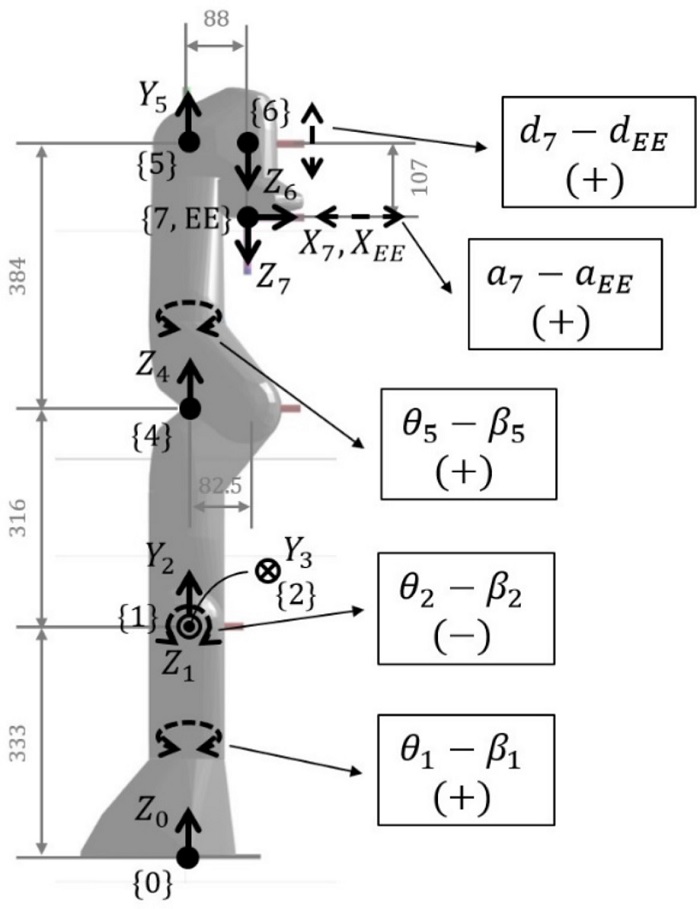
또한 다른 형태를 가진 7자유도 Franka Emika 사의 Panda모델에 대해 기구학 캘리브레이션 시뮬레이션을 진행하였고, Rainbow Robotics 사의 RB5 모델과 동일한 과정으로 기구학 파라미터의 중복성을 판별하였다. 자코비안 행렬을 피어슨 상관 분석하여 Tables 4와 6과 같이 상관 계수를 확인하였고, 절댓값이 1인 완전한 선형 관계를 갖는 a₇ - a_EE(1), d₇ - d_EE(1), θ₁ - β₁(1), θ₂ - β₂(-1), θ₅ - β₅(1) 의 기구학 파라미터들을 중복성으로 판별하였다.

Table 6

Pearson correlation coefficients of Franka Emika Panda manipulator for angular parameters

해당 결과를 Fig. 9와 같이 매니퓰레이터의 기구학 분석을 통해 확인해보면 각각 X₇ - X_EE방향의 병진, Z₆ - Z₇ 방향의 병진, Z₀ - Y₁ 방향의 회전, Z₁ - Y₂ 방향의 회전, Z₄ - Y₅ 방향의 회전에 대응되며 자유도가 중복되는 것을 확인하였다. 따라서 이를 통해 본 논문에서 제안한 기구학 파라미터의 중복성을 판별하는 방법의 정확성을 입증하였다.

Fig. 9

Kinematic analysis of Franka Emika Panda manipulator

4.3 기구학 파라미터의 중복성 제거 전/후 결과 비교

제안한 방법을 통해 판별한 기구학 파라미터의 중복성에 대해 일부 파라미터를 최적화 과정에서 제외시켜 중복성을 제거한 경우와 제거 없이 모든 파라미터를 사용한 경우를 나누어 최적화 과정을 진행하고, 그 결과를 비교하였다. 기구학 파라미터의 중복성을 제거할 때 최적화 과정에서 제외시키는 파라미터 선택에 따라 여러 가지 경우의 수가 존재하므로 모든 경우에 대해 비교를 진행하였고 동일한 결과가 나타났지만, 모든 결과를 첨부할 수 없어 몇 가지 경우에 대해서만 결과를 첨부하였다.

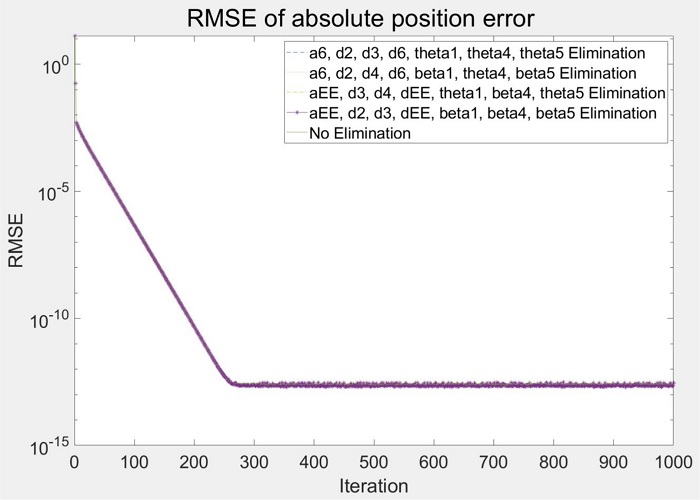
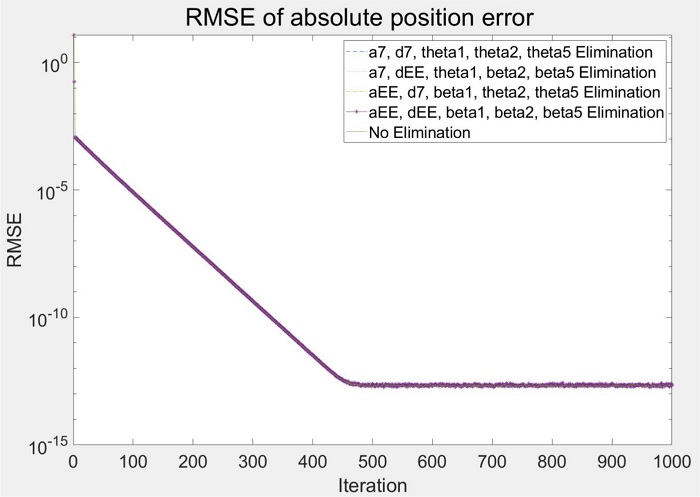
첫 번째로 최적화 과정에서 개선되는 엔드 이펙터의 절대 위치 오차 정확도의 일관성을 확인하기 위해 매 반복 과정에서 보정된 공칭 파라미터로 엔드 이펙터의 절대 위치 오차를 구하였고, 이에 대해 평균 제곱근 오차(Root Mean Square Error, RMSE)를 계산하여 그 수렴성을 그래프로 확인 및 비교하였다. Figs. 10과 11은 각각 RB5 모델과 Panda 모델에 대한 반복 횟수별 평균 제곱근 오차를 나타낸 그래프이고, Tables 7과 8은 각 모델에 대해 100 단위의 반복 횟수별로 중복성을 제거하지 않은 경우와 중복성을 제거한 각각의 경우의 평균 제곱근 오차값을 정리한 표이다.

Fig. 10

RMSE of absolute position error of end-effector (Rainbow Robotics RB5)

Fig. 11

RMSE of absolute position error of end-effector (Franka Emika Panda)

Table 7

RMSE of absolute position error of end-effector per 100 iterations (Rainbow Robotics RB5)

Table 8

RMSE of absolute position error of end-effector per 100 iterations (Franka Emika Panda)

그 결과 두 모델 모두 기구학 파라미터의 중복성을 제거한 경우와 제거 없이 모든 파라미터를 사용한 경우의 엔드 이펙터 절대 위치 오차 RMSE가 거의 동일하게 나타나는 것을 확인하였고, 이를 통해 기구학 파라미터의 중복성 제거 전과 후에 대해 기구학 캘리브레이션 결과의 일관성을 입증하였다.

두 번째로 기구학 파라미터 중복성 제거의 효율성을 입증하기 위해 최적화가 완료된 이후 보정된 중복 파라미터 값을 확인 및 비교하였다. 그 결과 모든 경우에 대해 중복 파라미터 각각의 보정 결과값은 다르지만, 결국 제로섬의 성질을 갖기 때문에 중복성을 고려하면 동일한 보정 결과를 갖는 것을 확인하였다. Tables 9와 10은 각각 RB5 모델의 d₂ - d₃ - d₄와 Panda 모델의 θ₁ - β₁에 대해 위에서 확인한 몇 가지 경우에서 나타난 파라미터 보정 결과와 최적화 과정에 사용한 파라미터 개수를 첨부한 것이다. 따라서 이를 통해 중복성 제거 전/후의 파라미터 보정 결과가 결국 동일하게 나타나는 것을 확인하였다. 또한 파라미터 중복성 제거로 최적화에 꼭 필요한 파라미터만을 사용하여 기구학 캘리브레이션을 진행할 수 있으므로 보정되는 파라미터의 개수를 줄일 수 있다는 측면에서 효율성을 입증하였다.

Table 9

Comparison of redundant parameters d2 - d3 -d4 after optimization (Rainbow Robotics RB5)

Table 10

Comparison of redundant parameters θ1 - β1 after optimization (Franka Emika Panda)