CMP에서 디바이스 패턴의 실 접촉 면적 측정을 통한 평탄화 규명

1. 서론

화학 기계적 평탄화(Chemical Mechanical Planarization, CMP) 공정은 디바이스의 고집적화 및 광역 평탄화를 위한 필수적인 반도체 공정이다[1]. CMP 공정은 연마 패드와 연마 입자에 의한 기계적 작용과 동시에 웨이퍼 박막에서 발생하는 슬러리의 화학적 작용으로 웨이퍼 표면의 결함을 제거하는 기술이다[2]. 웨이퍼에 작용된 외부 하중을 패드 돌기의 직접 접촉과 웨이퍼와 연마 패드 사이에 채워진 슬러리의 유막에 의해 전달되고 웨이퍼와 패드의 상대 회전에 의한 마찰로 재료가 제거된다[3]. 하지만 슬러리의 유체막에 의한 하중 전달은 매우 작아 주로 패드 돌기에 의해 하중이 전달된다[4,5]. 따라서, CMP 공정의 재료 제거에 큰 영향을 미치는 요소는 웨이퍼와 돌기의 접촉 면적들의 합을 의미하는 실 접촉 면적과 얼마나 많은 힘이 웨이퍼에 가해지는지를 의미하는 실 접촉 압력이다[6,7]. 균일한 압력을 받는 박막 웨이퍼와 달리 패턴 웨이퍼는 단차, 밀도, 크기와 같은 패턴의 지형적 특성에 따라 패드와의 접촉이 달라진다. 패턴 웨이퍼의 이상적인 CMP 메커니즘은 패턴의 상부 영역에서 재료 제거가 점진적으로 평탄하게 일어나 광역 평탄화를 이루는 것이지만, 실제 CMP 결과에서는 패턴 상부의 가장자리 영역에서 과연마가 발생하게 된다. 이러한 연마 불균일은 패턴의 지형적 특성에 따라 차이가 발생한다[8,9]. Ouma는 패턴의 밀도에 따라서 인접 패턴이 평탄화 길이에 미치는 영향을 가중치 함수를 이용하여 다이 내 평탄화를 예측하였다[10]. Vasilev는 패턴과 패드의 유효 돌기 곡률(Effective Asperity Curvature)을 고려하여 Greenwood-Williamson의 접촉 이론을 기반의 모델식을 제시하였다[11]. 또한, Jeong은 공정 시간에 따른 돌기의 마모와 실 접촉 면적의 상관관계를 고려한 모델을 제시하였고[6], Lee는 돌기의 변형에 따른 접촉 모드를 나누고 실 접촉 면적 기반 재료 제거 모델을 도출하였다[12]. 언급한 선행 연구는 패턴의 기하학적 특성 및 돌기의 실 접촉 면적을 기반으로 평탄화 모델을 제시하여 연마율을 예측하였지만 패턴에서 돌기의 접촉 분포를 고려하지 않아 패턴 내에서 발생하는 연마 불균일을 예측할 수 없다는 한계점이 존재한다. 따라서, 패턴의 지형적 특성에 따라 발생하는 패턴 내 돌기의 접촉 분포에 대한 연구가 필요하다.

본 연구에서는 디바이스 패턴 내에서 발생하는 연마 패드 돌기의 접촉 분포를 규명하고자 패턴 상하부의 대면적인 실 접촉 면적을 측정하였다. 패턴의 지형적 특성, 연마 시간에 따라 변화하는 패턴 형상과 단차 그리고 인가 압력에 따른 실 접촉 면적 측정을 통해 돌기의 접촉 분포를 분석하였다.

2. 디바이스 패턴과 CMP 패드의 접촉

2.1 CMP 패드

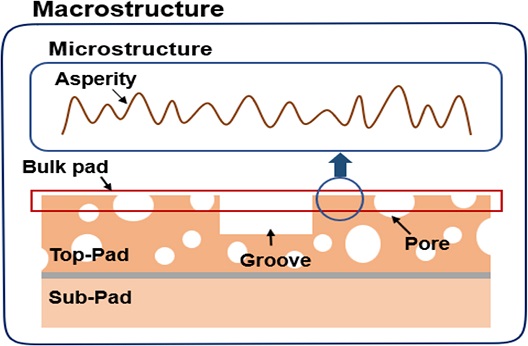
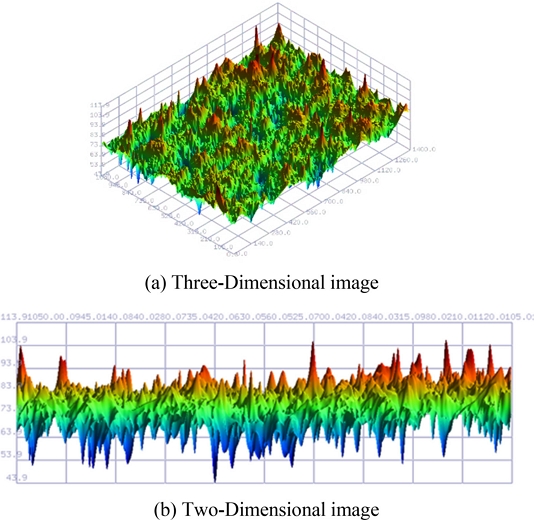
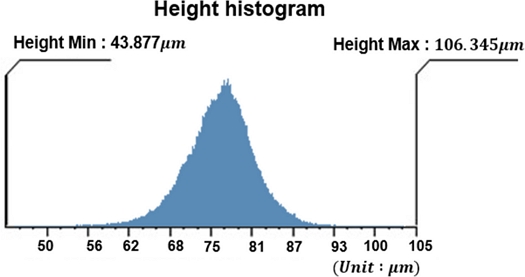
연마 패드는 발포 우레탄 소재로 만들어지며 Fig. 1과 같이 탄성계수가 작은 서브 패드와 탄성계수가 큰 상부 패드가 접착된 형태이다[13,14]. 연마 타겟과 접촉하는 패드의 상단에는 벌크 패드 층이 존재한다. 접촉부의 마이크로 스케일에서는 탄성 계수가 벌크 층에 비해 상대적으로 높고 무작위성을 띄는 돌기들이 존재한다. 일반적으로 연마 공정 전, 브레이크인(Break-In) 공정을 통해 돌기의 거칠기 및 높이를 이상적으로 만드는 과정을 거치게 된다. Fig. 2는 다이아몬드 컨디셔닝(Conditioning) 공정과 더미(Dummy) 공정을 거친 연마 패드를 공초점 현미경으로 측정한 이미지이다. 측정된 이미지의 높이를 분석하면 Fig. 3과 같다. 이와 같이 브레이크인 공정을 거친 연마 패드의 돌기는 일정한 높이와 곡률을 가진다고 가정할 수 있다[15].

Fig. 1

Cross-Section schematic of CMP pad

Fig. 2

Images of pad asperities measured through confocal microscopy

Fig. 3

Height histogram of CMP pad asperities

2.2 패턴-패드 돌기의 접촉

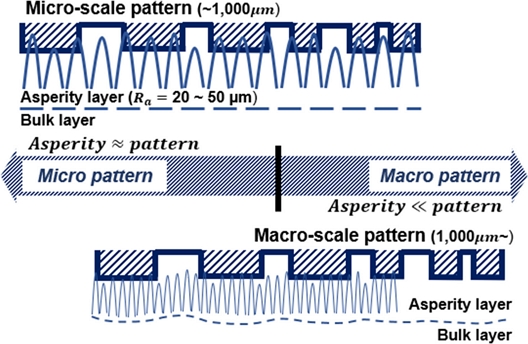
디바이스 패턴의 스케일에 따라 연마 패드와의 접촉을 구분할 수 있다. 1 mm 미만의 마이크로 스케일(Micro-Scale) 접촉과 1 mm 이상의 매크로 스케일(Macro-Scale) 접촉으로 구분할 수 있다. 마이크로 패턴과 연마 패드의 접촉인 경우 Fig. 4와 같이 패턴의 스케일(μm)과 패드 돌기의 스케일(μm)이 같아 기계적 재료 제거에 영향을 미치는 주요 요소는 패드 돌기로 판단할 수 있다. 반면, 매크로 패턴과 연마 패드의 접촉인 경우, 패드 돌기의 스케일에 비해 패턴의 스케일(mm)이 매우 크다. 따라서 재료 제거에 단일 돌기의 영향이 적어지고 돌기 더미와 벌크 층의 영향이 커진다. 돌기 층과 웨이퍼의 접촉은 단단하고 매끄러운 평면과 탄성을 지닌 거친 표면 사이의 접촉이다. Greenwood-Williamson의 접촉 이론을 바탕으로 무작위성을 띄는 돌기의 높이를 다음 식(1)과 같이 지수 함수로 표현할 수 있다[16,17].

$\[ \varphi \left(z\right)=\frac{1}{\text{σ}}\cdot exp\left(-\frac{z}{\text{σ}}\right) \]$

(1)

Fig. 4

Contact mechanism according to pattern scale

여기서 z는 돌기의 높이를 의미하며 σ는 돌기 높이 분포의 편차를 의미한다. 무작위의 돌기 높이에서 웨이퍼와의 접촉 시 발생하는 변형을 수식화하기 위해 가상의 거리인 패드의 참조면과 웨이퍼의 높이인 유효 돌기 높이 d를 정의한 후 돌기의 변형량을 다음 식(2)와 같이 나타낼 수 있다.

$\[ {\text{δ}}_a=d-z \]$

(2)

Greenwood-Williamson의 접촉 이론을 바탕으로 접촉 면적과 접촉 하중을 식(3)과 식(4)로 표현할 수 있다. 여기서 κ_a는 돌기의 곡률, N은 전체 돌기 개수이다. 또한, E는 패드의 탄성계수, υ는 패드의 포와송 비를 의미한다.

$\[ A_a=\frac{\pi }{{\kappa }_a}N{\int }_d^{\infty }{\delta }_a\varphi \left(z\right) dz \]$

(3)

$\[ F_a=\frac{4E}{3\sqrt{{\kappa }_a}\left(1-{\upsilon }^2\right)}N{\int }_d^{\infty }{\delta }_a^{\frac{3}{2}}\varphi \left(z\right) dz \]$

(4)

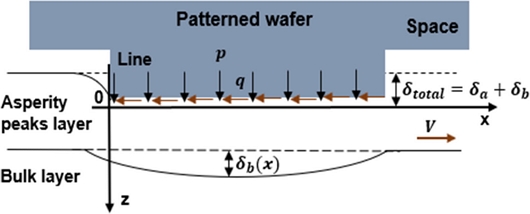
매크로 패턴의 접촉 메커니즘을 고려할 때는 Fig. 5와 같이 벌크 패드 층과 돌기 층으로 나누어 고려해야한다. 2개의 층에서 각각 변형이 일어난다[18]. 따라서 벌크 패드의 변형을 고려해야 한다. 벌크 변형량은 Fig. 4와 같이 단일 패턴 내에서 수평적 위치에 따라 다르다. 따라서 패드의 총 변형량은 식(5)로 나타낼 수 있으며 패턴 내 위치에 따라 다르게 된다. 여기서 δ_b는 벌크 패드의 변형량, δ_total는 패드의 총 변형량을 의미한다.

$\[ {\delta }_{total}\left(x\right)={\delta }_a+{\delta }_b\left(x\right) \]$

(5)

Fig. 5

Idealization of contact between CMP pad and macro pattern

이는 패턴의 접촉 응력이 패턴 내 위치에 따라 다르다는 것을 의미한다. 벌크 변형을 고려한 돌기의 접촉 면적과 접촉 압력 또한 다음과 같이 패턴에서 분포를 가지게 된다. 따라서 본 연구는 벌크의 영향이 큰 매크로 패턴에서의 돌기의 실 접촉 면적 측정을 통해 분포를 분석하여 패턴 내에서 발생하는 연마 불균일을 규명하고자 한다.

3. 실 접촉 면적 측정 및 분석

3.1 실 접촉 면적 측정 시스템

웨이퍼와 연마 패드의 접촉 계면을 측정하기 위해 Fig. 6(a)와 같은 실 접촉 면적 측정 장치를 제작하였다. 측정 장치는 박막을 이용한 멤브레인 타입의 구동 시스템으로 이루어졌다. 원하는 크기의 공압을 고무 재질의 박막에 전달하고, 박막에 부착된 연마 패드가 상단 창에 압착되어 접촉면을 형성한다. 패턴과 패드의 접촉 계면의 광학적 측정을 위해 상단 창은 Fig. 6(c)와 같은 패턴을 1.5 μm의 단차로 에칭한 23 × 23 mm² 크기의 유리 쿠폰을 사용하였다. 측정 시스템은 Fig. 6(b)와 같다. Nikon 사의 광학 현미경으로 측정되었고, 너비 1.6, 높이 1.2 mm의 측정 이미지를 스티칭(Stitching)하여 Fig. 7과 같이 너비 22, 높이 1.2 mm의 이미지로 분석하였다. 이미지는 Abode 사의 Photoshop을 이용한 대비 처리 후 접촉점의 개수 및 면적을 이미지 처리 소프트웨어인 Motic 사의 Motic Image Plus를 통해 분석하여 패턴의 상부와 하부에서의 돌기 접촉을 대면적으로 분석하였다.

Fig. 6

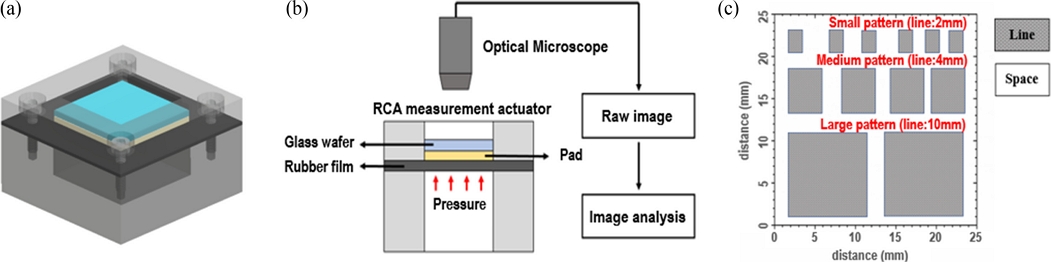
(a) Actuating system for real contact area (RCA) measurement, (b) Measurement system of RCA, and (c) Test layout of glass wafer

Fig. 7

Stitching method for analyzing large-area contact

3.2 디바이스 패턴의 지형적 특성에 따른 RCA 분포

3.2.1 측정 조건

다양한 사이즈와 밀도로 설계된 매크로 패턴의 실 접촉 면적 측정을 통해 패턴의 지형적 특성이 패드와의 접촉에 미치는 영향을 살펴보았다. 측정에는 Table 1과 같은 조건의 컨디셔닝 공정을 거친 23 × 23 mm² 크기의 샘플 패드를 사용하였다. 4 psi의 압력 조건에서 돌기의 압입으로 형성된 접촉 계면을 측정하여 패턴 내 돌기의 분포를 분석하였다.

Table 1

Break-In conditions of sample pads

3.2.2 측정 결과 및 분석

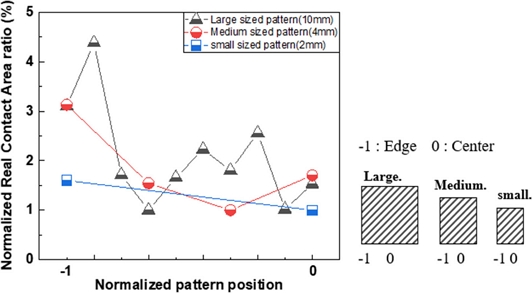
10, 4 그리고 2 mm 크기의 상부(Line)를 가지는 패턴에서의 돌기의 접촉 분포를 분석하였다. Fig. 8은 각 패턴에서 측정된 실 접촉 면적 비율을 패턴의 중심(0)을 기준으로 노멀라이징(Normalizing)하여 비교한 그래프이다. 한 점당 기준 면적 50 × 1,200 μm² 내에 나타나는 접촉 면적의 총합을 의미한다. 큰 패턴, 중간 패턴 그리고 작은 패턴에서 패턴의 중심 영역 대비 가장자리 영역에서 돌기 접촉 면적은 각 4.38, 3.13, 1.60배 높게 나타났다. 이를 통해 패턴의 크기가 클수록 중심 영역에 비해 가장자리 영역에서 돌기의 접촉이 집중되는 것을 확인할 수 있다.

Fig. 8

Normalized real contact area ratio according to normalized pattern position

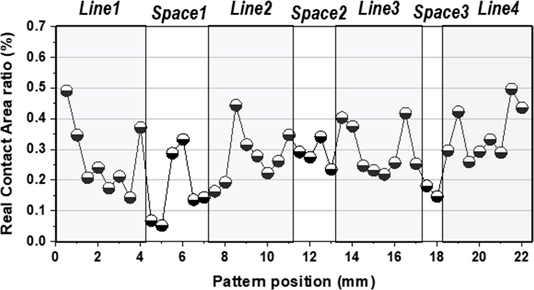
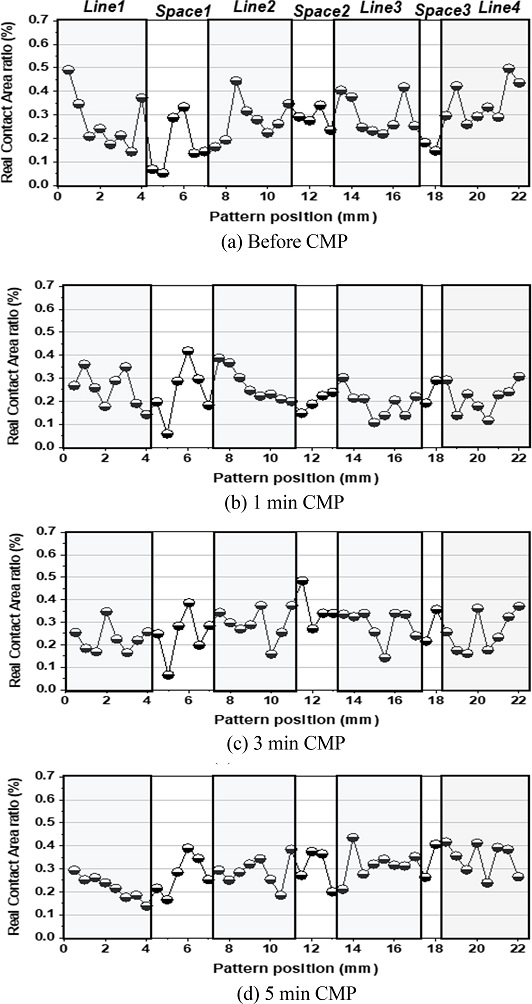
Fig. 9는 패턴의 밀도에 따른 돌기의 접촉 분포를 확인하기 위해 다이 내 다양한 밀도로 배치된 패턴의 상부와 하부(Space) 영역에서의 실 접촉 면적 분포를 나타낸 그래프이다. 패턴은 4 mm 너비의 상부를 가지고 57.1, 66.7, 80.0%의 밀도로 배치되었다. 밀도 57.1, 66.7, 80.0%인 패턴에서 상부의 가장자리와 중심 영역에서의 접촉 면적 비율 차이가 각 0.3173, 0.2209, 0.1995%로 나타났다. 즉 밀도가 낮은 패턴에서 가장자리와 중심 영역의 접촉 면적 분포 차이가 크다는 것을 확인할 수 있다. 이와 같이 패턴의 지형적 특성에 따른 돌기의 접촉 면적 측정을 통해, 크기가 크고 밀도가 낮은 패턴에서 돌기의 접촉 분포가 크게 나타나는 것을 확인하였다.

Fig. 9

Normalized real contact area ratio according to normalized pattern position

3.3 연마 시간에 따른 패턴 내 RCA 분포

3.3.1 연마 및 측정 조건

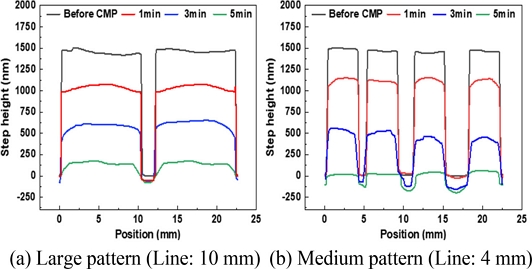
연마 실험은 Fig. 6(c)의 패턴을 1.5 μm의 단차로 에칭한 4인치 유리 웨이퍼를 대상으로 진행하였다. 연마기는 GnP Technology 사의 POLI-500을 사용하였고, 연마 패드는 KPX 사의 KONI 패드를 사용하였다. 브레이크인 조건은 Table 1과 같고, 연마 조건은 Table 2에 제시하였다. 연마 후 패턴의 프로파일은 Nanoscope사의 Nanoview로 측정되었고, Figs. 10(a)와 10(b)는 각 상부의 너비가 10인 큰 패턴, 4 mm인 중간 패턴의 연마 시간에 따른 패턴의 프로파일을 나타낸다. 연마가 진행됨에 따라 패턴의 단차가 줄어들고 패턴의 가장자리 쪽의 과연마로 인해 라운딩(Rounding) 현상이 발생하는 것을 확인할 수 있다. 연마된 쿠폰을 사용하여 4 psi의 압력 조건에서 실 접촉 면적 측정을 진행하였다.

Table 2

Polishing conditions of 4 inch glass patterned wafer

Fig. 10

Graphs of step height change according to polishing time

3.3.2 측정 결과

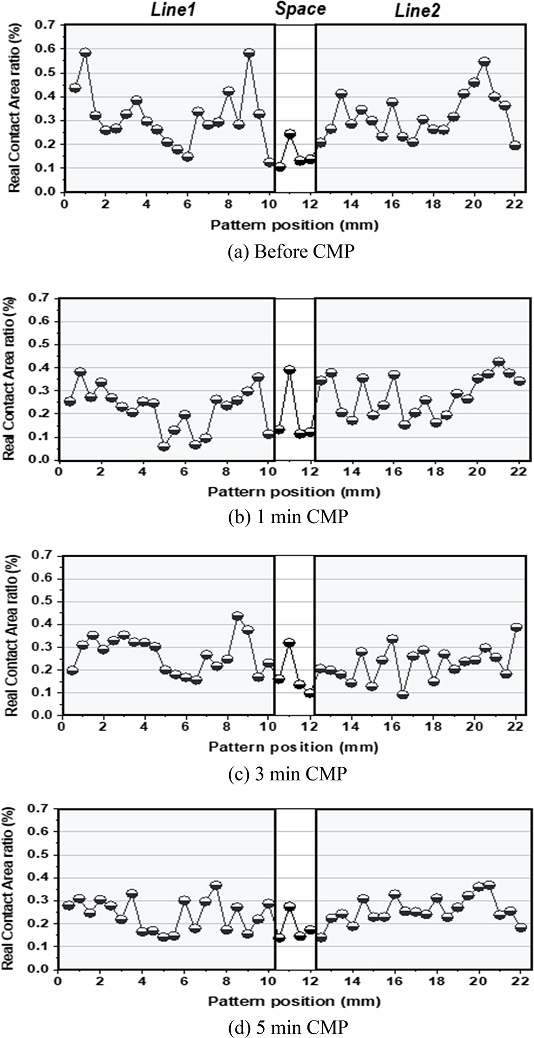
연마가 진행됨에 따라 감소하는 패턴의 단차와 라운딩에 의한 패턴의 형상이 패드 돌기와의 접촉에 미치는 영향을 분석하기 위해 연마 시간에 따른 실 패턴의 실 접촉 면적을 측정하였다. Fig. 11은 큰 패턴의 실 접촉 면적 분포 측정 결과이다. Figs. 11(a)부터 11(d)는 50 × 1,200 μm²의 기준 면적에서의 연마전과 1, 3, 5분 후의 돌기의 접촉 면적 분포를 나타낸 그래프이다. 패턴 상부에서 가장자리와 중심 영역의 최대 접촉 면적율 차이가 0.4368, 0.3233, 0.2806, 0.2556%로 점차 감소하였다. 패턴 상부와 하부의 접촉 면적률 차이 또한 감소하였다. 이를 통해 패턴의 평탄화가 진행되면서 패드 돌기의 접촉이 점차 균일해지는 것을 확인할 수 있다. Figs. 12(a)부터 12(d)는 중간 패턴에서의 연마 시간에 따른 실 접촉 면적 비율 분포를 나타낸 그래프이다. 밀도가 낮은 패턴의 가장자리와 중심의 접촉률 차이가 크고 연마 시간에 따라 감소율이 빠르다. 또한 밀도 0.571인 패턴에서 가장자리와 중심의 최대 접촉률 차이가 연마 시간에 따라 0.3173, 0.1828, 0.0589, 0.05443%로 줄어들었다. 큰 패턴과 비교해보면 크기가 작은 패턴이 가장자리와 중심의 접촉률 차이가 작고 감소율이 빠르다. 이를 통해 패턴의 라운딩 현상은 패턴의 밀도가 낮고 크기가 클수록 크게 나타나고, 평탄화 속도는 패턴의 밀도가 낮고 크기가 작을수록 빠른 것을 예측할 수 있다.

Fig. 11

RCA distribution in large pattern according to polishing time

Fig. 12

RCA distribution in medium pattern according to polishing time

Figs. 11과 12를 통해 패턴 형상과 벌크 패드 층의 변형 형상의 상관 관계를 예측할 수 있다. 연마 전 단차가 크고 패턴 형상이 직각일 때 벌크 패드의 변형에 의해 가장자리에 패드 돌기의 접촉이 집중된다. 연마가 진행되면서 패턴의 곡률이 줄어들면서 벌크 패드의 곡률 또한 감소하여 패턴 내 돌기의 접촉이 균일해지는 것을 예측할 수 있다.

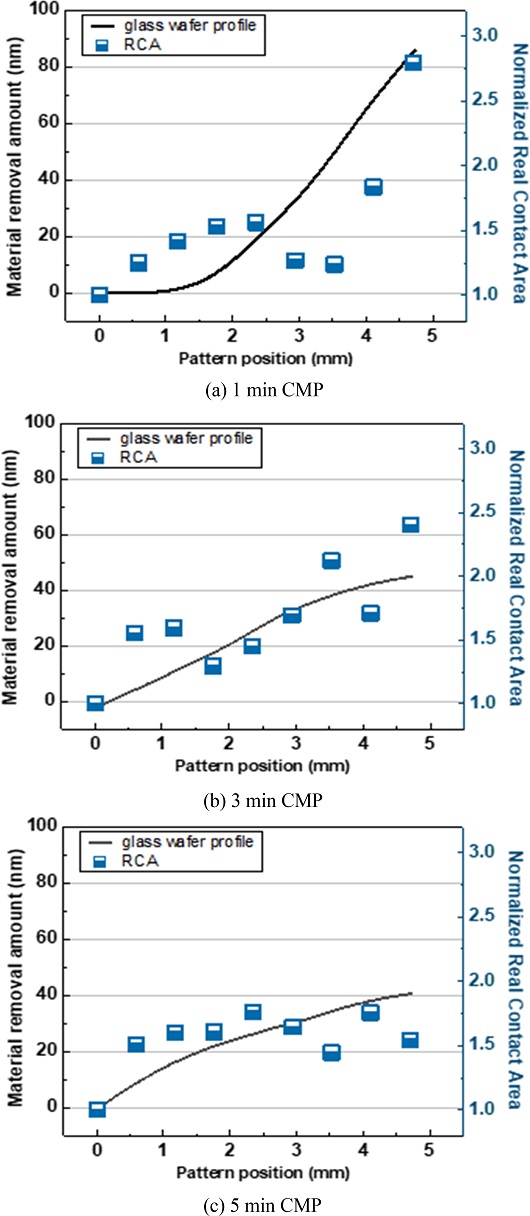
Fig. 13은 큰 패턴에서 유리 웨이퍼의 연마 결과와 측정된 실 접촉 면적 분포의 정합성을 비교한 그래프이다. Figs. 13(a)부터 13(c)는 각각 1분 동안의 연마량, 1분 연마 프로파일 기준 2분 동안의 연마량, 3분 연마 프로파일 기준 2분 동안의 연마량과 실 접촉 면적을 패턴의 중심 영역을 기준으로 패턴의 위치에 따른 분포를 비교한 그래프이다. 이를 통해 연마량과 실 접촉 면적 분포의 경향이 일치하는 것을 확인할 수 있다.

Fig. 13

Compatibility comparison between amount of removal rate and real contact area

3.4 압력 크기에 따른 패턴 내 RCA 분포

3.4.1 측정 조건

웨이퍼에 가해지는 외부 하중이 패턴과 패드 돌기의 접촉에 미치는 영향을 살펴보기 위하여 가압 크기를 변화시키며 실 접촉 면적을 측정하였다. Table 1의 조건으로 컨디셔닝 공정을 거친 샘플 패드를 사용하였고, 3.2.1절과 같은 조건에서 측정되었다. 압력 조건을 2에서 5 psi로 단계적으로 조절하며 접촉 면적을 측정하였다.

3.4.2 측정 결과

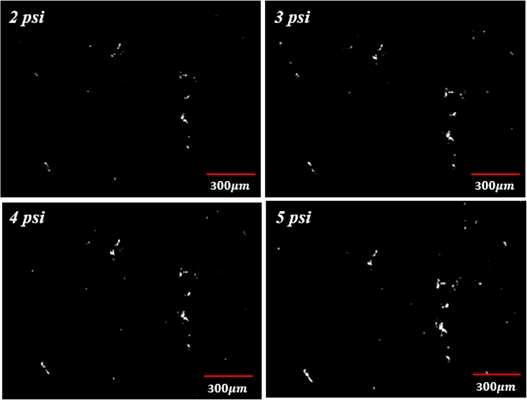
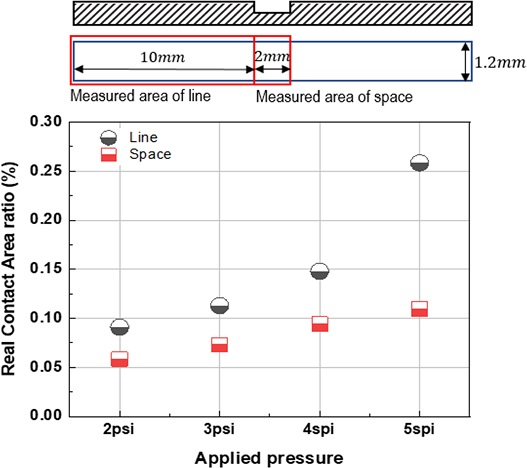
Fig. 14는 가압 크기에 따른 돌기들의 접촉을 측정한 이미지로, 흰색 점들은 돌기의 접촉점이다. 압력이 증가할수록 돌기의 접촉 면적과 접촉 개수가 증가하는 것을 확인할 수 있다. Fig. 15는 압력 크기에 따른 패턴의 상부와 하부 영역에서의 실 접촉 면적 비율을 비교한 그래프이다. 한 점당 기준 면적에서 나타나는 돌기들의 접촉 면적의 합을 의미하며, 상부의 기준 면적은 10 × 1.2 mm², 하부의 기준 면적은 0.2 × 1.2 mm²이다. 상부와 하부 모두 압력이 증가할수록 접촉 면적이 증가하였다. 2 psi의 압력 조건에 비해 5 psi에서 돌기의 접촉 면적이 하부는 87.79, 상부는 184.26% 증가하였다. 이를 통해 하부에 비해 상부 영역에서 압력 증가에 따른 접촉 면적 증가율이 큰 것을 확인할 수 있다.

Fig. 14

Images of real contact area according to applied pressure

Fig. 15

Real contact area ratio under various applied pressure values

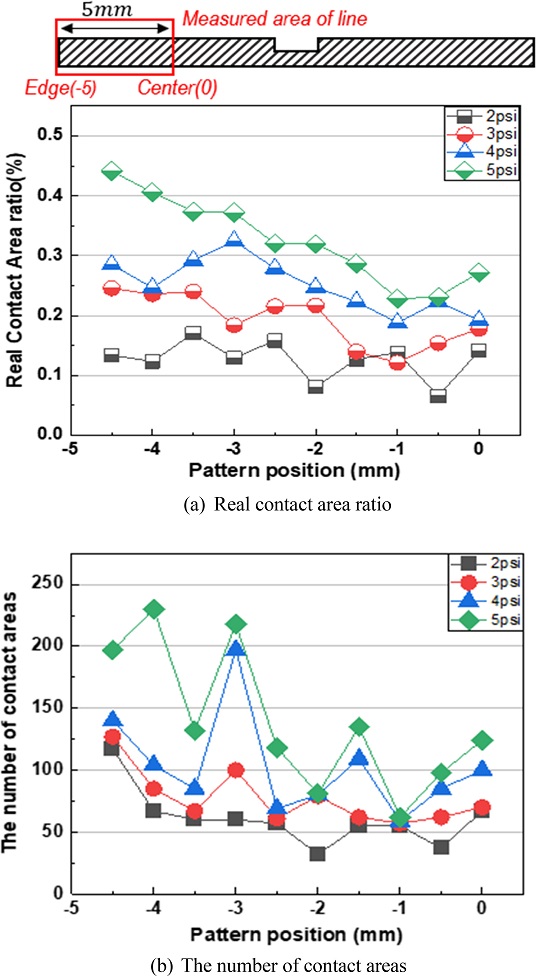
Figs. 16(a)와 16(b)는 패턴 상부의 중심(0)에서 가장자리(-5) 영역까지의 접촉 면적과 접촉점 개수의 분포를 나타낸 그래프이다. 모든 영역에서 압력이 증가할수록 접촉 면적과 접촉점 개수가 증가하는 것을 확인할 수 있다. 2와 3 psi 조건에서는 접촉점 개수의 증가율에 비해 접촉 면적의 증가율이 큰 것을 확인할 수 있다. 이는 압력에 의해 접촉된 단일 돌기들의 압입량이 증가하여 접촉 면적이 증가한 것으로 예측할 수 있다. 반면 4와 5 psi에서는 패턴 가장자리 영역에서 접촉점의 개수가 급격히 증가하는 것을 확인할 수 있다. 이는 압력이 증가함에 따라 높이가 낮은 돌기들이 접촉하게 되어 새로운 돌기들의 접촉에 의해 접촉 면적과 접촉점의 개수가 증가하는 것으로 예측할 수 있다.

Fig. 16

Graphs of contact distribution in line according to applied pressure

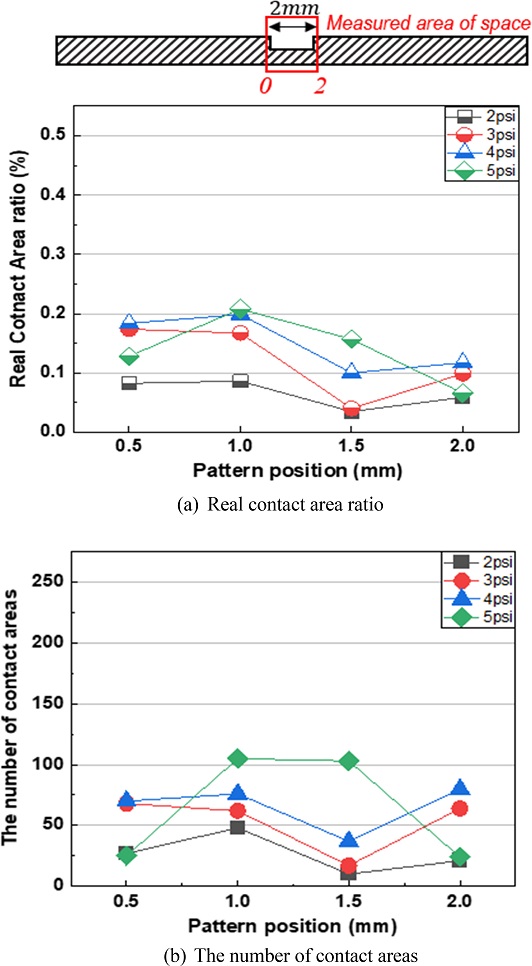
Figs. 17(a)와 17(b)는 패턴 하부에서의 압력에 따른 접촉 면적과 접촉점 개수의 분포를 나타낸 그래프이다. 압력 증가에 따라 접촉 면적이 증가하는데, 5 psi의 압력 조건에서는 하부의 중심 영역에서는 접촉 면적과 접촉점의 개수가 증가하는 반면 가장자리 영역에서는 감소하는 것을 확인할 수 있다.

Fig. 17

Graphs of contact distribution in line according to applied pressure

Figs. 16과 17을 통해 압력에 따른 벌크 패드의 변형을 예측할 수 있다. 상부 영역에서는 특정 압력에서 벌크 패드 변형이 나타나며 높이가 낮은 돌기들이 접촉하게 되면서 패턴의 가장자리 돌기의 접촉이 집중된다. 하부 영역에서는 특정 압력에 벌크 패드 변형에 의해 중심 영역에 돌기의 접촉이 집중되고, 가장자리 영역에서는 접촉을 하지 않는다. 즉 상부와 하부의 경계에서 PR‹접촉률이 급격하게 낮아진다. 이는 단차에 의한 높이의 불연속성에 의한 영향이라 판단된다.

4. 결론

본 연구는 CMP 공정을 대상으로 디바이스 패턴과 패드 돌기의 실 접촉 면적을 분석하고 평탄화 결과와의 상관관계를 규명하였다. 유리 패턴 웨이퍼를 이용한 측정과 이미지 스티칭을 통해 대면적인 실 접촉 면적 분석을 통해 돌기의 접촉 분포를 확인하고, 패턴의 지형적 특성에 따른 평탄화 경향을 확인하였다.

연마 초기의 패턴에서는 상부의 크기가 크고 밀도가 낮은 패턴에서 중심에 비해 가장자리 영역에서 돌기의 접촉이 집중되었다. 패턴 하부에서는 밀도가 낮은 영역에서 돌기의 접촉률이 높았다. 이를 통해 패턴의 크기가 크고 밀도가 낮은 패턴 형상의 라운딩이 크게 나타나는 것을 예측할 수 있다. 연마가 진행되면서 패턴의 단차와 형상 곡률이 감소함에 따라 상부와 하부 영역에서 돌기의 접촉 분포가 균일해지며 패턴이 평탄화를 이루는 것을 확인하였다. 또한 이러한 패드 돌기의 분포가 형성되는 원인에 대해 압력에 따른 돌기의 접촉 분포 분석을 통해 규명하였다. 특정 압력 전후로 접촉 면적 증가율의 원인이 변화하는 것을 확인하였다. 낮은 압력의 경우 접촉된 단일 돌기의 압입량이 증가하여 접촉 면적이 커지는 반면, 높은 압력의 경우 돌기의 접촉 개수가 급격하게 증가하여 접촉 면적이 증가하였다. 이는 탄성계수가 돌기에 비해 낮은 벌크 패드가 패턴의 가장자리에서 생기는 리바운딩으로 높이가 낮은 돌기들이 접촉하게 되면서 나타나는 현상이라 판단할 수 있다.

벌크 패드의 변형에 의해 돌기의 접촉 분포가 발생하면 패턴 내에서 연마 불균일을 초래하게 된다. 이러한 문제를 해결하기 위해서는 패드 개발을 통해 칩 내 패턴의 지형적 특성 및 특정 공정 조건에서 발생하는 패드 벌크 층의 변형에 의한 영향을 줄이는 것이 필요하다. 또한 디바이스 패턴 설계 시 벌크 층의 변형을 고려한 더미 패턴 설계를 통해 해결할 수 있으며, 이러한 연구 개발에 있어 본 연구의 활용을 기대할 수 있다.

그러나 본 연구에서 측정된 디바이스 패턴과 연마 패드의 접촉 분포는 패드 돌기의 무작위성과 탄성계수의 영향으로 결과가 상이할 수 있다. 이러한 조건에 가중치를 부여하여 대응할 수 있으며 돌기의 접촉 분포를 활용한 벌크 변형 모델 및 재료 제거 모델을 도출한다면 보다 정합성이 높은 평탄화 프로파일 시뮬레이터 개발을 기대할 수 있을 것이다.

Acknowledgments

이 과제는 부산대학교 기본연구지원사업(2년)에 의해 연구되었음.

REFERENCES

• Zantye, P. B., Kumar, A., Sikder, A., (2004), Chemical mechanical planarization for microelectronics applications, Materials Science and Engineering: R: Reports, 45(3-6), 89-220. [https://doi.org/10.1016/j.mser.2004.06.002]
• Lee, H., Sung, I.-H., (2019), Chemical mechanical polishing: A selective review of R&D trends in abrasive particle behaviors and wafer materials, Tribology and Lubricants, 35(5), 274-285.
• Luo, J., Dornfeld, D. A., (2001), Material removal mechanism in chemical mechanical polishing: theory and modeling, IEEE Transactions on Semiconductor Manufacturing, 14(2), 112-133. [https://doi.org/10.1109/66.920723]
• Wang, D., Lee, J., Holland, K., Bibby, T., Beaudoin, S., Cale, T., (1997), Von mises stress in chemical-mechanical polishing processes, Journal of the Electrochemical Society, 144(3), 1121. [https://doi.org/10.1149/1.1837542]
• Fu, G., Chandra, A., Guha, S., Subhash, G., (2001), A plasticity-based model of material removal in chemical-mechanical polishing (CMP), IEEE Transactions on Semiconductor Manufacturing, 14(4), 406-417. [https://doi.org/10.1109/66.964328]
• Jeong, H., Lee, H., Choi, S., Lee, Y., Jeong, H., (2012), Prediction of real contact area from microtopography on CMP pad, Journal of Advanced Mechanical Design, Systems, and Manufacturing, 6(1), 113-120. [https://doi.org/10.1299/jamdsm.6.113]
• Wang, L., Li, H., Zhou, P., Yan, Y., (2020), Impact of PAD micro contact size and distribution on the planarization in CMP, Proceedings of the 2020 China Semiconductor Technology International Conference, 1-4. [https://doi.org/10.1109/CSTIC49141.2020.9282530]
• Boning, D., Lee, B., Oji, C., Ouma, D., Park, T., Smith, T., Tugbawa, T., (1999), Pattern dependent modeling for CMP optimization and control, MRS Online Proceedings Library, 566, 197-209. [https://doi.org/10.1557/PROC-566-197]
• Gbondo-Tugbawa, T. E., (2002), Chip-Scale modeling of pattern dependencies in copper chemical mechanical polishing processes, Ph.D. Thesis, Massachusetts Institute of Technology.
• Ouma, D., Boning, D., Chung, J., Shin, G., Olsen, L., Clark, J., (1998), An integrated characterization and modeling methodology for CMP dielectric planarization, Proceedings of the IEEE 1998 International Interconnect Technology Conference, 67-69.
• Vasilev, B., Bott, S., Rzehak, R., Kücher, P., Bartha, J. W., (2012), A feature scale Greenwood-Williamson model predicting pattern-size effects in CMP, Microelectronic Engineering, 91, 159-166. [https://doi.org/10.1016/j.mee.2011.09.007]
• Lee, H., (2019), Semi-Empirical material removal model with modified real contact area for CMP, International Journal of Precision Engineering and Manufacturing, 20(8), 1325-1332. [https://doi.org/10.1007/s12541-019-00161-6]
• Yu, C., Wang, Z., Sun, F., Lu, S., Keer, L. M., Wang, Q. J., (2013), A deterministic semi-analytical model for the contact of a wafer and a rough bi-layer pad in CMP, ECS Journal of Solid State Science and Technology, 2(9), 368-374. [https://doi.org/10.1149/2.017309jss]
• Lee, S., Kim, H., Dornfeld, D., (2005), Development of a CMP pad with controlled micro features for improved performance, Proceedings of the IEEE International Symposium on Semiconductor Manufacturing, 173-176.
• Jeong, S., Jeong, K., Choi, J., Jeong, H., (2021), Analysis of correlation between pad temperature and asperity angle in chemical mechanical planarization, Applied Sciences, 11(4), 1507. [https://doi.org/10.3390/app11041507]
• Zhao, Y., Maietta, D. M., Chang, L., (2000), An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow, Journal of Tribology-Transactions of the ASME, 122(1), 86-93. [https://doi.org/10.1115/1.555332]
• Greenwood, J. A., Williamson, J. P., (1966), Contact of nominally flat surfaces, Proceedings of the Royal Society of London. Series A. Mathematical Physical and Engineering Sciences, 295(1442), 300-319. [https://doi.org/10.1098/rspa.1966.0242]
• Tichy, J., Levert, J. A., Shan, L., Danyluk, S., (1999), Contact mechanics and lubrication hydrodynamics of chemical mechanical polishing, Journal of the Electrochemical Society, 146(4), 1523. [https://doi.org/10.1149/1.1391798]