엔진 마운트 최적 댐핑 제어와 MR 마운트에의 적용

1. 서론

차량의 엔진과 차체 사이에 위치하는 엔진 마운트는 엔진의 장착하중에 대한 지지는 물론 차량의 승차감 향상을 위해 적절한 강성 및 감쇠를 가져야 한다. 엔진의 회전으로 발생되는 가진력은 엔진 마운트를 거쳐 차체에 전달되며, 또한 차체의 진동은 엔진 마운트를 거쳐 엔진의 진동을 유발한다. 승차감 측면에서 엔진 가진력이 차체에 전달되는 힘 전달률과 차체 진동이 엔진 진동으로 전달되는 변위 전달률 모두를 작게 설계하는 것이 바람직하다. 구체적으로 차체 진동에 의한 차체와 엔진의 상대진동을 작게 하기 위해서 엔진 마운트가 가져야 될 특성은 차체의 저주파 진동에 대해서는 높은 강성과 높은 감쇠계수, 고주파 진동에 대해서는 낮은 강성과 낮은 감쇠계수를 갖는게 이상적이다. 또한 엔진 가진력의 차체 전달률을 작게 하기 위해서는 마찬가지로 저주파 가진력에 대해서는 높은 강성과 높은 감쇠계수, 고주파 가진력에 대해서는 낮은 강성과 낮은 감쇠계수를 갖는게 이상적이다[1-3]. 하지만 이 조건은 서로 상반되는 특성을 가지므로 강성과 감쇠계수가 고정값을 갖는 일반적인 수동형 엔진 마운트로는 승차감 향상에 한계가 있다.

지금까지 엔진 마운트는 고무 마운트, 유압 마운트 등의 수동형 마운트가 사용되어 왔으며, 고무 마운트에 비해 유압 마운트는 유체의 점성을 이용한 댐핑 효과를 얻을 수 있어 많이 사용되고 있다. 그러나 수동형 마운트는 주파수 범위별로 상반되는 조건을 만족하기에 어려우므로 이를 개선하기 위해 MR 유체 또는 ER 유체를 사용하는 반능동 마운트 또는 능동 제어를 적용하는 능동 마운트가 사용되고 있다. 능동 마운트의 경우 제어를 위한 액튜에이터, 센서 등이 필요하므로 복잡성과 경제적인 측면에서 반능동 마운트가 선호되고 있다[4-8].

반능동 마운트의 대표적인 예가 MR 마운트이다. MR 마운트는 유압 마운트의 유압유 대신 MR 유체를 사용한다. MR 유체는 점성을 갖는 용매에 상자성(Paramagnetic) 입자를 분산시킨 유체로 MR 유체의 통로에 자기장을 가하여 유체의 유동 마찰력을 조정할 수 있다. MR 엔진 마운트는 실제 차량에 적용되고 있을 뿐 아니라, 기타 다양한 진동 저감 분야에 사용되고 있다[9-14].

본 연구에서는 차체 진동에 의한 차체-엔진 상대 진동 전달률과 엔진 가진력의 차체 전달률 모두를 관심 주파수 대역 범위에서의 H_∞-노옴(Norm)을 최소화할 수 있는 최적 댐핑의 해석적 설계 방법을 제안하며, 이를 MR 마운트로 구현하는 방법을 제시한다. 설계된 최적 댐핑 제어를 적용한 MR 마운트의 승차감 개선 효과를 MatLab을 이용한 시뮬레이션을 통해 검증한다.

2. 유압 엔진 마운트

2.1 유압 마운트 동역학 모델

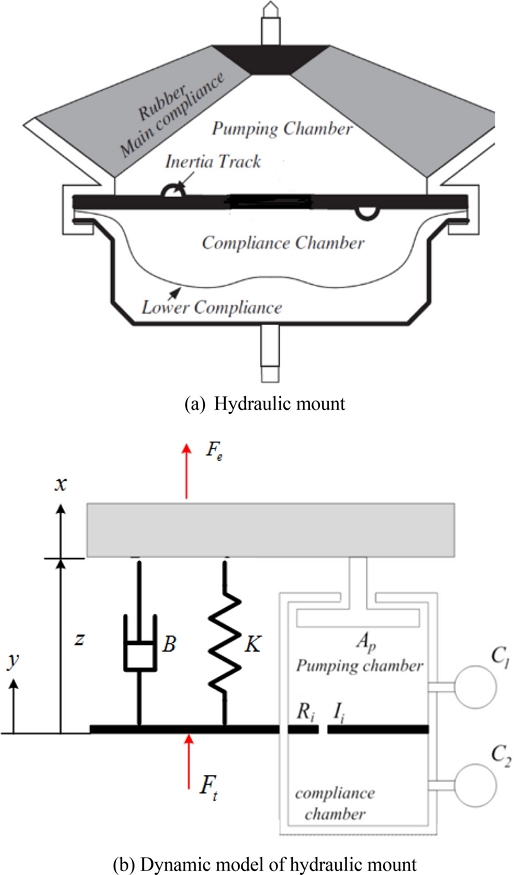
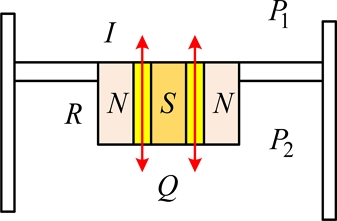
유압 마운트는 고무 마운트에 비해 점성 마찰을 추가할 수 있어 많이 이용되고 있다. Figs. 1(a)는 유압 마운트 개념도이며, 1(b)는 유압 마운트의 동역학 모델이다[2].

Fig. 1

Hydraulic mount and its dynamic model

Fig. 1(a)에서 엔진 마운트는 상부와 하부로 나누어지며, 상부의 펌핑챔버(Pumping Chamber)와 하부의 컴플라이언스챔버(Compliance Chamber)에는 점성 유체가 가득 충진된 상태이다. 상하챔버 사이에는 분리벽이 존재하며, 분리벽에는 관성트랙(Inertia Track)이 있어 상하부챔버에 있는 유체가 관성트랙을 통해 상하로 흐를 수 있다. 상부 펌핑챔버는 엔진에 연결되며, 중단의 분리벽은 차체에 고정 연결된다. 펌핑챔버의 고무는 강성과 점성을 가지며, 컴플라이언스챔버는 저탄성을 갖는 고무막으로 되어 있다. 이 유압 엔진 마운트는 상부에 연결된 엔진이 진동하면 챔버 내부의 유압의 압력 변화가 생기고, 이로 인해 유체가 관성트랙을 통해 상하부챔버로 흐르게 되고, 이때 관성트랙을 흐르는 유체의 점성 마찰이 진동 감쇠에 영향을 미친다. Fig. 1(b)에서 엔진 마운트의 운동방정식을 유도하면 식(1)과 같다.

$\[ \left\{\begin{array}{c}{P}_1-P_2=I\dot{Q}+RQ\hfill \\ c_1{\dot{P}}_1=A_p\left(\dot{y}-\dot{x}\right)-Q\hfill \\ c_2{\dot{P}}_2=Q\hfill \\ M\ddot{x}+B\left(\dot{x}-\dot{y}\right)+K\left(x-y\right)=A_p{P}_1+F_e\hfill \end{array}\right. \]$

(1)

여기서 M은 엔진의 질량, B, K는 고무 마운트의 점성계수와 강성계수, P₁, P₂는 상부와 하부 챔버의 압력, c₁, c₂는 상부와 하부 챔버의 컴플라이언스, Q는 관성트랙을 통해 흐르는 유량, R은 관성트랙의 댐핑, I는 유체의 관성 관련 변수, A_p는 엔진 변위에 따른 챔버 내부 압력 변화에 관계된 등가 단면적, y는 차체의 변위, x는 엔진의 변위, z는 차체와 엔진의 상대 변위를 나타낸다. 유체의 관성 I는 식(2.1)과 같으며, 관성트랙의 댐핑 계수 R은 트랙이 원형일 때와 이중 환형(Annular)일 때 각각 식(2.2)와 같다.

$\[ I=\frac{\rho L}{A_i} \]$

(2.1)

$\[ R=\left\{\begin{array}{c}\frac{8\mu L}{\pi r_o^4} for circular pipe\hfill \\ \frac{8\mu L}{\pi }\frac{1}{\left(r_o^4-r_i^4\right)-\frac{{\left(r_o^2-r_i^2\right)}^2}{In\left[\frac{r_o}{r_i}\right]}} for annular\hfill \end{array}\right. \]$

(2.2)

여기서 A_i, L은 각각 관성트랙의 단면적과 길이이며, ρ는 유체밀도, μ는 점성계수, r_o, r_i는 각각 이중환형단면의 장반경과 단반경이다. 식(1)을 정리하여 운동방정식 식(3)을 얻을 수 있다.

$\[ \left\{\begin{array}{c}I{\ddot{P}}_2+R{\dot{P}}_2+\left(\frac{1}{c_1}+\frac{1}{c_2}\right)P_2=-\frac{A_p}{c_1{c}_2}z\hfill \\ M\ddot{z}+B\dot{z}+\left(K+\frac{A_p^2}{c_1}\right)z=-M\ddot{y}-\frac{{c_{2}A}_p}{c_1}{P}_2+F_e\hfill \end{array}\right. \]$

(3)

식(3)에서 차체의 변위 Y(s)와 차체와 엔진의 상대변위 Z(s) 간의 전달함수 L(s)는 진동 전달률에 해당하며, 그 관계는 식(4)와 같다.

$\[ Z\left(s\right)=L\left(s\right)Y\left(s\right) \]$

(4)

여기서

$\[ L\left(s\right)=\frac{-M{s}^{2}G\left(s\right)}{H\left(s\right)G\left(s\right)-\frac{A_p^2}{c_1^2}} \]$

$\[ G\left(s\right)=I{s}^2+Rs+\left(\frac{1}{c_1}+\frac{1}{c_2}\right), H\left(s\right)=M{s}^2+Bs+\left(K+\frac{A_p^2}{c_1}\right) \]$

식(4)에서 진동 전달률의 주파수 응답함수(Frequency Response Function, FRF)는 식(5)와 같다.

$\[ L\left(j\text{ω}\right)=\frac{\left[\left\{\left(\frac{1}{c_1}+\frac{1}{c_2}\right)-I{\omega }^2\right\}+jR\omega \right]}{\left[\left\{\left(K+\frac{A_p^2}{c_1}\right)-M{\omega }^2\right\}+jB\omega \right]\left[\left\{\left(\frac{1}{c_1}+\frac{1}{c_2}\right)-I{\omega }^2\right\}+jR\omega \right]-\frac{A_p^2}{c_1}} \]$

(5)

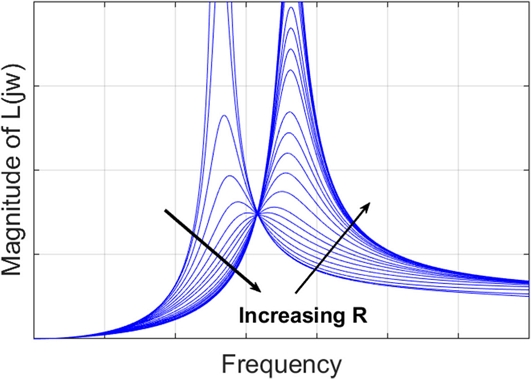
식(5)에서 유로댐핑 R의 변화에 따른 주파수 응답함수의 변화를 대표적으로 나타내면 Fig. 2와 같다[15]. 식(5)의 FRF에서 진동 전달률은 2개의 고유진동수가 존재한다. 따라서 R = 0일 경우 FRF는 2개의 첨두값을 갖지만, R이 증가하면 높은 고유진동수 진동모드는 낮은 고유진동수 모드에 비해 감쇠 증가가 빨라 그 첨두치가 작아지므로 Fig. 2와 같이 저주파 고유진동수의 영역의 변화가 지배적으로 나타난다. Fig. 2에서 FRF 크기는 유로마찰 R이 작을 경우 낮은 고유진동수에 의한 영향이 지배적으로 나타나며, R이 증가하면 FRF의 크기가 작아지고 고유진동수도 증가하는 특성을 보인다.

Fig. 2

FRF L(jω) with various friction R

여기서 R이 매우 작을 경우는 유체의 유동에 의한 마찰이 존재하지 않으므로 이때의 고유진동수는 고무 마운트의 고유진동수에 근접하게 된다. R이 일정 값보다 더 증가하면 높은 고유진동수에 의한 영향이 지배적으로 나타나며, R이 증가할수록 FRF의 크기가 증가하고 고유진동수도 증가한다. R이 매우 크면 관성트랙의 유동저항이 매우 커서 상하챔버 사이의 유체 유동이 없으므로 관성트랙이 막혀있는 상부챔버만 있는 마운트에 해당된다. 따라서 유동저항이 없는 낮은 고유진동수에 비해 상부챔버의 컴플라이언스의 영향만큼의 고유진동수 증가가 나타난다.

Fig. 2의 상대 진동 전달률은 소음과 진동 및 승차감 측면에서 작을수록 좋다. 하지만 R의 변화에 따른 FRF가 공통으로 통과하는 일정점 부근 주파수 이하의 저주파수 영역과 그 이상의 고주파수 영역에서의 댐핑의 요구 조건이 상반됨을 알 수 있다. 즉, 저주파수 영역에서는 큰 감쇠비가, 반대로 고주파수 영역에서는 작은 감쇠비가 요구된다. 엔진 가진력의 차체 전달률에서도 Fig. 2와 유사한 특성을 보인다. Fig. 1에서 차체에 전달되는 힘은 식(6)과 같다.

$\[ F_t\left(t\right)=B\dot{z}+Kz-A_p{P}_1 \]$

(6)

식(1)과 식(6)을 이용하여 정리하면 엔진 가진력 F_e(s)와 차체 전달력 F_t(s)간의 관계는 식(7)로 표현할 수 있다.

$\[ \frac{F_t\left(s\right)}{F_e\left(s\right)}=N\left(s\right) \]$

(7)

여기서 전달함수 N(s)는 힘 전달률에 해당하며, 진동 전달률과 식(8)의 관계를 갖는다.

$\[ N\left(s\right)=1+L\left(s\right) \]$

(8)

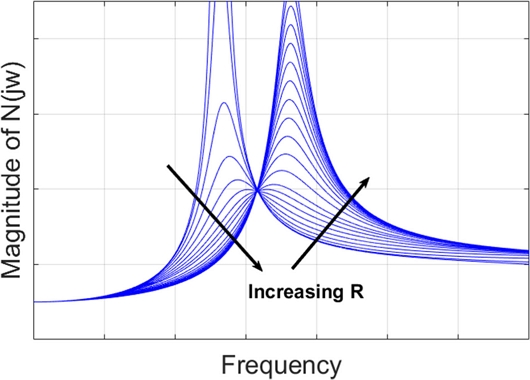
식(8)에서 유로댐핑 R의 변화에 따른 주파수 응답함수 N(jω)의 크기 변화는 대표적으로 Fig. 3과 같으며, 앞의 진동 전달률에서와 유사한 특성을 보인다. 즉, R이 작으면 낮은 고유진동수의 진동 특성이 지배적이며, 반대로 R이 크면 높은 고유진동수의 진동 특성이 우세하다. R이 작은 값에서 큰 값으로 증가할 때 일정점 부근의 좁은 영역을 통과한다.

Fig. 3

FRF N(jω) with various friction R

따라서 힘의 전달률을 작게 하기 위해서는 FRF가 공통으로 통과하는 일정점 부근 주파수 이하의 저주파수 영역에서는 큰 감쇠비, 고주파수 영역에서는 작은 감쇠비가 요구된다. 이상의 분석에서 진동 전달률과 힘 전달률 모두 공통적으로 저주파수 영역에서는 높은 감쇠비, 고주파수 영역에서는 작은 감쇠비가 요구됨을 알 수 있다. 이 요구는 서로 상반되는 관계이므로 수동형 엔진 마운트로는 만족시킬 수 없으며, 따라서 두 요구 조건을 적절히 타협하는 수준의 댐핑을 결정할 필요가 있다.

2.2 차체 진동 전달률 최소화 최적 댐핑

식(5)의 진동 전달률의 FRF 크기 |L(jω)|는 주파수에 대해 4차식으로 해석적으로 분석하기 어렵다. 하지만 실제 마운트에서 상부챔버 컴플라이언스가 하부챔버 컴플라이언스에 비해 매우 작고, 하부챔버의 강성(컴플라이언스의 역수)의 절대적인 크기도 작으며, (1/C₁)□ (1/C₂) ≅ 0, 유동 유체의 관성과 고무 마운트 점성계수가 상대적으로 작아 저주파 영역에서 Iω² ≅ 0, Bω ≅ 0으로 가정하면, 식(5)의 FRF 크기는 식(9)와 같이 주파수에 대한 2차식으로 근사화하여 간략히 나타낼 수 있다.

$\[ L\left(j\omega \right)=\frac{{\omega }^2\left\{\left(1/c_1\right)+jR\omega \right\}}{\left(1/c_1\right)\left\{{\omega }_1^2-{\omega }^2\right\}+jR\omega \left\{{\omega }_2^2-{\omega }^2\right\}} \]$

(9)

식(9)에서 FRF의 크기는 유로마찰 R의 변화에 관계없이 일정한 점을 지나는 특징을 갖고 있다. 이 점의 주파수는 식(9)의 크기의 제곱을 R²로 미분하여 0이 되는 점에서 찾을 수 있다. 즉, d[|L(jω)|²]/dR² = 0을 만족하는 주파수 $$ {\omega }_L^{\text{*}}$$는 식(10)과 같다.

$\[ {\left({\omega }_L^{\text{*}}\right)}^2=\frac{{\omega }_1^2+{\omega }_2^2}{2}, {\omega }_1^2=\frac{K}{M}, {\omega }_2^2=\frac{K}{M}+\frac{A_p^2}{M{c}_1} \]$

(10)

즉, FRF의 크기는 R에 관계없이 주파수 $$ {\omega }_L^{\text{*}}$$에서 항상 동일한 값을 갖는다. 따라서 모든 주파수 영역에서 FRF의 최대 크기가 $$ \left|L\left(j{\omega }_L^{\text{*}}\right)\right|$$가 되는 유로마찰 R을, H_∞-노옴을 최소화하는 최적 댐핑으로 정의할 수 있다. 이 최적 댐핑 R은 |L(jω)|를 주파수 ω로 미분한 결과가 $$ \omega ={\omega }_L^{\text{*}}$$에서 0이 되는 조건을 만족하는 R에 해당된다. 즉 식(11)을 만족하는 R이 최적 댐핑이 된다.

$\[ \frac{d}{d{\omega }^2}{\left|{\left.L\left({\omega }^2\right)\right|}^2\right|}_{\omega ={\omega }_L^{\text{*}}}=0 \]$

(11)

식(11)을 만족하는 최적 댐핑 $$ R_L^{\text{*}}$$는 식(12)와 같다.

$\[ R_L^{\text{*}}=\frac{1}{c_1}\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{2}{{\omega }_1^2+{\omega }_2^2}}=\sqrt{\frac{2MK}{\left(c_{1}K+A_p^2\right)\left({2c}_{1}K+A_p^2\right)}} \]$

(12)

이때 $$ \omega ={\omega }_L^{\text{*}}$$에서의 FRF의 크기는 식(13)과 같다.

$\[ \left|L\left(j{\omega }_L^{\text{*}}\right)\right|=\frac{{\omega }_1^2+{\omega }_2^2}{\left|{\omega }_2^2-{\omega }_1^2\right|}=1+\frac{2c_{1}K}{A_p^2} \]$

(13)

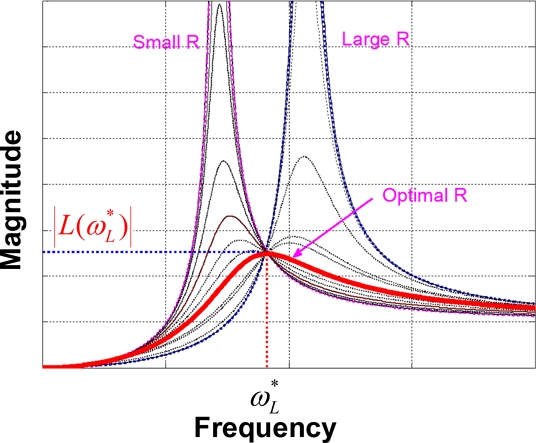
Fig. 4는 R의 증가에 따른 |L(jω)|이며, 최적의 유로마찰 $$ R_L^{\text{*}}$$일 때 FRF의 크기는 굵고 붉은색 곡선에 해당한다. 또한 R의 증가에 관계없이 모든 FRF의 크기는 $$ \omega ={\omega }_L^{\text{*}}$$에서 동일한 점을 지나며, $$ R_L^{\text{*}}$$일 때 |L(jω)|는 $$ \omega ={\omega }_L^{\text{*}}$$에서 최댓값을 갖는다. 즉, $$ R_L^{\text{*}}$$가 H_∞-노옴을 최소화하는 댐핑임을 확인할 수 있다.

Fig. 4

FRF |L(jω)| with optimal damping RL*

2.3 엔진 가진력 전달률 최소화 최적 댐핑

엔진 가진력의 차체 전달률은 식(8)에서 N(jω)가 L(jω)에 상수 1을 더한 관계를 가지므로 앞의 가정, (1/C₁)□ (1/C₂) ≅ 0, Iω² ≅ 0, Bω ≅ 0을 적용하면 FRF의 크기 |N(jω)|는 앞에서와 같이 유로마찰 R의 변화와 관계없이 일정점을 통과하며, 이 점을 최대치로 갖는, 즉 H_∞-노옴을 최소화하는, 최적의 댐핑 R을 구할 수 있다.

이 일정점의 주파수 $$ {\omega }_N^{\text{*}}$$는 d[|N(jω)|²]/dR² = 0에서 구할 수 있으며, 이 점을 최댓값으로 갖는 최적 댐핑 $$ R_L^{\text{*}}$$은 식(14)에서 구할 수 있다.

$\[ \frac{d}{d{\omega }^2}{\left|N\left({\omega }^2\right)\right|}^2{\left| \right.}_{\omega ={\omega }_N^{\text{*}}}=0 \]$

(14)

식(14)를 만족하는 최적 댐핑 $$ R_N^{\text{*}}$$는 식(15)와 같다.

$\[ R_N^{\text{*}}=\frac{1}{c_1}\frac{1}{{\omega }_2^2}\sqrt{\frac{{\omega }_1^2+{\omega }_2^2}{2}} \]$

(15)

또한 $$ \omega ={\omega }_N^{\text{*}}$$에서의 FRF의 크기는 식(16)과 같으며, 식(13)과 동일하다.

$\[ \left|N\left(j{\omega }_N^{\text{*}}\right)\right|=\frac{{\omega }_1^2+{\omega }_2^2}{\left|{\omega }_2^2-{\omega }_1^2\right|}=1+\frac{2c_{1}K}{A_p^2} \]$

(16)

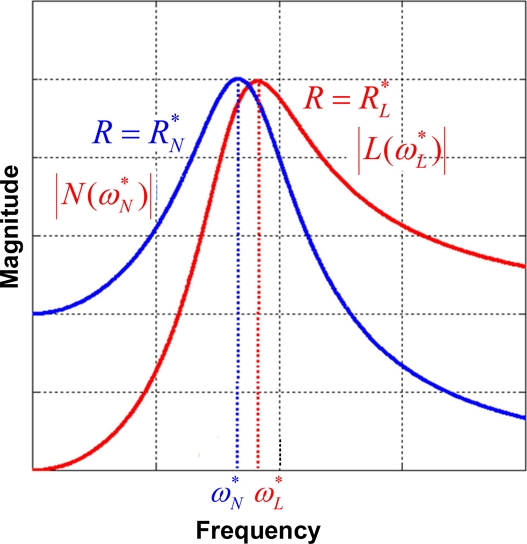
Fig. 5는 앞의 진동 전달률과 힘 전달률 기준 최적 댐핑 관련 분석 결과를 나타낸 것이며, Table 1에 이를 정량화하여 정리하였다. Fig. 5와 Table 1에서 $$ {\omega }_L^{\text{*}}>{\omega }_N^{\text{*}}, R_N^{\text{*}}>R_L^{\text{*}}, \left|L\left(j{\omega }_L^{\text{*}}\right)\right|=\left|N\left(j{\omega }_N^{\text{*}}\right)\right|$$의 관계를 얻을 수 있다.

Fig. 5

FRF |L(jω)| & |N(jω)| with optimal damping R*

Table 1

Summary of optimal damping design

이와 같이 Fig. 5와 Table 1에서 차체 변위의 엔진 전달률과 엔진 가진력의 차체 전달률을 최소화하는 최적 댐핑은 서로 다르며, 주파수 특성도 차이가 있다. 따라서 엔진 마운트의 설계 목적에 따라 취사선택하거나 두 최적 댐핑 사이의 값을 적절히 선택할 수 있겠다.

또한 앞의 최적 댐핑 설계에서 적용한 가정, (1/C₁)□ (1/C₂) ≅ 0, Iω² ≅ 0, Bω ≅ 0에 오차가 큰 경우 수치해석에 기반한 댐핑값의 조정은 있을 수 있겠다.

3. MR 마운트 최적 댐핑 제어

Fig. 1의 유압 마운트가 최적 댐핑을 갖도록 유체의 점성 및 관성트랙의 기하학적 형상을 설계할 수 있다. 하지만 기하학적 제한조건 등으로 최적 댐핑을 구현하지 못할 경우 외부적인 작용에 의해 댐핑을 조정할 수 있다. 특히 설계한 댐핑이 최적 댐핑에 미치지 못할 경우 MR 댐퍼를 이용하여 최적 댐핑을 갖도록 실시간으로 제어할 수 있다. 여기서 MR 댐퍼는 유압 마운트 구조를 기본으로 하며, 기존의 유압유 대신 MR 유체를 사용하고, 상하챔버 사이 유체의 통로인 관성트랙에 자기장을 형성할 수 있는 구조를 갖는다[11-13].

Figs. 6은 1의 유압 마운트에서 관성트랙 대신 환형튜브(Annular Tube)를 설치하고, 튜브 내면과 외면에 전자석을 설치하여 코일 전류 변화를 통해 유체 유동부의 자기장을 조정한다.

Fig. 6

Flow through inertia track

MR 댐퍼의 동역학적 특성은 Bingham Plastic 모델로 단순화할 수 있으며, 이때 MR 유체의 마찰저항 F_f은 다음 식(17)로 표현할 수 있다[2,13,16,17].

여기서 c₀는 MR 유체의 점성마찰계수, Q는 관성트랙을 통과하는 MR 유체의 유속이다. F_mr(i_mr)은 MR 댐퍼에서 MR 유체의 유동 통로에 자기장을 형성하는 코일의 전류가 i_mr일 때 MR 유체의 정지마찰력이다. 이 마찰력은 전류 i_mr에 의해 형성된 자기장의 크기에 따라 그 크기가 변한다. Fig. 6에서 유동 운동방정식은 식(18)로 쓸 수 있다.

단, MR 유체 마찰력은 쿨롱 마찰과 같은 특징을 갖는다. 즉, 식(18)을 식(19)로 나타낼 때

MR 유체의 마찰력은 식(20)과 같이 유체의 유동이 발생하기 전까지는 정지마찰력, 유동이 발생하면 쿨롱 마찰 특성을 갖는다. 즉, 유로를 통과하는 유체에 작용하는 외력 F_ext가 MR 유체의 마찰보다 작을 경우 MR 유체의 마찰력은 외력과 크기가 같고 방향이 반대로 작용하므로 유동은 일어나지 않는다.

유동이 발생할 때 유량방정식은 식(21)과 같으며,

식(3)과 식(21)을 이용하여 식(22)의 운동방정식을 유도할 수 있다.

식(1)에서 Q와 $$ {\dot{P}}_2$$ 의 부호는 같으므로 식(22)의 첫 번째 압력방정식에서 MR 댐퍼의 마찰력이 식(23)과 같으면 식(24)와 같이 최적 댐핑을 갖는 압력방정식을 얻게 된다.

Table 1과 식(10)에서 두 고유진동수는 ω₁ = 13.03 Hz, ω₂ = 18.22 Hz이므로 최적 댐핑 설계 방법을 적용한 주요 파라미터는 Table 3과 같이 결정된다.

식(23)에서 하부챔버의 압력은 대기압 수준에서 큰 변화가 없으므로 실제 적용 시 압력의 높은 측정정밀도가 필요하다. 반면 상부챔버의 압력은 평균압력이 높고 압력의 변화도 크므로 하부챔버의 압력 측정에 비해 용이한 장점이 있다. 상하부챔버의 압력의 관계는 식(1)에서 $$ c_1{\dot{P}}_1+c_1{\dot{P}}_2=-A_p\dot{z}$$이므로 이를 이용하여 식(23)을 다시 쓰면 식(25)에서 상부챔버의 압력변화율과 차체와 엔진 사이의 상대속도를 측정하고 되먹임하여 최적 댐핑을 갖는 제어를 할 수 있다. 즉 식(25)가 최적 댐핑 제어기가 된다.

4. 시뮬레이션 및 결과

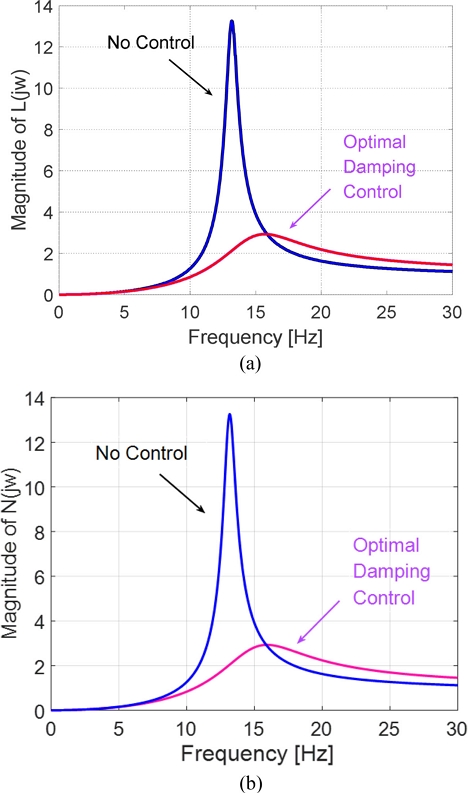
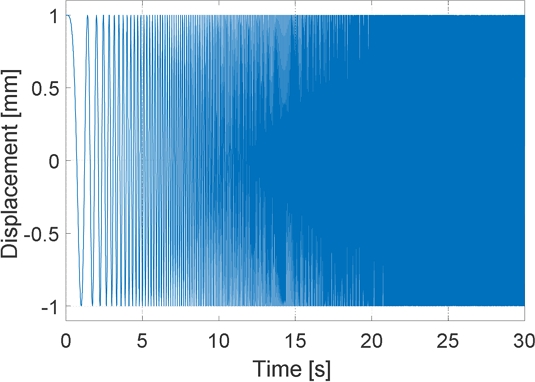
앞에서 제안한 최적 댐핑 제어 알고리즘의 타당성을 검증하기 위해 시뮬레이션을 실시하였으며, 시뮬레이션에 사용한 MR 마운트의 파라미터는 Tables 2와 3과 같다. Figs. 7(a)와 7(b)는 각각 비제어 시와 최적 댐핑 제어 적용 시 L(jω)의 크기, N(jω)의 크기이며, Table 3의 결과와 일치한다. L(jω)와 N(jω)는 비제어 시의 크기와 최적 댐핑 제어 시의 크기가 만나는 주파수에서 최댓값을 가지며, 그 이상의 주파수에서는 최적 댐핑 제어의 크기가 오히려 더 커진다. 이는 Figs. 2와 3에서의 결과와 일치함을 알 수 있다. Fig. 7은 주파수 영역에서 해석한 것이므로, 시간 영역에서 그 성능을 확인하기 위해 응답 특성을 MatLab/Simulink를 이용하여 시뮬레이션 하였다. 우선 진동 전달률을 분석하기 위해 차체의 변위는 Fig. 8과 같이 진폭이 1 mm로 일정하고, 주파수는 30초 동안 0.0-30 Hz 범위에서 선형으로 증가하는 Chirp 신호를 가정하였다. 따라서 Fig. 8의 x축 값은 시간 초(s)와 아울러 주파수 Hz를 나타낸다. 이 시간과 주파수 관계는 뒤의 Figs. 9와 10에서도 동일하다.

Table 2

System parameters for simulation

Table 3

System parameters

Fig. 7

(a) Magnitude of L(jω), and (b) Magnitude of N(jω) w/ and w/o optimal damping control

Fig. 8

Vehicle displacement

Fig. 9

Displacement transmission ratio w/ and w/o optimal damping control

Fig. 10

Control input force of optimal damping control

Fig. 8과 같이 차체가 진동할 때 제어하지 않은 경우와 식(25)의 최적 댐핑 제어를 적용한 경우 차체와 엔진의 상대변위를 구하였다. 여기서는 MR 유체의 동력학적 관계는 단순화하여 MR 전류에 비례하는 식(25)의 마찰력이 발생하는 것으로 가정하였다. 실제 Bingham Plastic 모델의 마찰력은 가하는 전류에 의한 포화응력에 해당되며 전류의 변화에 따른 포화응력 속응성은 MR 유체의 용매와 상자성 입자의 물리적 특성과 자기장 형성 장치의 특성에 따라 달라질 수 있으나 본 연구에서는 포화응력 도달까지의 시간 지연은 무시하였다.

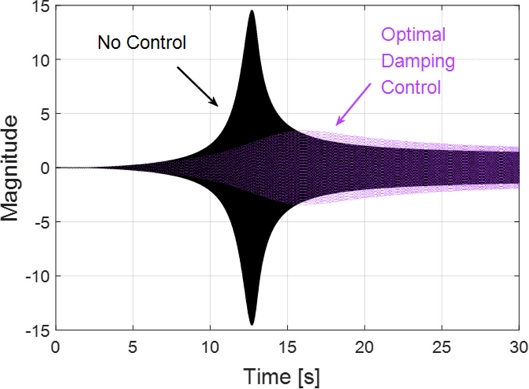
Figs. 9는 시뮬레이션 결과를 진동 전달률로 나타낸 것으로 Figs. 7(a)의 주파수 영역에서의 해석 결과와 같이 최적 댐핑 제어를 통해 진동 전달률의 H_∞-노옴을 감소시킬 수 있음을 확인할 수 있다. 또한 고주파 영역에서는 최적 댐핑 제어의 진동 전달률이 비제어 시에 비해 큰 특징이 일치함을 확인할 수 있다. Fig. 9에서 제어하지 않았을 경우 진동 전달률의 최대 크기는 13.36로 FRF 분석에서 구한 13.26보다 약간 큰 결과인데, 이는 입력신호가 FRF 분석에서와 달리 주파수가 시간에 따라 변화하는 Chirp 신호이며, 또한 수치해석에서 발생하는 오차로 분석된다. 최적 댐핑제어를 적용했을 때 진동 전달률의 최대 크기는 3.32로, Table 3의 이론적으로 구한 3.09보다 약간 큰 값을 보였는데, 이는 Table 3에서는 선형계로 가정한 값이며, 시뮬레이션에서는 식(20)의 MR 유체의 비선형적 요소를 고려하였기 때문으로 분석된다.

이 결과로부터 진동 전달률의 H_∞-노옴은 최적 댐핑제어를 통해 제어하지 않았을 때의 약 25% 수준으로 감소됨을 확인하였다.

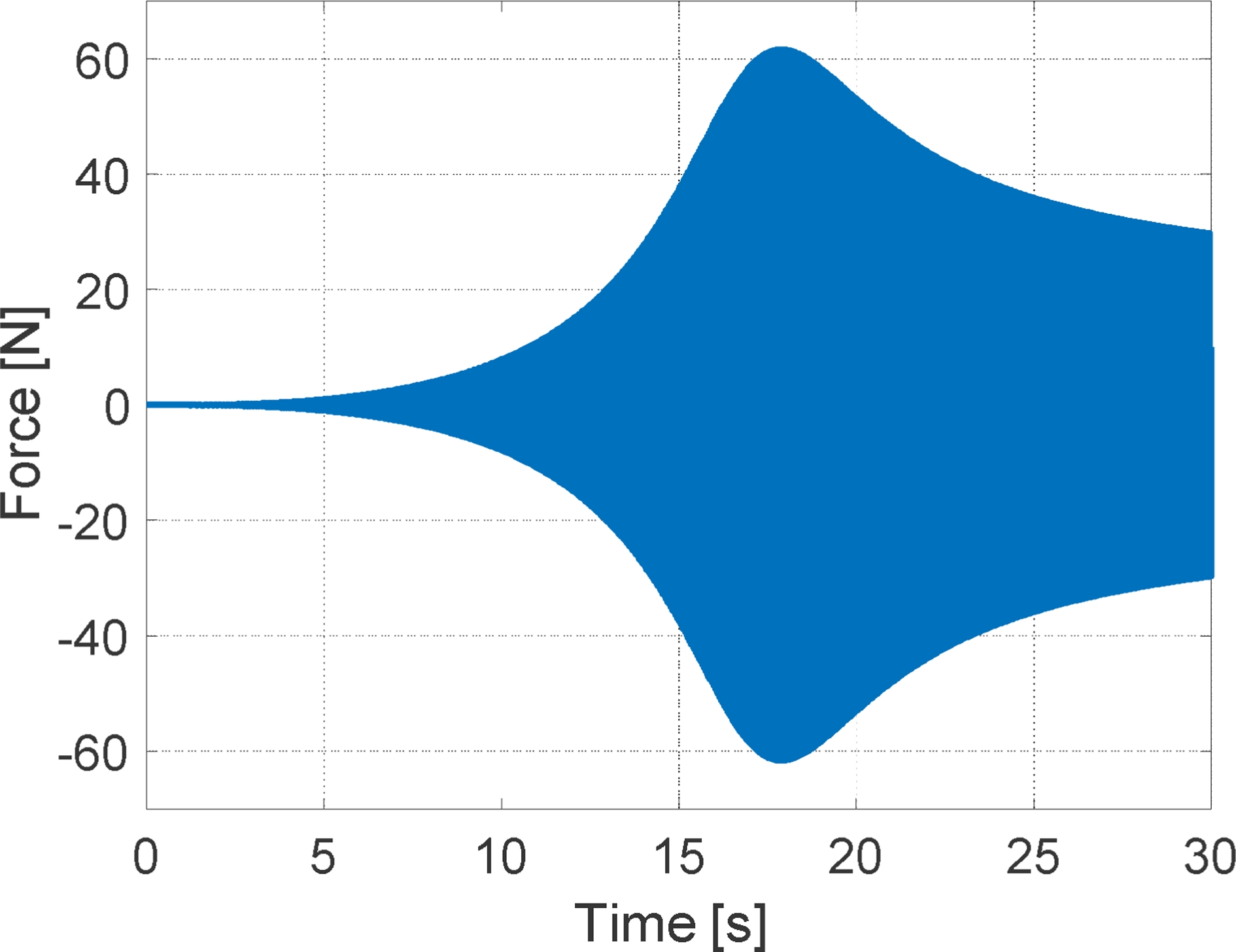
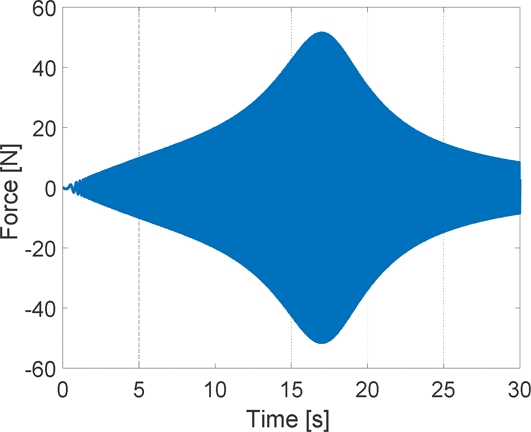
Fig. 10은 최적 댐핑 제어 적용 시, 식(25)의 제어입력으로 주파수 $$ {\omega }_L^{\text{*}}=15.84\mathrm{ }\mathrm{H}\mathrm{z}$$에서 최댓값을 갖는다. 다음으로 최적 댐핑 제어를 적용한 H 경우 엔진의 가진력이 차체에 전달되는 힘을 구하였다. Fig. 11은 가정한 엔진의 가진력으로 크기가 1,000 N, 주파수는 30초 동안 0.0-30 Hz 범위에서 선형으로 증가하는 Chirp 신호이다.

Fig. 11

Excitation force of engine

따라서 Fig. 11의 x-축 값은 시간 초(s)와 아울러 주파수 Hz를 나타낸다. 이 시간과 주파수 관계는 Figs. 12와 13에서도 동일하다.

Fig. 12

Force transmission ratio w/ and w/o optimal damping control

Fig. 13

Control input force of optimal damping control

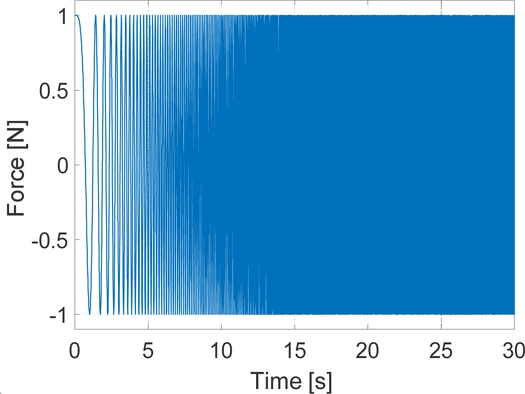
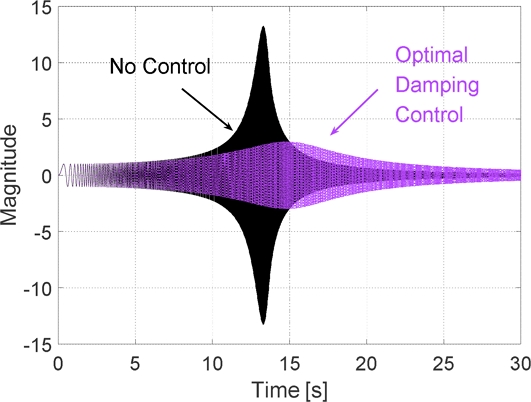
Figs. 12는 11의 엔진 가진력의 차체 전달력 시뮬레이션 결과를 힘 전달률로 나타낸 것으로, 7(b)의 주파수 영역에서의 해석결과와 같이 최적 댐핑 제어를 통해 힘 전달률의 H_∞-노옴을 감소시킬 수 있음을 확인할 수 있다. 또한 고주파 영역에서는 최적 댐핑 제어의 힘 전달률이 비제어 시에 비해 큰 특징 또한 일치함을 확인할 수 있다. Fig. 12에서 제어하지 않았을 경우 전달률의 최대 크기는 13.25로 FRF 분석에서 구한 13.26과 거의 같은 결과를 보였다. 최적 댐핑 제어를 적용했을 때 전달률의 최대 크기는 2.99로 Table 3의 이론적으로 구한 3.09보다 약간 작은 값을 보였는데, 이는 앞에서와 같이 식(20)의 MR 유체의 비선형적 요소와 수치해석에서 발생하는 오차 요인 때문으로 분석된다. 이 결과로부터 힘 전달률의 H_∞-노옴은 최적 댐핑 제어를 통해 제어하지 않았을 때의 약 23% 수준으로 감소시킬 수 있음을 확인하였다. Fig. 13은 최적 댐핑 제어 적용 시 식(25)의 제어입력으로 주파수 $$ {\omega }_N^{\text{*}}=14.99\mathrm{ }\mathrm{H}\mathrm{z}$$에서 최댓값을 갖는다.

5. 결론

차량의 엔진 마운트는 승차감 측면에서 저주파 외란에 대해서는 높은 강성과 높은 감쇠, 고주파 외란에 대해서는 낮은 강성과 낮은 감쇠가 요구되는 서로 상반되는 조건을 만족해야 한다. 이 요구 조건을 만족시킬 수 있는 해석적 방법으로 H_∞-노옴을 최소화하는 최적 댐핑 설계 방법을 제안하였으며, 이를 MR 마운트에서 실시간 제어를 통해 구현하는 방법을 제시하였다. 제안한 방법의 적용 가능성과 성능을 MatLab/Simulink를 이용한 시뮬레이션을 통해 분석하였으며, 수동 마운트에 비해 진동전달률과 힘 전달률을 개선할 수 있음을 검증하였다.

REFERENCES

• Lee, D.-Y., Sohn, J.-W., Choi, S.-B., (2009), A new type of active engine mount system featuring MR fluid and piezostack, Transactions of the Korean Society for Noise and Vibration Engineering, 19(6), 583-590. [https://doi.org/10.5050/KSNVN.2009.19.6.583]
• Ciocanel, C., Schroeder, C., Elahinia, M. H., (2008), Performance evaluation of a semi-active magnetorheological mount, SAE Technical Paper. [https://doi.org/10.4271/2008-01-0429]
• Mansour, H., (2010), Design and development of active and semi-active engine mounts, M.Sc. Thesis, Simon Fraser University.
• Rasekhipour, Y., Ohadi, A., (2011), Evaluating vibration performance of a semi-active MR engine mount, Proceedings of the 2nd International Conference on Control, Instrumentation and Automation, 90-95. [https://doi.org/10.1109/ICCIAutom.2011.6356636]
• Park, J. H., Do, X. P., Nguyen, Q. H., Kang, O. H., Choi, S.-B., (2013), Optimal design of magnetorheological mount for ship engines: maximum damping force, Transactions of the Korean Society for Noise and Vibration Engineering, 23(5), 472-478. [https://doi.org/10.5050/KSNVE.2013.23.5.472]
• Elahinia, M., Ciocanel, C., Wang, S., (2013), MR-and ER-based semiactive engine mounts: A review, Smart Materials Research, 831017. [https://doi.org/10.1155/2013/831017]
• Türkücü, T., Keleş, Ö., (2018), Magneto-rheological engine mount design and experimental characterization, Journal of Mechanical Science and Technology, 32(11), 5171-5178. [https://doi.org/10.1007/s12206-018-1015-y]
• Ahn, Y. K., Yang, B.-S., Ahmadian, M., Morishita, S., (2005), A small-sized variable-damping mount using magnetorheological fluid, Journal of Intelligent Material Systems and Structures, 16(2), 127-133. [https://doi.org/10.1177/1045389X05048041]
• Choi, S.-B., Seong, M.-S., Ha, S.-H., (2009), Vibration control of an MR vehicle suspension system considering both hysteretic behavior and parameter variation, Smart Materials and Structures, 18(12), 125010. [https://doi.org/10.1088/0964-1726/18/12/125010]
• Barber, D. E., Carlson, J. D., (2010), Performance characteristics of prototype MR engine mounts containing glycol MR fluids, Journal of Intelligent Material Systems and Structures, 21(15), 1509-1516. [https://doi.org/10.1177/1045389X09351957]
• Seong, M.-S., Choi, S.-B., Kim, C.-H., (2011), Design and performance evaluation of MR damper for integrated isolation mount, Journal of Intelligent Material Systems and Structures, 22(15), 1729-1738. [https://doi.org/10.1177/1045389X11421820]
• Sung, M. S., (2013), Tiny vibration control of ultra-precision stage using MR damper, Ph.D. Thesis, Inha University.
• Shirazi, F. A., Mohammadpour, J., Grigoriadis, K. M., Song, G., (2011), Identification and control of an MR damper with stiction effect and its application in structural vibration mitigation, IEEE Transactions on Control Systems Technology, 20(5), 1285-1301. [https://doi.org/10.1109/TCST.2011.2164920]
• Kim, S. H., Yoon, D. S., Choi, S. B., (2017), A design for improvement vibration comfort of wheel loader cabin MR mount, Proceedings of the Korean Society for Fluid Power & Construction Equipment Conference, 110-116.
• Lee, H. H., Choi, S. B., (2001), Vibration control of an engine mount featuring MR fluid, Proceedings of the Korean Society for Noise and Vibration Engineering Annual Autumn Conference, 213-218.
• Bingham, E. C., (1922), Fluidity and plasticity, McGraw-Hill.
• Bingham, E. C., Green, H., (1919), Plastic material and not a viscous liquid; The measurement of its mobility and yield value, Proceedings of the American Society for Testing Materials, 20(2), 640-675.