[ REGULAR ]

Journal of the Korean Society for Precision Engineering - Vol. 39, No. 8, pp.595-602

ISSN: 1225-9071 (Print) 2287-8769 (Online)

Print publication date 01 Aug 2022

Received 29 Mar 2022 Revised 07 Jun 2022 Accepted 13 Jun 2022

DOI: https://doi.org/10.7736/JKSPE.022.038

월류수심이 있는 가동보의 유체 구조 연성 해석

이해수¹ ; 박태현²^{, #}

1경상국립대학교 자동차공학과
2경남대학교 기계공학부

Fluid Structure Interaction Analysis of Movable Weir with Overflow Depth

Haesoo Lee¹ ; Taehyun Park²^{, #}

1Department of Automotive Engineering, Gyeongsang National University
2School of Mechanical Engineering, Kyungnam University

Correspondence to: ^#E-mail: taehyun@kyungnam.ac.kr, TEL: +82-55-249-2615

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Movable weir is a major system used to manage water level in a river to secure drinking water, agricultural water, and industrial water. It is critical to safely construct and operate movable weir, in any environmental circumstances. In this study, we performed an unsteady flow analysis, on the movable weir with overflow water depth. The continuity equation, with constant density and incompressible Navier-Stokes equation, were used for the flow analysis. The CFD results were applied for structural analysis, to evaluate the safety of movable weir. According to the analysis results, the movable weir has secured sufficient safety.

Keywords:

Movable weir, Overflow depth, FSI, Safety factor

키워드:

가동보, 월류수심, 유체 구조 연동, 안전계수

1. 서론

우리나라의 강과 하천에는 치수의 목적을 가진 댐이나 소형보가 설치되어 있다. 소형 보는 크게 수문이 없이 단순히 물을 가두고 월류의 방법으로 특정 수위를 유지하는 고정보와 보의 기울기나 높이를 변화시켜 수위를 인위적으로 제어할 수 있는 가동보가 있다[1]. 여기서 가동보의 경우 저장된 물의 수위 변화에 따라 수문에 작용하는 하중의 양과 그 하중의 작용점이 당연히 다르게 나타난다.

가동보는 철근 콘크리트 바닥이 있는 하천에 설치되며, 수위 조절을 통해서 여러 가지 외부 환경 변화에 능동적으로 대응할 수 있어 최근 설치 사례도 늘어나고 있으며 다양한 형태가 연구 개발되고 있다. 서경원 등은 수문의 운영 시 발생하는 여러 가지 진동 현상에 대해서 자세히 연구했으며 그 원인은 수문의 설계 컨셉, 구조 그리고 방류 형태 등이 복합적으로 작용하는 경우였다[2].

이해수 등은 정수압을 적용하여 다단제어 가동보의 구조해석을 수행하였다. 각각의 기립각도별(15, 30, 45, 60^o) 메쉬 의존성 테스트를 수행한 후 기립각도별 응력, 변형량, 최대 응력이 작용하는 위치 그리고 안전계수에 대해서 연구했다[3]. 최진우 등은 유압으로 작동되며, 저수층 배출장치를 갖추고, 문비(Gate Leaf)와 받침틀로 구성되어 있는 다단전도방식 가동보의 구조해석을 수행하였다[4]. 이때 적용한 하중은 저수에 의한 정수압(Hydrostatic Pressure)과 자중이 적용되었다.

최계운 등은 가동보 중 저층수 유입구가 있는 것을 설치할 경우 수위 상승효과를 분석하고 가동보 각도 변화가 상류측 수위에 미치는 영향과 갈수 시 저층수 배수를 위해 설치해 놓은 저층수 유입구에 따른 수위 변화를 실험적으로 연구하였다. 보설치에 따른 수위 변화가 수로에서의 거리보다는 하폭에 더 큰 영향을 미친다고 했으며, 저층수 유입구의 유무는 수위 변화에는 크게 영향을 주지 않고, 보 상단 부분에서 국부적인 수위 감소를 나타냄을 보고하였다[5].

박준우 등은 상용 CFD 툴과 오픈소스 CFD 툴을 이용한 2상 유동해석의 정량적 비교 연구를 수행하였다[6]. 물과 공기 2상 해석을 위해서 Volume of Fluid (VOF) 모형과 다상(Multi-Phase) 모형을 활용했으며 댐 붕괴 문제에 대해서 상용 툴과 오픈소스 툴에서 각각 해석을 수행하였다. 결과는 상용 CFD 툴이 오픈소스 툴보다 해일이 더 크게 관찰되었다. 즉 상용 툴 쪽의 VOF 모형의 움직임이 더 동적이라고 판단하였다.

기존의 연구들은 가동보에 대한 구조해석, 진동, 수위 문제 등을 수치해석이나 실험적으로 수행했었다. 하지만 보를 범람하는 월류수심이 발생했을 때 즉 비정상상태(Unsteady)의 유동이 구조물에 어떤 영향을 미치는가에 대한 연성해석은 없었다.

본 연구에서는 월류수심(Overflow Depth)이 발생했을 때 가동보가 받는 압력을 CFD 프로그램인 ANSYS FLUENT를 이용해서 계산하고 그 정보를 구조해석 툴로 전달해서 구조해석을 수행하는 유체-구조 연성(Fluid-Structure Interaction) 해석을 수행하였다. 유동해석에서 정상상태해석으로는 월류수심을 표현할 수 없기 때문에 공기와 물을 동시에 계산하는 VOF 모델을 이용하여 비정상상태에서 계산을 수행하였다.

2. 연성해석

2.1 2D 모델과 간략화한 3D 모델

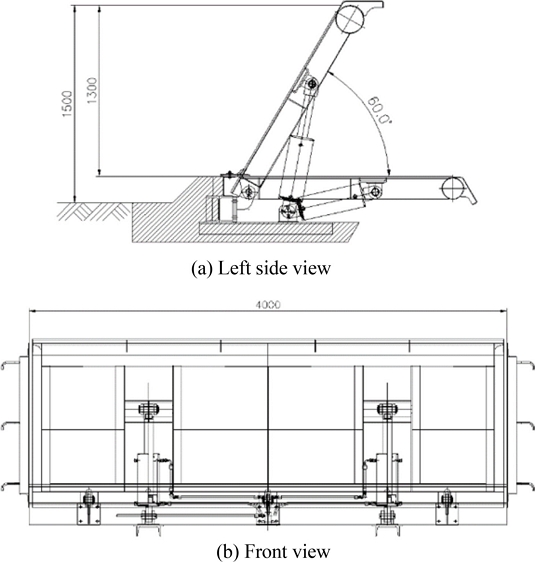
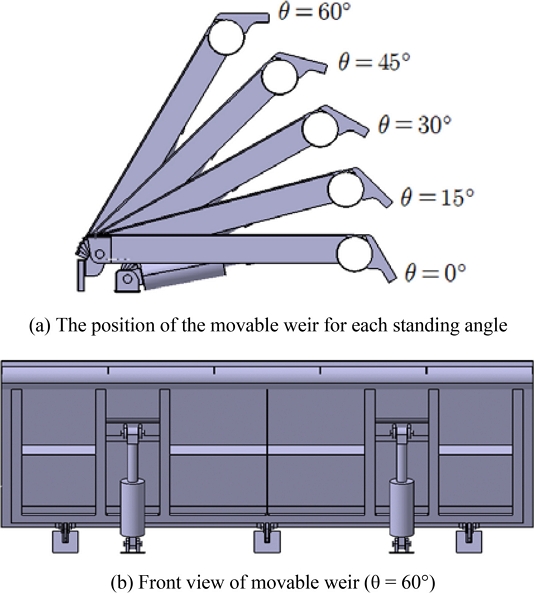
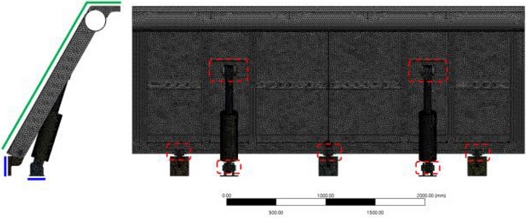
가동보의 2차원 모델은 Figs. 1(a)의 좌측면도와 1(b)의 정면도에 나타나 있다. 가동보는 철근 콘크리트 위에 설치되고 유압시스템에 의해 최대 60^o의 기립각을 가지며, 높이 1.3, 폭 3.95 m이다. 따라서 이론상 1.3 m의 최대 정수압을 가지지만 월류상태에는 이보다 더 높은 정수압을 받을 수 있다. Fig. 2는 가동보의 3D 모델을 나타내고 있다. Fig. 2(a)는 가동보가 기립하는 각도를 겹쳐서 나타낸 것이다. 0부터 60^o까지 나타내었지만, 해석은 15-60^o까지 연성해석을 수행하였다. Fig. 2(b)는 정면도이며 전면에 가동보의 기립을 위한 유압장치가 설치되어 있고, 해석에 불필요한 부분은 모두 생략했다.

Fig. 1

2D drawing of movable weir

Fig. 2

Simplified figures of the movable weir

2.2 유동해석을 위한 3D 모델

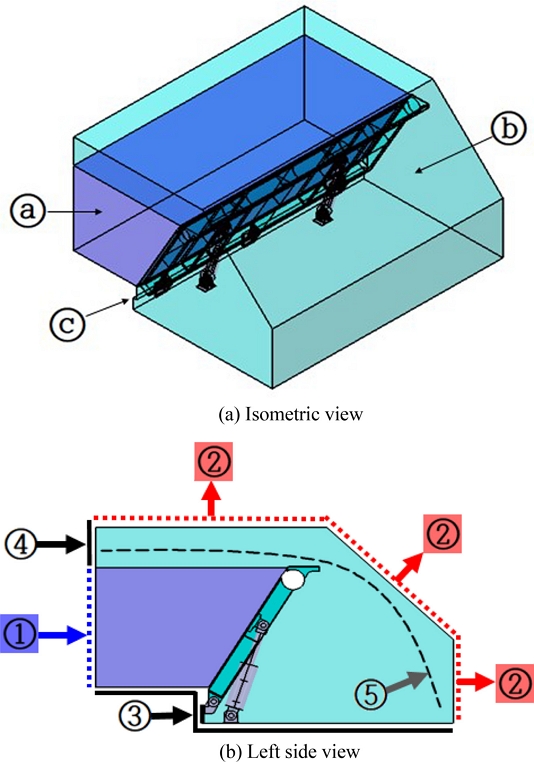
Figs. 3은 기립각도 60^o일 때 유동해석에 사용된 모델을 나타낸 것이며 3(a)는 등각도, 3(b)는 좌측면도이다. 가동보의 형상이 매우 복잡하기 때문에 유동해석 모델의 작도 방법은 먼저 가동보를 감싸고 있는 물과 공기가 계산될 영역을 생성한 후에 구조해석 모델을 부울 연산(Boolean Operation)을 통해서 추출해내는 방식을 사용했다. Fig. 3(a)에서 ⓐ는 계산 초기에 물이 적용될 영역, ⓑ는 공기가 적용될 영역 그리고 ⓒ는 가동보를 나타낸 것이다. 공기가 적용될 영역은 메쉬의 생성을 원활하게 하기 위해서 다시 2개의 영역으로 분할했고, 그 경계는 인테리어(Interior)로 지정해 질량이 이동할 수 있게 설정했다. Fig. 3(a)의 ⓑ 영역은 영역은 해석이 수행되면 물과 공기가 혼합되어 통과하는 영역이 된다. 유동해석에서는 고체(Solid)의 가동보는 필요하기 않기 때문에 가동보의 벽 부분만 적용했다. 또한 작업 유체인 물이 우측 상단 끝부분까지 도달하지는 않기 때문에 각각의 기립각도 별로 해석에 불필요한 영역은 제거해서 해석을 수행하였다. 따라서 그림은 매우 큰 모따기(Chamfer)가 된 형상이다. Fig. 3(b)에 ⑤번 점선은 유량이 증가하여 월류수심이 발생했을 때 생성될 수면을 가상으로 나타낸 것이다. 이것은 다음에 나오는 Fig. 4에서 물과 공기의 경계를 나타내는 굵은 실선 부분에 해당한다.

Fig. 3

3D model of the movable weir used in CFD (θ = 60o)

Fig. 4

Broad crested weir and overflow depth

Fig. 3(b)에서 파란색 점선 ①은 입구(Velocity Inlet)조건, 빨간색 점선 ②는 출구(Pressure Outlet), 검정색 굵은 실선 ③은 바닥(Wall), 검정색 굵은 실선 ④는 가상의 벽(Wall)으로 정의해 차오른 물이 가동보 쪽으로 이동하도록 했다. 그리고 좌측면도의 앞쪽과 뒤쪽은 대칭(Symmetry)으로 지정해서 길이 3,950 mm의 가동보가 주기적으로 배치된 상태의 해석을 수행하였다.

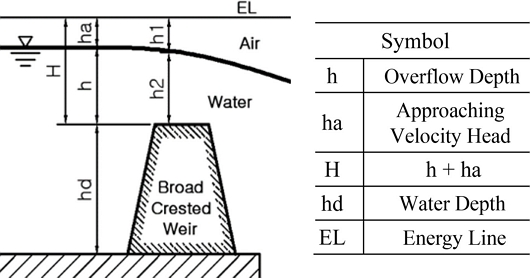
Fig. 4는 광정위어(Broad Crested Weir)의 개략도를 나타낸 것이다. 광정위어란 위어의 정상부가 접근유속으로 인한 월류수심의 수축에 영향을 줄 정도로 넓은 위어를 지칭한다[7]. 따라서, Fig. 4에서와 같이 최초 월류수심 h에서 하류로 갈수록 h2의 폭이 줄어들고 h1의 폭은 넓어지게 된다. 가동보의 경우 상단부에 사람이 도보로 이동 가능하도록 발판이 마련되어 있기 때문에 광정위어와 같은 월류수심의 수축이 일어나게 될 것이다.

2.3 지배방정식

본 해석에서는 작업 유체인 물과 공기를 동시에 계산하는 VOF (Volume of Fluid) 기반 비압축성 Navier-Stokes 방정식은 다음 식(1)부터 식(3)과 같다[6,8,9].

∇ ⋅ u = 0

(1)

∂ ρ α u ∂t + ∇ ⋅ ρ α uu = - ∇p + ∇ ⋅ μ α ∇u + ∇ u T + ρ α g + f σ

(2)

∂α ∂t + ∇ ⋅ αu = 0

(3)

단 여기서 u는 유체의 속도벡터, ρ(α)는 체적분율(Volume Fraction) α에 따른 유체의 밀도, t는 시간, μ는 점성계수, g는 중력항, f_σ는 표면장력(Surface Tension)이다. 밀도와 점성계수는 앞의 식(3)에 의해 결정된 체적분율 α에 의해 다음 식(4)와 식(5)와 같이 연산된다.

ρ α = αρ 1 + 1 - α ρ 2

(4)

μ α = αμ 1 + 1 - α μ 2

(5)

위의 식(4)와 식(5)에서 ρ와 μ의 아래첨자인 1과 2는 각각 FLUENT에서 지정하는 Primary Phase와 Secondary Phase의 물성치가 적용된다. 그리고 α는 기본 상의 체적분율로 설정되었다. 본 해석에서는 Primary Phase에는 공기를 적용하고, Secondary Phase에는 물을 적용했다. 단 여기서 점도비가 1,000을 초과할 경우 수렴이 어려울 수 있다.

2.4 유동해석

2.4.1 전처리

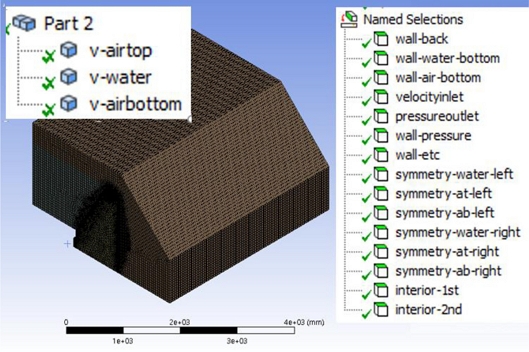
Fig. 5는 3D 모델을 ANSYS Workbench의 구성요소 중 하나인 DesignModeler에서 로딩하여 3개의 볼륨을 하나의 파트(Part)로 묶어(Form New Part) 두었다. 다시 ANSYS Meshing에서 로딩하여 각각의 경계에 이름을 부여하고 메쉬를 작성한 결과이다. 볼륨을 묶으면 볼륨의 경계가 보통 인테리어(Interior)로 자동 설정되며 또한 노드를 일치시켜 메쉬가 만들어진다. 만약 노드가 일치되지 않는다면 정보가 볼륨 간의 경계를 지날 때 매번 보간(Interpolation)을 통해서 전달되기 때문에 CPU에서 계산량이 많아지게 된다.

Fig. 5

Grid system

Fig. 5에서 좌측 상단에는 3개의 볼륨이 하나의 파트로 구성되어 있음을 나타내었고, 우측에는 각종 경계의 이름이 적용됨을 알 수 있다. 입구 경계조건 1개, 출구 경계조건 1개, 대칭 경계조건 6개, 경계 사이의 인테리어 2개, 그리고 기타의 벽이 적용되었다. DesignModeler에서는 6개의 면을 동시에 인테리어라고 명명했지만 ANSYS Meshing에서는 이를 자동으로 분리해서 각 볼륨의 면마다 대칭 조건의 이름을 적용시켰다.

Fig. 5에서 좌측 물 영역과 가동보 위쪽을 포함하는 공기영역은 육면체(Hexahedron)나 삼각기둥(Triangular Prism)의 메쉬가 만들어졌고, 가동보 바로 아래의 공기 영역은 사면체(Tetrahedron) 메쉬가 만들어졌다. 가동보 벽 근처는 상대적으로 조밀(Fine)한 메쉬가 만들어졌으며 멀어질수록 성긴(Rough) 메쉬가 만들어졌다.

Table 1에는 가동보의 기립각도별 해석 도메인(Domain)의 노드와 메쉬의 수가 나와 있다. 기립각도(θ)마다 계산해야 할 영역의 크기가 다르기 때문에 노드와 요소의 수도 달라진다. 각각의 기립각도별로 처음 계산한 모델이 계산되지 않거나 Courant Number의 문제로 계산이 멈추는 경우 메쉬의 크기를 줄여가면서 계산했다. Courant Number는 CFL No.로도 알려져 있는데 이는 과도상태(Transient) 해석 시 유체의 진행 길이가 시간 간격(Time Step)당 메쉬 하나의 길이보다 작도록 설정해야 좋은 결과를 얻을 수 있다는 것이다. 이를 수식으로 나타낸 것이 식(6)이며 여기서 u는 속도, t는 시간, x는 변위(메쉬의 길이)를 뜻한다. 하지만 너무 낮은 Courant Number는 해석 시간을 지나치게 소모한다는 단점이 있으므로 적당한 값을 찾아야 한다.

u⋅dt dx = C o u r a n t n u m b e r ≤ 1

(6)

Table 1

Number of nodes and elements by standing angle (θ) of movable wear

기립각 60^o에서 가장 많은 메쉬가 투자되었고, 30^o에서 가장 적은 메쉬가 투자되었다. 이는 월류수심이 보를 넘어오는 과정에서 어떤 형태를 보이느냐에 따라 달라졌다.

2.4.2 유동해석

해석 경계조건은 상류에서 속도 조건(Velocity Inlet, 0.1 m/s)으로 물이 유입되어 가동보의 상단을 통해서 월류수심이 발생하는 것을 가정했고 출구는 압력 조건(Pressure Outlet, 대기압 적용)을 적용했다. 계속해서 공급된 물은 가동보의 상단을 넘어서 아래로 떨어질 것이고, 이때의 조건은 단순히 가동보의 상단을 통과하는 것이 아니라 Fig. 3(b) 점선과 같이 가동보 상단의 발판을 통과할 때 월류수심의 수축을 동반하게 될 것이다. 이때 물이 가동보에 가하는 압력을 계산해서 구조의 정적 해석(Static Analysis)의 하중 조건(Loading Condition)으로 적용해서 연성해석을 수행할 것이다.

물과 공기가 한 도메인에서 계산되는 하천의 유동 현상을 계산하기 위해서 다상 모델(Multiphase)은 VOF 모델을 선택했으며 물(ρ = 998 kg_m/m³, μ = 1.003e-03 Pa·s)과 공기(ρ = 1.225 kg_m/m³, μ = 1.7894e-05 Pa·s)의 물성치가 적용되었다[11]. 추가로 물과 공기 사이의 상(Phase)의 상호작용을 위한 표면장력은 0.072 N/m가 적용되었다.

난류 점성 모델은 k-ω SST 모델이 적용되었다. 이 모델은 Menter가 제안한 것으로서 유동장의 특성에 따라서 Standard k-ε 난류 모델과 k-ω 난류 모델 및 Johnson-King 모델을 결합한 모델이다[10]. 이 모델은 벽면 근처에서는 k-ω 난류 모델을 사용하여 벽함수(Wall Function) 등이 필요 없이 경계조건만으로 계산이 가능하도록 하고 원방에서는 Standard k-ε 난류 모델을 사용하여 원방 경계값이 계산에 영향을 미치지 않도록 할 뿐만 아니라 역압력구배(Adverse Pressure Gradient)가 지배적인 부분에서는 Johnson-King 모델의 전단응력 이송 효과를 고려하도록 하고 있다[12].

Pressure-Velocity Coupling 알고리즘은 SIMPLE Scheme, Gradient는 Least Squares Cell Based, Pressure는 PRESTO, Momentum은 Second Order Upwind, 체적분율은 Geo-Reconstruct, 난류 운동에너지(Turbulent Kinetic Energy)는 Second Order Upwind, 소산율(Specific Dissipation Rate)은 Second Order Upwind를 적용했다. 부족완화계수(Under-Relaxation Factors)에서 압력(Pressure) 0.3, 밀도(Density) 1, 체적력(Body Forces) 1, 운동량(Momentum) 0.5, 난류 운동에너지 0.6, 소산율 0.6 그리고 난류 점성(Turbulent Viscosity) 0.8을 적용했다.

해석의 시간을 줄이기 위해서 Fig. 3(a)에서 ⓐ영역에 FLUENT의 Patch 기능을 이용해서 물을 먼저 적용하고 입구에서 추가로 물이 유입되도록 했다. 해석이 정상적으로 진행되는지를 알아보기 위해서 중간 단면을 지정하고, 이 단면에서 Water Volume Fraction을 관찰했다. Number of Time Steps를 3,000으로 지정하고, Time Step Size를 0.002로 지정해서 총 6초 동안 계산했으며, 전체적인 계산 시간을 고려해서 Time Step별 계산은 80회로 제한했다. 시스템의 저장 공간을 고려해서 해석 과정 파일은 6번의 Time Step마다 저장을 했다.

2.5 유동해석 결과

2.5.1 시간 경과에 따른 가동보의 벽면에 미치는 압력

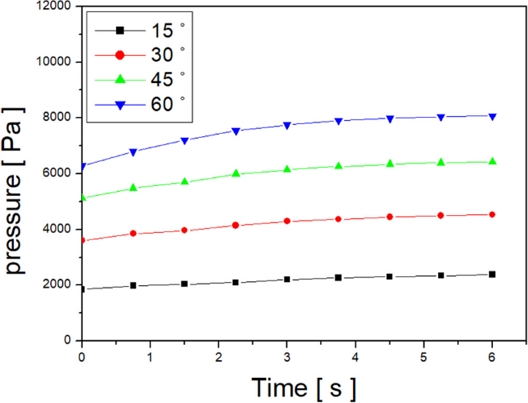
Fig. 6은 Time Step별로 가동보의 벽면에 미치는 면적 가중 평균 압력을 계산해서 나타낸 것이다. 가로축은 시간, 세로축은 압력을 나타내고 있다. 약 5초 이후부터는 가동보 벽면에 작용하는 압력의 변화가 미미했다. 따라서 계산 시간 및 PC의 계산 시간을 고려해서 6초까지 계산을 수행하였다.

Fig. 6

Area-Weighted average pressure acting on a movable weir over time

2.5.2 물의 체적분율과 가동보에 작용하는 압력

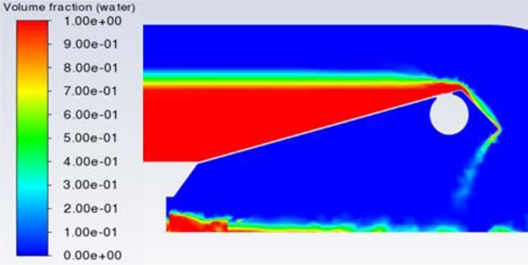
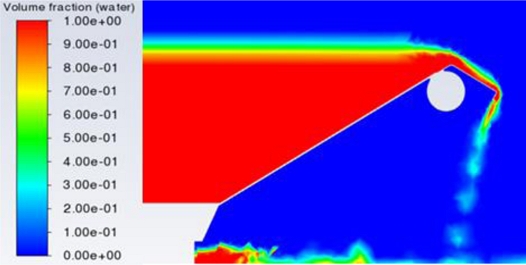
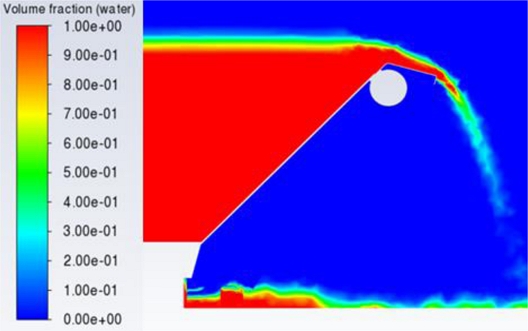
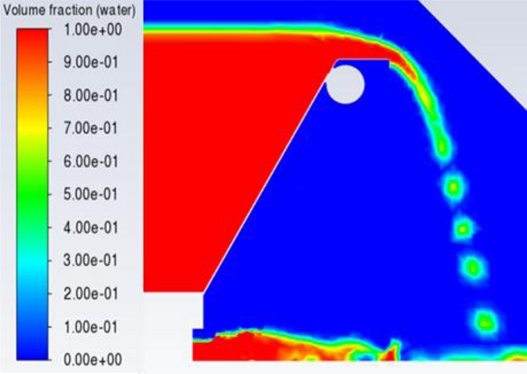
Figs. 7부터 10은 중앙의 단면(z = -2 m)의 등고선(Contour)으로 물의 체적분율을 나타낸 것이다. 이 그래프들에서 빨간색은 100% 물이고, 파란색은 100% 공기를 나타내며 그 중간의 색들은 메쉬 셀(Cell) 체적 내에 물의 비율에 따라서 파란색과 빨간색의 중간 단계 색들로 결정된다. Fig. 4의 광정위어처럼 가동보의 상단에 설치된 발판 위에서 월류수심의 수축이 잘 나타남을 알 수 있다.

Fig. 7

Water volume fraction at 15o of standing angle

Fig. 8

Water volume fraction at 30o of standing angle

Fig. 9

Water volume fraction at 45o of standing angle

Fig. 10

Water volume fraction at 60o of standing angle

가동보 상단의 발판 때문에 낙하하는 물의 형상도 각기 다르게 나타났다. 이 때문에 우측 출구 영역의 형상 모델링과 메쉬의 크기를 적절히 조절해야 했다. 그 결과 가동보 기립각 15^o에서의 도메인 체적이 30^o에서보다 더 작음에도 불구하고 더 많은 메쉬가 적용되었다.

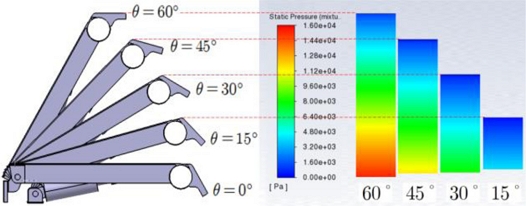
Fig. 11은 가동보의 벽면의 정압(Static Pressure) 분포를 일부분만 나타낸 것이다. 기립각도에 따라서 하단 부분이 조금씩 상승한 것도 그림으로 표시했다. 상단의 빨간색은 16,000 Pa에 해당되고, 하단의 파란색은 0 Pa에 해당되고 전체적으로 동일한 압력 스케일이 적용되었다. 작업 유체에 의한 압력 프리즘(Pressure Prism)이 잘 표현되었고, 가동보의 기립각도가 낮아짐에 따라서 벽면에 작용하는 압력도 낮아짐을 확인할 수 있었다. 이러한 결과들은 물리적으로 타당하다. 이 압력을 구조해석의 하중 조건으로 사용해서 구조해석을 수행하였다.

Fig. 11

Distribution of static pressure on the wall according to the standing angle of the movable weir

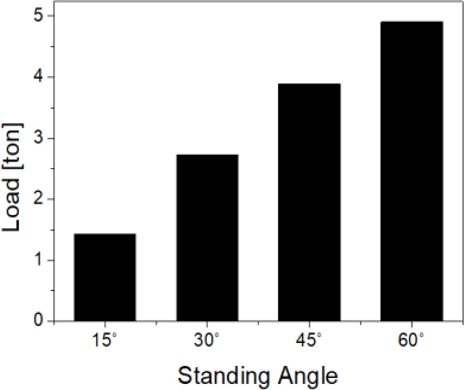
Fig. 12는 각각의 기립각도별로 가동보의 벽면에 작용하는 하중의 크기를 유동해석의 결과로부터 산출한 것이다. 이는 기립각도에 따라서 가둘 수 있는 물의 양이 정해지기 때문에 기립각도가 낮으면 수위가 낮기 때문에 보의 벽면에 가해지는 하중도 낮고, 기립각도가 높으면 수위가 높아져 하중도 높게 나왔으며 이는 물리적으로 타당한 결과이다. 가장 작은 하중은 기립각도 15^o에서 1.43 ton이었고, 가장 큰 하중은 기립각도 60^o에서 4.90 ton이었다.

Fig. 12

Load acting on the wall of the movable weir at each standing angle

2.6 구조해석

2.6.1 재료의 물리적 성질

가동보의 재질은 바닥에 매립될 구조물과 유압시스템 부분은 SS400이며 나머지는 모두 STS304가 적용되었다. SS400과 STS304의 물성치는 Table 2에 나타내었으며 기존 구조해석 논문과 같게 적용했다[3].

Table 2

Material properties of SS400 and STS304 [3]

2.6.2 구속조건 및 메쉬

Fig. 1(a)에서 보는 것과 같이 보의 경첩이 바닥에 고정된 부분은 철근 콘크리트에 고정되어서 완전구속상태이다. 그래서 Fig. 13에서 파란색 실선의 경우 각 방향으로 모두 구속시키는 Fixed Support 조건을 적용했으며, 초록색의 실선 구간인 보의 벽 부분과 상단의 발판은 유동해석 결과로부터 압력을 전달받아 적용했다. 빨간색 점선 구간인 경첩(Hinge)과 핀(Pin) 부분의 경우 접촉 부분이 분리될 수는 없지만 약간의 미끄러짐(Sliding)이 허용되는 No Separation 조건이 적용되었다.

Fig. 13

Finite element modeling of movable weir

메쉬의 경우 가동보의 형상이 매우 복잡하기 때문에 보의 벽면의 경우 20, 다른 부분들은 10 mm로 지정해 자동을 메쉬를 구성했다. 핀과 같은 간단한 구조는 육면체 메쉬가 생성되고 나머지 부분들은 모두 4면체의 메쉬가 생성되었다. 그리고 큰 응력이 발생되는 보의 중앙 하단부에는 Sphere of Influence 기능을 적용해서 메쉬의 크기를 2 mm로 지정했다. 기립각도 60^o인 경우 노드의 수는 963,712개, 요소의 수는 558,814개로 구성되었다.

2.6.3 변형량

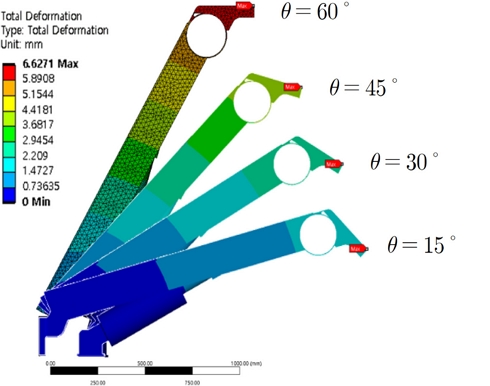
Fig. 14는 구조해석을 수행한 후 기립각도별 변형량(Total Deformation, mm)을 하나의 그림으로 나타낸 것이다. 참고문헌의 결과처럼 기립각도가 클수록 물의 수위가 높아지기 때문에 더 많은 변형량이 나타났다[3]. 기립각도 60^o에서부터 차례로 6.63, 4.34, 2.93 그리고 1.83 mm가 나왔다.

Fig. 14

Total deformation by standing angle of movable weir

2.6.4 응력

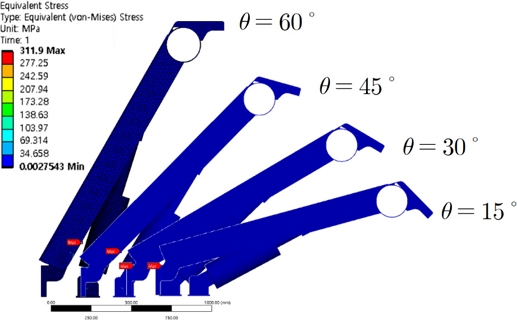
Fig. 15는 기립각도별 가동보가 받는 등가 응력(von-Mises, MPa)을 나타낸 것이다. 최대 응력이 나타나는 위치가 기립각도별로 조금씩 다르기 때문에 가동보를 겹치지 못하고 임의의 간격으로 배치했다. 기립각도가 큰 경우인 60^o에서 최대 응력이 나타났으며 기립각도가 낮아질수록 작은 응력이 나왔고 이를 Table 3에 정리하였다. 하지만 Fig. 16처럼 최대 응력이 나오는 위치는 달랐다. 응력의 크기 면에서는 전체적으로 변형량의 결과와 동일한 경향을 보였다.

Fig. 15

Stress (von-Mises) by standing angle of movable weir

Table 3

Maximum stress for each standing angle of a movable weir

Fig. 16

Maximum stress generation point for each standing angle of the movable weir

3. 결과 및 토의

3.1 최대 응력 발생 지점

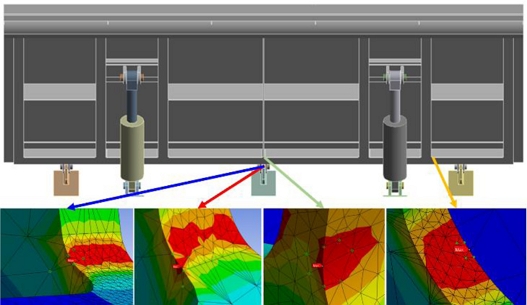
Fig. 16은 가동보의 기립각도별 최대 응력이 발생한 위치를 나타내고 있다. 기립각이 15와 30^o는 중앙의 힌지 뒷부분, 45^o에서는 정면의 우측 하단 노치 부분 그리고 60^o에서는 정면 중앙의 하단부에 있는 노치에서 발생했다. 이처럼 최대 응력의 발생 위치가 다른 것은 가동보의 기립각도에 따른 작용점(Center of Pressure)의 위치가 변경되었기 때문으로 생각된다. 기립각도가 낮아지면 가동보의 벽면 위에 담긴 물의 무게중심이 Fig. 15 기준으로 점차 가동보의 오른쪽으로 이동해서 나타나는 결과로 생각된다.

3.2 안전계수

Table 3은 기존 구조해석[3] 결과와 연성해석 결과를 나타낸 것이다. 기존 구조해석(Structural Analysis, SA)의 경우 가동보의 수심만 적용해서 계산했지만, 월류수심이 있는 연성해석(Fluid-Structure Interaction, FSI)의 경우 상승된 수위만큼 더 큰 전압력이 작용한다. 따라서 응력이 더 크게 발생했고 식(8)의 FSI 안전계수도 식(7)의 SA 안전계수에 비해 더 낮게 나왔으며, 이는 물리적으로 타당한 결과이다. 여기서 S는 안전계수, σ_u는 인장강도 그리고 σ_max는 구조해석에서 계산한 최대 응력이다.

S A : S = σ u σ max,SA = 590 228.71 = 2.579686 … ≒ 2.58

(7)

F S I : S = σ u σ max, F S I = 590 271.86 = 2.170268 … ≒ 2.17

(8)

소재의 물성치가 잘 알려져 있으며 하중의 종류와 크기 그리고 응력의 크기가 쉽게 결정될 수 있는 경우에는 약 1.5-2 정도의 안전계수가 필요(Joseph Vidosic의 제한값)하다. 이 연성해석에서는 월류수심으로 인해서 전압력이 더 크게 작용했음에도 불구하고 가장 취약한 곳에서 2.17 이상의 안전계수를 유지하고 있기 때문에, 구조물은 충분한 안전을 확보했다고 판단된다.

4. 결론

가동보의 최대 저수량에 추가로 물이 유입되어 월류수심이 발생하는 가혹한 상황을 가정해서 유동해석을 수행하고 그 결과를 이용하여 구조해석을 수행하고 유동해석은 ANSYS Workbench의 FLUENT를 사용했고 구조해석은 Static Structure를 사용했으며 다음의 결론을 얻었다.

(1)비정상 유동해석에서 월류수심의 수축이 잘 표현되었다.
(2)가동보의 벽면에 작용하는 압력은 약 4.5초에 해당되는 900 time step을 지나면서 일정하게 유지된 것으로 판단된다.
(3)월류수심의 영향으로 더 많은 전압력이 적용되어 변형량과 응력은 구조해석의 결과보다 증가한 값이 나왔으며 이는 물리적으로 타당하다.
(4)가장 취약한 노치부의 안전계수가 2.17로 가동보는 안전성을 확보한 것으로 판단된다.

Acknowledgments

해석에 사용된 정보들은 세광산업으로부터 제공받았으며, 이에 감사드립니다.

REFERENCES

Yeo, C., Kim, Y., Seo, G., Song, J., Yeo, C., Kim, Y., Seo, G., Song, J., (2009), The study for hydraulic influence by installing movable weir, Proceedings of the Conference of the Korean Society of Civil Engineers, 1452-1455.
Seo, G. W., Ko, D. S., Ryu, G. S., (2015), Case study for gate vibration of the movable weir, Proceedings of the KFMA Annual Meeting, 45-47.
Lee, H., Park, T., (2021), An aanalytical study of structural performance evaluation for multi-stage control movable weir, Journal of the Korean Society of Manufacturing Process Engineers, 20(5), 61-68. [https://doi.org/10.14775/ksmpe.2021.20.05.061]
Choi, J. W., Joo, H. J., Kim, J. M., Lee, K. S., Yoon, S. J., (2013), An analytical study on the structural performance evaluation of the multistage overturing movable gate, Journal of Korean Society of Steel Construction, 25(6), 613-622. [https://doi.org/10.7781/kjoss.2013.25.6.613]
Choi, G., Kim, Y., Cho, S., Kim, J., (2006), Variation of water elevation by setting angle of movable weir with bottom flow gate, Proceedings of the Korean Society of Civil Engineers Conference & Civil Expo, 2661-2664.
Park, J., Pham, Q. D. T., Choi, S., A comparative study of two-phase flow simulations between a commercial software (ANSYS Fluent) and an open source-based (OpenFOAM) computational fluid dynamics, Journal of Computational Fluids Engineering, 26(2), 31-38. [https://doi.org/10.6112/kscfe.2021.26.2.031]
Paik, J., Lee, N. J., (2015), Numerical modeling of free surface flow over a broad-crested rectangular weir, Journal of Korea Water Resources Association, 48(4), 281-290. [https://doi.org/10.3741/JKWRA.2015.48.4.281]
Youn, S. B., Im, I. T., Seo, L. S., (2016), Fluid mechanics 2nd, Munundang.
Ansys, Inc., ANSYS Fluent theory guide 2020 R2. http://www.ansys.com/
Menter, F. R., (1994), Two-Equation eddy-viscosity turbulence models for engineering applications, AIAA Journal, 32(8), 1598-1605. [https://doi.org/10.2514/3.12149]
Çengel, Y. A., Cimbala, J. M., (2010), Fluid mechanics: Fundamentals and applications, McGraw-Hill Higher Education.
Lee, B. S., Lee, D. H., Lee, S. S., (1998), Analysis of unsteady turbulent flow fields around 2 dimensional square cylinder using k- SST turbulence model, Proceedings of the Korean Society for Aeronautical & Space Sciences 1998 Spring Conference, 104-107.

Haesoo Lee

Ph.D. Lecturer at Gyeongsang National University. His research interest is the fluid machinery and CFD.

E-mail: haesoolee@gnu.ac.kr

Taehyun Park

Professor in the School of Mechanical Engineering, Kyungnam University. His research interest is CFD, smart manufacturing, nano&micro technology.

E-mail: taehyun@kyungnam.ac.kr

θ	60^o	45^o	30^o	15^o
Nodes	1,116,774	738,588	624,190	664,010
Elements	2,944,931	1,686,557	1,413,734	1,537,818

Material	SS400	STS304
Density [kg_m/m³]	7,800	8,000
Young’s modulus [GPa]	200	193
Poisson’s ratio	0.3	0.29
Yield strength [MPa]	230	330
Tensile strength [MPa]	515	590

Standing anlge [^o]	60	45	30	15
Structural analysis σ_average [MPa]	199.2	158.2	151.6	93.1
Couple field analysis σ_average [MPa]	271.9	252.4	172.5	120.9