유한요소 모델을 이용한 머리뼈의 영률에 따른 골전도 반응 차이 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The bone compression and the inertia from cochlear fluid or middle ear (ME) ossicles, are generally considered to be important components inducing bone-conducted (BC) hearing. To clarify the bone compression effect on the BC hearing caused by variation of Young’s modulus of skull, two different types of three-dimensional finite-element models were used in this study. The FE models were (1) Isolated cochlea model comprising ME and cochlea containing basilar membrane (BM) and (2) Head model comprising the isolated cochlea structure. The model was validated by comparison of cochlear responses such as BM velocities with those of otosclerosis patients’ clinical data. Additionally, results showed that the bone compression effects on a BC hearing is highly depended on the Young’s modulus of a skull. Also, the bone compression effects could be underestimated at low frequencies in temporal bone experiments, whereas the effects could be overestimated at high frequencies in cadaver experiments.
Keywords:
Temporal bone, Cadaver head, Otosclerosis, Finite element model, Bone compression, Bone conduction키워드:
측두골, 사체 머리, 이경화증, 유한요소 모델, 골압축, 골전도1. 서론
골전도(Bone Conduction, BC)를 야기하는 여러 요인 중 가장 주요한 요소로 중이의 관성, 달팽이관 내부의 유체 관성과 달팽이관 주변 뼈의 압축 효과가 주로 언급된다[1-3]. 이러한 주요 요소가 골전도에 미치는 영향을 정량화하고 골전도 메커니즘을 밝히고자 하는 실험에서는 Temporal Bone과 Cadaver Head가 주로 사용되어 왔다.
예를 들어 Stieger, et al. (2018)은 골전도 메커니즘을 설명하기 위해 Temporal Bone을 사용하여 Promontory 속도와 달팽이관 내압을 측정했다[4]. 그들은 Cochleostomy를 수행하여 Laser Vibrometer로 Promontory 속도를 측정하였다. Temporal Bone을 사용한 연구는 Stenfelt, et al. (2002)에 의해서도 수행되었다. 이들은 Temporal Bone을 Shaker에 고정하여 상하 진동을 이용한 골전도 자극을 가하고 이에 상응하는 Umbo와 Stapes Footplate의 움직임을 측정했다[5]. 그들은 이러한 실험 세팅을 이용하여 중이의 질량 증가에 따른 골전도 청력의 변화, 즉 골전도에 있어 중이의 관성의 영향을 정량화하여 보여주었다. 골전도 메커니즘의 이해를 돕기 위한 실험에는 Temporal Bone 외에도 Cadaver Head가 많이 사용된다.
Cadaver Head를 이용한 실험은 Eeg-Oloffson, et al. (2018)의 연구에서 볼 수 있다. 이들은 가장 큰 달팽이관 반응을 야기하는 골전도 자극 위치를 찾기 위해 Cadaver Head로부터 Mechanical Point Impedance와 Promontory 속도를 측정하였다. Promontory 속도를 측정하기 위해, 고막과 함께 Malleus와 Incus를 제거한 후 Promontory에 작은 유리 반사판을 부착하였다. 일반적인 골전도 보청기(Bone Conduction Devices, BCDs) 부착점과 Ear Canal과 가까운 위치 사이의 여러 위치에서 진동 자극을 가했으며 Laser Doppler Vibrometer로 Promontory 속도를 측정하였다. 이를 통해, 진동 자극을 표준 BCDs 위치보다 달팽이관에 더 가깝게 가하면 Promontory 속도가 증가한다는 것을 밝혔다[6].
이러한 실험 결과들이 골전도 메커니즘을 이해하는데 크게 기여했으나, 골전도의 또 다른 주요 요소인 달팽이관 주변 뼈의 압축 효과에 대한 설명 및 연구는 이에 비해 상대적으로 미흡했다. 뼈의 압축 효과는 뼈의 기계적 물성치에 매우 의존하므로, 달팽이관을 포함하는 두개골의 영률 측정에 관한 연구가 중요하다. 예를 들어, Auperrin, et al. (2014)은 Density Measurements, Geometrical Measurements, Three-Point Bending Tests와 Statistical Analysis를 통해 두개골의 평균적인 영률을 측정하였다[7]. 그 결과 Frontal Bone은 3.81±1.55, Parietal Bones는 5.00±3.12, Temporal Bones는 9.70±5.75 GPa이었다. 또, Rho, et al. (1993)이 측정한 Cortical Bone의 Tensile 영률은 18.6 GPa이었다[8]. 이처럼 두개골의 영률은 여러 값으로 측정되고, 이러한 영률의 차이가 골전도 청력에 미치는 영향, 특히 영률의 차이에 의해 Temporal Bone과 Cadaver의 뼈 압축 효과에 따른 골전도 변화에 대한 연구는 많이 이루어지지 않은 상황이다.
본 연구에서는 청각 기관을 포함하는 전체 Head의 3D 유한 요소(Finite Element, FE) 모델을 사용하여 영률 차이에 따른 Temporal Bone과 Cadaver Head 사이의 골전도 반응에 대한 영향을 조사하였다. 이 모델은 이경화증(Otosclerosis) 환자로부터 얻은 임상 데이터와 청력 상실을 비교하여 검증되었다. 또한, 이경화증 상태를 통해, 골전도에 대한 뼈의 영률에 따른 뼈의 압축 효과는 Temporal Bone과 Cadaver Head 모델 모두에서 조사되었다.
2. 방법
2.1 유한요소 모델
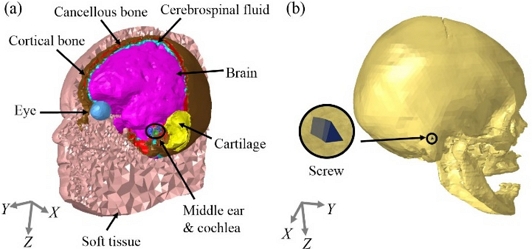
Temporal Bone을 시뮬레이션하기 위해, 두 개의 Fluid Chamber (Scala Vestibuli, Scale Tympani)로 구성된 달팽이관 구조를 만들었고, 이 Fluid Chamber 사이에 기저막(Basilar Membrane, BM)을 삽입하여 청신경과 연결된 기저막의 속도가 클수록 청력이 우수하다는 가정을 적용하였다. 또한 Fig. 1에서 보듯이 고막과 이소골, 그리고 인대 등으로 구성된 중이 구조를 결합시켜 이를 Isolated Model로 칭하였다. Cadaver Head 모델은 두개골, 눈, 뇌, 뇌척수액 등으로 구성하였다. 특히 피부, 혈관과 근육과 같은 조직은 하나의 Soft Tissue로 정의하였고, 앞서 보인 Isolated Model을 머리 모델 속에 삽입하여 기저막의 속도를 계산할 수 있도록 하였다. 두 모델에 대한 자세한 설명은 이전 연구[9-11]에서 설명되었지만, 본문에서는 독자의 편의를 위해 모델에 대해 다음과 같은 간략한 설명을 추가한다.
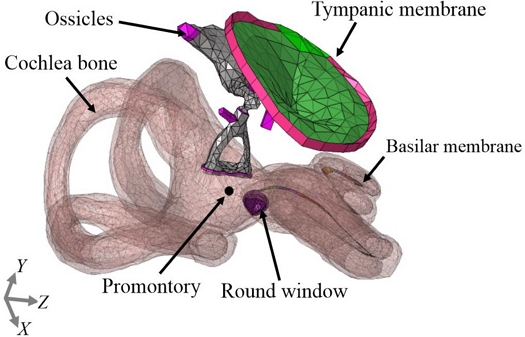
The FE model of the isolated model consisting of the middle ear and cochlea. It is assumed that outer cochlear bone and end of the ligaments are completely connected with the temporal bone
머리 유한요소 모델은 Cadaver Head의 Cryosectional 이미지를 사용하여 3D 재구성에 의해 생성되었으며, 각각 약 258,000개 및 144,000여 개의 고체 및 유체 사면체 요소로 구성되었다. Isolated 모델의 경우, 청각 주변부의 Geometry를 생성하기 위해 μCT 이미지를 사용했다. Isolated 모델은 약 104,000개, 507,000개의 고체 및 유체 사면체 요소로 구성되었다. 또한, 기저막은 약 18,000개의 고체 오면체 요소로 나타내었다. Isolated 모델과 머리 유한요소 모델은 각각 Figs. 1 및 2에 나타내었다.
2.2 골전도 자극
본 연구에서는 외부 자극의 입력 주파수를 0.1에서 10까지 0.1 kHz씩 증가시키며 시뮬레이션을 수행하였다. FE 시뮬레이션은 상용 소프트웨어인 ACTRAN (MSC Software, Newport Beach, CA, USA)을 통해 수행되었다. 골전도 청력을 시뮬레이션으로 구현하기 위해 두 가지 다른 자극 방법이 사용되었다.
첫 번째 방법은 Head Model에 적용된 방법으로, Mastoid 위치에서 Sinusoidal Force를 접면에 수직인 방향으로 가했다. 이는 머리에 부착된 BCDs로부터의 골전도 자극과 매우 유사하다. 두 번째 방법은 Isolated Model에 적용된 방법으로 외측 달팽이관 뼈와 고막의 끝, 그리고 중이 구조를 지지하는 각 인대의 끝에 Sinusoidal Displacement 조건을 할당하였고 이를 통해 구조물의 관성을 통한 골전도 자극을 살펴보았다. 또한 Isolated 모델에서는 달팽이관의 주변 뼈가 없기 때문에 Head 모델에 비하여 뼈의 압축 효과가 크게 감소할 것을 감안하여 Isolated 모델의 뼈 바깥 표면에 Distributed Pressure를 가했다. 두개골을 통과하는 실제 압력파는 상당히 복잡하지만, 시뮬레이션에서 달팽이관의 압력파는 파장의 길이가 달팽이관의 길이보다 훨씬 크다는 가정하에 평면파로 단순화되었다. 추가 압력을 가하는 자세한 방법은 이전 연구[12]에서 확인할 수 있다.
이경화증의 경우 이전 연구[13]에서 설명한 바와 같이 Stapdes Anuular Ligament의 영률을 뼈의 영률과 같은 값으로 설정하여 인대의 경화를 시뮬레이션 상에서 구현하였다. 또한 정상 상태에서의 기저막 속도와 이경화증 조건의 기저막 속도 차이를 이용하여 이경화증에 의한 청력 손실을 계산하였다. 계산된 청력 손실은 시뮬레이션 결과를 검증하는데 뿐만 아니라 Carhart’s Notch [14]를 보여주는 임상 데이터와 비교하여 골전도 반응에 대한 뼈의 압축 효과를 조정하는 데에도 사용되었다.
3. 결과 및 고찰
Fig. 3은 정상 상태와 이경화증 상태의 기저막 속도 차이를 통해 계산한 주파수별 청력 손실을 나타낸다. 이 청력 손실은 Figs. 3(a)부터 3(c)에서 흑색 점선으로 표시된 임상 데이터[12]와 비교되었다. 임상 데이터는 이경화증 환자의 골전도 청력을 측정한 Carhart의 데이터를 사용하였다. Fig. 3(a)는 Isolated 모델에 관성을 이용한 시뮬레이션 결과를 나타내며, 흑색과 적색 실선은 각각 뼈의 압축 효과가 없을 때와 있을 때를 나타낸다. Isolated 모델의 시뮬레이션에서 관성뿐만 아니라 뼈의 압축 효과가 있는 경우(적색 실선), 계산된 청력 손실은 약 10 dB의 차이 내로 임상 데이터와 유사함을 나타내었다. 하지만, 골전도 자극에 관성만을 사용한 경우, 600 Hz 미만의 저주파에서 임상 데이터와 비교하여 20-30 dB의 커다란 청력 손실 차이가 관찰되었다. 따라서, Isolated 달팽이관에 Shaker를 사용하여 실험을 할 경우, 추가적인 뼈의 압축을 고려하여 적절한 보상을 감안하지 않는다면 1 kHz 미만의 저주파수에서 얻어질 실험값이 다소 왜곡될 가능성이 있음을 추론할 수 있다.
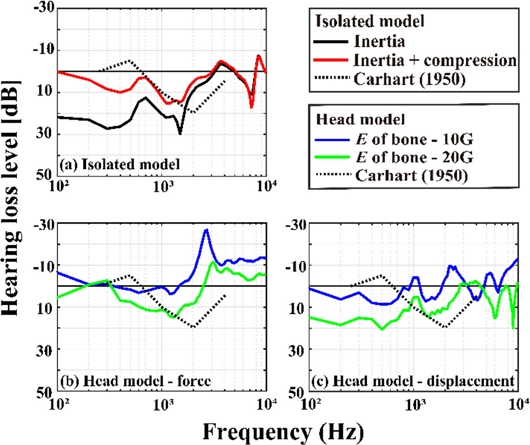
Comparison of the hearing loss level calculated in the simulation with clinical data. The used FE models are (a) The isolated cochlear model, and (b)-(c) The full head model. In (a), the black-solid line represents the only inertia input whereas the red-solid line indicates the inertia and bone compression inputs. In (b) and (c), the blue-solid line means the case when the Young’s modulus for cortical bone and cochlear bone was 10 GPa. On the other hand, the green-solid line describes the case when the Young’s modulus was 20 GPa. In all the figures, the black-dotted line represents the clinical data obtained by Carhart. The BC input is the dynamic force in (b) whereas the input is the sinusoidal displacement in (c). The displacement in (c) was applied on a few nodes on the surface of skull
Figs. 3(b)와 3(c)의 청색과 녹색 실선은 각각 Cortical Bone과 Cochlear Bone의 영률이 10과 20 GPa인 경우를 나타낸다. Fig. 3(b)는 골전도 입력값으로 Sinusoidal Force를 가했을 경우 이경화증에 의한 청력 손실을 나타낸다. 뼈의 영률이 10 GPa일 경우, 1 kHz 이상에서는 이경화증 환자의 골전도 청력 손실이 크지 않아 임상 데이터와 비교했을 때 상대적으로 이경화증 환자로부터 청력 증가가 나타났다. 반면, 영률이 20 GPa의 경우에는, 1 kHz 이상에서 임상데이터와 10 dB 이내의 차이를 보이며 약 1.3 kHz 부근에서 Notch (Carhart’s Notch)가 나타났다.
Fig. 3(c)는 Head 모델을 Shaker에 고정하여 Sinusoidal Displacement 조건을 할당한 실험[14]과 같이 골전도 입력값으로 머리 유한요소 모델에 Sinusoidal Displacement를 적용하여 시뮬레이션을 수행했을 때 청력 손실을 나타낸다. 영률이 10 GPa(청색)일 때보다 20 GPa(녹색)일 때, 1 kHz 이하의 저주파에서 10-15 dB 정도의 보다 큰 청력 손실이 발생했다. 이는 주변 뼈의 영률이 클 때 뼈의 압축 효과가 더 적게 발생함을 보여준다. 다시 말해, 골전도 입력값이 BCDs와 같은 Sinusoidal Force일 경우 두개골의 영률이 고주파에서 골전도 청력에 큰 영향을 미치는 것을 알 수 있다.
이 결과를 실험 조건에 적용해 보았을 때, Cadaver Head를 사용한 골전도 실험은 두개골의 특성상 시간이 지날수록 굳어지기 때문에 영률 차이에 따른 골전도 청력에 대한 뼈의 압축 효과를 보다 신중하게 고려할 필요가 있다. 또한 이전 연구[7,8]에 따르면, 두개골의 영률은 약 2-19 GPa 범위로 보고되고 있다. 두개골 영률에 있어 존재하는 개인차는 골전도 청력에 영향을 끼칠 것으로 예측된다. 따라서, 정확한 실험값 도출이나 환자에 따른 올바른 BCDs 사용을 위해서는 각 개인의 두개골 영률을 고려하는 것이 필요할 것으로 사료된다.
본 연구는 머리뼈의 영률에 따른 골전도 반응 차이 분석을 위해 두개골에 직접 자극을 주는 Implantable Device를 가정하여 시뮬레이션을 진행하였다. 하지만, 최근 부착형 골전도 보청기도 많이 보급되는 것을 상기할 필요가 있다. 기본적인 에너지 전달 과정 및 머리뼈가 골전도에 미치는 영향은 삽입형과 부착형 서로 간에 큰 차이가 없을지라도 부착형 골전도 보청기에 대한 연구가 추후 진행될 필요가 있다.
4. 결론
본 연구에서는 두개골의 영률이 골전도 청력에 미치는 영향을 두 종류의 3차원 청각기관 유한요소 모델(Isolated Cochlear Model과 Head Model)을 이용하여 연구하였다. 이경화증으로 인한 청력 손실을 임상 데이터와 비교하여 모델을 검증하였고, 이를 통해 두개골의 영률이 골전도 청력에 미치는 영향, 특히 뼈 압축력이 골전도 청력에 미치는 영향을 살펴보았다. Temporal Bone에 Shaker가 사용된 골전도 실험의 경우, 저주파에서 뼈의 압축력이 더 고려되어야 하는 반면, Cadaver Head를 이용한 실험의 경우 고주파에서 뼈의 압축력이 지나치게 강조되지 않도록 주의를 기울여야 할 것이다.
NOMENCLATURE
| FE : | Finite Element |
| μCT : | Micro Computed-Tomography |
| BM : | Basilar Membrane |
| kHz : | Kilohertz |
| GPa : | Gigapascal |
| dB : | Decibel |
Acknowledgments
이 성과는 2017년도 및 2019년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(Nos. 2017M3A9E2065287 and 2019R1C1C1007907).
REFERENCES
-
Stenfelt, S., (2011), Acoustic and physiologic aspects of bone conduction hearing, Implantable Bone Conduction Hearing Aids, 71, 10-21.
[https://doi.org/10.1159/000323574]

-
Stenfelt, S., Goode, R. L., (2005), Bone-conducted sound: Physiological and clinical aspects, Otology & Neurotology, 26(6), 1245-1261.
[https://doi.org/10.1097/01.mao.0000187236.10842.d5]

-
Stenfelt, S., (2020), Investigation of mechanisms in bone conduction hyperacusis with third window pathologies based on model predictions, Frontiers in Neurology, 11, 966.
[https://doi.org/10.3389/fneur.2020.00966]

-
Stieger, C., Guan, X., Farahmand, R. B., Page, B. F., Merchant, J. P., Abur, D., Nakajima, H. H., (2018), Intracochlear sound pressure measurements in normal human temporal bones during bone conduction stimulation, Journal of the Association for Research in Otolaryngology, 19(5), 523-539.
[https://doi.org/10.1007/s10162-018-00684-1]

-
Stenfelt, S., Hato, N., Goode, R. L., (2002), Factors contributing to bone conduction: The middle ear, The Journal of the Acoustical Society of America, 111(2), 947-959.
[https://doi.org/10.1121/1.1432977]

-
Eeg-Olofsson, M., Stenfelt, S., Tjellström, A., Granström, G., (2008), Transmission of bone-conducted sound in the human skull measured by cochlear vibrations, International Journal of Audiology, 47(12), 761-769.
[https://doi.org/10.1080/14992020802311216]

-
Auperrin, A., Delille, R., Lesueur, D., Bruyère, K., Masson, C., Drazétic, P., (2014), Geometrical and material parameters to assess the macroscopic mechanical behaviour of fresh cranial bone samples, Journal of Biomechanics, 47(5), 1180-1185.
[https://doi.org/10.1016/j.jbiomech.2013.10.060]

-
Rho, J. Y., Ashman, R. B., Turner, C. H., (1993), Young's modulus of trabecular and cortical bone material: Ultrasonic and microtensile measurements, Journal of Biomechanics, 26(2), 111-119.
[https://doi.org/10.1016/0021-9290(93)90042-D]

-
Chang, Y., Kim, N., Stenfelt, S., (2016), The development of a whole-head human finite-element model for simulation of the transmission of bone-conducted sound, The Journal of the Acoustical Society of America, 140(3), 1635-1651.
[https://doi.org/10.1121/1.4962443]

-
Kim, N., Steele, C. R., Puria, S., (2014), The importance of the hook region of the cochlea for bone-conduction hearing, Biophysical Journal, 107(1), 233-241.
[https://doi.org/10.1016/j.bpj.2014.04.052]

-
Lim, J., Dobrev, I., Röösli, C., Stenfelt, S., Kim, N., (2022), Development of a finite element model of a human head including auditory periphery for understanding of bone-conducted hearing, Hearing Research, 421, 108337.
[https://doi.org/10.1016/j.heares.2021.108337]

-
Carhart, R., (1950), Clinical application of bone conduction audiometry, Archives of Otolaryngology, 51(6), 798-808.
[https://doi.org/10.1001/archotol.1950.00700020824003]

-
Kim, N., Steele, C., Puria, S., (2013), Carhart's notch: A window into mechanisms of bone-conducted hearing, Proceedings of the Meetings on Acoustics ICA2013, 050133.
[https://doi.org/10.1121/1.4799725]

-
Nicole, L. G., Patterson, J. N., Rodriguez, A. I., Fitzpatrick, D., Gordon, K. R., Janky, K. L., (2020), Bone conduction vibration vestibular evoked myogenic potential (VEMP) testing: Reliability in children, adolescents, and young adults, Ear and Hearing, 42(2), 355.
[https://doi.org/10.1097/AUD.0000000000000925]


M.S. researcher in the Department of Mechanical Engineering, Sogang University. His research interest is bone conduction, acoustic psychology and finite element method.
E-mail: imbellcow94@gmail.com

B.S. in the Department of Mechanical Engineering, Incheon National University. Her research interest is bone conduction and machine learning.
E-mail: strong_water99@inu.ac.kr

Associate Professor in the Department of Mechanical Engineering, Sogang University. His research interest is hearing mechanics including cochlear and middle-ear mechanics, and bone conduction.
E-mail: nkim@sogang.ac.kr