특이성을 고려한 엑소수트의 전신 기반 제어 전략 시뮬레이션

1. 서론

실제 산업현장에서 노동자들은 단순하고 반복적인 업무들을 주로 수행하게 된다. 그중에서도, 물건을 들어 올리거나 내리는 동작들은 허리나 무릎 관절에 큰 부담을 야기한다. 이러한 부담을 줄이기 위해 웨어러블 로봇인 엑소수트가 보조력을 전달하는 연구들이 다양하게 수행되어왔다. 우선 초기에는 패시브한 엑소수트를 이용한 연구들이 진행되었는데, 스프링 혹은 탄성 물질을 이용하여 외부 구동력 없이 착용자를 보조하였다[1,2]. 이러한 연구들은 관절이 최대로 구부러졌을 때 에너지를 저장한 뒤 들어올리는 과정에서 이를 이용하는 방식으로 부담을 줄여주었다. 구동기가 없기 때문에 다른 엑소 시스템보다 상대적으로 가벼우며 추가적인 제어기가 필요하지 않다는 장점이 있다[3-5]. 그러나 패시브한 시스템으로는 보조력에 한계가 있기 때문에 다양한 액티브 시스템을 이용한 연구들이 많이 개발되었다.

일반적인 리프팅 동작에서는 최저점에서 무릎에 큰 모멘트가 발생하기 때문에 무릎 보조에 대한 연구가 중점적으로 진행되었고[6,7], 뿐만 아니라 다른 관절에도 보조 토크를 전달하기 위해 발목, 허리 등에도 구동기를 결합하여 만든 엑소 시스템도 활발히 개발되었다[8]. 이렇게 다양한 관절에서의 보조력들은 직접 가해지는 신체 부위뿐만 아니라 전체 시스템 다이나믹스를 변화시키기 때문에 각각의 값은 적절하게 분배되어야 한다. 높은 퍼포먼스를 보이기 위해서는 주어진 동작에 맞춰 최적으로 제어기가 구성되어야 하며, 사람과의 상호작용 또한 고려되어야 그 효율을 극대화시킬 수 있다.

이러한 보조 토크를 생성하는 연구들은 다양한 방향으로 진행되었는데, 위치 기반 제어부터 모델 기반의 토크 제어까지 다방면으로 진행되었다. 모델 기반 제어의 경우 비선형 모델 예측 제어기[9], 마비 환자를 위한 임피던스 제어기[10] 등의 연구가 존재하며, 최근에는 컴퓨팅 성능 향상과 AI (Artificial Intelligence)의 발전으로 인해 강화학습을 이용한 연구도 활발하게 진행 중이다[11].

본 논문에서 제시하는 제어기는 전신 제어기(Whole-Body Control)이다. 로보틱스 분야에서 최근 많이 사용되고 있으며, 다양한 태스크들을 동시에 만족시키는 최적 해를 찾는 방식이다[12,13]. 상대적으로 좀 더 긴 시간을 고려하는 모델 예측 제어기와는 다르게 전신 제어기는 매 순간마다 최적값을 계산한다는 장점이 있다. 또한, 다양한 태스크들을 구성하고 각각의 중요도에 따라 가중치를 쉽게 부여할 수 있다는 특징을 갖는다. 이러한 방식의 제어기는 다양한 목적으로 연구가 진행되어 왔는데 예를 들어, 계층적 최적화 방법을 통해 순차적으로 최적화 문제를 푸는 방법이 존재하며[14], Underactuated 시스템에서 내력을 고려한 방법이 존재한다[15]. 사족보행에서 사용되는 Whole-Body Impulse Control의 경우에는[16] 지면 반력을 효과적으로 생성하기 위하여 모델 예측 제어기와 전신 기반 제어기 형태를 통합하였다. 앞서 말한 연구들의 경우 일반적으로 족형의 로봇 시스템에 많이 쓰이기 때문에 본 논문에서 적용하고자 하는 시스템인 엑소수트에서도 적절하게 사용될 수 있을 것이다.

엑소 시스템은 족형 로봇들과 비슷한 구조를 지니긴 하나 특이성(Singularity) 문제를 직면하게 된다. 족형 로봇들의 경우에는 다리가 완전히 펴진 상태는 일반적으로 고려하지 않는다. 보행제어의 경우 다리를 어느 정도 구부린 형태로 진행이 되기 때문이다. 그러나 엑소수트에서의 리프팅 동작의 경우 최종적으로 무릎과 허리를 완전히 펴게 되는 구조에 도달해야 하기 때문에 특이성 문제는 피할 수 없다.

토크 제어에서 특이성 문제를 해결하기 위한 연구는 이전부터 다양하게 진행되어 왔다. 적응 제어기를 설계하여 해당 문제를 극복한 사례가 존재하며[21], 최소 자승법 혹은 가중치 역행렬 계산을 통해 해결한 연구가 있다[22]. 그러나 본 연구에서는 최적화 문제에서의 특이성 해결방법이 필요하므로 영공간(Null Space)을 이용한 방법을 사용하여 제어기를 구성하였다[20].

최종적으로 전신 제어기(Whole-Body Control)에 특이성 문제를 해결하기 위한 항을 추가하여 리프팅 과정에서 안정적인 토크를 생성하고자 한다.

2. 리프팅 인체 동작 생성

2.1 인체 다이나믹스

다양한 동작을 묘사하기 위한 인체 모델의 경우 12 자유도로 표현될 수 있다. 그러나 리프팅 동작의 경우 2D 평면상에서 동작한다고 가정할 수 있으므로 롤과 요 모션은 무시할 수 있게 된다. 이러한 2D 모델의 경우 논문[17]을 보면 인체를 3-Link 모델 혹은 4-Link 모델로 묘사하였으며 논문[18]에서는 7-Link 모델로 표현하였다.

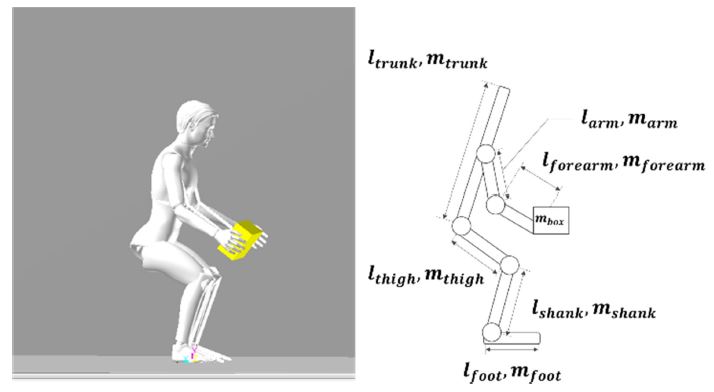
만일 목관절을 고정 관절로 가정한다면 모델링은 Fig. 1과 같이 나타내어진다. 각각의 링크들은 발, 종아리, 허벅지, 상체, 팔, 전완으로 구성된다.

Fig. 1

A 6-link human model for the lifting motion

한편 사람의 신장과 무게의 경우 개개인에 따라서 다르기 때문에 착용자에 따라서 적합하게 물리적 값을 반영하여 모델을 구성해야 한다. 논문[19]의 경우 인체를 여러 개의 링크들로 나누어 표현하였으며 실험을 통하여 각 링크의 상대적인 무게와 길이를 얻어냈다. 이러한 물리량은 신장과 무게에 따라서 변수화가 가능하며 Table 1과 같이 표현된다. 이를 기반으로 착용자의 신체 정보에 따라 모델링이 가능하게 된다.

Table 1

Human body distribution rate

마지막으로 인체의 다이나믹스 행렬을 라그랑지안 방법을 통하여 얻어냈으며 식(1)과 같이 나타내어진다. Floating Base Dynamics Model로 구성되었으며 허리 부분의 링크를 베이스로 두고 계산되었다.

$\[ \begin{array}{c}M\dot{\nu }+b+g=S^T\tau +J_C^{T}B\rho \\ M=\left[\begin{array}{ccc}{M}_{com, l}& 0_{3\times 3}& 0_{3\times n_{joint}}\\ 0_{3\times 3}& M_{com, a}& 0_{3\times n_{joint}}\\ 0_{n_{joint\times 3}}& 0_{n_{joint\times 3}}& M_q\end{array}\right]\in {\mathbb{R}}^{\left(6+n_{\text{joint }}\right)\times \left(6+n_{\text{joint }}\right)}\end{array} \]$

(1)

은 Mass Matrix를 의미하며(M_{com, l}은 베이스의 선 운동에 관련된 항, M_{com, a}은 베이스의 각 운동에 관련된 항, M_q는 베이스를 기준으로 각 링크들에 관련된 항임),

$\[ \mathrm{b}+\mathrm{g}=\left[\begin{array}{c}{0}_{6\times \left(6+n_{joint}\right)}\\ C_q\end{array}\right]\nu +\left[\begin{array}{c}mg\\ 0_{n_{joint}}\end{array}\right]\in {\mathbb{R}}^{\left(6+n_{joint}\right)\times \left(6+n_{joint}\right)} \]$

는 코리올리 및 중력에 관련된 항을 의미한다(C_q ∈ $$ \mathbb{R}$$^{n_joint×(6+n_joint)}, $$ g= {\left[g_0^T 0_3^T\right]}^T$$).

또한 $$ S=\left[0_{n_{joint}\times 6}{ I}_{n_{joint}}\right]\in {\mathbb{R}}^{\left(6+n_{joint}\right)\times n_{actuated}}$$는 전체 (6+n_joint 자유도 중 관절 토크를 가할 수 있는 자유도만 선정하는 행렬, $$ J_c^T\in {\mathbb{R}}^{\left(6+n_{joint}\right)\times 12}$$는 지면 접촉 자코비안, $$ \mathrm{B}\mathrm{\rho }\left(=\mathrm{F}\right)\in \mathrm{ }{\mathbb{R}}^{12\times 1}$$는 지면 반력을 나타낸다(B는 힘 벡터를 구성하는 기저 벡터, ρ는 각 기저 벡터의 가중치를 의미).

2.2 인체 동작 생성

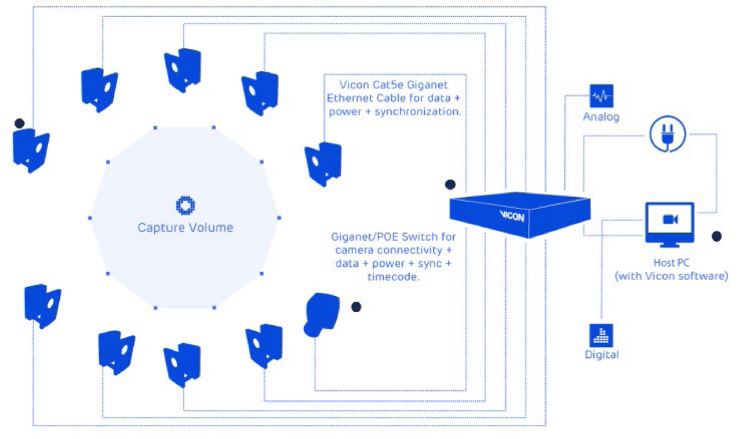
시뮬레이션 상에서 인체의 동작을 묘사하기 위하여 인체운동 분석 실험을 진행하였다. VICON 사의 NEXUS 1.8.5.를 활용하여 실험 환경이 구성되었으며, 동작분석 카메라는 4 M 픽셀의 T-40 8대가 사용되었다. 분석을 위한 마커들은 Fig. 2와 같이 하지의 경우 골반, 꼬리뼈, 허벅지, 무릎, 종아리, 발목, 발등, 발뒤꿈치에 부착하였으며 상지의 경우 쇄골, 명치, 경추, 요추, 견갑골, 어깨, 상박, 팔꿈치, 하박, 손목, 손등에 부착하였다. 부착 후 실험자는 주어진 무게의 박스를 들고 반복적으로 리프팅 동작을 수행하였다. 시스템 환경 구성은 Figs. 3과 같으며 실험 과정은 2의 사진과 같이 진행하였다. 최종적으로 얻은 궤적은 시뮬레이션 상에서 위치 피드백으로 토크 값을 생성하였으며 해당 값을 사람의 모션 인풋으로 설정하였다.

Fig. 2

Motion capture experiment: Lifting operation

Fig. 3

Motion capture experiment: System communication and configuration

3. 전신 제어 기반의 엑소수트 보조 전략

3.1 제어 시스템 다이나믹스

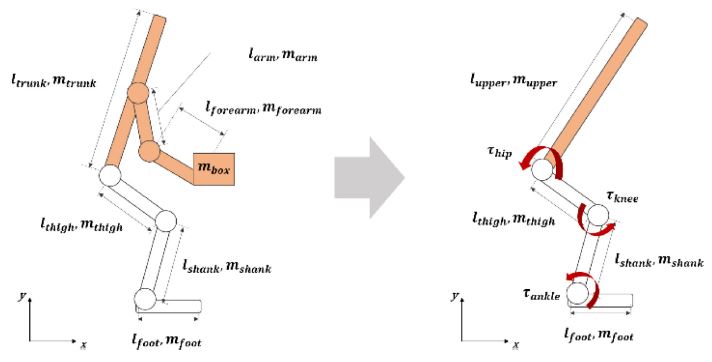
앞서 2장에서 6자유도로 리프팅 동작을 묘사하였다. 복잡한 모델을 구성할수록 인체 동작을 좀 더 정확하게 묘사할 수 있으나, 실제로 정밀한 모델링을 하는 것은 매우 어렵다. 또한 복잡한 모델링은 제어기 구성에도 큰 어려움을 주게 된다. 한편, 리프팅 동작 중에는 전완과 팔의 움직임이 크지 않기 때문에 Fig. 4와 같이 좌측의 6-Link 모델을 4-Link로 근사할 수 있다.

Fig. 4

Approximate box lifting model for control

앞서 언급한 내용과 같이 사람의 상체를 하나의 강체로 근사하여 제어 시스템을 구성하였으며 이를 기반으로 제어기를 설계하였다. 추가적으로 엑소수트를 착용한 인체모델을 시뮬레이션에서 구성하기 위하여 각 부분의 물리량을 병합하였다. 시스템의 제어 입력은 토크 값인 τ_hip, τ_knee, τ_ankle이며 얻게 되는 센서 값은 IMU 값과 각 관절의 엔코더 값으로 구성된다.

3.2 전신 제어(Whole-Body Control) 프레임워크

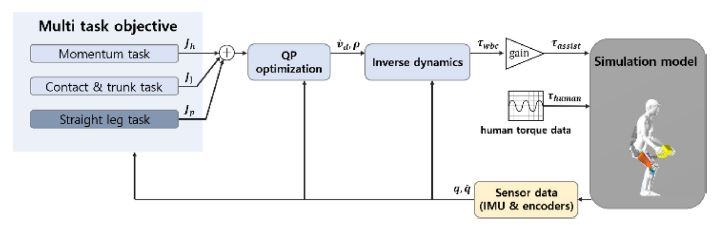
이 장에서는 전신 제어(Whole-Body Control) 기반의 리프팅 보조 전략에 대한 설명을 포함한다. 전신 제어 기반의 제어기는 일반적으로 다양한 태스크의 동작을 하나의 목적 함수로 구성하게 되고 이를 최소화하는 최적 변수들을 찾아내는 과정으로 진행된다. 최적화된 변수들을 기반으로 시스템에 맞는 최종 아웃풋을 계산하게 되는데 일반적으로 족형 로봇의 경우 토크 값이 이에 해당된다. 엑소수트를 위해 본 연구에서 구성한 시스템은 Fig. 5의 블록 다이어그램과 같이 표현된다.

Fig. 5

Whole-body control framework for the exoskeleton system

리프팅 동작을 위한 태스크들은 CoM (Center of Mass)을 이동시키는 부분, 발의 접촉을 유지시키는 부분, 트렁크 각도를 제어하는 부분, 그리고 특이성 문제를 해결하는 부분으로 구성되었다. 첫 번째로 CoM 움직임에 관한 부분의 경우 레퍼런스 궤적에 PD 피드백을 통해서 제어되도록 하였으며, 세부적으로는 x 방향은 초깃값을 유지하는 방향으로, y 방향은 물체를 들어올릴 수 있는 수직 궤적으로 생성하였다. 이렇게 생성된 궤적을 기반으로 지면 반력을 계산할 수 있으며 이를 기반으로 태스크를 구성하게 된다. 두 번째는 지면 접촉에 관련된 부분으로 해당 접촉점이 리프팅 동작 동안 움직이지 않음을 의미한다. 마지막으로는 다리가 완전히 펴진 상태에서의 특이성(Singularity) 문제를 방지하기 위한 부분으로 구성된다. 세부적인 내용은 식(3)과 식(4)와 Table 2에 표기하였다.

Table 2

Physical meaning of the variables

일반적으로는 족형 시스템 제어에서는 완전히 다리가 펴진 상태를 인위적으로 피하기 때문에 특이성 문제가 발생하지 않는다. 그러나 리프팅 동작에서는 물건을 들어 올리는 최종 지점에서 특이성 문제에 직면하기 때문에 본 연구에서는 이러한 문제를 추가적인 목적 함수를 추가하여 해결하고자 하였다. 관련된 목적 함수는 논문[20]을 참고하였다. 해당 방법론에 따르면 무게 중심을 직접적으로 제어하는 대신에, 해당 부분을 목적 함수의 영공간(Null Space)에 넣어 간접적으로 제어하여 특이성 문제를 해결한다.

우선적으로 다리의 구조를 완전히 편 상태로 유지하기 위해 리프팅 과정에서의 무릎 관절 궤적을 미리 정의해야 하는데 이는 식(2)와 같이 구성되었다. $$ \stackrel{-}{q}$$는 미리 정해진 관절 각도를, q는 현재 각도를 의미하며(K_p, k_d는 각각 P Gain, D Gain), 간단한 PD 피드백 형태로 가속도 단위의 값을 얻어낸다. 이 가속도 값은 식(4)의 Straight Leg Cost 부분에서 사용된다.

$\[ \stackrel{-}{a}=K_p(\stackrel{-}{q}-q)+K_d\nu \]$

(2)

식(4)의 Straight Leg Cost의 역할은 다음과 같다. 식(2)에서 얻어진 값으로 관절 각도를 움직이면서 기존의 목적함수들을 만족시킬 수 있는 해답을 얻어내는 것이 궁극적인 목표이며, 수식에서 J_task는 전체 목적함수인 Momentum Cost, Contact & Trunk Cost를 의미하고 $$ \stackrel{-}{S}A$$는 시스템의 모멘텀을 구성하는 행렬인 A [24]에 수직 방향에 관련된 부분을 제거하는 $$ \stackrel{-}{S}$$ 행렬을 곱하여 얻어지는 값이다. 이는 수직방향 모멘텀에 대한 제어를 직접적으로 제어하지 않고 남겨두기 위해서이다. 최종적으로 $$ {∥\left(I-J_{task}^{+}{J}_{tsak}\right){\dot{\nu }}_{proj}∥}^2$$와 같이 목적 함수를 구성하여 미리 정해진 각도로 다리를 펴는 동작을 수행하면서 나머지 목적 함수들도 만족시킬 수 있는 해를 얻어낼 수 있게 된다. 해당 식에서 $$ J_{task}^{+}$$는 J_task의 유사 역행렬 Pseudo Inverse)을 의미한다.

최종적인 QP (Quadratic Programming) 구성은 식(3)과 같이 표현되는데, 최적화 변수의 경우 $$ {\dot{\nu }}_d$$, ρ값으로 각각은 관절 각가속도와 지면 반력을 구성하는 변수이다. 식의 각 부분들은 Table 2에 그 의미를 표기하였다. Quadratic Programming이란 목적함수가 이차식이고, 제약함수가 모두 Affine인 컨벡스 최적화 문제를 말하며, 본 연구에서는 해당 문제의 해답을 얻어내기 위하여 qpOASES [23] 솔버를 사용하였다.

$\[ \begin{array}{c}\underset{\rho ,{\dot{\nu }}_d}{min} J_h+J_J+J_p\\ s.t A{\dot{\nu }}_d+\dot{A}{\nu }_d=W_g+W_{grf}\\ {\rho }_{min}\le \rho \le {\rho }_{max}\\ {\tau }_{min}\le \tau \le {\tau }_{max}\end{array} \]$

(3)

(4)

최소화하고자 하는 목적 함수들의 전체 수식은 식(4)와 같이 정의되고, p는 원하는 무게중심의 위치 벡터, P_h, P_i, P_o는 중요도에 따른 가중치 행렬이다. Momentum Cost의 경우 무게중심의 위치를 원하는 위치로 이동하게 만드는 역할, Contact & Trunk Cost의 경우 리프팅 동작 중 두 발의 양 끝이 지면과 접촉을 유지하도록 만들어주며 상체의 각도가 심하게 구부러지거나 움직이지 않도록 하는 역할을 한다. Straight Leg Cost의 경우 앞 단락에서 설명했으므로 생략한다. 각 목적 함수를 구성하는 행렬 및 벡터들은 Table 2와 같이 요약하였다.

Table 2의 v = [v_x, v_v, v_z, w_x, w_y, w_z, $$ {\dot{q}}_1$$, ⋯$$ {\dot{q}}_{n_{joint}}$$]는 다이나믹스를 묘사하는 속도이며 각 부분은 베이스의 선 속도, 가속도 및 관절 각속도로 구성되어 있다. $$ \mathrm{A}\in {\mathbb{R}}^{\left(6+n_{joint}\right)\times \left(6+n_{joint}\right)}$$는 시스템 무게중심의 운동량을 계산하는 행렬로 논문[16]에 그 자세한 구성이 소개되어 있으며, W_g, $$ {\mathrm{W}}_{\mathrm{e}\mathrm{r}\mathrm{f}}\in {\mathbb{R}}^{\left(6+n_{joint}\right)\times 1}$$는 중력과 지면 반력이 시스템에 가하는 힘 및 모멘트를 의미한다. 토크 범위 제한의 경우 절댓값 50 Nm로 제한하였으며, 마지막으로 지면 반력의 경우 F = Bρ와 같이 기저 벡터와 가중치로 나타내게 되는데 가중치인 ρ의 범위를 제한함으로써 내고자 하는 지면 반력의 값을 한정하게 된다.

최종적으로 최적 문제를 풀어 얻어낸 최적화 변수들을 기반으로 Inverse Dynamics를 계산하게 되고, 이를 기반으로 토크 값을 계산해낸다. 앞서 구성한 시스템의 식(1)을 변형하여 얻어낸 Inverse Dynamics 수식은 식(5)와 같이 표현된다.

$\[ \tau =S\left(-J_c^{T}B\rho +M{\dot{\nu }}_d+b+g\right) \]$

(5)

4. 시뮬레이션 및 결과

4.2 시뮬레이션 결과

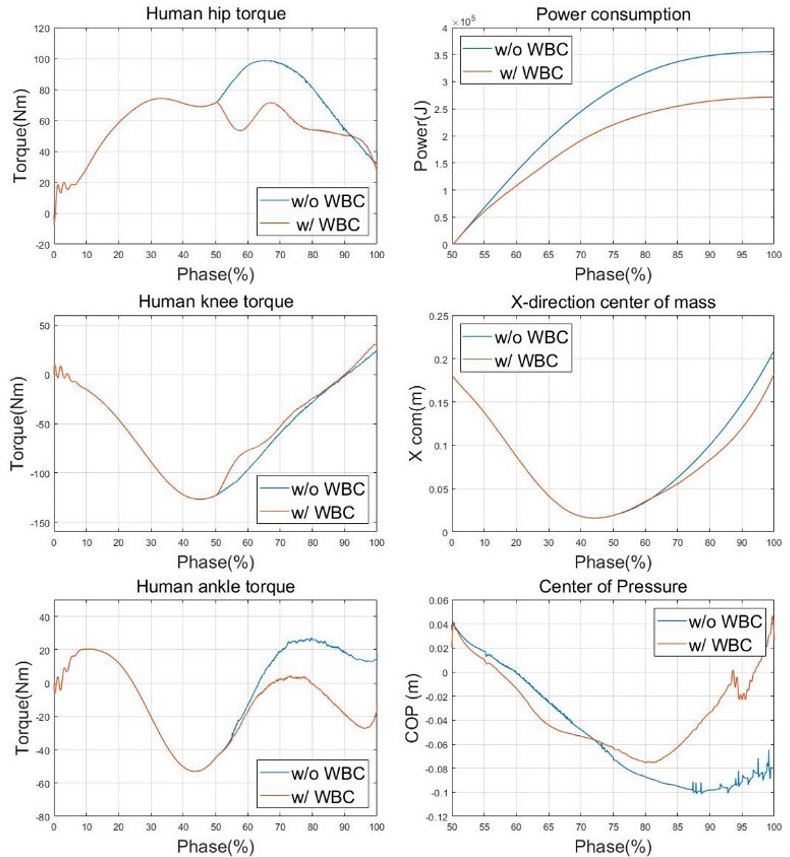
시뮬레이션 결과는 Figs. 6과 7과 같다. Fig. 7은 전신 제어기의 사용 유무에 따라서 사람의 토크 값을 비교하였으며, 무게중심의 위치, 발의 압력 중심(Center of Pressure), 에너지 소모율 등을 확인하였다. 결과를 보면 알 수 있듯이 무릎과 허리 부분의 요구 토크 값이 감소하는 것을 알 수 있으며, 발목 부분의 요구 토크 값은 절대적인 크기는 비교할 수 없으나 최종적으로 에너지 소모율이 제어기를 사용하지 않았을 때에 비해 23%까지 감소한 사실을 확인했다. X 방향 무게 중심의 경우 보조력의 증가에 따라 발의 중심좌표인 x = 0에 가까워지는 결과를 얻어내었으며 균형 지표가 되는 압력 중심(Center of Pressure) 또한 발의 중심 부근으로 이동하였다. 해당 결과들로 인해 제안하는 전신 제어기가 주어진 태스크들을 만족시키기 위한 토크를 생성하여 균형 지표 및 에너지 효율을 증가시킨 것을 알 수 있다.

Fig. 6

Lifting simulation results (w/ straight leg term, w/o straight leg term)

Fig. 7

Lifting simulation results (w/ WBC (Whole-body control), w/o WBC (Whole-body control))

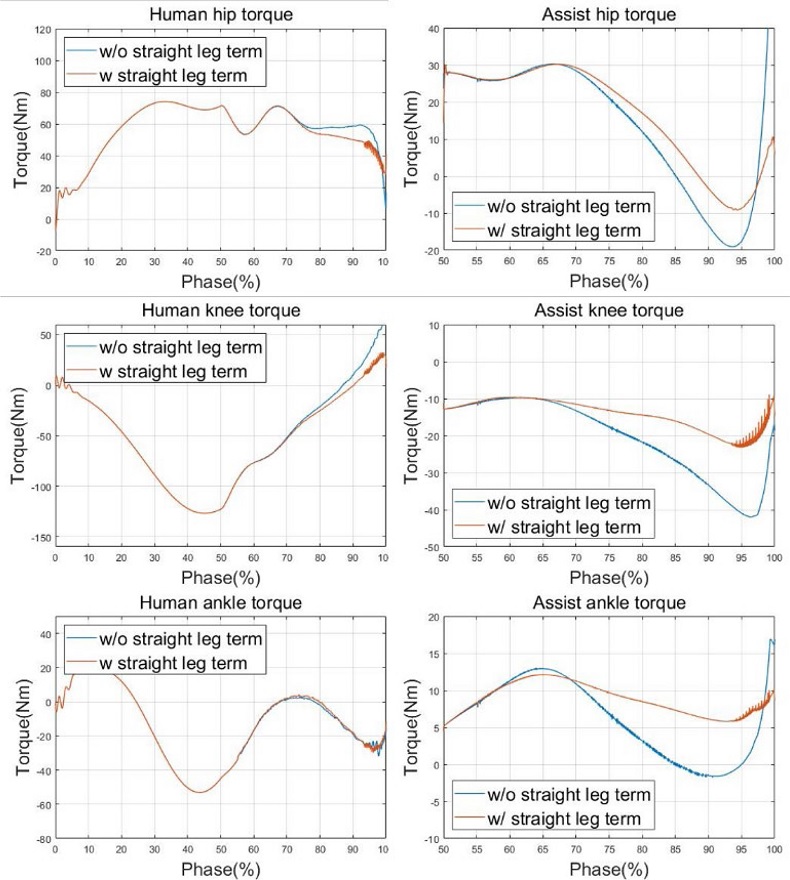
Fig. 6에서는 Straight Leg 목적함수의 유무에 따른 토크 값을 비교하였다. 오른쪽 열에서 보이는 엑소수트가 가하게 되는 보조 토크의 경우 리프팅 페이즈(Phase)의 최종 지점에 가까워지면서 특이성 문제가 발생하게 되며, 각 관절의 토크 값이 모두 증가하는 것을 알 수 있다. 특히 허리와 발목 관절의 경우에는 그 증가량이 상당히 크고 구동기의 토크 제한 값을 만족시키지 못하는 정도까지 문제가 되는 것을 알 수 있다. 이는 특이성 부근에서 필요한 수평방향 힘 성분을 관절 토크 값으로 생성하기 어렵기 때문이다. 그러나 Straight Leg 관련 목적 함수가 추가된 경우에는 해당 지점에서 우선적으로 물건을 들어올리는 관절 레퍼런스에 관련된 동작을 수행하게 되어 안정적으로 보조 토크를 생성하게 된다.

결론적으로 제안하는 제어기가 효율적으로 리프팅 동작을 진행할 수 있도록 보조하는 것을 확인하였고, 특이성 문제 또한 해결하였음을 알 수 있다.

5. 결론

본 논문에서는 사람 모델과 엑소수트를 병합하여 시뮬레이션을 진행하였으며, 엑소수트의 보조 토크의 경우 전신 제어 기반으로 구성하였다. 리프팅 동작을 만족시키기 위한 여러 가지 태스크들로 목적 함수를 구성하였고, 특이성 문제를 피하기 위한 부분을 추가적으로 통합하였다.

전신 제어기(Whole-Body Controller)의 경우 무게중심의 궤적에 관련된 Momentum Cost, 상체 각도에 관련된 Trunk Cost, 지면 접촉 조건에 관련된 Contact Cost, 그리고 마지막으로 특이성 문제를 해결하기 위한 Straight Leg 관련 목적함수로 구성된다. 결과적으로 해당 보조토크 생성으로 인해 리프팅 과정에서의 사람의 총에너지 사용량이 감소하였으며, 무게중심 및 Center of Pressure가 발의 중심부와 점차 가까워지는 것을 확인하여 균형 지표 또한 상승하였다고 판단된다. 마지막으로 특이성 문제가 발생될 수 있는 리프팅 동작의 최종 지점에서도 안정적인 토크 생성이 가능하였으며, 이를 통해 해당 제어기가 효과적임을 입증하였다.

추후 개발된 실제 하드웨어를 통해서 해당 알고리즘을 검증하려 한다. 하드웨어의 경우 제작이 완료된 상태이며 500 Hz 정도의 토크 제어 주기를 지닌다. 토크 제어 기반의 시스템에서 제안하는 제어기가 안정적으로 동작할 것으로 예상되나 엑소시스템과 착용자의 상호작용을 고려하지 않았기 때문에 해당 문제는 추후 과제로 해결하고자 한다.

Acknowledgments

본 연구는 대한민국 정부(산업통상자원부 및 방위사업청) 재원으로 민군협력진흥원에서 수행하는 민군기술협력사업(상호연동 모듈형 근력보조 엑소수트 기술개발 과제)의 연구비 지원으로 수행되었습니다(No. 19-CM-GU-01).

REFERENCES

• Penzlin, B., Enes Fincan, M., Li, Y., Ji, L., Leonhardt, S., Ngo, C., (2019), Design and analysis of a clutched parallel elastic actuator, Actuators, 8(3), 67. [https://doi.org/10.3390/act8030067]
• Näf, M. B., Koopman, A. S., Baltrusch, S., Rodriguez-Guerrero, C., Vanderborght, B., Lefeber, D., (2018), Passive back support exoskeleton improves range of motion using flexible beams, Frontiers in Robotics and AI. [https://doi.org/10.3389/frobt.2018.00072]
• Abdoli-E, M., Agnew, M. J., Stevenson, J. M., (2006), An on-body personal lift augmentation device (PLAD) reduces EMG amplitude of erector spinae during lifting tasks, Clinical Biomechanics, 21(5), 456-465. [https://doi.org/10.1016/j.clinbiomech.2005.12.021]
• Whitfield, B. H., Costigan, P. A., Stevenson, J. M., Smallman, C. L., (2014), Effect of an on-body ergonomic aid on oxygen consumption during a repetitive lifting task, International Journal of Industrial Ergonomics, 44(1), 39-44. [https://doi.org/10.1016/j.ergon.2013.10.002]
• Lotz, C. A., Agnew, M. J., Godwin, A. A., Stevenson, J. M., (2009), The effect of an on-body personal lift assist device (PLAD) on fatigue during a repetitive lifting task, Journal of Electromyography and Kinesiology, 19(2), 331-340. [https://doi.org/10.1016/j.jelekin.2007.08.006]
• Ranaweera, R., Gopura, R., Jayawardena, T., Mann, G. K., (2018), Development of a passively powered knee exoskeleton for squat lifting, J. Robotics Netw. Artif. Life, 5(1), 45-51. [https://doi.org/10.2991/jrnal.2018.5.1.11]
• Mohri, S., Inose, H., Arakawa, H., Yokoyama, K., Yamada, Y., Kikutani, I., Nakamura, T., (2017), Development of non-rotating joint drive type gastrocnemius-reinforcing power assist suit for squat lifting, Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 851-856. [https://doi.org/10.1109/AIM.2017.8014124]
• Wei, W., Zha, S., Xia, Y., Gu, J., Lin, X., (2020), A hip active assisted exoskeleton that assists the semi-squat lifting, Applied Sciences, 10(7), 2424. [https://doi.org/10.3390/app10072424]
• Tahamipour-Z, S., Sani, S. H., Akbarzadeh, A., Kardan, I., (2018), An assistive strategy for compliantly actuated exoskeletons using non-linear model predictive control method, Proceedings of the Iranian Conference on Electrical Engineering (ICEE), 982-987. [https://doi.org/10.1109/ICEE.2018.8472699]
• Dos Santos, W. M., Siqueira, A. A., (2019), Optimal impedance via model predictive control for robot-aided rehabilitation, Control Engineering Practice, 93, 104177. [https://doi.org/10.1016/j.conengprac.2019.104177]
• Luo, S., Androwis, G., Adamovich, S., Su, H., Nunez, E., Zhou, X., (2021), Reinforcement learning and control of a lower extremity exoskeleton for squat assistance, Frontiers in Robotics and AI, 8, 702845. [https://doi.org/10.3389/frobt.2021.702845]
• Koolen, T., Bertrand, S., Thomas, G., De Boer, T., Wu, T., Smith, J., Englsberger, J., Pratt, J., (2016), Design of a momentum-based control framework and application to the humanoid robot atlas, International Journal of Humanoid Robotics, 13(1), 1650007. [https://doi.org/10.1142/S0219843616500079]
• Kim, D., Jorgensen, S. J., Lee, J., Ahn, J., Luo, J., Sentis, L., (2020), Dynamic locomotion for passive-ankle biped robots and humanoids using whole-body locomotion control, The International Journal of Robotics Research, 39(8), 936-956. [https://doi.org/10.1177/0278364920918014]
• Henze, B., Dietrich, A., Ott, C., (2015), An approach to combine balancing with hierarchical whole-body control for legged humanoid robots, IEEE Robotics and Automation Letters, 1(2), 700-707. [https://doi.org/10.1109/LRA.2015.2512933]
• Kim, D., Zhao, Y., Thomas, G., Fernandez, B. R., Sentis, L., (2016), Stabilizing series-elastic point-foot bipeds using whole-body operational space control, IEEE Transactions on Robotics, 32(6), 1362-1379. [https://doi.org/10.1109/TRO.2016.2597314]
• Kim, D., Di Carlo, J., Katz, B., Bledt, G., Kim, S., (2019), Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control, arXiv:1909.06586, . [https://doi.org/10.48550/arXiv.1909.06586]
• Tözeren, A., (1999), Human body dynamics: Classical mechanics and human movement, Springer Science & Business Media.
• Inose, H., Mohri, S., Yamada, Y., Nakamura, T., Yokoyama, K., Kikutani, I., (2016), Development of a lightweight power-assist suit using pneumatic artificial muscles and balloon-amplification mechanism, Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), 1-6. [https://doi.org/10.1109/ICARCV.2016.7838564]
• Drillis, R., Contini, R., Bluestein, M., (1964), Body segment parameters, Artificial Limbs, 8(1), 44-66.
• Griffin, R. J., Wiedebach, G., Bertrand, S., Leonessa, A., Pratt, J., (2018), Straight-leg walking through underconstrained whole-body control, Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), 5747-5754. [https://doi.org/10.1109/ICRA.2018.8460751]
• Koessler, A., Bouton, N., Briot, S., Bouzgarrou, B. C., Mezouar, Y., Linear adaptive computed torque control for singularity crossing of parallel robots, ROMANSY 22-Robot Design, Dynamics and Control, Springer, 2019, 222-229. [https://doi.org/10.1007/978-3-319-78963-7_29]
• Chung, C., Lee, B. H., Kim, M., Lee, C., (2000), Torque optimizing control with singularity-robustness for kinematically redundant robots, Journal of Intelligent and Robotic Systems, 28(3), 231-258. [https://doi.org/10.1023/A:1008152705719]
• Github, Open-source C++ implementation of the recently proposed online active set strategy. https://github.com/coin-or/qpOASES
• Orin, D. E., Goswami, A., (2008), Centroidal momentum matrix of a humanoid robot: Structure and properties, Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, 653-659. [https://doi.org/10.1109/IROS.2008.4650772]