정면충돌을 고려한 전동 킥보드 연결부의 2차원 위상최적설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Electric kickboards provide personal mobility with a simple structure and easy operation. With these advantages, the number of users is increasing annually. However, as the number of users of electric kickboards increases, related accidents are also increasing. To prevent accidents, this study proposes the topological optimization of an electric kickboard connecting part to improve structural strength during a front collision. The results confirmed that as the volume fraction increased, the structure connecting the board and the bottom of the handle support changed to a toroidal shape, thereby lowering the maximum stress and improving the uniformity of the stress distribution. In addition, the topological optimization was safer than the connecting parts of two typical electric kickboards sold in the Korean market. These findings can contribute to improving the safety and optimizing the design direction of electric kickboards.
Keywords:
Electric kickboard, Finite element analysis, Front collision, Optimality criteria method, Safety improvement, Topology optimization키워드:
전동 킥보드, 유한요소해석, 정면충돌, 최적성 기준법, 안전성 개선, 위상최적설계1. 서론
전동 킥보드는 간단한 구조와 쉬운 조작법이 특징인 대표적 퍼스널 모빌리티(Personal Mobility)이다. 최근에는 공유 서비스와 함께 전동 킥보드 이용자가 급격히 증가하고 있다[1]. 다만, 관련 사고 역시 지속적으로 증가하고 있어 사회적 관심을 받고있다. 일반적으로 전동 킥보드 관련 사고는 크게 사용자에 의한 운행 사고와 제품의 결함으로 인한 파손 사고로 나눌 수 있다. 운행 사고에 대한 예방은 다양한 법적 규제를 통해 이뤄지고 있지만, 제품의 결함으로 인한 사고에 대해서는 아직까지 확실한 대안이나 방지책이 부족한 실정이다. 따라서 전동 킥보드의 결함을 줄여 사고를 예방하는 것이 매우 중요하다.
전동 킥보드의 대표적인 결함은 외부 하중에 의한 구조적 파손이다. 이러한 파손을 예방하기 위해 구조적 안전성이 개선된 많은 설계안들이 제시되었다. 김민규는 파손 사고율이 가장 높은 연결부에 대한 구조적 안전성을 형상별로 분석하고 안전성이 개선된 연결부의 형상을 제시하였다[2]. Dong은 마그네슘 합금 기반의 설계를 통해 강성과 강도가 개선된 킥보드 프레임을 제시하였다[3]. Hsia는 도로 테스트를 통해 얻은 응력 및 피로 내구성을 기반으로 프레임을 재설계하였다[4]. Chou는 탑승 자세를 고려한 인체공학적 성능이 개선된 프레임을 제시하였다[5]. Shivhare는 작동 및 충격 부하 시나리오를 고려한 설계 및 모델링을 제시하였다[6]. 제시된 설계안들이 구조적 안전성 개선에도 불구하고, 연구자들의 직관과 경험에 의존하는 경향이 있어 최적의 결과로서는 한계를 가진다.
연구자들의 직관과 경험으로부터 자유로운 설계를 위해서는 수학적 이론과 컴퓨터 연산 기반의 접근법이 필요하다. 이러한 필요성으로 인해 제안된 방법이 위상최적설계이다[7]. 위상최적설계는 주어진 하중 조건 아래 제한된 재료로 최적의 재료 분포를 찾기 때문에 설계 시 다양한 위상을 고려할 수 있다는 장점이 있다. 또한 위상최적설계는 형상 최적설계, 치수 최적설계보다 상위 단계로 전체 설계에 미치는 영향이 크기 때문에 자동차[8-10], 의료[11], 로봇[12], 건설[13,14] 등 다양한 분야에서 활용되고 있다. 특히 최근에는 복잡한 구조의 제작을 위한 3차원 프린팅 기술[15]과 대규모 연산을 위한 컴퓨터의 하드웨어가 급격히 발전하였다. 위상최적설계의 단점인 높은 가공 난이도와 낮은 계산 효율성이 점차 극복되어 활용도가 높아지고 있다.
본 연구는 정면충돌 상황에서 전동 킥보드의 구조적 안전성 향상을 위한 연결부의 위상최적설계를 목표로 한다. 이를 위해 전동 킥보드의 대표 프레임 구조를 선정하고 연결부를 설계영역으로 할당하였다. 앞바퀴 정면충돌 하중 조건 아래 위상최적설계를 수행하고, 기존 모델과의 충돌 성능 비교를 통해 최적설계안의 검증을 수행하였다.
2. 본론
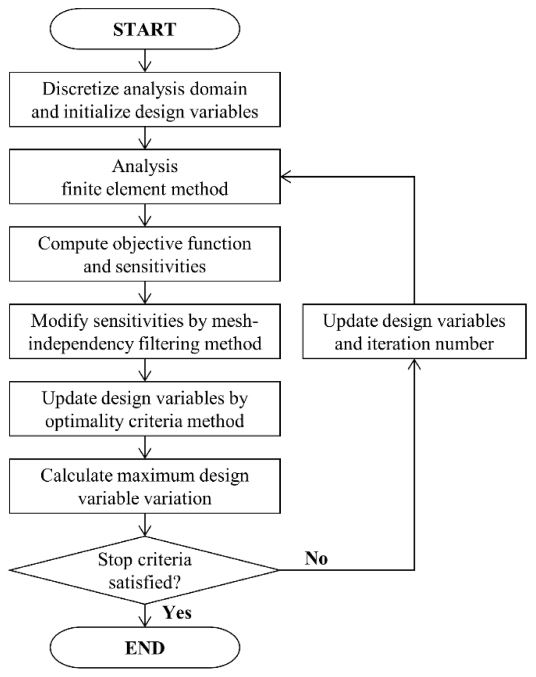
본 연구에서 전동 킥보드 연결부의 위상최적설계는 크게 유한요소해석 기반의 구조적 거동 분석 단계와 분석 기반의 설계변수값 갱신 단계로 구성된다(Fig. 1). 이를 위한 유한요소모델링은 2.1장에 위상최적설계 과정은 2.2장에 나타낸다. 그리고 전동 킥보드의 최종 위상최적설계안의 비교 검증은 2.3장에 나타낸다.
2.1 유한요소모델링
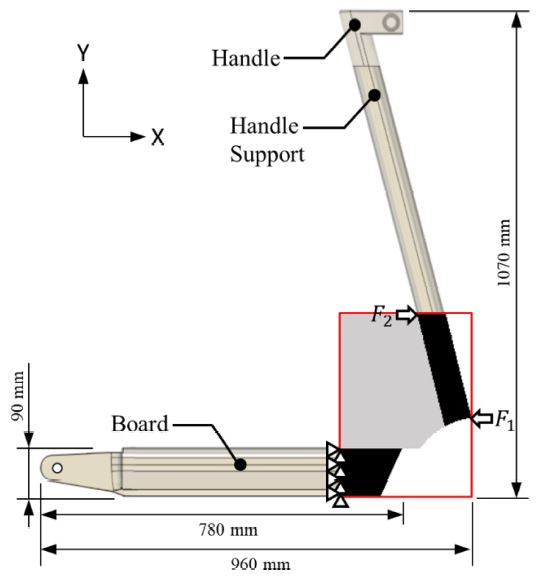
본 연구에서는 공유형 전동 킥보드로 가장 많이 보급된 Segway-Ninebot 사의 Ninebot Max (G30)를 연구 대상으로 선정하고 유한요소모델로 생성하였다. 해당 킥보드의 프레임은 960 mm의 길이와 1,070 mm의 높이를 가지며, 발판은 780 mm의 길이와 90 mm의 높이를 가진다(Fig. 2). 핸들 지지대의 직경은 50 mm이다. 다만, 해당 모델은 정면충돌 시 좌우 대칭 구조로 인해 시상면(Longitudinal or Sagittal Plane)에서 최대 응력이 발생하는 특징을 가진다. 이러한 특징적·구조적 거동을 반영하고 연결부의 효율적인 위상최적설계를 위해 본 연구에서는 3차원 형상을 2차원으로 축소하여 유한요소 모델을 생성하였다. 더불어 구조적 거동 영향도가 적은 킥 스탠드와 핸들 같은 부분들은 모델 생성 단계에서 제외하였다. 핸들부는 이전 연구들에서 정면충돌 시 연결부 대비 매우 적은 응력이 발생한다고 보고된 바 있다[2,16]. 그리고 평면 응력(Plane Stress) 상황을 가정하였다.
유한요소모델은 23,975개의 2차원 정사각형 4절점 요소(Four-Node Quadrilateral Element)로 구성하였다. 요소는 각 절점에서 2개의 자유도를 가지며, 요소의 거동(i.e. 절점 간의 변위)은 이중선형(Bilinear) 형상함수로 표현하였다. 각 요소의 탄성계수는 식(1)과 같이 요소의 밀도 값을 SIMP (Solid Isotropic Material Penalization) 기반으로 변환하여 부여하였으며, Poisson’s Ratio는 0.3으로 동일하게 부여하였다[17,18].
| (1) |
여기서 Ei는 i번째 요소의 탄성 계수이며, ρi는 i번째 요소의 상대 밀도 값이다(0.001 ≤ ρi ≤ 1). 그리고 E0는 상대 밀도 값이 1일 때의 탄성계수로 1의 값을 가진다.
본 연구에서 정면충돌 상황을 모사하기 위해 이전 연구[2]에서 제안된 경계조건과 하중조건을 사용하였다. 발판 뒷부분의 수직 위 절점들을 완전 고정하였다. 그리고 위상최적설계는 하중의 크기가 아닌 하중 분포(또는 패턴)에 의존하므로 핸들 지지대의 우측 하단과 좌측 상단의 절점들에 각각 동일한 크기 (1 N)의 충돌 힘 (F1, F2)을 반대 방향으로 부여하였다(Fig. 2).
2.2 위상최적설계
본 연구는 핸들 지지대와 발판 사이의 부분을 위상최적설계 영역으로 설정하였다. 설계 영역은 가로 274mm, 세로 350mm의 크기를 가진다. 다만, 앞바퀴와 간섭이 일어나는 부분은 설계영역에서 제외하였다(Fig. 2). 설계 변수는 각 요소의 밀도 값이며 총 23,975개이다.
정면충돌에 대한 구조적 안전성을 향상시키기 위해 본 연구에는 식(2)와 같이 외부 하중에 대한 구조의 컴플라이언스(Compliance: Sum of Strain Energy)를 목적함수로 선정하였으며 부피분율(Volume Fraction)을 제한조건으로 선정하였다[19].
| (2) |
여기서 ρi는 설계변수로 각 요소의 밀도이다. N은 전체 요소수, ui는 변위벡터, k0는 요소의 강성행렬을 의미한다. 제한 조건에서 Vo는 전체 설계영역 부피를 의미하며, VF는 부피분율이다. 그리고 본 연구에서는 요소 크기에 따른 위상최적설계의 수치적 불안정성(Numerical Instabilities)을 줄이기 위해 설계변수 갱신 시 식(3)과 같이 민감도를 필터링하여 적용하였다[20,21].
| (3) |
여기서 dist(i,j)는 i번 요소와 j번 요소의 유클리드 거리이다. j는 dist(i,j) ≤ rmin의 조건을 만족하는 요소 번호를 말한다. rmin은 필터 영역을 결정하기 위한 필터 크기를 의미한다.
본 연구는 식(4)와 같이 Optimality Criteria Method [22]를 이용하여 위상최적설계를 수행하였다. 설계의 종료 조건으로 축차(Iteration)간 설계변수 값의 최대 변화량(Tolerance: 0.01)을 사용하였다.
| (4) |
여기서 m은 양수 이동 제약(Positive Move-Limit)이고, η는 0.5로 수치 감쇠 계수(Numerical Damping Coefficient)이다. 그리고 Bi는 최적 조건에서 식(5)에 의해 결정된다.
| (5) |
여기서 λ는 이분법 알고리즘(Bi-Sectioning Algorithm)에 의해 결정되는 라그랑지 승수(Lagrangian Multiplier)이고, 분모의 항은 목적함수의 민감도를 의미한다.
마지막으로 본 연구는 제한조건의 부피분율(0.2, 0.3, 0.4, 0.5)과 민감도 필터링 크기(1, 2, 3, 4 px)에 따른 전동 킥보드 연결부의 위상 변화를 분석하기 위해 하이퍼 파라미터(Hyperparameter) 값으로 선정하여 총 16개의 연결부 위상을 도출하였다. 위상최적설계는 MATLAB R2017a의 In-House 코드를 작성하여 수행되었다. 그리고 각 위상최적설계는 DESKTOP (CPU: AMD Ryzen 3700X, GPU: GeForce 1,660, RAM: 8 GB) 기준 평균 10시간을 요구하였다.
2.3 충돌 성능 비교
본 연구에서는 도출된 위상을 검증하기 위해 시중에 판매되고 있는 2개의 대표적인 전동 킥보드 연결부와 충돌 성능을 비교하였다. 이를 위해 Ninebot MAX의 입방체형(Cubic) 연결부와 Minimoters Dualtron Eagle의 토로이드형(Toroid) 연결부를 구현하였다. 토로이드형 위상의 경우에는 시중 판매 모델 중 가장 좋은 정면충돌 성능을 가진다고 보고된 바 있다[2]. 마지막으로 동일한 부피분율, 경계조건, 하중조건에서 계산된 각 모델의 컴플라이언스를 충돌 성능 지표로 가정하여 비교 분석하였다.
3. 위상최적설계 결과
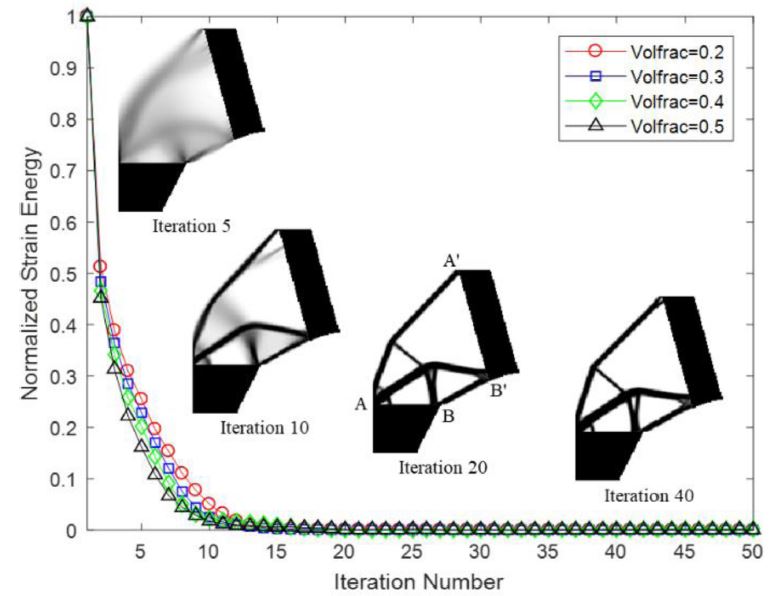
Fig. 3은 전동 킥보드 연결부의 위상최적설계 과정의 목적함수 값과 제한조건 값의 변화를 나타낸다. 부피분율의 크기에 상관없이 공통적으로 목적함수와 제한조건의 값이 설계 과정 초반에 많은 감소를 보였으며, 설계 후반에서는 적은 변화를 보였다. 이러한 수치적 수렴 특성은 위상최적설계 과정에서의 주요 구조물의 생성 전, 후의 결과로 설명이 가능하다[23]. 우선적으로 발판과 핸들 지지대의 양 끝(A-A’, B-B’)이 연결되는 주요 구조물의 생성이 목적함수 감소에 큰 영향을 미치는 것을 확인할 수 있다(Fig. 3). 이어서 구조물 내부에 세부 구조들을 생성시키면서 목적함수 값을 수렴시키고 제한조건의 값을 만족시키는 형태로 볼 수 있다. 그리고 설계 과정 후반에서는 요소의 밀도 값의 벌칙화를 강조하여 구조물의 위상이 더욱 선명해지는 형태로 진행되었다.
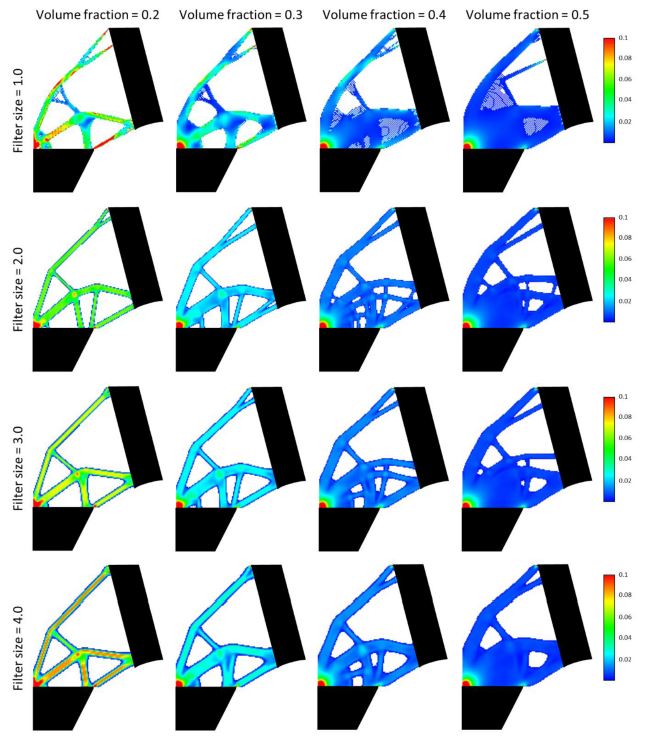
Fig. 4는 부피분율과 필터링 크기에 따른 전동 킥보드 연결부의 위상최적설계 결과를 나타낸다. 도출된 결과들은 공통적으로 발판과 핸들 지지대의 상단과 하단이 각각 연결되는 위상들을 보였다. 이는 핸들 지지대의 작용점으로부터 발판까지 연결부를 통해 충돌 하중을 분포 및 전파하기 위한 결과로 볼 수 있다. 또한 부피분율이 높을수록 구조의 두께가 두꺼워지며 세분화되는 것을 확인하였으며, 발판 하단과 핸들 지지대 하단을 연결하는 구조가 토로이드형으로 변화하는 것을 확인하였다. 이러한 변화는 핸들 지지대에 작용한 우력(Couple of Force)으로 인한 굽힘 모멘트를 효과적으로 지지하기 위한 결과로 볼 수 있다. 이러한 결과들은 본 연구의 방법이 구조 역학적인 특징을 잘 모사하여 올바르게 수행되었음을 의미한다.

Topology optimization results of electric kickboard’s connection according to filter size and volume fraction values
본 연구에서는 민감도의 필터링 크기에 따른 위상의 변화에 대한 분석도 수행하였다. 필터링의 크기가 1 px인 경우 필터링이 작동하지 않아 연결부에서 체커보드(Checker Board) 패턴의 구조물이 생성되었다. 이는 경첩(Hinge) 구조이며, 실제 제조가 불가능한 수치적 불안정성에 의해 생성된 결과이다. 따라서 본 연구는 필터링 크기가 2-4 px인 경우의 변화를 분석하였다(Figs 4와 5). 필터링의 크기가 증가할수록 두께가 얇은 구조물은 사라지고 주요 구조물이 두꺼워지는 현상을 확인하였다. 이러한 결과는 최적설계과정 후반부에서의 변화량을 줄여 위상최적설계 수렴 속도에도 영향을 미쳤다. 필터링 크기가 2 px인 경우 수렴을 위해 평균 289회의 축차가 필요하였으나, 4 px인 경우 평균 82회만 필요하였다(Table 1). 다만, 필터링의 크기가 커질수록 구조물과 주변부와의 경계가 모호(Blurred)해지는 현상도 발견하였다.
Fig. 5는 도출된 위상들의 변형률 에너지 분포를 보여준다. 모든 위상은 공통적으로 발판 상단의 양 끝에서 높은 변형률 에너지를 가졌다. 구체적으로는 핸들 지지대의 긴 길이로 인해 더 높은 모멘트가 발생하는 발판의 좌측 상단에서 더 높은 변형률 에너지가 발생하였다. 이러한 현상으로 인해 해당 지점들로부터 구조의 연결성이 생성되었으며, 특히 발판 좌측 상단을 기준으로 하는 구조물이 우측 상단보다 더 많은 것을 확인할 수 있다. 더불어 부피분율의 증가에 따라 좌측 상단의 구조가 세분화되고 많아지는 현상이 발견되었다. 이러한 현상은 최대 변형률 에너지를 낮추고 변형률 에너지 분포의 균일성을 향상시키는데 영향을 미쳤다. 따라서 본 연구의 위상최적설계가 구조적인 효율성을 높이기 위한 방향으로 진행되었음을 확인할 수 있으며, 이는 일반적인 위상최적설계의 목적[24]과 부합한다.
Strain energy distribution of electric kickboard’s connection according to filter size and volume fraction values
Fig. 6과 Table 2는 본 연구에서 도출한 위상(VF: 0.2, Filter size: 4.0 px)과 시중 모델 간의 충돌 성능 비교에 대한 결과이다. 총 3개의 연결부 중 위상최적설계안의 충돌 성능(164 N·mm)이 나머지 연결부들(입방체형: 485 N·mm, 토로이드형: 892 N·mm)과 대비하여 최소 66% 이상의 높은 성능을 보였다. 이는 충돌시 발생하는 변형률 에너지 분포와 관련성이 있다. 위상최적설계 결과물의 구조들은 정면충돌에 의해 발생한 변형률 에너지를 구조물 전체에 고르게 분포하여 컴플라이언스를 낮췄다(Std.: 0.04 N·mm). 반면 나머지 시중의 2가지 모델들은 에너지를 고르게 분포시키지 못하고 에너지가 집중되는 현상이 발생하였다. 특히 앞바퀴부에 가까운 짧은 구조물일수록 에너지 집중 현상이 심화되었다. 이러한 결과는 위상최적설계 결과가 정면충돌에서 안전성을 개선하여 파손 예방에 기여할 수 있음을 의미한다. 다만, 본 연구에서는 입방체형의 연결부가 토로이드형보다 더 높은 성능을 보였는데 이는 이전 연구[2]와 불일치하는 결과이다. 이러한 결과는 부피분율에 대한 제한조건이 없었던 이전 연구와는 달리, 본 연구에서의 부피분율은 동일하게 제한 적용하였기 때문에 발생한 차이로 볼 수 있다.
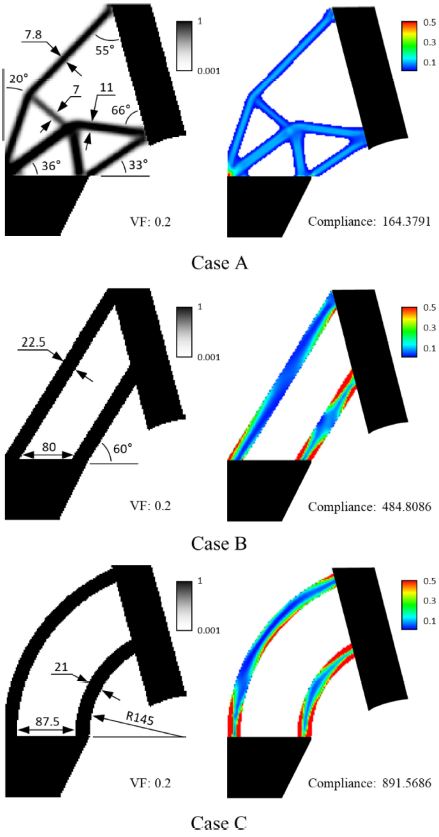
Collision performance of the topology optimization result and two models on the market: Density map (Left column) and strain energy distribution (Right column)
본 연구는 다음과 같은 한계점을 가진다. 첫째, 탑승자의 체중으로 인한 하중을 고려하지 않았다. 둘째, 단순화를 통해 세부적인 전동 킥보드의 구조들을 고려하지 않았다. 셋째, 평면 응력을 가정한 2차원 위상최적설계를 수행하였다. 그럼에도 불구하고, 본 연구에서 위상최적설계를 통해 도출된 전동 킥보드 연결부는 시중 모델 대비 정면충돌에 대한 개선된 안전성을 보였다.
4. 결론
본 연구에서는 정면충돌에 대한 전동 킥보드 연결부의 구조적 안전성 개선을 위해 위상최적설계를 수행하였다. 이를 위해 연구 모델을 2차원 모델로 구성하였으며 정면충돌 상황에서의 위상최적설계를 수행하였다. 연구 결과로 발판 하단과 핸들 지지대 하단을 연결하는 구조가 토로이드형으로 변화하여 최대 변형률 에너지를 낮추고 분포의 균일성을 향상시키는 변화를 확인하였다. 대표 위상최적설계안과 시중에 판매되고 있는 2개의 대표적인 전동 킥보드 연결부 위상과의 충돌 성능 비교를 통해 위상최적설계 결과를 검증하였다. 위상최적설계를 통해 기존 전동 킥보드의 연결부보다 충돌 성능을 최소 66% 이상 개선할 수 있음을 확인하였다. 본 연구 결과를 바탕으로 전동 킥보드의 안전성이 개선되기를 기대한다.
Acknowledgments
본 과제(결과물)는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 디지털 신기술 인재양성 혁신공유대학사업의 연구결과입니다.
REFERENCES
- Lee, U.-Y., Kim, S.-I., (2021), A study on user experience of scooter-sharing system, Journal of Digital Convergence, 19(2), 425-431.
-
Kim, M. G., Kim, J. J., (2021), Structural safety analysis of electric kickboard according to shape of connection parts using finite element analysis, Journal of the Korean Society of Manufacturing Process Engineers, 20(12), 65-70.
[https://doi.org/10.14775/ksmpe.2021.20.12.065]

-
Dong, H. B., Zhang, W., (2011), Lightweight design of electric scooter frame by finite element optimization, Advanced Materials Research, 201-203, 49-53.
[https://doi.org/10.4028/www.scientific.net/AMR.201-203.49]

-
Hsia, S. Y., Chou, Y. T., (2013), Analysis of welding fatigue on electric scooter using CAE approach, Applied Mechanics and Materials, 291-294, 920-924.
[https://doi.org/10.4028/www.scientific.net/AMM.291-294.920]

-
Chou, J.-R., Hsiao, S.-W., (2005), An anthropometric measurement for developing an electric scooter, International Journal of Industrial Ergonomics, 35(11), 1047-1063.
[https://doi.org/10.1016/j.ergon.2005.06.001]

-
Shivhare, G., Kundu, K., Narayan, J., Dwivedy, S. K., (2021), Design and modeling of a compact lightweight electric-scooter, Proceedings of the 2021 International Conference on Computational Performance Evaluation (ComPE), 944-949.
[https://doi.org/10.1109/ComPE53109.2021.9752193]

-
Sigmund, O., Maute, K., (2013), Topology optimization approaches, Structural and Multidisciplinary Optimization, 48(6), 1031-1055.
[https://doi.org/10.1007/s00158-013-0978-6]

-
Kim, J., Kim, J. J., Jang, I. G., (2022), Integrated topology and shape optimization of the five-spoke steel wheel to improve the natural frequency, Structural and Multidisciplinary Optimization, 65(3), 1-12.
[https://doi.org/10.1007/s00158-022-03183-3]

-
Lee, W. G., Kim, J. S., (2015), Lightweight design of brake bracket for composite bogie using topology optimization, Transactions of the Korean Society of Mechanical Engineers A, 39(3), 283-289.
[https://doi.org/10.3795/KSME-A.2015.39.3.283]

-
Kim, J., Roh, H. S., Min, Y., Hur, S.-H., Jang, I. G., (2018), Lightweight design of the stub axle using topology optimization, Journal of the Korean Society for Precision Engineering, 35(7), 695-700.
[https://doi.org/10.7736/KSPE.2018.35.7.695]

-
Kim, J. J., Jang, I. G., (2016), Image resolution enhancement for healthy weight-bearing bones based on topology optimization, Journal of Biomechanics, 49(13), 3035-3040.
[https://doi.org/10.1016/j.jbiomech.2016.06.012]

-
Briot, S., Goldsztejn, A., (2018), Topology optimization of industrial robots: Application to a five-bar mechanism, Mechanism and Machine Theory, 120, 30-56.
[https://doi.org/10.1016/j.mechmachtheory.2017.09.011]

-
Kim, Y.-C., Hong, J.-K., Jang, G.-W., (2011), Lightweight crane design by using topology and shape optimization, Transactions of the Korean Society of Mechanical Engineers A, 35(7), 821-826.
[https://doi.org/10.3795/KSME-A.2011.35.7.821]

-
Baandrup, M., Sigmund, O., Polk, H., Aage, N., (2020), Closing the gap towards super-long suspension bridges using computational morphogenesis, Nature Communications, 11(1), 1-7.
[https://doi.org/10.1038/s41467-020-16599-6]

-
Shahrubudin, N., Lee, T. C., Ramlan, R., (2019), An overview on 3D printing technology: Technological, materials, and applications, Procedia Manufacturing, 35, 1286-1296.
[https://doi.org/10.1016/j.promfg.2019.06.089]

- Choi, K., Cho, J., (2020), A study on structural analysis at front collision according to the shape of electric kick board, Journal of the Korean Society of Mechanical Engineers, 22(3), 457-462.
-
Bendsøe, M. P., (1989), Optimal shape design as a material distribution problem, Structural Optimization, 1(4), 193-202.
[https://doi.org/10.1007/BF01650949]

-
Rozvany, G. I., Zhou, M., Birker, T., (1992), Generalized shape optimization without homogenization, Structural Optimization, 4(3), 250-252.
[https://doi.org/10.1007/BF01742754]

-
Sigmund, O., (2001), A 99 line topology optimization code written in Matlab, Structural and Multidisciplinary Optimization, 21(2), 120-127.
[https://doi.org/10.1007/s001580050176]

- Sigmund, O., (1994), Design of material structures using topology optimization, Technical University of Denmark. https://www.researchgate.net/profile/Ole-Sigmund/publication/261173987_Design_of_Material_Structures_Using_Topology_Optimization/links/55de078b08aeaa26af0f20d3/Design-of-Material-Structures-Using-Topology-Optimization.pdf
-
Sigmund, O., (1997), On the design of compliant mechanisms using topology optimization, Journal of Structural Mechanics, 25(4), 493-524.
[https://doi.org/10.1080/08905459708945415]

-
Bendsøe, M. P., (1995), Optimization of structural topology, shape, and material, Springer.
[https://doi.org/10.1007/978-3-662-03115-5]

- Lee, S.-J., Park, G.-I., (2013), A matlab code for structural topology optimization, Journal of the Architectural Institute of Korea Structure & Construction, 29(10), 11-18.
-
O’Shaughnessy, C., Masoero, E., Gosling, P. D., (2022), Topology optimization using the discrete element method. Part 1: Methodology, validation, and geometric nonlinearity, Meccanica, 57(6), 1213-1231.
[https://doi.org/10.1007/s11012-022-01493-w]


MS. candidate in the Department of Mechanical Engineering, Keimyung University. His research interest is topology optimization for vehicular mobility.
E-mail: dhdvndtm@gmail.com

Ph.D. candidate in the Department of Mechanical Engineering, Keimyung University. Her research interest is topology optimization-based bone remodeling.
E-mail: eclipse0403@gmail.com

Assistance Professor in the Department of Mechanical Engineering, Keimyung University. His research interest is biomechanical engineering based on optimization and artificial neural network.
E-mail: kjj4537@gmail.com