Digital Mask를 이용한 STED Lithography 기술의 분석적 검증
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, a digital mask-based STED lithography technique was proposed, and the effective resolution of the proposed system was calculated analytically. The proposed STED lithography system uses two spatial light modulators to modulate the phase of an excitation beam and a depletion beam, respectively. The excitation spatial light modulator acts as a digital mask to form the patterning image, while the depletion spatial light modulator creates an image surrounding the projected excitation image. Thus, photopolymerization is suppressed by stimulated emission occurring in the depletion focus region surrounding the excitation focus, thereby improving lithographic resolution. Electromagnetic field and intensity distribution were calculated, and the resolution of the proposed STED lithography was simulated based on vectorial diffraction theory. An effective resolution of 72 nm was calculated under the condition of Is 0.1, which is similar to the resolution of conventional STED lithography at 70 nm. These results analytically confirmed that the proposed STED lithography system could pattern a two-dimensional region simultaneously without the loss of resolution compared to conventional STED lithography.
Keywords:
Photolithography, Nanostructure fabrication, Optical phase modulation, Spatial light modulator, Superresolution키워드:
포토리소그래피, 나노구조체 제조, 광위상 변조, 공간 광 변조기, 초고해상도1. 서론
광학 시스템의 물리적인 한계인 회절한계를 극복하기 위해 1994년 S. W. Hell이 STED를 제안한 이래로, STED는 초고해상 형광 이미징과 패터닝 분야에서 활발하게 연구되고 있으며[1-3], 특히 패터닝 분야에서는 회절한계 이하의 미세 구조를 적층 제조할 수 있는 기술로 각광받고 있다[4,5]. STED 리소그래피는 여기빔(Excitation Beam) 초점의 외곽에서 발생하는 광중합(Photo Polymerization) 반응을 억제하기 위해 공핍빔(Depletion Beam)의 초점을 여기빔의 초점에 중첩시킴으로써, 수십 nm급의 해상도를 달성할 수 있다. 여기 초점 영역의 주변에 공핍빔이 중첩되어 있으므로, 공핍빔에 의한 유도 방출로 인해 여기빔 PSF 외부 영역의 광중합이 억제되어 결과적으로 회절한계 이하의 유효 PSF를 획득하는 것이 가능하다. 결과적으로 여기빔의 PSF와 공핍빔의 PSF는 모두 광학적 특성에 의해 좌우되지만, STED 리소그래피의 유효 PSF는 회절한계를 극복할 수 있어 회절한계 이하의 패턴을 제조하는 것이 가능해진다.
SETD의 해상도를 결정하는 유도 방출은 광강도에 의해 결정되기 때문에, 공핍 초점의 형상에 의해 크게 영향을 받는다. 유효 PSF의 등방성을 확보하기 위해 공핍빔은 중심부의 광강도가 0인 도넛 형상을 사용하는 것이 가장 일반적인 방식이며[6,7], 공핍빔의 위상을 부분적으로 지연시킨 후 집광함으로써 도넛형상의 초점을 형성하게 된다. 도넛 형상의 공핍 초점은 여기 초점에 중첩되어 초점의 중앙을 제외한 부분에서 광중합을 억제시키며, 이렇게 형성된 회절한계 이하의 유효 초점으로 시료를 스캔하는 직접 묘화 방식으로 패턴을 제조하게 된다.
이 연구에서는 직접 묘화 방식으로 패턴을 제조하는 STED 리소그래피와는 다르게 SLM을 디지털 마스크로 이용하여 2차원 패턴을 한 번에 노광할 수 있는 2D 디지털 STED 리소그래피 방법을 제안하고 이에 대한 해석을 진행하였다. 방위(Azimuthal) 편광된 빛은 집광될 경우 중심의 광강도가 0인 도넛 형상의 초점을 형성하게 된다[8]. 따라서 제작하려는 패턴의 형상에 맞춰 SLM의 각 픽셀의 위상을 변조하여 입사되는 공핍빔의 편광을 유사 방위 편광으로 변조시키고 시료의 표면으로 투영시킴으로써 제작하려는 패턴을 감싸는 형상의 공핍 초점을 형성할 수 있으며, 이를 통해 스캔 없이 2차원 면적을 한 번에 패터닝하는 것이 가능하다. 벡터 회절 이론을 통해 위상변조에 의해 형성되는 도넛 초점의 형상과 이에 의한 STED 해상도를 분석하였으며, 기존 방식 STED 해상도와의 비교를 통해 제안하는 2D 디지털 STED 리소그래피의 성능을 해석적으로 검증하였다.
2. 해석 모델
2.1 제안 광학 시스템
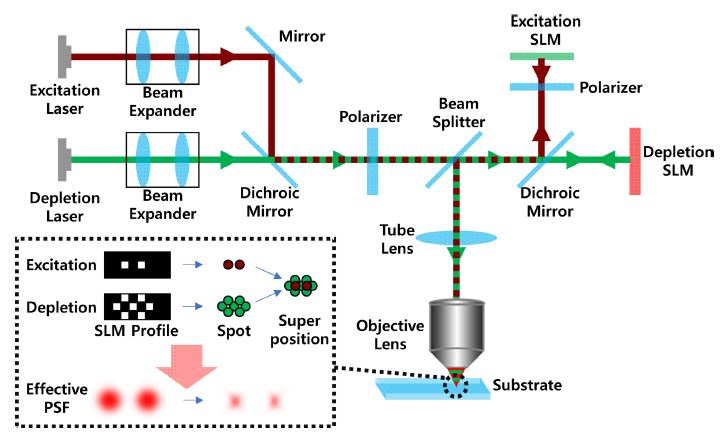
이 연구에서 제안하는 광학 시스템은 Fig. 1과 같다. 여기빔과 공핍빔의 위상을 각각 변조하기 위하여 2대의 SLM을 사용하게 된다. SLM1과 SLM2는 각각 여기빔과 공핍빔의 편광을 변조하기 위해 사용되며 투영광학계를 통해 초점면에서 각 SLM의 픽셀의 위치를 동기화시킨다. 이때, 여기빔은 SLM1에 의해 위상이 변조된 후 편광판을 통과함으로써 SLM에 의해 변조된 픽셀과 동일한 형상, 즉 노광하려는 패턴의 형상을 초점면으로 투영시키게 된다. SLM1이 여기빔의 투과 여부를 결정하는 디지털 마스크로 작용하게 된다. 반면 공핍빔은 SLM2에 의해 위상이 변조된 후 편광판 없이 광학계를 통해 초점면으로 투영된다. 따라서 공핍빔은 여기빔과 다르게 SLM에 의한 광강도의 형상 변화 없이 초점면으로 투영되나, SLM2에 의해 변조된 편광성분이 남아있는 상태로 전달된다. 이때, SLM2의 각 픽셀이 SLM1에서 형성된 노광 패턴을 감싸는 형태로 방위 편광을 형성하게 되면 투영된 여기 초점을 둘러싸는 도넛 광초점을 형성하게 된다. 이와 같은 광학시스템 구성에서 여기빔과 공핍빔이 동시에 조사될 경우, 여기 초점의 외곽을 둘러싸는 공핍 초점에서 유도 방출 현상이 발생하여 유효 PSF를 감소시키게 되어 회절한계 이하의 패터닝이 가능하다. 이때, 형성된 도넛 초점 중심부의 크기는 광학 회절한계에 의해 결정되며 초점면으로 투영된 SLM1의 픽셀 주변을 정확하게 감싸도록 만들기 위해서는 광학시스템의 회절한계와 시스템의 배율을 조절할 필요가 있다. 이 연구에서는 상용 대물렌즈와 SLM을 고려한 Table 1의 조건을 이용하여 해석을 진행하였으며 여기빔은 펨토초 레이저, 800 nm 파장의 이광자 중합 조건을, 공핍빔은 532 nm 파장의 연속파(Continuous Wave) STED 조건을 가정하였다.
2.2 벡터 회절 이론 기반 광학 시스템 해석
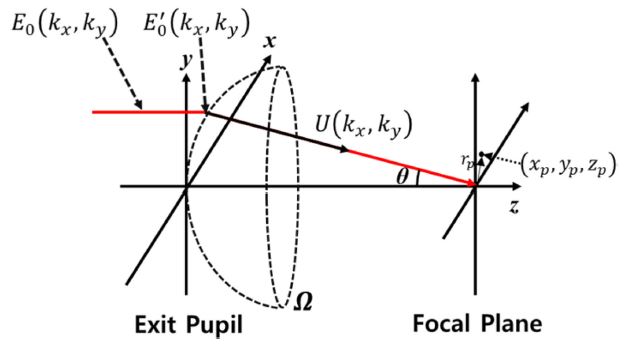
Fig. 2는 2D 디지털 STED 리소그래피의 초점면 근처에서 전자기장 분포와 그에 따른 PSF를 계산하기 위한 Abbe의 사인 조건을 따르는 이상적인 광학시스템의 구성이다. 원형, 대칭적으로 입사되는 광학 시스템의 초점 근처의 전자기장을 해석할 때, 출사동(Exit Pupil)의 회절 적분을 베셀 함수(Bessel Function)로 단순화시켜 계산하기 위해 원통형 좌표계를 사용하는 것이 일반적이다. 그러나 디지털 마스크를 적용한 2D 디지털 STED 리소그래피의 경우, 원통형 좌표계를 사용할 경우 SLM의 각 픽셀에 의해 변조된 편광 성분을 고려하여 계산하는 것이 어렵다. 따라서 SLM의 픽셀에 의해 변조된 편광의 영향을 고려하기 위해 직교 좌표계(Cartesian Coordinate)를 이용하여 초점 근처의 위치(xp, yp, zp)에서 회절된 전자기장 E를 아래의 식(1)과 같이 계산하였다[9,10].
| (1) |
출사동에서의 U는 고개구수(High Numerical Aperture) 렌즈에 의한 E0의 회전을 고려하여 식(2)와 같이 유도된다[11].
| (2) |
이때, kx, ky, kz는 각각 k의 x, y, z축 성분을 의미하며, E0는 편광 상태를 포함한 평면파 입사광을 나타낸다. 간단한 예로 x축으로 선형 편광된 입사광 E0는 [Ex ; Ey ; Ez] 성분에 대해 E0 = [1 ; 0 ; 0]으로 표현된다. 이 연구에서는 위와 같이 유도된 수식들을 통해 디지털 마스크가 투영된 광학시스템 초점면의 전자기장 분포를 해석하였다.
2.3 디지털 마스크 해석 모델
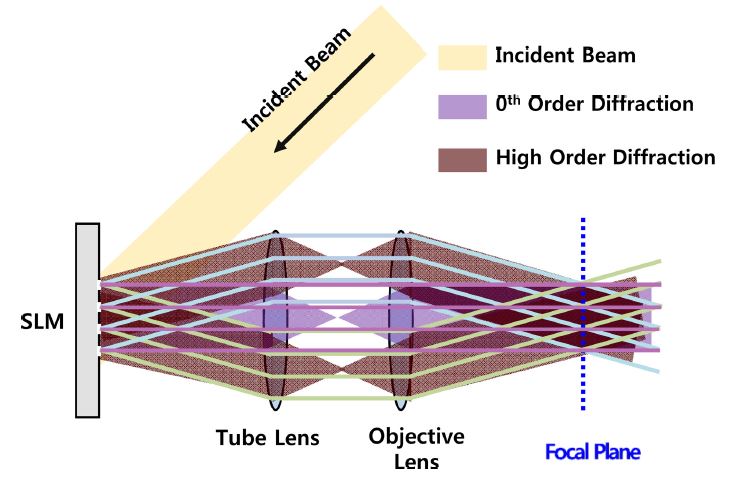
SLM, 디지털 마이크로미러 디바이스 등 마이크로 소자를 이용해 빛의 경로/위상을 변조할 경우에는 소자 표면에서 발생하는 회절 특성을 고려해야 한다. 특히 펨토초 레이저를 여기 광원으로 사용하는 STED 리소그래피의 경우 회절에 의해 시공간적으로 펄스가 스트레치(Stretch)되어 펄스폭이 늘어남으로써 물질을 여기시키지 못하는 문제가 발생할 수 있다. 그러나 이 연구에서 제안하는 시스템처럼 바이-텔레센트릭(Bi-Telecentric) 구조의 광학계를 사용할 경우, Fig. 3과 같이 회절된 빛들이 광학계의 초점면에서 다시 시공간적으로 집광됨으로써 회절에 의한 이미지 품질의 저하와 펄스의 스트레치 문제를 해결하는 것이 가능하다[12]. 따라서 이 연구에서는 고차 회절 성분의 광강도 분포 및 펄스 스트레치에 의한 영향을 별도로 계산하지 않고 0차 회절의 광강도 분포로 이를 대체하였다.
리소그래피 시스템에서 마스크에 의해 초점에서 형성되는 광강도 분포는 마스크 함수 M과 PSF의 컨볼루션으로 표현되며, 코히런트 시스템의 경우 식(3)과 같이 정리된다[13].
| (3) |
| (4) |
고개구수 대물렌즈의 각 PSF의 전자기장 분포는 식(1)을 통해 계산될 수 있으며, 초점면으로 투영된 마스크 함수 M은 식(4)와 같이 오브젝트 면의 마스크 함수 M0인 SLM의 각 픽셀 좌표와 투영광학계의 배율 fobj/ft로 표현될 수 있다. 여기빔의 경우 SLM1을 통해 위상이 변조된 후, 편광판에 의해 필터링되기 때문에 SLM1의 위상변조 여부에 따라 마스크 함수의 진폭(Amplitude)가 0과 1로 구성된다. 반면 공핍빔의 경우 SLM2에 의해 위상이 변조된 후 별도의 필터링 없이 초점면으로 투영되므로 마스크 함수의 진폭은 전 영역에서 1이며, SLM2 각 픽셀의 위상변조 여부에 따라 전자기장의 편광성분이 변조된다. 위의 수식들을 통해 초점면에서의 전자기장 분포를 해석하였으며, 여기빔의 이광자 중합을 고려하여 여기빔 광강도의 제곱 조건하에서의 STED 리소그래피의 해상도를 계산하였다.
3. 해석 결과 및 분석
먼저 상쇄간섭을 일으켜 초점면에서 공핍빔의 광강도를 0으로 만들 수 있는지 여부를 확인하였다. 공핍빔의 경우 여기빔과 다르게 편광성분을 필터링해주는 광학소자를 통과하지 않기 때문에 SLM 각 픽셀에서 입사되는 빛이 모두 초점면으로 투영된다. STED를 발현하기 위한 높은 광강도의 공핍빔이 지속적으로 투영될 경우 제조된 패턴을 열화시킬 수 있기 때문에 SLM 각 픽셀의 위상 변조를 통해 초점면에서 상쇄간섭을 일으킴으로써 공핍빔의 광강도를 조절할 수 있는 방법을 해석하였다.
공핍빔의 광강도를 조절하기 위해 4개의 픽셀을 하나의 도메인으로 구성하여 편광을 변조하였다. Figs. 4(a)는 공핍빔의 상쇄간섭을 일으키기 위한 빛의 편광 조건을 나타내며, 4(b)는 초점면에서의 광강도 분포를 나타낸다. SLM의 픽셀 크기는 8 μm, 시스템의 배율은 1/111배이므로 초점면으로 투영된 SLM의 픽셀은 회절한계보다 작게 된다. 따라서 SLM의 각 픽셀은 인접한 픽셀의 전자기장 분포에 영향을 미치게 되므로 구성된 전체 도메인의 편광을 Fig. 4(a)와 같이 변조시켜줄 경우 각 픽셀의 성분들이 인접한 픽셀들과 상쇄되어 광강도가 감소하게 된다. 따라서, 패터닝 영역을 제외한 부분은 위와 같이 편광을 변조하여 광강도를 감소시키고 패터닝할 영역은 정상적으로 편광 변조해줄 경우 패터닝할 영역만 선택적으로 높은 광강도의 빛을 집광시키는 것이 가능하다.
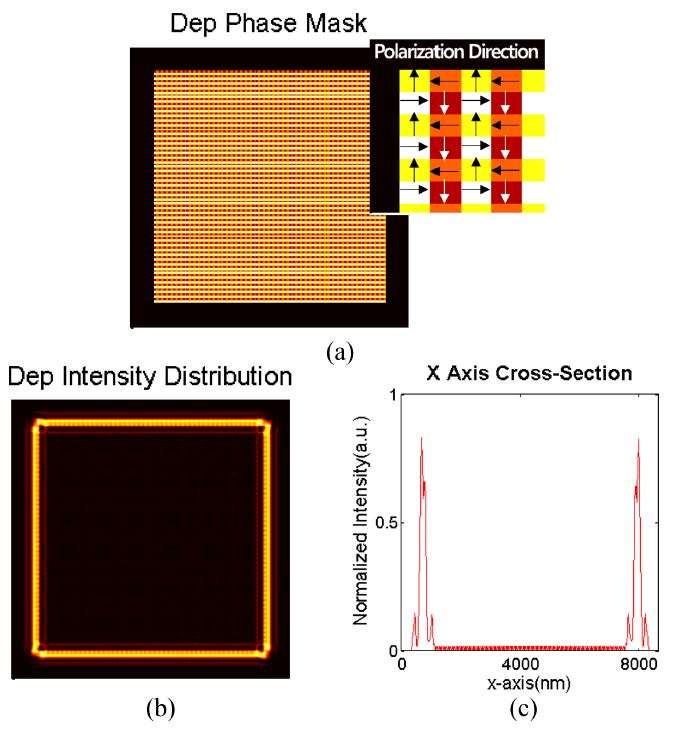
Simulation results of 0 depletion intensity at focal point through pixel modulation of SLM. (a) Phase modulation at SLM, (b) Intensity distribution by modulated phase, and (c) Its cross-section profile
다음으로 리소그래피의 해상도를 향상시키기 위한 공핍 초점의 형상을 해석하였다. 앞서 언급한 바와 같이 제조하려는 패턴의 형상을 감싸는 형상의 유사 방위 편광을 형성하게 될 경우, 중심부에서는 상쇄간섭에 의해 광강도가 0으로 감소하고, 패턴의 주변부에서는 높은 광강도를 유지함으로써 유도방출에 의한 해상도 향상이 일어날 것으로 예상하였다. 따라서, 다양한 패턴들에 대해 유사 방위 편광을 형성함으로써 제안한 STED 리소그래피가 임의 패턴에 대해 해상도를 향상시킬 수 있을지에 대해 검증하였으며, 이에 대한 결과가 Fig. 5에 정리되어 있다.
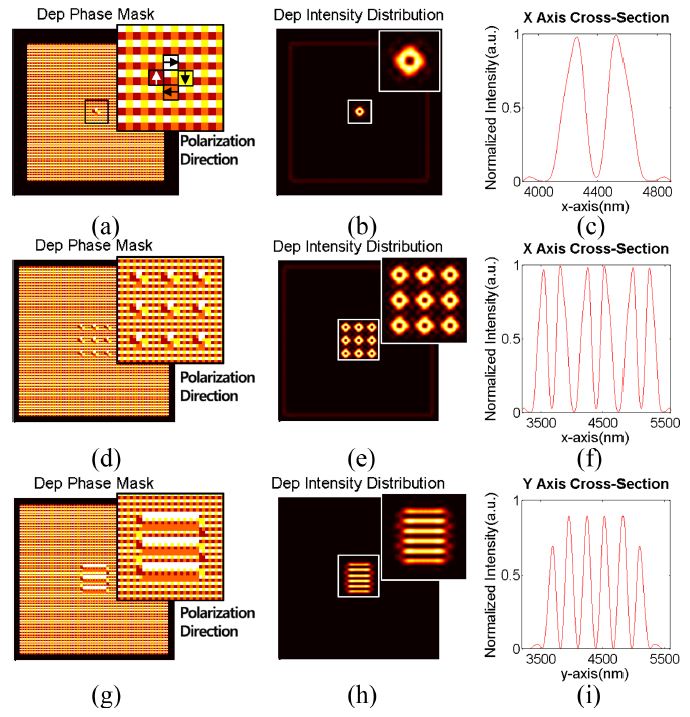
Calculated depletion intensity profile of various pattern. Phase modulation, depletion intensity distribution, and its cross-section profile for (a)-(c) Single spot, (d)-(f) Multi-spot, and (g)-(i) Multi-line pattern
Figs. 5(a)부터 5(c)는 단일 초점의 해상도를 향상시키기 위한 공핍 초점을 해석한 결과이며, 5(a)는 공핍 초점을 형성하기 위한 편광 성분을, 5(b)는 이에 의한 초점면의 광강도 분포를, 5(c)는 광강도의 단면 프로파일을 각각 나타낸다. 편광 성분은 도넛 형상의 공핍 초점을 형성하려는 도메인에서만 유사 방위 편광으로 변조시키고 그 외의 도메인에서는 광강도를 0으로 만들어주기 위한 편광으로 변조하였다. 예상했던 바와 같이, 공핍 초점의 중심부의 광강도는 0으로 감소되었으며 주변부에서는 높은 광강도를 갖는 도넛 형상의 초점이 형성됨을 확인할 수 있었다.
Figs. 5(d)부터 5(f)는 다중 초점의 해상도를 향상시키기 위한 공핍 초점을 해석한 결과이다. 마찬가지로, 도넛 형상의 초점을 형성하려는 도메인 외의 영역에서는 광강도를 0으로 만들기 위한 편광으로 변조하였으며 도넛 초점의 영역에서는 유사 방위편광으로 변조하여 해석을 진행하였다. 다중 초점에서의 결과 역시 중심부의 광강도가 0인 다수의 도넛 초점이 형성됨을 확인할 수 있었다.
Figs. 5(g)부터 5(i)는 선형 패턴의 공핍 초점을 형성하기 위한 편광 조건 및 이에 대한 해석 결과이다. 마찬가지로, 중심부의 광강도가 0인 초점이 형성됨을 확인할 수 있었다. 다만, 최외곽의 선에서는 내부의 선에 비해 광강도가 상대적으로 약한 것을 확인할 수 있으며 이는 최와곽 패턴의 경우 인접 패턴들의 전자기장 영향을 상대적으로 덜 받기 때문으로 판단된다. 따라서, 대면적 패턴을 제작할 경우 최외곽 패턴의 광강도를 보상하기 위해 패턴 외부에 더미 공핍 패턴을 형성할 필요가 있다. 위 결과를 통해, 제안한 방식의 STED 리소그래피 시스템에서 임의 형상의 패턴에 대한 공핍 초점을 형성할 수 있음을 확인할 수 있었다.
마지막으로, 제안한 2D 디지털 STED 리소그래피에서의 해상도 향상에 대해 계산하였다. STED의 해상도는 유도 방출 효율에 의해 결정되므로 공핍 빔의 광강도와 물질의 특성에 의해 영향을 받는다. 따라서 STED의 유효 광강도 분포는 아래의 식(5)와 같이 표현되며[14], 이 수식을 기반으로 제안한 디지털 STED 리소그래피와 기존 STED 리소그래피의 해상도를 해석하여 비교하였다. 이때, 여기빔의 경우 이광자 중합 조건을 고려하여 광강도의 제곱 조건으로 계산을 진행하였으며 동일한 광세기 조건 하에서의 정량적 비교를 위해 여기 빔과 공핍 빔의 광강도를 정규화(Normalization)하여 계산하였다.
| (5) |
기존 STED 리소그래피의 해상도를 고려하여 이와 동등한 수준의 해상도를 도출할 수 있는 값으로 Is를 설정하였으며, 기존 STED 리소그래피의 해상도인 ~70 nm에 맞춰 Is를 0.1로 설정하고 해석을 진행하였다[15]. 이때 2D 디지털 STED 리소그래피의 반치폭(Full Width at Half Maximum)은 72 nm로 기존 STED 리소그래피의 실험적 해상도와 동등한 값을 나타낸다. 2D 디지털 STED 리소그래피의 여기 초점, 공핍 초점, 유효 광강도 분포 및 단면 프로파일는 각각 Figs. 6(a)부터 6(d)와 같다.
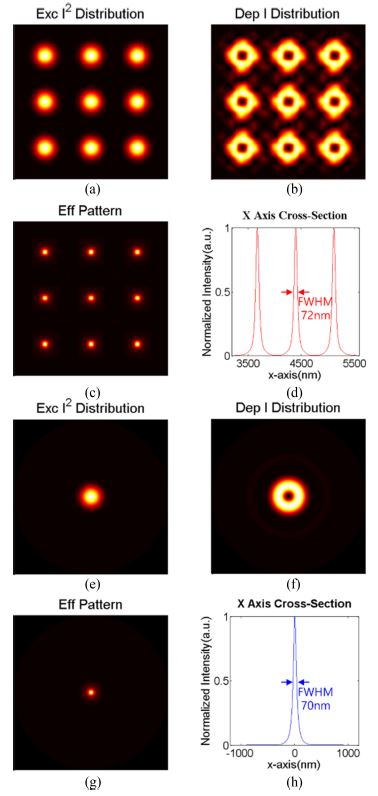
Calculated effective STED profile. Excitation intensity [2] distribution, depletion intensity distribution, effective STED profile and its cross-section profile for (a)-(d) Proposed STED, and (e)-(h) Conventional SETD lithography
비교를 위한 기존 STED 리소그래피의 광강도 분포는 Figs. 6(e)부터 6(h)에 나타나있다. 그림에서 보이는 바와 같이 디지털 STED 리소그래피 시스템의 여기 초점 및 공핍 초점의 광강도 분포는 기존 STED 리소그래피와 동등한 수준인 것을 확인할 수 있었으며, 따라서 STED의 유효 광강도 분포 역시 동일할 것임을 예상할 수 있다. 기존 STED 리소그래피 역시 Is를 0.1로 설정하여 STED의 유효 광강도 분포를 계산하였으며, 이때 반치폭은 2D 디지털 STED 리소그래피와 동등 수준인 70 nm로 계산되었다. 특히 해석 결과에서 확인할 수 있는 것처럼 제안한 2D 디지털 STED 리소그래피 시스템에서는 공핍 초점의 형상을 변조함으로써 2D 패턴을 한 번에 제조하는 것이 가능하다. 이 결과를 통해 제안한 2D 디지털 STED 리소그래피 시스템이 단일 초점을 사용해 직접 묘화 방식으로 패턴을 제작하는 기존 STED 리소그래피와 비교하여 해상도의 손실 없이 2차원 영역을 한 번에 패터닝함으로써 고해상/고속 패턴 제조가 가능함을 확인하였다.
4. 결론
이 연구에서는 SLM을 디지털 마스크로 이용하여 2차원 패턴을 한 번에 노광할 수 있는 2D 디지털 STED 리소그래피 기술을 제안하고 해석을 통해 제안한 시스템의 성능 및 유효 해상도를 확인하였다. 제안하는 STED 리소그래피 시스템은 2대의 SLM을 이용해 각각 여기빔과 공핍빔의 위상을 변조함으로써 패턴 형상의 여기 초점과 이를 둘러싼 도넛 형상의 공핍 초점을 형성하게 된다. 여기 초점 외곽의 공핍 초점 영역에서 발생하는 유도 방출에 의해 광중합이 억제되어 리소그래피 해상도를 향상시키는 것이 가능하다. 벡터 회절 이론에 기반한 해석 모델을 통해 제안한 시스템의 여기 초점 및 공핍 초점에 대해 전자기장 분포 및 광강도 분포 해석을 수행하였으며, 해석 결과 중심부의 광강도가 0인 도넛 형상의 초점이 여기 초점을 둘러싼 형태로 형성되는 것을 확인할 수 있었다. 여기 초점과 공핍 초점의 광강도 해석 결과를 기반으로 2D 디지털 STED 리소그래피의 해상도를 계산하였으며, Is 0.1 조건에서 72 nm의 유효 해상도 결과를 확인하였다. 이는 기존 STED 리소그래피의 Is 0.1 조건에서의 해상도 70 nm와 동등한 수준의 결과로, 2D 디지털 STED 리소그래피 시스템이 기존 STED 리소그래피와 비교하여 해상도의 손실 없이 2차원 영역을 한 번에 패터닝하는 것이 가능함을 해석적으로 확인할 수 있었으며, SLM의 스크린 크기과 광학시스템의 배율을 고려하여 138 × 77 μm 영역을 70 nm 급의 해상도로 한 번에 패터닝할 수 있을 것으로 예상된다.
이 결과들을 통해 제안한 STED 리소그래피 시스템이 고해상/고속 패턴 제조가 가능함을 확인할 수 있었으며, 고속으로 회절한계를 극복한 패턴 제조가 가능한 새로운 기술로 나노구조체 제조 분야에 기여할 수 있기를 기대한다.
Nomenclature
| STED : | Stimulated Emission Depletion |
| PSF, h : | Point Spread Function |
| SLM : | Spatial Light Modulator |
| E : | Electric Field Distribution |
| I : | Intensity Distribution |
| Is : | Saturation Intensity of Material |
| λexp : | Wavelength of Excitation Beam |
| λdep : | Wavelength of Depletion Beam |
| NAobj : | Numerical Aperture of Objective Lens |
| fobj : | Focal Length of Objective Lens |
| ft : | Focal Length of Tube Lens |
| k : | Wavenumber |
| Ω : | Integral Domain |
| M : | Mask Function |
Acknowledgments
본 연구는 한국기계연구원 기본사업(NK236E)의 일환으로 수행되었습니다.
REFERENCES
-
Hell, S. W., Wichmann, J., (1994), Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy, Optics Letters, 19(11), 780-782.
[https://doi.org/10.1364/OL.19.000780]

-
Willig, K. I., Harke, B., Medda, R., Hell, S. W., (2007), STED microscopy with continuous wave beams, Nature Methods, 4(11), 915-918.
[https://doi.org/10.1038/nmeth1108]

-
Klar, T. A., Wollhofen, R., Jacak, J., (2014), Sub-abbe resolution: From STED microscopy to STED lithography, Physica Scripta, 2014(T162), 014049.
[https://doi.org/10.1088/0031-8949/2014/T162/014049]

-
Wollhofen, R., Katzmann, J., Hrelescu, C., Jacak, J., Klar, T. A., (2013), 120 nm resolution and 55 nm structure size in STED-lithography, Optics Express, 21(9), 10831-10840.
[https://doi.org/10.1364/OE.21.010831]

-
Müller, P., Müller, R., Hammer, L., Barner-Kowollik, C., Wegener, M., Blasco, E., (2019), STED-inspired laser lithography based on photoswitchable spirothiopyran moieties, Chemistry of Materials, 31(6), 1966-1972.
[https://doi.org/10.1021/acs.chemmater.8b04696]

-
Leutenegger, M., Eggeling, C., Hell, S. W., (2010), Analytical description of STED microscopy performance, Optics Express, 18(25), 26417-26429.
[https://doi.org/10.1364/OE.18.026417]

-
Moneron, G., Hell, S. W., (2009), Two-photon excitation STED microscopy, Optics Express, 17(17), 14567-14573.
[https://doi.org/10.1364/OE.17.014567]

-
Hao, X., Kuang, C., Wang, T., Liu, X., (2010), Effects of polarization on the de-excitation dark focal spot in STED microscopy, Journal of Optics, 12(11), 115707.
[https://doi.org/10.1088/2040-8978/12/11/115707]

-
Wolf, E., (1959), Electromagnetic diffraction in optical systems-I. An integral representation of the image field, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 253(1274), 349-357.
[https://doi.org/10.1098/rspa.1959.0199]

-
Richards, B., Wolf, E., (1959), Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 253(1274), 358-379.
[https://doi.org/10.1098/rspa.1959.0200]

- Zijp, F., (2007), Near-field optical data storage, Ph.D. Thesis, Delft University of Technology.
-
Saha, S. K., Wang, D., Nguyen, V. H., Chang, Y., Oakdale, J. S., Chen, S.-C., (2019), Scalable submicrometer additive manufacturing, Science, 366(6461), 105-109.
[https://doi.org/10.1126/science.aax8760]

-
Ma, X., Arce, G. R., (2011). Computational lithography, John Wiley & Sons.
[https://doi.org/10.1002/9780470618943]

-
Willig, K., Keller, J., Bossi, M., Hell, S., (2006), STED microscopy resolves nanoparticle assemblies, New Journal of Physics, 8(6), 106.
[https://doi.org/10.1088/1367-2630/8/6/106]

-
Buchegger, B., Kreutzer, J., Plochberger, B., Wollhofen, R., Sivun, D., Jacak, J., Schütz, G. J., Schubert, U., Klar, T. A., (2016), Stimulated emission depletion lithography with mercapto-functional polymers, ACS Nano, 10(2), 1954-1959.
[https://doi.org/10.1021/acsnano.5b05863]


Senior researcher in the Department of Nano-Manufacturing Technology of KIMM. His research interest is maskless digital lithography and STED microscopy.
E-mail: wslee@kimm.re.kr

Senior researcher in the Department of Nano-Manufacturing Technology of KIMM. His research interest is laser-material interaction process.
E-mail: hyunmin@kimm.re.kr

Professor in the Department of Nano-Mechatronics, Korea University of Science and Technology and the Head of the Department of Nano-Manufacturing Technology of KIMM. His research interest is nano mechatronics.
E-mail: paul@kimm.re.kr