코너링 오차 및 기구학적 제한값 간의 관계를 활용한 공구경로 계획
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The kinematic constraints used in a computerized numerical control (CNC) interpolator are one of the main factors determining a machine tool’s machining accuracy. The CNC generates velocity profiles by applying kinematic constraints such as jerk and acceleration. Therefore, changing the kinematic constraints values can adjust the cycle time and cornering error. This study proposes a method to adjust the kinematic constraint values. First, the relationship between CNC kinematic constraints and cornering errors were analyzed. The relationship between the kinematic constraints and the cornering error was expressed as an analytical solution. Kinematic constraint values that satisfy specific cornering error values were selected using the analytical solution of cornering error. Finally, a method was devised to apply the appropriate kinematic constraint values to each machining section within a part program. The analytical solutions for cornering errors and using different machining segments to control cornering errors were verified using tool path generation simulation.
Keywords:
Interpolator, Cycle time, Corner smoothing키워드:
보간기, 사이클타임, 코너 스무딩1. 서론
공구경로를 생성하는 CNC 보간기는 고속 고정밀 가공을 위한 핵심 기능 중 하나이다. CNC 제조사는 접선방향 및 공작기계 각 축 방향의 허용 가속도 및 저크 등의 기구학적 제한값을 몇 개의 단계로 미리 지정하는 기능을 제공한다. 적절한 기구학적 제한값을 사용하면 가공정밀도의 향상, 사이클타임의 저감 등을 달성할 수 있다. 반대로 기구학적 제한값을 적절히 선정하지 못하는 경우 가공의 비효율성이 발생할 수 있다. 예를 들어, 신속한 절삭이 허용되는 부품임에도 느린 가감속 때문에 과도한 시간이 소요될 수 있다. 또는 정밀한 가공이 요구되는 부품에서 지나치게 빠른 가감속 사용으로 인한 위치제어 오차가 발생하여 공차를 만족하지 못할 수 있다.
기구학적 제한값이 가공정밀도와 가공속도에 미치는 영향을 분석한 연구가 다수 수행된 바 있다. Yu, et al.은 반복된 실험으로부터 기구학적 제한값에 따라 변화하는 사이클타임과 이송계의 궤적을 분석하여 적절한 기구학적 제한값을 선정하는 방법을 제안하였다[1]. Ward, et al.은 여러 개의 유한 임펄스 응답(Finite Impulse Response, FIR) 필터를 중첩하여 실제 공작기계의 공구경로를 추정하고, 이로부터 사이클타임과 코너링 오차(Cornering Error)를 추정하는 시뮬레이션을 제안하였다[2]. Lee, et al.은 공구경로 생성 모델과 이송계 동역학 모델로 구성된 시뮬레이션을 활용하여 파트프로그램에 대한 최적의 기구학적 제한값을 결정하였다[3].
그러나 이러한 선행연구는 코너링 오차와 기구학적 제한 간 관계를 일반화된 함수로 표현하지 못하였다. 실험적인 방법은 공작기계에 적합한 파라미터를 선정하기 위하여 장비의 반복적인 운전을 요구한다는 단점이 있다. 시뮬레이션을 활용한 방법은 최적의 기구학적 제한값을 선정하기 위하여 정해지지 않은 횟수의 시뮬레이션을 실행하므로 충분한 연산 시간이 필요하다는 특징이 있다. 결국 공작기계 사용자는 주어진 파트프로그램에 적합한 기구학적 제한값을 선정하기 위하여 사용자의 경험에 의존하거나, 실험에서의 시행착오를 겪거나, 수렴까지의 연산에 소요되는 시간의 범위가 보장되지 않는 시뮬레이션을 사용할 수밖에 없다.
본 논문에서는 주어진 파트프로그램에서 요구되는 코너링 오차를 만족하는 기구학적 제한값의 선정 방법을 제안한다. 선독 기능이 적용된 보간 기능에서 활용하는 기구학적 제한과 코너링 오차 간의 관계를 일반화된 함수로 표현한다. 또한 유도한 일반해를 활용하여 특정 코너링 오차를 만족하는 기구학적 제한값을 선택한다. 주어진 파트프로그램 내 여러 구간에 대하여 적합한 기구학적 제한값을 적용하여 코너링 오차를 제한하는 방법을 제안한다.
2. 기구학적 제한과 코너링 오차 사이의 관계
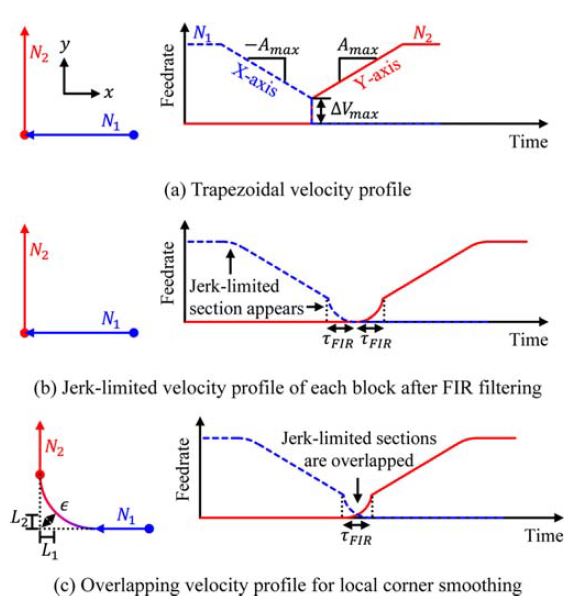
일반적인 파트프로그램에서는 서로 다른 진입 및 출입 각도를 갖는 블록이 이어진다. 또한 직선과 직선, 직선과 원호, 원호와 원호 등 서로 다른 형태의 경로가 만나 코너를 형성한다. 따라서 모든 진출입 각도 및 경로 형태에 대한 해석에는 어려움이 있다. 본 논문에서는 Fig. 1과 같이 X축으로 이송하는 직선보간 선행블록 N1과 Y축으로 이송하는 직선보간 후행블록 N2가 만나는 직각 코너를 기준으로 기구학적 제한과 코너링 오차 사이의 관계를 분석하였다. 두 개 블록에 지령된 이송 거리는 충분히 길어서 지령된 속도를 달성하기 위한 가감속을 수행할 수 있다고 가정하였다.
생성된 공구경로를 CNC 공작기계의 제어기가 높은 정밀도로 추종하기 위해서는 부드러운 가속 및 감속이 중요하다. 가감속 방법 중 하나인 사다리꼴 속도 프로파일은 가속이 변화하는 순간에 무한대의 저크가 발생한다. 급격한 가속도의 변화는 공작기계에 대한 충격과 진동을 유발하여 가공정밀도를 저하시킨다. 따라서 여러 CNC는 가속도의 부드러운 변경이 가능한 저크 제한 속도 프로파일을 사용한다.
본 논문에서는 저크가 제한된 공구경로를 생성하기 위하여 저자가 Ref. 3에서 제안한 방법을 사용하였다. 이 방법에는 각 축의 기구학적 제한 내에서의 고속가공을 위하여 선독 기능을 활용한다. 먼저, 기구학적 제한이 적용된 사다리꼴 속도 프로파일이 생성된다. Fig. 1(a)와 같이 각 축의 가속도는 Amax이고, 코너링 전후에 허용되는 각 축의 속도차는 ΔVmax이다. 선행블록의 감속구간 및 후행블록의 가속구간의 속도 프로파일은 각각 식(1) 및 식(2)로 표현된다. t는 시간, tC는 선행블록이 종료되고 후행 블록이 시작되는 시점이다.
| (1) |
| (2) |
가속도가 변화하는 순간 발생하는 무한대의 저크와, 선행블록의 종점과 후행블록의 시점에서의 순간적인 속도차에 의한 충격을 완화하기 위하여 추가적인 가감속이 필요하다. 식(3)과 같이, 사다리꼴 속도 프로파일 Vi(t)와 길이 τFIR을 갖는 유한 임펄스 응답 필터 h(t)의 합성곱(Convolution)을 통하여 저크 제한속도 프로파일 가 생성된다. u(t)는 단위 계단 함수(Unit Step Function)로, 식(4)와 같다.
| (3) |
| (4) |
선행블록 종료 시 및 후행블록의 시작 시 저크 제한 속도 프로파일은 각각 식(5), 식(6)으로 표현된다. Fig. 1(b)는 합성곱으로부터 생성된 저크 제한 속도 프로파일이다. 이때의 저크가 제한된 구간에서 나타나는 유효 저크 JE 및 유효 가속도 AE는 식(7), 식(8)과 같이 기구학적 제한 Amax, ΔVmax, τFIR에 의하여 결정된다.
| (5) |
| (6) |
| (7) |
| (8) |
t에 대하여 식(5), 식(6)를 적분하여, 저크가 제한된 공구경로는 각각 식(9), 식(10)으로 표현된다.
| (9) |
| (10) |
그러나 FIR 필터를 사용하면 각 블록을 실행하는 시간이 τFIR 만큼 연장된다. 또한 Fig. 1(b)처럼 블록의 종점 및 시점에서 모든 축이 정지한다. 블록 실행 시간의 연장을 최소화하고 모든 축이 정지하는 현상을 해소하기 위하여 연속된 두 블록을 τFIR만큼 중첩하는 국소적인 코너 스무딩(Corner Smoothing)이 사용되었다. 저크가 제한된 구간이 실행되는 시간이 τFIR이므로, 선행블록과 후행블록의 저크가 제한된 구간끼리 서로 중첩된다.
또한 선행블록의 실행이 완료되기 전에 후행블록이 실행되기 시작한다. 따라서 Fig. 1(c)와 같이 기존 코너 부근에 부드러운 경로가 나타난다. 코너링 오차 ε는 기존 코너와 부드러운 코너사이 거리의 최솟값으로, 중첩된 구간의 중간시점에서 발생한다. 식(11)의 선행블록의 저크 제한 구간의 중간시점부터 종료시점까지 이송하는 구간의 길이 L1, 후행블록의 시작시점부터 저크제한 구간의 중간시점까지 이송하는 거리 L2를 활용하여 ε를 식(12)와 같이 유도하였다.
| (11) |
| (12) |
식(7), 식(8), 그리고 식(12)로부터 기구학적 제한값이 코너링 오차를 결정함을 확인할 수 있다. 따라서 적절한 기구학적 제한 값을 선정하여 코너에서의 정밀도를 조정할 수 있다. Amax 및 ΔVmax를 증가시키면 가감속에 필요한 시간이 단축되어 사이클 타임이 저감되지만 코너링 오차가 증가한다. τFIR이 증가하면 코너링 오차가 증가한다. 블록 중첩의 효과로 인하여 τFIR의 증가가 사이클타임에 미치는 영향은 저감된다.
3. 파트프로그램 내 가공구간별 코너링 오차 제한
파트프로그램은 황삭 및 정삭 등 여러 가공전략을 포함할 수 있다. 따라서 파트프로그램 내에는 신속한 재료 제거가 중요한 구간, 정밀한 가공이 요구되는 구간 등이 존재할 수 있다. 그러므로 파트프로그램 전체에 대하여 동일한 기구학적 제한값을 적용하기보다는, 가공전략에 적합하게 기구학적 제한값을 변경하는 것이 유리하다. 본 장에서는 황삭구간, 정삭구간을 구분하여 각각 코너링 오차 제한 εr, εf을 만족하는 기구학적 제한값을 적용하는 방법에 대하여 제안한다.
먼저, 파트프로그램을 여러 개의 가공구간으로 구분하여야 한다. 본 논문에서는 급이송 블록 사이의 절삭이송 블록들의 묶음을 가공구간이라고 정의하였다. 또한 공작물의 최종형상을 결정하는 가공구간을 정삭구간으로 정의하였다. 최종형상을 결정하지 않는 가공구간은 모두 황삭구간으로 정의하였다.
Fig. 2는 급이송, 직선보간, 원호보간, 공구교체를 포함하는 예시이다. 공구는 급이송으로 하강하여 사각형을 가공하고, 다시 급이송 이후 원을 가공하고, 급이송으로 원점으로 복귀한다. 공구교체 후 다시 급이송, 사각형 가공, 급이송, 원 가공, 급이송 원점 복귀를 수행한다. 본 논문의 가공구간에 대한 정의를 따르면, 급이송 사이의 연속된 절삭이송 블록의 묶음이 총 4개의 가공구간으로 나타난다. 또한 주어진 예시에서는 같은 Z축 높이에서 상대적으로 안쪽에 위치한 경로가 최종형상을 결정한다고 할 때, 가공구간 #1, #2는 황삭구간, 가공구간 #3, #4는 정삭구간으로 분류된다.
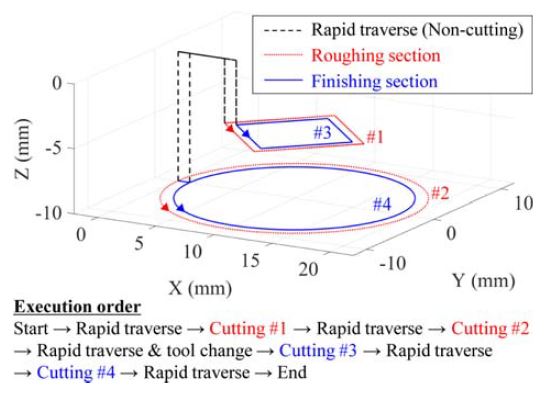
Determination of the machining section in a part program according to the cutting and non-cutting motion
분류된 황삭구간 및 정삭구간에서 각각 서로 다른 코너링 오차 제한을 적용하기 위하여 식(12)를 활용할 수 있다. 식(12)는 Fig. 1과 같이 충분히 긴 G01 직선보간 블록이 만나 형성된 직각 코너에 대한 분석 결과이다. 식(12)를 활용하여 선정한 기구학적 제한값은 짧은 블록, 원호보간 블록, 직각이 아닌 코너 등이 포함된 일반적인 경우에 대하여 코너링 오차를 엄격히 제한할 수는 없으나, 지정된 코너링 오차를 지나치게 초과하는 것은 억제할 수는 있다. 따라서 εr, εf가 포함된 코너링 오차 범위를 여러 개의 정밀도수준으로 나누고, 각 수준의 기구학적 제한 값을 식(12)를 활용하여 선정한다. 또한 각 정밀도수준이 적용된 공구경로 생성 시뮬레이션을 수행하여 가공구간마다 발생하는 최대 코너링 오차를 계산한다. 이로부터 황삭구간에서는 εr, 정삭구간에서는 εf를 초과하지 않는 정밀도수준을 선정한다. 경우에 따라서, 코너링 오차 제한이 만족되지 못한 시뮬레이션 결과가 발생할 수 있다. 이런 경우에는 기존보다 더 넓은 코너링 오차 범위에서 정밀도수준별 기구학적 제한값을 재선정하는 상기 과정을 반복하여야 한다.
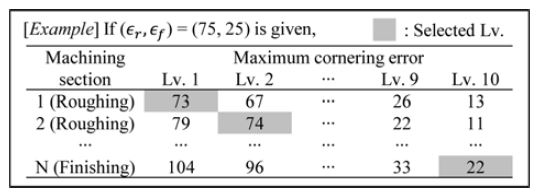
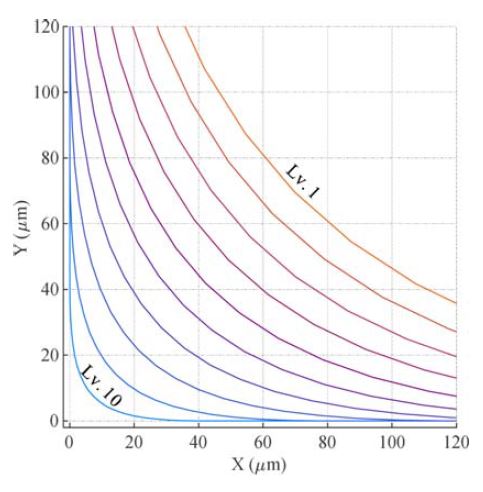
Fig. 3은 εr, εf가 각각 75, 25 μm까지 허용되는 예시이다. Table 1과 같이, εr, εf를 포함하는 10 μm부터 100 μm의 범위를 10개의 정밀도수준으로 나누고, 각 수준별 기구학적 제한값을 선정하였다. 각 정밀도수준을 적용하였을 때 발생하는 가공구간 마다의 최대 코너링 오차를 공구경로 생성 시뮬레이션으로부터 계산하였다. 이로부터 εr, εf를 초과하지 않는 정밀도수준을 가공구간마다 별도로 적용할 수 있다. 사이클타임의 저감을 위하여 코너링 오차 제한이 만족되는 가장 낮은 정밀도수준을 적용하여야 한다.
4. 공구경로 생성 시뮬레이션을 활용한 검증
기구학적 제한 및 코너링 오차 사이의 관계식 식(12)의 검증을 위하여 공구경로 생성 시뮬레이션을 활용하였다. 공구경로 생성 시뮬레이션은 C++ 언어로 작성하였다. Fig. 4는 Table 1의 정밀도수준마다 생성된 공구경로이다. Table 2는 직각 코너에서 식(12)를 활용하여 예측한 코너링 오차와 공구경로 시뮬레이션으로 계산한 코너링 오차를 비교한 표이다. 코너링 오차 예측정확도는 97% 이상으로, 식(12)를 코너링 오차 예측과 기구학적 제한값 선정에 활용될 수 있음을 확인하였다.
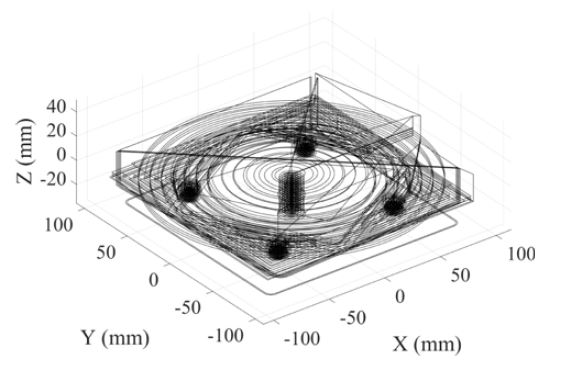
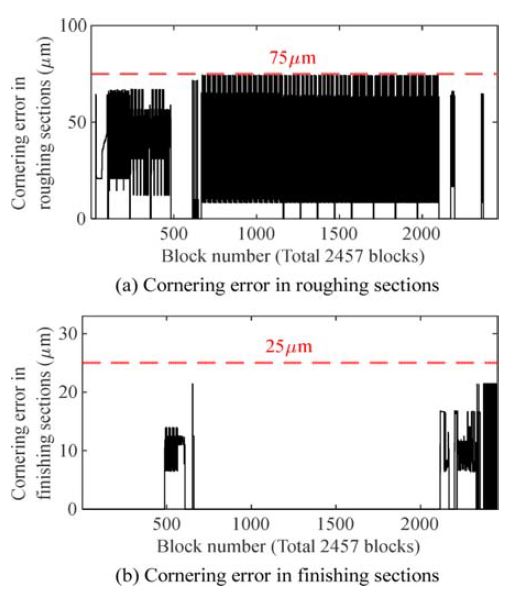
또한 ISO 10791-7:2020 M1-160에 지정된 표준 시편 형상[4] 가공용 파트프로그램에 대하여 가공구간마다 다른 기구학적 제한값을 지정하는 방법을 검증하였다. Fig. 5는 파트프로그램에서 지령한 경로이며, G00 급이송, G01 직선보간, G02/03 원호보간 등 총 2,457개의 블록을 포함한다. 파트프로그램 내 황삭구간과 정삭구간은 각 구간의 최종형상 결정 여부를 확인하여 수작업으로 구분하였다. 황삭구간은 18개, 정삭구간은 14개였다. εr은 75 μm, εf는 25 μm로 지정하였다.
코너링 오차를 제한하기 위하여 공구경로 생성 시뮬레이션을 활용한 기구학적 제한값 선정 기법을 적용하였다. Table 1의 기구학적 제한값을 활용하여 코너링 오차를 제한한 결과를 황삭구간 및 정삭구간에 대하여 Figs. 6(a), 6(b)에 각각 표시하였다. Fig. 6(a)와 같이 황삭구간에는 75 μm의 코너링 오차 제한을 초과하지 않도록 정밀도수준 1, 2, 5, 6이 사용되었다. Fig. 6(b)와 같이 정삭구간에서는 정밀도수준 9, 10이 적용되어 코너링 오차 제한 25 μm를 만족함을 확인하였다. 황삭구간, 정삭구간마다 별도로 정밀도수준을 적용하여 주어진 코너링 오차 제한 εr, εf가 각각 만족되었음을 확인하였다.
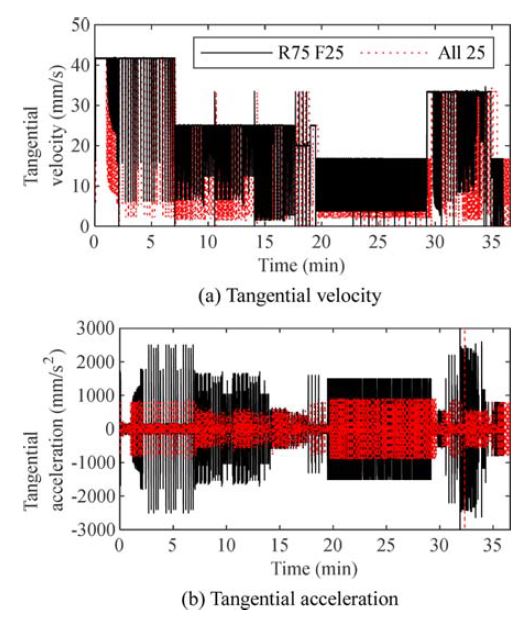
또한, 제안한 방법과, 파트프로그램 전체에 대하여 εf만을 적용하는 경우를 비교하였다. 제안한 방법이 적용된 경우, 접선방향 속도가 상대적으로 높게 유지되고 있음을 Fig. 7(a)에서 확인할 수 있다. 또한 제안한 방법이 적용되었을 때 접선방향 가속도의 크기가 상대적으로 큼을 Fig. 7(b)에서 확인할 수 있다. 제안한 방법을 적용하여 황삭구간에서 높은 접선방향 가속도를 사용하면 사이클타임의 저감이 가능하다. 제안한 방법을 적용한 경우 36분 1초, εr, εf 구분 없이 전체 파트프로그램에 25 μm의 코너링 오차 제한을 적용한 경우 36분 35초의 사이클타임이 소요되었다. 따라서 제안한 황삭 및 정삭구간에 대한 코너링 오차를 개별 적용하는 방법을 활용하여 사이클타임이 저감됨을 확인하였다.
5. 결론
본 논문에서는 코너링 오차에 따른 기구학적 제한값을 선택하는 방법을 제안하였다. 코너링 오차가 각 축별 가속도 및 코너에서의 허용 속도 차와 같은 기구학적 제한을 변수로 갖는 일반화된 함수로 표현될 수 있음을 확인하였다. 유도한 관계식을 활용하여 97% 이상의 정확도로 직각 코너에 대한 코너링 오차를 예측하였다. 공구경로 생성 시뮬레이션을 활용하여 지정된 코너링 오차 제한을 초과하지 않는 기구학적 제한값을 가공구간마다 적용하였다. 또한 제안한 방법을 활용하여 사이클타임 저감이 가능함을 확인하였다.
Acknowledgments
본 연구는 산업통상자원부의 기계장비산업기술 개발사업(20000285, 장비제어공정 통합 가상공작기계 기술 및 이에 기반한 공작기계 지능화 원천기술 개발)의 지원으로 수행되었다.
REFERENCES
-
Yu, B.-F., Chen, J.-S., (2020), Development of an analyzing and tuning methodology for the CNC parameters based on machining performance, Applied Sciences, 10(8), 2702.
[https://doi.org/10.3390/app10082702]

-
Ward, R., Sencer, B., Jones, B., Ozturk, E., (2021), Accurate prediction of machining feedrate and cycle times considering interpolator dynamics, The International Journal of Advanced Manufacturing Technology, 116(1), 417-438.
[https://doi.org/10.1007/s00170-021-07211-2]

-
Lee, C.-Y., Hwang, S.-H., Min, B.-K., (2022), Simulation-based optimization of CNC interpolator parameters for machining accuracy improvement, The International Journal of Advanced Manufacturing Technology, 119, 3757-3770.
[https://doi.org/10.1007/s00170-021-08434-z]

- ISO 10791-7, (2020), Test conditions for machining centres-Part 7: Accuracy of finished test pieces.

Ph.D. candidate in the School of Mechanical Engineering, Yonsei University. His research interests are CNC interpolation and machine tool simulation.
E-mail: hwang.soonhong@yonsei.ac.kr

Ph.D. candidate in the School of Mechanical Engineering, Yonsei University. His research interests are CNC interpolation and reinforcement learning.
E-mail: sangwon.kang@yonsei.ac.kr

Senior researcher in the Korea Institute of Machinery & Materials. His research interests are CNC interpolation and digital twin simulation.
E-mail: cylee@kimm.re.kr

Professor with the School of Mechanical Engineering, Yonsei University. His research interests include machine tool control, precision manufacturing processes and intelligent manufacturing systems.
E-mail: bkmin@yonsei.ac.kr