강 파이프의 고주파 전기저항 용접공정에 대한 수치 해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The high-frequency electric resistance welding (HF-ERW) process is widely used in the steel pipes production because it can weld at a high speed, has excellent weldability, and attains clean and precise shapes. However, for process improvement, analytic studies on electromagnetic field and temperature distributions, and selection of appropriate process variables are required. In this study, finite element analysis models that can analyze the electromagnetic field distribution and temperature distribution in the HF-ERW of a steel pipe were proposed, in consideration of the characteristics of the process, including electromagnetic phenomena localized to the workpiece surface and fast welding speed. By applying the proposed analysis models, changes in current density, magnetic flux density, generated heat density, and fused width in the pipe could be predicted according to changes in process variables such as the V angle of the strip, the electrode position, and the source voltage. Through comparison with the analysis and the limited-case experiment, the analysis result predicted the actual fused width fairly well, and the validity of the proposed model could be verified.
Keywords:
High frequency electric resistance welding, Electromagnetic field, Temperature distribution, Numerical anaysis키워드:
고주파 전기저항 용접, 전자기장, 온도 분포, 수치 해석1. 서론
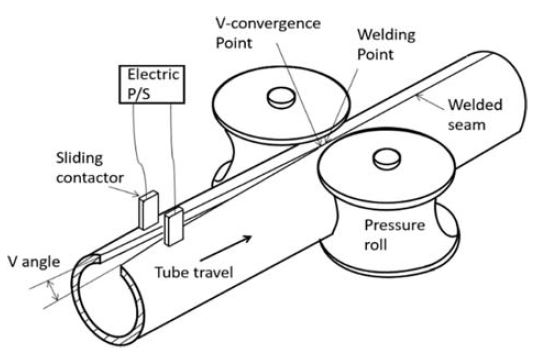
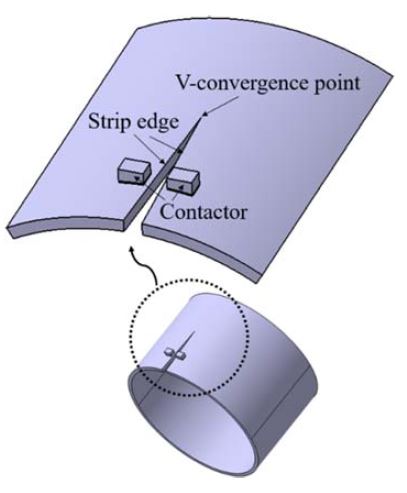
고주파 전기저항용접(High Frequency Electric Resistance Welding, HF-ERW)에서는 Fig. 1에 보인 바와 같이 원통형으로 성형된 대강(Skelp)을 V자 형태로 공정 위치에 진입시키고, 진입하는 접합부 주위에서 접촉 전극(Sliding Contactor)을 통해 고주파 전류를 인가하여, 대강의 모서리(Edge) 표면이 서로 만나는 V-수렴점(Convergence Point)인 용접 위치(Welding Point)의 표면을 국부적으로 가열하게 한다. 국부적으로 가열된 파이프가 이송되어 압착롤(Pressure Roll)의 위치에서 압착력이 가해지면 표면의 용융 가열부는 산화물과 함께 배출되고 접합부는 고상 압접이 된다. 이와 같은 고주파 전기저항용접 공정은 빠른 속도로 용접이 가능하고 용접부의 강도와 인성이 높으며 용접부가 청정한 표면과 정확한 형상 치수를 갖게 되어, 중소 구경의 강파이프(Steel Pipe) 제작에 널리 적용되고 있다[1,2]. 한편, HF-ERW에 의한 강 파이프 제조 공정은 300 kHz 이상의 고주파 전류를 이용하므로 표피효과(Skin Effect)가 발생하고, 전극에서 용접 위치로 근접할수록 대강의 두 모서리 표면 사이 거리가 점점 가까워져 고주파 전류에 의한 근접효과(Proximity Effect)가 크게 나타나는 특징을 갖고 있다[3]. 따라서 용접 위치에 가까워지면 표피효과와 근접효과가 중첩되어 전류 흐름이 대강 모서리 표면에 밀집되며 이로 인한 저항 열로 모서리 표면 부분이 집중적으로 가열된다[4]. 이 과정에서, 모서리 표면에 작용하는 전자기력에 의한 접합부의 청정 효과와 압착롤의 가압에 의한 산화물 배출 효과는 우수한 용접부를 얻기 위해 매우 중요한 현상이고, 이는 접합부에서의 적정한 가열 여부에 따라 영향을 받게된다.
HF-ERW 공정에서 용접부의 품질과 신뢰성을 향상하기 위하여 용융부 표면에서 형성되는 금속 산화물의 배출과 잔류에 관련한 연구가 다수 수행되었다. 용접부의 입열량이 낮은 경우에는 두께 방향 표면이 충분히 용융되지 못하는 냉접 결함이 발생하고, 입열량이 너무 높은 경우에는 산화물이 접합부에 잔존하는 침입 결함이 발생하게 된다[5-7]. 용접 입열량이 적정 크기보다 과대하게 증가함에 따라 V-수렴점과 용접 위치가 분리되고 두 위치 사이의 접합 면에는 좁은 간극(Narrow Gap)이 존재하게 되어, 여기에서 산화물을 포함한 표면 금속의 배출과 침입현상이 나타나게 된다[4]. 이와 같은 현상은 주로 고속 카메라 등을 활용한 실험적 방법으로 규명되어져 왔으며, HF-ERW 공정에서 발생하는 용접 현상에 대한 해석적 규명을 시도하여 공정을 단순화하고 전자기장에 관한 간이화된 해석식을 유도하고 전류밀도와 자속밀도 그리고 전자기력을 해석하여 활용한 사례가 있다[8]. 전극과 용접 위치를 하나의 평면에 두고 2차원 유한 요소해석법으로 전기자기장과 열전도 해석을 하여 용접 현상을 규명하고자 하였고[9], 전자기장 및 온도 분포에 관한 수치해석 모델로서 용융 금속과 산화물의 거동에 미치는 용접 조건의 영향을 규명하고자 하였다[4,10].
HF-ERW 공정의 이론적 해석에 대한 시도가 다수 있었음에도 불구하고, 자기장 분포 및 온도 분포에 관한 3차원적 해석 연구와 이를 통한 적정 공정 변수의 선정에 관한 연구는 미흡하다고 할 수 있다. 이는, 구조물에 비해 가열부의 깊이가 매우 좁고 가열 범위가 국부적인 공정의 특징으로 인해 해석 기법의 적용에 어려움이 있기 때문으로 판단된다. 그럼에도, 소재 표면에 국한하여 나타나는 전자기적 현상과 빠른 용접 속도 등 공정이 갖는 특징을 활용하면 해석 범위를 크게 축소한 해석 모델의 제시가 가능할 수 있다.
본 연구에서는 강 파이프의 HF-ERW 공정에서 전자기장 해석을 위해 임피던스 경계조건을 활용한 유한요소해석 모델을 제시하여 공정 변수의 변화에 따라 용접부 주위에 나타나는 전류밀도 분포, 자속밀도 분포, 발열량을 구하였고, 공정의 열전달 해석을 위한 유한요소해석 모델을 제시하여 전자기장 해석에서의 발열량을 열원으로 용접부에서의 온도 분포를 해석하였다. 제한된 경우의 실험 결과와 비교하여 제안된 모델의 타당성을 검증하였다.
2. 전자기장 및 온도 분포 해석
2.1 전자기장 해석 모델
HF-ERW 공정에서는 대강 소재에 고주파 교류 전류가 인가되며 이로 인해 와전류가 생성되는 전자기장 현상이 발생하게 되고, 전류의 전기저항에 의해 발생하는 열을 용접 열원으로 이용하게 된다. 이때의 전자기장 현상을 묘사하는 모델은 맥스웰 방정식으로부터 유도하여 다음과 같은 방정식으로 나타낼 수 있다[11].
| (1) |
| (2) |
여기서, μ는 투자율, 는 자기 벡터 포텐셜, σ는 전기전도도, 는 전원 전류밀도, 는 와전류밀도, 는 전기장의 세기이다.
식(1)에서 를 구하고, 이를 이용하여 식(2)에서 와전류를 구할 수 있다. 따라서, 소재에 인가된 전원 전류와 이로 인해 생성된 와전류에서 소재에 발생하는 줄열(Joule Heat), q는 식(3)과 같이 나타낼 수 있다.
| (3) |
방정식(1)에 대한 해는 유한요소해석 등 수치해석적 방법으로 구할 수 있고, 식(3)의 줄열을 구하면 이는 열전달 해석에서의 입력 열원인 발열량이 된다.
한편, HF-ERW에서 활용하는 300 kHz 이상의 고주파 전원과 강 소재의 경우, 침투깊이는 대략 0.0065 mm 이하 크기로 예측된다[12]. 따라서 표면을 제외한 소재 내부 영역에서는 전자기장이 존재하지 않는다고 가정할 수 있고, 줄열은 대부분이 소재 표면에서 발생한다고 판단할 수 있다. 이러한 문제에서는 표면 임피던스 경계조건(Surface Impedance Boundary Condition, SIBC)을 적용하면 시간과 용량을 크게 줄여 해석할 수 있다[12,13].
Fig. 2는 해석에 사용된 강 파이프 모델로서 대강 소재와 두 전극으로 구성된 기하학적 형상을 보이고 있다. 대강의 두 모서리 표면이 서로 만나는 V-수렴점과 용접 위치는 동일하다고 가정하고 전자기 현상은 용접부 주위에 국한하여 나타나므로, 전체 길이가 400 mm인 파이프를 대상으로 파이프의 중심에서 용접선을 기준으로 ±30o 이내를 해석 영역으로 설정하였다.
파이프 끝에서 전극 중심까지는 80 mm, 전극에서 용접 위치까지는 130 mm로, 전극 단면은 가로 22 mm, 세로 30 mm의 사각형으로, 전극 중심 간은 58 mm로, 파이프와 전극 사이 간극은 0.1 mm로 전극의 크기와 상대 위치를 각각 설정하였다. 한편, 파이프 모델로부터 일정 거리로 이격된 공간 위치까지는 전자기장의 영향이 발생한다고 가정하고 그 내부는 공기층으로 설정하였다.
용접 공정을 모사하기 위한 전기 회로는 전압이 공급되는 좌측 전극, 좌측 전극과 파이프 표면 사이의 좌측 공극, 파이프, 우측 공극, 우측 전극 등의 요소로 구성되고, 전극의 상부 표면에 주파수 320 kHz의 전압이 인가된다. 고주파수의 특성을 이용하여, 전극과 파이프는 표면 임피던스 경계를 가진 전도체로 가정하였다. 강재의 비투자율은 300, 전기 저항은 0.5 × 10-6 Ω로, 전극의 비투자율은 1, 전기 저항은 1.72 × 10-8 Ω로 각각 일정하다고 가정하였다. 전극이 파이프와 접촉되는 공극에서의 접촉 저항은 10-4 Ω로 가정하였다.
2.2 온도 분포 해석 모델
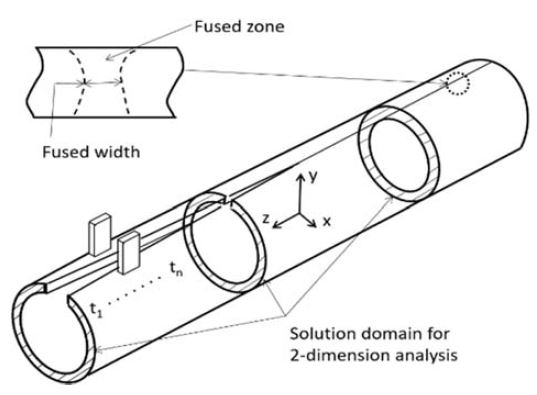
전자기장 해석에서 산출된 발열량 분포를 열원으로 하여, HF-ERW 공정 중 파이프의 온도 분포를 해석하였다. 이때, 파이프의 이송 속력이 열전도보다 매우 빠르다면 파이프의 이송 방향(z축 방향)으로 열전도가 없다고 가정할 수 있다. 이에 따라, Fig. 3과 같이 시간의 변화에 따라 변화되는 해석 영역이 나타나 있듯이, x−y축 해석 단면을 파이프의 진행 속도에 의한 시간 변화(t1, t2, ..., tn)에 따라 변형하면서 z축 방향 위치의 해당 발열량을 열원으로 하는 2차원 과도상태로 공정을 모델화하고 온도분포 해석을 수행할 수 있다. 2차원 해석영역에서 시간 변화에 따른 과도상태의 열전달 지배방정식은 다음과 같다.
| (4) |
여기서, T는 온도, k는 열전도 계수, Qi는 발열량, ρ는 밀도, ci는 비열, t는 시간이고, 초기조건은 상온으로 설정할 수 있다.
경계조건은 다음과 같은 표면에서의 대류 조건을 사용하였다.
| (5) |
여기서, n은 경계면에 수직한 방향 벡터, h는 대류 계수, Ta는 대기 온도, Ts는 경계면 온도이다.
파이프의 온도 분포 해석에서는 전자기장 해석과 동일한 기하학적 모델을 적용하였다. 용접 속도는 파이프 이송 속도인 220 mm/s로 설정하였고, 밀도, 비열, 열전도도 등 파이프 소재의 열적 물성치는 온도변화에 따라 변화되는 특성을 고려하였다[14].
2.3 유한요소해석
두께 15.4 mm의 X65 급 대강 소재로써 외경 609.6 mm, 내경 578.8 mm의 파이프를 제작하는 공정에 대한 전자기장 및 온도 분포에 관한 모델을 유한요소해석 모델로 구현화하였다.
전자기장 유한요소해석 모델의 해를 구하기 위해서 상용소프트웨어인 FLUX3D를 사용하여 3차원 정상상태 AC 해석을 수행하였다[15]. 해석영역은 용접부 주위는 크기를 줄여 분할하여, 특히 V-수렴점 주위에서 0.01 mm 크기로 사면체 요소 약 450,000개의 요소로 분할하였다.
공급 전압, 전극 거리(전극에서 V-수렴점 위치까지의 거리), 대강 V 각도 등의 변화에 따른 공정 현상을 해석하고자 하였고, Table 1은 입력 변수의 변화를 보여 주고 있다. 공급 전압의 변화에 대한 해석에서는 전극 거리와 대강 각도를 각각 130 mm와 6o로, 거리 변화의 해석에서는 전압과 각도를 각각 240 V와 6o로, 각도 변화의 해석에서는 전압과 거리를 각각 240 V와 130 mm로 일정하게 두고 해석하였다.
전자기장 해석에서는 전류밀도, 자속밀도, 발열량 분포를 계산하여 용접부에서의 전류 밀집 효과를 분석하고, 소재 표면에 작용하는 자속밀도의 크기를 파악하며 온도 분포 해석을 위한 열원을 도출한다.
HF-ERW에서 파이프의 온도 분포에 대한 유한요소해석 모델의 해는 상용소프트웨어인 ABAQUS를 활용하여 구하였다[16]. 해석 영역의 분할은 사각형 요소를 사용하였으며 접합부 부근에는 조밀하게 하여 전체 27,480개 요소로 분할하였다.
강관의 3차원 정상상태 전자기장 해석으로 먼저 발열량을 구하고, 각 위치에서의 발열량을 이용하여 파이프 길이 방향 각 2차원 단면에서의 천이 과정 온도 분포 해석을 수행하였다. 이를 위해, 해석영역 내의 파이프 단면 형상을 시간에 따라 변형하여 파이프 이송에 따라 모서리 간격이 줄어들어, 모서리가 접합되는 V-수렴점 위치의 형상에 도달하게 될 때까지의 열전달 과정을 모사하여 해석하였다. 온도 해석 결과 분석을 위해, 용접부에서 용융 온도 이상에 도달하는 크기를 추출하였으며 두께 중앙부의 폭을 용융 폭으로 나타내었다.
3. 결과 및 고찰
3.1 전자기장 해석
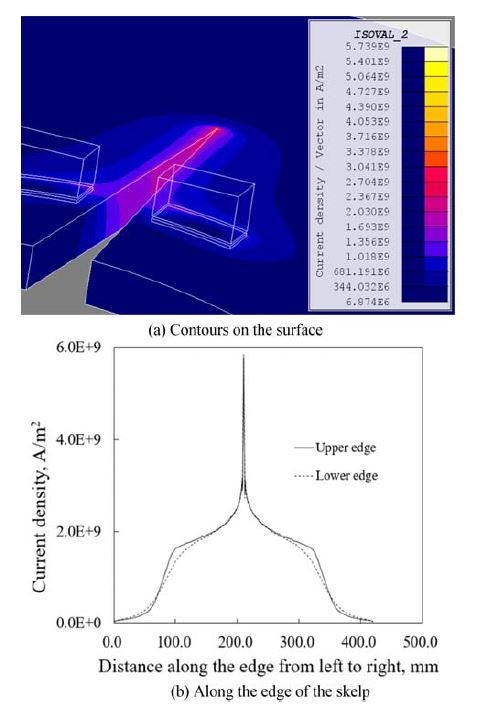
Fig. 4는 파이프의 전류밀도(Current Density)에 대한 해석 결과를 보여 주고 있다. Fig. 4(a)는 두 전극과 대강 소재 표면에 나타난 전류밀도 분포를 보이고 있다. 소재 모서리 표면에서 전류밀도가 소재 두께에 걸쳐 대칭적 분포를 보이며, 용접 위치에 근접할수록 크기가 증가하는 것을 알 수 있다.
Fig. 4(b)는 대강 소재의 한쪽 끝에서 다른 쪽 끝까지 상부 모서리를 따르는 경로 그리고 하부 모서리를 따르는 경로의 각각에 대하여 전류밀도를 나타내고 있다. 주위에 좌측 전극이 존재하고 있는 80 mm 근방에서 전류밀도가 크게 증가하고, 용접 위치라고 할 수 있는 V-수렴점 근방에서는 전류밀도가 급격히 증가하고 있다. 우측 전극이 존재하는 340 mm 근방에서부터 전류밀도는 감소하게 된다. 용접부 주위에서의 급격한 증가는 고주파 전류가 반대 방향으로 흐르는 두 표면이 매우 근접해, 표피효과에 더하여 근접효과가 뚜렷하게 나타나는 결과로 판단된다. 모서리 간격이 어느 정도 벌어져 있는 V-영역에 비하여 용접 위치에서 전류가 표피로 2배 이상 더 밀집되고 있다. 전극은 소재의 외부 표면에서 위치하고 있으나, 전류밀도 분포는 상부와 하부모서리에서 유사하게 나타나고 있다. 전류밀도의 분포로 인하여 자속밀도 분포와 발열량 분포도 유사한 형태로 나타나게 된다.
Fig. 5는 전극에 인가하는 입력 전압의 크기를 220 V에서 300 V까지 변화하는 경우, V-수렴점에서, 소재 두께 방향에 분포하는 전류밀도, 자속밀도(Magnetic Flux Density), 발열량(Generated Heat Density)의 변화를 나타내고 있다. 여기서 두께 방향은 파이프 소재의 외면에서 내면까지의 반경 방향을 나타낸다. 모든 결과에서 두께 중앙에서는 대체로 일정한 분포를 보이나, 소재의 표면과 이면에 해당하는 가장자리에서 크기가 급격히 증가하고 있다. 전압이 증가할수록 전류밀도, 자속밀도, 발열량은 비례적으로 증가하고 있으며 가장자리에서의 비례 폭이 중앙부보다 더 크게 나타나고 있다.
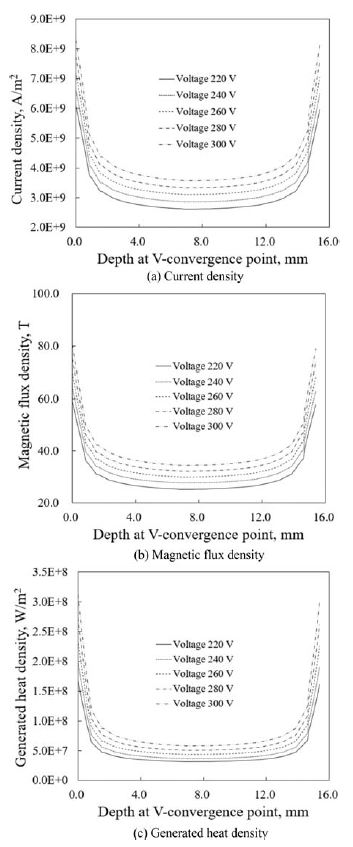
Results of the analysis along the thickness of workpiece at V-convergence point with change of input source voltage
발열량은 소재에 흐르는 전류의 제곱에 비례하는 크기를 가지므로 발열량의 분포는 전류밀도의 분포와 유사하게 된다. 발열량 분포로서는 용접 위치에서 소재의 두께 방향 중심부보다 외면과 내면에서 가열이 크게 발생하게 되는 것을 예측할 수 있다.
공급 전압에 의해 양 전극 사이에 흐르는 전류는 전압의 변화에 따라 Table 2와 같이 계산되었다. 이는 전압에 비례하며 소재 표면에서의 임피던스와 와전류에 의해 결정된 크기로 판단된다.
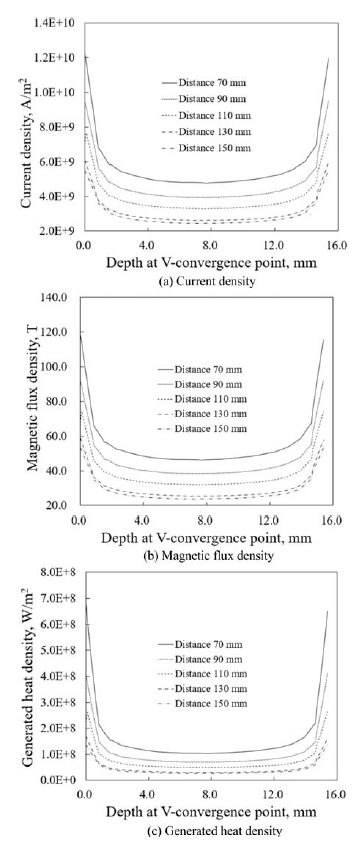
Fig. 6은 전극과 용접 위치 사이의 거리 변화에 따라 V-수렴점에서 소재 두께 방향에 분포하는 전류밀도, 자속밀도, 발열량의 변화를 보여 주고 있다. 두께의 중앙부에서는 일정한 크기를 나타내고, 가장자리에서는 크기가 급격하게 증가하고 있다. 거리가 근접할수록 전류밀도가 크게 증가하고 있고, 자속밀도와 발열량도 이에 비례하는 형태로 나타나고 있다. 이는 거리가 증가할수록 전기저항이 증가하고, 이로 인해 전류가 감소하고, 자속의 감소와 이로 인한 와전류의 감소 등에 기인한 결과로 판단된다. 특히 용접 위치 부근에서의 감소가 크게 나타나고 있다. 한편, 거리가 130 mm 이상에서는 거리에 의한 효과가 크게 줄어들고 있다.
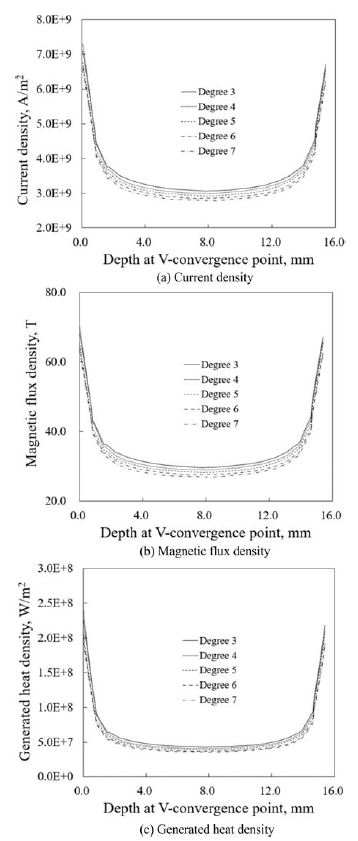
Fig. 7은 대강 소재가 용접 위치로 진입하는 각도의 변화에 따라, 용접 위치에서의 소재 두께 방향으로 나타낸 전류밀도, 자속밀도, 발열량 분포를 보여주고 있다. 전류밀도는 소재의 두께에 걸쳐 대체로 일정하게 나타나나, 외면과 내면 주위에서는 매우 크게 나타나고 있고 두께 중심을 기준으로 외부와 내부가 대칭적 분포를 보이고 있다. 대강의 진입각도가 작아질수록 전류밀도가 크게 나타나고 있다. 자속밀도와 발열량의 분포는 두께 방향으로의 분포, 그리고 대강의 진입각도 등의 변화에 대하여 전류밀도의 분포와 유사한 형태를 나타내고 있다.
3.2 온도 분포 해석
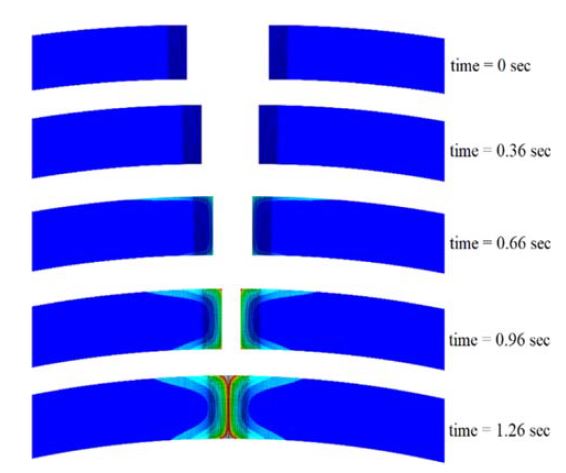
파이프의 단면을 파이프의 이송에 따라 변형하면서 2차원 과도상태 온도 분포 해석을 수행한 결과, 파이프 소재 두께 방향에 나타나는 온도 분포를 시간변화에 따라 얻을 수 있었다. Fig. 8은 파이프의 이송 속력을 고려한 시간의 경과에 따라 단면의 형상이 변화되고 단면 내의 온도 분포가 변화되는 현상을 보여주고 있다. 대강의 모서리는 용접 위치로 근접될수록 간격이 좁아지고 용접 위치에서는 두 모서리가 접합된 상태를 보여 주고 있다. 대강이 용접 위치로 근접할수록 단면 내의 온도가 높아지는 분포 상태를 나타내고 있다.
Fig. 9는 용접된 소재의 두께 방향에서 실제 용접부의 한 쪽과 이에 해당하는 해석의 결과를 동시에 보여 주고 있다. 공급전압이 240 V, 전극과 용접 위치 사이 거리가 130 mm, 대강의 진입 각도를 6o, 파이프의 이송 속도를 220 mm/s로 수행한 용접결과를 비교하였다.
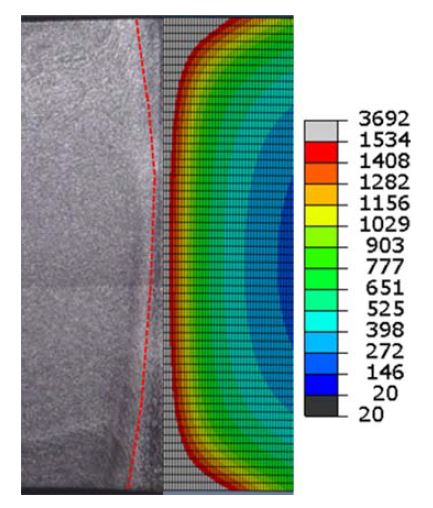
Comparison between actual welded surface and predicted temperature distribution of the model surface
결과에서 위는 파이프 소재의 외부 표면, 아래는 내부 표면에 해당한다. 두께의 중앙부에서 실제 용융 반폭은 0.3 mm이고, 해석 결과의 용융 반폭은 0.2 mm로 유사하게 나타나고 있다. 그러나 두께의 가장자리 부분인 파이프의 외면과 내면에서는 실제와 예측의 결과에서 차이가 발생하고 있다. 실제 용접부는 압축롤에 의한 업셋을 기계 가공하여 제거한 후의 결과이고, 해석에서는 전자기력에 의한 소재 밀착 현상과 업셋에 의한 용융부의 유동을 고려하지 않은 결과이다. 이로써 가장자리 부근에서의 결과에서는 다소 차이가 발생한 것으로 판단된다.
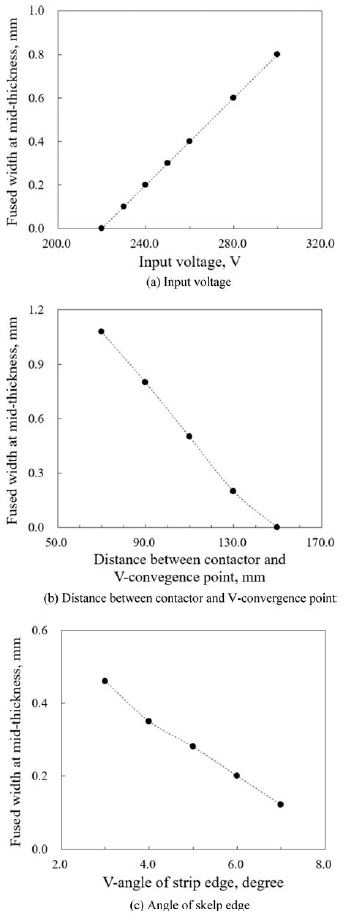
Fig. 10은 유한요소해석으로 예측한 용접 조건에 따라 V-수렴점에서 두께 중앙부 용융 폭의 변화를 나타내고 있다. Fig. 10(a)는 전극에 인가하는 입력 전압을 220 V 조건에서 300 V 조건까지 변화할 때 용융 폭의 변화로, 0-0.8 mm까지 비례적으로 증가하고 있음을 보여 주고 있다.
Fig. 10(b)는 전극의 위치가 용접 위치로부터 70 mm 이격된 조건에서 140 mm 이격된 조건까지 변화한 경우, 용융 폭의 변화가 1.08 mm에서 0 mm로 나타나고 있다. 특히 70-130 mm까지는 용융 폭은 거리 변화에 비례적으로 감소하고, 거리가 150 mm인 경우는 용융부가 나타나지 않았다. 거리에 따른 용융 폭의 변화는 전자기장 해석에서 나타난 거리에 따른 전류밀도와 발열량의 분포로써 경향성을 유추할 수 있다.
Fig. 10(c)는 용접 위치로 진입하는 대강의 진입각도가 3o인 조건에서 7o인 조건까지 변화할 때 용용지 폭은 0.46 mm에서 0.12 mm로 비례적으로 축소되고 있다. 이는 전자기장해석의 결과에서 예측된 바와 같이 대강 모서리의 진입 각도가 커질수록 전류밀도와 이와 인한 발열량이 작아지는 결과에 기인한다고 판단할 수 있다.
4. 결론
강 파이프의 고주파 전기저항용접 공정에서 공정의 특성을 고려하여 전자기장 분포와 온도 분포를 해석할 수 있는 유한요소해석 모델을 제안하였다. 제안된 해석 모델을 적용하여 공급전원의 크기, 용접 위치로부터의 전극 위치, 용접 위치로의 소재진입 각도 등 공정 변수의 변화에 따른 용접부에서의 전자기장 및 온도 분포를 해석하고, 용융 폭의 변화를 예측하였다. 입력 전압을 220 V에서 300 V까지 변화할 때 용융 폭은 0-0.8 mm까지 비례적으로 증가되었고, 전극의 위치를 용접 위치로부터 70 mm 이격에서 140 mm 이격까지 변화한 경우 용융 폭은 1.08 mm에서 0 mm로 변화되었으며, 대강의 진입각도가 3o에서 7o까지 변화할 때 용용 폭은 0.46 mm에서 0.12 mm로 비례적으로 축소되었다. 제안된 해석 모델은 파이프 제작 과정에서 적정한 가열 크기, 재료적 열화와 변형의 최소화 등 공정의 최적화를 위해 효과적으로 활용되고, 추후 용접부 주위에 나타나는 금속유동의 규명에도 활용될 것으로 판단된다.
NOMENCLATURE
| μ : | Permeability |
| : | Magnetic Vector Potential |
| σ : | Electric Conductivity |
| : | Source Current Density |
| : | Eddy Current Density |
| : | Electric Potential |
| T : | Temperature |
| Qi : | Generated Heat |
| t : | Time |
REFERENCES
-
Tian, P., Xu, K., Lu, G.-P., Qiao, G.-Y., Liao, B., Xiao, F.-R., (2018), Evaluation of the mechanical properties of the X52 high frequency electric resistance welding pipes, International Journal of Pressure Vessels and Piping, 165, 59-67.
[https://doi.org/10.1016/j.ijpvp.2018.06.006]

- Kim, Y., (1998), High-frequency electrical resistance welding of pipes, Journal of Korean Welding Scociety, 16(5), 45-47.
- Jang, S., Seo, J., Kim, H., Lee, J., (1997), Analysis of the skin effect on the coil with high frequency current source, Proceedings of the Korean Institute of Electrical Engineers Conference, 288-290.
- Haga, H., Aoki, K., Sato, T., (1980), Welding phenomena and welding mechanisms in high-frequency electric resistance welding-1st report, Welding Journal, 59(7), 208s-212s.
- Kang, D. I., Choi, J. H., Jang, Y. S., Kim, Y. S., (1998), Analysis of high frequency electric resistance welding phenomena using high speed cinematography, Journal of Korean Welding Scociety, 16(2), 29-36.
- Kim, C. M., (2009), Defect occurrence mechanism and fatigue crack propagation behavior in high frequency electric resistance weld joint, Ph.D. Thesis, Hanyang University.
-
Kim, C.-M., Kim, J.-K., (2009), The effect of heat input on the defect phases in high frequency electric resistance welding, Metals and Materials International, 15(1), 141-148.
[https://doi.org/10.1007/s12540-009-0141-5]

- Lee, J. Y., Kim, S. S., Yoo, C. D., (2001), Analysis of high frequency resistance welding, Journal of Korean Welding Scociety, 19(3), 23-26.
-
Okabe, T., Yasuda, K., Nakata, K., (2016), Dynamic observations of welding phenomena and finite element analysis in high-frequency electric resistance welding, Welding International, 30(11), 835-845.
[https://doi.org/10.1080/09507116.2016.1142203]

-
Okabe, T., Toyoda, S., Goto, S., Kato, Y., Yasuda, K., Nakata, K., (2014), Numerical analysis of welding phenomena in high-frequency electric resistance welding, Key Engineering Materials, 622-623, 525-531.
[https://doi.org/10.4028/www.scientific.net/KEM.622-623.525]

- Jang, S., Seo, J., Lee, H., Hong, J., Lee, J., (1996), The skin effect and current distribution characteristics of a coil streaming with high frequency, Proceedings of the Korean Institute of Electrical Engineers Conference, 222-224.
- Hwang, S.-R., Shin, P. S., (2017), A study on the minimization of tie-plate loss of cast resin transformer using surface impedance boundary condition, The Transactions of the Korean Institute of Electrical Engineers, 66(9), 1334-1340.
-
Dumont, B., Gagnoud, A., (2000), 3D finite element method with impedance boundary condition for the modeling of molten metal shape in electromagnetic casting, IEEE Transactions on Magnetics, 36(4), 1329-1332.
[https://doi.org/10.1109/20.877684]

-
Bae, K.-Y., Yang, Y.-S., Yi, M.-S., Park, C.-W., (2018), Numerical analysis of heat flow in oxy-ethylene flame cutting of steel plate, Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 232(4), 742-751.
[https://doi.org/10.1177/0954405416654183]

- Altair, Altair flux™ 2019.1 user guide. https://blog.altair.co.kr/wp-content/uploads/2019/07/AltairFlux2019.1_NewFeatures.pdf
- Washington University in St.Louis, Abaqus/cae user's manual. https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.5/books/usi/default.htm?startat=pt01ch05s05hlb05.html

Professor in the Department of Mechanical Engineering, Chonnam National University. His research interests are in manufacturing processes.
E-mail: ysyang@chonnam.ac.kr

Professor in the School of Mechatronics Engineering, Gyeongsang National University. His research interests are in manufacturing processes and mechatronics.
E-mail: kybae9@gnu.ac.kr