자동차용 판재의 Subtle Feature의 성형 조건에 따른 곡률 반경 예측 모델에 대한 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The subtle feature is one of the characteristic lines and represents the most noticeable line in the automotive panel. In this study, we proposed a method to predict the radius of curvature of products according to the material, its thickness, its punch angle, and its punch radius. The radius of curvature was divided into three regions, namely, the non-linear, transition, and linear regions. In the non-linear region, the prediction model for the radius of curvature with different forming conditions was derived using the finite element analysis. In the linear region, the radius of curvature was assumed to be the sum of the punch radius and the thickness of the material. In the transition region, a model connecting two regions (Non-linear and linear region) was developed based on the continuity condition. The prediction model presented a very small RMSE with the value of 0.314 mm. Using the prediction model, the radius of curvature with various forming variables could be predicted and the required radius of punch, to obtain a certain value of the radius of curvature, could be precisely predicted.
Keywords:
Automotive panels, Stamping, Prediction model, Subtle feature키워드:
자동차용 부품, 스탬핑, 예측 모델, 특징 형상1. 서론
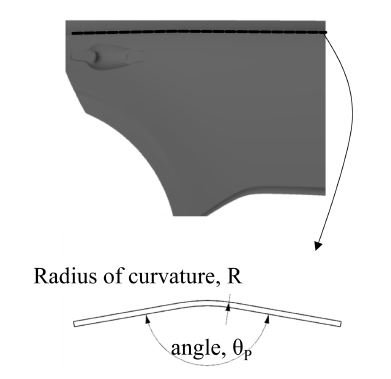
최근 자동차 외형 판재에서 형상에 대한 특징을 표현할 수 있는 특징선(Characteristic Line)의 설계의 중요성이 증대되고 있다[1]. 이와 같은 특징선 중 Subtle Feature Line은 제품의 각도가 155o 이상이며, 외측 곡률 반경이 48 mm 이하의 특징선을 의미한다. Subtle Feature Line의 개략도는 Fig. 1과 같다. 자동차용 외판재에서 이와 같은 특징선은 자동차의 외형을 평가하는데 주요 요소 중 하나이다[2].
이와 같은 최소 성형 가능 곡률 반경은 금형의 설계에 있어서 중요한 부분이다. 보통 낮은 곡률 반경의 제품을 얻기 위해 펀치의 반경을 0 mm에 가깝도록 날카로운 형상으로 가공하는 경우가 많다[3,4]. Lee et al. [1]은 비드를 사용하여 인장과 굽힘이 동시에 발생할 수 있는 Subtle Feature Line 성형 공정을 제안하였다. 해당 연구에서 펀치 반경이 0 mm로 수렴하여도 제품곡률 반경은 일정 값으로 수렴하였고, 이를 최소 성형 가능 곡률 반경으로 정의하였다. 이 결과는 자동차용 외판재의 성형 금형을 설계하는 과정에서 펀치 및 다이를 일정 곡률 반경 이하로 설계 및 가공이 불필요하다는 것을 의미한다. 또한 펀치를 매우 날카롭게 제작하는 경우, 성형 공정 중 응력 집중으로 재료의 마모 및 파손이 발생할 수 있다. 따라서 금형 설계 과정에서 제작 가능한 제품 곡률 반경과 해당하는 펀치 반경을 정확히 예측하여 설계하는 것이 필요하다.
본 연구에서는 재료 종류, 두께, 펀치 각도, 펀치 반경에 따른 제품 외측에서의 곡률 반경을 예측하는 방법을 제안하고자 한다. 일정 펀치 반경 이하에서는 해석 결과를 사용하여 다항식으로 반응 표면 모델(Response Surface Model) [5,6]을 구성하고 제품 곡률 반경을 예측하였다. 특정 펀치 반경 이상에서는 일반적인 재료의 변형 특성을 고려하여 제품 곡률 반경이 재료 두께와 펀치 곡률 반경의 합이라는 가정으로 결과를 예측하였다. 성형 후 제품의 곡률 반경이 최소 성형 가능 곡률 반경으로 수렴하는 영역과 제품 곡률 반경이 펀치 반경과 비례하는 영역 사이에서는 3차식을 구성하여, 모든 영역에서 해석 모델의 결과가 연속성을 유지할 수 있도록 하였다.
2. Subtle Feature Line의 성형 공정 및 해석 모델
본 연구에서는 Subtle Feature Line의 성형 공정을 단순화하였다. 제품을 성형하기 위한 펀치의 제작은 CNC 밀링 절삭 가공 후 표면조도계(Surface Profiler)로 가공된 펀치의 곡률반경을 측정하여 정확도를 확인하였다. 이후 일반적인 만능 성형 시험기(Universal Tensile Machine)에서 실험 가능하도록 비드를 먼저 성형하고, 제품의 최종 형상을 성형하였다. 이와 같이 비드를 먼저 성형한 후 비드 형상을 통해 재료를 고정하면 제품의 중심부에서 인장과 굽힘 성형이 동시에 발생한다. 성형된 소재의 외측 반경을 포면조도계를 통해 표면에 대한 데이터를 얻은 후 Lee et al. [7]에서 제안한 알고리즘을 이용하여 제품의 각도와 곡률 외측 반경을 측정하였다.
위 알고리즘은 다음과 같다. 첫 번째로 입력된 데이터를 총 3개의 그룹으로 구분한다. 두 번째로 구분된 그룹 중 중간 그룹을 원으로 근사시킨 후 호의 양쪽에 있는 두 개의 접선이 추정되는 방법이다.
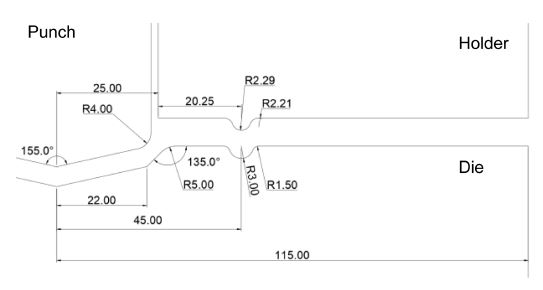
해석에서 펀치 및 다이의 치수는 실험에서와 동일하다. 펀치, 다이, 홀더 형상은 Fig. 2와 같다. 홀더는 스프링을 통해 재료와 먼저 접촉하며 이후 홀더에 스프링에 의해 압축력이 가해지고 펀치가 소재와 접촉한다. 이때, 소재는 비드 형상으로 고정되어 있으며 펀치가 하강하여 중심부의 인장과 굽힘을 발생시킨다.
Fig. 3은 펀치 각도 165o, 펀치 반경 12 mm, 두께 0.65 mm CR3 재료의 해석 결과 및 실험 결과이다. 성형 실험 및 해석 결과에서 중심부의 굽힘 각도와 곡률 반경(Radius of Curvature)을 측정하였다.
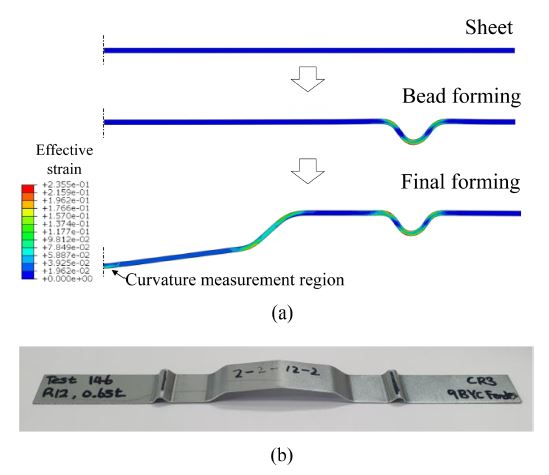
(a) Simulation results and (b) Experimental result of the subtle feature line with the punch angle of 165o, punch radius of 12 mm and CR3 material with the thickness of 0.65 mm
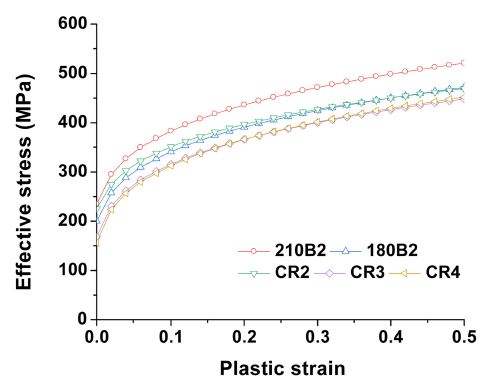
실험은 펀치각도 155, 165, 175o에 대해 진행하였다. 또한 재료는 자동차용 외판재 재료로 사용하고 있는 CR2, CR3, CR4, 180B2, 210B2에 대해 진행하였으며, 해당 재료의 유동 응력 선도는 Fig. 4와 같다. 재료 두께는 0.6, 0.65, 0.7 mm를 사용하였다.
해석은 상용 프로그램인 ABAQUS 6.14v의 Static/Implicit 코드를 사용하였다. 소재는 평면 변형률 조건을 사용하였으며 요소는 CPE4R을 사용하였다. 펀치의 경우 강체 조건으로 가정하여 Analytical Rigid를 사용하였다. 모든 재료의 탄성 계수는 207 GPa, 밀도는 7,650 kg/m3, 푸아송 비는 0.33, 등방성 경화 모델로 해석을 진행하였다.
3. 제품 곡률 반경과 펀치 곡률 반경의 관계 및 예측 방법
3.1 실험 및 시뮬레이션 결과 비교
두께 0.6 mm의 210B2 재료의 펀치각도 155o에서 펀치 반경과 제품의 곡률 반경에 대한 해석 결과, 펀치 반경이 0 mm로 감소하여도 성형 가능한 최소 제품 곡률 반경은 4.37 mm로 수렴하였다. 일반적으로 펀치 곡률 반경이 감소함에 따라 제품 곡률 반경이 감소한다. 하지만 실험 및 해석에서 확인 가능하듯이 펀치 반경이 0 mm로 감소하여도 성형 가능한 제품의 곡률 반경 값이 발생한다. 해석과 실험에서 모두 특정 곡률 반경 이하로 성형이 불가능하였다. 이와 같이 성형 가능한 최소 곡률 반경을 최소 성형 가능 곡률 반경으로 정의하였다.
두께 0.7 mm의 210B2 재료를 펀치 각도 155o로 성형할 시 펀치 반경에 따른 실험 결과와 해석 결과를 Fig. 5에 비교하였다. 두께 0.7 mm의 210B2 재료를 펀치 반경 0 mm, 펀치각도 155o 로 성형할 시 제품의 곡률 반경 실험 및 해석 결과는 각각 4.28, 5.18 mm이다. 실험 및 해석에서 얻을 수 있는 최소의 제품 곡률 반경을 최소 성형 가능 곡률 반경으로 정의하였다. 또한 같은 155o에서 펀치 곡률 반경에 따른 실험 결과와 해석 결과, 평균 제곱근 오차(Root Mean Square Error, RMSE)는 0.466 mm의 값을 보였다. 게다가 같은 두께에서 펀치각도에 따른 해석 결과와 실험 결과의 비교에서도 RMSE는 2 이하의 값을 확인하였다. 이를 통해 해석 결과가 실험 결과를 정확히 예측할 수 있음을 확인할 수 있었다[8].
3.2 펀치 반경과 제품 곡률 반경의 관계의 예측 모델
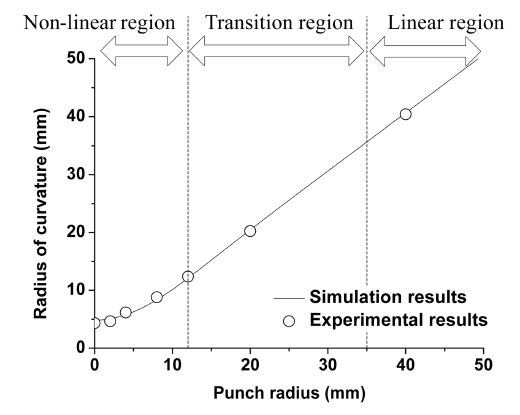
본 연구에서는 Fig. 5의 펀치 반경과 제품 곡률 반경의 관계에서 펀치 반경과 성형 후 발생하는 제품 곡률 반경의 관계를 펀치 반경과 제품 곡률 반경이 비례하는 영역(Linear Region), 비선형 영역(Non-Linear Region), 중간 영역(Transition Region)의 3개 영역으로 구분하였다.
한편, 본 연구에서는 CR2, CR3, CR4, 180B2, 210B2의 총 5가지 재료를 사용하였다. 5개의 재료에 대해 재료는 비선형 모델의 변수로 사용하지 않았다. 재료의 특징은 탄성계수, 항복강도, 가공경화지수 등으로 표현 가능하지만 이 모든 특성을 한개의 비선형 영역의 모델 식에 포함하기에는 해석 결과가 부족하므로, 재료마다 다른 다항식 모델을 사용하였다. 따라서 비선형 영역의 입력 변수는 재료 두께(t), 펀치 각도(θ), 펀치 반경(PR)만으로 다항식 모델을 구성하였다.
먼저 펀치 반경이 작은 경우, 펀치 반경이 감소함에 따라 제품 곡률 반경은 일정 값으로 수렴하였다. 이 영역에서는 제품 곡률 반경을 3차식의 관계로 구성하였다. 또한 재료 종류, 각도, 두께에 대한 영향은 2차식으로 모사하여 3차식과 2차식 조합의 다항식을 구하였다. 재료 종류, 두께, 각도에 대한 식은 2차식을 사용하여도 충분히 모사할 수 있어 이를 2차식으로 모사하였다. 하지만 펀치 반경에 대한 관계를 2차식으로 모사하는 경우, 펀치 반경이 0에 가까운 경우에 곡률 반경의 변화를 모사하기 어렵다. 따라서, 펀치 반경은 3차식을 사용하였고, 재료 두께와 펀치 각도는 2차식을 사용하였다.
제품 곡률 반경 예측 식은 다음과 같으며, 각각의 비선형 모델은 11개의 변수를 갖는다. 각 경우의 해석 결과는 펀치 곡률 반경(PR) 0 mm에서 20 mm까지, 두께 0.6, 0.65, 0.7 mm, 펀치 각도 155, 165, 170, 175o의 값을 사용하였다. 해석 결과는 기존 연구 논문의 결과[7]에 정리되어 있다. 다항식을 활용한 반응 표면 모델 식은 식(1)과 같다. 해당 다항식은 펀치 반경, 펀치 각도, 재료 두께에 대한 식이다. 여기서, 펀치 반경(PR)은 3차식을 사용하였다. 이는 2차식으로는 펀치 반경 0인 영역을 정확하게 모사하기 어렵기 때문이다[7]. MATLAB 2020R을 사용하여 계수를 찾았다. 계수는 Table 1과 같다.
| (1) |
비선형 영역의 범위는 재료 두께에 대해 0.6-0.7 mm, 펀치 각도 155-175o이다. 펀치 반경은 0 mm 에서 20 mm의 값을 사용하여 RSM 모델을 제작하였다. 각 재료에 따른 식(1)의 변수는 Table 1과 같다.
일반적인 굽힘 공정에서 제품 외측의 곡률 반경은 제품의 두께와 펀치 곡률 반경의 합으로 표현된다. 본 연구에서는 펀치 반경이 35 mm 이상인 경우, 펀치 곡률 반경과 제품 곡률 반경은 비례 관계를 보인다고 가정하였다. 보통 굽힘 공정에서 재료가 펀치와 접촉한 이후 펀치의 표면을 따라 변형하는 경우, 재료의 내측이 펀치의 외측 반경과 동일하게 성형된다. 이 경우, 펀치 반경과 제품 곡률 반경은 서로 비례한다. 따라서 재료는 펀치 형상에 적합하도록 변형하며, 재료의 두께 감소를 제외하면 다른 영향을 크게 받지 않는다.
본 연구에서는 선형 관계가 시작되는 시점을 펀치 반경 35 mm 이상으로 가정하였다. 선형 영역에서 제품의 곡률 반경은 재료 두께와 펀치 반경의 합이다. 이전 연구에서, 성형 공정 중 재료 두께는 약 4% 감소하였다[1]. 따라서 선형 영역에서도 두께가 4% 감소한다고 가정하였고, 이때 선형 영역에서 dκ/dPR = 1이기 때문에 선형 영역에서는 식(2)와 같이 펀치 반경과 제품 곡률 반경의 관계를 정의할 수 있다.
| (2) |
비선형 영역과 선형 영역 사이의 영역에서의 예측 모델을 활용하여 중간 영역에서의 근사식을 만들어 제품 곡률 반경을 예측하였다. 비선형 영역에서의 끝 지점에서 변수값과 제품 곡률 반경을 알고 있고, 선형 영역에서 선형 모델의 시작 지점에서 변수값과 제품 곡률 반경을 알고 있으므로 이 4개의 데이터를 사용하여 근사식을 만들 수 있다. 근사식을 펀치 반경에 대해 3차식으로 만들어 주면 4개의 초기값으로부터 3차식을 구성 할 수 있다.
비선형 영역의 곡률 반경 예측 식을 κ = f (PR, t, θ)라고 하였을 때, dκ/dPR = 1이 되면 선형 모델을 적용할 수 있다. 따라서, 비선형 모델에서 dκ/dPR이 증가하여 1이 되면 선형 모델을 적용할 수 있다. 하지만 펀치 각도가 증가함에 따라 dκ/dPR의 최댓값이 1이 아닌 경우가 있다. 이 때는 dκ/dPR이 최댓값을 갖는 PR을 찾는다. 이는 dκ2/dPR2 = 0을 만족하는 PR을 찾는다. 이때의 PR이 비선형 모델의 끝점이 된다.
이로부터, 다음 2가지 경우를 나눌 수 있으며, dκ/dPR은 다음과 같은 조건으로 구분할 수 있다.
1) max (dκ/dPR) ≥ 1인 경우: dκ/dPR = 1이 되면, 이 지점부터 선형 모델을 사용한 제품 곡률 반경 예측을 진행한다. 이와 같은 경우 중간 영역은 발생하지 않는다.
2) max (dκ/dPR) < 1인 경우: dκ/dPR가 1을 넘지 않기 때문에, d2κ/dPR2 = 0을 만족하는 PR를 구한다. d2κ/dPR2 = 0에서 κ가 최댓값을 갖기 때문이다. 중간 영역의 시작점이 바로 d2κ/dPR2 = 0인 지점이다.
max (dκ/dPR) < 1인 경우, dκ2/dPR2 = 0인 지점에서부터 PR이 35 mm인 지점이 중간 영역이 된다. dκ2/dPR2 = 0을 만족하는 PR을 찾고, 이 점에서의 dκ/dPR을 구한다. 그리고 선형 영역이 시작되는 지점(펀치 반경 35 mm)과 그 지점에서의 제품 곡률반경, 기울기를 알고 있고, 비선형 모델의 끝점과 해당 지점에서의 기울기를 구하였다. 4개의 조건을 사용하여, 중간 영역에서의 식을 만들 수 있다. 2점에서의 함수값과 그 점에서의 기울기를 알고 있기 때문에 펀치 반경에 대한 3차식을 구성할 수 있다. 일반 3차식에, 비선형 모델이 종료되는 지점의 좌표의 끝점 좌표 PR1, κ1을 대입하면 아래 식이 된다. 식(3)에 나머지 경계 조건을 대입하면 각 재료, 두께, 펀치 각도에 대한 식(3)을 구할 수 있다.
| (3) |
본 연구에서는 입력한 펀치 반경, 펀치 각도, 재료 두께, 재료 종류에 따라 식(3)을 계산하여, 중간 영역의 예측식을 도출하였다. 재료에 대해서는 분기 문(if 문)을 사용하여 계산하였고, 나머지는 입력 조건에 따라 실시간으로 계산하였다. 전체 해석은 Microsoft Excel 2016의 매크로를 통해 작업하였다. 또한 모든 작업이 Excel을 통해 가능하도록 프로그래밍하였다.
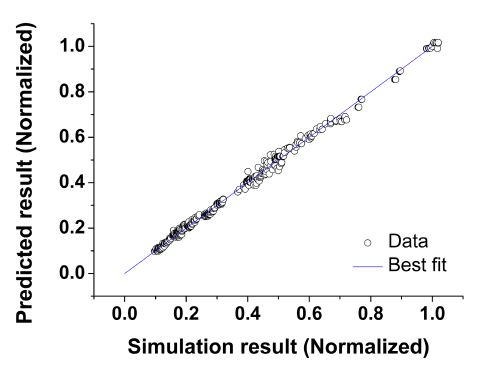
전체 결과에 대해 해석 결과와 본 연구를 통해 개발한 예측 모델의 결과를 비교한 그래프는 Fig. 6과 같다. 또한 전체 결과에 대한 RMSE는 0.314 mm로, 전체 영역에 대해 예측 모델이 결과를 잘 예측할 수 있음을 확인할 수 있었다.
4. 예측 모델을 사용한 예측 결과 및 고찰
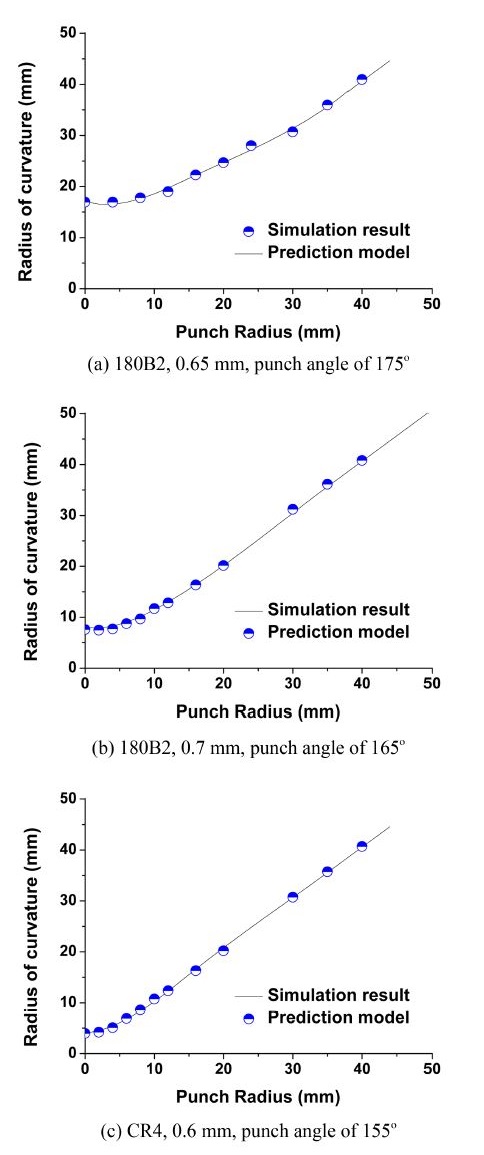
앞서 설명한 피팅 모델을 사용하여 다양한 경우에 대해 제품 곡률 반경 예측 결과를 해석 결과와 비교한 결과는 Fig. 7과 같다. 먼저 180B2, 두께 0.65 mm 재료에 대해 펀치 각도 175o에서 펀치 반경에 따른 제품 곡률 반경을 비교하였다. 또한 180B2, 두께 0.7 mm, 펀치 각도 165o인 경우, CR4, 두께 0.6 mm, 펀치 각도 155o인 경우에 대해 예측 결과와 해석 결과를 비교하였다. 그림에서 확인 가능하듯이 매우 정확히 예측 가능한 것을 볼 수 있다.
또한 식(1) 피팅 모델을 사용하는 경우, 해당 조건에서 펀치 반경에 따른 제작 가능한 최소 성형 가능 곡률 반경을 계산할 수 있다. Fig. 8은 CR3 소재의 재료 두께와 펀치 각도에 따른 최소 성형 가능 곡률 반경을 나타낸 그래프이다. 최소 성형 가능 곡률 반경은 재료의 두께가 감소함에 따라 낮아진다. 또한 펀치 각도가 증가함에 따라 감소하는 경향을 보인다.
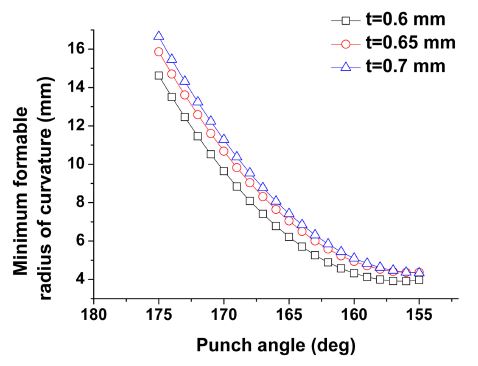
The relationship between the punch angle and the minimum formable radius with different thickness (CR3)
본 연구에서는 유한요소해석 결과와 일반적으로 알려진 재료 변형 특성을 사용하여, 펀치 반경에 대해 연속한 제품 곡률 반경 예측 모델을 개발하였다. 식(1)을 사용하여 전체 영역을 피팅하는 경우, 선형 영역에서 예측 정확도가 떨어진다. 이 부분에서의 정확도를 향상시키기 위해 선형 영역을 정하고 일반적인 재료 변형 특성을 적용하여 식(2)의 예측 모델을 구성하였다. 그리고 중간 영역은 식(3)과 같이 예측 모델의 연속을 유지할 수 있도록 3차식을 사용하였다. 이와 같은 다양한 모델의 조합을 통해 만들어진 예측 모델은 연속성을 유지할 수 있으며, 다양한 범위에서 정확히 예측할 수 있는 장점이 있다.
그리고 개발한 예측 모델을 활용해, 자동차 외판 성형 공정에서 성형 가능한 최소 굽힘 반경을 구하여 설계에 적용할 수 있다. 게다가 제작하고자 하는 제품의 굽힘 반경에 대해 필요한 펀치 각도 역시 도출할 수 있다. 해당 연구에서의 결과를 금형 설계에 적용하는 경우, 성형 가능한 제품 반경을 구할 수 있어, 무리하게 펀치 반경을 날카롭게 가공할 필요가 없다. 그러므로 적절한 펀치 반경으로 금형을 설계할 수 있어, 응력 집중, 마모에 의한 금형 파손을 방지할 수 있다.
5. 결론
본 연구에서는 자동차용 외판재에서 각도가 높고 곡률 반경이 작은 Subtle Feature Line의 성형 공정 예측에 대한 연구를 진행하였다. 자동차용 외판재로 사용되는 180B2, 210B2, CR2, CR3, CR4 소재에 대해 실험 결과를 기반으로 하여, 펀치의 반경과 제품의 곡률 반경을 3개의 영역으로 구분하였다.
3개의 영역은 펀치 반경과 제품 곡률 반경이 비례하는 선형 영역, 펀치 반경이 감소함에 따라 일정 값으로 수렴하는 비선형 영역, 그리고 두 개의 영역을 연결하는 중간 영역으로 구분하였다. 또한 곡률 반경 예측 모델은 재료의 종류에 따라 다르며, 실시간으로 재료 두께, 펀치 각도를 입력받아 펀치 반경에 따른 제품 곡률 반경을 계산할 수 있도록 하였다. 해석 결과와 예측 결과를 전체 영역에서 비교하였을 때, 평균 제곱근 오차는 0.314 mm로 제품 곡률 반경에 비해 매우 낮아, 본 연구에서 제안한 해석 모델을 통해, 다양한 성형 조건에서 제품의 곡률 반경을 정확히 예측할 수 있음을 확인하였다.
NOMENCLATURE
| κ : | Radius of Curvature |
| PR : | Punch Radius |
| θ : | Angle of the Punch |
| t : | Thickness of the Material |
Acknowledgments
본 연구는 정부의 재원으로 한국연구재단(NRF)의 지원(No. NRF-2020R1C1C1014412)을 받아 수행되었습니다. 또한 실험에 도움을 주신 GM Korea에 감사드립니다.
REFERENCES
-
Lee, C.-W., Yu, J., Youn, H. W., Chung, Y., (2021), The minimum formable radius of subtle feature lines in automotive outer panel stamping, International Journal of Automotive Technology, 22(4), 993-1001.
[https://doi.org/10.1007/s12239-021-0089-0]

-
Nam, S., Patil, A. K., Patil, S., Chintalapalli, H. R., Park, K., Chai, Y., (2013), Hybrid interface of a two-dimensional cubic Hermite curve oversketch and a three-dimensional spatial oversketch for the conceptual body design of a car, Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 227(12), 1687-1697.
[https://doi.org/10.1177/0954407013502327]

-
Yoshida, M., Yoshida, F., Konishi, H., Fukumoto, K., (2005), Fracture limits of sheet metals under stretch bending, International Journal of Mechanical Sciences, 47(12), 1885-1896.
[https://doi.org/10.1016/j.ijmecsci.2005.07.006]

-
Huang, Y.-M., (2007), Finite element analysis on the V-die coining bend process of steel metal, The International Journal of Advanced Manufacturing Technology, 34(3), 287-294.
[https://doi.org/10.1007/s00170-007-1054-4]

-
Hu, W., Enying, L., Yao, L. G., (2008), Optimization of drawbead design in sheet metal forming based on intelligent sampling by using response surface methodology, Journal of Materials Processing Technology, 206(1-3), 45-55.
[https://doi.org/10.1016/j.jmatprotec.2007.12.002]

-
Mosbah, H., Attyaoui, S., Nasri, R., (2021), Optimization of the countersinking parameters based on the response surface method, The International Journal of Advanced Manufacturing Technology, 117(1), 501-510.
[https://doi.org/10.1007/s00170-021-07645-8]

-
Lee, C.-W., Chung, Y.-C., (2022), Curve-fitting algorithm for the inspection of subtle feature lines on automotive outer panels, Materials, 15(18), 6323.
[https://doi.org/10.3390/ma15186323]

-
Chung, Y.-C., Yu, J.-H., Jung, K.-S., Song, Y.-H., Jeon, Y.-B., Kim, Y.-J., Jun, S.-M., Kwon, S.-O., Lee, C.-W., (2022), Effects of the material properties and thickness on the minimum formable radius in the subtle feature forming process. https://assets.researchsquare.com/files/rs-1825545/v1/8a87db1f-c6f4-49b6-bbec-57b893e15c40.pdf?c=1663875919
[https://doi.org/10.21203/rs.3.rs-1825545/v1]


Received M.E degree in Department of Mechanical Design and Manufacturing Engineering in Seoul National University of Science and Technology.
E-mail: jhyu9190@seoultech.ac.kr

Received M.E. degree in Department of Mechanical Design and Manufacturing Engineering in Seoul National University of Science and Technology.
E-mail: ksjung@seoultech.ac.kr

Professor in the Department of Mechanical System Design Engineering, Seoul National University of Science and Technology. His research interests are developing tools to design and realize shapes. He has developed tool-path generation algorithms and systems for die and mold making, and has studied the automatic design processes for automotive stamping dies. His current research interests are algorithms for additive manufacturing and digital manufacturing.
E-mail: ychung@seoultech.ac.kr

Assistant professor in the Department of Product Design And Manufacturing Engineering, Seoul National University of Science and Technology. His research interests include simulation and development of the metal forming process and lightweight materials.
E-mail: cwlee@seoultech.ac.kr