Scheduling for Assembly Line with Human–Robot Collaboration
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the scheduling of assembly lines with human–robot collaboration, variations in workload caused by differences in the available working hours of workers and robots must be minimized. A scheduling method that considers buffers shared by automated guided vehicles and cooperative assembly by multiple workers is proposed herein. In particular, cooperative work requires an assembly schedule that minimizes the make span and satisfies the delivery date, while accounting for the possibility of work partitioning, the number of workers, as well as their available time slots and skills. Hence, it is difficult to obtain an exact optimal solution within a reasonable computation time using existing methods such as mathematical programming. Heuristic or metaheuristic approaches are effective for solving this problem. However, these approaches are not suitable for cooperative assembly by multiple workers. Therefore, a genetic algorithm supported by dispatching rules with four genes is proposed. Computational experiments are conducted based on multiple worker skills. The results showed that when the worker skills are the same, the genetic representation of the job name and part processing order is effective, whereas when the worker skills are different, the genetic representation of the cooperative process with the worker for each operation is effective.
Keywords:
Assembly scheduling, Skill, Cooperative assembly, Collaborative assembly, AGV1. Introduction
In the manufacturing industry of a society where the labor force is declining, automation is necessitated to improve the production volume per worker. However, in assembling high-value-added products, many tasks exist that are difficult unless humans are involved, and the effective operation of an assembly line involving human–robot collaboration is required. Since humans and robots differ not only in terms of production capacity per unit time, but also in workable time zones, the workload of each process fluctuates significantly. Furthermore, the workload of each process fluctuates owing to changes in product specifications and high-mix production. When the workload variation between processes is significant, the production volume is restricted by processes involving high workloads; therefore, variations in workload must be suppressed. In this study, we focused on a shared buffer that aggregates intermediate products on an assembly line and cooperative work in which multiple workers perform multiple processes simultaneously for the same assembly target to reduce the variation in workload on the assembly line, where human–robot collaboration is involved.
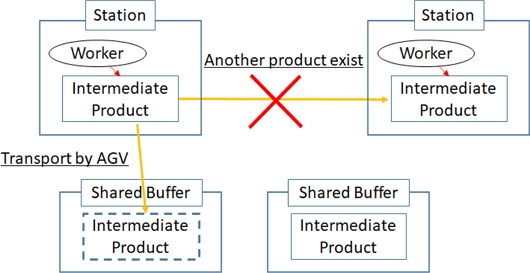
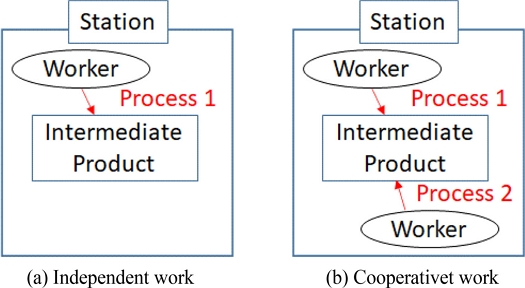
In a shared buffer, the buffer capacity is shared by aggregating the intermediate products of an entire assembly line to effectively exploit the buffer capacity even when the workload of each process fluctuates. It can be easily realized by transporting the assembly target to a place other than the workplace in the next process using an automated guided vehicle (AGV). Figure 1 shows the shared buffers for intermediate products transported by AGV. In case that another intermediate product exists in next station, the intermediate product cannot go to next station. When the intermediate product is transported to a shared buffer, the station will be ready for other intermediate product to be placed. In cooperative work, multiple workers perform multiple processes simultaneously for the same assembly target to dynamically allocate the production capacity based on fluctuations in the workload of each process. Figure 2 shows the deference between independent work and cooperative work. An intermediate product can be assembled faster by cooperative work. Cooperative work cannot be performed at all times owing to restrictions such as the possibility of work division, number of workers, and workable time zone. Moreover, even if cooperative work can be conducted, the effectiveness degree can change depending on the skill difference among the workers.
In an assembly line where the workload of each process fluctuates significantly, the scheduling of each production resource such as workers and robots becomes increasingly important to effectively suppress variations in the workload. Therefore, a model that can collectively manage elements such as unit transport by AGVs, evacuation to a buffer, a workable time zone between workers and robots, worker skills, and cooperative work is required. Furthermore, because many factors must be considered and scheduling becomes more complicated, an algorithm that derives a feasible and efficient schedule within a permissible time is required. The objectives of this study are to make such a model and scheduling algorithm.
Studies that model the assembly line typically describe the constraints of intermediate products [3,4,6-9] and AGVs [2,3,13]; however, none of these studies involve worker skills or shifts. Some studies consider worker skills [5,12] but shifts and intermediates are not considered. Meanwhile, other studies involve cooperative work by multiple workers [1] but do not consider worker skills.
Regarding the scheduling algorithm, in studies that involve the occupancy constraint of the location where the intermediate product is placed, a method for deriving the exact optimum solution of the schedule via mathematical programming has been proposed. However, it has been shown that as the scale of the problem increases, it becomes difficult to solve it in an acceptable time [3,6,8]. In addition, by lengthening the scheduling time unit, a solution can be derived in an acceptable time even for a complicated problem that manages cooperative work by multiple workers [1]; however, this results in a low time resolution of scheduling.
Heuristic and metaheuristic methods can be used to derive a solution to this problem in an acceptable time regardless of the time resolution of scheduling [2-4,7-9,13]. Among them, the genetic algorithm is applicable to many areas; for example, in studies that consider worker skills, a method based on the arrangement of workers as a gene [5,11] has been proposed. However, no method has been proposed for assigning cooperative work by multiple workers.
In this study, we target scheduling problems that consider cooperative work by multiple workers with different skills in an assembly line where robots collaborate with multiple workers with a limited work time zone, where units are transported by AGVs and evacuated to a buffer. We propose a solution based on the modeling of an assembly line and the genetic algorithm. Additionally, we conduct a numerical experiment in which different skills and shifts are set for each worker while targeting the assembly line of machine tools, as well as verify the usefulness of the proposed method.
2. Scheduling Problem Setting
2.1 Assembly Line Model to Be Scheduled
The model of the assembly line targeted in this study is described. In the assembly line, multiple units are assembled individually and then combined; finally, all the units are combined. In the assembly of machine tools, the bed and column are individually assembled as a unit and then combined. Assembly per assembly target is defined as one job, and one job comprises multiple processes. A predetermined order relationship exists between processes, and one worker or robot performs work for one process. The processes of different units can be performed in parallel. Furthermore, cases exist where processes of the same unit can be performed in parallel. For example, when assembling multiple components to one unit, one worker may perform individual assemblies, or multiple workers may assemble components in parallel. In cooperative work, multiple workers perform multiple processes of the same unit simultaneously. Examples of processes in assembling a machine tool include mounting a unit on an AGV by a worker, assembling components to a unit by a worker or robot, and connecting a bed and column by a worker or robot.
The location wherein the process is executed is called the workplace, and the location wherein one or more workplaces where the same type of process is performed is called the station. Multiple processes are preset for one station, and processes of different units may be set. For example, bed and column assembly processes may be executed at station A. One unit is transferred to the workplace at a time, and a preset process is performed.
Subsequently, the worker goes to an arbitrary workplace and executes one process at a time. The worker’s skills are predetermined, whereas the ability to execute a specific process and the execution time change depending on the skill. In addition, the shift is predetermined for the worker, and the process can be executed during the shift, not outside the shift.
The robot is fixed to a specific station and executes one process at a time. Executable processes are preset for a specific robot. Within the station, the robot can perform processes in multiple preset workplaces. For example, different processes can be performed in two workplaces reachable by the robot arm. The operating time of the robot is set in advance, and the robot can be operated 24 h a day.
A unit is mounted on an AGV and transported between stations. The occupancy of an AGV is released when units (a bed and a column) are combined or when a finished product is unloaded.
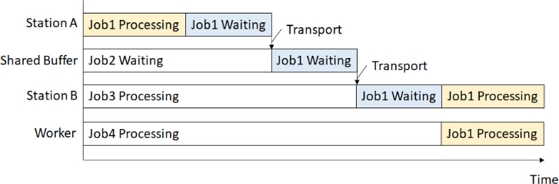
If the destination station is occupied when it traverses between stations of a unit, the AGV equipped with the unit traverses to the shared buffer space and waits for the destination station to become available. If no free space is available in the shared buffer space, it remains at the source station and waits for the destination station or shared buffer space to become available. The capacity of the shared buffer space is to be predetermined. Figure 3 shows the processes: a unit of job 1 waits at the station where previous process of job 1 is executed, then waits at shared buffer, then waits at the next station until next process starts in the form of a Gantt chart. The movement time of the unit is sufficiently small with respect to the execution time of the process and is thus negligible.
2.2 Condition Setting for Machine Tool Assembly Line
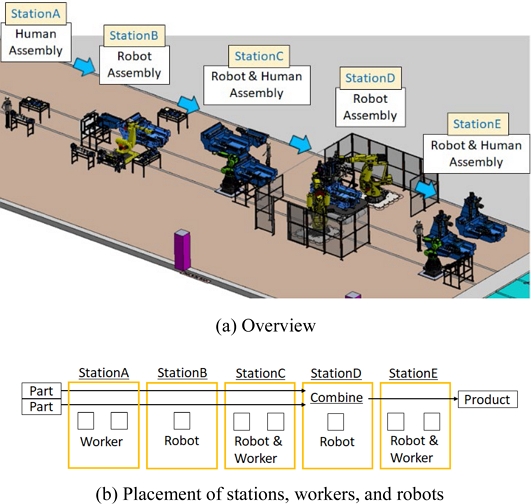
The machine tool assembly line shown in Figure 4 is represented by the model described in Section 2.1 above as an example of the assembly line. The assembly line in Fig. 4 comprises stations A to E. One machine tool is assembled by assembling the necessary components to the bed and column and connecting them. One job is executed by performing the following processes:
(1) Station A comprises two workplaces, and workers perform their tasks.
(2) Beds and columns are appropriately transported from station A to the workplace of station B. Station B comprises one workplace, and components are assembled by a robot.
(3) Beds and columns are appropriately transported from station B to the workplace of station C. Station C comprises two workplaces, and components are assembled by a worker and robot.
(4) Beds and columns are transported from station C to the workplace of station D. Station D comprises one workplace, and a robot connects the bed and column.
(5) The combined bed and column are transported from station D to the workplace of station E. Station E comprises two workplaces, and the workers and robots perform their tasks.
The following specific conditions are set:
- • Workers can shift stations A, C, and E as appropriate to perform arbitrary work.
- • At stations B, C, and E, only one robot can perform its task. At station D, two robots can perform their tasks, but they are considered as one robot because the processes are always synchronized.
- • The worker’s day shift comprises a continuous work time of 4 h in the first half, a break time of 0.75 h, and a continuous work time of 4 h in the second half. The night shift begins immediately after the day shift and involves a continuous work time of 4 h in the first half, a break time of 0.75 h, and a continuous work time of 3.5 h in the second half.
- • The robot operates 24 h a day.
- • Two workers are assigned each to the day and night shifts.
3. Scheduling Method based on GENETIC Algorithm
3.1 Gene Expression for Scheduling
Herein, we propose a scheduling method based on a parameter-free genetic algorithm (PFGA) [10,12]. Table 1 shows the genes assigned to the three jobs, which are represented by genes assigned to four classes. The four classes are (1) job name, (2) processing order of bed/column, (3) cooperative process with workers for each operation, and (4) assigned worker number for each operation. These genes are considered as one chromosome. The parameter values of these genes in Table 1 show an example of a genetic representation of three jobs in which four workers and three cooperative processes are assigned. The genes of each class are described as follows:

Example of genetic representation of three jobs (A job is represented by genes assigned to four classes)
① Job name
Genes are represented by integers from 1 to the total number of jobs. By changing the gene that represents the job name assigned to the job processing order, the job processing order will change.
② Processing order of bed/column
Genes 1 and 2 represent a bed and a column, respectively, which are processed in the order in which the genes are listed. For example, the notation “1, 2” represents scheduling in which the bed is processed first, and the notation “2, 1” represents scheduling in which the column is processed first. It is assigned to the process before the bed and column are connected at station D, i.e., the process of stations A, B, and C.
③ Cooperative process with workers for each operation
Regarding the processes performed by the operator, the processes for which cooperative work is realizable by the operator are flagged; the gene of processes 1 and 0 indicate that the cooperative work is performed and not performed, respectively. For example, cooperative work can be performed in three steps, then three genes will be assigned in order. When a gene of this class is “1, 0, 1,” it is scheduled to perform cooperative work, not perform cooperative work, and perform cooperative work, in that order.
④ Assigned worker number for each operation
The worker number is a gene assigned to the process performed by the worker. The order of genes of the worker number is arranged in the order of the bed process, the column process, and the process after the bed and column are integrated.
3.2 Scheduling Process
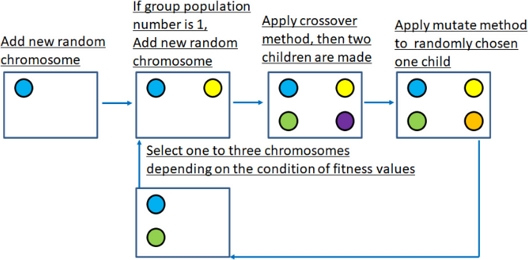
Figure 5 shows the entire flow of the scheduling process using PFGA. The flow is as follows:
- • Step 1: An empty local population is generated.
- • Step 2: In all jobs, for genes in classes (1) job name, (2) processing order of bed/column, (3) cooperative process with workers for each operation, and (4) assigned worker number for each operation, the genes that should be included in each class are randomly arranged and assigned. However, only when Step 2 is performed for the first time, “(1) job name” is not random but is arranged in the order of the delivery date set for each job.
- • Step 3: The genes of classes (1) job name, (2) processing order of bed/column, (3) cooperative process with workers for each operation, and (4) assigned worker number for each operation assigned in Step 2 are combined into one chromosome and stored in the local population. After performing Step 3 for the first time, Steps 2 to 3 are repeated because only one chromosome exists in the local population.
- • Step 4: Two chromosomes in the local population are randomly extracted and crossed as parent chromosomes to generate two child chromosomes (The crossover method is described in Section 3.3.).
- • Step 5: Two child chromosomes generated in Step 4 are selected randomly and mutated (The mutation method is described in Section 3.4.).
- • Step 6: A total of 1 to 3 chromosomes from the two parent chromosomes extracted in Step 4, and the two child chromosomes generated in Steps 4 and 5 are returned to the local population (The method for selecting chromosomes to be returned to the local population is described in Section 3.5.).
- • Step 7: If only one chromosome exists in the local population, return to Step 2; if two or more chromosomes exist, return to Step 4, and repeat the process up to Step 6. This repetition is performed for a predetermined number of generations.
3.3 Chromosome Crossover Method
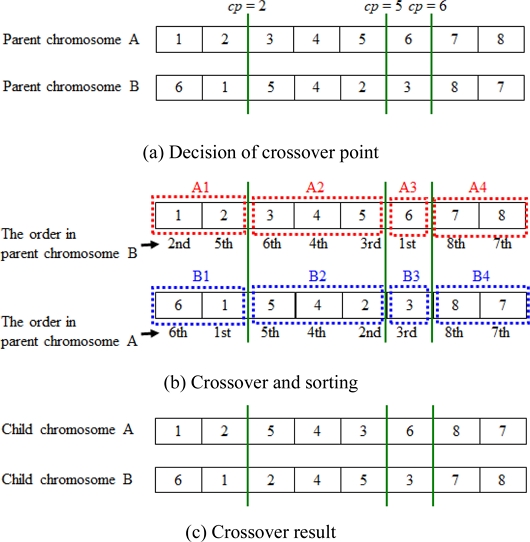
Multipoint crossover is applied to the “(1) job name” gene on the chromosome. Figure 6 shows an example of crossover for a chromosome with eight jobs. The numbers shown in the figure represent the “(1) job name” in the genes that constitute the chromosome. In Step 4 of Section 3.2, two parent chromosomes are extracted from the local population, as shown in Fig. 6(a). The number of chromosome cuts, n, in crossover is randomly determined between 1 and the number of jobs, -1. For example, if the number of jobs is eight, then the number of disconnections will be one to seven. For the two parent chromosomes, the cleavage position cp is randomly determined, the cleavage is performed with the number of cleavage n, and the genes are crossed to generate a child chromosome. In the example shown in Fig. 6, the number of cuts n is three, and the cut position cp is 2, 5, and 6.
When a crossover is performed, child chromosomes are generated in the following processes (Steps 1 to 3) such that the same job number does not overlap in the chromosome.
Step 1: As shown in Fig. 6(b), two parent chromosomes A and B randomly selected from the local population are cleaved by the number of cuts n to achieve subparents A1, ..., An + 1, B1, ..., Bn + 1.
Step 2: Regarding the job name genes of the even-numbered subparents of parent chromosome A, as shown in Fig. 6(b), the order of the job name genes arranged in parent chromosome B is verified, and within each even-numbered subparent of parent chromosome A, they are rearranged based on the order to generate child chromosome A, as shown in Fig. 6(c).
Step 3: Regarding the job name genes of the even-numbered subparents of parent chromosome B, as shown in Fig. 6(b), the order of the job name genes arranged in parent chromosome A is verified, and within each even-numbered subparent of parent chromosome B, they are rearranged based on the order to generate child chromosome B, as shown in Fig. 6(c).
When moving the position of the “(1) job name” gene, the “(2) processing order of bed/column,” “(3) cooperative process with workers for each operation,” and “(4) assigned worker number for each operation” genes that represent the job move simultaneously. Multipoint crossover is applied to the “(3) cooperative process with workers for each operation” and “(4) assigned worker number for each operation” genes related to the same “(1) job name.” For the “(2) processing order of bed/column” gene on the chromosome, the randomly selected parent gene is inherited without modification.
3.4 Chromosome Mutation Method
One child chromosome is randomly selected from the two child chromosomes generated by crossover. The numerical value m is randomly determined from 1 to the number of jobs possessed by the selected child chromosome, and the jobs in the child chromosome are randomly selected m times. One class is randomly selected from the four classes of the selected job, and the gene is mutated as follows:
If the selected mutation class is “(1) job name,” when the processing order “O-order” before the mutation of the job is smaller than the processing order “M-order” after the mutation, then the processing order of the jobs in between is shifted forward individually. When the O-order before the mutation of the job is larger than the M-order after the mutation, the processing order of the jobs in between is shifted individually.
When the selected mutation class is “(2) processing order of bed/column,” only one mutant gene exists, but two genes are mutated simultaneously. For example, if the original gene is 1, 2, then genes 2, 1 are mutated; if it is 2, 1, then genes 1, 2 are mutated.
If the selected mutation class is a “(3) cooperative process with workers for each operation,” then the gene to be mutated is randomly selected from the genes of that class, and genes 1 and 0 are switched.
If the selected mutation class is “(4) assigned worker number for each operation,” a gene to be mutated is randomly selected from the genes of that class, and the gene is mutated to a gene randomly selected from the worker’s name.
3.5 Chromosome Selection Method
The selection of chromosomes to be returned to the local population in Step 6 of Section 3.2 is performed in one of the following cases (Cases 1 to 4) based on the fitness evaluation value derived using the method shown in Section 3.8.
- • Case 1: If two child chromosomes have a higher fitness rating than the two parent chromosomes, then the two child chromosomes and the parent chromosome with the higher fitness rating are returned to the local population. This operation increases the number of chromosomes in the local population by one.
- • Case 2: If two child chromosomes have a lower fitness rating than the two parent chromosomes, then the parent chromosome with the higher fitness rating is returned to the local population. This procedure reduces the number of chromosomes in the local population by one.
- • Case 3: If one parent chromosome has a higher fitness evaluation value than two child chromosomes, then the parent chromosome and the child chromosome with the higher fitness evaluation value are returned to the local population. This operation does not change the number of chromosomes in the local population.
- • Case 4: If one child chromosome has a higher fitness evaluation value than the two parent chromosomes, then the child chromosome is returned to the local population, and Steps 2 and 3 in Section 3.2 are performed. This operation does not change the number of chromosomes in the local population.
3.6 Scheduling Policy
In this study, the scheduling policies A to C shown in Table 2 were set, and a comparative evaluation was performed.
Policy A: Scheduling is performed by the genes of two classes: “(1) job name” and “(2) processing order of bed/column.” The genes of “(3) cooperative process with workers for each operation” and “(4) assigned worker number for each operation” are not used. Cooperative work should always be performed when possible. If multiple worker candidates are present simultaneously, then the worker with higher skills is prioritized. If the skill levels of the workers are the same, then the workers are assigned in the ascending order of the worker number.
Policy B: Scheduling is performed based on three classes of genes: “(1) job name,” “(2) processing order of bed/column,” and “(3) cooperative process with workers for each operation.” The gene of “(4) assigned worker number for each operation” is not used. If multiple worker candidates are present simultaneously, as in policy A, then the workers with higher skills are prioritized. If the skill levels are the same, then the workers are assigned in the ascending order of the worker number.
Policy C: Scheduling is performed based on four classes of genes: “(1) job name,” “(2) processing order of bed/column,” “(3) cooperative process with workers for each operation,” and “(4) assigned worker number for each operation.” By performing the genetic manipulation of (4), the assignment of highly skilled workers to processes that do not require high skill levels can be avoided. If multiple worker candidates are present simultaneously, then the worker defined by the gene is prioritized.
3.7 Process Allocation (Dispatching) Policy
The process was dispatched based on the following rules:
- • Rule 1: For each job, the high-priority unit (bed or column) process, low-priority unit (bed or column) process, and post-bonding unit (bed and column) process are allocated from the genetic information described in the “(2) processing order of bed/column” class.
- • Rule 2: Each process is allocated to the earliest possible time.
- • Rule 3: If multiple workers who can be assigned are present simultaneously, then they are assigned based on the policy shown in Section 3.6.
- • Rule 4: When the process is completed, if the next workspace is available, the unit is shifted to the next workspace; if the next workspace is not available but the shared buffer space is, the unit is shifted to the shared buffer space; if neither the next workspace nor the shared buffer space is available, then the unit will remain in the same workspace.
- • Rule 5: Even if a new process exists that can be assigned to the same workplace immediately before the assigned process, if the shared buffer space is full and waiting is necessitated in the workplace, the waiting time zone may interfere with the schedule of the allocated process. In this case, a new process is assigned after the assigned process.
3.8 Schedule Evaluation: Calculation of Fitness Evaluation Value
For the schedule generated based on the dispatching rule, the gene fitness is evaluated by the total time from the start of the first work to the end of all work (makespan), as well as the delivery date penalty. Because the job end time does not exceed the delivery date, the fitness evaluation value EV is calculated based on Rules 1 and 2 below, and the schedule is evaluated.
- • Rule 1: If the job end time exceeds the delivery date, then the penalty is calculated by adding the fixed penalty and the penalty proportional to the exceeded time (Fixed penalties and proportionality constants are preset.).
- • Rule 2: The penalty calculated in Rule 1 is added to the makespan and then used as the fitness EV (The formula for calculating EV is shown in Section 4.1.).
4. Evaluation Experiment
4.1 Experimental Conditions
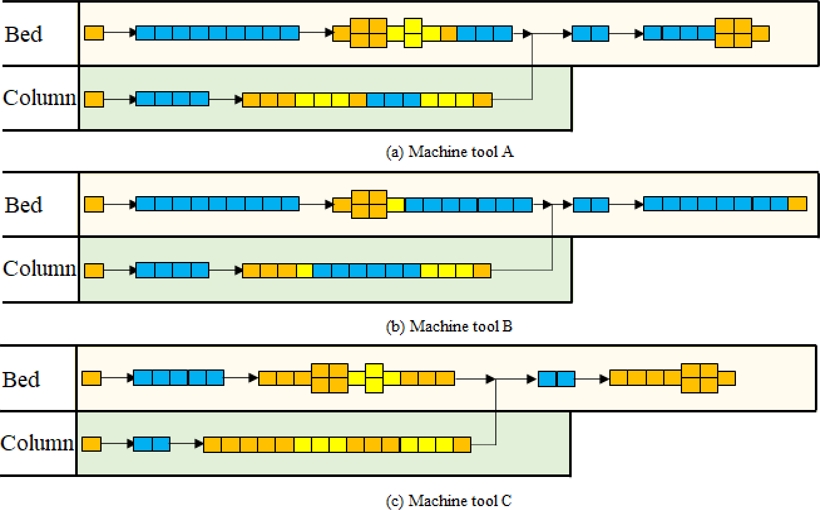
Numerical experiments were conducted to verify the effectiveness of the proposed scheduling method. In the numerical experiment, scheduling was performed using an assembly comprising seven types of machine tools. Figure 7 shows the assembly process of machine tools A, B, and C, and the processes performed by the robot and operator to assemble the bed and column are shown separately. The orange, blue, and yellow boxes shown by the black frames in the figure represent one process. The process is performed in order from left to right. Arrows indicate that the station being processed will change. The blue box represents the robot process. The orange box represents normal work, i.e., a process that can be performed by all workers who do not require advanced skills. The yellow boxes represent high-difficulty tasks, i.e., tasks that require a high degree of skill, and processes that can be performed by a limited number of workers. The process in which two boxes are lined up vertically represents a process in which two workers can work simultaneously. For processes that allow cooperative work, if the skill levels of two workers who work simultaneously are equal, then the work time is also equal. Machine tools D and E have the same assembly process as machine tool A; however, their total processing times are 1.5 and 0.7 times, respectively. Machine tool F has the same assembly process as machine tool B, but its total processing time is 1.4 times longer. Machine tool G has the same assembly process as machine tool C, but its total processing time is 0.7 times longer.
Job combinations I, II, III, and IV with 15, 20, 25, and 30 number of jobs, respectively, were set (see Table 3). Additionally, Table 3 shows the breakdown and delivery date for machine tools A to G in job combinations I, II, III, and IV. These job combinations were determined based on job data from an actual conventional assembly line. The scheduling dates for each job combination (I, II, III, and IV) were verified to be April 1 and April 7. In addition, as shown in Table 4, combination patterns 1, 2, and 3 of the worker’s skill values and the shift of the workers (day shift/night shift) were set. Worker skill values were set for each of two types of processes, i.e., normal and high-difficulty work. The actual work time RT can be expressed by the skill value of the worker corresponding to the process, S, and the standard time of the process, ST, as shown in Eq. (1). When the skill value S of the worker corresponding to the process is 0, the work cannot be performed. Although it is desirable that the skills of all workers should be equal, some workers have lower skills. As a result, in some cases, lower skill workers cannot perform some tasks. We then assumed that they would be covered by a combination with higher-skilled workers, as shown in Table 4.
| (1) |
The EV for each scheduling is calculated using Eq. (2).
| (2) |
In Eq. (2), MS represents the makespan, PE the delivery penalty, and the time unit for each is one hour. The makespan and delivery date are weighted by w1 and w2, respectively. In this evaluation experiment, w1 = 1 and w2 = 5 were prioritized to satisfy the delivery date. PE is calculated using Eqs. (3) and (4) based on the conditions. The smaller the EV, the higher is the evaluated value.
| (3) |
| (4) |
Equation (3) is applied when the job completion date FI is earlier than the job delivery date DU. Equation (4) is applied when the job completion date FI exceeds the job delivery date DU. In Eq. (4), i is the penalty coefficient proportional to the time over the delivery date, and j is the fixed penalty value assigned when the delivery date is exceeded; in this numerical experiment, i = 1 and j = 24 h (1 day). FI-DU is the period between FI and DU, expressed in units of h.
4.2 Scheduling Results and Discussion
Figure 8 shows the result of dividing the EV of schedule policies A, B, and C shown in Section 3.6 by the number of jobs to obtain the EV per job when scheduling on April 1 and April 7 for job combinations I, II, III, and IV (whose number of jobs are 15, 20, 25, and 30, respectively) shown in Table 3 for each of the worker skill value combination (1, 2, and 3) shown in Table 4. The average value of 10 trials is shown. Based on a preliminary experiment, the number of generations of the genetic algorithm was set to 300. The calculation times per trial based on a computer with a Core i7-6600U CPU and 16 GB of memory, regardless of the rules, were as follows: 2 min when the number of jobs was 15; 4 min, 20; 6 min, 25; 8 min, 30.
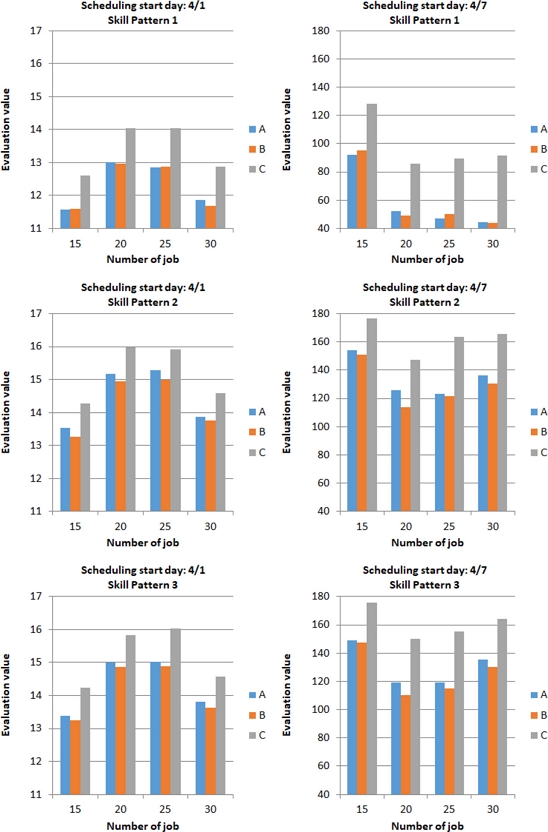
Evaluation values of makespan and delivery penalty for three different worker skill patterns calculated based on three different scheduling policies. Scheduling policy B is effective for skill patterns 2 and 3, where skill of each worker differs
Although policies A and B are similar, policy B yielded slightly higher evaluation scheduling results. Since policy C comprises more gene combinations than policies A and B, it can yield highly evaluated scheduling results, although they are lower than those yielded by policies A and B. In dispatching policy B, rules are set for consecutive processes, and if the skills are the same, the same worker is assigned in the ascending order of the worker number; furthermore, the possibility of assigning the same worker is high. In policy C, workers are assigned to each process. Therefore, cases exist where the workers are different for each process; consequently, some processes require a wait time for the appropriate workers.
Therefore, policy C yields lower scheduling results than policies A and B.
In skill value combination pattern 1, policy B resulted in lower evaluation results than policy A in some cases. In the abovementioned pattern, since the skill values of all the workers are the same, the work time of each process by two workers who perform cooperative work is the same, and no waiting time is generated during the cooperative work. Because cooperative work is always performed in policy A whereas the presence or absence of cooperative work is considered in policy B, it is assumed that scheduling evaluation results lower than those yielded by policy A will be obtained when cooperative work is not performed in policy B. However, when the number of jobs is 20 or 30, policy B yields a higher evaluation scheduling result than policy A. Under the scheduling conditions of this study, the work time per day using only robots is 8.5 h. Therefore, to efficiently perform work using only the robot, storing AGVs in the middle of multiple processes in the buffer may be more effective than proceeding with the process via cooperative work. Hence, it is assumed that the scheduling result of policy B, which considers the presence or absence of cooperative work, yields a higher evaluation value than policy A, which always performs cooperative work.
In skill value combination patterns 2 and 3, policy B always yielded a higher evaluation scheduling result than policy A. If the skills of two workers who perform cooperative work are different and their work times differ, then waiting time may be incurred. Hence, it is assumed that high evaluation scheduling results are obtained when cooperative work is not performed, and that those results are obtained by policy B, which considers the cooperative work, instead of policy A, which always performs the cooperative work.
The evaluation values between skill value combination patterns 2 and 3 did not differ significantly. Pattern 3, which includes workers with low skill values, yielded a worse evaluation value than combination pattern 2; however, the number of high-difficulty work processes was less than that of normal work. Therefore, it is assumed that even if a process exists that cannot be performed based on the situation, it will not impose a significant effect.
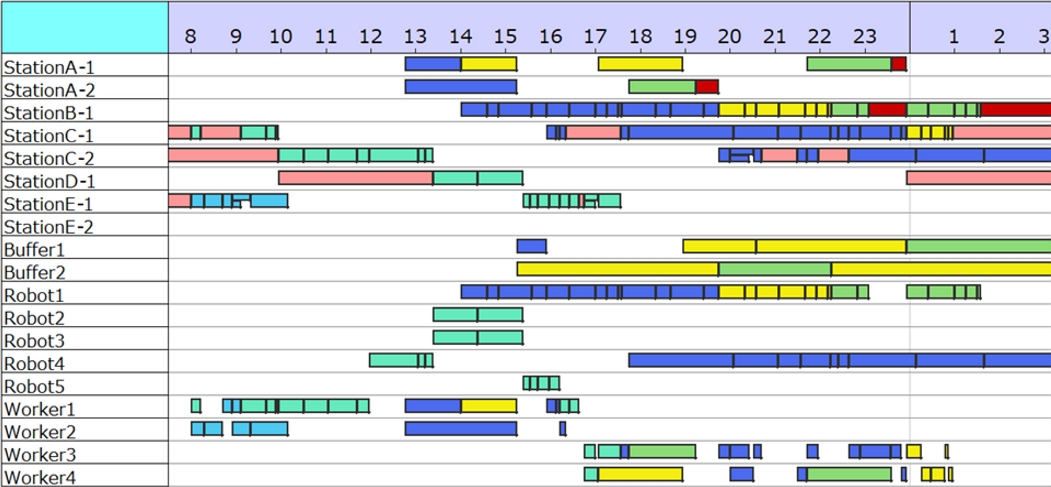
Figure 9 shows the obtained scheduling results partially in the form of a Gantt chart. The horizontal axis represents time, and the bars in the Gantt chart represent the state in which a bed or column is placed in each station or shared buffer space, as well as the state in which the robot/worker is operating. The red bar of the station indicates that the bed or column is waiting in the workplace after work, and the light red bar of the station indicates that the bed or column has shifted to the workplace where the next process is to be performed and is waiting for work. Colors other than red and light red indicate the difference between jobs.
5. Conclusion
Scheduling issues in assembly lines that include unit transport by AGVs, evacuation to buffer, different skills, and collaborative work of multiple workers and robots with workable time zones, and cooperative work by multiple workers were investigated in this study. Subsequently, an assembly line model was proposed, as well as a scheduling method that combines a genetic algorithm and dispatching rules based on that model. In the proposed method, the machine tool assembly line is represented by the genes of four classes: “(1) job name,” “(2) processing order of bed/column,” “(3) cooperative process with workers for each operation,” and “(4) assigned worker number for each operation.” We successfully achieved a schedule based on the EV of the schedule.
A scheduling system was constructed based on the proposed method, and numerical experiments were conducted to determine the appropriate conditions for reducing the makespan and fulfilling the delivery date. When the worker skills were the same, the scheduling evaluation results that accounted for the job name and processing order of bed/column, or those that accounted for the account job name, the processing order of bed/column, and cooperative process with workers for each operation did not differ significantly. However, when the worker skills differed, the scheduling that accounted for the job name, the processing order of bed/column, component priority, and cooperative process with workers for each operation was effective. Hence, the appropriate allocation of cooperative work by considering worker skills can effectively improve the production volume in a complicated assembly line, where the workload of each process fluctuates significantly.
REFERENCES
-
Borreguero-Sanchidrián, T., Pulido, R., García-Sánchez, Á., Ortega-Mier, M., (2017), Flexible job shop scheduling with operators in aeronautical manufacturing: A case study, IEEE Access, 6, 224-233.
[https://doi.org/10.1109/ACCESS.2017.2761994]

- Chen, C., Tiong, L. K., Chen, I.-M., (2019), Using a genetic algorithm to schedule the space-constrained AGV-based prefabricated bathroom units manufacturing system, International Journal of Production Research, 57(10), 3003-3019.
-
Elmi, A., Topaloglu, S., (2013), A scheduling problem in blocking hybrid flow shop robotic cells with multiple robots, Computers & Operations Research, 40(10), 2543-2555.
[https://doi.org/10.1016/j.cor.2013.01.024]

- Fu, G., (2004), A method for solving jobshop scheduling problems with limited common buffers, transactions of the institute of systems, Control and Information Engineers, 17(3), 113-121. Japanese
-
Gong, G., Deng, Q., Gong, X., Liu, W., Ren, Q., (2018), A new double flexible job-shop scheduling problem integrating processing time, green production, and human factor indicators, Journal of Cleaner Production, 174, 560-576.
[https://doi.org/10.1016/j.jclepro.2017.10.188]

-
Heger, J., Voss, T., (2018), Optimal scheduling of AGVs in a reentrant blocking job-shop, Procedia Cirp, 67, 41-45.
[https://doi.org/10.1016/j.procir.2017.12.173]

-
Hino, R., Kusumi, T., Yoo, J. K., Shimizu, Y., (2005). Job shop scheduling focusing on role of buffer, Transactions of the Japan Society of Mechanical Engineers, Series C, 71(702), 685-692. Japanese
[https://doi.org/10.1299/kikaic.71.685]

-
Liu, S. Q., Kozan, E., Masoud, M., Zhang, Y., Chan, F. T., (2018), Job shop scheduling with a combination of four buffering constraints, International Journal of Production Research, 56(9), 3274-3293.
[https://doi.org/10.1080/00207543.2017.1401240]

-
Maleki-Darounkolaei, A., Modiri, M., Tavakkoli-Moghaddam, R., Seyyedi, I., (2012), A three-stage assembly flow shop scheduling problem with blocking and sequence-dependent set up times, Journal of Industrial Engineering International, 8(1), 1-7.
[https://doi.org/10.1186/2251-712X-8-26]

- Matsui, S., Yamada, S., (2007), An empirical performance evaluation of a parameter-free genetic algorithm for job-shop scheduling problem, 2007 IEEE Congress on Evolutionary Computation, 3796-3803.
-
Peng, C., Fang, Y., Lou, P., Yan, J., (2018), Analysis of double-resource flexible job shop scheduling problem based on genetic algorithm, Proceedings of the 2018 IEEE International Conference on Networking, Sensing and Control (ICNSC), 1-6.
[https://doi.org/10.1109/ICNSC.2018.8361360]

-
Sawai, H., Kizu, S., (1998), Parameter-free genetic algorithm inspired by “disparity theory of evolution”, Proceedings of the International Conference on Parallel Problem Solving from Nature, 702-711.
[https://doi.org/10.1007/BFb0056912]

-
Zeng, C., Tang, J., Yan, C., (2014), Scheduling of no buffer job shop cells with blocking constraints and automated guided vehicles, Applied Soft Computing, 24, 1033-1046.
[https://doi.org/10.1016/j.asoc.2014.08.028]


Ph.D. candidate in the Department of System Design Engineering, Keio University.
E-mail: inoueko@makino.co.jp

Professor in the Department of System Design Engineering, Keio University.
E-mail: haoyama@sd.keio.ac.jp