밀폐형 공압회로 내 정밀압력제어를 위한 기계 구동식 가스 압력제어기의 제어특성 평가
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this work, precise gas pressure control based on a closed pneumatic circuit was achieved with a mechanically driven gas pressure controller (MDGPC), consisting of a variable-volume bellows chamber and linear actuator. The linear actuator was employed to change an axial dimension of the bellows chamber with the proportional (P) and proportional-integral (PI) controls for fast, stable, and precise pressure control of the gas inside the bellows chamber. The pressure control stability and resolution of the MDGPC were approximately 1.5 Pa and 10 Pa for the P control and 1 Pa and 5 Pa for the PI control, respectively. Despite the more stable and precise control characteristics of the PI control method, overshoots and undershoots observed during the set-point pressure changes and recoveries from pressure disturbances rendered it unsuitable for the MDGPC control method. In contrast, the MDGPC operated under the P control did not show any significant overshoots or undershoots when the set-point pressure abruptly changed or when the MDGPC was exposed to pressure disturbances. Therefore, it was concluded that a fast, precise, and stable gas pressure control in a closed manner was attainable with the MDGPC under the P control.
Keywords:
Closed pneumatic circuit, Gas pressure controller, Proportional control, Proportional integral control, Mechanically driven gas pressure controller키워드:
밀폐형 공압회로, 가스 압력제어기, 비례 제어, 비례 적분 제어, 기계 구동식 가스 압력제어기1. 서론
정밀 가스 압력제어는 첨단 산업분야의 필수 공정제어 기술이며, 공정 자동화로부터 항공기 내부 환경조절시스템 제어에 이르기까지 다양한 산업 분야에서 수요가 증가하고 있다[1]. 특히, 정밀 가스 압력제어를 달성할 수 있는 가스압력제어기(Gas Pressure Controller, GPC)는 위 산업분야에서의 응용에 더해 압력 및 관련 물리량 측정기의 정밀 교정 및 시험 수행을 위한 필수 장비로 사용되고 있으며[2,3], 이에 따라 GPC의 구성 및 최적 제어에 대한 관련 산업의 관심이 고조되고 있다. 이러한 GPC의 가스 압력제어 방식은 제어회로의 개폐여부에 따라 외부의 압력소스 또는 싱크를 이용하는 개방형 공압회로 압력제어(Open Pneumatic Circuit Control)와 별도의 압력소스와 싱크가 존재하지 않는 밀폐형 공압회로 압력제어(Closed Pneumatic Circuit Control)로 분류된다[4].
개방형 공압회로 압력제어 관련 연구는 제어기 특성에 따라 다양한 방향으로 진행되었으며, 접속부의 전달특성 변화를 보상하는 강건 압력제어가 가능한 제어기 설계 관련 연구들이 주요하게 수행된 바 있으며[5-7], 이와 관련하여 구동 밸브의 에너지 손실과 열적 민감성을 보완하기 위한 압전 구동기 기반 압력 조절기[8] 및 응답특성 보완을 위한 PID-PWM (Proportional Integral Derivative-Pulse Width Modulation) 제어기와 관련된 연구가 진행된 바 있다[9,10]. 또한, 기화된 액화천연가스의 압력제어 중 외란에 대해 압력제어 안정도를 향상시킬 수 있는 압력변화 보상 제어기 설계와 관련된 연구들 역시 진행된 바 있다[11,12]. 다만, 개방형 공압회로 압력제어는 제어의 편리성에도 불구하고 별도의 압력소스와 싱크 구성이 어려운 환경에서 적용에 제약을 받는다는 한계를 가져, 이를 극복할 수 있는 밀폐형 공압회로 압력제어에 대한 필요성 역시 다양한 분야에서 제기되었다.
밀폐형 공압회로 압력제어 관련 연구로는 체내 일정유량 혈액 순환을 위한 밀폐형 공압회로 기반 공압 펌프[4,13]와 병원균 유출에 따른 감염을 방지한 코로나 감염자용 산소공급기[14] 개발 관련 연구가 진행된 바 있으나, 이들 연구는 유체의 유량 제어가 주 목적이며 밀폐형 공압회로 내 가스 압력제어와 관련된 연구는 수행된 예가 많지 않다. 특히, 압력제어를 통해 정밀 온도제어를 구현하는 압력제어식 온도제어(Pneumatic Temperature Control) [15,16]나 잉크젯 프린팅 기반 디스플레이 생산 공정[17,18]과 같이 수십Pa 수준의 압력 안정도를 요하는 응용분야에 대해 밀폐형 공압회로를 적용한 정밀 가스 압력제어 관련 연구는 현재까지 보고된 바가 없는 실정이다.
이에 본 연구에서는 밀폐형 공압회로 압력제어 방식을 적용하여 수십Pa 수준의 압력제어 안정도를 달성할 수 있는 가스 압력제어기술을 확립하고자 하였다. 이를 위해 본 연구에서는 축방향 길이변화가 가능한 용접 주름관(Welded-Bellows) 형태의 가변체적형 챔버와 선형 구동기(Linear Actuator)로 구성된 기계 구동식 가스 압력제어기(Mechanically Driven Gas Pressure Controller, MDGPC)를 개발하였으며, 가변체적형 챔버의 축길이와 연동된 선형 구동기 구동축의 변위제어는 압력 외란에 대한 강건성 확보를 위해 미분 제어(Derivative Control)를 제외한 비례 제어(Proportional Control, P제어) 및 비례-적분 제어(Proportional-Integral Control, PI제어)를 적용하여 밀폐형 공압회로 내 고속·정밀 압력제어를 구현하고자 하였다. 이와 같이 개발된 MDGPC의 압력제어 특성은 압력제어 안정도, 분해능, 순간 압력제어 특성, 압력외란에 대한 회복 능력 측면에서 평가하였으며, MDGPC 기반 정밀 가스압력제어를 달성하기 위한 최적 제어방식을 도출하고자 하였다.
본 논문에서는 MDGPC의 제어방식에 대한 이론적 배경을 2장에서 소개하고, 3장에서 MDGPC의 제작 및 최적 제어이득 선정 결과 및 압력제어특성 평가를 위한 시험방법을 소개한다. 4장에서는 MDGPC의 압력제어특성 시험결과를 제시하고, 마지막으로 5장에서 본 연구의 결론을 요약하여 제시한다.
2. 이론적 배경
본 연구에서는 압력 피드백을 갖는 선형 구동기 구동축 변위 제어를 통해 구동축과 연결된 가변체적형 챔버의 축방향 길이 변화에 따른 체적변화를 유도하고, 이를 통해 챔버 내부 가스압력을 제어하고자 하였다. 이를 위해 본 연구에서는 단순하면서도 효과적인 제어특성으로 인해 다양한 산업 및 공학 시스템에서 널리 사용되는 PID 제어[19,20]의 각 제어성분을 적용하여 선형 구동기 구동축 변위제어를 수행함으로써 밀폐형 공압회로 방식의 정밀·고속 가스 압력제어를 달성하고자 하였다.
PID 제어는 비례(Proportional) 성분, 적분(Integral) 성분, 미분(Derivative) 성분의 제어성분을 조합하여 목표값(Set-Point Value)과 측정값(Process Value)의 차인 제어오차(Error, e(t))에 대해 조작변수(Manipulated Variable, m(t)) 값을 결정하는 제어이다[21]. 이러한 PID제어는 각 제어 성분의 조합을 통해 제어 방식이 결정되며, 대표적으로 P제어, PI제어, PID제어가 사용된다. P제어는 제어대상의 제어오차에 비례하는 값을 제어기에 조작 변수로 입력하는 제어이며, P제어를 통해 결정된 조작변수는 아래의 식(1)과 같이 비례 성분에 대한 제어이득(Kp)을 이용하여 표현된다.
| (1) |
이러한 P제어는 일반적인 단순 온-오프 제어 대비 부드럽고 빠른 제어가 가능하나, 제어오차에 비례하는 값을 조작변수로 지속 입력하므로 측정값이 목표값에 근접할 시 미세한 정상상태 오차(Steady-State Error)가 유지되는 특성을 가진다[21]. 이러한 P제어의 한계를 극복하기 위해 제안된 제어방식이 PI제어이다. PI제어는 제어오차의 비례 성분과 시계열 적분 성분을 조작변수 결정에 사용하며, PI제어를 통해 결정된 조작변수는 아래의 식(2)와 같이 비례 성분에 대한 제어이득(Kp) 및 적분 성분에 대한 제어이득(KI)을 이용하여 표현된다.
| (2) |
이러한 PI제어는 제어오차의 적분값을 조작변수에 지속적으로 더해주므로 정상상태 오차를 줄이는 장점을 가지나, 외란이 발생할 경우 회복에 일정 시간이 요구되어 P제어 대비 느린 제어가 이루어질 수 있다[21]. 이와 같은 PI제어의 단점을 해결하기 위해 제시된 PID제어는 제어오차의 비례 성분과 적분 성분에 미분 성분을 더해 조작변수를 결정한다. PID제어를 이용하여 결정된 조작변수는 식(3)과 같이 비례, 적분, 및 미분 성분에 대한 제어이득(KP, KI, KD)을 이용하여 표현된다.
| (3) |
PID제어의 미분 성분은 제어오차의 현재 기울기를 외삽하여 계산하므로 시스템의 응답속도를 빠르게 하고 안정성에 기여할 수 있으나, 고주파 외란이 시스템 제어에 직접적 영향을 미칠 경우 외란을 증폭시켜 시스템의 불안정을 악화시킬 수 있다[20]. 이러한 미분 성분의 특성으로 인해 본 연구에서 제작된 가스 압력제어기와 같이 가스 압력변화 등의 외란이 시스템에 직접적인 영향을 미치는 분야에서는 일반적으로 미분 제어를 사용하지 않는다[21].
이에 따라 본 연구에서는 가변체적형 챔버의 축방향 길이 제어를 위해 D제어를 제외한 P제어 및 PI제어를 적용하여 챔버 내부가스의 압력제어를 수행하고자 하였다. P제어 및 PI제어는 각 성분의 제어이득 선정에 따라 압력제어 특성이 크게 변할 수 있으므로, 전체 공압회로의 동특성을 기반으로 그에 맞는 최적 제어이득 선정이 요구된다. 이에 본 연구에서는 개발된 MDGPC의 고속·정밀 가스압력제어 달성을 위해 P제어 및 PI제어에 대한 최적 제어이득을 선정한 후, 이를 적용한 MDGPC의 압력제어특성을 평가하고자 하였다.
3. 실험 장치 및 방법
3.1 실험 장치
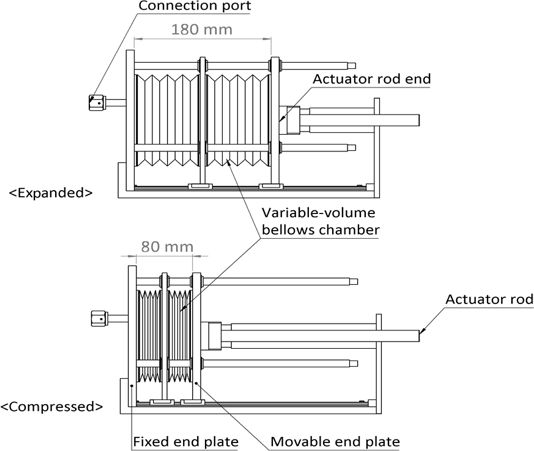
본 연구에서는 밀폐형 공압회로 기반 정밀 가스압력제어를 달성하기 위해 가변체적형 챔버 및 선형 구동기로 이루어진 MDGPC를 제작하였다. MDGPC에 사용된 가변체적형 챔버는 0.02 mm 두께의 스테인리스 스틸 용접 주름관으로 제작하였으며, 축방향 길이 변화에 의한 체적변화를 통해 내부 압력변화가 유도되도록 설계하였다. 선형 구동기 구동축 변위 제어를 통해 제어되는 가변체적형 챔버의 축방향 길이는 외력이 가해지지 않을 때의 축 길이 130 mm를 기준으로 ±50 mm의 변위범위를 갖도록 제작되었다.
Fig. 1은 이와 같이 제작된 MDGPC 내 가변체적형 챔버의 압축 및 팽창과정에서의 외형변화를 보여준다. 가변체적형 챔버의 체적은 챔버와 연결된 선형 구동기 구동축(rod)의 위치제어를 이용하여 제어하였다. 이를 위해 0.01 mm/s부터 2 mm/s의 속도범위에서 250 mm의 이동범위와 0.01 mm의 변위제어 분해능을 갖는 상용 선형 구동기를 사용하였다.
선형 구동기의 구동축 위치변화는 가변체적형 챔버 축방향 길이변화와 역비례관계를 가지므로, 본 연구에서는 가변체적형 챔버의 축방향 길이를 제어변수로 사용하였다. MDGPC의 압력 제어 매질인 제어가스는 불활성 기체인 헬륨(He)을 사용하였으며, 가변체적형 챔버 내부 제어가스의 압력측정은 상대 교정불확도(U(p)pFS) 0.005(약 95% 신뢰의 수준)의 정밀 압력측정기를 이용하여 실시간 측정하였다. 이와 같이 측정된 가변체적형 챔버 내부 제어가스 압력은 선형 구동기 변위제어를 위한 제어변수로 사용하였다.
3.2 P제어 최적 제어이득 결정
본 연구에서 개발한 MDGPC는 제어변수와 조작변수로 각각 가변체적형 챔버 내 제어가스 압력과 챔버의 축방향 길이를 사용하였으며, 설정압력과 측정압력의 차를 제어오차로 하여 가스 압력제어를 수행하였다. 먼저 P제어 적용 MDGPC의 가스 압력 제어의 조작변수는 식(4)와 같이 선형 변위로 변환된 제어오차(Δp(dl/dp))에 비례제어이득(KP)을 곱하고 초기 선형 변위에 더하여 결정한다. 본 연구에서는 압력변화에 대한 길이변화율(dl/dp)을 불안정성을 야기하지 않는 가장 큰 압력에 대한 변위 변화율인 1 mm/kPa로 설정하였다. 아울러 설정압력과 측정압력 간 차가 1 kPa 이상에 해당하는 큰 제어오차의 발생 시 MDGPC의 안정도 유지를 위해 1 mm 이상의 변위가 가해지지 않도록 조작변수의 상하한을 각각 1 mm와 -1 mm로 설정하였다.
| (4) |
본 연구에서는 P제어의 최적 비례제어이득을 도출하기 위해 1.0에서 2.0의 범위에서 비례제어이득을 0.1의 단위로 상승시키며 ±1 kPa의 계단형 설정압력 변화에 대한 응답을 확인하였다. 본 연구에서는 제어압력 안정도에 주안점을 두고 평가하였으나 오버 슈트 및 언더 슈트 특성 역시 비교하여 불안정한 거동 발현이 제한되는 제어이득을 최적 제어이득으로 선정하고자 하였다.
Table 1은 이와 같은 비례제어이득 변화에 따른 응답특성 시험 결과를 보여주며, 각 비례제어이득에서 설정압력 유지 구간 내 30분간 측정한 측정압력 변화의 표준편차로 정의된 제어 안정도(Control Stability), 설정압력 유지 구간 내 최대값과 최소값의 차로 정의된 첨두치 간 진폭(Peak-to-peak Amplitude), 설정 압력 변화 시 발생한 첨두치와 정상상태 측정압력의 차로 정의한 오버 슈트(Overshoot) 및 설정압력 변화 시 발생한 최저치와 정상상태 측정압력의 차로 정의한 언더 슈트(Undershoot)의 값을 확인할 수 있다. 표를 통해 확인할 수 있듯이 비례제어이득 1.5에서 가장 안정적인 압력제어가 이루어짐을 확인할 수 있으며, 첨두치 간 진폭 역시 최소수준을 보임을 알 수 있다. 또한, 오버 슈트 및 언더 슈트의 경우 상대적으로 낮은 수준인 약 1 Pa의 값을 가짐을 확인하였다. 이에 따라 본 연구에서는 P제어를 위한 최적 비례제어이득으로 가장 안정적인 압력제어특성과 더불어 상대적으로 작은 오버 슈트 및 언더 슈트 특성을 보인 1.5를 최적 비례제어이득으로 선정하였다.
3.3 PI제어 최적 제어이득 결정
전술한 바와 같이 P제어를 통한 제어는 측정압력이 설정압력에 근접하는 경우 설정압력에 완전히 도달하지 못하거나 설정압력에서 일정 범위 내 진동하는 정상상태 오차를 가질 수 있다. 본 연구에서는 MDGPC를 이용한 가스 압력제어 시 발생할 수 있는 정상상태 오차를 없애기 위해 PI제어 역시 적용하고자 하였으며, PI제어 구동을 위한 최적 제어이득을 결정하고 이를 이용한 가스 압력제어 수행결과를 P제어 적용 결과와 비교하고자 하였다. 본 연구에서 사용한 PI제어 기반 조작변수는 식(5)와 같이 표현되며, 앞 절의 P제어와 동일하게 압력변화에 대한 길이 변화율(dl/dp)을 1 mm/kPa로 설정하고 조작변수의 상하한을 각각 1 mm, -1 mm로 설정하였다.
| (5) |
본 연구에서는 PI제어를 위한 최적 비례제어이득(KP)과 적분제어이득(KI) 조합 결정을 위해 1.0부터 2.0까지의 비례제어이득 범위에 대해 적분제어이득을 0.005부터 0.05까지 변경시켜 가며 ±1 kPa의 계단형 설정압력변화에 대한 MDGPC의 응답특성을 시험하였다. 본 연구에서는 PI제어를 위한 최적 제어이득 조합의 선정 시, P제어를 위한 최적 비례제어이득의 선정과 동일한 기준을 적용하여 최적 제어이득 조합을 선정하였다.
Figs. 2(a)와 2(b)는 비례 및 적분제어이득 별 ±1 kPa의 계단형 설정압력 변화에 대해 각 설정압력 유지 구간 내 제어압력 안정도와 첨두치 진폭 변화를 보여준다. 그림에서 보이는 바와 같이 비례제어이득이 증가함에 따라 제어압력 안정도가 향상되었으며, 제어이득이 KP = 2.0 과 KI = 0.01 의 조합을 가질 때 가장 안정적인 압력제어 달성이 가능하였다. 또한, Fig. 2(b)에서 볼 수 있듯이 첨두치 진폭의 경우 적분제어이득 변화에 따른 큰 차이를 보이지 않았으나, KP = 2.0 과 KI = 0.01 의 조합을 가질 때 약 8 Pa로 상대적으로 낮은 값을 가져 위 제어이득 조합을 사용할 경우 상대적으로 안정적인 제어가 가능함을 확인하였다. Figs. 2(c)와 2(d)는 각각 비례 및 적분제어이득 별 계단형 설정압력 변화에서 측정된 오버 슈트 및 언더 슈트 변화 경향을 보여준다. 그림에서 볼 수 있듯이 KP = 2.0 과 KI = 0.01의 조합을 가질 때 상대적으로 낮은 수준의 오버 슈트 및 최저 언더 슈트가 발생하였다. 이와 같은 거동에 따라 본 연구에서는 KP = 2.0 과 KI = 0.01 를 PI제어의 최적 제어이득 조합으로 선정하였다.
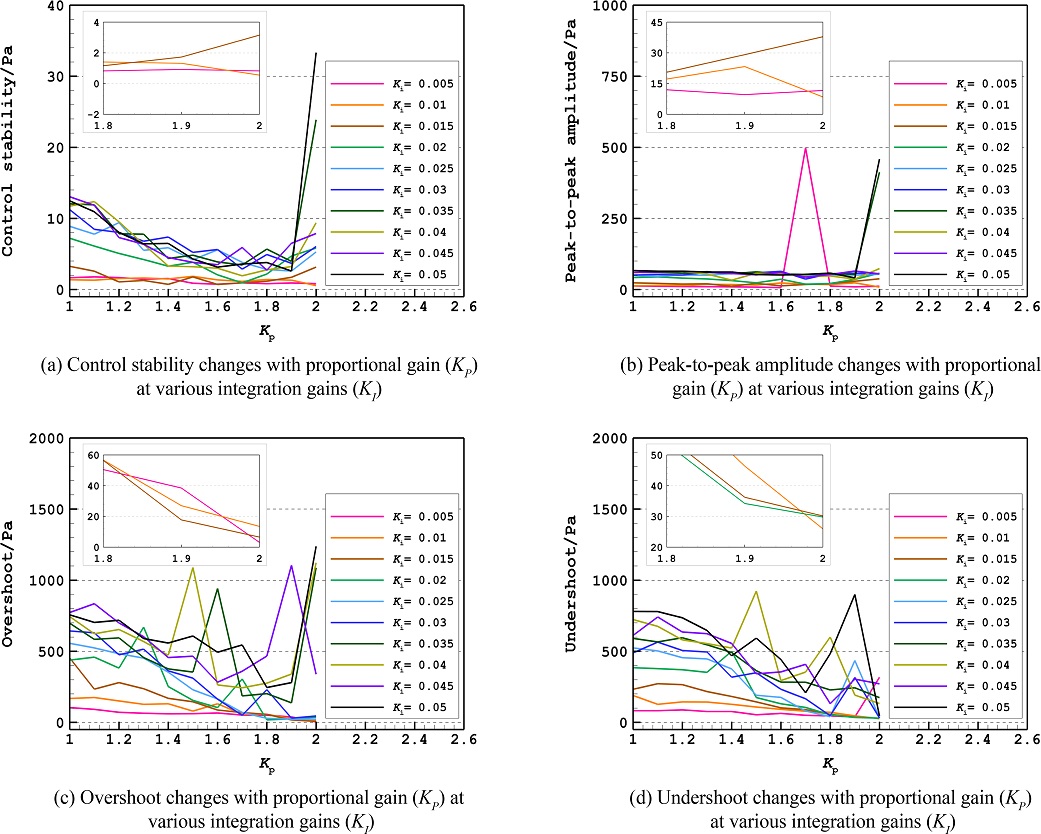
Control responses of the MDGPC to ±1 kPa step changes in the set-point value at various proportional gains (KP) and integral gains (KI). Insets show the magnified view of the responses
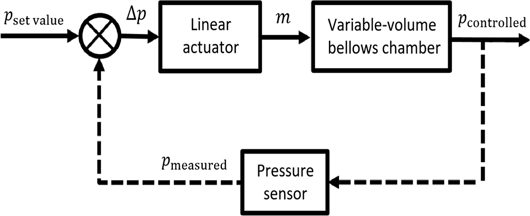
본 연구에서 제작된 MDGPC는 이와 같이 결정된 최적 비례 및 적분제어이득을 적용하여 가변 체적형 챔버의 선형 변위제어를 수행하였으며, 압력제어 과정을 블록 선도로 표현하면 Fig. 3과 같다. 그림과 같이 MDGPC에 설정압력이 입력되면 측정압력과 설정압력의 차(Δp) 및 dp/dl과 최적 제어이득에 의해 조작변수가 결정되어 선형 구동기로 입력된다. 조작변수 입력에 의한 가변체적형 챔버의 축방향 길이변화(체적변화)는 내부 압력변화를 유도하며, 변화된 압력 측정값을 바탕으로 연속 피드백 제어함으로써 MDGPC의 가변체적형 챔버 내부 가스압력을 설정압력으로 정밀 제어하고자 하였다.
3.4 MDGPC 압력제어특성 시험 방법
본 연구에서는 위와 같이 결정된 최적 P제어 및 PI제어이득을 적용하여 MDGPC를 구동하였으며, 압력제어 안정도 및 분해능, 계단형 설정압력 변화를 통한 순간 압력제어능력, 외부 압력 외란에 대한 회복능력 등의 측면에서 MDGPC의 압력제어 특성을 시험하였다. 본 연구에서 제작된 MDGPC는 가변 체적형 챔버가 단열처리 없이 외부에 노출되어 있으므로 외기 온도 변화에 따라 내부 압력변화가 유발될 수 있다. MDGPC를 이용한 정밀 가스 압력제어 달성을 위해서는 이와 같은 실온변화에 대한 압력변화를 보상할 수 있는 안정적 압력제어능력 검증이 필수적이다. 이에 따라 본 연구에서 수행한 압력제어 안정도 시험은 가변체적형 챔버 주변 외기 온도변화에 의한 챔버 내부 가스압력 변화 보상 및 설정압력 유지능력에 초점을 맞추어 진행하였다. 해당 시험은 불규칙적으로 변화하는 외기 온도에 대해 압력제어 전후 가변체적형 챔버 내부 압력 안정도 변화를 비교함으로써 수행하였으며, 정량적 비교를 위한 압력제어 안정도는 12 h 기준 압력변화의 표준편차로 정의하였다.
이와 더불어 본 연구에서는 개발된 MDGPC 기반 가스 압력제어의 정밀도를 결정할 수 있는 압력제어 분해능 역시 평가하였다. MDGPC의 압력제어 분해능은 안정도를 벗어나는 명시적 제어압력 변화가 관측되는 설정압력 변화로 정의하여 평가하고자 하였으며, 상기와 같이 결정된 압력제어 안정도를 바탕으로 압력제어 안정도 내의 설정압력 변화로부터 시작하여 일정한 비율로 설정압력 변화를 증가시켜 가며 분해능 평가를 수행하였다.
본 연구에서 제작된 MDGPC는 안정적이고 정밀한 압력제어 특성 외에도 수kPa 수준의 설정압력 변화에 대해 오버 슈트나 언더 슈트와 같은 불안정성 없이 빠른 설정압력에 도달하는 것이 요구된다. 이에 따라 본 연구에서는 MDGPC의 순간 압력제어특성을 평가하기 위해 70 kPa에서 90 kPa의 범위에서 ±5 kPa의 계단형 설정압력 변화에 대한 압력제어 응답특성을 시험하였다. 이와 같은 시험에 있어, 각 설정압력 유지 구간에서의 압력제어 안정도 및 설정압력 변화 시 오버 슈트 및 언더 슈트 발생 여부를 중요한 지표로 설정하여 평가하였다.
본 연구의 제작한 MDGPC는 밀폐형 공압회로 내 가스 압력제어를 목적으로 하므로 공압회로 내·외부의 직·간접적 외란에 노출될 수 있으며, 이에 따라 제어 중 노출되는 압력 외란에 대한 설정압력 회복능력은 역시 평가되어야 할 중요 특성 중 하나이다. 이에 본 연구에서는 80 kPa의 설정압력으로 제어 중인 MDGPC에 외부에서 ±5 kPa의 압력 외란을 일정시간 동안 인가했을 때 MDGPC의 설정압력 회복 시간 및 회복 후 제어압력 안정도를 주요지표로 하여 MDGPC의 외란에 대한 회복능력을 평가하고자 하였다. 해당 시험에서 외부 압력 외란은 별도의 상용 가스 압력제어기를 이용하여 75 kPa 및 85 kPa의 압력을 발생시킨 후 약 5 s의 시간 동안 MDGPC의 가변체적형 챔버를 해당 압력에 노출시키는 방식으로 인가하였으며, 설정압력 회복시간은 압력 외란 인가 후 설정압력의 99.99%에 해당하는 압력으로의 회복까지 소요된 시간으로 정의하였다.
4. 시험결과
4.1 압력제어 안정도 평가
Figs. 4(a)와 4(b)는 약 ±2oC의 외기 온도변화 환경에서 각각 P 및 PI제어를 적용한 MDGPC의 압력제어 전후 가변체적형 챔버 내부 압력변화를 보여준다. 해당 시험에 있어 압력제어 전의 가변체적형 챔버는 축방향 길이를 고정하여 고정체적 모드(Fixed-Volume Mode)로 운용하였다. 그림에서 보이듯이 가변체적형 챔버 내부 압력은 고정체적 운용 시 외기 온도변화에 따라 크게 변하는 특성을 보였다. 반면, 선형 구동기 제어를 통한 압력제어를 실시할 경우 외기 온도변화와 무관하게 가변체적형 챔버 내부 가스압력이 설정압력으로 제어되었으며, 이에 따라 압력제어 안정도가 크게 향상되었다.
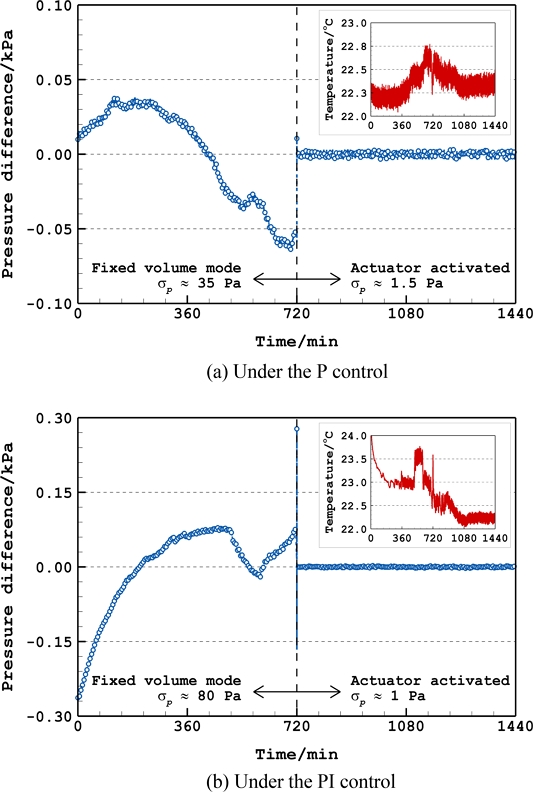
Stability changes in the gas pressure inside the variable-volume chamber when the MDGPC was in operation with the P or PI control method. The insets show the variation in the room temperature
가변체적형 챔버 내부 가스압력은 압력제어 전 약 80 Pa의 안정도로 변하였으나, P제어 및 PI제어를 적용한 MDGPC 구동하였을 시 각각의 제어 방식에 따라 약 1.5 Pa 및 약 1 Pa의 안정도로 매우 안정적인 가스 압력제어가 이루어졌음을 확인할 수 있다. MDGPC의 제어압력 안정도는 위와 같이 PI제어가 P제어 대비 다소 우수한 특성을 보였으나, 첨두치 진폭은 P제어와 PI제어에 따라 각각 약 7 Pa 및 약 20 Pa로 확인되어 P제어 시 보다 좁은 폭의 압력제어가 가능함을 확인하였다.
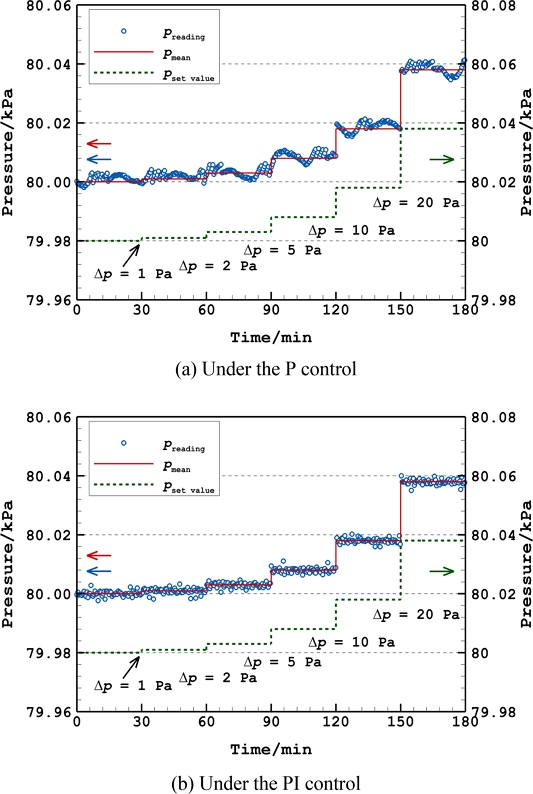
본 연구에서는 압력제어 안정도 시험에 이어 MDGPC의 압력제어 정밀도를 정량화하기 위한 분해능 평가를 수행하였다. 본 연구에서 압력제어 분해능은 1 Pa부터 20 Pa까지 설정압력을 약 두 배씩 증가시키며 측정압력 변화가 안정도를 벗어나 명확히 구분되는 설정압력 변화로 결정하였다. Figs. 5(a)와 5(b)는 각각 P제어 및 PI제어를 적용하였을 때 얻어진 가변체적형 챔버 내부 측정압력(청색 표식)의 설정압력(녹색 점선) 변화에 대한 응답특성을 보여주며, 각 설정압력 유지 구간에서의 측정압력 평균(적색 실선) 역시 도시되어 있다. 그림에서 확인할 수 있듯이 P제어 및 PI제어 시, 각각 설정압력 10 Pa 및 5 Pa 증가 시 측정압력의 명확한 변화가 관측되어 MDGPC의 압력제어 분해능이 P제어 및 PI제어에 따라 각각 약 10 Pa 및 약 5 Pa임을 확인하였다.
위 시험결과를 바탕으로 본 연구에서 제작된 MDGPC의 압력제어 안정도는 P제어와 PI제어에 대해 각각 약 1.5 Pa과 약 1 Pa로 확인되었으며, 제어 정밀도를 지시하는 압력제어 분해능은 P제어와 PI제어에서 각각 약 10 Pa과 약 5 Pa로 평가되었다. 이를 통해 압력제어 안정도는 PI제어 시 P제어 대비 다소 우수한 특성을 가짐을 확인하였으나, 첨두치 진폭의 경우 PI제어 대비 P제어 적용 시 더 좁은 폭의 압력제어가 가능함 역시 확인하였다.
4.2 순간 압력제어특성 평가
본 연구에서는 MDGPC의 순간 압력제어특성 평가를 위해 ±5 kPa의 계단형 설정압력 변화에 대한 압력제어 응답특성을 시험하였다. Figs. 6(a)와 6(b)는 각각 P 및 PI제어를 적용하였을 경우 얻어진 계단형 설정압력 변화에 대한 MDGPC의 압력제어 응답특성을 보여준다. 그림에서 볼 수 있듯이, 설정압력 변화(적색 점선) 시 선형 구동기 구동축 위치(녹색 점선)변화에 따라 측정압력(청색 표식)이 P 및 PI 제어 방식에 대해 각각 최대 약 1.9 kPa/s 및 2.4 kPa/s의 압력변화율로 계단형 변화를 근사하여 제어됨을 확인할 수 있다. Fig. 6(c)는 90 kPa에서 P제어 및 PI 제어를 통한 압력제어 중 제어압력의 변화를 보여준다. 그림에서 보이는 바와 같이, P제어를 적용한 MDGPC의 경우 측정압력(청색 표식)이 설정압력(적색 실선) 기준 약 3 Pa의 폭 내에서 제어되며 약 1.5 Pa의 제어압력 안정도를 가진 반면, PI제어 적용 시 측정압력(녹색 표식)이 설정압력(적색 실선) 기준 약 2 Pa의 폭 내에서 약 1 Pa의 제어압력 안정도로 제어됨을 확인할 수 있다. 다만, PI제어 시 외부 온도 변화에 따른 외란에 의해 간헐적으로 크게 압력이 변하는 특성을 보였다. Fig. 6(d)는 P제어 및 PI제어 중 설정압력(적색 실선)이 70 kPa에서 75 kPa로 변경될 때의 오버 슈트 특성을 보여준다. 그림에서 보이는 것과 같이 P제어를 적용할 경우 측정압력(청색 표식)에서 오버 슈트의 발생은 확인되지 않았으나, PI제어를 적용할 경우 측정압력(녹색 표식)에서 약 290 Pa의 오버 슈트가 발생하였음을 확인하였다.
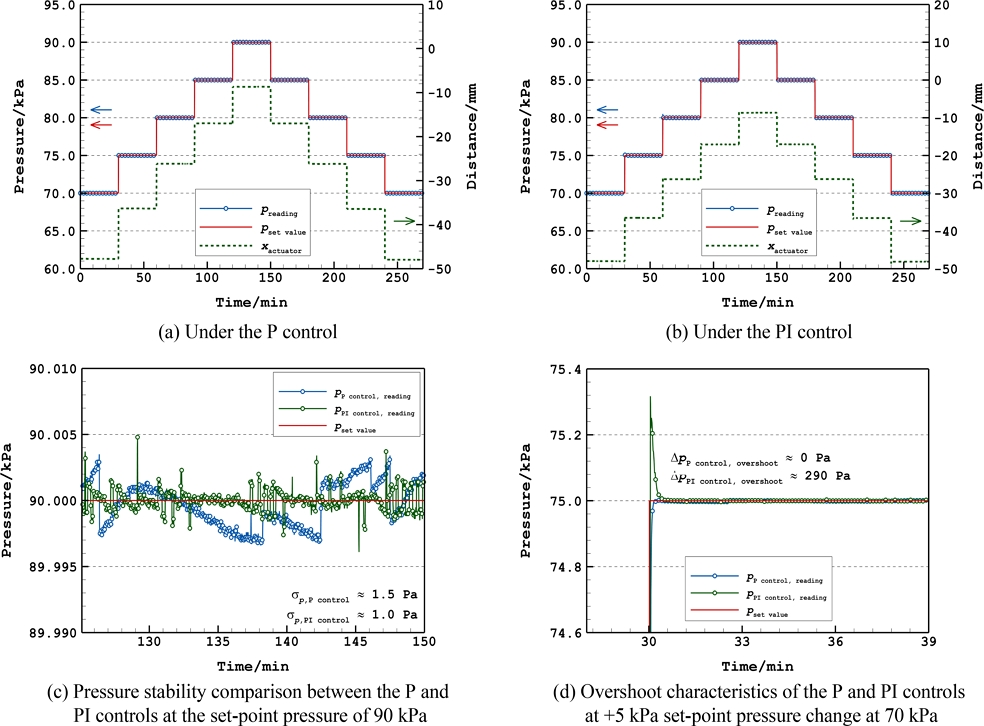
Response of the control gas pressure to stepwise set-point value changes with enlarged figures at specific pressure
위 시험결과들을 종합하여 볼 때, 설정압력 유지 구간의 제어압력 안정도는 PI제어의 경우 약 1 Pa로 약 1.5 Pa의 제어 안정도를 보인 P제어 대비 근소하게 우수하나, 설정압력 변화 시 PI제어에서 오버 슈트가 발생하여 제어 안정성을 악화시킬 수 있다는 점에서 설정압력 유지 및 변화를 아우르는 전반적인 압력제어를 위한 제어방식으로 P제어가 더욱 적절할 수 있음을 확인하였다.
4.3 외란에 대한 회복능력 평가
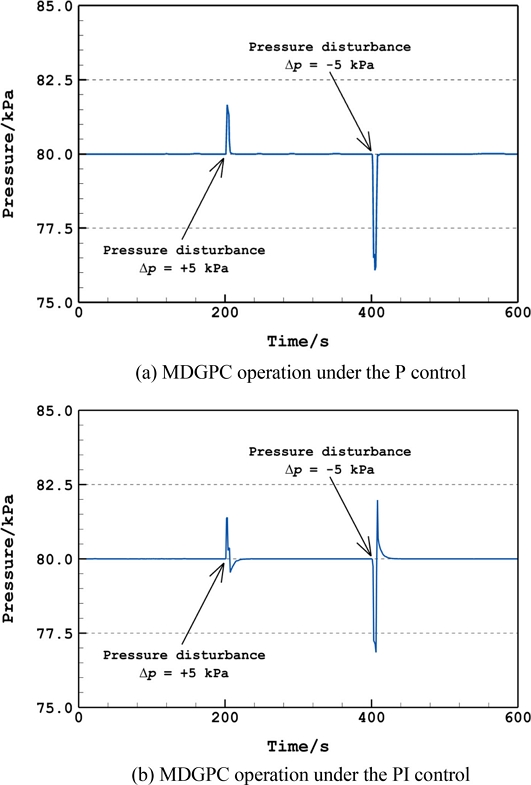
MDGPC의 압력 외란에 대한 설정압력 회복능력은 80 kPa의 설정압력으로 제어 중인 MDGPC에 ±5 kPa 압력 외란을 약 5초간 인가하였을 때 얻어진 설정압력으로의 회복 거동을 통해 평가하였다. Figs. 7(a)와 7(b)는 각각 P제어 및 PI제어를 통한 설정압력제어 중 ±5 kPa의 압력 외란에 노출된 후 얻어진 압력 회복과정을 보여준다. 그림을 통해 확인할 수 있듯이, 가변체적형 챔버 내부 압력은 압력 외란에 의해 잠시 영향을 받았으나 P제어 및 PI제어 시 각각 약 5초 및 약 20초 이내에 설정압력으로 회복하였으며, 회복 후 압력 안정도는 P제어와 PI제어 시 각각 1.5 Pa과 1 Pa로 평가되었다. 이에 따라, 본 연구에서 시험한 MDGPC는 압력 외란에 대해 제어 안정도 이내의 설정압력 회복능력을 가지고 있음을 확인하였다. 다만, 그림에서 확인할 수 있듯이, P제어의 경우 설정압력 회복 시 오버 슈트 또는 언더 슈트 없이 즉각적인 회복을 보인 반면, PI제어 시 제어압력에서 오버 슈트 및 언더 슈트가 발생하여, 압력 외란에 노출가능성이 존재하는 MDGPC의 운용에 있어 PI제어보다 P제어의 적용이 더욱 적합한 것으로 평가되었다. 또한, 그림에서 보이는 바와 같이 MDGPC는 설정압력보다 높은 값의 압력외란에 노출될 경우 낮은 값의 압력외란에 노출되는 경우 대비 더욱 강건한 특징을 보였는데, 이는 MDGPC의 가변체적형 챔버의 팽창과정 시 부피증가에 의한 압력 변화율이 감소하는 특징에 기인한다.
5. 결론
본 연구에서는 밀폐형 공압회로 내 고속·정밀 가스 압력제어를 실현하기 위해 가변체적형 챔버와 선형 구동기로 이루어진 밀폐형 기계 구동식 가스 압력제어기(MDGPC)를 제작하였다. MDGPC의 구동에 적합한 제어방식을 특정하기 위해 본 연구에서는 P제어 및 PI제어를 적용한 MDGPC의 가스 압력제어 특성을 시험하고자 하였다. 이를 위해 본 연구에서는 먼저 MDGPC의 구동에 적합한 P제어 및 PI제어의 최적 제어이득을 결정하였으며, 이와 같이 결정된 최적 P제어 및 PI제어 방식을 적용한 MDGPC의 압력제어특성을 시험하였다.
MDGPC의 압력제어 안정도 시험 결과, P제어와 PI제어를 적용할 시 모두 MDGPC 구동을 통해 가변체적형 챔버 내부 압력 안정도가 크게 향상됨을 확인하였으며, P제어 및 PI제어 시 각각 약 1.5 Pa와 1 Pa의 제어압력 안정도를 가짐을 확인하였다. 이어 수행된 ±5 kPa의 순간 설정압력 변화 및 압력 외란에 대한 MDGPC의 압력제어 및 압력회복 시험에서, MDGPC는 설정압력 변화를 따르는 계단형 압력변화 구현 및 압력 외란에 대해 제어 안정도 이내의 설정압력 회복 능력을 갖추고 있음을 확인하였다. 다만, PI제어를 통한 설정압력 변화 또는 압력 외란에 대한 설정압력 회복 시, P제어에서는 발현되지 않은 오버 슈트 및 언더 슈트가 발생하였다는 점에서 압력변화가 수반되는 제어에 있어 PI제어보다는 P제어가 더욱 적합함을 확인하였다. 이를 통해, 최적 P제어를 적용한 MDGPC를 사용할 경우 밀폐형 공압회로 기반 고속·정밀·고안정 가스 압력제어를 달성할 수 있음을 확인하였다.
NOMENCLATURE
| t : | Time |
| m : | Manipulated Variable |
| KP : | Coefficient for the Proportional Term (P gain) |
| KI : | Coefficient for the Integral Term (I gain) |
| KD : | Coefficient for the Derivative Term (D gain) |
| e : | Steady-State Error |
| l0 : | Initial Axial Dimension of the Bellows Chamber |
| σp : | Stability of the Controlled Gas Pressure |
| Δtext : | External Temperature Change |
| Δpcont : | Magnitude of the Pressure Change |
| Δpdist : | Magnitude of the Pressure Disturbance |
Acknowledgments
This paper was presented at KSPE Autumn Conference 2022
이 논문은 부경대학교 자율창의학술연구비(2021년)에 의하여 연구되었음.
REFERENCES
- Yun, S., Han, S., Kim, M., (2009), The world-wide market and technique trends of process & hydraulic-pneumatic valve, Journal of Drive and Control, 6(3), 2-9.
- Korea Association of Standards & Testing Organizations, (2017), Altermeters, (Report No. KASTO 17-20401-427).
- Korea Association of Standards & Testing Organizations, (2019), Absolute pressure gauges, (Report No. KASTO 19-20406-391).
- Kim, B.-S., Lee, J.-J., Nam, K.-W., Jeong, G.-S., Ahn, C.-B., Sun, K., (2007), Pressure regulation system for optimal operation of the pneumatic vad with bellows-type closed pneumatic circuit, Journal of Biomedical Engineering Research, 28(4), 569-576.
- Jang, J., (2001), A study on the pressure control of a pneumatic pressure vessel considering dynamic characteristics of pneumatic transmission line, Journal of Power System Engineering, 5(4), 90-96.
- Jang, J. S., Lee, K. K., (2001), A study on the pressure control of a pneumatic pressure vessel, Proceedings of the Korean Society for Power System Engineering 2001 Autumn Conference, 296-301. https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE01039826
- Jang, J. S., Koh, D. K., Kim, Y. B., (2006), Pressure control in a pneumatic pressure chamber, Proceedings of the Korean Society for Power System Engineering 2006 Spring Conference, 333-338. https://www.dbpia.co.kr/Journal/articleDetail?nodeId=NODE01028097
- Yun, S., Kim, C., Seo, S., Park, J., Ham, Y., (2006), Pressure regulator for piezoelectric valve, Transactions of the Korea Fluid Power Systems Society, 3(2), 1-6.
- Yun, S., Kim, C., Ham, Y., Park, J., Youn, D., (2007), Digital control for PZT type electro-pneumatic regulator, Proceedings of the Korean Society of Precision Engineering Conference, 93-94.
- Yun, S., Lee, K., (2008), Digital control of electro-pneumatic regulator with two piezoelectric microvalves, Journal of Drive and Control, 5(2), 17-23.
-
Kim, B.-W., (2011), A study on the characteristics of high pressure regulator for vehicle CNG, Journal of the Korea Academia-Industrial Cooperation Society, 12(12), 5997-6003.
[https://doi.org/10.5762/KAIS.2011.12.12.5997]

- Jung, J.-H., Nam, C.-W., Kim, M.-K., (2021), A study on the pressure control process of gas regulators through numerical analysis, Journal of the Korean Institute of Gas, 25(5), 37-51.
- Yoo, C. Y., Kang, S. M., Choi, S. W., (2020), Method for determination of pump ejection quantity through in vitro experiment of ECMO using pneumatic pulsatile pump, Proceedings of the Korean Society Mechanical Engineers 2020 conference, 1996-1998.
-
Cavaglià, M., Olivieri, C., Morbiducci, U., Raparelli, T., Jacazio, G., Ivanov, A., Chiesa, A., Savino, D., Chiarenza, S. M., Romiti, A., (2021), Noninvasive mechanical ventilation in the COVID?19 era: Proposal for a continuous positive airway pressure closed?loop circuit minimizing air contamination, oxygen consumption, and noise, Artificial Organs, 45(7), 754-761.
[https://doi.org/10.1111/aor.13888]

-
Joung, W., Gam, K. S., Kim, Y.-G., Yang, I., (2015), Hydraulic operating temperature control of a loop heat pipe, International Journal of Heat and Mass Transfer, 86, 796-808.
[https://doi.org/10.1016/j.ijheatmasstransfer.2015.03.056]

- Joung, W. C., (2015), Loop heat pipe-based hydraulic temperature control technique and its application to the precision thermometry, Proceedings of the Korean Society Mechanical Engineers 2015 conference, 1517-1519. https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE06575881
- Kim, J.-W., Choi, K.-H., Kim, D.-S., (2008), A study for micro-patterning using an electrostatic inkjet, Proceedings of the Korean Society Mechanical Engineers Conference, 1103-1106.
-
Yang, Y.-J., Ko, J.-B., Dang, H.-W., Kim, H.-C., Choi, K.-H., Cho, K.-H., (2012), Development of pneumatic ink supply system for electrostatic head on meniscus control, Journal of the Korean Society for Precision Engineering, 29(4), 455-460.
[https://doi.org/10.7736/KSPE.2012.29.4.455]

- Desborough, L., Miller, R., (2002), Increasing customer value of industrial control performance monitoring-Honeywell's experience, Proceedings of the AIChE Symposium Series, 169-189. https://www.researchgate.net/profile/Lane-Desborough/publication/228814712_Increasing_Customer_Value_of_Industrial_Control_Performance_Monitoring_-Honeywell's_Experience/links/573cb75b08aea45ee8419a26/Increasing-Customer-Value-of-Industrial-Control-Performance-Monitoring-Honeywells-Experience.pdf
-
Lei, G., (2020), Feedback and uncertainty: Some basic problems and results, Annual Reviews in Control, 49, 27-36.
[https://doi.org/10.1016/j.arcontrol.2020.04.001]

-
Smith, C. A., (2003), Automated continuous process control, John Wiley & Sons.
[https://doi.org/10.1002/0471218839]


M.Sc. candidate in the Department of Intelligent Robot Engineering, Pukyong National University. His research interest is on precision thermal control.
E-mail: cypark9015@gmail.com

Assistant Professor in the School of Mechanical Engineering, Pukyong National University. His main research interest is on precision thermal control and thermometry.
E-mail: wukchuljoung@pknu.ac.kr