고장진단을 위한 영구자석형 동기모터 유한요소 모델 개발

1. 서론

최근, 직면한 환경 문제 해결을 위해 다양한 산업 분야에서 전동화와 함께 전기 모터 사용이 빠르게 증가하고 있다. 다양한 전기모터 중 영구자석형 동기모터(Permanent Magnet Synchronous Motor, PMSM)는 높은 에너지 효율 및 출력 밀도를 갖는 장점 덕분에 전기자동차 산업을 포함한 다양한 산업분야에서 각광받고 있다. 영구자석형 동기모터에 대한 관심이 증가함에 따라 모터 출력 향상, 토크 리플 및 진동 저감 등 관련분야에 대한 연구가 지속적으로 진행되어 왔으며[1,2], 영구자석형 동기모터 사용량이 증가함에 따라 안정성 또한 중요한 문제로 대두되고 있다. 영구자석형 동기모터는 영구 자석, 권선, 베어링과 회전체 등 다양한 부품들로 구성되어 있으며 하나의 부품에만 이상이 발생해도 전체 시스템의 정상적인 구동이 불가능하다. 따라서 모터시스템 상태감시 및 고장진단과 관련된 연구 또한 활발하게 진행 중이다[3].

모터는 전류가 인가되어 발생하는 회전 자기장과 영구자석의 자기장의 상호 작용을 통해 전기적인 에너지를 기계적인 에너지로 변환하여 토크를 발생시킨다. 일반적으로 고장 발생 시 인가되는 전류 특성이 변화하기 때문에 전류를 감시하여 고장을 구별하는 MCSA (Motor Current Signature Analysis) 기법에 대해서 많은 연구가 수행되었다[4]. 해당 기법은 전류 데이터를 통해 쉽게 고장 감지가 가능하지만, 모터 공간 정보를 담아내지 못해 고장이 어디에 발생했는지 정확히 규명하기 어렵다. 이러한 단점 보완을 위해 모터에서 전기에너지를 기계에너지로 변환 시 발생하는 열 및 진동을 기반으로 고장을 탐지하는 기법 또한 지속적으로 연구되고 있다[5]. 하지만 이런 기계적 신호 기반 진동 신호 감시 기법은 추가 센서를 설치해야 하기 때문에 비용 증가의 단점이 존재한다.

최근 컴퓨터 연산속도 향상 및 다변량 데이터 수집 용이함이 인공지능(Artificial Intelligence, AI) 기반 모터 고장진단 연구를 활발하게 하였다. 구체적으로, 측정된 모터 응답을 기반으로 고장 여부를 판별하는 방법이 제시되었으며[6], 모터의 응답을 학습하여 응답 자체를 모사하는 연구 또한 진행되었다[7]. 또한 디지털 트윈 기술을 도입하여 모터 고장 시 응답변화 가상데이터를 산출하고 이러한 가상데이터를 기반으로 인공지능을 학습하는 연구 또한 주목받고 있다. 구체적으로, 모터 회전체의 경우 베어링 부품에서 고장이 자주 발생하지만 실제 데이터를 측정하기 어렵기 때문에, 가상 고장데이터를 생성하고 학습 가능하다면 고장진단에 용이하다[8]. 따라서 고정확도 유한요소해석을 통해 모터를 모델링하고 고장데이터를 생성하는 연구 또한 활발히 진행되는 연구분야이다. 구체적으로, 모터 단면을 이차원 모델링하여 모터 운전조건에서 발생하는 전자기장을 계산하고 이를 기반으로 진동과 열에 영향을 주는 인자들을 연성하여 정상상태 및 고장에 의해 변동하는 진동 및 온도특성을 분석하면 효율적 고장 진단 알고리즘 개발이 가능하다고 사료된다[9-11]. 이러한 디지털 트윈 기반 고장진단 연구를 수행하기 위해서는 우선 정확도 높은 모터 전자기장 모델을 구현해야 하기 때문에 본 연구에서는 다양한 운전 조건에서 영구자석형 동기모터의 전자기 특성을 예측 가능한 유한요소 모델을 개발하였다. 구체적으로 모터에 전류가 인가될 때 발생하는 전자기장 관련 지배방정식을 연성하여 2차원 전자기력 산출할 수 있는 유한요소 모델을 구현하였으며, 상세 형상은 대상 모터를 분해하여 구체적 제원을 산출하였다. 또한 테스트 베드를 구축하여 제안 모델의 정확도 및 성능을 정량적으로 검증하였다. 본 연구에서 제시하는 고정밀 유한요소 해석모델은 고장을 포함한 영구자석형 모터의 다양한 운전조건에서의 전자기장 응답을 예측 가능하기 때문에, 디지털 트윈 기반 설계최적화 및 고장진단 분야 등 다양한 정밀공학분야에 활용이 가능할 것으로 사료된다.

2. 영구자석형 동기모터 유한요소 모델 구축 및 고장 모사

2.1 영구자석형 동기모터 유한요소 모델

영구자석형 동기모터는 고정자에 권선된 코일에 3상 전류가 인가되면, 3상 교류 전류로 인해 회전 자기장이 형성되는 원리이다. 구체적으로, 영구자석이 부착된 회전자가 전류로 인해 회전하는 자기장의 위상에 동기(Synchronization)되어 회전하며 자기력이 생성된다. 또한 이렇게 생성된 자기장은 고정자와 회전자 사이 공극(Air Gap)에서 생성되는 전자기력을 기반으로 회전자에 기계에너지인 토크를 생성한다. 모터에 흐르는 전류로 인해 공극에서는 Maxwell Equation(식(1))을 통해 자기 벡터 포텐셜을 계산한다.

$\[ \nabla \times \left(\frac{1}{\mu }\nabla \times A\right)=J \]$

(1)

여기서 μ는 자기 투자율(Permeability), A는 자기 벡터 포텐셜, J는 전류 밀도를 나타낸다. 자기 벡터 포텐셜을 기반으로 공극에서의 자속 밀도 B를 계산할 수 있다. 유한요소 모델의 전자기 해석의 빠르며 높은 정확도를 갖는 2D 단면으로 간소화하여 계산한다. 모터의 단면인 원을 중심으로 r, θ, z 좌표계를 지정하여, 자기 벡터 포텐셜의 z 방향 성분만 고려하는 것이 가능하다. 이 때 자기 벡터 포텐셜에 의한 자속 밀도 B는 식(2) 및 식(3)을 이용하여 계산된다.

$\[ B=\nabla \times A \]$

(2)

$\[ B=\left[\frac{1}{r}\frac{\partial A_z}{\partial \theta }\right]\widehat{r}+\left[-\frac{\partial A_z}{\partial r}\right]\widehat{\theta } \]$

(3)

계산된 자속 밀도는 회전자에 자기력으로 작용하여 회전을 유도하고 이를 통해 모터는 전기적인 에너지로부터 기계적인 에너지인 토크를 발생시킨다. 회전자에 가해지는 단위체적당 힘 f는 Maxwell 방정식에 의해 식(4)와 같이 정의되며, 이로부터 Maxwell Stress Tensor σ를 정의할 수 있다.

$\[ f=\frac{1}{\mu }\left[\left(\nabla \cdot B\right)B+\left(B\cdot \nabla \right)B-\frac{1}{2}{B}^2\right] \]$

(4)

$\[ f=\nabla \cdot \sigma \]$

(5)

$\[ \sigma =\frac{1}{\mu }\left[\begin{array}{ccc}\frac{B_r^2-B_{\theta }^2-B_z^2}{2}& B_r{B}_{\theta }& B_r{B}_z\\ B_{\theta }{B}_r& \frac{B_{\theta }^2-B_r^2-B_z^2}{2}& B_{\theta }{B}_z\\ B_z{B}_r& B_z{B}_{\theta }& \frac{B_z^2-B_r^2-B_{\theta }^2}{2}\end{array}\right] \]$

(6)

Maxwell Stress Tensor σ로부터 2D 형상의 회전자에 가해지는 토크 T는 다음과 같이 유도된다.

$\[ T={\int }_S r\times \sigma \cdot ds \]$

(7)

$\[ T=\frac{1}{{\mu }^2}{\int }_0^{2\pi } r^2{B}_r{B}_{\theta }d\theta \]$

(8)

이때 ε 길이의 공극을 가지는 모터의 경우 가해지는 토크는 공극에서의 면적분으로 계산된다(식(9)).

$\[ T=\frac{1}{\mu \epsilon }{\int }_S r{B}_r{B}_{\theta }dS \]$

(9)

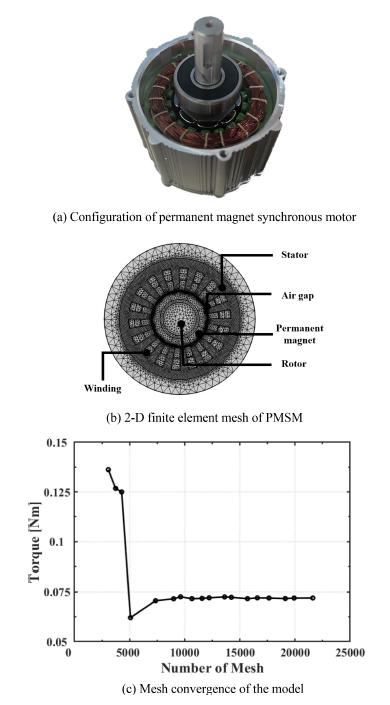
본 연구에서는 식(9)를 바탕으로 모터의 전자기 해석을 위한 2D 유한요소 모델을 구축하였다. 모델 형상은 3장에서 후술된 실험에 사용한 모터의 단면인 Fig. 1(a)를 참고하였으며, 해당 모델의 구조 및 물성치는 Table 1에 명시하였다. 토크는 모터의 구조 변수 및 자속 밀도 값으로 계산되며, 토크 값이 실제 모터의 토크 값과 유사하다면 유한요소 모델이 실제 모터의 전자기 특성을 매우 정확하게 모사한다.

Fig. 1

PMSM used for experiments and finite element model

Table 1

Specification of PMSM FE model

유한요소 모델이 실제 모터의 토크 특성을 정확하게 예측하기 위해서는 모터의 구조 및 물성뿐만 아니라 모터 구동에 필요한 입력 정보 데이터도 규명되어야 한다. 토크 값 계산에 필요한 자속 밀도는 공극 내에 회전하는 회전자 및 전류에 의한 자기장으로 생성되기 때문에, 본 연구에서는 정확한 토크 특성 모사를 위해 유한요소 모델에 실제 모터의 구동 및 제어에 따른 회전자의 위치 및 전류 값을 그대로 대입하여 공극 내에 자기장이 계산하였다. 본 연구에서는 실측 데이터를 적용하여 정상 및 과도 상태의 토크 응답뿐만 아니라 토크 리플 또한 표현 가능하도록 구성하였다.

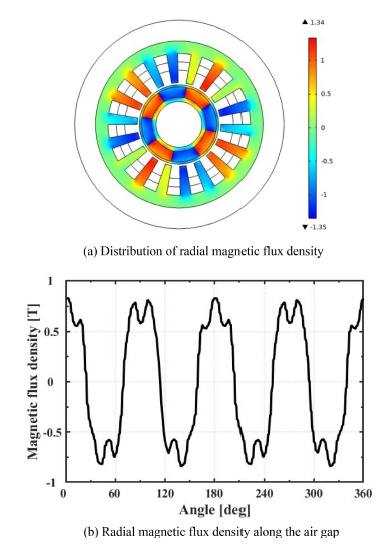
Fig. 1(b)에 유한요소 모델 해석을 위한 메쉬(Mesh) 구성을 도시하였다. 메쉬는 모터의 부품별로 다르게 구성하여 유한요소 해석의 정확성 및 계산 시간을 최적화하였다. 특히 자기장계산에서 정밀도에 큰 영향을 미치는 각 부품 간 경계 영역은 세밀한 메쉬를 갖도록 구성하였다. 즉, 토크 계산은 공극 내의 자속 밀도의 적분을 통해 계산되기 때문에 해당 영역에서 오차가 크게 발생 가능하며, 이러한 특성을 고려할 때 이 관심영역에서는 정교하게 메쉬를 구성하여야 정확도가 보장된다. 충분할 정도의 정교한 메쉬 구성을 위해 메쉬 수렴성을 조사하였다. 해당 유한요소 전자기 모델은 측정된 모터 전류 및 회전자의 위치 데이터를 입력으로 사용하여 전자기장 및 토크가 계산되는데, 메쉬 수를 늘려가며 같은 입력 데이터에 대해 계산되는 토크 값의 경향을 확인하였다. Fig. 1(c)을 근거로 유한요소 모델은 총 17,643개의 메쉬로 구성하였다. 계산된 특정 시간에서의 자기장 특성은 Fig. 2에 예시로 도시하였다. 본 연구에서 모사한 8극 모터의 경우 반경 방향의 자속 밀도는 공극 내에서 극수의 절반에 해당하는 고조파 성분을 가지게 되고 4^th 고조파 성분을 크게 갖는 것을 Fig. 2(b)에서 확인할 수 있다. 따라서 제안 모델의 실제 영구자속형 모터의 특성을 잘 모사함을 추론 가능하다.

Fig. 2

Magnetic flux density profile of PMSM FE model

2.2 고장모사: 편심

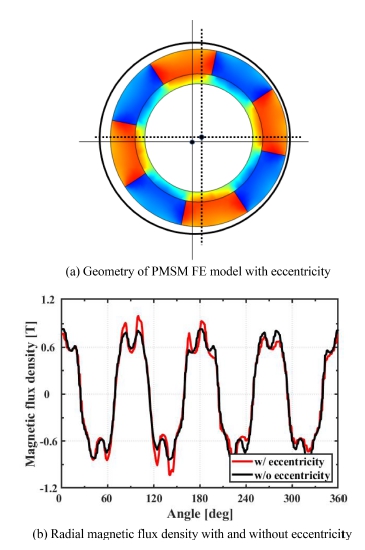
모터는 고장이 발생함에 따라 전자기 특성이 달라진다. 본 연구에서는 유한요소 모델을 이용하여 고장 상태에 대한 전자기응답을 예측하고자 대표적인 고장 모드인 편심을 구현하였다. 모터의 회전축 편심은 설계 공차 및 연결 축 불량으로 모터 내에 가장 자주 발생하는 고장 모드이다. 편심이란 회전자의 회전 축이 고정자의 중심축으로부터 벗어나 회전하게 되는 상태로 정의되며, 이로 인해 모터는 불필요한 진동 및 소음에 노출되고 베어링의 부하로 연결되어 고장이 가속화되고 수명이 감소한다. 따라서 이러한 편심을 감시하고 고장이 발생하기 전 적절한 예방정비가 필요하다. 본 연구에서는 Fig. 3(a)에 도시된 바와 같이 회전자의 중심이 고정자의 중심과 불일치하도록 유한요소 모델을 구축하여 편심 고장을 모사하였다.

Fig. 3

PMSM FE model with eccentricity

모터는 고정자와 회전자 사이 공극에서 자기장이 형성된다. 하지만 회전자의 회전축이 편심될 경우 공극에 불균형이 발생하고 이러한 구조 변형은 형성되는 자기장의 불균형을 야기시켜 전체적인 전자기적인 거동의 변화를 유발한다. 첫 번째로 모터 공극에서 발생하는 기자력 F (Magnetomotive Force)는 고정자 인가 전류 및 회전자의 영구자석으로부터 생성된다. 기자력으로부터 발생하는 자기장은 투과율(Permeance)로부터 결정되고 투과율 Λ는 식(10)과 같이 정의된다.

$\[ \Lambda \left(t,\alpha \right)=\frac{\mu }{\delta \left(t,\alpha \right)} \]$

(10)

식(10)에서 δ(t, α)는 편심이 존재할 때 시간 t와 공극의 위치각 α에 따라 변화하는 공극 길이이며, 기자력에 의한 자속밀도는 식(11)로 정의된다.

$\[ B_r=F(t,\alpha )\times \mathrm{\Lambda }(t,\alpha ) \]$

(11)

결과적으로 공극의 비대칭은 자기장의 불균형에 직접적으로 영향을 미치게 된다. 편심 모델에서는 회전자 위치를 고정자의 중심에서 0.15 mm 이격시켰고, 이에 따른 전자기 응답을 편심이 없을 때와 비교하여 Fig. 3(b)에 도시하였다. 나머지 조건은 동일한 채로 편심의 조건만 주었을 때, 자속 밀도는 편심으로 인한 공극의 비대칭으로 인해 불균형한 모습을 보이는 것을 확인할 수 있다.

3. 테스트베드 구축 및 실험

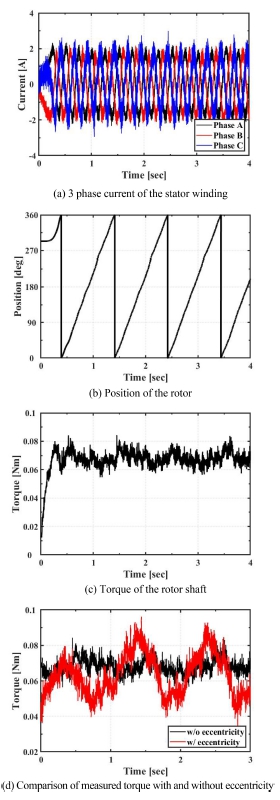
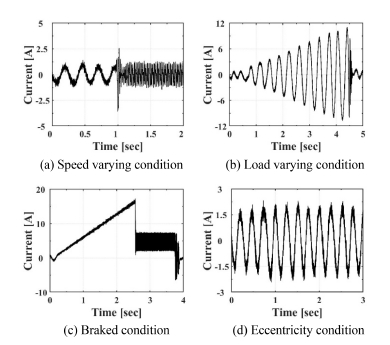
정상 및 고장 상태 모터에 대한 유한요소 모델의 검증을 위한 테스트베드를 Fig. 4와 같이 구축하였다. 모터는 드라이버 및 컨트롤러를 통해 FOC (Field Oriented Control) 제어로 구동된다. 정상상태 모터의 경우 여러 조건에서 구동 데이터를 취득하였고, 대표 고장 모드인 편심 조건에서도 실험을 진행하여 데이터를 취득하였으며, 상세 운전조건은 Table 2에 기술하였다. 정상(Steady) 및 과도(Transient) 상태에서 모터 전자기 특성 관찰을 위해 다양한 운전조건에서 실험을 진행하였다. 모터가 제어됨에 따라 측정되는 전류 및 회전자의 위치는 모터의 드라이버 및 내장 엔코더(Encoder)를 통해 수집하였고 Table 2의 첫 번째 실험에서 측정한 데이터를 대표적인 예시로 Figs. 5(a) 및 5(b)에 도시하였다. 또한 실험 시 인가되는 해당 데이터를 구축한 유한요소 모델에 입력으로 인가하여 산출된 전자기 해석 결과를 기반으로 토크 값을 산출하였다. 산출된 토크 값은 테스트베드에 설치된 토크 센서 측정값과 정량적 비교/분석을 실시하여 본 연구에서 제안하는 영구자석형 전기 모터 유한요소 모델의 정확도를 검증하였다. 첫 번째 실험의 토크 측정값은 Fig. 5(c)에 예시로 도시하였다.

Fig. 4

PMSM experimental setup

Table 2

List of various operating condition of PMSM experiment

Fig. 5

Measured data from PMSM testbench setup

또한 모터 주요 고장 모드인 정적 편심 상태를 모사하기 위해 실험에서 Fig. 4의 고정된 영구자석형 동기모터의 고정자를 포함한 하우징을 이격시킨 채로 고정하였다. 회전자는 토크센서의 축과 커플링으로 단단하게 연결되어 있어 고정된 반면 고정자의 중심축을 이동시킴으로써 회전자의 중심 회전축이 고정자의 중심으로부터 벗어난 정적 편심 상태 모사가 가능하다. 이러한 실험조건은 2장에서 기술한 편심 모델과 동일한 상황으로서 편심이 인가된 상황에서 모터 전자기 특성을 검증할 수 있다. 편심된 모터 전자기 특성은 비대칭 공극으로 인한 불균형한 자기장 형성된다는 것인데, 결과적으로 회전자 토크 또한 불균일하게 나타나는 것을 Fig. 5(d)에 도시된 측정결과에서 확인 가능하다.

4. 결과분석 및 고찰

유한요소 모델을 통해 계산된 토크 값과 위 구축된 테스트베드를 통해 측정한 토크 값의 비교를 통해 다양한 구동조건 및 고장 조건에서 모델의 검증을 진행하였다. Table 2에 기술한 첫번째 운전 조건으로, 정지해 있던 무부하 모터를 60 RPM으로 구동했을 때 실험 및 해석 모델의 토크를 비교 및 검증하여 Fig. 6에 도시하였다. 정지되어 있던 모터는 0초부터 구동되어 0.2초까지 과도응답 상태를 거쳐 정상 상태의 토크 특성이 관찰 가능하다. 모터 구조 및 물성치뿐만 아니라 영구자석형 동기모터의 제어에 필요한 전류 및 위치 데이터를 유한요소 모델에 그대로 입력으로 사용하여 단순히 정상 상태에서의 토크만 예측하는 것이 아니라 과도 상태 및 토크 리플 또한 유한요소 모델을 통해 정확하게 모사 가능한 것을 Fig. 6을 통하여 관찰할 수 있다.

Fig. 6

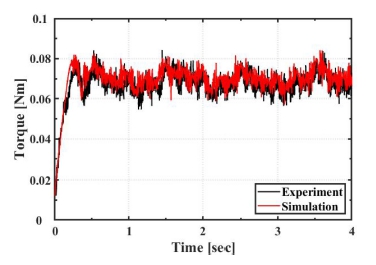
Comparison of torque characteristics between measured and calculated torque during no load operating condition

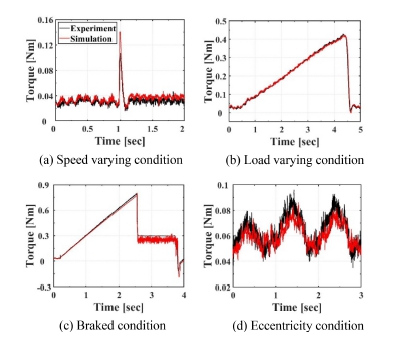
나머지 구동 조건에서 유한요소 모델에서 산출되는 토크 값과 측정한 값 또한 동일한 경향을 보이는 것을 Fig. 7에서 관찰가능하다. 구체적으로, 1초에 60 RPM으로부터 600 RPM까지 속도를 급격하게 증가시키는 속도 가변 조건(Table 2 두 번째 운전조건)에서 나타나는 토크 과도 응답, 무부하 상태부터 0.4 Nm까지 토크가 점차적으로 증가하는 가변 부하 조건에서 나타나는 토크 응답(Table 2 세 번째 운전조건) 또한 유한요소 모델 추정결과가 실험결과와 유사함을 확인 가능하다. 브레이크를 이용하여 구동 토크보다 큰 힘으로 구동 중인 모터를 정지할 때의 토크(Table 2 네 번째 운전조건)의 경우, 2.5초 이후 해석상 토크 값의 리플이 크게 나타난다. 이는 모터에 정격 전류가 흐를 때, 드라이버를 통해 측정되는 전류에 잡음이 포함되어 측정되는 현상이 있었는데(Fig. A1), 해당 전류를 그대로 유한요소 모델에 사용하여 실험값과 차이가 발생하였다. 하지만 정격 토크 이상의 하중이 지속되는 상태를 제외하고, 즉 정상적인 모터 구동 상황에서는 이 경우 또한 매우 정확하게 토크 값 예측이 가능한 것으로 보인다. 요약하면, 본 연구에서 제안하는 고정밀 유한요소 해석모델은 다양한 운전조건에서 영구자석형 전기모터의 전자기 특성을 매우 잘 반영하여 실제 모터의 응답에 해당하는 실험값과 매우 유사한 토크 값을 도출해 낼 수 있다. 마지막으로, 모터의 고장 상태인 편심에 대한 모델 응답을 Fig. 7(d)과 같이 실험값과 비교/분석하여 모델 정확도를 검증하였다(Table 2다섯 번째 운전조건). 비대칭을 갖는 공극을 유한요소 모델로 구현하여 편심에 따라 달라지는 토크 응답을 계산하면 실험값과 유사한 결과가 산출됨을 관찰 가능하며, 이를 통하여 앞서 서술한 불균형한 자기장 모사가 가능함을 추론 가능하다. 따라서 제시된 모델은 모터의 고장 상태에서 달라지는 응답 또한 산출 가능하기 때문에, 고장진단에 사용할 수 있는 데이터 생성이 가능하다고 간주할 수 있다.

Fig. 7

Validation of calculated torque of finite element model of PMSM in various operating conditions

유한요소 모델의 정량적 검증을 위해 토크 계산 값과 실험값의 RMSE (Root Mean Squared Error)를 계산하여 Table 3에 구동 조건별로 도시하였다. 해당 실험에서 구동 조건에 따라 토크 스케일이 크게는 10배까지 변하는데 이로 인해 RMSE 값은 비례하여 증가하기 때문에 각 구동 조건별 RMSE를 정량적으로 정확하게 비교하기 위해 각각 계산 값과 실험값에 대해 토크 평균 값에 대한 RMSE 값도 함께 표에 도시하였다. Figs. 6, 7의 토크 개형 비교 및 Table 3의 RMSD를 근거하여 제안한 모터의 유한요소 전자기 모델은 고장 상태를 포함한 여러 조건에서 의미 있는 해석 결과를 도출하고 고장 진단을 위해 활용도가 높음을 확인할 수 있다.

Table 3

Comparison between experimentally measured torque and simulated torque

5. 결론

본 연구에서는 고장 상태를 포함한 여러 운전 조건에서 영구 자석형 동기 모터 전자기 응답특성을 예측 가능한 유한요소 모델을 제시하였다. 해당 유한요소 모델은 실제 실험에서 사용된 모터의 구조 및 물성을 반영하여 구축하였으며, 관심모터의 전자기 특성을 정확하게 반영하기 위해 유한요소 모델 토크 값이 계산되기에 필요한 대입되는 전류 및 회전자의 위치 데이터를 가상으로 생성하지 않고 실험에서 직접 측정한 값을 사용하였다. 또한, 다양한 운전 조건에서 정상 상태, 과도 상태와 토크 리플을 매우 정확하게 구현이 가능한 것을 실험과 비교분석을 통해 검증하였으며, 편심을 갖는 모터의 달라지는 전자기 응답 또한 유한요소 모델을 통해 구현 가능하다는 것을 검증하였다. 모터 편심은 토크만 불균일하게 만들뿐 아니라 회전자 전체 불평형 자기력(Unbalanced Magnetic Pull, UMP)을 형성하여 심한 진동 및 베어링 부하를 야기시키는데 이러한 상황에 대한 구현 방법을 본 연구에서는 제시하였다. 향후 연구에서 영구자석형 전기모터에 대해 제시된 전자기 모델을 근간으로 고장진단에 사용 가능한 다물리 응답을 산출하는 모델을 구현할 계획이다.

Acknowledgments

본 연구는 한국기계연구원의 기본사업(NK244B) 지원을 받아 수행되었습니다.

REFERENCES

• Kang, G.-H., Son, Y.-D., Kim, G.-T., Hur, J., (2009), A novel cogging torque reduction method for interior-type permanent-magnet motor, IEEE Transactions on Industry Applications, 45(1), 161-167. [https://doi.org/10.1109/TIA.2008.2009662]
• Jang, I.-S., Kim, W.-H., (2020), Study on electromagnetic vibration analysis process for PM motors, IEEE Transactions on Applied Superconductivity, 30(4), 1-6. [https://doi.org/10.1109/TASC.2020.2976070]
• Bhuiyan, E. A., Akhand, M. M. A., Das, S. K., Ali, M. F., Tasneem, Z., Islam, M. R., Saha, D., Badal, F. R., Ahamed, M. H., Moyeen, S., (2020), A survey on fault diagnosis and fault tolerant methodologies for permanent magnet synchronous machines, International Journal of Automation and Computing, 17, 763-787. [https://doi.org/10.1007/s11633-020-1250-3]
• Ebrahimi, B. M., Roshtkhari, M. J., Faiz, J., Khatami, S. V., (2013), Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis, IEEE Transactions on Industrial Electronics, 61(4), 2041-2052. [https://doi.org/10.1109/TIE.2013.2263777]
• Tsypkin, M., (2011), Induction motor condition monitoring: Vibration analysis technique-A practical implementation, Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), 406-411. [https://doi.org/10.1109/IEMDC.2011.5994629]
• Ince, T., Kiranyaz, S., Eren, L., Askar, M., Gabbouj, M., (2016), Real-time motor fault detection by 1-D convolutional neural networks, IEEE Transactions on Industrial Electronics, 63(11), 7067-7075. [https://doi.org/10.1109/TIE.2016.2582729]
• Lopes, T. D., Raizer, A., Valente Júnior, W., (2021), The use of digital twins in finite element for the study of induction motors faults, Sensors, 21(23), 7833. [https://doi.org/10.3390/s21237833]
• Tadina, M., Boltežar, M., (2011), Improved model of a ball bearing for the simulation of vibration signals due to faults during run-up, Journal of Sound and Vibration, 330(17), 4287-4301. [https://doi.org/10.1016/j.jsv.2011.03.031]
• Martinez, J., Belahcen, A., Detoni, J., (2016), A 2D magnetic and 3D mechanical coupled finite element model for the study of the dynamic vibrations in the stator of induction motors, Mechanical Systems and Signal Processing, 66, 640-656. [https://doi.org/10.1016/j.ymssp.2015.06.014]
• Xie, Y., Chen, P., Li, F., Liu, H., (2019), Electromagnetic forces signature and vibration characteristic for diagnosis broken bars in squirrel cage induction motors, Mechanical Systems and Signal Processing, 123, 554-572. [https://doi.org/10.1016/j.ymssp.2019.01.030]
• Taras, P., Li, G.-J., Zhu, Z.-Q., Foster, M. P., Stone, D. A., (2018), Combined multiphysics model of switched flux PM machines under fault operations, IEEE Transactions on Industrial Electronics, 66(9), 6737-6745. [https://doi.org/10.1109/TIE.2018.2877089]