벽 등반 드론 자세에 따른 모듈형 영구자석 휠-레그의 부착력

1. 서론

임무 범위와 수행 시간 확장을 위해 드론 관련 기술이 지속해서 개발되고 있다. 배터리 성능개선이 중요하지만, 개별 부품 개발로도 임무 수행 능력을 확장하고 작동 시간을 늘릴 수 있다. 예를 들어 열 적외선 카메라와 이미지 처리 프로그램으로 드론 수색 및 관측 능력이 확장된 것과 같이, 개별 부품 개발로 임무수행 범위 및 효율성을 확장했다[1,2]. 드론이 벽면 등반이 가능하면 시설물 정밀검사와 같이 임무 수행 범위 및 효율성 향상이 가능하다.

기존 드론은 벽면 부착이나 이동을 위해 계속해서 에너지를 사용한다[3]. 또한 타이밍 풀리형 자석 바퀴, 강자성체 영구자석 바퀴, 흡착식 패드 등의 기존 벽면 부착/이동 장치는 강자성체자로(Magnetic Flux Path)나 공기 압축기 등이 필요하여 드론에 적용하기 어렵지만 휠-레그는 가능하다[4-6].

영구자석 휠-레그(Wheel-leg)는 테두리 없이 몇 개의 바퀴살(Spoke)로 구성되어 가볍고 부가장치가 필요 없다[7,8]. 하지만 벽면을 부착 및 이동을 위한 휠-레그 부착력 관련 연구가 부족하다.

이 논문에서는 벽 등반 드론 자세에 따른 모듈형 영구자석 휠-레그의 부착력을 연구했다. 자석 휠-레그 개수는 3개로 결정하여 드론의 질량을 최소화하고 드론의 치수, 강자성 벽면의 기울기, 드론의 자세 등을 고려하여 영구자석 휠-레그의 필요 부착력 식을 유도했다. 유도한 부착력의 유효성을 검증하기 위해 간략 실험 모델을 제작하고 역학적 요소들을 변화시키며 부착력을 측정했다. 마지막으로 역학적 요소 변화에 따라 부착력을 잃는 벽면 각도를 측정하고 유도한 부착력 식과 비교하여 그 유효성을 검증했다.

2. 본론

2.1 벽 등반 드론

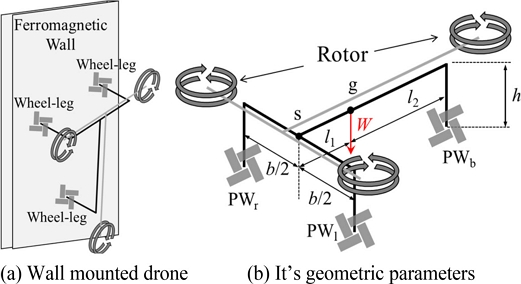
이 논문의 벽면 등반 드론은 Fig. 1(b)와 같이 비행을 위한 3개의 동축 로터(Co-axial Rotor) 트라이콥터(Tricopter) 추력부를 가지며 벽면 부착 및 이동을 위해 3개의 휠-레그(PW_l,_r,_b)를 가진다. Fig. 1(a)는 벽면 등반 드론이 강자성 벽면에 부착되어 있는 모습을 나타내었다.

Fig. 1

Wall mounted drone

2.2 영구자석 휠-레그와 부착력

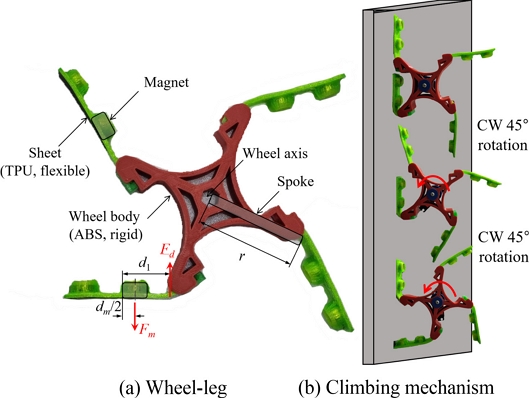
Fig. 2(a)의 벽면 등반 드론의 영구자석 휠-레그는 바퀴살과 영구자석 시트(Sheet)로 구성되며 Fig. 2(b)와 같이 강자성체 벽면에 부착하여 등반한다. 영구자석의 견인력에 의해 영구 자석 시트가 변형하며 강자성체 변멱에 부착하고 휠 축(Wheel Axis)에 연결된 구동 모터 토크에 의해 휄-레그가 회전하며 최소 하나의 휠-레그 시트가 강자성체 벽면에 부착하게 된다[8].

Fig. 2

Wheel-leg and its climbing mechanism

휠-레그 바퀴살 가장자리 수직 항력(F_d)과 모멘트 평형을 이루는 영구 자석 부착력(F_m)은 식(1)과 같다. 영구자석 끝부터 수직항력까지 거리를 d₁, 자석 직경을 d_m이라 할 때 모멘트 평형을 이용해 영구자석 부착력 최소값을 식(1)과 같이 유도했다.

$\[ F_m\ge \frac{2F_d{d}_1}{d_m} \]$

(1)

2.3 영구자석 필요 부착력

2.3.1 힘 평형에 의한 필요 부착력

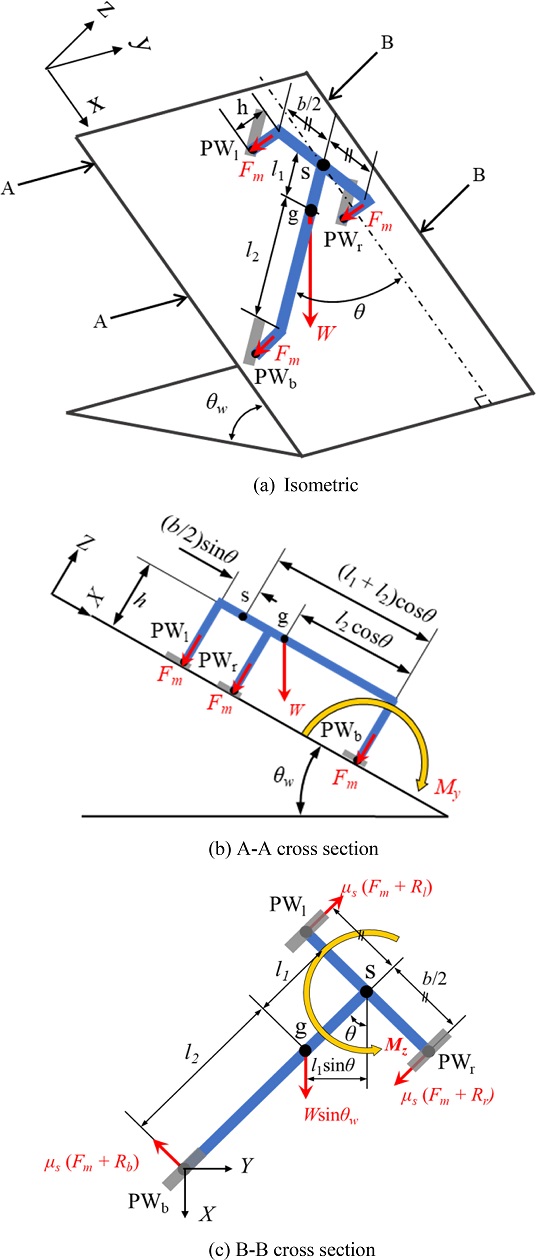
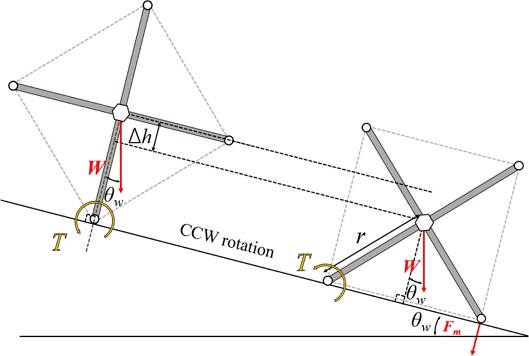
Fig. 1의 드론이 벽면 각도(θ_w)만큼 기울어진 강자성 벽 면에 x축 기준 드론의 부착 각도(θ)만큼 기울어져 부착할 때 자유물체도를 Fig. 3에 나타냈다.

Fig. 3

Free body diagram of the wall-climbing drone

Figs. 3(a)와 3(b)의 벽면과 평행한 방향(x축) 힘 평형을 이용하여 벽면에서 미끄러지지 않기 위한 부착력 조건은 식(2)와 같다.

$\[ F_m\ge \frac{\mathrm{W}\text{sin}{\theta }_w-{\mu }_s\mathrm{W}\text{cos}{\theta }_w}{3{\mu }_s} \]$

(2)

2.3.2 모멘트 평형에 의한 필요 부착력

Fig. 3(a)의 A-A 단면(X-Z 평면)에서 바라보았을 때, Fig. 3(b)와 같이, 뒤 휠-레그(PW_b) 기준 모멘트 평형(ΣM_y = 0)으로 드론의 영구자석 휠-레그 부착력을 계산한다. 이 때 모멘트 암(Arm)은 드론 부착 각도(θ)에, 힘은 벽면 각도(θ_w)에 영향을 받는다[9].

Fig. 3(b)와 같이 앞쪽 오른 휠-레그(PW_r)가 뒤쪽 휠-레그(PW_b)보다 위에 있을 드론의 부착 각도 조건은 식(3)과 같고 이때 모멘트 M_y의 받침점은 뒤쪽 휠-레그로 유지된다. 휠-레그 기준 모멘트 평형에 의한 영구자석 휠-레그의 필요 부착력은 식(4)와 같다.

$\[ \frac{b}{2}\text{sin}\theta \ge \left(l_1+l_2\right)\text{cos}\theta \]$

(3)

$\[ F_m\ge \frac{W\left\{\left(l_2\text{cos}\theta \right)\text{cos}\left({\theta }_w-h\sin {\theta }_w\right)\right\}}{-2\left(l_2+l_2\right)\text{cos}\theta } \]$

(4)

식(3)을 만족하지 않고 앞쪽 오른 휠-레그가 뒤쪽 휠-레그보다 아래 있는 드론 자세 각의 경우, 앞쪽 오른 휠-레그가 받침점인 모멘트 평형에 의한 영구자석 휠-레그의 필요 부착력은 식(5)와 같다.

$\[ F_m\ge \frac{W\left\{\left(\frac{b}{2}\sin \theta -l_1\text{cos}\theta \right)\text{cos}{\theta }_w-h\sin {\theta }_w\right\}}{-\left\{\frac{b}{2}\sin \theta -\left(l_1+l_2\right)\text{cos}\theta +b\sin \theta \right\}} \]$

(5)

0^o ≤ θ_w ≤ 90^o, 0^o ≤ θ ≤ 180^o에서 드론이 B-B 단면(X-Y 평면) 위에 안정적으로 부착하기 위해 앞 휠-레그의 중심 점(s) 기준, 모멘트 M_z 평형에서 구한 영구자석 휠-레그의 필요 부착력은 식(6)과 같다.

$\[ F_m\ge \frac{T_{g1}-\left(l_1+l_2\right){\mu }_s{R}_{P{W}_b}}{b{\mu }_s}-W\cos {\theta }_w \]$

(6)

여기서, $$ T_{g1}=W\sin {\theta }_w{l}_1\sin \theta ,R_{P{W}_b}=\frac{l_1}{2\left(l_1+l_2\right)}W\cos {\theta }_w$$

90^o ≤ θ_w ≤ 180^o, 0^o ≤ θ ≤ 180^o에서 벽면 각도가 90^o보다 크면 지면 반력(수직 항력)을 무시할 수 있어 영구자석 휠-레그 필요 부착력은 식(7)과 같이 축약된다.

$\[ F_m\ge \frac{W\cos \left({\theta }_w-90\right)l_1\sin \theta }{b{\mu }_s} \]$

(7)

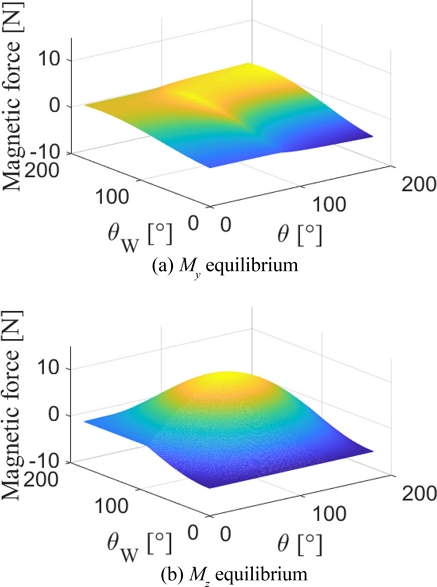
실험 검증에 사용할 간략 모델 사양을 Table 1에 나타냈고 이를 이용하여 M_y 평형에서 계산한 벽면 각도와 부착 각도에 따른 필요 부착력을 Fig. 4(a)에 표시했다. 면 각도와 부착 각도가 증가할수록 필요 부착력이 커진다. 벽면 각도가 작을 때 필요 부착력이 음이 된다. 즉, 드론 자중으로 벽면 수직 항력이 커져 부착력이 음(척력)이더라도 벽면에 부착할 수 있다.

Table 1

Parameters to calculate the required magnetic force

Fig. 4

Required magnetic force for attachment

일정한 벽면 각도에서 부착 각도가 증가할 때, 필요 부착력이 한 번의 급격한 증가가 있는데 이는 받침점이 변경되기 직전, 음의 방향을 가지는 M_y 모멘트 암이 양의 방향을 가지는 M_y 모멘트 암에 비해 급격히 감소하기 때문이다. 이후, 부착 각도가 180도에 가까워지면 M_y에 의한 필요 부착력이 소폭 감소하는 구간이 존재한다. 이것은 드론 질량 중심까지의 높이와 l₁ 값이 감소하고 부착 각도가 증가할수록 필요 부착력 감소구간의 기울기가 완만해지기 때문이다. 또한, 일정한 부착 각도에서 벽면 각도가 180도에 가까워지면 M_y에 의한 필요 부착력이 식(4)의 분자가 작아져 최댓값을 가진 후, Fig. 4(a)와 같이 소폭 감소한다.

벽면 및 부착 각도에 따른 M_z 평형으로 계산한 부착력을 Fig. 4(b)에 표시했다. 드론에 작용하는 M_z는 부착 및 벽면 각도가 90도일 때 모멘트 암(l₁sinθ)과 힘(Wsinθ_w)이 커져 최대 부착력(Wl₁/bμ_s)이 필요하며 자중의 약 1.8배이다.

M_y와 마찬가지로 벽면 각도가 90도인 영역에서 음 M_z 값이 존재하며 이는 드론 자중에 의한 지면 반력으로 휠-레그의 척력에도 드론은 벽면에 부착할 수 있기 때문이다. 그러나 벽면 각도가 90도보다 크면 지면 반력이 없어지고 양의 부착력이 필요하게 된다.

2.4 영구자석 휠-레그와 토크

휠-레그의 회전에 따라 회전 축과 질량 중심 높이(h)가 변한다. 식(8)와 같이 바퀴살(Spoke) 개수(n)가 증가할수록 질량 중심 변화가 적다.

$\[ \mathrm{\Delta }h=r\left(1-\cos \frac{\pi }{n}\right) \]$

(8)

휠-레그 모터는 드론 자중과 휠-레그 자력에 의한 토크를 이기고 회전해야 한다. 휠-레그 모터의 필요 토크는 드론 질량 중심 높이(h), 바퀴살의 길이(r), 바퀴살 개수(n), 벽면 각도(θ_w), 드론 자중(W) 그리고 영구자석 부착력(F_m)에 영향을 받는다. 벽면 각도가 90도이고 휠-레그가 3개인 경우 최대 필요 토크는 식(9)와 같으며 영구자석 부착력에 의한 토크가 지배적이다. 휠-레그 회전에 따른 변화를 Fig. 5에 나타냈다.

$\[ T_{max}\approx Wr\left(\frac{1}{3}+\frac{l_1}{b{\mu }_s}\right)\cos \frac{\pi }{n} \]$

(9)

Fig. 5

Torque to drive the wheel-legs with 4 spokes

3. 실험을 통한 검증

3.1 휠-레그 자석의 필요 부착력

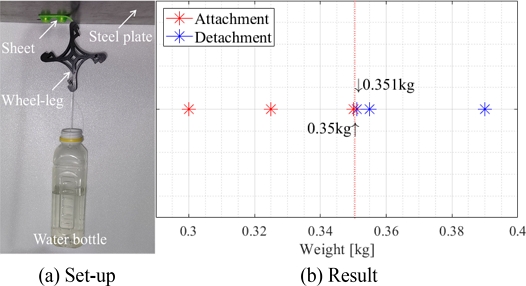
Fig. 6(a)와 같이 휠-레그를 강자성 면(Steel)에 부착시킨 후 물통(Water Bottle)을 매달고 물을 주입하며 휠-레그가 떨어지는 물통 질량을 Fig. 6(b)와 같이 측정했다. Table 2의 휠-레그 형상 변수와 측정한 F_d를 식(1)에 대입하며 측정값(F_m^E) 13.66 N이 도출되었다. 이는 카탈로그를 통해 확인한 자석의 이론값(F_m^T) 14.11 N과 3.13%의 오차를 보이며 유도한 부착력의 유효성을 검증했다.

Fig. 6

Measurement of the wheel-leg’s magnetic force

Table 2

Parameters of the wheel-leg

3.2 벽면 및 드론 부착 각도에 따른 부착력

3.2.1 실험 모델 파라미터

Fig. 7과 같이 드론을 모사하여 3개 다리를 가진 간략한 실험 모델을 제작했다. 본체(Main Body) 다리 하단에 고무자석판(Rubber Magnet Plate)을 부착했다. 본체에 알루미늄 바(Aluminum Bar)로 자중을 늘려 특정 조건에서 강자성체 벽면과 분리되게 했다.

Fig. 7

Test model for wall detachment experiment

실험모델의 각종 파라미터를 측정하기 위한 실험 과정을 Fig. 8에 나타냈다. Fig. 8(a)와 같이 고무자석판을 강자성체에 부착하고 물통에 물을 주입하며 강자성체와 분리되는 질량을 측정한 결과 고무자석판 자력(F_m)은 1.41 N이었다. Fig. 8(b)와 같이 고무자석판을 붙인 배터리가 철판 위에서 움직이기 시작하는 물통 질량을 측정하여 정지마찰계수(μ_s)가 0.62임을 확인했다.

Fig. 8

Experiments to measure parameters of the test model

3.2.2 실험방법

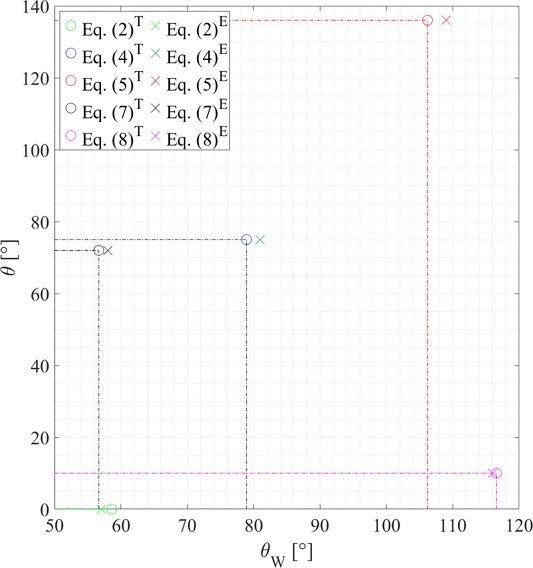
Table 3과 같이 M_y의 범위를 식(3)의 경계 부착 각도(78.11^o)에 따라 나누고, M_z는 벽면 각도 90^o를 기준으로 나누어 실험을 수행한다. 주어진 부착각도 θ와 Table 1의 변수를 이용하여 드론이 탈착되는 이론적 벽면 각도 값을 계산한다. 주어진 부착각도로 실험 모델을 벽면에 부착시키고 벽면각도 θ_w를 변화시키며 벽면으로부터 분리되는 실제 각도(θ_w^E)측정한다.

Table 3

Experimental results of detach conditions

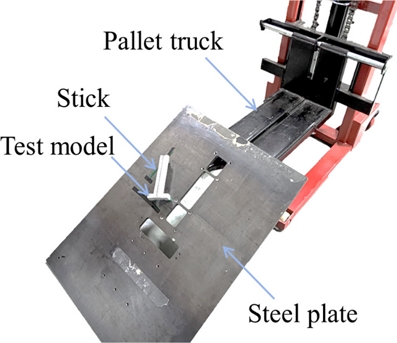
Fig. 9과 같이 얇은 막대(Stick)로 불필요한 벡터 성분들의 영향을 제거하고 실험 모델이 벽면으로부터 분리되는 벽면 각도(θ_w^E)를 측정했다.

Fig. 9

Experimental set-up for detach conditions

3.2.3 실험 결과

이론적 탈착 벽면 각도와 측정된 탈착 벽면 각도를 Table 3과 Fig. 10에 나타냈다. X 방향 힘 평형으로 유도한 식(2)의 이론값과 측정값은 가장 큰 오차인 3.4%였고 모멘트(M_y와 M_z)의 경우는 2.5% 이하의 상대 오차를 보여 유도한 부착력 식의 유효성을 검증했다.

Fig. 10

Experiment result

4. 결론

이 논문에서는 벽 등반 드론 자세에 따른 모듈형 영구자석 휠-레그의 부착력을 연구했다. 자석 휠-레그 개수는 3개로 결정하여 드론의 질량을 최소화하고 드론의 치수, 강자성 벽면의 기울기, 드론의 자세 등을 고려하여 영구자석 휠-레그의 필요 부착력 식을 유도했다. 간략 실험 모델을 제작하고 역학적 요소들을 변화시키며 영구자석의 부착력을 측정했다. 마지막으로 역학적 요소 변화에 따라 부착력을 잃는 벽면 각도를 측정하고 유도한 부착력 식과 비교하여 그 유효성을 검증했다. 이 연구 결과로 적절한 자력을 가지는 영구자석을 선정하여 모듈형 영구자석 휠-레그를 설계할 수 있고 향후 영구자석뿐만 아니라 다양한 벽면 탈부착 및 이동 장치 개발에 도움이 될 것이다.

Acknowledgments

This paper was presented at KSPE Autumn Conference 2022

REFERENCES

• Ha, K. H., Kim, J. H., Choi, J. W., (2021), A study on the application of drone in firefight field, Journal of the Korea Academia-Industrial Cooperation Society, 22(4), 321-330.
• Lee, S. B., Lim, J. T., (2021), A study on the creation of mission performance data using search drone images, The Journal of Korea Institute of Convergence Signal Processing, 22(4), 179-184.
• Myeong, W., Myung, H., (2018), Development of a wall-climbing drone capable of vertical soft landing using a tilt-rotor mechanism, IEEE Access, 7, 4868-4879. [https://doi.org/10.1109/ACCESS.2018.2889686]
• Han, S.-C., Yi, H.-C., (2002), A study on a detachment of a permanent magnet wheel for a wall-climbing mobile robot using magnetic inducement, Journal of the Korean Society for Precision Engineering, 19(1), 143-149.
• Kim, D. Y., Park, Y. J., Hong, S. B., Kim, S. Y. (2011), The development of an autonomous mobile platform using timing pulley-type magnet wheels, Proceedings of the Spring Conference of the Korean Society of Manufacturing Technology Engineers, 361-362.
• Lee, J. H., Ryu, S. M., Choe, H. R., (2000), Design of wall climbing robot with closed loop kinematic chains, Transactions of the Korean Society Mechanical Engineers A, 24(8), 2065-2073.
• Sell, R., Aryassov, G., Petritshenko, A., Kaeeli, M., (2012), Kinematics and dynamics of configurable wheel-leg, Proceedings of the 8^th International DAAAM Baltic Conference Industrial Engineering, 19-21.
• Daltorio, K. A., Wei, T. E., Horchler, A. D., Southard, L., Wile, G. D., Quinn, R. D., Gorb, S. N., Ritzmann, R. E., (2009), Mini-whegs TM climbs steep surfaces using insect-inspired attachment mechanisms, The International Journal of Robotics Research, 28(2), 285-302. [https://doi.org/10.1177/0278364908095334]
• Han, S. C., Yi, H. C., Kim, E. C., (2004), Study on the design constraints of the wall-climbing mobile robot using permanent wheels (Part 1-Design Guideline), 21(9), 69-76.