Fuzzy AHP-TOPSIS 기법을 이용한 최적 미세 가공 공정의 다기준 의사 결정

1. 서론

최근 전자, 통신, 광학, 의료, 자동차, 항공 등의 산업에서 부품의 고집적화와 고정밀화로 인한 초소형 부품 및 제품에 대한 수요가 급격히 증가하고 있다[1]. 이러한 부품 및 제품의 예로는 마이크로 센서 및 구동 장치, 마이크로 엔진 및 열교환기, 의료용 임플란트 및 진단 장치 등이 있는데, 이의 제작을 위해서는 미세 가공 기술이 요구된다. 따라서 미세 가공 기술의 발전도 비약적으로 이루어져 왔는데, 그 결과로서 가공 가능한 최소 크기, 치수 정밀도, 표면 품질, 소재 종류, 그리고 경제성 및 생산성 등에서의 제한이 점차 줄어들고 있다.

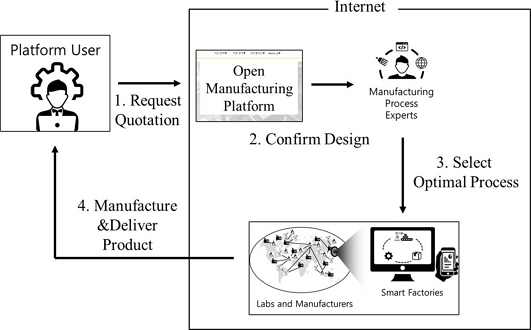
하지만 이러한 미세 가공에 대한 수요 증가와 기술 발전에도 불구하고 공정 개발자가 아닌 공정 수요자 측면에서의 미세 가공에 대한 접근은 쉽지 않다고 할 수 있다. 예를 들어 CNC 가공, 사출 성형, 3D 프린팅과 같은 일반 가공의 경우에는 해당 공정에 대한 전문 지식이 없는 사람도 개방형 제조 플랫폼(Fig. 1 참조)을 통해 최적의 가공 방법 및 서비스를 제공받을 수 있지만[2,3], 미세 가공의 경우에는 전문가를 통한 문제 해결은 물론 관련 기술에 대한 정보 탐색마저도 쉽지 않은 것이 현실이라고 할 수 있다. 이는 미세 가공을 활용한 제품 또는 부품 개발을 저해하는 요소로서 작용할 수 있으므로 이에 대한 보완이 요구된다고 할 수 있다.

Fig. 1

Concept of open manufacturing platform

지금까지 개발된 미세 가공 공정에는 많은 종류가 있다. 전통적인 방식의 기계 가공 공정부터 전기적, 화학적, 열적 반응 등을 활용한 다양한 종류의 특수 가공 공정들이 존재한다. 미세 가공 공정들은 각기 나름대로의 장점과 단점을 가지고 있기 때문에, 제품 또는 부품 개발 시 이러한 가공법들의 특징들을 최대한 활용하는 것이 요구된다. 하지만 부품 또는 제품의 특성에 따라 다수의 요구 조건이 존재하고, 이러한 요구 조건에 대해 각각의 미세 가공 공정들이 부합하는 정도가 다르기 때문에 모든 요구 조건을 고려한 가장 적절한 가공법을 선택하는 것은 매우 어려운 일이다.

이처럼 많은 선택지와 요구 조건이 존재하는 환경에서 최적의 선택지를 결정하는 것을 다기준 의사결정이라 한다[4]. 지금까지 다기준 의사결정을 위한 많은 기법들이 개발되었는데, 본 연구에서는 그 중에서도 AHP-TOPSIS 기법에 Fuzzy 논리를 적용한 Fuzzy AHP-TOPSIS 기법을 활용하여 최적의 미세 가공 공정을 찾는 방법을 제시한다[5]. 보다 구체적으로는 미세 가공과 관련된 제품 또는 부품의 요구 조건 각각에 대한 중요도를 AHP (Analytic Hierarchy Process) 기법을 이용하여 계산한 후, 이를 TOPSIS (Technique for Order Performance by Similarity to Ideal Solution) 기법에 연계하여 최적의 미세 가공 공정을 결정하는 방법을 제시한다. 이때 주어진 요구 조건에 대한 평가와 미세 가공 공정에 대한 평가에 Fuzzy 논리를 적용함으로써 참, 거짓의 이분법적 평가나 절대적 수치에 의한 정량적인 평가가 아니라 언어로 표현되는 정성적 평가가 가능토록 한다[6]. Fuzzy 논리의 이러한 장점은 로봇이나 자율 주행 등 다양한 분야에서 널리 활용되고 있다[7,8].

Fuzzy AHP-TOPSIS 기법을 활용하여 제조 환경의 다양한 분야에서 다기준 의사결정 문제를 해결한 사례들이 많이 있다[9,10]. 그 중에서 가공과 관련된 사례들을 살펴보면 적층제조(Additive Manufacturing)에서 최적의 가공 방법을 선택하기 위해 Fuzzy AHP-TOPSIS 기법을 활용한 경우가 있다[11]. 또한, 방전가공(Electro Discharge Machining)에서 가공 조건의 최적화를 위해 Fuzzy AHP-TOPSIS 기법을 활용한 경우도 있다[12]. 하지만, 주어진 부품 또는 제품의 다수 요구 조건에 맞는 최적의 미세 가공 방법을 선택하기 위해 다기준 의사결정 기법을 적용한 사례는 찾기가 쉽지 않다. 따라서 이에 대한 해법을 제시하는 본 연구가 충분한 의의를 갖는다고 할 수 있다.

본 논문의 순서는 다음과 같다. 먼저, 1장에서는 본 연구의 배경과 목적을 소개한다. 2장에서는 본 연구 방법의 토대가 되는 Fuzzy AHP, Fuzzy TOPSIS 기법을 보다 구체적으로 설명한다. 3장에서는 주어진 부품의 최적 미세 가공 방법 결정 사례를 통해 제안된 방법의 유효성을 검증한다. 마지막으로 4장에서는 본 연구가 갖는 의미를 정리한다.

2. 제안된 방법

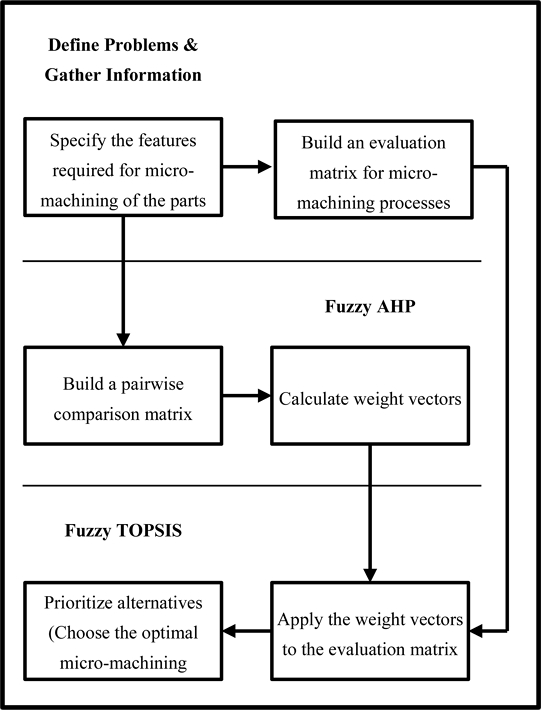
Fig. 2는 본 논문에서 제안한 Fuzzy AHP-TOPSIS 기법을 활용한 미세 가공 공정의 다기준 의사결정 과정을 보여 주는 흐름도이다. 흐름도는 크게 세 단계로 구성되어 있는데, 첫 번째 단계에서는 주어진 제품 및 다양한 미세 가공 공정들에 대한 정보가 수집되어 정리된다. 두번째 단계에서는 제품 가공을 위해 고려되는 요구 조건들의 가중치가 Fuzzy AHP 기법을 이용하여 구해진다. 마지막 세번째 단계에서는 전 단계에서 얻어진 가중치를 토대로 Fuzzy TOPSIS 기법을 사용하여 미세 가공 공정들의 최종 순위가 결정된다. 이 과정에서 Fuzzy AHP 기법 및 Fuzzy TOPSIS 기법이 어떻게 적용되는지는 다음에 보다 구체적으로 기술된다.

Fig. 2

Proposed methodology for prioritizing a micro machining process by Fuzzy AHP-TOPSIS

2.2 Fuzzy AHP

AHP는 Saaty가 고안한 다기준 의사결정 기법이다[13]. 여기에 Fuzzy 논리를 접목한 Fuzzy AHP는 Table 1에서와 같이 고려 항목들에 대한 언어적 평가를 삼각 Fuzzy 수로 나타내어 고려 항목의 정량적인 비교가 가능하도록 한 것이다. 이 경우 삼각 Fuzzy 수는 하한값, 중앙값, 상한값 (l, m, u)으로 이루어지는데, 두 삼각 Fuzzy 수 A₁ = (l₁, m₁, u₁), A₂ = (l₂, m₂, u₂) 가 있을 때 이들 사이의 연산은 다음과 같이 정의된다.

$\[ \begin{array}{c}{A}_1\otimes A_2=\left(l_1,m_1,u_1\right)\otimes \left(l_2,m_2,u_2\right)\\ =\left(l_1\mathrm{*}{l}_2,m_1\mathrm{*}{m}_2,u_1\mathrm{*}{u}_2\right)\end{array} \]$

(1)

$\[ a\otimes A_1=\left(a\mathrm{*}{u}_1,a\mathrm{*}{m}_1,a\mathrm{*}{l}_1\right) \]$

(2)

$\[ A_1^{-1}={\left(l_1,m_1,u_1\right)}^{-1}=\left(\frac{1}{u_1},\frac{1}{m_1},\frac{1}{l_1}\right) \]$

(3)

Table 1

Triangular fuzzy number for pairwise comparison

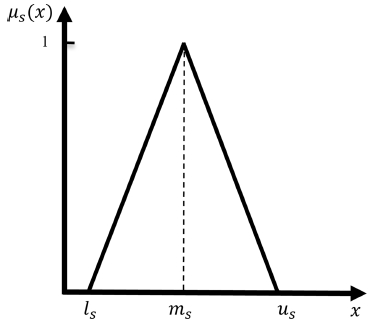
한편 삼각 Fuzzy 수 A_s = (l_s, m_s, u_s)가 있을 때 임의의 값을 갖는 변수 x가 Fuzzy 집합에 소속되는 정도를 나타내는 Fuzzy 멤버십 함수(Fuzzy Membership Function) μ_s(x) 는 식(4)와 같이 정의되는데, 이를 도식으로 나타내면 Fig. 3과 같이 중앙값(m_s)에서는 1을 가지면서 하한값(l_s)과 상한값(u_s)에서는 0을 갖는 이등변삼각형의 형태가 된다.

$\[ {\mu }_s\left(x\right)=\text{max}\left(\text{min}\left(\frac{x-l_s}{m_s-l_s},\frac{u_s-x}{u_s-m_s}\right),0\right) \]$

(4)

Fig. 3

Triangular fuzzy membership function

본 연구에서는 부품 또는 제품의 미세 가공을 위해 요구되는 조건들의 상대적인 중요도를 평가하기 위해 Fuzzy-AHP를 적용하여 요구 조건들의 가중치를 계산한다. 이 경우, n개의 요구 조건들에 대한 상대적 중요도는 Table 2에 주어진 것과 같은 쌍대 비교 설문을 통해 수요자로부터 얻게 된다. 즉, j번째 요구 조건에 대한 i번째 요구 조건의 상대적 중요도는 Table 1을 통해 언어적 평가의 삼각 Fuzzy 수 M_i,j(i = 1, 2, ..., n)로 변환된다. 반대로 i번째 요구 조건에 대한 j번째 요구 조건의 상대적 중요도를 나타내는 삼각 Fuzzy 수 M_i,j 는 식(3)을 사용하여 $$ M_{j,i}=M_{i,j}^{-1}$$ 의 관계를 이용하여 구할 수 있다.

Table 2

Pairwise comparison survey for Fuzzy AHP

n × n 크기의 삼각 Fuzzy 수 M_i,j 에서 n개의 요구 조건에 대한 가중치를 계산하기 위해서는 Chang이 고안한 범위 분석법(Extent Analysis Method)을 적용한다[14]. i번째 요구 조건에 대한 Fuzzy 합성 범위 값(Synthetic Extent Value), S_i 는 다음과 같이 삼각 Fuzzy 수 M_i,j 을 정규화하여 구한다.

$\[ \begin{array}{c}{S}_i=\sum _{j=1}^n{M}_{ij}\otimes {\left[\sum _{i=1}^n\sum _{j=1}^m{M}_{ij}\right]}^{-1}\\ \sum _{j=1}^m{M}_{ij}=\left(\sum _{j=1}^m{l}_{ij},\sum _{j=1}^m{m}_{ij},\sum _{j=1}^m{u}_{ij}\right)\\ {\left[\sum _{i=1}^n\sum _{j=1}^m{M}_{ij}\right]}^{-1}=\left(\frac{1}{\sum _{i=1}^n\sum _{j=1}^m{u}_{ij}},\frac{1}{\sum _{i=1}^n\sum _{j=1}^m{m}_{ij}},\frac{1}{\sum _{i=1}^n\sum _{j=1}^m{l}_{ij}}\right)\end{array} \]$

(5)

한편, 범위 분석법에서 정의된 Fuzzy 합성 범위 값 S₂가 S₁ 값보다 높을 확률 V(S₂≥S₁)은 다음과 같다.

$\[ V\left(S_2\ge S_1\right)=\left\{\begin{array}{c}1 if m_2\ge m_1\\ 0 if l_1\ge u_2\\ \frac{l_1-u_2}{\left(m_2-u_2\right)-\left(m_1-l_1\right)} otherwise \end{array}\right. \]$

(6)

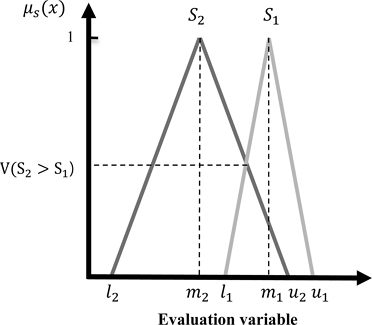
이렇게 구한 확률 V(S₂≥S₁) 은 Fig. 4에서처럼 두 삼각 Fuzzy 수의 교차점에서의 y값에 해당한다. 한편, 합성 범위 값 S_i 가 다른 모든 합성 범위 값 S_k 보다 클 확률, d’(A_i)은 다음과 같다.

$\[ \begin{array}{c}{d}^{\mathrm{\text{'}}}\left(A_i\right)=V\left(S_I\ge S_1,S_2,\dots ,S_n\right)=V\left[\left(S_i\ge S_1\right),\left(S_i\ge S_2\right),\dots ,\right.\\ \left.\left(S_i\ge S_{i-1}\right),\left(S_i\ge S_{i+1}\right),\dots ,\left(S_i\ge S_n\right)\right]=\text{min}V\left(S_i\ge S_k\right),\\ k=\mathrm{1,2},\dots ,n;k\ne i,\end{array} \]$

(7)

Fig. 4

The intersection of fuzzy numbers

이를 이용하여 n가지 요구 조건에 대한 가중치 백터 W’를 다음과 같이 정의할 수 있다.

$\[ W^{\mathrm{\text{'}}}=\left(d^{\mathrm{\text{'}}}\left(A_1\right),d^{\mathrm{\text{'}}}\left(A_2\right),\dots ,d^{\mathrm{\text{'}}}\left(A_n\right)\right) \]$

(8)

정규화된 가중치 백터 W 는 다음과 같이 주어진다.

$\[ W=\left(d\left(A_1\right),d\left(A_2\right),\dots ,d\left(A_n\right)\right);d\left(A_i\right)=\frac{d^{\mathrm{\text{'}}}\left(A_i\right)}{\sum _i^n{d}^{\mathrm{\text{'}}}\left(A_i\right)} \]$

(9)

2.3 Fuzzy TOPSIS

TOPSIS는 Hwang과 Yoon에 의해 제시된 다기준 의사 결정방법 중의 하나이다[15]. TOPSIS의 기본 원리는 최선의 선택지는 긍정적인 해결책(Positive Ideal Solution, PIS) 과는 최대한 가깝게 있어야 하는데 반해 부정적인 해결책(Negative Ideal Solution, NIS)과는 최대한 멀리 떨어져 있어야 한다는 것이다. Fuzzy TOPSIS는 해결책의 평가에 있어 모호성과 부정확함이 존재할 때 활용하는 것이 보다 바람직하다. 본 연구에서는 여러 미세 가공 공정 중 주어진 부품 또는 제품의 가공에 최적인 공정을 선택하기 위해 Fuzzy-TOPSIS 방법을 적용하였다. 구체적인 적용 방법은 다음과 같다.

앞서 Fuzzy AHP에서 정의된 n개의 요구 조건에 대해 m개의 선택 가능한 미세 가공 공정이 존재할 때, 이에 대한 평가표는 Table 3에 제시된 정량적 언어 평가를 이용하여 작성할 수 있다. 이 때 주의할 점은 각각의 요구 조건을 정량적으로 큰 것이 선호되는 혜택 기준(Benefit Criteria) 또는 정량적으로 작은 것이 선호되는 비용 기준(Cost Criteria)으로 나누고, 이를 Table 3에 제시된 언어를 이용하여 정량적으로 평가하여야 한다는 것이다. 그다음에는 선택지 평가표를 삼각 Fuzzy 수 P_ij = (l_ij, m_ij, u_ij)로 변환한 후 정규화 과정을 거친다. 정규화 시, i번째 요구 조건이 혜택 기준일 경우 식(10), 비용 기준일 경우 식(11)을 각각 사용한다.

Table 3

Triangular fuzzy number for linguistic ratings

$\[ \begin{array}{c}{\widehat{p}}_{ij}=\left(\frac{l_{ij}}{u_j^{+}},\frac{m_{ij}}{u_j^{+}},\frac{u_{ij}}{u_j^{+}}\right) and u_j^{+}\\ =max u_{ij}\left(benefit criteria\right)\end{array} \]$

(10)

$\[ {\widehat{p}}_{ij}=\left(\frac{l_j^{-}}{u_{ij}},\frac{l_j^{-}}{m_{ij}},\frac{l_j^{-}}{l_{ij}}\right) and l_j^{-}=min{ l}_{ij}\left(cost criteria\right) \]$

(11)

다음으로는 Fuzzy AHP에서 구한 가중치 벡터를 정규화된 Fuzzy 수 행렬에 식(12)와 같이 적용한다.

$\[ v_{ij}={\widehat{p}}_{ij}\otimes {\left(W\right)}^T \]$

(12)

이후 모든 개별 요구 조건에 대한 이상적 해결책(PIS)과 부정적 해결책(NIS)을 식(13), 식(14)를 적용하여 찾는다. 식(13), 식(14)에서 알 수 있듯이, 이상적 해결책과 부정적 해결책은 요구 조건이 혜택 기준일 때는 정규화된 Fuzzy 수 행렬 행값의 최대값과 최소값이 되나 비용 기준일 때는 반대로 행값의 최소값과 최대값이 된다.

$\[ v_i^{+}=\left\{\left\{\begin{array}{c}\left(max{ v}_{i,j}|i\in benefit criteria \right)\\ \left(min{ v}_{i,j}|i\in cost criteria\right)\end{array}\right\}\right\}i=\mathrm{1,2},\dots ,n \]$

(13)

$\[ v_i^{-}=\left\{\left\{\begin{array}{c}\left(max{ v}_{i,j}|i\in benefit criteria \right)\\ \left(min{ v}_{i,j}|i\in cost criteria\right)\end{array}\right\}\right\}i=\mathrm{1,2},\dots ,n \]$

(14)

그 다음으로는 j번째 선택지와 PIS, NIS의 거리($$ d_j^{+}$$, $$ d_j^{-}$$)를 아래의 식(15), 식(16)을 이용하여 각각 구한다.

$\[ \begin{array}{c}{d}_j^{+}=\sum _{i=1}^n\left(v_{ij}-v_i^{+}\right)\\ =\sum _{i=1}^n\sqrt{\left\{{\left(a_{ij}-a_j^{+}\right)}^2+{\left(b_{ij}-b_j^{+}\right)}^2+{\left(c_{ij}-c_j^{+}\right)}^2\right\}}\\ j=\mathrm{1,2},\dots ,m\end{array} \]$

(15)

$\[ \begin{array}{c}{d}_j^{-}=\sum _{i=1}^n\left(v_{ij}-v_i^{-}\right)\\ =\sum _{i=1}^n\sqrt{\left\{{\left(a_{ij}-a_j^{-}\right)}^2+{\left(b_{ij}-b_j^{-}\right)}^2+{\left(c_{ij}-c_j^{-}\right)}^2\right\}}\\ j=\mathrm{1,2},\dots ,m\end{array} \]$

(16)

마지막으로 각 선택지의 근접도 계수(Closeness Coefficient)를 다음 식을 이용하여 구하게 되며, 계산된 근접도 계수를 내림차순하여 최종 순위를 결정하게 된다.

$\[ C{C}_j=\frac{a_j^{-}}{d_j^{-}+d_j^{+}},j=\mathrm{1,2},\dots ,m \]$

(17)

3. 연구 사례

3.1 미세 가공 및 제품 정보 수집

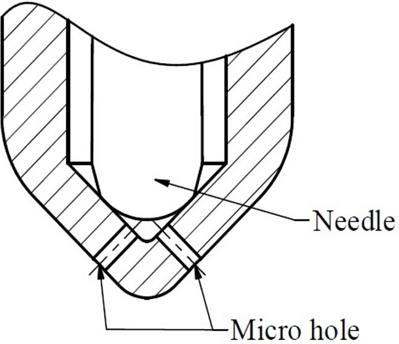
본 연구에서는 최적의 미세 가공법 선정을 위한 Fuzzy-AHP-TOPSIS 방법의 활용 예로 Fig. 5에 보이는 것과 같은 가솔린 직접 분사(Gasoline Direct Injection, GDI) 엔진의 연료 주입 노즐을 선정하였다. GDI 엔진은 연료와 공기를 혼합하여 엔진 실린더에 넣는 방식이 아니라 연료와 공기를 분리하여 공급하는 방식이다. GDI 엔진 성능을 유지하기 위해서는 연료 주입 노즐에서 분사되는 연료 압력을 일정하게 유지해야 한다. 이때 연료 주입 노즐의 구멍은 이 분사 압력에 직접적인 영향을 주게 되므로 높은 품질의 구멍 가공이 요구된다[16].

Fig. 5

Fuel injection nozzle

미세 가공법 선정 시 고려해야 할 요구 조건으로는 최소 직경, 최대 종횡비, 표면 거칠기, 가공 속도, 경제성 총 5가지를 선정하였다. Fuzzy AHP를 활용하여 선정된 5가지 요구 조건의 중요도를 계산하기 위해서는 먼저 수요자로부터 Table 2의 쌍대 비교 설문을 받아야 한다. 일단 설문이 완성되면 그 결과를 토대로 5가지 요구 조건을 2개씩 짝지은 모든 조합에 대해 중요도를 평가하게 된다. 이때 중요도 평가는 Table 1의 언어적 평가를 토대로 수행된다.

연료 주입 노즐의 적절한 연료 분사 압력 조절을 위해서는 작은 구멍 직경과 작은 표면 거칠기가 요구된다. 따라서 쌍대 비교 설문에서 다른 요구 조건보다 가공 가능한 최소 구멍 직경과 표면 거칠기에 대한 중요도가 더 높게 평가될 거라고 예상할 수 있다. 또한, 연료 분사 노즐의 구멍 깊이가 상대적으로 작기 때문에 최대 종횡비에 대한 중요도는 다른 항목에 비해 보다 낮게 평가될 거라고 예상할 수 있다. 위와 같은 각 요구 조건들의 상대적 중요도를 고려하여 Table 2의 쌍대 비교 설문을 진행한다.

연료 주입 노즐을 가공할 미세 가공법 후보로서는 전통적인 방식의 드릴 가공, 레이저 가공, 방전 가공(EDM), 전해 가공(ECM), 전해 방전 가공(ECDM), 전자빔 가공(EBM), 초음파 가공을 선정하였다. 여기서 전통적인 방식의 드릴 가공은 보통 크기의 가공에 흔히 사용하는, 공구를 척에 끼워 돌리는 절삭 가공을 의미한다. 여기에는 Twist 드릴, Spade 드릴, D-shaped 드릴, Single 드릴과 같이 드릴 공구의 형태에 따라 세부 분류된 미세 가공법들이 포함된다.

3.2 Fuzzy AHP

요구 조건의 가중치를 구하기 위해 Table 2의 쌍대 비교 설문을 받아 쌍대 비교표를 작성해야 한다. Table 4와 같은 쌍대 비교표 M_n,m를 작성할 때, i행의 요구 조건이 j열의 요구 조건보다 중요할 경우에는 M_ij에 Table 3의 언어적 평가를 입력하고 M_ji에는 빈칸을 입력한다. 반대로 j열의 요구 조건이 i행의 요구 조건보다 중요할 경우에는 M_ji에 언어적 평가를 입력하고 M_ij에는 빈칸을 입력한다. 이후 언어적 평가를 Table 3의 삼각 퍼지수로 변환한 후, 빈칸에는 대각선 대칭 원소의 역수값을 식(3)을 이용하여 기입한다. 이렇게 완성된 쌍대 비교표는 Table 5와 같다.

Table 4

Pairwise comparison survey

Table 5

Pairwise comparison table

이후 각 요구 조건의 Fuzzy 합성 범위 값을 식(5)를 사용하여 구하고, 범위 분석법을 통해 각 Fuzzy 합성 범위 값을 비교하여 각 요구 조건의 가중치를 식(6)부터 식(9)를 통해 구한다. 이렇게 구한 Fuzzy 합성 범위 값과 가중치는 Table 6과 같다.

Table 6

Fuzzy AHP result

3.3 Fuzzy TOPSIS

Fuzzy TOPSIS에 사용될 미세 가공법에 대한 요구 조건 별 평가표는 Table 7과 같다. 미세 가공법들에 대한 평가표를 삼각 퍼지수로 변환한 후, 식(10), 식(11)을 이용하여 정규화한다. 다음으로는 Fuzzy AHP에서 구한 가중치를 식(12)을 통해 가공법 평가표에 적용한다. 이렇게 정규화와 가중치가 적용된 가공법들에 대한 평가표는 Table 8과 같다. 가공법 평가표에서 식(13), 식(14)에 따라 각 요구 조건의 긍정적인 해결책(PIS)과 부정적인 해결책(NIS)를 찾는다. 최소 직경의 경우 그 값이 작을수록 좋기 때문에 ECDM이 PIS(0.096, 0.112, 0.134), Spade, D-shaped가 NIS(0.168, 0.224, 0.336)이다. 모든 요구 조건에 대해 PIS와 NIS를 구한 후, 식(15), 식(16), 식(17)을 적용하여 근접도 계수 CC_i 를 구한 결과는 Table 9와 같다. 본 예시에서는, 근접도 계수가 0.854로 가장 큰 레이저 가공이 요구 조건을 충족시키는 최적 가공 방법이라 할 수 있다.

Table 7

Evaluation of Micro drilling

Table 8

Normalized weighted evaluation table

Table 9

Fuzzy TOPSIS result

4. 결론

본 연구에서는 최적의 미세 가공 방법 선택을 위해 Fuzzy AHP-TOPSIS 기법을 활용하는 방법을 제시하였다. 보다 구체적으로는 미세 가공과 관련된 제품 또는 부품의 요구 조건 각각에 대한 중요도를 AHP (Analytic Hierarchy Process) 기법을 이용하여 계산한 후, 이를 TOPSIS (Technique for Order Performance by Similarity to Ideal Solution) 기법에 연계하여 최적의 미세 가공 공정을 결정하는 방법을 제시하였다. 이 과정에서 요구 조건의 중요도 평가와 미세 가공 공정의 적합도 평가에 Fuzzy 논리를 적용함으로써 참, 거짓의 이분법적 평가나 절대적 수치에 의한 평가가 아니라 언어로써 표현되는 평가가 가능토록 하였다. 제안된 방법의 실효성은 엔진의 연료 주입 노즐 사례를 통해 확인할 수 있었다.

본 논문에서 제시한 Fuzzy AHP TOPSIS 기법은 요구 조건이나 선택지들을 임의로 늘려도 적용할 수 있다는 장점이 있다. 예를 들어, 연료 주입 노즐 사례에서 요구 조건으로 치수 정밀도나 기하 공차를 추가하거나 미세 가공 방법으로 AJM (Abrasive Jet Machining)을 추가해도 동일한 방법을 적용하여 문제를 해결할 수 있다. 또한, 이 방법은 확장성이 좋아 구멍 가공뿐만 아니라 형상 가공 등 다른 분야에도 쉽게 적용할 수 있다는 장점이 있다. 더불어 요구 조건의 중요도 평가나 가공 공정의 적합도 평가에 언어적 평가를 활용함으로써 평가의 수월성이 높다는 장점이 있다.

따라서 본 연구에서 제시된 방법을 보다 적극적으로 활용할 필요성이 있다고 판단된다. 이를 위해서는 추후 미세 가공과 관련된 다양한 데이터베이스 및 사례 구축, 그리고 미세 가공 공정에 대한 보다 정확한 이해와 평가가 필요하다고 할 수 있다. 그 결과로서 미세 가공과 관련된 다양한 요구 조건으로 인해 최적의 결정이 어려운 설계 및 제조 문제에서 보다 적합한 해결 방법을 보다 손쉽게 찾을 수 있으리라 기대된다. 또한 미세 가공을 위한 개방형 제조 플랫폼에서 최적 공정 선정을 위한 엔진으로서 활용될 수 있으리라 기대된다.

Acknowledgments

이 연구는 서울과학기술대학교 교내 학술연구비 지원으로 수행되었습니다.

REFERENCES

• Gao, S., Huang, H., (2017), Recent advances in micro-and nano-machining technologies, Frontiers of Mechanical Engineering, 12(1), 18-32. [https://doi.org/10.1007/s11465-017-0410-9]
• Son, J., Kang, H., Bae, H., Lee, E., Han, H., Park, J., Kim, H., (2015), IoT-based open manufacturing service platform for mass personalization, The Journal of the Korean Institute of Communication Sciences, 33(1), 42-47.
• Kang, H. S., Do Noh, S., Son, J. Y., Kim, H., Park, J. H., Lee, J. Y., (2018), The FaaS system using additive manufacturing for personalized production, Rapid Prototyping Journal, 24(9), 1486-1499. [https://doi.org/10.1108/RPJ-11-2016-0195]
• Jahan, A., Edwards, K. L., Bahraminasab, M., (2016). Multi-criteria decision analysis for supporting the selection of engineering materials in product design. Butterworth-Heinemann.
• Ishak, A., (2020), Analysis of fuzzy AHP-TOPSIS methods in multi criteria decision making: Literature review, Proceedings of the IOP Conference Series: Materials Science and Engineering, 012147. [https://doi.org/10.1088/1757-899X/1003/1/012147]
• Zadeh, L. A., (1988), Fuzzy logic, Computer, 21(4), 83-93. [https://doi.org/10.1109/2.53]
• Ko, J. H., Bae, J. H., Hong, D., (2016), Variable impedance control and fuzzy inference based identification of user intension for direct teaching of a mobile robot, Journal of the Korean Society for Precision Engineering, 33(8), 647-654. [https://doi.org/10.7736/KSPE.2016.33.8.647]
• Ahn, K. K., Yoon, J. I., Khoa, L. D., (2011), A study on the path-tracking of electric wheelchair robot, Journal of the Korean Society for Precision Engineering, 28(11), 1265-1271.
• Carnero, M. C., (2014), Multicriteria model for maintenance benchmarking, Journal of Manufacturing Systems, 33(2), 303-321. [https://doi.org/10.1016/j.jmsy.2013.12.006]
• Prakash, C., Barua, M. K., (2015), Integration of AHP-TOPSIS method for prioritizing the solutions of reverse logistics adoption to overcome its barriers under fuzzy environment, Journal of Manufacturing Systems, 37, 599-615. [https://doi.org/10.1016/j.jmsy.2015.03.001]
• Anand, M., Vinodh, S., (2018), Application of fuzzy AHP–TOPSIS for ranking additive manufacturing processes for microfabrication, Rapid Prototyping Journal, 24(2), 424-435. [https://doi.org/10.1108/RPJ-10-2016-0160]
• Roy, T., Dutta, R. K., (2019), Integrated fuzzy AHP and fuzzy TOPSIS methods for multi-objective optimization of electro discharge machining process, Soft Computing, 23(13), 5053-5063. [https://doi.org/10.1007/s00500-018-3173-2]
• Saaty, T. L., (1990), How to make a decision: The analytic hierarchy process, European Journal of Operational Research, 48(1), 9-26. [https://doi.org/10.1016/0377-2217(90)90057-I]
• Chang, D.-Y., (1996), Applications of the extent analysis method on fuzzy AHP, European Journal of Operational Research, 95(3), 649-655. [https://doi.org/10.1016/0377-2217(95)00300-2]
• Hwang, C.-L., Yoon, K., Hwang, C.-L., Yoon, K., (1981), Methods for multiple attribute decision making, Multiple Attribute Decision Making: Methods and Applications a State-of-the-art Survey, 58-191. [https://doi.org/10.1007/978-3-642-48318-9_3]
• Jadhav, P. D., Mallikarjuna, J., (2018), Effect of fuel injector hole diameter and injection timing on the mixture formation in a GDI engine-a cfd study, Computational and Experimental Studies, 6(4), 737-748. [https://doi.org/10.2495/CMEM-V6-N4-737-748]