사출성형제품 이형 후 상온 냉각 중 크립 현상에 관한 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Recently, with the expansion of application of polymer composite materials, high levels of deformation compensation actions have been developed. However, there is a problem of high-temperature viscoelasticity that occurs over time after completing the injection molding process. In this study, changes of mechanical properties of the Moldflow program for injection molding were analyzed to verify the viscoelasticity phenomenon through deformation analysis. In addition, deformation analysis of plastic injection molded products according to arrangement of three ribs was conducted and two products with different geometric shapes of the same function were compared. As a result, it was possible to reflect the viscoelastic effect by reducing the elastic modulus and shear modulus of the material. It was confirmed that the geometric shape with thick ribs formed in multiple longitudinal directions was mainly responsible. On the surface of the product where the rib arrangement was parallel and perpendicular to the flow direction, the orientation was orthogonal to the linear direction and the maximum residual stress was 81.17 MPa, which showed the largest value. It was judged that viscoelastic phenomena could be predicted and that an arrangement of parallel and perpendicular ribs that might intersect should be avoided.
Keywords:
Fiber-reinforced polymer, Composite materials, Injection molding, Viscoelasticity키워드:
섬유강화플라스틱, 복합재료, 사출성형, 점탄성1. 서론
최근 FRP (Fiber Reinforced Plastics)와 같은 고분자 복합재료가 사출성형 공법을 통하여 복잡한 형태의 제품을 대량생산하는 방식으로 기존 다이 캐스팅 공법 등으로 생산되던 제품을 대체하며 그 적용 분야가 확대 및 기대되고 있다. 우수한 기계적 성능과 유리한 용적중량(Volumetric Weight)을 가진 고분자 복합재료는 고강도 및 경량화가 요구되는 분야에 주로 사용되고 있지만 이러한 장점에도 불구하고 비교적 성형공정이 까다로워 종래에는 다이 캐스팅을 통한 단순한 형상의 부품에 일부 소량생산 방식으로 생산되어왔다. 특히 높은 비강도와 비탄성계수 등의 우수한 기계적 특성을 가진 FRP와 같은 고분자 복합재료는 성형공정 및 대량생산에 불리하여 그 한계가 명확하다[1-5].
하지만 앞서 언급한 사출성형 공법을 통한 적용 분야의 확대로 인해 적용제품에 대한 다양한 강도, 성능, 기능적 조건들이 새롭게 요구되고 있다. 특히 사출성형제품에 대한 정밀기하공차 요구는 제품 내 수축편차 발생이 불가피한 사출성형공법 특성상 기술적 어려움이 매우 많은 과제로, 지난 수년간 CAE (Computer-aided Engineering), 모핑(Morphing) 및 역공학(Reverse Engineering) 기술 등을 활용한 일정 수준의 변형 보완대책들이 개발되었다[6-8].
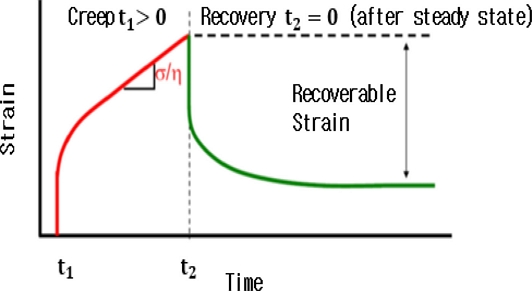
이러한 진보에도 불구하고 사출성형 공정 완료 후에 상온에서 냉각 중인 제품에서 변형 해석 결과와 달리 매우 큰 변형이 시간이 경과함에 따라 나타나는 경우가 있다. 이는 고분자 재료의 대표적 특성인 시간에 따른 고온 점탄성 효과가 두드러짐에 의한 것이다. 플라스틱은 일정한 하중을 가했을 때, 탄성변형을 일으키고 하중을 계속 유지하면 점탄성 변형이 시간에 따라 증가하게 된다. 이후 하중을 제거하면 플라스틱은 바로 탄성 회복을 하고, 서서히 점탄성 회복을 하게 되는데 이러한 현상을 Creep Compliance라 한다. Fig. 1은 일정한 Stress를 받는 플라스틱 재료의 Creep 현상의 시간이 경과함에 따른 Strain 변형률을 나타낸 것이다. 본 연구에서는 이러한 사출성형제품 이형 후 상온 냉각 중 크립 현상을 고려한 변형 해석을 체계적으로 고찰하고자 한다[9-11].
2. 연구 방법
2.1 고온 크립의 점탄성 효과 반영
본 연구에서 사용된 소재는 섬유강화 고분자 복합 재료 CTS P6635이며, 모재는 폴리프로필렌(Polypropylene)이고, 강화제인 유리섬유 함유율은 35%이다. 추천되는 성형 온도 조건은 금형온도 95oC, 제품 이형 온도 206oC, 용융점은 220oC이며, 유리전이온도는 50oC이다. 재료의 기계적 물성은 Table 1에 나타내었다.
제품 이형 후 발생하는 점탄성 변형에 대해서는 섬유 강화제의 기계적 물성이 지배적인 섬유 배향 방향(Fiber Orientation Direction)에 대해서는 극히 미소할 것으로 판단되며, 주로 섬유 배향 방향에 수직인 방향에 대해서 발생한다고 볼 수 있다.
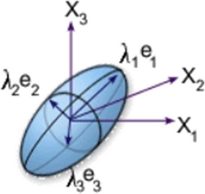
3차원 섬유 배향 계산은 동일한 유한 요소 메쉬에서 금형 충전 해석과 동시에 수행된다. 각 요소에 대한 3차원 배향 솔루션은 2차 텐서로 설명된다. 그래픽 표현을 위해 배향 텐서의 고유값과 고유 벡터가 생성되며 고유 벡터는 섬유 정렬의 기본 방향을 나타내고 고유 값은 해당 방향을 기준으로 정렬된 섬유의 통계 비율(0-1)을 제공한다. Fig. 2 는 각 요소에 대한 섬유의 정렬 분포를 설명하는 배향 타원체를 정의한다. 횡단등방성물성치(Transversely Isotropic Material Data)의 2차 기본방향(2nd Principal Direction)은 섬유 배향 방향에 수직인 방향으로 응력 변형률 선도에서 기울기 즉, 탄성계수 및 전단탄성계수를 줄이는 방법으로 항복 및 점탄성 변형효과를 반영하고자 한다.
점탄성 효과를 고려하기 위해 2차 기본방향의 탄성계수 및 1, 2차 기본방향의 전단탄성계수를 기본값을 기준으로 50-100%로 적용시켜 고온 크립 해석을 수행하였다.
2.2 기하학적 형상에 따른 해석
섬유강화 고분자 복합재료 사출성형시 필연적으로 휨(Warpage)이 발생하게 된다. 이는 제품 내부의 수축 편차에 의해 발생하며, 제품 내부 수축 편차는 금형 내부에서 제품이 고화 되는 순간 밀도차와 재료 이방성에 의한 수축 편차에 의해 주로 발생된다. 재료가 이방성을 가지는 경우에는 방향성 첨가제가 포함되지 않았을 때와 비교하여 미소하지만, 섬유 강화제와 같은 방향성 첨가제가 포함된 경우는 수축 편차의 주원인이 될 수 있다.
본 연구에서는 섬유 배향 텐서로부터 2, 3차 기본방향을 판단하고, Mises-Hencky 응력 값을 고찰하여 과도한 편향응력(Deviatoric Stress)을 유발하는 기하학적 형상을 규명하였다.
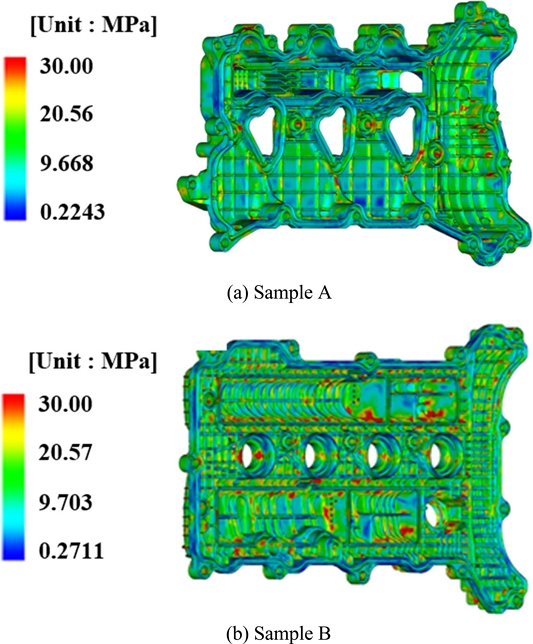
또한 섬유 강화 고분자 복합재료의 사출성형 시 기하학적 형상에 따른 고온 크립 특성을 고찰하고자 동일 기능의 제품 중 변형 해석 값과 제품 이형 후 실제 변형 결과 값의 오차가 약 30%인 Sample “A”와 약 300% 수준인 Sample “B”에 대해 기하학적 형상에 따른 평균 섬유 배향 텐서와 잔류응력 값을 비교 평가하고자 한다.
2.3 리브 배치에 따른 해석
과도한 편향응력은 섬유 배향 방향의 급작스러운 변화에 의해 발생하는 것으로 판단되며, 주로 리브 배치의 배열과 상관관계가 있는 것으로 판단된다. 따라서 이러한 영향을 고찰하기 위해, 본 연구에서는 다음 세 가지 경우의 리브 배치에 따른 평균 섬유 배향 텐서와 잔류응력 해석 비교를 통해 고온 크립 특성을 고찰하고자 하였다.
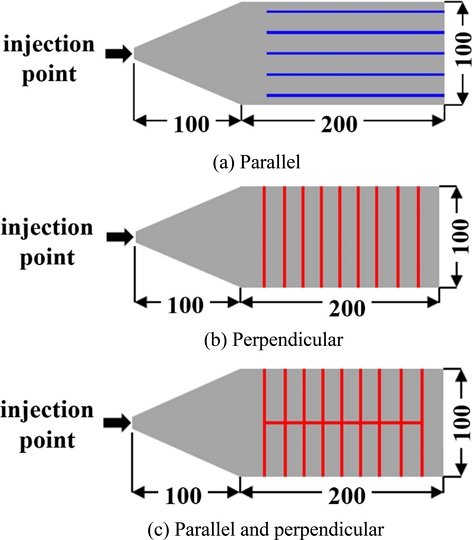
Fig. 3(a)는 유동 방향에 평행인 리브 배치를 나타낸 것이다. 사출 주입점의 효과를 최소화하기 위해 리브를 사출 주입점으로부터 100 mm 이상에 위치시켰으며, 기본 두께 3 mm, 리브 두께 2 mm, 리브 높이는 10 mm로 적용하였다.
Fig. 3(b)는 유동 방향에 수직인 리브 배치를 나타낸 것이다. Fig. 3(a) 유동 방향에 평행인 리브 배치의 해석 모델과 동일하게 리브 배치를 사출 주입점으로부터 100 mm 이상에 위치시켰으며, 기본 두께 3 mm, 리브 두께 2 mm, 리브 높이 10 mm로 적용하였다.
Fig. 3(c)는 유동 방향에 평행 및 수직인 리브 배치를 나타낸 것이다. 유동 방향에 평행인 리브 배치의 플로우 리더(Flow Leader) 역할을 통해 점탄성 효과 검증을 위하여 Table 2 Sample “B”를 기준으로 해석 모델에 플로우 리더 역할을 하는 유동 방향에 평행 및 수직인 리브 배치를 적용하여, 기본 두께 2.2 mm, 유동 방향에 평행인 리브 두께 3 mm, 수직인 리브 두께 2.5 mm, 리브 높이 10 mm로 적용하였다.
3. 연구 결과 및 고찰
3.1 고온 크립의 점탄성 효과 검증
본 연구에서는 섬유 강화 고분자 복합 재료의 사출성형 시 발생하는 고온 크립 현상을 반영하기 위해 2차 기본방향의 탄성계수 및 1, 2차 기본방향의 전단계수를 기본값을 기준으로 50-100%로 적용시켜 변형해석을 수행하여 해당 제품의 점탄성 변형 이후 나타난 변형과 재현되었는지 검토하였다.
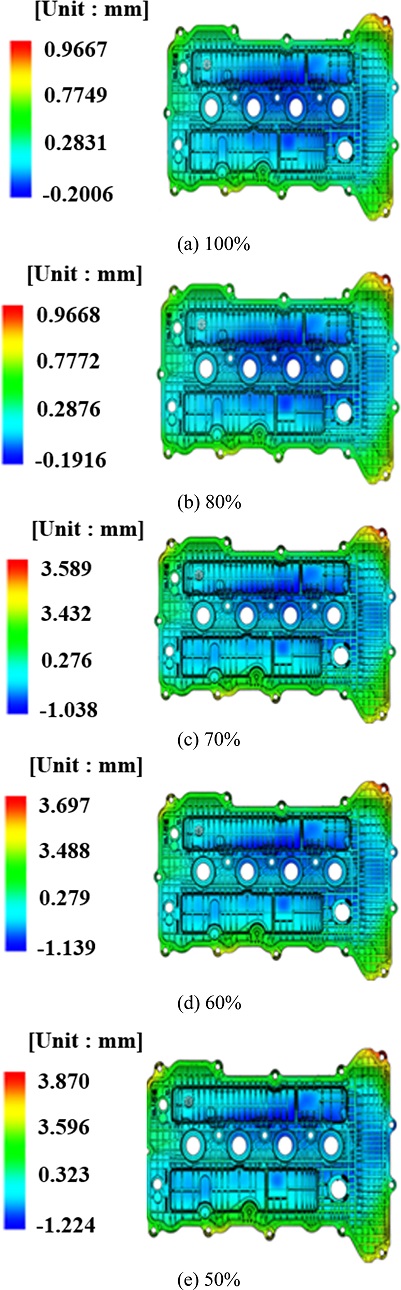
Fig. 4는 횡단등방성물성치를 2차 기본방향에 대한 탄성계수와 1차, 2차 기본방향의 전단탄성계수를 기본값을 기준으로 (a) 100%, (b) 80%, (c) 70%, (d) 60% 및 (e) 50%로 적용하여 변형해석을 한 결과를 나타낸 것이다.
2차 기본방향에 대한 탄성계수 및 1, 2차 기본방향의 전단계수를 Figs. 4(b)로 적용시켰을 경우에는 최대변형량이 0.0001 mm로 큰 영향이 없었고, 4(c), 4(d), 4(e)로 적용시켰을 경우에는 각각 3.589, 3.697, 3.870 mm로 증가하였다. 이는 해당 제품의 점탄성 변형 이후 나타난 변형과 유사한 결과를 나타냈다.
이는 폴리머 기지(Polymer Matrix)의 강성이 제품 강성에 기여하는 효과가 감소함으로써 나타나는 결과로 보이며, 폴리머 기지에서 점탄성 및 소성변형이 일어난 결과로 판단된다. 따라서, 섬유강화 고분자 복합 재료의 2차 기본방향 탄성계수 및 1, 2차 기본방향 전단계수의 수정을 통한 변형 특성을 고찰한 결과, 해당 제품의 점탄성 변형 이후와 유사한 결과를 통해 점탄성 효과를 검증할 수 있었다[12].
3.2 기하학적 형상에 따른 특성
Fig. 5는 제품 외측의 평균 섬유 배향 텐서를 나타낸 것이다. Fig. 5(a)는 Sample A의 결과에 해당하며, Fig. 5(b)는 Sample B의 결과에 해당한다. Figs. 5(a), 5(b) 모두 게이트 주변에서 배향 방향의 변화가 있으나, 전체적으로 직사각형 형상의 길이 방향으로 1차 기본방향이 배향되었다.
Fig. 6은 제품 내측의 평균 섬유 배향 텐서를 나타낸 것이다. Fig. 6(a)는 외측과 동일하게 게이트 주변에서 배향 방향의 변화가 있으나 전체적으로 길이 방향으로 1차 기본방향이 배향되는 결과가 나타났다. Fig. 6(b)는 다수의 길이 방향으로 배치된 두꺼운 리브 형상에서 레이스트랙 효과(Racetrack Effect)에 의해 플로우 리더 역할이 수행되는 것으로 보이며, 그에 따라 유동 방향에 수직인 리브 배치에서 직사각형 형상의 짧은 변 방향으로 배향성이 나타남을 확인할 수 있다.
사출 성형품에 변형이 생기는 원인 중 하나는 잔류응력이다. 수지가 고온과 고압으로 금형에 채워지고 냉각되는 과정에서 성형품에 잔류응력이 형성된다. 잔류응력은 시간이 지나면서 스스로 이완되면서 제품에 변형을 일으킨다[13].
Fig. 7은 섬유강화 고분자 복합재료의 사출성형시 기하학적 형상에 따른 고온 크립 특성을 고찰하기 위한 제품 내측의 잔류 응력 결과를 나타낸 것이다. Figs. 7(a)에서는 배향 방향의 급작스러운 변화가 발생하는 일부 구간에서 비교적 큰 값이 나타났으며, 7(b)에서는 대부분의 유동 방향과 수직으로 배치된 리브 형상에서 큰 값이 나타남을 확인할 수 있었다. 이는 급격한 배향 방향의 변화로 인한 것으로 판단된다. 이를 통해 Fig. 7(b)의 기하학적 형상이 다소 문제됨을 알 수 있었다.
3.3 리브 배치에 따른 특성
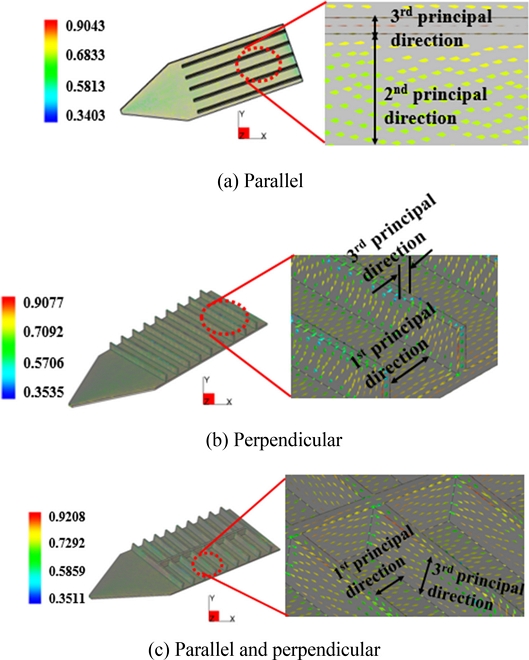
Fig. 8(a)는 유동 방향에 평행인 리브 배치의 평균 섬유 배향 텐서 결과를 나타낸 것이다. 섬유 배향 텐서를 고찰해본 결과, 해석 모델의 상하면 모두에서 1차 기본방향은 X축 방향으로 배향되었으며, 2차 기본방향은 바닥 면에서는 Y축 방향으로 균일하게 정렬되었다. 그러나 리브 구간에서는 제품의 두께 방향으로 정렬되는 3차 기본방향 특성에 의해, Y축 방향으로 2차 기본방향과 리브 구간에서 3차 기본방향이 교대로 나타났다.
Fig. 8(b)는 유동 방향에 수직인 리브 배치의 평균 섬유 배향 텐서 결과를 나타낸 것이다. 해석 모델의 제품 표면에서 1차 기본방향은 X축 방향으로 배향되었으며, 리브 구간에서는 말단면에서 말단 효과에 의한 배향 효과가 나타났으나 짧은 구간에서 나타나 영향이 크지 않은 것으로 보인다. 대부분의 리브 구간에서 3차 기본방향이 배향되어 1차와 3차 기본방향이 교대로 나타남을 확인할 수 있다.
Fig. 8(c)는 유동 방향에 평행 및 수직인 리브 배치의 평균 섬유 배향 텐서 결과를 나타낸 것이다. 해석 모델의 제품 표면에서 유동 방향에 평행인 리브에서 플로우 리더 역할을 하여 유속이 빨라짐을 알 수 있다. 또한 바닥 면에서는 느린 유속을 나타내어 바닥 면과 유동 방향에 수직인 리브에서 제품 표면에서 1차 기본방향에 직교배향 양상을 보였다.
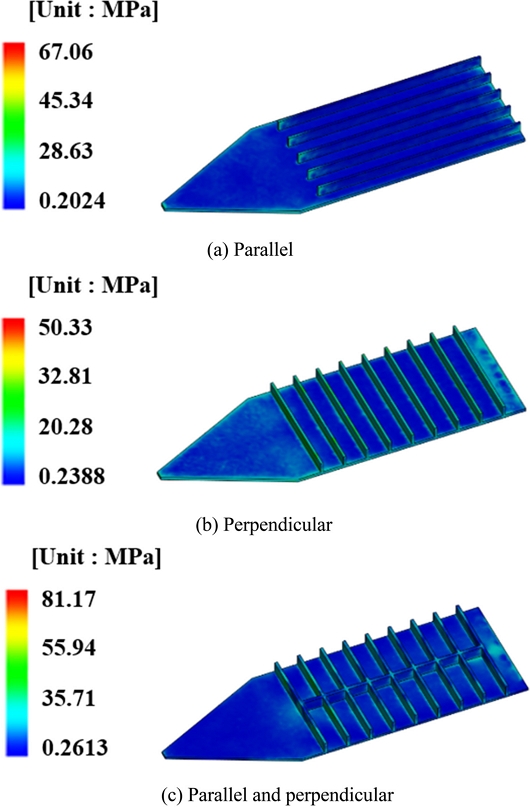
Fig. 9(a)는 유동 방향에 평행인 리브 배치의 잔류응력 해석 결과를 나타낸 것이다. 최댓값은 67.06 MPa로 나타났으며, 일부 배향 방향이 급격히 변화하는 부분에서 값이 크게 나타났지만 전체적으로 균일한 1차 기본방향에 의해 낮은 값을 나타낸다.
Fig. 9(b)는 유동 방향에 수직인 리브 배치의 잔류응력 해석 결과를 나타낸 것이다. 최댓값은 50.33 MPa로 나타났으며, 제품 표면에서 배향 방향은 유지됐지만, 리브 진입 구간에서 수직으로 급격히 꺾여, 리브와 제품 접합 구간에서 비교적 큰 값을 나타낸다. 이 경우 제품 표면에서의 배향은 균일하게 유지되었으므로 제품 표면을 따라 항복이나 점탄성 변형을 일으킬 정도의 인장 또는 전단응력은 발생하지 않은 것으로 보인다.
Fig. 9(c)는 유동 방향에 평행 및 수직인 리브 배치의 잔류응력 해석 결과를 나타낸 것이다. 최댓값은 81.17 MPa로 나타났으며, 제품 표면에서 1차 기본방향에 직교 배향 양상을 보였으며 큰 값이 나타나 이 경우 소성변형 및 점탄성 효과가 예상된다.
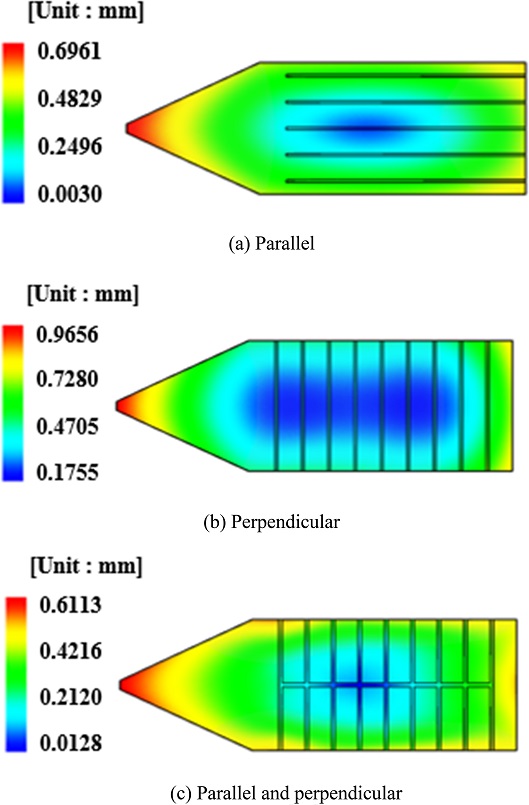
따라서, 섬유강화 고분자 복합재료의 사출성형 시 리브 배치에 따른 고온 크립 특성을 고찰하기 위해 세 가지 경우의 리브 배치에 따른 잔류응력 값을 비교한 결과, Fig. 9(c)와 같이 유동 방향에 평행 및 수직인 리브 배치에서 최댓값이 81.17 MPa으로 세 가지 리브 배치 중 가장 큰 값을 나타내었다. Fig. 10은 변형 해석 결과를 나타낸 것이다. Fig. 10(c)의 리브가 교차되는 배치의 경우 변형량이 비교적 적은 값을 보이는 것을 확인할 수 있다. 이 경우 변형량은 다소 작지만 잔류응력이 가장 큰 값을 나타내므로 소성변형 및 점탄성 효과가 가장 클 것으로 예상되기 때문에, 리브가 교차되는 배치를 지양해야 할 것으로 판단된다.
4. 결론
본 연구에서는 사출성형공정 해석을 통하여, 섬유강화 고분자 복합재료의 이형 후 상온 냉각 중인 사출성형제품의 기하학적 형상 및 리브 배치에 따른 크립 현상의 특성을 규명하고자 하였다.
1) 고온 점탄성 효과는 결정형 수지 종류의 엔지니어링 플라스틱(Engineering Plastic) 경우도 제품 이형 온도가 유리 전이온도보다 상당히 높을 시, 제품 이형 후 점탄성 변형은 비결정형 구간에서 충분히 발생함을 확인할 수 있었다.
2) 기하학적 형상에 따른 특성으로는 외곽 형상이 비대칭인 Sample A 해석 모델의 경우 부분적으로 배향 방향의 급격한 변화가 발생하는 구간에서 잔류응력이 비교적 큰 값이 나타났다.
다수의 리브 형상을 가진 Sample B 해석 모델의 경우 대부분의 유동 방향과 수직인 리브 구간에서 급격한 배향 방향 변화로 인해 잔류응력이 큰 값이 나타남을 통해 Sample B의 기하학적 형상이 다소 문제됨을 알 수 있었다.
3) 세 가지 경우의 리브 배치에 따른 섬유 배향 텐서 및 효과 해석 결과, 유동 방향에 평행 및 수직인 리브 배치에서 제품 표면의 유동 방향에 평행인 리브에서 Flow Leader의 영향을 받아 1차 기본방향에 직교 배향 양상을 보였다.
또한, 유동 방향에 평행 및 수직인 리브 배치에서 잔류응력이 가장 큰 값을 나타내므로, 이 경우 소성변형 및 점탄성 효과가 가장 클 것으로 예상되기 때문에 리브가 교차되는 배치를 지양해야 할 것으로 판단된다.
특히 리브설계 시 잔류응력, 구조적 강성, 변형 등의 관계가 복잡하므로 본 연구에서는 리브 설계에 따른 대략적인 경향성을 살펴보았다. 명확한 결론 도출을 위해서는 향후 이에 대한 추가적인 연구가 필요할 것으로 사료된다.
Acknowledgments
This paper was presented at KSPE Autumn Conference 2022
REFERENCES
- Cho, D.-H., Kim, H.-J., (2009), Naturally cyclable biocomposites, Elastomers and Composites, 44(1), 13-21.
- Strong, A. B., (2008), Fundamentals of composites manufacturing: Materials, methods and applications, Society of Manufacturing Engineers.
- Schwartz, M. M., (1984), Composite materials handbook, Second Edition, McGraw-Hill. https://archive.org/details/compositemateria0000schw/mode/2up
- Jang, B., (1994), Advanced polymer composites: Principles and applications. ASM International.
- Lee, J., (2016), Research on the residual fiber length in injection molding process for glass fiber reinforced polypropylene, M.Sc. Thesis, Ajou University.
- Lee, H. K., Kim, H. C., Yang, G. E., (2002), A study on process of injection mold in reverse engineering, Journal of the Korean Society of Precision Engineering, 19(6), 160-165.
- Hwang, S., Han, S.-R., Lee, H., (2021), A study on the improvement of injection molding process using CAE and decision-tree, Journal of the Korea Academia-Industrial Cooperation Society, 22(4), 580-586.
- Wu, Z., (2018), Analytical study on various process conditions for improving quality of injection molding, M.Sc. Thesis, Hannam University.
-
Moon, H., Kim, H., Choi, C., Jeong, K., (2008), Thermal viscoelastic analysis of plastic part considering residual stress, Transactions of Materials Processing, 17(7), 496-500.
[https://doi.org/10.5228/KSPP.2008.17.7.496]

-
Kim, J. S., Han, J. W., (2022), Enhanced first-order shear deformation theory for thermo-mechanical-viscoelastic analysis of laminated composite structures, Journal of the Korean Society of Manufacturing Process Engineers, 21(4), 53-59.
[https://doi.org/10.14775/ksmpe.2022.21.04.053]

-
Reissner, E., (1945), The effect of transverse shear deformation on the bending of elastic plates, Journal of Applied Mechanics, 12(2), A69-A77.
[https://doi.org/10.1115/1.4009435]

-
Xie, X.-L., Mai, Y.-W., Zhou, X.-P., (2005), Dispersion and alignment of carbon nanotubes in polymer matrix: A review, Materials Science and Engineering: R: Reports, 49(4), 89-112.
[https://doi.org/10.1016/j.mser.2005.04.002]

-
Lee, M., Kim, H., Lyu, M.-Y., (2012), A study on the warpage of glass fiber reinforced plastics for part design and operation condition: Part 1. Amorphous Plastics, Polymer (Korea), 36(5), 555-563.
[https://doi.org/10.7317/pk.2012.36.5.555]


Master student under the supervisor of Professor Hee-Seon Bang in Department of Welding and Joining Science Engineering, Chosun University. Her research interests include the smart welding process and design.
E-mail: yujung4171@naver.com

A Professor in the Department of Welding and Joining Science Engineering, Chosun University. Her research interests include the smart welding process and design.
E-mail: banghs@chosun.ac.kr