AAM 덕트 내 스트럿 형상에 따른 블레이드 공력 음향 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Lately, due to the concentration of population in metropolitan areas, traffic congestion in the hub city has occurred, and future mobility AAM development is undergoing active progress to solve this situation. Accordingly, reducing noise pollution, which is pointed out as one of the problems of AAM, is an essential technical issue for urban operation. In this study, a duct, which is a representative aerodynamic noise reduction method, was used, and numerical analysis was performed using ANSYS FLUENT, a CFD software, according to the shape of struts in the duct. The FW-H of the transient-state LES model was used, and the steady-state analysis value was used as the initial value to save analysis time. Case 1 without strut, Case 2 with strut of an airfoil section, and Case 3 with strut of a rectangle section were designed and compared at a rotational speed of 6,000 RPM. Compared to Case 1, Case 2 and Case 3 showed improved thrust by about 7% and 2%, respectively. Compared to Case 2, Case 3 showed reduced OASPL from a minimum of 0.0793 dB to a maximum of 1.0072 dB. It was found that shapes of strut in the duct significantly affect thrust and aerodynamic noise.
Keywords:
Advanced air mobility, Electric vertical take-off and landing, Aerodynamic noise, Ducted blade, Sound pressure level키워드:
미래 항공 모빌리티, 전동 수직 이착륙기, 공력 소음, 덕트 블레이드, 음압 레벨1. 서론
최근 전 세계적으로 대도시로의 인구 집중화로 인해 환경 문제와 도심 내 심각한 교통 체증 문제가 발생하며, 이를 해결하기 위해 미래 항공 모빌리티(Advanced Air Mobility, AAM) 개발이 활발하게 진행되고 있다.
AAM은 도심 내 교통 체증을 해결하기 위한 도심 항공 모빌리티(Urban Air Mobility, UAM)와 주요 도시·지역 간 항공 이동을 위한 지역 간 항공 모빌리티(Regional Air Mobility, RAM)의 개념을 포괄한다. AAM은 전동 수직 이착륙기(Electric Vertical Takeoff and Landing, e-VTOL)로 개발되어 활주로 없이 수직으로 이착륙이 가능하며, 내연기관이 아닌 전기 모터를 사용하여 유해가스의 배출이 없다는 이점이 존재한다. 또한 전기 모터의 사용은 이착륙 및 비행 시 발생하는 엔진 소음을 저감시킬 수 있어 AAM에 적용되고 있다. 하지만 AAM은 모터에서 발생하는 엔진 소음보다 블레이드의 와류 간섭으로 인해 생기는 Blade-vortex Interaction (BVI) 소음이 지배적[1]이기 때문에 도심 항공에서 비행하기 위해서는 블레이드를 중점으로 공력 소음 저감 연구가 진행되어야 한다. 대표적인 공력 소음 저감 방법으로는 덕트를 사용한 연구[2]가 있다. 덕트를 사용하였을 때 생기는 이점으로는 제자리 비행(Hovering) 시 추력(Thrust) 증가 및 블레이드 끝단 와류를 제어하여 소음을 저감시키며, 덕트가 블레이드로 향하는 이물질 등을 막아 안전성 향상을 기대할 수 있다.
덕트 형상은 공력 성능뿐만 아니라 소음에도 영향을 미치기 때문에 덕트를 활용한 기존 연구도 활발히 수행되고 있다. Zhao 등[3]은 제자리 비행 시 덕트의 지면 효과(Ground Effect)에 초점을 맞추어 공기역학적 특성 및 소음에 대한 연구를 수행하였다. Ventura Diaz 등[4]은 덕트 및 동축 로터에서의 공기역학적 특성 및 소음에 대해 비교하여 각각의 성능을 평가하였다. Jang 등[5]은 덕트에 Shroud를 활용하여 블레이드 끝단 와류 제어를 통한 소음 저감 효과를 연구하였으며, Guo 등[6]은 다공성 덕트와 일반 덕트의 비교를 통해 다공성 구조를 사용한 덕트의 소음 저감 효과에 대한 연구를 수행하였다.
또한 덕트의 형상을 변경하여 소음을 저감하려는 연구도 수행되고 있다. Kim 등[7]은 덕트 전연(Leading Edge) 형상에 따른 유동 박리 연구를 진행하여 소음 저감 연구에 유의미한 해석 값을 제시하였다. Zhang 등[8]은 덕트와 블레이드의 비틀림 분포를 변경하여 소음 해석 연구를 수행하였다. 하지만 블레이드의 형상을 변경하여 소음을 저감하려는 연구는 활발히 진행되고 있지만, 덕트 및 덕트 내 스트럿의 형상을 변경하는 연구는 많이 수행되지 않았다. 또한 덕트와 AAM 기체를 고정하는 스트럿(Strut)은 수치 해석을 진행할 때 해석 시간을 고려하여 무시하고 진행되기 때문에 스트럿에 관한 연구는 거의 수행되지 않았다. 그러나 Park 등[9]의 연구에 의하면 덕트 내 스트럿은 블레이드의 추력 및 공력 소음에 영향을 미치는 것을 알 수 있다.
본 연구에서는 스트럿이 없는 덕트와 스트럿 단면 형상을 에어 포일 및 직사각형 형태로 설계 및 해석하였다. 블레이드의 추력 및 공력 음향에 대해 가상해석을 진행하였으며, 가상해석을 통해 덕트 내 스트럿 유무에 따라 블레이드의 추력 및 공력 음향에 미치는 영향에 대해 비교 후 스트럿 형상에 따라 공력 소음 및 추력 성능을 수치적으로 해석하는데 연구목표를 두었다.
2. 해석 모델 설계 및 가상해석
2.1 블레이드 및 덕트 설계
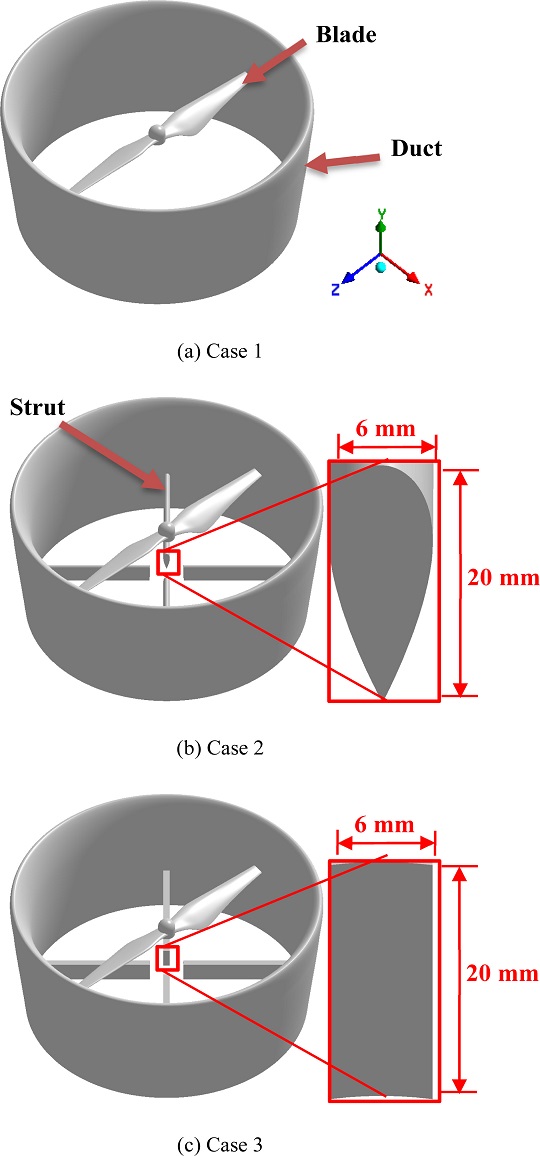
본 연구에서는 블레이드 모델로 D 社의 9450 블레이드를 사용하였으며, 덕트의 형상은 Yilmaz 등[10]의 연구를 참조하여 NACA 4312 에어 포일을 사용하였다. 블레이드 직경은 240 mm이며, 덕트의 길이는 140 mm다. 블레이드의 위치는 덕트 전연으로부터 단면 길이의 0.3에 해당하는 부분에 블레이드 중심점을 위치시켰다. 본 연구에서 사용한 모델의 제원은 Table 1에 정리하였다. Fig. 1은 효과적으로 가상해석을 수행하기 위해 공력 및 소음에 지배적인 영향을 미치지 않는 블레이드 뒤 포드(Pod)의 형상을 제거하여 단순화한 형상이다. Fig. 1(a)는 스트럿이 없는 Case 1 형상이며, Figs. 1(b)와 1(c)는 각각 스트럿 단면 형상을 에어 포일과 직사각형으로 설계한 Cases 2, 3 형상이다. 덕트 내 스트럿의 단면 형상을 같은 크기(높이 20 mm, 폭 6 mm)로 설정하였다.
2.2 격자 생성 및 의존도 검사
본 연구에서는 격자 생성을 위해 ANSYS MESH를 사용하였고, 유동 해석에 적합하게 Volume을 기준으로 벽면 인근 조밀한 격자 Sizing을 주었으며, 사면체와 육면체를 혼합하는 비정렬 격자를 사용하였다. 블레이드, 덕트 및 스트럿에서의 7층 이상의 경계층을 고려하였다. 경계층 해석 특성상 벽면 격자에서 적절한 Y+ 값을 고려하여 격자를 생성하였다. 격자 생성 조건을 따른 모든 Cases의 유동장을 포함한 격자 수와 노드 수는 Table 2에 정리하였다.
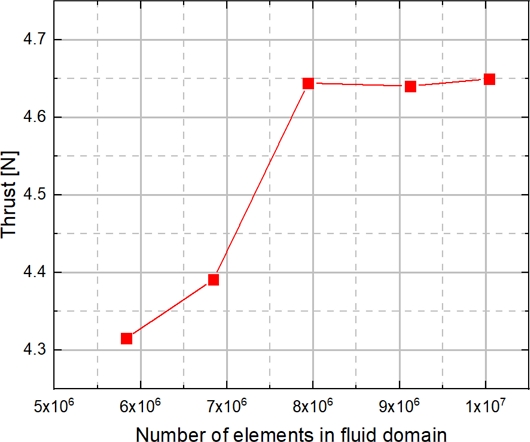
본 연구에서 생성된 격자의 신뢰성을 확인하기 위해 격자 의존도 검사를 수행하였다. 격자 의존도를 검사하기 위해 스트럿이 없는 Case 1 형상을 블레이드 및 덕트의 격자 수를 차이를 두어 생성한 후, 추력을 비교하였다. 약 600만개부터 1,000만개까지 5개의 격자 모델을 생성하였으며, 수렴성 및 해석 시간을 고려하여 약 900만개의 격자 수를 선정하였다. 격자 의존도 검사 결과를 Fig. 2에 표시하였다.
2.3 경계 조건
본 연구에서는 저고도 비행체인 AAM의 비행 조건을 고려한 성능 분석을 위해 입·출구에서의 경계조건(Boundary Conditions)을 대기압으로 가정하여 가상해석을 수행하였다. 블레이드 팁 부근 높은 선속도로 인해 발생하는 공기역학적 특성 및 소음의 변화가 명확하게 예측되는 최대 회전속도인 6,000 RPM으로 설정하였다. 블레이드 직경이 크지 않아 압축성 효과가 적을 것으로 예상되어 주변 유체는 비압축성으로 계산하였다. 상세한 경계 조건은 Table 3에 정리하였다.
k-ω Shear Stress Transport (SST) 모델에 기반하여 초기값을 계산 후, 계산된 초기값을 Large Eddy Simulation (LES) 모델을 사용하여 계산하였다. 공력 음향 연구에서는 청취자까지의 매질에 대한 물성치도 고려되어야 하기 때문에, 대기를 매질로 사용하였다. 수치적 음향해는 Table 4의 12개의 청취자(Listener) 위치에서 예측하였다.
2.4 가상해석
상용 전산 유체 역학(Computational Fluid Dynamics, CFD) 코드인 ANSYS FLUENT를 활용하여 가상해석을 수행하였다. 블레이드 및 덕트의 공기역학적 특성인 제자리 비행을 수치적으로 분석하기 위해 운동량 방정식과 연속 방정식을 고려하였다. 운동량 방정식을 계산하기 위해 유동장 영역을 고정 영역과 회전 영역으로 나누었다. 고정 유동장에서는 직교 좌표를 기준으로 운동량 방정식을 계산하였으며, 블레이드 인근 회전 유동장은 회전 운동을 계산하기 위해 기준 좌표에 회전 좌표를 추가한 방정식을 계산하였다.
공력 음향 해석에서는 과도상태(Transient State) 해석이 필수적이지만, 수치적으로 수렴하는데 상당한 시간이 소요된다. 본 연구에서는 해석 시간을 절약하기 위한 방법으로 정상상태(Steady State) 해석을 통해 얻은 해석 값을 과도상태 해석의 초기값으로 사용하였다. 회전 영역 주위 난류를 해석하기 위해 상류에서 자유 난류의 현상 설명 및 벽면 근처 유동에 적합한 모델인 Reynoldsaveraged Navier-Stokes (RANS)의 k-ω SST 모델을 사용하여 해석하였다. 과도상태 해석은 LES 모델을 사용하였으며, 이는 유동해석에서 RANS 모델에 비해 정확하고 현실적인 결과를 생성할 수 있다. 정상상태 및 과도상태 해석에서 회전 유동장은 Moving Reference Frame (MRF) 방법을 사용하여 식(1)로 계산하였다.
| (1) |
여기서, 2ω × vr, ω × ω × r은 각각 Coriolis 가속도, 구심가속도이며, α × r와 α는 모두 선형 가속도를 의미한다. 정상 상태 해석을 통해 얻은 초기값은 우측 첫번째 항을 제외하여 계산하였으며, 과도상태 해석에서는 모든 항을 사용하여 시간에 따른 변화를 고려하여 MRF를 계산하였다.
수치해석적으로 블레이드 및 덕트의 공력 음향해를 계산하기 위한 대표적인 예측 방법인 Lighthill [11]의 음향 상사법(Aeroacoustic Analogy)을 바탕으로 하는 Ffowcs Williams-Hawkings (FW-H) 방정식[12]을 활용하여 식(2)로 계산하였다.
| (2) |
여기서, a0와 p′는 각각 원거리 장 음속, 음압이며, H(f)는 단위 계단 함수, δ(f)는 Dirac Delta 함수를 의미한다.
3. 결과 및 고찰
본 연구에서는 AAM 덕트 내 스트럿 유무에 따라 블레이드의 추력 및 공력 음향에 미치는 영향을 분석하기 위해 Fig. 1(a)의 스트럿이 없는 Case 1 형상과 Figs. 1(b)와 1(c)의 스트럿 단면 형상을 에어 포일과 직사각형으로 설계한 Cases 2와 3 형상의 가상해석을 수행하였다. 적절한 스트럿 단면 형상을 설계하기 위해 전체 음압 레벨(Overall Sound Pressure Level, OASPL) 및 주파수에 따른 음압 레벨(Sound Pressure Level, SPL)을 비교하여 공력 음향에 대해 해석하였다. Intel Xeon Phi 7250 1.4 GHz, 68 core, 96 GB, 6Ch per CPU 성능의 수퍼컴퓨터를 활용하여 해석의 신뢰성을 확인하였다.
3.1 추력 성능
덕트를 사용하는 공력 음향 연구에서 스트럿을 고려하여 설계하였을 때 블레이드에 미치는 영향을 확인하기 위해 덕트 내 스트럿 유무 및 형상에 따라 추력 값을 비교하였다. 총 3가지 Case에서 블레이드를 6,000 RPM으로 회전시켰을 때 생기는 추력 값을 Table 5에 정리하였다. Case 1에서 추력은 약 4.64 N으로 계산되었으며, Cases 2와 3에서는 각각 약 4.98, 4.74 N으로 Case 1에 비해 각각 약 7, 2% 향상된 추력이 계산되었다. 이는 블레이드 하부에 있는 스트럿 유무 및 형상에 따라 덕트를 통과하는 공기의 흐름에 영향을 미치는 폐색 효과(Blockage Effect)[9]로 인해 스트럿 상단과 하단에서 정압 차이가 발생하여 향상된 값을 확인할 수 있었다.
3.2 와도 분포
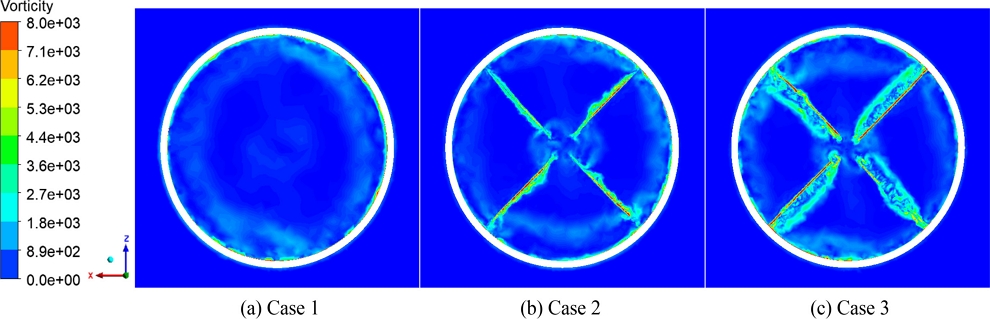
스트럿 후연에서 발생하는 와도가 공력 음향에 영향을 미칠 것으로 판단되어 덕트 내 스트럿 유무 및 형상에 따라 변동하는 공력 음향을 예측하기 위해 스트럿 후연에서 와도 분포를 비교하였다. 와도 발생 지점에서의 차이를 명확하게 비교하기 위해 범위를 0-8,000 [s−1]으로 제한하여 Fig. 3에 표시하였다. Case 1과 다르게 Cases 2와 3은 스트럿 후연에서 발생하는 와도 분포를 확인할 수 있었다. Case 2는 에어 포일 스트럿 형상에 의해 와도가 스트럿 후연에 집중되는 것을 확인할 수 있으며, Case 3은 직사각형 스트럿 형상에 의해 박리가 발생하는 것을 확인할 수 있었다. 이는 청취자 위치에서 공력 음향을 예측할 때 와도가 한 곳으로 집중되는 Case 2보다 박리가 발생하는 Case 3에서 와도 강도가 감소되어 Case 3에서 공력 소음 저감 효과가 클 것으로 예측할 수 있었다. 스트럿 후연에서 발생하는 와도 분포의 비교를 통해 덕트 내 스트럿 유무 및 형상이 공력 음향에 영향을 미치는 것을 알 수 있었다. 따라서 덕트에서의 공력 소음 저감 설계를 위해서는 스트럿 단면 형상 개선이 필수적이라고 판단할 수 있었다.
3.3 압력계수 분포
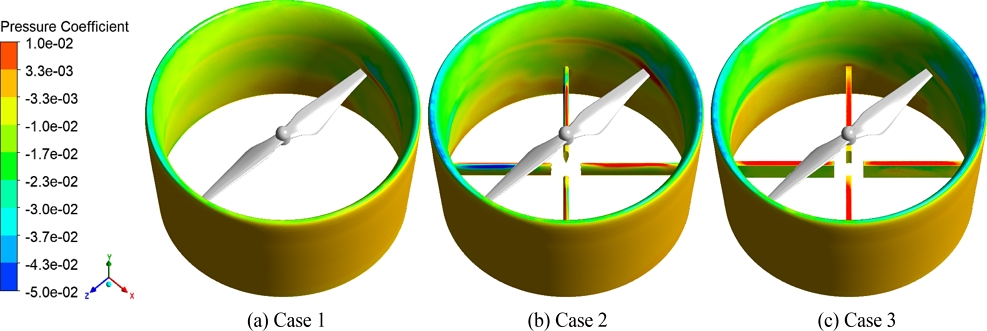
블레이드의 회전으로 인해 생기는 덕트 내 스트럿에서의 압력 저항을 압력계수(Pressure Coefficient, Cp)를 통해 비교하였다. Fig. 4는 6,000 RPM으로 회전하는 블레이드 및 덕트에서 스트럿 주변 압력계수를 비교하기 위해 덕트 및 덕트 내 스트럿에서 계산한 압력계수 분포이다. 스트럿에서의 압력계수를 명확하게 비교하기 위해 범위를 -0.05~0.01로 제한하였다. Case 1과 다르게 Cases 2와 3을 통해 스트럿에서 압력계수 편차가 크게 나타남을 알 수 있었다. Case 2와 3에서 공력 소음이 최대로 발생할 수 있는 국소 위치에서 압력계수 차이는 각각 약 0.11, 0.06으로 Cases 2가 3에 비해 약 83% 높은 것을 확인할 수 있었다. 이는 스트럿이 블레이드가 회전할 때 생기는 와류와 상호작용하면서 와류의 발생과 흐름에 변화를 주게 되어 압력 변동이 다르게 발생하는 것을 알 수 있었다. Case 2보다 Case 3에서 공력 소음에 직접적인 영향을 미치는 급격한 압력 변동이 개선되며, 이는 스트럿 형상에 따라 압력 변동 크기에 영향을 미치는 것을 의미한다. 압력계수 분포를 비교를 통해 덕트를 활용한 연구에서 공력 음향을 정확히 예측하기 위해서는 스트럿을 고려해야 할 것으로 판단한다.
3.4 덕트 내 스트럿 형상에 따른 공력 음향 비교
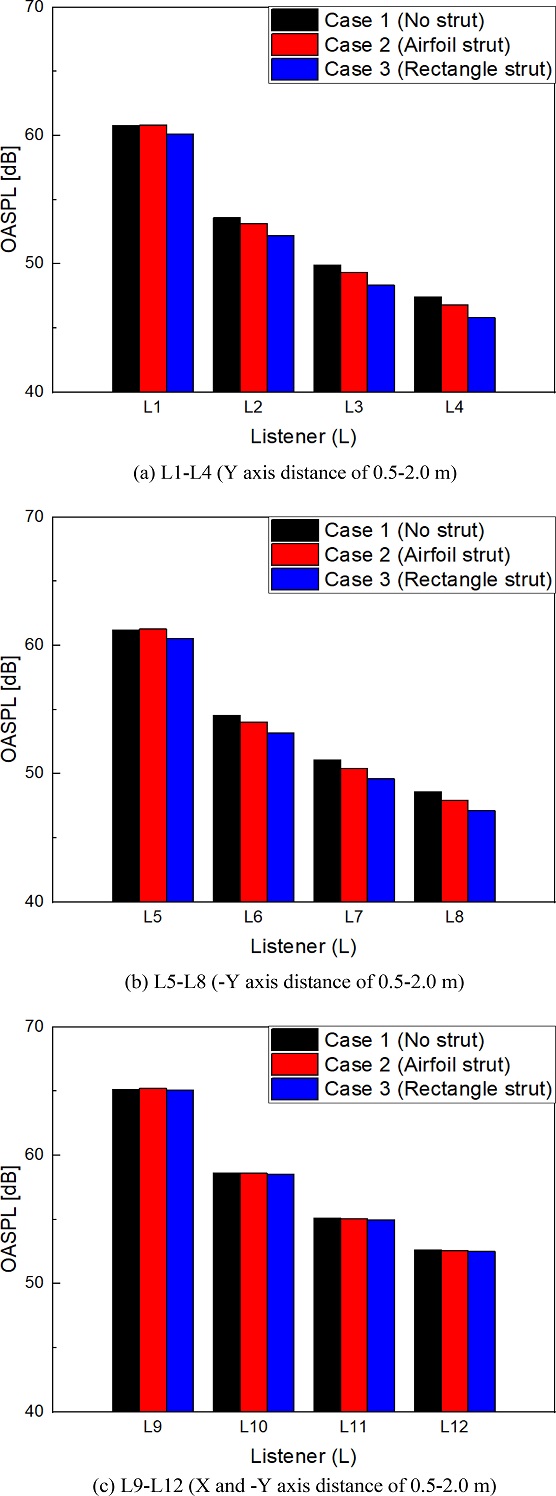
Fig. 5의 그래프는 Table 4의 12개의 청취자 위치에 따라 Cases 1-3의 OASPL을 보여준다. OASPL은 소음의 강도를 평가하는 중요한 지표이며, 넓은 스펙트럼의 주파수에서 발생하는 음압 레벨의 적분형으로 식(3)과 식(4)로 계산하였다.
| (3) |
| (4) |
여기서, Pref는 기준 음압, f는 주파수를 의미하며, 본 연구에서는 1 kHz에서 청취자가 들을 수 있는 최소 음압 레벨인 20 μPa로 계산하였다.
L1-L4는 Y축을 기준으로 회전하는 블레이드 상단에서 거리 0.5-2.0 m까지 0.5 m 간격으로 비교하였으며, L5-L8은 블레이드 하단에서 비교하였다. L9-L12는 L5-L8과 같은 조건에서 X축으로 거리를 0.5-2.0 m까지 0.5 m 간격으로 계산하였다. Figs. 5(a), 5(b), 5(c)에서 같은 방향으로 측정된 소음은 거리가 멀어짐에 따라 감소하는 경향을 확인할 수 있었다. 각 방향별 0.5 m 거리의 청취자 위치에서는 스트럿 효과가 미미하며, 오히려 일부 소음에 악영향을 미친다. 하지만 각 방향별 1.0-2.0 m의 청취자 위치에서는 스트럿을 통한 균일한 유체의 흐름 특성으로 오히려 소음에 긍정적인 영향을 미친다. 그리고 L2-L4, L6-L8에서는 스트럿으로 인한 소음 저감이 크고 L9-L12에서는 덕트 내 스트럿의 영향을 미미하게 받는다. 이는 덕트 내 스트럿에 의한 공력 소음 저감 효과가 적게 미치는 청취자 위치로 덕트 내 스트럿 유무 및 형상에 의한 OASPL의 차이가 적게 나타나는 것을 확인할 수 있었다. Fig. 5에서 덕트 내 스트럿의 형상과 소음의 상관 관계는 Case 1 대비 Case 3 에서 가장 많은 소음이 저감되었으며, OASPL은 Case 1 대비 최소 0.033 dB에서 최대 1.607 dB가 저감되었다.
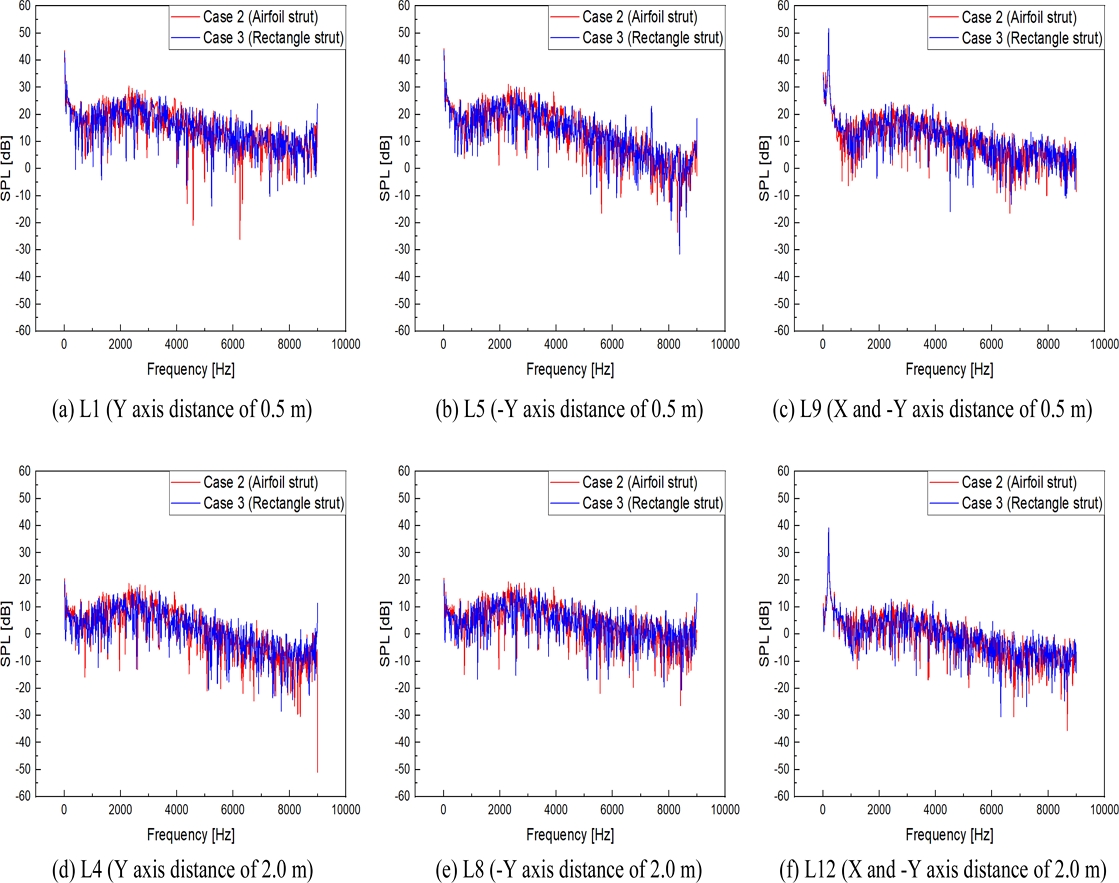
OASPL은 넓은 스펙트럼의 주파수에서 발생하는 음압 레벨의 적분형으로 소음의 크기 비교를 하기에 적합하나, 청취자의 위치별 구체적인 소음의 특성을 비교하는 것은 어렵다. 따라서 청취자의 위치에 따라 주파수 별로 자세하게 분석하기 위해 Fast Fourier Transform (FFT)를 사용하였다. Fig. 6은 청취자 위치별 가장 가까운 거리인 0.5 m의 L1, L5, L9와 가장 먼 거리인 2.0 m의 L4, L8, L12에서 주파수별 SPL을 나타낸 그림이다. Fig. 6의 청취자 위치에서 전체적인 주파수 경향은 비슷하게 나타나며, 2,500-3,000 Hz 사이에서 타 주파수 대비 약 73-135% 높은 소음이 발생하였다. Fig. 6 L1, L4, L5, L8, L9, L12의 청취자 위치에서 SPL은 Case 2 대비 Case 3은 각각 약 1.5, 3.7, 1.6, 4.3, 8.4, 25.1% 저감되었다. 이를 통해 같은 위치에서의 청취자는 거리가 멀어짐에 따라 소음이 감소하는 것을 알 수 있었다. 스트럿 형상에 따라 전반적인 소음의 경향은 비슷하지만, 특정 주파수 대역에서 톤 소음(Tonal Noise) 특성이 다르게 나타났다. 또한 스트럿 형상이 전체적인 소음 수준의 차이는 보이지만, 전반적인 소음 특성에 미치는 영향은 미미한 것을 알 수 있었다. 따라서 Figs. 5와 6을 통해 덕트 내 스트럿의 형상에 따라 공력 소음 저감을 위한 유효한 지표가 나타남을 알 수 있었다. 하지만 Table 5에 나타내었듯 소음 저감만 고려한 형상 설계는 추력의 저하를 초래할 수 있다. 이를 통해 공력 소음 저감 극대화 및 추력 저하의 최소화를 적절히 고려하여 최적의 덕트 내 스트럿 형상을 설계하는 작업이 요구된다.
4. 결론
최근 도심 내 교통 체증 문제가 발생함에 따라 해결책으로 떠오르는 AAM이 도심에서 운용되기 위해서 공력 소음을 줄이는 연구는 필수적이다. 따라서 본 연구에서는 대표적인 공력 소음 저감 방법인 덕트를 활용하였으며, 덕트 내 스트럿 유무 및 형상에 따라 추력 및 공력 음향 해석을 수행하였다. 총 3가지의 스트럿 유무 및 형상에 따라 설계된 Cases에 대한 결론은 다음과 같다.
(1) 회전 속도는 6,000 RPM으로 고정하였으며, 3가지 Cases에서 추력 값을 비교하였다. Case 1 대비 Cases 2와 3에서 각각 추력은 약 7, 2% 향상되는 것을 알 수 있었다. 이는 스트럿에서 폐색 효과가 발생하기 때문이다.
(2) 공력 음향에 직간접적으로 영향을 미치는 유동인자를 확인할 수 있는 와도 분포를 스트럿 후연에서 비교하였다. 청취자 위치에서 공력 음향을 예측할 때 직사각형 스트럿 형상의 Case 3는 스트럿에 의해 박리가 발생하기 때문에 와도 강도가 감소되어 공력 소음 저감 효과가 Case 2 대비 클 것으로 예측할 수 있었다.
(3) 덕트 내 스트럿에서 공력 음향에 영향을 미치는 압력계수 분포를 비교하였다. Cases 2와 3에서 공력 소음이 최대로 발생할 수 있는 국소 위치에서 압력계수 차이는 Case 2가 Case 3에 비해 약 83% 높은 것을 확인할 수 있었다. 이를 통해 스트럿 형상에 따라서 압력계수가 다르게 나타나는 것을 확인할 수 있었다. 또한 Case 2보다 Case 3에서 공력 소음에 직접적으로 영향을 미치는 급격한 압력 변동이 개선되는 것을 알 수 있었다.
(4) 총 12개의 청취자 위치에서 OASPL 및 주파수에 따른 SPL을 비교하였다. 전체적으로 Case 3에서 가장 많은 소음이 저감되었으며, OASPL은 스트럿 형상에 따라 Case 1 대비 Case 3에서 최소 0.033 dB에서 최대 1.607 dB가 감소되었다. 또한 SPL은 Fig. 6의 6가지 청취자 위치에서 Case 2 대비 Case 3이 각각 약 1.5, 3.7, 1.6, 4.3, 8.4, 25.1% 저감되었다. 이를 통해 스트럿 형상에 따라 공력 소음 저감 효과의 차이를 볼 수 있었다.
(5) 본 연구를 통해 덕트 내 스트럿 유무 및 형상에 따라 추력 및 공력 음향에 영향을 미치는 것을 알 수 있었으며, 추력 향상은 에어 포일 스트럿에서, 공력 소음 저감은 직사각형 스트럿에서 성능이 가장 우수하게 나오는 것을 확인할 수 있었다. 이는 블레이드가 회전할 때 생기는 와류와 스트럿은 상호작용하며 와류의 흐름에 변화를 주게 되는데, 스트럿 유무 및 형상에 따라 추력과 공력 음향에 밀접한 연관이 있는 와류에 미치는 영향이 차이가 있음을 알 수 있었다.
(6) 따라서 스트럿 유무에 따라 추력 및 와도 분포, 압력계수를 비교하였을 때 확연한 차이를 볼 수 있었으며, 이는 앞으로 진행될 AAM의 덕트를 활용한 공력 소음 저감 연구에서 스트럿도 고려하여 설계하여야 함을 알 수 있었다. 본 연구를 기반으로 AAM 덕트 내 스트럿의 배치 및 개수에 따른 블레이드 공력 음향에 대해 연구할 것이고, 추력 저하의 최소화 및 공력 소음 저감을 고려한 스트럿 형상을 설계할 것이다.
Acknowledgments
이 결과물은 2023년도 대구가톨릭대학교 학술연구비 지원에 의한 것임.
REFERENCES
-
Yung, H. Y., Gmelin, B., Splettstoesser, W., Philippe, J. J., Prieur, J., Brooks, T. F., (1997), Reduction of helicopter blade-vortex interaction noise by active rotor control technology, Progress in Aerospace Sciences, 33(9-10), 647-687.
[https://doi.org/10.1016/S0376-0421(97)00006-7]

- Kim, D. H., Yi, D. K., Hwang, N. Y., Park, J. H., Ahn, J., (2022), Analysis of aerodynamic performance and noise of propellers according to the presence or absence of duct, Proceedings of the Korean Society for Aeronautical and Space Sciences 2022 Fall Conference, 897-899.
-
Zhao, Y., Tian, Y., Wan, Z., (2022), Aerodynamic characteristics of a ducted fan hovering and transition in ground effect, Aerospace, 9(10), 572.
[https://doi.org/10.3390/aerospace9100572]

-
Ventura Diaz, P., Caracuel Rubio, R., Yoon, S., (2019), Simulations of ducted and coaxial rotors for air taxi operations, Proceedings of the American Institute of Aeronautics and Astronautics Aviation 2019 Forum, 2825.
[https://doi.org/10.2514/6.2019-2825]

-
Jang, C. M., Furukawa, M., Inoue, M., (2001), Noise reduction by controlling tip vortex in a propeller fan, Journal of the Japan Society of Mechanical Engineers International Journal Series B Fluids and Thermal Engineering, 44(4), 748-755.
[https://doi.org/10.1299/jsmeb.44.748]

-
Guo, J., Zhou, T., Fang, Y., Zhang, X., (2021), Experimental study on a compact lined circular duct for small-scale propeller noise reduction, Applied Acoustics, 179, 108062.
[https://doi.org/10.1016/j.apacoust.2021.108062]

- Kim, D. Y., Kwun, S. M., Hong, W. S., Ahn, J., (2021), A study on the inlet flow separation of ducted fan system with duct lip shape under crosswind conditions, Proceedings of the Korean Society for Aeronautical and Space Sciences 2021 Spring Conference, 11-12.
-
Zhang, T., Barakos, G. N., (2021), High-fidelity numerical analysis and optimisation of ducted propeller aerodynamics and acoustics, Aerospace Science and Technology, 113, 106708.
[https://doi.org/10.1016/j.ast.2021.106708]

-
Park, M., Jang, J., Lee, D., (2017), Noise prediction of ducted fan unmanned aerial vehicles considering strut effect in hover, International Journal of Aeronautical and Space Sciences, 18(1), 144-153.
[https://doi.org/10.5139/IJASS.2017.18.1.144]

-
Yilmaz, S., Erdem, D., Kavsaoglu, M., (2013), Effects of duct shape on a ducted propeller performance, Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 803.
[https://doi.org/10.2514/6.2013-803]

-
Lighthill, M. J., (1952), On sound generated aerodynamically I. General theory, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 211(1107), 564-587.
[https://doi.org/10.1098/rspa.1952.0060]

-
Ffowcs Williams, J. E., Hawkings, D. L., (1969), Sound generation by turbulence and surfaces in arbitrary motion, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 264(1151), 321-342.
[https://doi.org/10.1098/rsta.1969.0031]


B.Sc. candidate in the School of Mechanical and Automotive Engineering, Catholic University of Daegu. His research interest is electric vehicle, advanced air mobility and aero-dynamics.
E-mail: shwyoun99@cu.ac.kr

Engineer in the Rotorcraft Flight Dynamics team, Korea Aerospace Industries (KAI). His research interest is aeroacoustics, aerodynamics, propeller/rotorcraft, optimization, and turbo machinery.
E-mail: jihun.song@koreaaero.com

Professor in the Department of Mechanical Engineering, Daegu Catholic University. His research interest is heat transfer, fluid engineering, electric vehicle, and advanced air mobility.
E-mail: dlee@cu.ac.kr