필름 열성형에 의한 선폭 변화를 최소화하기 위한 인쇄 회로의 형상에 관한 연구

1. 서론

그동안 가전, IT기기, 자동차 등 핵심 요소부품인 전자부품, 센서 등을 제작하기 위해 금속을 인서트하고 사출성형하는 방법, 전자회로가 인쇄된 기판을 플라스틱 하우징과 기계적으로 조립하거나 열/초음파로 융착하는 방법 등이 주로 사용되어 왔다[1].

그러나 이러한 방법은 전자부품의 크기와 무게를 줄이는데 한계가 있으며, 3차원 곡면형상의 디자인을 구현하기 어려운 단점이 있다. 또한 조립공정이 복잡하고, 충격에 약하기 때문에 내구성이 떨어지는 문제가 있다[1].

최근 IoT 환경, 스마트시티, U-health 환경 등에서 요구되는 센서, 바이오소자 등 첨단 스마트기기는 대부분 3차원 형상으로 두께가 얇고 가벼우며, 높은 내구성을 요구하기 때문에 전자부품의 고성능화, 고집적화가 매우 중요하다[2].

이에 대응하기 위하여 하중의 지지나 내부 부품을 보호하는 플라스틱 구조물과 인쇄전자 소자를 일체화 성형할 수 있는 새로운 방식의 제조기술이 요구되고 있다. 최근 주목받고 있는 제조기술의 하나인 IME (In-Mold Electronics) 공법은 기존의 FIM (Film Insert Molding) 공법[3]을 더욱 발전시킨 것으로 필름 표면에 전자회로 인쇄, 전자소자 마운팅, 3차원 형상으로의 필름 열성형 및 트리밍, 필름 인서트 사출성형 등으로 구성되어 있다[4]. 전자회로 및 소자가 실장된 필름이 플라스틱 기구물과 일체화 성형되는 것이 특징이며, IME 공법을 적용할 경우 전자제품의 제반 기능과 함께 다양한 형상의 제품을 얇고 가볍게 제조할 수 있는 장점이 있다[4-6]. 특히, 핀란드의 Tacto Tek 사에 따르면 제품의 무게를 약 70% 이상 줄일 수 있으며, 두께를 2 mm정도로 얇게 제작 가능한 것으로 보고되고 있다[4].

한편 전자 제품의 기능이 다양할수록 전자회로가 고밀도화 되고 더 많은 소자를 마운팅하는 것이 필요하기 때문에 필름에 인쇄하는 전자회로의 선폭을 최소화하는 것이 필요하다[5]. 최근에는 미세화 공정 연구를 통해 최소 2-5 nm의 선폭까지 구현할 수 있다는 연구결과가 있다[6]. 그러나 선폭이 작은 전자회로를 필름에 인쇄할 경우 3차원 형상으로 필름을 열성형하는 공정에서 연신에 의해 회로의 선폭이 감소하게 된다. 이로 인해 회로가 끊어지거나 크랙이 발생하여 전자회로의 기능이 제대로 구현되지 못하는 문제가 발생할 수 있다.

지금까지 필름에 인쇄된 전자회로가 열성형 공정에서 발생하는 회로의 변형으로 인해 저항과 전류의 변화를 회로 형상에 따라 고찰한 연구결과가 발표되어 있다[7-9]. 그러나 회로의 형상이 열성형에 의한 선폭 변화에 미치는 영향에 대한 연구결과는 아직까지 보고된 바 없다.

본 연구진에서는 선행연구를 통해 필름 열성형 과정에서 발생하는 인쇄 패턴의 변형량을 예측하고, 해석과 실험 결과가 잘 일치함을 확인하였다[10]. 본 논문에서는 필름 열성형 해석과 실험을 통해 회로 형상이 열성형에 의한 선폭 변화에 미치는 영향에 대하여 고찰하였다. 이를 위해 말발굽 형상, 코일 형상 등 새로운 인쇄회로 형상을 제안하였으며, 각각의 형상에 대해 열성형 이후의 선폭변화를 측정하고, 직선 형상 회로인 경우의 선폭변화와 비교하였다.

2. 회로 형상 및 금형설계

2.1 인쇄회로 형상

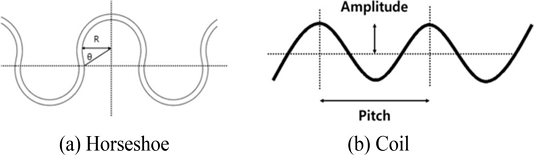
회로 형상이 열성형에 의한 선폭 변화에 미치는 영향을 고찰하기 위하여 말발굽 형상, 코일 형상, 직선 형상의 회로에 대해 각각 해석과 실험을 수행하였다.

말밥굽 형상의 경우 반지름과 각도가 열성형 이후 전기저항에 미치는 영향이 매우 큰 것으로 알려져 있다[11]. 이를 반영하여 Fig. 1(a)와 같이 반지름과 각도를 설계변수로 사용하였으며, 또한 코일 형상에서는 Fig. 1(b)와 같이 피치와 진폭을 설계변수로 사용하였다. 이때 선폭은 0.5 mm로 고정하였다.

Fig. 1

Circuit shape

2.2 적용모델 및 금형설계

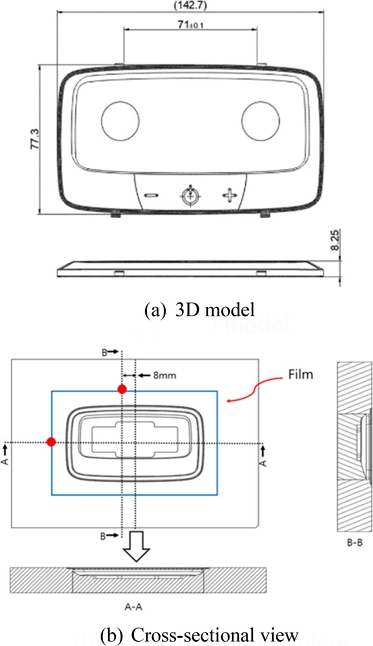
가로, 세로 길이가 각각 142.7, 77.3 mm이고, 높이 8.25 mm인 자동차용 룸램프를 적용모델로 선정하였으며, Fig. 2는 3차원 형상과 단면형상을 각각 나타낸다.

Fig. 2

Application model of a room lamp

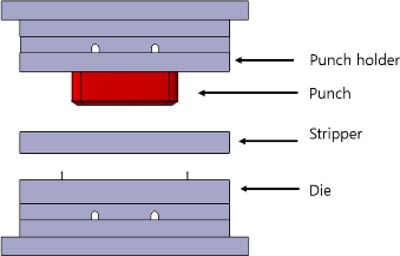
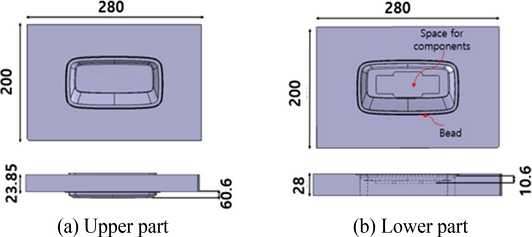
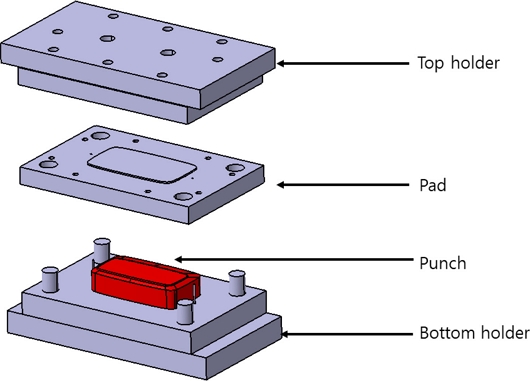
Fig. 3과 같이 스트리퍼, 펀치, 다이로 구성된 열성형 금형을 설계하였으며, 필름을 고정하기 위하여 4개의 고정핀을 사용하였다. Fig. 4는 상측과 하측 금형의 개략도를 나타낸 것으로 필름을 연신시키기 위해 하측 다이에 돌출된 비드를 설치하였고, 전자소자가 마운팅된 필름 성형에서 소자가 펀치와 접촉하지 않도록 중앙 부분에 회피 공간을 설치하였다.

Fig. 3

Structure of thermoforming mold

Fig. 4

Schematics of thermoforming mold

Fig. 5는 열성형 실험을 위하여 제작한 금형을 나타낸 것이며, 하측 금형이 고정된 상태에서 상측 금형이 67.5 mm/s의 속도로 하강하며 필름을 성형하도록 하였다.

Fig. 5

Thermoforming mold

열성형한 이후에 필름을 컷팅하기 위하여 Fig. 6과 같이 트리밍 금형을 설계하였다. 펀치 위에 필름을 위치시키고, 양측 2개의 핀을 사용하여 필름을 고정하도록 하였다. 상부 금형이 하강하면서 펀치와 상측 다이가 형폐되고, 가압을 통해 펀치의 형상대로 필름이 컷팅되도록 하였다. Fig. 7은 제작한 트리밍 금형을 나타낸다.

Fig. 6

Structure of trimming mold

Fig. 7

Trimming mold

3. 열성형 해석 및 실험

3.1 해석 방법

K-BKZ 비선형 점탄성 모델을 기반으로 T-SIM [12]을 사용하여 필름 열성형 해석을 수행하였다. Table 1은 공정조건을 나타낸 것으로, 상측과 하측 금형온도 85^oC, 필름 표면 온도 113^oC, 가압시간 20초, 라이너 두께 0.6 mm인 경우에 대하여 열성형 해석을 수행하였다. 금형과 필름 사이의 마찰계수는 일반적으로 필름 온도에 따라 다르기 때문에 참고문헌[13] 데이터를 사용하였으며, 필름 표면 온도 113^oC에 대하여 마찰계수 0.11을 해석에 적용하였다.

Table 1

Processing conditions used in T-SIM analysis

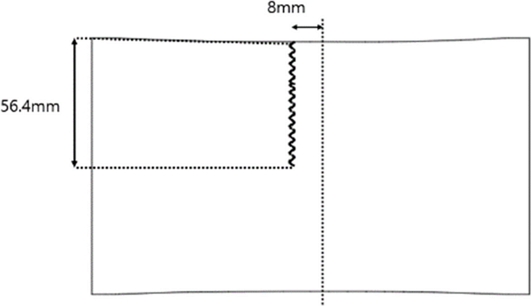
적용모델이 좌우 대칭이므로 Fig. 8과 같이 중심으로부터 8 mm 떨어진 위치에서 길이 56.4 mm 지점까지의 선폭을 측정하였다.

Fig. 8

Measuring range for line width

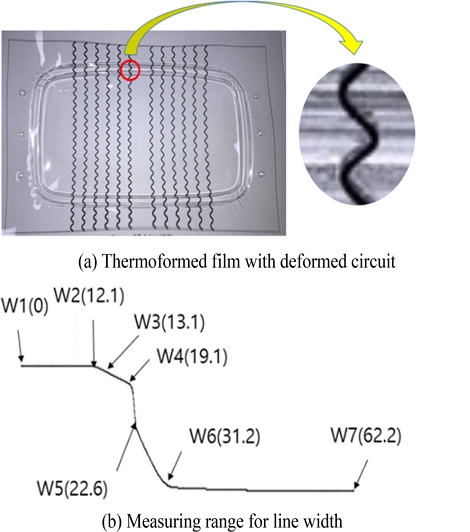
Fig. 9는 열성형에 의해 Fig. 8의 회로가 필름과 함께 변형된 형상을 나타낸 것이며, Fig. 9(b)와 같이 W1-W7 지점까지를 측정범위로 설정하였다. 이때 그림에서 괄호 안의 숫자는 W1을 기준점으로 하는 거리를 mm 단위로 나타낸 것이다. 수직 방향 연신율이 작게 발생하는 바닥부분(W6-W7)에서의 선폭 측정은 제외하였으며, W1-W6 구간에서만 선폭을 측정하였다.

Fig. 9

Circuit deformation after thermoforming

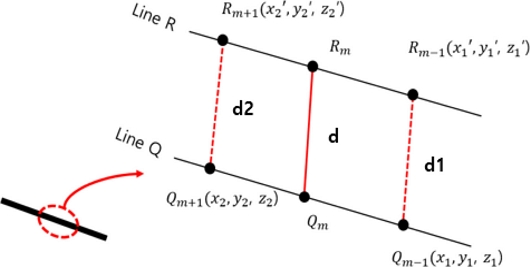
Fig. 10은 열성형 해석결과를 적용하여 선폭을 계산하기 위한 과정을 나타낸 것이다. 선폭을 표현하기 위하여 하나의 선을 서로 평행한 두 개의 선(Line Q, Line R)으로 분리하고, 열성형 이전의 선 사이 간격을 0.5 mm로 설정하였다. 선폭 계산을 위해 두 개의 선(Line Q, Line R)을 각각 길이를 따라 1 mm 간격으로 100등분 하였다. 열성형 이후 Qm지점에서의 선폭을 계산하기 위해 인접한 Qm-1에서의 선폭(d1)과 Qm+1에서의 선폭(d2)을 각각 계산하여 평균값(d)을 취하였다. 선폭이 라인 형상변화에 민감하게 변화하여 불연속 현상이 발생하기 때문에 인접한 지점에서의 선폭 평균값을 사용해 민감도를 감소시킬 수 있도록 하였다.

Fig. 10

Calculation of line width

3.2 실험 방법

적용모델이 좌우 대칭 형상이기 때문에 Fig. 11과 같이 한 장의 필름에 2가지 유형의 회로 형상을 인쇄하였다. 이때 사용한 필름은 PC (LonghuaPC- 1811T)이며, 전도성 잉크(Dupon-ME603)를 사용하여 0.01 mm 두께로 회로를 스크린 인쇄하고, 오븐 120^oC에서 40분 동안 건조하였다.

Fig. 11

Circuit patterns printed on film

Fig. 12는 실험에서 사용한 열성형 장비를 나타낸 것으로 다이에 설치된 4개의 핀으로 필름을 고정하였다. 세라믹 히터를 이용하여 일정한 시간 동안 필름을 가열한 이후 상측 금형이 하강하며 스트리퍼와 다이가 형폐되고, 펀치의 압력에 의해 필름이 성형되도록 하였다. 이때 사용한 공정조건은 하측과 상측 금형 85^oC, 필름 가열시간 9초, 필름 가압시간 20초, 라이너 두께 0.6 mm이다.

Fig. 12

Thermoforming machine

열성형 이후의 선폭을 측정하기 위하여 Fig. 13의 공구현미경(STV-C-2010, SOMETECH)을 사용하였다. Fig. 14와 같이 회로를 100배로 확대한 상태에서 회로 형상에 접하는 직선(Line m)상의 A점을 기준으로 직선(Line n)상에 있는 수직한 점 B를 구하고, A점과 B점 사이의 거리를 측정하였다. 이때 0.5 mm 간격으로 선폭을 측정하였다.

Fig. 13

Photograph of microscope

Fig. 14

Measurement of line width (all dimensions in mm)

4. 회로 형상이 선폭에 미치는 영향

4.1 직선 형상

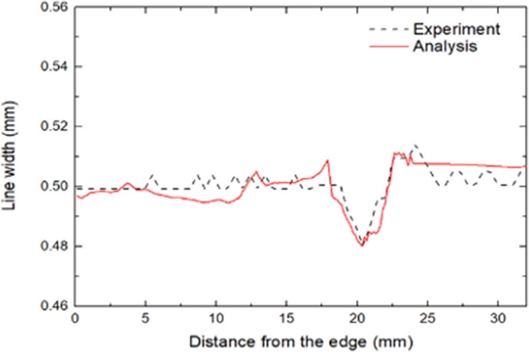
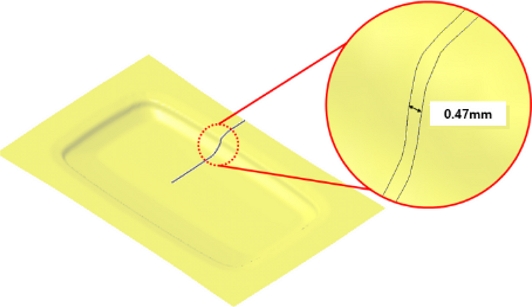
Fig. 15는 직선 회로에 대해 열성형 이후 변형된 선폭에 대한 해석과 실험을 비교한 것이다. 해석과 실험결과가 비교적 잘 일치하고 있음을 알 수 있다. Fig. 9에서 나타낸 W3-W5 구간에서 수직축 연신율에 의해 선폭이 크게 감소하는 것을 확인할 수 있다. 선폭이 최소인 영역은 Fig. 16에서 도시한 바와 같이 가장자리로부터 20 mm 떨어진 지점으로서 연신이 많이 발생하는 코너 부분이다. 해석과 실험에 의한 선폭 값은 0.478 mm로 나타났으며, 이때 선폭 변화율은 4.4%임을 알 수 있다.

Fig. 15

Line width for straight line shape

Fig. 16

Minimum line-width for straight line shape

4.2 말발굽 형상

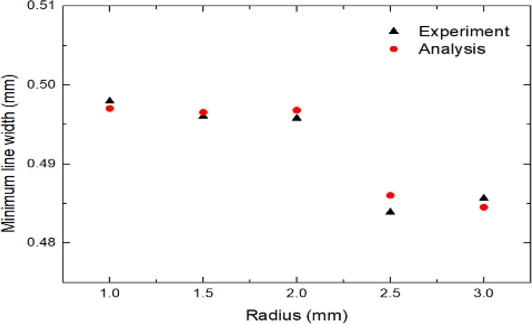
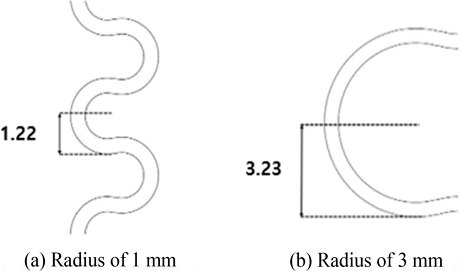
말발굽 형상의 각도를 15^o로 고정하고, 1^-3 mm의 범위에서 반지름에 따른 선폭 변화를 고찰하였다. Fig. 17은 열성형 이후 Fig. 16과 동일한 코너 부분에서 발생하는 반지름에 따른 최소 선폭을 나타낸 것이다. 해석과 실험결과가 비교적 잘 일치하고 있으며, 반지름이 증가함에 따라 선폭이 감소하는 것을 알 수 있다. Fig. 18은 반지름이 클수록 회로가 수직방향으로 배열되는 것을 나타낸다. 본 모델의 경우 코너부분에서 수직 방향 연신율이 수평 방향 연신에 비해 크기 때문에 반지름이 클수록 수직 방향 연신의 영향을 많이 받아 선폭이 더욱 감소하는 것으로 판단된다. 반지름 1 mm인 경우의 최소선폭은 0.498 mm이며, 이때 선폭 변화율은 0.4%에 불과하다. 따라서 위에서 고찰한 직선 회로의 선폭 변화율 4.4%에 비해 크게 감소함을 알 수 있다.

Fig. 17

Minimum line-width according to horseshoe radius

Fig. 18

Arc length in vertical direction for two types of radius

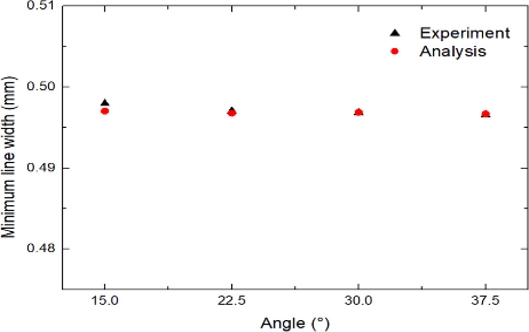
말발굽 형상의 반지름을 1 mm로 고정하고 15-37.5^o 사이에서 각도를 변경하며 열성형에 의한 선폭 변화를 고찰하였다. Fig. 19는 각도에 따른 최소선폭을 나타낸 것으로 각도가 선폭 변화에 미치는 영향은 크지 않음을 알 수 있다. 그 이유는 각도가 15^o에서 37.5^o로 증가할 때 선의 곡률 변화가 크지 않기 때문에 선폭 변화에 미치는 영향이 거의 없는 것으로 판단된다.

Fig. 19

Minimum line-width according to horseshoe angle

4.3 코일 형상

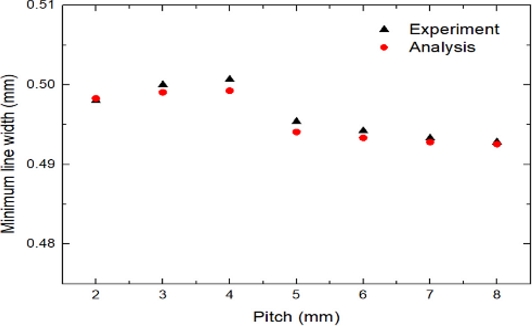
코일 형상의 진폭을 1 mm로 고정하고, 2-8 mm의 범위에서 피치에 따른 선폭 변화를 고찰하였다. Fig. 20은 피치 변화에 따른 열성형 이후의 최소선폭을 나타낸 것으로 해석이 실험결과보다 약간 작게 나타났으나, 경향은 매우 유사한 것을 볼 수 있다. 피치가 2 mm에서 4 mm로 증가하면서 선폭이 약간 증가하는 구간이 있지만 전체적으로 피치가 증가함에 따라 선폭이 감소하는 것으로 나타났다. 그 이유는 본 모델의 경우 수직 방향 연신율이 더 크며, 코일 형상의 피치가 증가할수록 수직 형상에 가까워지기 때문에 수직방향 연신의 영향으로 선폭이 다소 감소하는 것으로 판단된다. 결과적으로 피치 2-4 mm 구간에서 열성형에 의한 선폭 변화율은 약 0.2%에 불과함을 알 수 있다. 따라서 위에서 고찰한 말발굽 형상의 선폭 변화율 0.4%, 직선 형상의 선폭 변화율 4.4%에 비해 코일 형상의 선폭 변화율이 가장 작음을 알 수 있다.

Fig. 20

Minimum line-width according to coil pitch

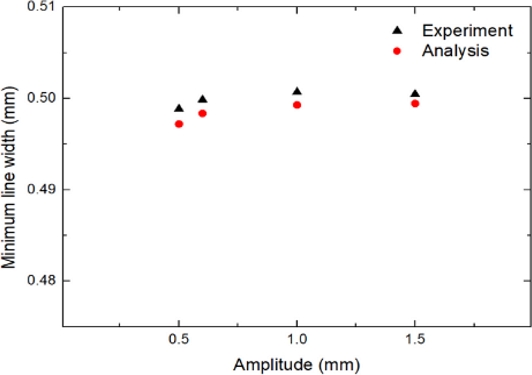
피치를 4 mm로 고정하고 0.5-1.5 mm의 범위에서 진폭을 변경하며 열성형에 의한 선폭 변화를 고찰하였다. Fig. 21은 진폭 변화에 따른 열성형 이후의 최소선폭을 나타낸 것으로, 진폭이 증가할수록 최소선폭이 약간 증가하고 있으나, 그 영향은 크지 않은 것으로 나타났다. 그 이유는 본 모델의 경우 수직 방향 연신율이 더 크게 발생하는데 코일의 진폭이 증가할수록 상대적으로 연신이 작게 일어나는 수평방향으로 배열되기 때문에 선폭이 증가하는 경향을 나타낸 것으로 판단된다.

Fig. 21

Minimum line-width according to coil amplitude

5. 결론

필름 열성형 해석과 실험을 적용하여 필름에 인쇄된 회로 형상이 열성형에 의한 선폭 변화에 미치는 영향에 대하여 고찰하였으며, 이를 통해 얻은 결론은 다음과 같다.

(1) 직선 형상, 말발굽 형상, 코일 형상 등 각각의 인쇄 회로의 형상에 대하여 점탄성 모델을 기반으로 해석한 열성형에 의한 선폭 예측결과는 실험과 비교적 잘 일치하였다.

(2) 말발굽 형상의 회로에서 반지름이 증가함에 따라 수직 방향 연신의 영향을 많이 받아 선폭이 감소하였다. 반면에 각도는 곡률 변화에 미치는 영향이 작고, 열성형에 의한 선폭 변화에 미치는 영향이 미미하였다.

(3) 코일 형상의 회로에서 피치가 2 mm에서 4 mm로 증가하면서 선폭이 약간 증가하고 있지만 전체적으로 피치가 증가함에 따라 수직 방향 연신의 영향을 많이 받게 되어 선폭이 감소하는 것으로 나타났다. 반면에 진폭이 증가할수록 선폭이 약간 증가하고 있으나, 그 영향은 크지 않은 것으로 나타났다.

(4) 직선 형상, 말발굽 형상, 코일 형상의 회로에서 열성형에 의한 선폭변화율은 각각 4.4, 0.4, 0.2%로 나타났으며, 이를 통해 열성형에 의한 선폭변화를 최소화하기 위하여 코일 형상의 회로가 가장 바람직함을 알 수 있었다.

(5) 코일 형상의 회로를 사용할 경우 적용하고자 하는 모델형상에 따른 연신특성을 고려해 피치, 진폭 등 설계변수 최적화가 필요하다. 이를 위해 필름의 점탄성 모델을 기반으로 한 열성형 해석에 의한 진폭 예측이 유용할 것으로 판단된다.

(6) 필름 열성형해석에서 점탄성모델을 적용하기 위한 필름 물성측정, 필름 두께 및 마찰계수 등을 고려한 연신율 변화 등 추가적인 연구가 필요하다.

Acknowledgments

본 연구는 중소벤처기업부의 기술개발사업(S3157893)의 지원과 2023년 한국교통대학교 산학협력단 지원을 받아 수행하였음.

REFERENCES

• Neeli, M. R., (2015), An investigation into electronic circuit production in thermoplastics, Ph.D. Thesis, Griffith University.
• Russo, A., Ahn, B. Y., Adams, J. J., Duoss, E. B., Bernhard, J. T., Lewis, J. A., (2011), Pen-on-paper flexible electronics, Advanced Materials, 23(30), 3426-3430. [https://doi.org/10.1002/adma.201101328]
• Leong, Y., Yamaguchi, S., Mizoguchi, M., Hamada, H., Ishiaku, U., Tsujii, T., (2004), The effect of molding conditions on mechanical and morphological properties at the interface of film insert injection molded polypropylene-film/polypropylene matrix, Polymer Engineering & Science, 44(12), 2327-2334. [https://doi.org/10.1002/pen.20260]
• Oulu, P. N., Kempele, J. S., Kempele, P. R., Oulu, M. H., Oulunsalo, M. S., Kempele, J. T., Oulu, A. K., (2017), Multilayer structure for accommodating electronics and related method of manufacture, US9724869.
• Simula, T., Niskala, P., Heikkinen, M., Rusanen, O., (2018), Component packages for IMSE™ (Injection Molded Structural Electronics), Proceedings of the 2018 IMAPS Nordic Conference on Microelectronics Packaging (NordPac), 50-54. [https://doi.org/10.23919/NORDPAC.2018.8423845]
• Rusanen, O., Simula, T., Niskala, P., Lindholm, V., Heikkinen, M., (2019), Injection molded structural electronics brings surfaces to life, Proceedings of the 2019 22nd European Microelectronics and Packaging Conference & Exhibition (EMPC), 1-7. [https://doi.org/10.23919/EMPC44848.2019.8951795]
• White, K., Yeager, M., Sherwood, J., Bogetti, T., Cline, J., (2018), Material characterization and finite element modeling for the forming of highly oriented UHMWPE thin-film and unidirectional cross-ply composites, Proceedings of the 33rd ASC Technical Conference, 1-16. [https://doi.org/10.12783/asc33/25944]
• Madadnia, B., Bossuyt, F., Vanfleteren, J., (2022), Technological development for the reduction of out-of-plane deformation of metallic meander structures in thermoformed electronics, The International Journal of Advanced Manufacturing Technology, 119(9-10), 6649-6663. [https://doi.org/10.1007/s00170-022-08680-9]
• Xu, S., Zhang, Y., Cho, J., Lee, J., Huang, X., Jia, L., Fan, J. A., Su, Y., Su, J., Zhang, H., (2013), Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems, Nature Communications, 4(1543), 1-8. [https://doi.org/10.1038/ncomms2553]
• Seong, G.-S., Lee, H.-S., (2018), A study on the thickness distribution and pattern deformation of films in vacuum-assisted thermoforming, Journal of the Korea Society of Die & Mold Engineering, 12(2), 5-10.
• Plovie, B., Vanfleteren, J., Vervust, T., Quintero, A. V., Bossuyt, F., (2018), Design automation of meandered interconnects for stretchable circuits, IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 38(9), 1648-1660. [https://doi.org/10.1109/TCAD.2018.2859222]
• Accuuform, (2005), Computer simulations of transforming and blowing molding. https://www.t-sim.com/WebPages/EN/ProductTSIM.html
• Lee, J. K., Scott, C. E., Virkler, T. L., (2001), Effects of rheological properties and processing parameters on ABS thermoforming, Polymer Engineering & Science, 41(2), 240-261. [https://doi.org/10.1002/pen.10725]