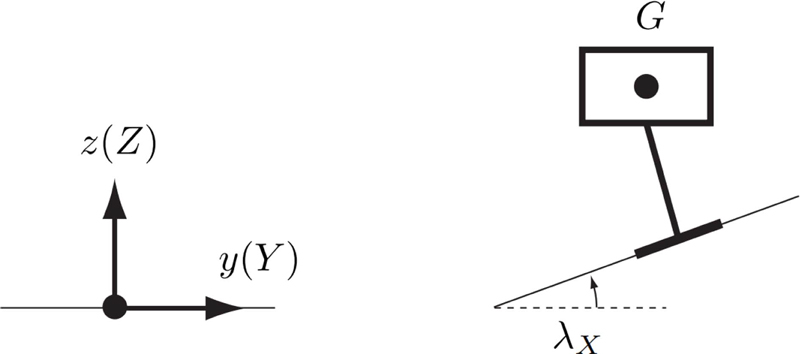하이브리드 이동 로봇의 다리 보행과 스케이트 주행을 위한 역기구학의 해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Hybrid mobile robot is the system that will practically combine legged walking and skated driving in the same system. Therefore, this robot has own problems of inverse kinematics that are not considered in typical walking robots. In this paper, I fully categorized the inverse kinematics problems for hybrid mobile robot with general motion by walking and driving on an inclined plane, including switching end-effectors between foots and blades. I also solved the inverse kinematics for each case of problems. I here actively adopted the coordinate transformation derived from the inclined plane to cope with the random motion of foots and blades on the plane. I then presented several examples of the inverse kinematics problems with specific situations, and verified the validity of the analysis method from the results.
Keywords:
Hybrid mobile robot, Legged walking, Skated driving, Inverse kinematics, Switching end-effectors키워드:
하이브리드 이동 로봇, 다리 보행, 스케이트 주행, 역기구학, 말단 교체1. 서론
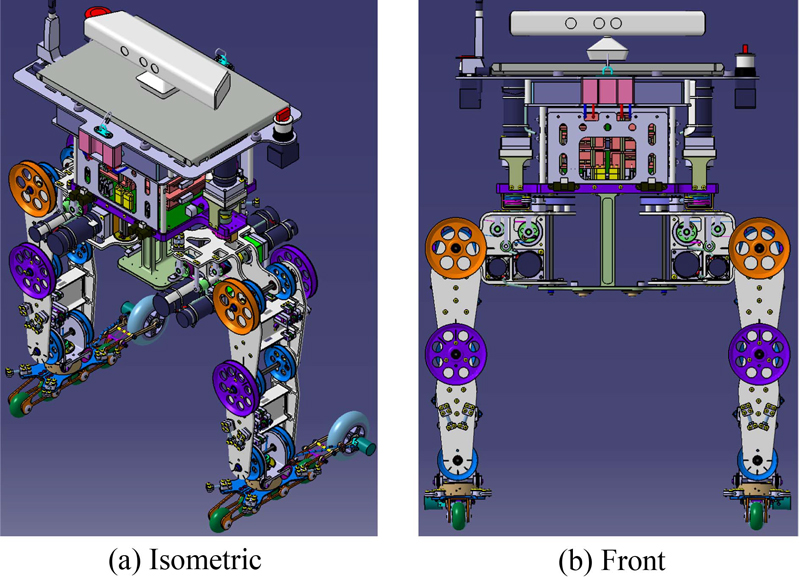
하이브리드 이동 로봇은 1개의 시스템에 2개 이상의 이동 방법을 통합한 형태[1-4]인데, 이 연구에서는 다리에 의한 보행과 스케이트에 의한 주행을 동일한 시스템에 통합하는 것을 목표로 한다. 사람은 걷거나 뛰는 것보다 자전거나 인라인 스케이트 등의 도구를 이용하면 훨씬 적은 에너지로 매우 빠르고 멀리 갈 수 있는데, 사람이 그렇다면 로봇도 마찬가지일 것이다. 따라서 주변 상황과 지면 상태에 맞게 저속의 다리 보행과 고속의 스케이트 주행을 적절히 결합해서, 로봇의 이동 능력을 극대화하면서 에너지 효율적인 이동 방법을 제시하고자 한다. 아울러 인간의 스케이트 동작을 공학적으로 구현하는 것만으로도 충분한 의미가 있다고 생각한다. 2족 로봇에 의한 보행 및 주행은 지금까지 수많은 이론 연구[5-7]가 진행되었고, 다양한 동영상[8-12]으로 연구 결과를 실증하고 있다. 하이브리드 이동 로봇을 개발하기 위해서는 스케이트 주행의 구현이 가장 큰 난관인데, 이 연구에서는 스케이트 주행의 기초적인 이론 연구[13,14]를 진행했고, Fig. 1과 같이 몸통과 2족 10자유도의 구성인 스케이트 로봇(SkaBot)을 개발해서 부족하지만 동영상[15]으로 연구 결과를 예시했는데, 백문이 불여일견(百聞不如一見)이다.
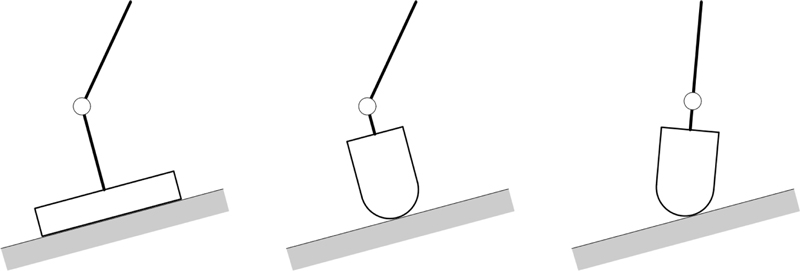
로봇의 역기구학은 일반적으로 주어진 End-effector의 위치와 자세로부터 관절 변수를 구하는 문제인데, 더이상 연구할 것이 남아있지 않다는 소극적인 인상을 가지기 쉽다. 그러나 보편적인 상황에 대한 일반 해법이 존재하더라도, 제한적인 상황에 대한 특수해가 필요한 경우가 있는데, 이 논문은 후자에 해당한다. 스케이트 주행의 경우에는 전방에서 간략하게 본 Fig. 2와 같이 발목의 불편한 부담을 덜기 위해서 스케이트를 옆으로 기울이게 되는데, 이것은 주어진 발목의 각도를 맞추기 위한 스케이트의 기울기를 구하는 문제가 된다. 그리고 다리 보행의 경우에는 경사면의 기울기와 발바닥의 자세가 기본적으로 서로 같지만, 스케이트 주행의 경우에는 경사면의 기울기와 스케이트 날의 자세가 기본적으로 서로 같지 않다. 따라서 하이브리드 이동 로봇의 스케이트 주행에는 일반적인 보행 로봇에서 상정할 수 없는 고유한 역기구학 문제가 발생한다. 이것은 기존의 역기구학[5,6,16]에서 다루지 않은 내용인데, 보행 로봇에서는 기지(旣知)의 End-effector의 위치와 자세로부터 미지(未知)의 관절 변수를 구하는 것이 주된 문제가 되지만, 스케이트 주행 로봇에서는 기지의 관절 변수에서 미지의 End-effector의 위치와 자세를 구하는 것이 주된 문제가 되는데, 미지수의 개수는 서로 같다.
이 논문에서는 하이브리드 이동 로봇의 다리 보행과 스케이트 주행을 위한 역기구학 문제를 고찰한다. 역기구학 문제를 경사 지면에서 다리 보행과 스케이트 주행에 의한 일반적인 이동, 발바닥과 스케이트 날의 교체 등을 포함해서 체계적으로 분류하고, 각각에 대해서 해석한다. 그리고 구체적인 상황에 대한 역기구학 예제를 계산하고, 결과로부터 해석 방법의 유효성을 확인하고자 한다.
2. 보행, 주행에 대한 역기구학의 해석
2.1 보행, 주행에 대한 역기구학 문제의 분류
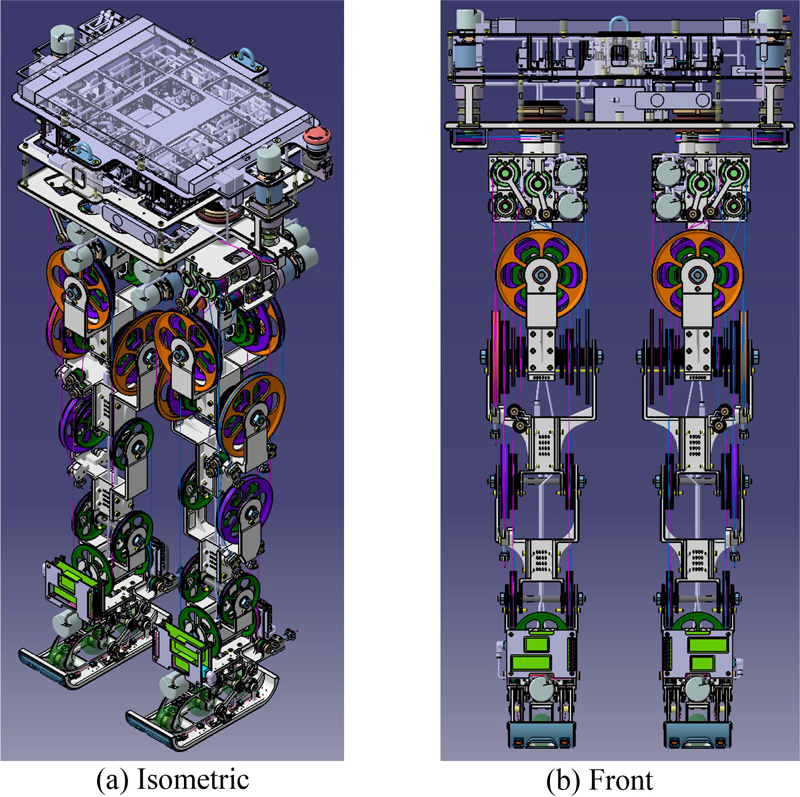
Fig. 3은 개발 중인 로봇으로 몸통과 2족 12자유도의 구성인데, Fig. 1과 같이 스케이트 주행만이 가능한 2족 10자유도의 스케이트 로봇[15]과 달리 다리 보행과 스케이트 주행이 동일한 시스템에서 가능하기 때문에 진정한 의미의 하이브리드 이동 로봇이라고 할 수 있다. 여기서는 역기구학 문제를 다루므로 3장에 기하학적인 정보만을 언급하겠다.
모든 좌표계는 일반적으로 원점과 좌표축으로 구성되는데, 평탄 수평면의 기준 및 고정 좌표계는 0 – XYZ 좌표계이고, 수평 지면이 XYZ축 방향의 병진 및 회전으로 일정한 경사 지면이 된다. 로봇의 기준 및 고정 좌표계는 0 – xyz 좌표계인데, 평탄 수평면의 0 – XYZ 좌표계와 서로 같다. 여기서 몸통, 다리의 좌표축은 xyz와 같이 소문자로 표시하고, 경사면, 발바닥, 스케이트 날의 좌표축은 XYZ와 같이 대문자로 표시한다. Fig. 4와 같이 로봇은 경사면 위에서 다리 보행 또는 스케이트 주행에 의해서 직진 또는 선회로 이동한다. 2족 로봇의 입장에서 오른 다리가 제1 다리, 왼 다리가 제2 다리이다.
보행과 주행의 역기구학에 필요한 동차 변환 행렬을 Table 1에 정리했는데, 예를 들면 오른 발바닥의 Ψ1은 0 – XYZ 고정 좌표계에서 병진과 XYXYZ-X+ Euler Angles인 λX, λY, γX, γY, βZ, βX 의 회전으로 이동 좌표계가 되는 것을 의미하고, 오른 스케이트의 Ψ1은 고정 좌표계에서 병진과 XYXYZ-Y- Euler Angles인 λX, λY, γX, γY, βZ, βY 의 회전으로 이동 좌표계가 되는 것을 의미한다. 여기서 Z- Euler Angle인 βZ는 -Z축 중심의 회전각이고, 생략된 상첨자의 부호는 +이고, i = 1, 2이다. 우좌(右左) 발바닥의 자세는 XYXYZ-X± Euler Angles로 나타낼 수 있는데, 이것은 경사면의 XYXY 기울기인 Euler Angles에 발바닥의 회전인 Z-X± Euler Angles을 추가한 형태로서 경사면 위의 자유로운 발바닥의 운동을 나타낸다. 특히 γY는 보행과 주행의 좌우 다리에서 축과 축이 서로 대칭적인 바깥쪽을 가리키도록 추가한 회전각인데, 오른 다리에서 γY = 0°, 왼 다리에서 γY = 180°이다. Table 1에 포함된 부호의 구분으로 좌우 발바닥에서 회전각은 서로 대칭이 되는데, βZ는 바깥으로 돌리는 것이 양이고, βX는 앞으로 드는 것이 양이 된다. 그리고 우좌(右左) 스케이트의 자세는 XYXYZ-Y+ Euler Angles로 나타낼 수 있는데, 이것은 경사면의 기울기인 XYXY Euler Angles에 스케이트 날의 회전인 Z-Y± Euler Angles을 추가한 형태로서 경사면 위의 자유로운 스케이트 날의 운동을 나타낸다. Table 1에 포함된 부호의 구분으로 좌우 스케이트에서 회전각은 서로 대칭이 되는데, βZ는 바깥으로 돌리는 것이 양이고, βY는 바깥으로 드는 것이 양이 된다. 따라서 경사면 위의 발바닥과 스케이트의 자유로운 운동을 나타내기 위해서 경사면을 기준으로 하는 좌표 변환을 적극적으로 사용했다.
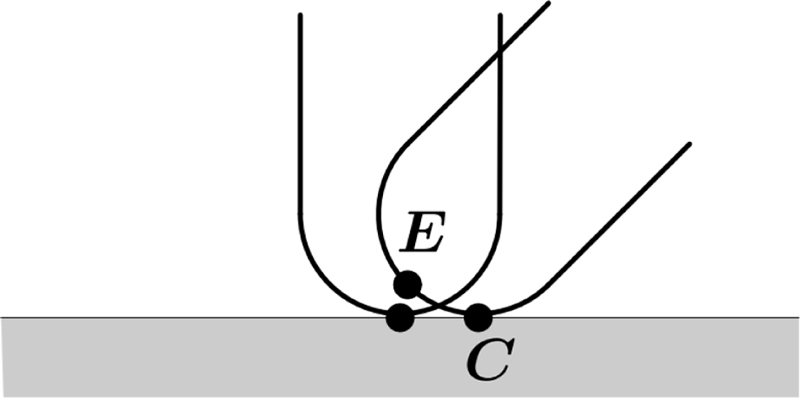
그리고 Fig. 5와 같이 인라인 스케이트 휠의 끝부분이 종단면으로 원호의 형상이다. End-effector의 교체 중에 스케이트 날과 지면의 접촉 조건이 미끄럼이 없는 Pure Rolling이라고 하면, 접촉 상태는 수직인 선 접촉 또는 경사인 선 접촉으로 서로 변하기 때문에 End-effector의 위치인 E와 접촉점의 위치인 C가 바뀌게 된다. 실제로 스케이트 날의 마찰력에는 방향성이 있어서 날 방향의 마찰력이 그 수직 방향의 값보다 대단히 작기 때문에 옆으로 미끄러지지 않는 논홀로노믹(Nonholonomic) 구속이 작용한다. 그리고 많은 4족 보행 로봇[17,18]의 발끝이 마찰력 증가를 위해서 고무 재질의 원기둥 또는 구 형상이므로 Fig. 5와 유사한 상황이 발생하지만, 발목의 자세를 고려하지 않아도 되므로 충분히 회피할 수 있다.
경사 지면에서 보행을 위한 발바닥과 주행을 위한 스케이트날의 교체를 고찰하는데, Fig. 2와 같이 스케이트 날은 발바닥 안에 수납되어 있다. Fig. 6과 같이 발목의 관절각을 θ6 이라고 하면, Fig. 2와 같이 보행에서 주행으로 교체하는 경우에는 미지의 θ6과 기지의 βX = 0°으로 발바닥과 지면이 수직의 면 접촉인 상태, 미지의 θ6과 기지의 βY = 0°으로 스케이트와 지면이 수직의 선 접촉인 상태, 기지의 θ6 = 0°과 미지의 βY ≠ 0°으로 스케이트와 지면이 경사의 선 접촉인 상태의 순서로 바뀐다. 특히 기지의 βY = βYa = 0°에서 꺾인 발목을 얼마나 돌려야 미지의 βY = βYb에서 θ6 = 0°인 곧게 뻗은 발목이 되는가를 해석하는 것이 핵심이다. 그리고 주행에서 보행으로 교체하는 경우에는 기지의 θ6 = 0°과 미지의 βY ≠ 0°으로 스케이트와 지면이 경사의 선 접촉인 상태, 미지의 θ6과 기지의βY = 0°으로 스케이트와 지면이 수직의 선 접촉인 상태, 미지의 θ6과 기지의 βX = 0°으로 발바닥과 지면이 수직의 면 접촉인 상태의 순서로 바뀐다. 특히 기지의 βY = βYa에서 θ6 = 0°인 곧게 뻗은 발목을 얼마나 돌려야 기지의 βY = βYb = 0°에서 꺾인 발목이 되는가를 해석하는 것이 핵심이다. 여기서 스케이트와 지면이 경사의 선 접촉인 상태는 발목의 불편한 꺾임을 막으면서 부담을 더는 안락한 주행을 위한 것으로 현실적인 선택이다. 따라서 일반적인 이동, 말단(End-effector)의 교체 등을 포함해서 보행과 주행의 역기구학을 분류하면 크게 다음과 같이 3종류의 문제로 정리할 수 있다.
- ● 기지의 말단 위치, 기지의 말단 자세에 대한 보행과 주행의 역기구학
- ● 기지의 말단 위치, 미지의 말단 자세에 대한 주행의 역기구학
- ● 미지의 말단 위치, 미지의 말단 자세에 대한 주행의 역기구학
각각의 문제에 대해서 구체적으로 설명하고, 역기구학을 해석하기로 한다. 아울러 해석 과정은 계산의 연속적인 순서가 매우 중요하므로, 대표적인 저술[19]과 같이 순차적으로 나열하고자 한다.
2.2 기지 말단 위치, 기지 말단 자세의 보행, 주행에 대한 역기구학의 해석
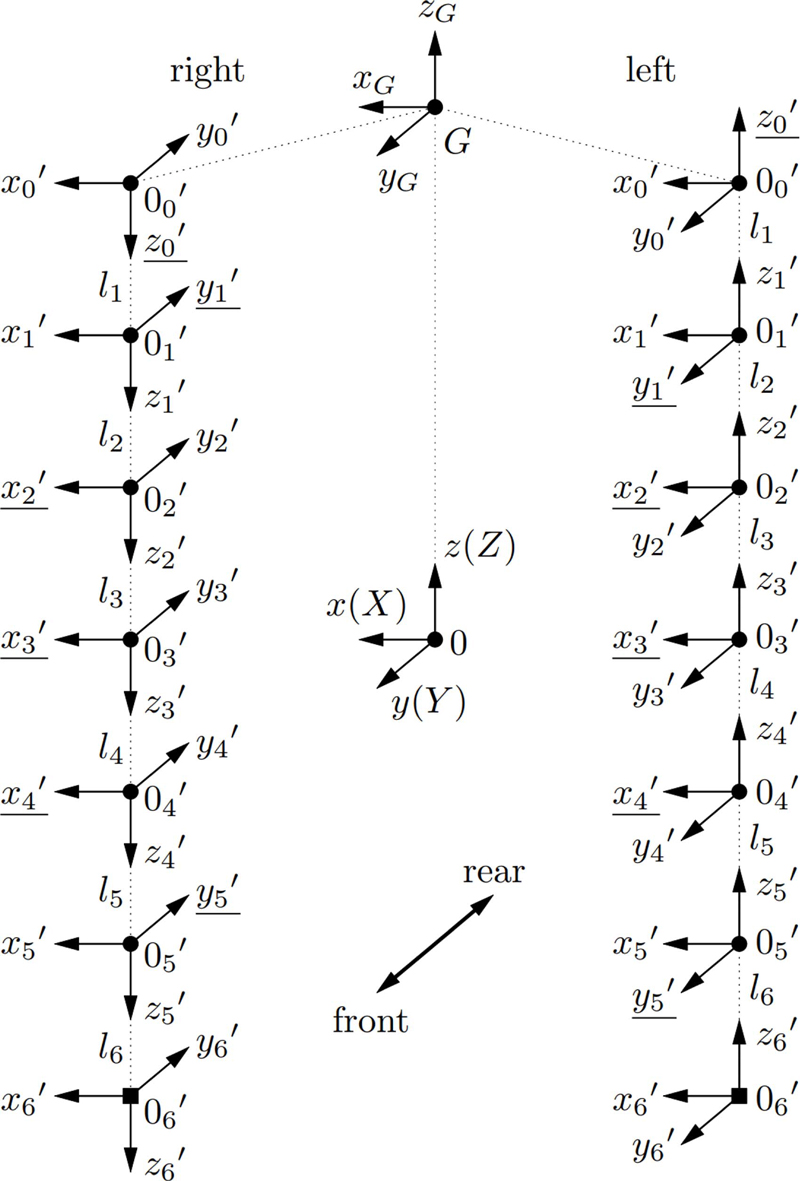
Fig. 3의 로봇에 대한 좌표계는 Fig. 6과 같은데, 0 – xyz 좌표계는 기준 및 고정 좌표계, G – xGyGzG 좌표계는 몸통의 무게 중심인 G에 고정한 이동 좌표계, 좌표계는 다리의 제i 관절에 고정한 이동 좌표계, 좌표계는 다리의 End-effector에 고정한 이동 좌표계 등이고, i = 1, 2, … , 6이다. 몸통의 자세는 xyz Fixed Angles로 나타낼 수 있는데, θx, θy, θz는 각각 xyz축 중심의 회전각을 의미한다. θz = 0°인 경우에 로봇의 입장에서 오른쪽이 +x축, 앞쪽이 +y축, 위쪽이 +z축이다. 특히 간단한 수식을 위해서 θx = 0°, θy = 0°으로 놓지만,θx ≠ 0°, θy ≠ 0°인 경우도 용이하게 계산할 수 있다. 다리는 2족 12자유도의 구성으로 각 다리에는 6개의 회전 관절이 있고, 관절의 배치는 다른 휴머노이드 로봇[6]과 같이 JRz – JRy – JRx – JRx – JRx – JRy이다. 여기서 JRx, JRy, JRz는 각각 축, 축, 축 중심의 회전 관절을 의미한다. 좌우 다리에서 관절각은 서로 대칭이 되도록 정했는데, 똑바로 선 자세에서 JRx는 앞으로 드는 것이 양이고, JRy는 바깥으로 드는 것이 양이고, JRz는 바깥으로 돌리는 것이 양이다. 사람의 다리와 비교하면 제1, 2, 3 관절은 고관절에, 제4 관절은 무릎에, 제5, 6관절은 발목에 각각 해당한다. 그리고 제i 관절의 회전각은 θi, 제i 링크의 길이는 li이다. 각 관절의 실질적인 가동 범위는 θ1 = ±90°, θ2 = ±90°, θ3 = ±90°, θ4 = ±150°, θ5 = ±90°, θ6 = ±90°이고, 간단한 표기를 위해서 C ≡ cos, S ≡ sin, T ≡ tan 등이다. 특히 가장 일반적인 경우인 의 범위를 이론적으로 고민하기보다는 ±90°에는 arctan 함수를, ±180°에는 arctan2 함수를 구분해서 사용하기로 하는데, 다리의 가동 범위는 팔보다 좁으므로 큰 무리가 없다고 판단된다. 따라서 Fig. 6과 같이 몸통을 포함한 오른 다리의 동차 변환 행렬은 다음과 같다.
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
| (1f) |
| (1g) |
| (1h) |
여기서 , 은 좌표계 원점 사이의 상대 위치이다. 그리고 기준 및 고정 좌표계에 의한 End-effector의 위치와 자세는 다음과 같은 동차 변환 행렬로 사전에 주어진다.
| (2) |
여기서 은 좌표계 원점 사이의 상대 위치이고, 은 End-effector의 자세를 나타낸다. 특히 End-effector의 자세는 Table 1의 Ψ1로 주어지는데, 오른 발바닥과 오른 스케이트 날에서 축 방향의 단위 벡터를 각각 이라고 하면, Fig. 6에서 인 것에 유의하자. 따라서 Ψij를 Ψ1의 (i, j) 성분이라고 하면, T와 Ψ1의 자세 행렬은 다음과 같게 된다.
| (3) |
식(1), 식(2)에서 몸통을 포함한 오른 다리의 동차 변환 행렬과 End-effector의 동차 변환 행렬은 다음과 같이 동일한 것이다.
| (4) |
이 문제는 주어진 T = Ψ1에서 미지의 θ1, θ2, θ3, θ4, θ5, θ6을 구하는 것이 되고, 미지수는 6개이다. 먼저 θ1, θ2, θ6을 구하기 위해서 식(4)에서 다음을 계산한다.
| (5) |
θ1, θ2를 구하기 위해서, 식(5)의 (1, 2) 성분을 정리하면 다음과 같다.
| (6) |
여기서 이다. θ1, θ2를 구하기 위해서, 식(5)의 (1, 3) 성분을 (1, 4)성분에 대입해서 정리하면 다음과 같다.
| (7) |
여기서 이다. 식(6), 식(7)에서 각각 Tθ2를 구한 다음에 Tθ2 = Tθ2를 정리하면 다음과 같다.
| (8) |
가동 범위가 θ1 = ±90°이므로, 식(8)에서 θ1은 다음과 같이 구할 수 있다.
| (9) |
여기서 분자인 P1P6 – P3P4와 분모인 P2P6 – P3P5가 이 아니어야 한다. 가동 범위가 θ2이므로, 식(7)에서 θ2는 다음과 같이 구할 수 있다.
| (10) |
여기서 분자인 P4Cθ1 + P5Sθ1와 분모인 P6가 이 아니어야 한다. 특히 2.3.2항에서 언급하는 것과 같이 End-effector의 위치 정보를 포함한 P4, P5, P6을 반드시 사용해야 한다. 그리고 θ6을 구하기 위해서, 식(5)의 (1, 1) 성분과 (1, 3) 성분을 정리하면 다음과 같다.
| (11a) |
| (11b) |
여기서 이다. 식(11)에서 θ6은 다음과 같이 구할 수 있다.
| (12) |
그러므로 식(9), 식(10), 식(12)에서 θ1, θ2, θ6은 1쌍의 해가 존재한다. 다음으로 θ3, θ4, θ5를 구하기 위해서 식(4)에서 다음을 계산한다.
| (13) |
θ3, θ4, θ5를 구하기 위해서, 식(13)의 (2, 2) 성분과 (3, 2) 성분을 정리하면 다음과 같다.
| (14a) |
| (14b) |
식(14)에서 θ3, θ4, θ5는 다음과 같이 구할 수 있다.
| (15) |
θ4를 구하기 위해서, 식(13)의 (2, 4) 성분과 (3, 4) 성분을 제곱해서 Cθ4로 정리하면 다음과 같다.
| (16) |
여기서 이고, 분모인 2l3l4가 영이 아니어야 하고, –1 ≤ Cθ4 ≤ 1이어야 한다. 삼각함수의 관계에서 이므로, θ4는 다음과 같이 구할 수 있다.
| (17) |
θ3을 구하기 위해서, 식(13)의 (2, 4) 성분과 (3, 4) 성분을 Cθ3, Sθ3에 대한 연립 방정식으로 정리하면 다음과 같다.
| (18a) |
| (18b) |
여기서 이다. 식(18)에서 θ3은 다음과 같이 구할 수 있다.
| (19) |
여기서 분모인 가 영이 아니어야 하고, –1 ≤ Cθ3 ≤ 1, –1 ≤ Sθ3 ≤ 1이어야 한다. θ5는 다음과 같이 구할 수 있다.
| (20) |
그러므로 식(9), 식(10), 식(12), 식(17), 식(19), 식(20)에서 θ1, θ2, θ6, θ4, θ3, θ5는 전체적으로 2쌍의 해가 존재하므로 적절하게 선택해야 한다. 특히 사람과 같이 θ4 ≤ 0°이라고 하면, Table 2와 같이 전체적으로 1쌍의 해가 해석적으로 존재하게 된다. 그리고 가장 일반적인 경우인 ±180°의 범위에서 계산하면 식(8)에서 2쌍, 식(7)에서 2쌍, 식(17)에서 2쌍으로 전체적으로 8쌍의 해가 존재하는데, 구체적인 해석 과정은 생략하기로 한다. 아울러 왼 다리의 경우도 용이하게 해석할 수 있다.
2.3 기지 말단 위치, 미지 말단 자세의 주행에 대한 역기구학의 해석
이 문제는 주어진 스케이트의 위치에서 주어진 θ6을 만족하기 위한 스케이트의 자세인 βY와 미지의 θ1, θ2, θ3, θ4, θ5를 구하는 것이 되고, 미지수는 6개이다. 특히 2.2 절과 같이 오른 스케이트의 자세는 Table 1의 ∆1, Ψ1로 나타내는데, 미지수인 βY를 구하기 위해서 따로 분리해야 한다. 따라서 ∆ij를 ∆1의 (i, j) 성분이라고 하면, 식(3)과 같이 T와 Ψ1의 자세 행렬은 다음과 같게 된다.
| (21) |
이 문제는 Table 3와 같이 크게 3경우로 나눌 수 있는데, 각각의 경우에 대해서 역기구학을 해석하기로 한다.

Solutions of inverse kinematics for comfortable skating with known position and unknown orientation of end-effector
θ6 = 0°인 경우에, 먼저 θ1, θ2, βY를 구하기 위해서 식(5)를 계산한다. θ1, θ2를 구하기 위해서, 식(5)에서 βY를 포함하지 않는 (1, 2) 성분과 (1, 4) 성분을 정리하면 각각 식(6)과 식(22)와 같다.
| (22) |
여기서, 이다. 식(6), 식(22)에서 각각 Tθ2를 구한 다음에 Tθ2 = Tθ2를 정리하면 다음과 같다.
| (23) |
가동 범위가 θ1 = ±90°이므로, 식(23)에서 θ1은 다음과 같이 구할 수 있다.
| (24) |
여기서 분자인 P1P6 – P3P4와 분모인 P2P6 – P3P5가 이 아니어야 한다. 가동 범위가 θ2 = ±90°이므로, 식(22)에서 θ2는 다음과 같이 구할 수 있다.
| (25) |
여기서 분자인 P4Cθ1 + P5Sθ1와 분모인 P6가 이 아니어야 한다. 특히 2.3.2항에 언급하는 것과 같이 말단의 위치 정보를 포함한 P4, P5, P6을 반드시 사용해야 한다. 그리고 βY를 구하기 위해서 식(5)의 (1, 1) 성분과 (1, 3) 성분을 CβY, SβY에 대한 연립 방정식으로 정리하면 다음과 같다.
| (26a) |
| (26b) |
여기서 이다. 식(26)에서 βY는 다음과 같이 구할 수 있다.
| (27a) |
| (27b) |
여기서 분모인 V1V4 – V2V3가 영이 아니어야 한다. 그러므로 θ6 = 0°인 경우에 식(24), 식(25), 식(27)에서 θ1, θ2, βY는 1쌍의 해가 존재한다.
다음으로 θ3, θ4, θ5를 구해야 하는데, 나머지 과정은 2.2절의 내용과 기본적으로 동일하므로 2.2절을 참고하길 바란다. 특히 식(16)에서
등인 것에 유의하자. 그러므로 사람과 같이 θ4 ≤ 0°이라고 하면, Table 3과 같이 θ6 = 0°인 경우에 θ1, θ2, βY, θ4, θ3, θ5는 전체적으로 1쌍의 해가 해석적으로 존재하게 된다. 그리고 가장 일반적인 경우인 ±180°의 범위에서 계산하면 식(23)에서 2쌍, 식(22)에서 2쌍, 식(17)에서 2쌍으로 전체적으로 8쌍의 해가 존재하는데, 구체적인 해석 과정은 생략하기로 한다. 아울러 왼 다리의 경우도 용이하게 해석할 수 있다.
θ6 ≠ 0인 경우에, θ1, θ2, βY를 구하기 위해서 식(5)를 계산한다. θ1, θ2를 구하기 위해서, 식(5)에서 βY를 포함하지 않는 (1, 2) 성분과 (1, 4) 성분을 정리하면 각각 식(6)과 식(28)과 같다.
| (28) |
여기서 P4 ~ P6은 식(22)와 서로 같고, P7 = l6Sθ6 ≠ 0이다. 수평 지면에서 θx = θy = θz = 0°인 몸통으로 똑바로 서면 식(2)에서 R11 = 1, R22 = R33 = -1, R12 = R13 = R21 = R23 = R31 = R32 = 0이므로 식(6), 식(28)에서 P1 = P3 = P4 = P5 = 0, P2 ≠ 0, P6 ≠ 0등이 되는데, 이것은 지극히 평범한 상황이므로 역기구학의 해석이 반드시 가능해야 한다. 하지만 P3 = P4 = P5 = 0이면 식(6), 식(28)이 (P1Cθ1 + P2Sθ1)Cθ2 = 0, P6Cθ2 = P7이 되어서 Cθ2, Sθ2 에 대한 연립 방정식의 일반적인 해법으로 θ2 = arc tan2(Sθ2, Cθ2)를 구할 수 없다. 따라서 운동 상황을 고려한 해석 방법을 고민하게 되었는데, 수많은 시행착오로부터 Table 3과 같이 θ6 ≠ 0°인 경우를 크게 θ6 ≠ 0°, P3 = 0인 경우와 θ6 ≠ 0°, P3 ≠ 0인 경우로 구분하는 것이 타당하다고 판단했다. 간단히 설명하면 P3 = 0인 경우에 식(6), 식(28)을 연립해서 θ1을 구할 수 없지만, P3 ≠ 0인 경우에 θ1을 구할 수 있다.
θ6 ≠ 0°, P3 = 0인 경우에, 먼저 θ1, θ2를 구하기 위해서 식(5)를 계산한다. 식(5)의 (1, 2) 성분인 식(6)이 성립하기 위해서 Cθ2 ≠ 0, P1Cθ1 + P2Sθ1 = 0을 만족해야 하므로, 가동 범위가 ±90°인 θ1은 다음과 같이 구할 수 있다.
| (29) |
여기서 분자인 P1와 분모인 P2가 이 아니어야 한다. θ2를 구하기 위해서, 식(5)의 (1, 4) 성분을 정리하면 다음과 같다.
| (30) |
여기서 U1 = P4Cθ1 + P5Sθ1, U2 = P6, U3 = P7이고, P4 ~ P7은 식(28)과 서로 같다. 식(30)에서 θ2는 다음과 같이 구할 수 있다.
| (31) |
여기서 이어야 한다. 그러므로 θ6 = 0°, P3 = 0인 경우에 식(29), 식(31)에서 θ1, θ2는 2쌍의 해가 존재한다.
다음으로 βY, θ3, θ4, θ5를 구해야 하는데, 나머지 과정은 2.3.1항의 내용과 기본적으로 동일하므로 2.3.1항을 참고하길 바란다. 그러므로 사람과 같이 θ4 ≤ 0° 이라고 하면, Table 3과 같이θ6 ≠ 0°, P3 = 0인 경우에 θ1, θ2, βY, θ4, θ3, θ5는 전체적으로 2쌍의 해가 해석적으로 존재하게 된다. 그리고 가장 일반적인 경우인 ±180°의 범위에서 계산하면 식(29)인 P1Cθ1 + P2Cθ1 = 0에서 2쌍, 식(31)에서 2쌍, 식(17)에서 2쌍으로 전체적으로 8쌍의 해가 존재하는데, 구체적인 해석 과정은 생략하기로 한다. 아울러 왼 다리의 경우도 용이하게 해석할 수 있다.
θ6 ≠ 0°, P3 ≠ 0인 경우에, 먼저 θ1, θ2를 구하기 위해서 식(5)를 계산한다. 식(5)의 (1, 2) 성분과 (1, 4) 성분을 연립해서 Cθ1, Sθ1을 구하면 다음과 같다.
| (32a) |
| (32b) |
여기서 P1 ~ P7은 식(6), 식(28)과 서로 같고, 분모인 (P1P5 – P2P4)Cθ2가 영이 아니어야 하고, –1 ≤ Cθ1 ≤ 1, –1 ≤ Sθ1 ≤ 1이어야 한다. θ2를 구하기 위해서, 식(32)의 Cθ1, Sθ1을 에 대입해서 새롭게 Sθ2에 대해서 정리하면 다음과 같이 Sθ2에 관한 2차 방정식이 된다.
| (33) |
여기서
이다. 가동 범위가 θ2 = ±90°이므로, 식(33)에서 θ2는 다음과 같이 구할 수 있다.
| (34) |
여기서 –1 ≤ Sθ2 ≤ 1이어야 한다. 2.3.2항에 언급한 것과 같이 P4 = P5 = 0이 자주 발생하므로, θ1을 구하기 위해서 식(5)의 (1, 2) 성분을 정리하면 다음과 같다.
| (35) |
여기서 이다. 식(35)에서 θ1은 기본적으로 식(30), 식(31)과 같은 형태로 구할 수 있는데, 여기서 이어야 한다. 특히 P4 = P5 = 0이면, 식(32)에서 분모가 영이 되어서 θ1을 구할 수 없으므로 θ1은 반드시 식(35)에서 구해야 하고, 게다가 2.3.2항에 언급한 것과 같이 식(6), 식(28)의 연립 방정식으로 θ2를 제대로 구하지 못하게 된다. 그러므로 θ6 ≠ 0°, P3 ≠ 0인 경우에 식(34), 식(35)에서 θ2, θ1은 최대 4쌍의 해가 존재한다.
다음으로 βY, θ3, θ4, θ5를 구해야 하는데, 나머지 과정은 2.3.1항의 내용과 기본적으로 동일하므로 2.3.1항을 참고하길 바란다. 그러므로 사람과 같이 θ4 ≤ 0°이라고 하면, Table 3과 같이 θ6 ≠ 0°, P3 ≠ 0인 경우에 θ2, θ1, βY, θ4, θ3, θ5는 전체적으로 최대 4쌍의 해가 해석적으로 존재하게 된다. 그리고 가장 일반적인 경우인 ±180°의 범위에서 계산하면 식(34)에서 최대 4쌍, 식(35)에서 2쌍, 식(17)에서 2쌍으로 전체적으로 최대 16쌍의 해가 존재하는데, 구체적인 해석 과정은 생략하기로 한다. 아울러 왼 다리의 경우도 용이하게 해석할 수 있다. 2.3절에 대한 시행착오를 언급하자면, 식(7)을 포함해서 연립 방정식을 해석적으로 풀고자 했지만 수많은 조합으로도 해를 구할 수 없었고, 3개의 미지수인 θ1, θ2, βY를 한꺼번에 수치해석적인 방법으로 풀고자 했지만 해를 구할 수 없었다.
2.4 미지 말단 위치, 미지 말단 자세의 주행에 대한 역기구학의 해석
Fig. 2와 같이 기지의 βY = βYa에서 꺾인 발목을 얼마나 돌려야 미지의 βYa = βYb와 기지의 θ6에서 안락하게 뻗은 발목이 되는가를 해석하는 것인데, 이 문제는 주어진 θ6을 만족하기 위한 스케이트의 위치, 스케이트의 자세인 βYb, 미지의 P1, P2, P3, P4, P5를 구하는 것이 되고, 미지수는 6개이다. 특히 오른 스케이트의 위치는 Table 1의 ∆1, Ψ1로 나타내는데, 미지수인 βYb를 구하기 위해서 따로 분리해야 한다. Table 1 의 ∆1에서 축 방향의 단위 벡터를 각각 이라고 하면, Fig. 5와 같이 βY = 0°인 기지의 C0 = E0과 Pure Rolling을 기준으로 βY, C, E가 기지의 βY, Ca, Ea에서 미지의βYb, Cb, Eb로 바뀌게 되는데, Ca, Cb, Ea, Eb는 다음과 같다.
| (36a) |
| (36b) |
| (36c) |
| (36d) |
| (36e) |
| (36f) |
여기서 rw는 Fig. 5와 같이 스케이트 휠의 반지름이고, δC = Cb – Ca, δE = Eb – Ea는 C, E의 증분이다. 특히 스케이트의 위치는 기지의 Ea에서 미지의 Eb = Ea + δE로 바뀌는데, δE = (δxE, δyE, δzE)T를 미지수인 βYb로 나타내면 다음과 같다.
| (37a) |
| (37b) |
| (37c) |
여기서 이다. 그리고 2.3 절과 같이 오른 스케이트의 자세는 Table 1의 ∆1, Ψ1로 나타내는데, 미지수인 βYb를 구하기 위해서 따로 분리해야 한다. 따라서 자세 행렬은 식(21)에서 회전각인 βY를 βYb로 바꾼 것과 서로 같다. 이 문제는 Table 4와 같이 크게 2경우로 나눌 수 있는데, 각각의 경우에 대해서 역기구학을 해석하기로 한다.
θ1, θ2, βYb를구하기 위해서 식(5)를 계산한다. 식(5)에서 βYb를 포함하지 않는 (1, 2) 성분을 정리하면 식(6)과 같다. 2.3.2항과 2.3.3항에서 설명한 것과 같이 식(6)에 대한 해석 방법은 크게 P3 = 0인 경우와 P3 ≠ 0인 경우로 구분하는 것이 타당하다고 판단했다.
P3 = 0인 경우에, 먼저 θ1, θ2, βYb를 구하기 위해서 식(5)를 계산한다. 식(5)의 (1, 2) 성분인 식(6)이 성립하기 위해서 Cθ2 ≠ 0, P1Cθ1 + P2Sθ1 = 0을 만족해야 하므로, θ1은 식(29)와 같이 구할 수 있다. βYb를 구하기 위해서 식(5)의 (1, 1) 성분과 (1, 3)성분을 CβYb, SβYb에 대한 연립 방정식으로 정리하면 다음과 같다.
| (38a) |
| (38b) |
여기서 V1 ~ V4, P8 ~ P21은 식(26)과 서로 같다. 식(38)에서 식(27)과 같은 형태로 CβYb, SβYb을 구하면 다음과 같다.
| (39) |
여기서 분모인 V1V4 – V2V3가 영이 아니어야 한다. 따라서 βYb는 βYb = f(θ2)와 같이 θ2의 함수이다. θ2를 구하기 위해서, 식(5)에서 βYb를 포함하는 (1, 4) 성분을 βYb, CβYb, SβYb에 대해서 정리하면 다음과 같다.
| (40) |
여기서
이다. 식(40)에 식(39)를 대입하면 최종적으로 θ2의 함수가 되므로, 식(40)에서 θ2는 수치해석적으로 구할 수 있다. 회전 범위가 βYb = ±90°이므로, 식(39)에서 βYb는 다음과 같이 구할 수 있다.
| (41) |
여기서 분자인 P21V1 – P14V3와 분모인 P21V2 – P14V4가 이 아니어야 한다. 그러므로 P3 = 0인 경우에 식(29), 식(40), 식(41)에서 θ1, θ1, βYb는 1쌍의 해가 존재한다.
다음으로 θ3, θ4, θ5를 구해야 하는데, 나머지 과정은 2.2절의 내용과 기본적으로 동일하므로 2.2절을 참고하길 바란다. 특히 식(16)에서
등이고, 식(37)에서
인 것에 유의하자. 그러므로 사람과 같이 θ4 ≤ 0°이라고 하면, Table 4와 같이 P3 = 0인 경우에 θ1, θ2, βYb, θ4, θ3, θ5는 전체적으로 1쌍의 해가 수치해석적으로 존재하게 된다. 그리고 가장 일반적인 경우인 ±180°의 범위에서 계산하면 식(29)에서 2쌍, 식(17)에서 2쌍으로 전체적으로 4쌍의 해가 존재하는데, 구체적인 해석 과정은 생략하기로 한다. 아울러 왼 다리의 경우도 용이하게 해석할 수 있다.
P3 ≠ 0인 경우에, 먼저 θ1, θ2, βYb를 구하기 위해서 식(5)를 계산한다. θ2를 구하기 위해서, 식(5)에서 βYb를 포함하는 (1, 2) 성분을 정리해서 Tθ2를 구하면 다음과 같다.
| (42) |
따라서 θ2는 θ2 = f(θ1)과 같이 θ1의 함수이다. βYb를 구하기 위해서 식(5)의 (1, 1) 성분과 (1, 3) 성분을 CβYb, SβYb에 대한 연립 방정식으로 정리하면 식(38)과 같다. 식(38)에서 CβYb, SβYb를 구하면 식(39)와 같다. 따라서 βYb는 βYb = f(θ1)과 같이 θ1의 함수이다. θ1을 구하기 위해서, 식(5)에서 βYb를 포함하는 (1, 4) 성분을 βYb, CβYb, SβYb에 대해서 정리하면 식(40)과 같다. 식(40)에 식(39)를 대입하면 최종적으로 θ1의 함수가 되므로, 식(40)에서 θ1은 수치해석적으로 구할 수 있다. 가동 범위가 θ2 = ±90°, 이므로, 식(42)에서 θ2는 다음과 같이 구할 수 있다.
| (43) |
여기서 분모인 P3가 영이 아니어야 한다. 회전 범위가 βYb = ±90°이므로, βYb는 식(41)과 같이 구할 수 있다. 그러므로 P3 ≠ 0인 경우에 식(40), 식(43), 식(41)에서 θ1, θ2, βYb는 1쌍의 해가 존재한다.
다음으로 θ3, θ4, θ5를 구해야 하는데, 나머지 과정은 2.4.1항의 내용과 기본적으로 동일하므로 2.4.1항을 참고하길 바란다. 그러므로 사람과 같이 θ4 ≤ 0°이라고 하면, Table 4와 같이 P3 ≠ 0인 경우에 θ1, θ2, βYb, θ4, θ3, θ5는 전체적으로 1쌍의 해가 수치해석적으로 존재하게 된다. 그리고 가장 일반적인 경우인 ±180°의 범위에서 계산하면 식(43)인 (P1Cθ1 + P2Sθ1)Cθ2 + P3Sθ2에서 2쌍, 식(17)에서 2쌍으로 전체적으로 4쌍의 해가 존재하는데, 구체적인 해석 과정은 생략하기로 한다. 아울러 왼 다리의 경우도 용이하게 해석할 수 있다. 2.4절에 대한 시행착오를 언급하자면, 식(7)을 포함해서 연립 방정식을 해석적으로 풀고자 했지만 수많은 조합으로도 해를 구할 수 없었고, 3개의 미지수인 θ1, θ2, βYb를 한꺼번에 수치해석적인 방법으로 풀고자 했지만 해를 구할 수 없었다.
3. 보행, 주행에 대한 역기구학의 해석 예제
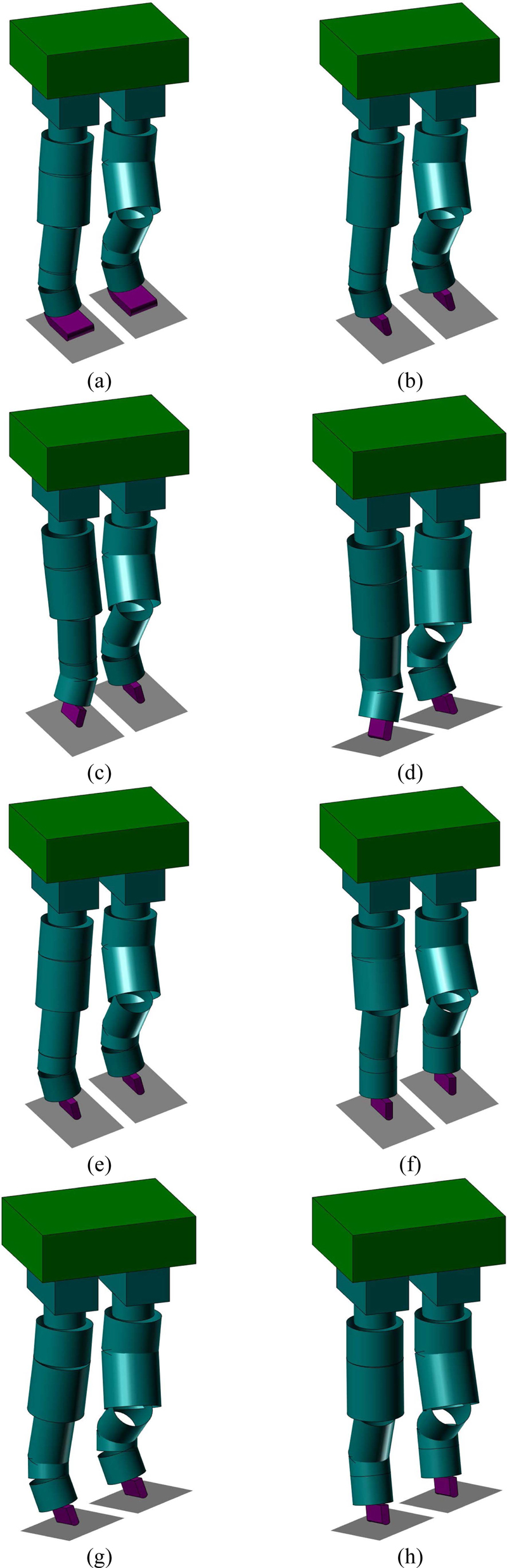
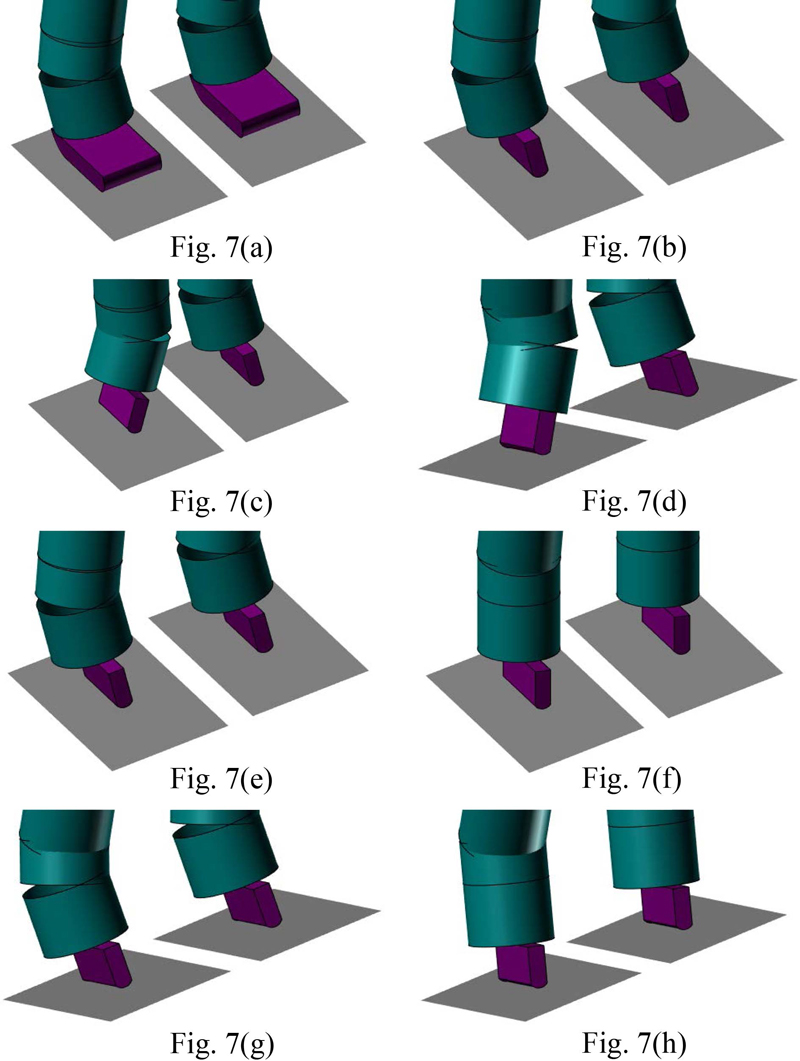
이 논문에서는 역기구학 문제만을 다루기 때문에 Fig. 3의 로봇을 Fig. 7과 같이 간략하게 표현했다. 여기서 다리 사이의 간격이 220[mm], 링크의 길이가 l1[mm], l2[mm], l3[mm], l4[mm], l5[mm], l6[mm] 등이다. 그리고 Table 5와 같이 예제의 경사 지면은 0i –XiYiZi좌표계의 위치와 자세로 나타내었는데, Fig. 8과 같이 로봇의 입장에서 Table 5(a)는 우저좌고(右低左高)의 지면이고, Table 5(b)는 우저좌고(右低左高)와 전고후저(前高後低)의 지면인데, Fig. 7과 Fig. 8은 동일한 시점에서 본 것이다.
Fig. 7은 역기구학을 해석한 예제인데, Fig. 8과 같이 Endeffector와 경사면에 주목하길 바란다. Fig. 7(a)는 Table 5(a)의 경사면에서 Table 2(a)의 βX = 0°인 보행을 계산한 예제이고, Fig. 7(b)는 Table 5(a)의 경사면에서 Table 2(a)의 βY = 0°인 주행을 계산한 예제이다. Fig. 7(c)는 Table 5(a)의 경사면에서 Table 3(b)의 계산 예제이고, Fig. 7(d)는 Table 5(b)의 경사면에서 T able 3 (c )의 계산 예제인데, θ6 = 20°이다. 그리고 Fig. 7(e)(f)는 Table 5(a)의 경사면에서 Table 4(a)의 계산 예제이고, Fig. 7(g)(h)는 Table 5(b)의 경사면에서 Table 4(b)의 계산 예제인데, 꺾인 발목을 곧게 뻗게 되는 과정에서 전후(前後)의 상황이고, θ6 = 0°이다. 아울러 모든 예제는 역기구학과 정기구학의 계산 결과를 서로 비교해서 검산했다. Table 6에 Fig. 7의 결과를 단위가 도(度)인 수치로 간단히 정리했는데, qi는 제i 다리의 관절각을 의미한다.
4. 결론
하이브리드 이동 로봇의 다리 보행과 스케이트 주행을 위한 역기구학 문제를 고찰했다. 역기구학 문제를 경사 지면에서 다리 보행과 스케이트 주행에 의한 일반적인 이동, 발바닥과 스케이트 날의 교체 등을 포함해서 체계적으로 분류했고, 각각의 문제에 대해서 역기구학을 해석했다. 특히 경사면 위에서 발바닥과 스케이트 날의 자유로운 운동을 포괄하기 위해서 경사면을 기준으로 하는 좌표 변환을 적극적으로 사용했고, 해석적인 방법과 수치해석적인 방법을 혼용했다. 그리고 구체적인 상황에 대해서 역기구학 예제를 계산했고, 결과로부터 해석 방법의 유효성을 확인했다.
References
-
Endo, G., Hirose, S., (2012), Study on roller-walker— improvement of locomotive efficiency of quadruped robots by passive wheels, Advanced Robotics, 26(8-9), 969-988.
[https://doi.org/10.1163/156855312X633066]

- Roller-walker. https://www.youtube.com/watch?v=P5ay5VC9ba4
-
Bjelonic, M., Grandia, R., Harley, O., Galliard, C., Zimmermann, S., Hutter, M., (2021), Whole-body MPC and online gait sequence generation for wheeled-legged robots, Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 8388-8395.
[https://doi.org/10.1109/IROS51168.2021.9636371]

- The future of robotic mobility. https://www.youtube.com/watch?v=RJyhZUqj3hM
- Nenchev, D. N., Konno, A., Tsujita, T., (2018), Humanoid robots: Modeling and control, Butterworth-Heinemann.
-
Goswami, A., Vadakkepat, P., (2019), Humanoid robotics: A reference, Springer.
[https://doi.org/10.1007/978-94-007-6046-2]

- Kaul, L. S., (2019), Human-inspired balancing and recovery stepping for humanoid robots, KIT Scientific Publishing.
- ASIMO robot demo 2/9: Walking over an uneven surface. https://www.youtube.com/watch?v=nVScax9uviM
- ASIMO robot running fast. https://www.youtube.com/watch?v=D6VG9E06LyI
- Atlas, The next generation. https://www.youtube.com/watch?v=rVlhMGQgDkY
- Getting some air, Atlas?. https://www.youtube.com/watch?v=vjSohj-Iclc
- ‘Cassie’ sets world record for fastest 100 meters by a bipedal robot. https://www.youtube.com/watch?v=64hKiuJ31a4
- Hwang, C.-S., (2009), Dynamic consideration of athletic constraints on skating motion, Journal of the Korean Society for Precision Engineering, 26(3), 55-67.
- Hwang, C.-S., (2009), Gaits control for skating motion with nonholonomic constraint, Journal of the Korean Society for Precision Engineering, 26(6), 59-67.
- SkaBot 1 (part 1). https://www.youtube.com/watch?v=Sr23tFqCvkg
-
Inoue, K., Shiina, K. I., Takano, M., Sasaki, K., (1996), Study on total computer-aided design system for robot manipulators, Journal of the Robotics Society of Japan, 14(5), 710-719.
[https://doi.org/10.7210/jrsj.14.710]

- UpTown spot. https://www.youtube.com/watch?v=kHBcVlqpvZ8
-
Bledt, G., Powell, M. J., Katz, B., Di Carlo, J., Wensing, P. M., Kim, S., (2018), MIT cheetah 3: Design and control of a robust, dynamic quadruped robot, Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2245-2252.
[https://doi.org/10.1109/IROS.2018.8593885]

- Craig, J. J., (1989), Introduction to robotics: Mechanics and control 2nd edition, Addison-Wesley.

He joined Kyungpook National University in 2005, where he is currently a Professor with the School of Mechanical Engineering. His current research interests include robotic systems for hybrid moving and object manipulating.
E-mail: robot@knu.ac.kr

He joined Kyungpook National University in 2006, where he is currently a Professor with the School of Convergence. His current research interests include smart manufacturing and measurement, robot gripper.
E-mail: holee@knu.ac.kr

She joined Kyungpook National University in 2009, where she is currently a Professor with the School of Convergence. Her current research interests include artificial intelligence implementation for intelligent devices.
E-mail: kby09@knu.ac.kr