다구치 방법과 그레이 관계분석을 이용한 전기화학 수소압축기 엔드플레이트의 구조분석 및 최적화

1. 서론

최근 에너지 소모, 압축 방법, 수소오염 등의 단점이 있는 기계적 압축에 대한 대안으로 비기계적 압축 방식 중 전기화학적 수소압축기가 주목을 받고 있다[1]. 전기화학적 수소압축기는 전기화학적 원리를 이용하여 수소를 압축하는데, 낮은 전력 소비와 열 손실, 높은 효율, 고순도 압축 등의 장점이 있다[2]. 전기화학적 수소압축기의 높은 출력과 내구성 향상을 위해 엔드플레이트에 대한 정확한 디자인의 최적화 연구가 필요하다. Jo et al.은 유한요소분석(FEA)을 사용하여 물 전기분해(PEMWE)스택에서의 엔드 플레이트의 두께가 성능에 미치는 영향을 평가하고 최적화하였다[3]. 그들은 엔드 플레이트의 두께에 따라 PEMWE 스택의 성능의 영향을 분석하였다. Choi et al. 연료전지 스택의 엔드플레이트에 대한 토폴로지 최적화에 대해 연구하였다. 토폴로지 최적화로 얻은 설계 값을 제작성을 고려한 설계로의 전환 시 유의점들을 미리 파악하고 유한요소분석(FEA)을 적용하여 최적설계를 수행하였다[4]. Chung et al.은 양성자 교환막 연료전지(PEMFE) 스택의 기계적 설계 및 분석에 대한 방법론을 제시하였다. 이를 위해 PEMFC 스택의 기계적 반응을 설계, 분석 및 개선하는 방법을 연구했다[5]. Yu et al.은 엔드플레이트의 경량화와 더 나은 열특성을 갖도록 설계하기 위해 공리적 설계방법과 유한요소해석을 사용하여 탄소섬유강화 복합재질로 된 외부판과 열 절연폼이 내재된 샌드위치 구조의 엔드플레이트에 대한 연구 수행하였다[6]. Zhou et al.은 양성자 교환막 연료전지(PEMFC)의 기계적 상태를 예측하기 위한 복합모델과 재료 특성 등가를 기반으로 유한요소모델(FEM)을 사용하여 스택 시스템을 모델링했다. 유한요소모델의 정확성을 검증하기 위해 스탬프 처리된 분리판(Bipolar Plate)을 사용한 실험을 수행하였다[7]. Yoon et al.은 스택 조립과정 시 발생하는 조립오차에 대해 스택의 안전성확보와 성능향상을 위해 다구치 방법을 이용해서 양성자 교환막 연료전지(PEMFC)의 가스켓(Gasket)의 강건설계를 수행하여 구조적 신뢰성을 확인하였다[8]. Caponetto et al.은 압축 압력이 700 Bar로 작동하는 전기화학 수소 압축기의 엔드플레이트의 모양과 두께를 유한요소법(FEM) 분석을 사용하여 최적화하였다[9]. Kim et al.은 유한요소 방법(FEM)과 DOE를 활용하여 스택의 성능에 영향을 주는 기체 확산층의 압력 분포에 대한 설계 매개변수의 영향을 분석하고 최적화를 수행하였다[10]. 지금까지 엔드플레이트에 대한 연구들은 주로 고분자 전해질 연료전지(PEMFC)의 적용되는 엔드플레이트의 디자인 및 성능향상을 위한 최적화 연구들이 진행되었다. 따라서 전기화학적 수소압축기의 엔드플레이트 경우 구조적으로 더 높은 작동압력으로 확장해서 설계되고 검증되어야 한다. 하지만 전기화학적 수소압축기의 엔드플레이트에 대한 디자인과 구성품들에 대한 구조적 검증 연구는 거의 수행되지 않았다.

이 연구에서는 고압 작동 조건에서 전기화학적 수소압축기 스택의 성능과 내구성을 극대화하기 위해 스택 구성품 중 엔드플레이트의 개념적 설계 방법론을 제시하였다. 또한 다구치-그레이 관계분석을 이용하여 엔드플레이트 파라미터 최적화를 시행하였다. 최적화된 엔드플레이트가 전기화학적 수소 압축기의 스택의 성능과 내구성에 미치는 영향을 검토하기 위해 Dummy Cell을 적층하여 구조분석을 통해 전기화학적 수소 압축기의 스택 내부의 구성품(분리판, 기체확산층) 사이에 분포되는 접촉압력의 균일도 경향을 분석하였다.

2. 전기 화학적 수소압축기 엔드플레이트 구조 최적화

2.1 전기 화학적 수소압축기

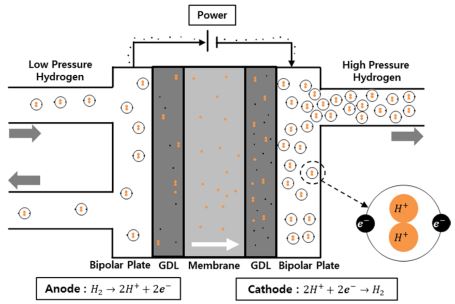
전기화학 수소 압축기(EHC)는 고분자 전해질 연료전지(PEM-FC)와 동일한 구조를 가지고 있다[11]. 양쪽에 전해질로 작용하는 막이 두 개의 촉매가 함유된 전극 사이에 위치해 있으며, 양극(Anode)에서 수소가 산화되고 음극(Cathode)에서는 전원 공급에 의해 환원된다. 이러한 방식으로, 수소가 저압 양극구획(Fig. 1, Left)에서 고압(높은 압력) 음극 구획(Fig. 1, Right)으로 이동하게 된다[12].

Fig. 1

How an electrochemical hydrogen compressor works

2.3 다구치방법을 이용한 엔드플레이트 구조 최적화

2.3.1 설계인자 및 설계조건 결정

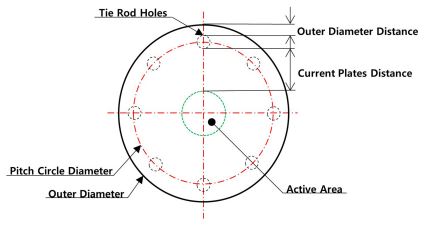
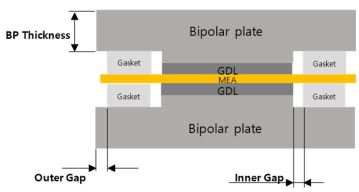
먼저 다구치 방법을 적용하여 전기 화학적 수소 압축기(Electrochemical Hydrogen Compressor)의 엔드플레이트 설계 및 유효성 평가를 수행하였다. 엔드플레이트의 형상 설계 인자는 Fig. 2에서 명시한 각 설계인자들을 선택하였다. 또한, 전기 화학적 수소압축기 작동 시 주변 환경 (온도, 습도)과 스택 조립 시 발생하는 유격과 같은 제어 불가능한 인자도 고려되었다. 엔드플레이트 초기 설계를 위해 제공된 정보는 단위 Cell 활성화면적 28.26 cm² 과 압축과정 중 스택 내부에서 발생하는 최대 압력 300 Bar이다. 제공된 초기 설계 값을 기반으로 엔드플레이트와 관련된 설계 파라미터와 범위를 Table 1과 같이 선정하였다. 엔드플레이트 모양은 Caponetto et al.가 최적의 형상임을 증명한 원형으로 선정하였다[7]. 엔드플레이트의 안전성을 유지하고 스택 내부 압력을 지탱하는 Tie Rod의 Size와 개수는 스택 내부의 압력(300 Bar)을 버틸 수 있도록 안전률까지 고려하여 결정하였다. 이 연구에서 Tie Rod Nominal Size가 M16, 개수 8개를 수준 1로, Tie Rod Nominal Size를 M12, Tie Rod개수 14개를 2 수준으로, Tie Rod Nominal Size M10, 개수 20개를 3 수준으로 선정하였다. 부적절한 Tie rod Size와 개수는 시스템의 안정성 문제를 초래할 수 있다. 엔드플레이트의 외경, 활성화 면적 최대활용 및 Tie Rods 배치에 영향을 주는 항목인 Current Plate Distance, Outer Diameter Distance는 활성화면적을 고려하여 Current Plate Distance, Outer Diameter Distance가 최소치인 경우에도 Tie Rod 간의 배치배열을 이룰 수 있도록 각각의 수준을 결정하였다. 엔드플레이트 구조강도와 무게에 영향을 주는 항목인 엔드플레이트의 두께는 임의로 75 mm를 1수준으로 하였고 25 mm씩 늘어나도록 각각의 수준을 결정하였다. 엔드플레이트의 봉인 및 압축과정에서 필요한 압력 제어에 영향을 주는 항목인 Clamping Pressure도 제시된 값이 없기 때문에 스택 내부에서 발생하는 압력을 같은 값을 1수준으로 하였고 5 MPa씩 늘어나도록 각각의 수준을 결정하였다.

Fig. 2

Definition of design parameters for end plate

Table 1

End plate design parameter table

결과적으로 5개의 3수준 설계인자가 결정되었다. 직교배열표는 설계 파라미터 사이의 교호작용을 고려하지 않고, 주 효과만을 고려하여 L18로 결정한 후, 각 경우에 대하여 유한요소법(FEM) 시뮬레이션을 수행하였다. FEM 해석을 위하여 ANSYS Design Modeler (ANSYS Workbench 18.2.2)을 이용하여 18가지 Case의 모델링 데이터를 생성하였다. 격자(Mesh)는 단일 엔드플레이트 형상이 단순하므로 Mechanical Auto-Mesh를 적용하여 생성하였고, 격자(Mesh)의 요소 편차를 줄이기 위해 격자(Mesh) 밀도를 +100으로 설정하였다. 엔드플레이트의 재질로 수소에 대한 내식성이 우수한 Stainless 316L을 선택하였고 그물성치가 Table 2에 주어졌다. 체결 압력은 엔드플레이트의 바닥면 모서리에 Remote Fixed 조건으로 고정시켰다. 스택 내부에서 발생하는 내압은 Current Plate를 통해 엔드플레이트로 전달되는 형태로 모사하였다. Current Plate 작동 압력은 Cell의 최대압력인 300 Bar (30 MPa)를 적용하였다.

Table 2

Mechanical properties of stainless steel 316L

2.3.2 시뮬레이션 결과 및 데이터 분석

각 목적 함수에 대한 시뮬레이션 조건과 해석결과, 그리고 식 (2)로 계산한 S/N비를 Table 3에 표시하였다.

$\[ \eta =-10{\mathit{log}}_{10}{y}^2 \]$

(2)

Table 3

End plate simulation results for deformation, stress, weight

2.3.3 S/N비의 분산분석(ANOVA)

Table 4에 최소 총 변형 결과에 대한 분산 분석이 보여졌다. 여기서 변형에 가장 큰 영향을 미치는 인자는 F 값이 가장 큰 Clamping Force임을 알 수 있다. 응력 최소화에는 두께가 가장 중요함이 Table 5에 보여졌는데 이는 엔드플레이트의 두께가 증가할수록 응력 값이 낮아질 것이라는 직관과 일치한다. 무게 최소화 분산분석이 주어진 Table 6에서 엔드플레이트의 두께가 가장 큰 영향을 미치는 것으로 확인되었다. 여기서 체결력은 엔드플레이트의 무게에 거의 영향이 없음을 알 수 있다.

Table 4

ANOVA Table of minimum deformation

Table 5

ANOVA Table of minimum equivalent stress

Table 6

ANOVA Table of minimum weight

2.3.4 최적조건 결정

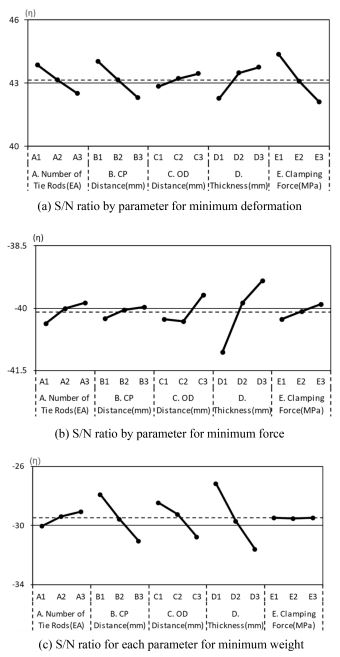
Fig. 3에서 각 목적 함수에 대한 설계 파라미터의 수준별 S/N비를 그래프로 보여졌다. 여기서 얻어진 엔드플레이트의 Total Deformation, Equivalent Stress, 그리고 Weight의 최적조건이 Table 7에 보여졌는데 목적함수에 따라 최적조건이 다르다. 이를 극복하기 위해 그레이 관계분석이 이용되었다.

Fig. 3

Parameter mean response graph by objective function

Table 7

Optimization conditions and simulation results for each objective function

2.4 그레이 관계 분석

2.3절에서는 최소 Total Deformation, 최소 Equivalent Stress, 최소 Weight를 만족시키기 위한 엔드플레이트의 최적 설계 파라미터를 독립적으로 분석하고 결정했다. 그러나 각 목적 함수의 최적화 조건이 상이하므로 그레이 관계 분석(Gray Relational Analysis)을 이용하여 다목적 함수의 최적 조건을 동시에 충족시키도록 시도하였다[13]. 이때 각 목적함수에 동일한 가중치 1/3씩을 할당하여 그레이 관계등급을 구하였다(Table 8).

Table 8

Gray correlation coefficient and gray correlation rating for analysis results

Table 8에서 계산된 그레이 상관관계 등급을 이용하여 분산 분석을 수행한 후, 그 결과를 Table 9에 정리하였다. 각 목적함수에 각각 0.33의 가중치를 주고 분석했을 때, CP Distance가 첫번째, 엔드플레이트의 두께가 두번째 큰 영향을 끼침을 알 수 있다. 다른 설계 파라미터들은 큰 영향을 주지 않아 오차로 처리하였다. 그레이 상관분석으로 결정한 파라미터와 각 목적 함수 별 최적 조건 파라미터에 대한 시뮬레이션 결과가 Table 10에 제시되었다. 그레이 상관분석으로 얻어진 결과는 3가지 최적 조건 결과의 중간값을 가짐을 알 수 있다.

Table 9

Analysis of variance table of gray relational ranks

Table 10

Optimization conditions and simulation results for each objective function

3. Dummy Cell 적층 FEM 시뮬레이션

3.1 전기 화학적 수소압축기 스택 모델

최적화된 엔드플레이트에 안전성 및 성능을 평가하기 위해 스택 내부에 전달되는 셀 접촉압력분포와 압력의 균일 여부를 분석하고 및 평가하였다. 위를 위해 12개의 Dummy Cell을 적층한 스택 시뮬레이션을 실시하였다.

3.1.1 유한요소해석 구조 모델링

전기 화학적 수소압축기 스택은 엔드플레이트, Bipolar Plate, Gasket, GDL, 그리고 MEA로 구성되어 있다. 본 연구에서는 모델의 간소화를 위해 Tie Rod와 Nut는 고려하지 않았다. 스택 시뮬레이션을 위해 제공된 활성화 면적(28.26 cm²), 작동압력(300 Bar)을 기준으로 설계된 단일 Dummy Cell 구성 요소의 치수와 기계적 특성이 Table 11에 자세히 기술되었다

Table 11

Dimensions and mechanical properties of cell components

3.1.2 경계조건 및 하중조건

본 모델에서 가스확산층(GDL)과 엔드플레이트 사이, Current Plate와 Bipolar Plate 사이, 가스확산층(GDL)과 Bipolar Plate 사이, 그리고 Gasket과 Bipolar Plate 접촉조건을 ‘Bonded’로 구성하였다. 또한 엔드플레이트의 모서리를 X, Y, Z, Xθ, Yθ, Zθ의 자유도는 0으로 가정하여 움직임을 구속하였다. Clamping Pressure는 엔드플레이트에 있는 와셔의 투영된 엔드플레이트 표면에 작용하는 것으로 모델링하였다.

3.1.3 적절 체결력

본 연구에서는 GDL의 최대 효율을 도출하기 위해 Dummy Bipolar Plate와 Dummy GDL의 접촉압력을 1.0 MPa로 설정하였다[14]. 또한, 스택 내부 압력 누수 방지를 위해 GDL에 적정 접촉압력을 가정하였다. 이를 위해 식(3)을 사용하여 스택 내부에서 발생하는 300 Bar (30 MPa)의 압력을 엔드플레이트에 있는 와셔의 단면적으로 나누어 힘 평형 체결압력과 적정 체결압력을 계산하여 적정 체결압력을 65.5 MPa로 도출하였다. 이를 통해 GDL에 적절한 압력을 적용하여 최적의 연료전지 성능을 도출하기 위한 설계 기준을 제시하였다.

$\[ P_{internel }=\frac{F_{Clamping Force }}{A_{Washer Area }} \]$

(3)

3.2 FEM 시뮬레이션 결과 및 토론

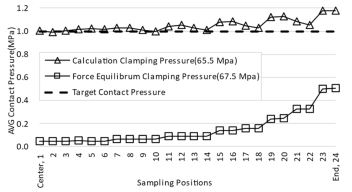
스택 내부에 전달되는 평균 접촉압력을 평가하기 위해 Dummy GDL의 위치별로 24개의 Sampling Data를 취득하고 이를 기반으로 평균 접촉압력을 계산하였다. Fig. 4는 힘-평형 방정식과 적정체결압력을 이용하여 얻은 결과이다. 힘-평형 방정식으로 시뮬레이션한 결과, 스택 중심에서는 평균 접촉압력이 거의 0이었지만, 엔드플레이트에 가까워질수록 평균 접촉압력이 증가하는 경향을 보였다. 반면, 적정 체결압력으로 시뮬레이션한 결과 평균 접촉압력이 목표 평균 접촉압력인 1.0 MPa에 근접하였고, 엔드플레이트에 가까워질수록 평균 접촉압력이 증가하였다.

Fig. 4

Dummy stack configuration schematic

3.2.1 체결압력 파라미터 분석

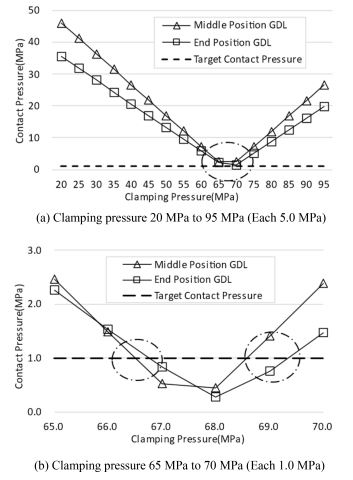
이 절에서는 Dummy GDL의 체결압력 변화에 따른 평균 접촉압력의 변화를 연구하였다. 체결압력을 20 MPa부터 5 MPa 단위로 증가시키면서 95 MPa까지 시뮬레이션을 수행한 결과, Fig. 5(a)에서 보듯이 체결압력이 65-70 MPa 구간까지 평균 접촉압력이 목표로 한 1 MPa에 가까워지다가 다시 증가하였다. 목표값에 근접한 체결압력구간에 대해 체결압력을 1 MPa 단위로 증가시키면서 시뮬레이션을 수행한 결과, Fis. 5(b)에서 보듯이 체결압력이 68 MPa을 기점으로 두 구간에서 목표로 한 평균접촉압력, 1 MPa에 근접하였다. 두 체결압 중 낮은값을 결정해야 Middle Position GDL과 End Position GDL의 평균접촉압력 차가 낮아 스택내부에 좀 더 균일한 접촉압력이 전달됨을 알 수 있었다.

Fig. 5

Average contact pressure according to clamping pressure conditions

4. 접촉압력 최적화

4.1 Dummy Single Cell 디자인 파라미터 최적화

4.1.1 Dummy Single Cell 디자인 파라미터 설정

셀 내부 구성품의 균일 압력분포를 위해 단일 셀 최적화 연구를 수행하였다. 단일 셀은 분리판(Bipolar Plate), 가스확산층(GDL), 가스켓(Gasket), 그리고 막 전극 접합체(MEA)로 구성되어 있다. 단일 셀의 최적화를 위해 각 구성품의 초기 디자인값은 Table 11에 제시되었고 다양한 디자인 변수의 범위는 Table 12에 제시하였다.

Table 12

Single cell design parameters and levels

4.1.2 경계조건 및 하중 조건

경계조건으로 단일 셀의 상부와 하부 Bipolar Plate 모서리를 X, Y, Z 방향 및 Xθ , Yθ , Zθ 각도로 고정하였다. 단일 셀의 압착 상태를 시뮬레이션하기 위해 압축하중을 Bipolar Plate 외부 노출면에 적용하였다. 압축하중은 단일 셀에 1.5 MPa부터 6.0 MPa까지 1.5 MPa 간격으로 적용하여 목표 평균 접촉압력인 1.0 MPa에 도달할 수 있는 초기 체결압력을 도출하였다. 이를 통해 단일 셀 디자인 변수 최적화를 위한 2.5 MPa의 압축하중을 적용하였다.

4.1.3 스택 시뮬레이션 결과 및 분석

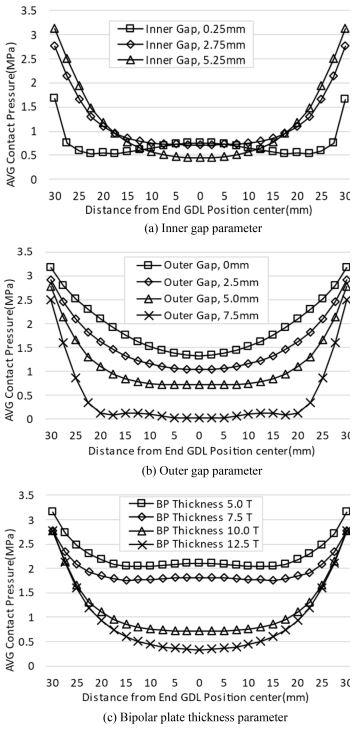
시뮬레이션 결과가 Fig. 6에 보여졌다. Figs. 6(a), 6(b)에서는 Gasket과 구성품 간의 Gap 수준에 따라 특정 값에서 균일한 접촉압력이 발생하는 것이 관찰되었다. 또한, Fig. 6(c)에서는 Bipolar Plate의 두께가 증가할수록 접촉압력의 균일도가 향상되고 GDL 중심 부근에서 발생하는 접촉압력이 증가하는 것을 확인하였다. 이러한 결과를 토대로, 균일한 접촉압력 전달을 위한 단일 Cell의 최적 디자인을 도출하였으며, 해당 결과는 Fig. 7에 제시되었다.

Fig. 6

GDL contact pressure distribution according to design parameters

Fig. 7

Dummy single cell optimal design

4.2 Dummy Single Cell 적층

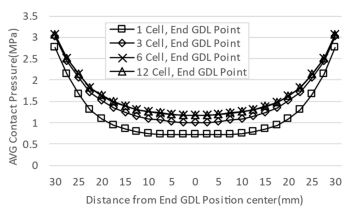
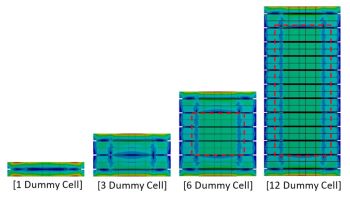
이 절에서는 최적화된 Dummy 단일 셀을 적층 하여 접촉압력 분포와 균일도에 대한 영향을 조사하였다. 적층 된 Dummy 단일 셀 간의 접촉조건으로는 Frictional Coefficient을 0.3으로 적용하였다. Fig. 8는 단일 셀 적층 별 End GDL 위치의 접촉압력 분포를 보여줍니다. 단일 셀의 적층이 증가할수록 평균 접촉압력과 균일도가 향상되는 것을 확인되었다. Fig. 9은 단일 셀 적층별 Von-Mises Stress결과이다. 단일 셀이 6 Cell 이상 적층되었을 때 스택의 중심, 양쪽 끝 부분에서 접촉압력이 안정화되는 것을 확인하였다. 따라서 안정화된 접촉압력을 얻기 위해서는 최소 6 Cell 이상의 셀을 적층해야 함을 알 수 있다.

Fig. 8

Contact pressure distribution for each layer of dummy single cell

Fig. 9

Dummy cell stacked section (Von-Mises Stress)

4.3 스택 작동 상태 시뮬레이션

4.3.1 경계조건 및 하중 조건

시뮬레이션을 통해 실제와 거동이 유사한 결과를 얻기 위해 Tie Rod와 Nut, 와셔 등을 추가로 모델링하여 스택 적층 해석을 수행하였다. 이 과정에서 기존의 고무 타입 Gasket 대신 내구성이 높은 PTFE 재질을 사용하여 높은 내압과 체결압력을 견딜 수 있도록 설계하였다. 구성품의 기계적 특성치는 Table 11에 보여졌다. 또한, 시뮬레이션의 수렴성 개선을 위해 엔드플레이트와 셀 구성품에는 Web Mesh 형태를, Tie Rod, Nut, 와셔에는 Hex Domination Mesh를 적용하였다. 각 구성품 간의 접촉 조건이 Table 13에 주어졌다.

Table 13

Dimensions and mechanical properties of single cell components

4.3.2 내압발생상태 시뮬레이션

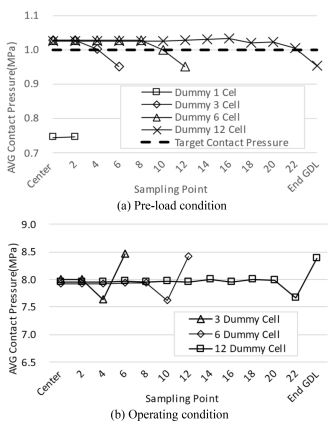
스택 내부의 운전조건에 따라 전달되는 평균접촉압력 분포와 균일도 분석을 위해 추가적인 시뮬레이션을 수행하였다. 먼저 초기 부하상태를 시뮬레이션하기 위해 Bolt-Pretension 조건을 적용하여 Tie Rod에 450 N의 하중을 적용하였다. 그 이후에는 스택이 작동하는 상황을 가정하여 설계상 최대 내부압력인 300 Bar에 도달하는 순서로 하중을 가하였다. Fig. 10(a)에서 초기부하상태 때 Dummy 단일 셀을 적층한 경우 목표로 한 평균 접촉압력보다 낮은 분포를 보였지만, 3, 6, 12 Cell을 적층했을 때는 End Position을 제외한 위치에서 균일한 접촉압력 분포를 확인할 수 있었다. 스택의 초기 부하 상태에서 스택 작동에 따라 Cell 내부의 가스확산층(GDL)에 대한 평균 접촉압력 분포는 Fig. 10(b)에 보여졌다. 결과적으로, 초기 부하 상태보다 높은 평균 접촉압력이 발생했다. 그러나 End Position에 평균 접촉압력을 제외하면 초기 부하 상태와 유사한 평균 접촉압력 값이 다른 위치에서 균일한 형태로 발생하는 것을 확인하였다. 또한, End Position에 접촉압력은 다른 위치에 있는 평균 접촉압력보다 높은 값을 나타내는 것을 알 수 있다.

Fig. 10

GDL average contact pressure distribution by location

5. 결론

이 연구에서는 전기화학적 수소 압축기의 작동 압력(300 Bar)에서 무게를 최소화하고, 변형과 응력을 최소화하면서 안전성과 성능을 최적화하는 엔드플레이트를 설계하기 위해 구조분 및 최적화를 수행하였다. 다구치 방법을 이용하여 Number of Tie Rods, CP Distance, OD Distance, Thickness, Clamping Force, 그리고 엔드플레이트의 설계 인자들이 변형, 응력, 무게에 미치는 영향을 분석하였다. 목적함수에 따라 변형, 응력, 무게에 각각 0.3의 가중치를 부여하여 다목적 최적화를 수행하였고, 그레이 상관 관계 분석법을 이용하여 최적수준을 구했다. 결과적으로, CP Distance가 가장 큰 영향을 미치는 것으로 확인되었으며, 또한 엔드플레이트 두께도 영향을 주었다. 최적조건은 그레이 상관분석 결과의 중간값을 가짐을 확인하였다. 최적화된 엔드플레이트의 안전성과 성능을 평가하기 위해 스택 내부의 셀 접촉압력 분포와 균일성을 분석하였다. 12개의 더미 셀을 적층한 스택 시뮬레이션을 수행하였고, 힘 평형 방정식을 이용하여 셀 체결압력을 결정하여 시뮬레이션을 진행했다. 결과적으로, 최적의 평균 접촉압력이 1.0 MPa에 근접하였고, 셀 체결압력이 증가하면 Dummy GDL의 평균 접촉압력이 감소-증가하는 경향을 확인하였다. 더불어, 균일한 접촉 압력분포를 위해 단일 셀 구성품의 최적화 및 적층 시뮬레이션을 수행하였고, 6개 이상의 셀을 적층한 경우 스택 내부의 평균 접촉압력이 균일화되는 것을 확인하였다. 또한, 운전조건에 따라 초기 부하 상태와 유사한 평균 접촉압력을 얻을 수 있었다. 이러한 연구 결과는 수소 에너지 저장 시스템의 설계와 안정성 향상을 위한 유용한 정보를 제공하며, 다목적 최적화 문제에 그레이 상관 관계 분석법과 다구치 방법이 유용한 접근 방법임을 보여준다.

Acknowledgments

이 논문은 2022년도 서울시립대학교 교내학술연구비에 의하여 지원되었음.

REFERENCES

• Sdanghi, G., Maranzana, G., Celzard, A., Fierro, V., (2020), Towards non-mechanical hybrid hydrogen compression for decentralized hydrogen facilities, Energies, 13(12), 3145. [https://doi.org/10.3390/en13123145]
• Zou, J., Han, N., Yan, J., Feng, Q., Wang, Y., Zhao, Z., Fan, J., Zeng, L., Li, H., Wang, H., (2020), Electrochemical compression technologies for high-pressure hydrogen: Current status, challenges and perspective, Electrochemical Energy Reviews, 3, 690-729. [https://doi.org/10.1007/s41918-020-00077-0]
• Jo, M., Cho, H.-S., Na, Y., (2020), Comparative analysis of circular and square end plates for a highly pressurized proton exchange membrane water electrolysis stack, Applied Sciences, 10(18), 6315. [https://doi.org/10.3390/app10186315]
• Choi, W.-S., Oh, S.-J., Kim, S.-J., Hong, B.-S., (2003), Topology optimization for end plate of fuel cell stack, Proceedings of the Korean Society of Mechanical Engineers Conference, 456-461.
• Chung, T.-T., Lin, C.-T., Shiu, H.-R., (2016), Mechanical design and analysis of a proton exchange membrane fuel cell stack, Journal of the Chinese Institute of Engineers, 39(3), 353-362. [https://doi.org/10.1080/02533839.2015.1101810]
• Yu, H. N., Kim, S. S., Do Suh, J., (2010), Axiomatic design of the sandwich composite endplate for PEMFC in fuel cell vehicles, Composite Structures, 92(6), 1504-1511. [https://doi.org/10.1016/j.compstruct.2009.10.026]
• Caponetto, R., Privitera, E., Mirone, G., Matera, F., (2022), Structural analysis of electrochemical hydrogen compressor end-plates for high-pressure applications, Energies, 15(16), 5823. [https://doi.org/10.3390/en15165823]
• Zhou, Z., Qiu, D., Zhai, S., Peng, L., Lai, X., (2020), Investigation of the assembly for high-power proton exchange membrane fuel cell stacks through an efficient equivalent model, Applied Energy, 277, 115532. [https://doi.org/10.1016/j.apenergy.2020.115532]
• Yoon, J.-Y., Park, J.-S., (2008), Structural robust design of PEMFC gasket using taguchi method, Journal of the Korean Society for Aeronautical & Space Sciences, 36(8), 740-746. [https://doi.org/10.5139/JKSAS.2008.36.8.740]
• Kim, C., Sohn, Y., Park, G., Kim, M., Lee, J., Kim, C., Choi, Y., Cho, S., (2012), The stress distribution analysis of PEMFC GDL using FEM, Transactions of the Korean Hydrogen and New Energy Society, 23(5), 468-475. [https://doi.org/10.7316/KHNES.2012.23.5.468]
• Bampaou, M., Panopoulos, K. D., Papadopoulos, A. I., Seferlis, P., Voutetakis, S., (2018), An electrochemical hydrogen compression model, Chemical Engineering Transactions, 70, 1213-1218.
• Grigoriev, S., Shtatniy, I., Millet, P., Porembsky, V., Fateev, V., (2011), Description and characterization of an electrochemical hydrogen compressor/concentrator based on solid polymer electrolyte technology, International Journal of Hydrogen Energy, 36(6), 4148-4155. [https://doi.org/10.1016/j.ijhydene.2010.07.012]
• Jung, J. H., Kwon, W. T., (2010), Optimization of EDM process for multiple performance characteristics using Taguchi method and Grey relational analysis, Journal of Mechanical Science and Technology, 24(5), 1083-1090. [https://doi.org/10.1007/s12206-010-0305-8]
• Chen, R., Qin, Y., Du, Q., Peng, J., (2018), Effects of clamping force on the operating behavior of PEM fuel cell, SAE Technical Paper, 2018-01-1718. [https://doi.org/10.4271/2018-01-1718]