유정압베어링 설계 최적화 모듈 개발

1. 서론

유정압베어링은 직선이나 회전운동을 하는 표면에서 비접촉 방식으로 부하를 지지하고, 원하는 방향으로 운동을 안내하는 기계요소로, 부하용량과 강성이 클 뿐만 아니라 저마찰로 인한 정밀한 이송이 가능하여 공작기계, 연삭기와 같은 다양한 생산 장비의 베어링으로 널리 사용되고 있다[1-3]. 유정압베어링은 구름 베어링과 달리 규격품이 없는 관계로 설계자가 직접 설계해서 사용해야 하며, 따라서 모세관이나 패드 사이즈, 공급압력, 간극 등의 설계정보로부터 부하용량이나 강성, 유량 등의 성능 해석을 통해 설계가 이루어진다. 그러나 목표로 하는 성능을 만족하지 못할 경우 이런 설계변수를 변경하여 재설계가 이루어져야 하며, 이때 유정압베어링의 특성에 대해 완벽하게 이해하지 못하면 설계변수 변경 시 상당한 어려움에 직면하게 된다. 특히, 성능에 대해 서로 상반된 결과를 도출하는 설계변수들이 있는 경우에는 유정압베어링에 대한 배경지식이 있다 해도 직접적인 설계가 어려울 수 있다.

따라서 이러한 문제 해결을 위해 유정압베어링의 설계 최적화에 대한 연구[4-15]가 진행되었다. 70-80년대에 수행된 연구[4-8]는 적절한 최적화 알고리즘의 부재로 인해 최적화 알고리즘을 직접적으로 적용한 것이 아니라 해석적인 방법을 통해 도표를 작성하고 이로부터 최적의 파라미터를 선정하는 방식으로 이루어져 복잡한 최적화 설계 문제에 대응하지 못하는 한계를 보이고 있다. 최근의 유정압베어링 최적설계 동향에 대해 살펴보면, 유정압베어링의 에너지(Minimum Power Loss) 측면에서의 최적화를 위해 순차적 이차 프로그래밍(Sequential Quadratic Programming, SQP) [9]과 향상된 회색늑대 알고리즘(Enhanced Grey Wolf Optimizer, EGWO) [10]을 사용한 연구가 진행되었다. 유정압베어링의 모세관 저항요소를 서보밸브로 대체한 서보 제어형 능동 유정압베어링을 개발하고, 제어 및 제어시스템의 최적화를 통해 유정압베어링의 성능을 향상시켰으며[11], 전산유체역학(CFD) 해석 결과를 기반으로 유정압베어링 패드의 기하학적 최적화(포켓 면적 및 위치)를 수행하였다[12]. 유정압베어링이 적용된 유니트, 장비 측면에서의 최적화를 살펴보면, 연삭기용 유정압 스핀들의 선단강성만을 대상으로 황금분할법(Golden Section Search) 알고리즘을 사용하여 최적화를 수행한 연구[13] 및 전체 공작기계 가이드웨이 설계측면에서의 유정압베어링 최적화를 다룬 연구가 진행되었다[14]. 이 논문에서는 기계 프레임의 구조적인 변형을 유한요소해석(FEM)을 통해 예측하고 이를 유정압베어링 설계(패드 위치 및 개수 등)에 반영하였다. 이와 비슷하게, 슬라이드 캐리지(Carriage) 내의 유정압 램(Ram)의 정동적 성능을 향상시키기 위해 이분법(Bisection Method)을 이용하여 최적의 공급압력과 패드 사이즈를 결정한 연구도 있다[15].

이와 같이 유정압베어링의 최적화는 설계목적에 맞게 부분적으로 진행되어 왔으나, 유정압베어링 자체의 다양한 설계변수 및 성능, 제한조건을 동시에 고려하여 종합적으로 최적설계를 수행한 연구는 찾아보기 어렵다. 따라서 본 연구에서는 이들을 모두 고려할 수 있도록 설계 최적화 모듈을 개발하였으며, 구축된 최적화 모듈을 통해 유정압베어링의 최적화를 수행하고, 실험장치를 제작하여 최적화 설계 결과를 검증하였다.

2. 유정압베어링 설계 최적화 모듈

2.1 설계 최적화 모듈의 구성

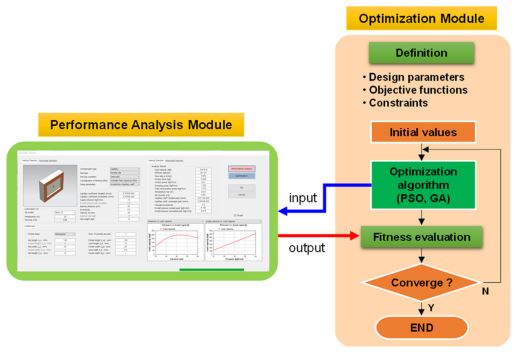
유정압베어링 설계 최적화 모듈은 기본적으로 유정압베어링의 성능을 해석하는 성능해석 모듈과 해석된 성능을 최적화하여 설계변수를 결정하는 최적화 모듈로 구성되어 있다. Fig. 1은 설계 최적화 모듈의 전체적인 구성도를 보여준다. 최적화 모듈에서 최적화를 위한 설계변수 및 목적함수, 제한조건 등을 정의하고, 주어진 조건에서 성능해석을 한 후 적합도를 평가하여 목표로 하는 성능을 달성할 때까지 최적화 알고리즘을 통해 반복적인 계산이 수행된다.

Fig. 1

Overall configuration of the design optimization module

2.2 유정압베어링 성능해석 모듈

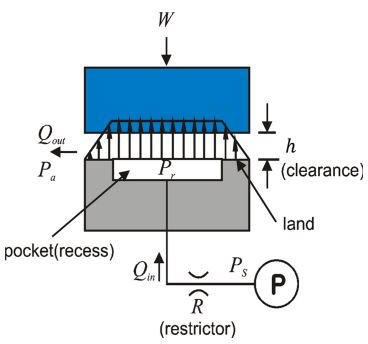
유정압베어링은 저항요소(Restrictor)의 종류에 따라 크게 모세관(Capillary)과 정유량(Constant Flow) 타입으로 구분할 수 있으며, Fig. 2는 일반적으로 많이 사용되는 모세관형 유정압베어링의 구조 및 주요 변수를 보여준다. P_s는 공급압력, P_a는 대기압력, P_r은 포켓 압력, h는 간극, W는 외부하중, Q_in과 Q_out은 각각 유입유량 및 유출 유량을 의미한다.

Fig. 2

Structure of capillary-type hydrostatic bearing

유정압베어링의 주요성능은 레이놀즈 방적식으로부터 유도할 수 있으며[1-3], 최종적으로 부하용량(C_p), 강성(K), 유량(Q)에 대한 수식을 간단히 정리하면 식(1)과 같다. A_eff는 베어링 유효면적, b는 압력비, B는 베어링 유량계수, μ는 점성계수를 의미한다.

$\[ \begin{array}{c}{C}_p=A_{eff}\left(P_r-P_a\right)\\ K=\frac{3C_p\left(1-\beta \right)}{h}\\ Q=B{h}^3/\text{μ}\left(P_r-P_a\right)\end{array} \]$

(1)

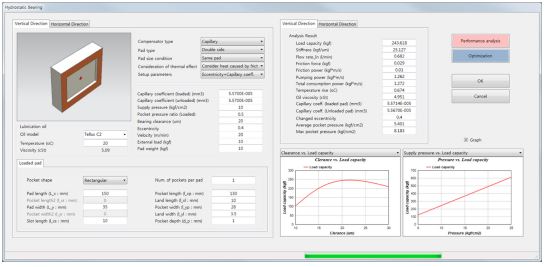
Fig. 3은 유정압베어링에 대해 개발된 성능해석 모듈(S/W)을 보여주고 있다.

Fig. 3

Performance analysis module for hydrostatic bearings

2.3 설계 최적화 모듈

2.3.1 최적화 알고리즘

최적화 알고리즘에는 크게 도함수(Derivative)에 기반한 방법과 도함수가 필요 없는 방법이 있다[16]. 도함수가 필요한 대표적인 방법 중 구배법은 빠른 계산속도를 보이지만 초기값을 잘못 선정하면 국소해에 빠지기 쉬우며 반드시 도함수가 필요한 단점이 있다. 유정압베어링의 경우, 성능 계산 시 비선형 방정식 사용으로 인해 도함수를 구하기 어려우므로 다수의 초기해를 이용하여 전역적으로 탐색하는 전역 최적화 방법을 이용하였다. 전역 최적화 방법 중 대표적으로 유전자 알고리즘(Genetic Algorithm, GA)과 입자 군집 최적화 알고리즘(Particle Swarm Optimization, PSO)을 이용하여 최적화를 수행하였다.

유전자 알고리즘[16]은 해의 잠재적인 집단이 형성된 후, 이로부터 각 개체에 대한 목적함수가 계산되고 각 개체들의 강점과 약점을 나타내는 적합도 함수가 평가되어 최적의 개체가 선택된다. 만약 종료 조건을 만족하지 않으면, 재생산, 교배, 돌연변이 연산자를 통해 새로운 해의 집단이 생성되고 이전과 같은 방법을 되풀이하여 최적화 과정이 수행된다. 입자 군집 최적화 알고리즘[17]은 비교적 최근에 개발된 알고리즘으로, 군집의 움직임과 지능에 기반한 최적화 방법이다. 각 입자는 하나의 군집내에서 자신의 이전 최적해와 모든 군집들 중 현재까지 발견된 이전 최적해를 향하도록 앞으로의 탐색 궤적을 조정한다.

2.3.2 최적화 모듈

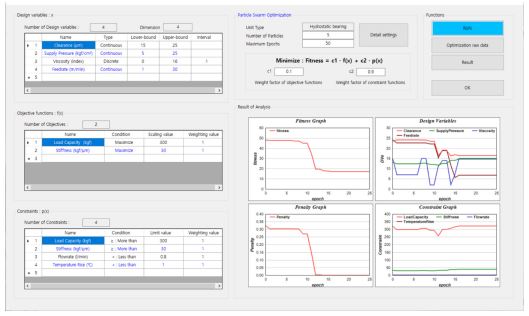
최적화 모듈에서 최적화를 위한 설계변수 및 목적함수, 제한 조건 등을 정의하고, 최적화 알고리즘과 연계하여 최적화를 수행하게 된다. 본 논문에서는 제한조건을 갖는 최적화 문제를 다루기 위해 벌점함수(Penalty Function)을 이용하였다. 벌점함수는 제약조건을 위반한 정도를 평가하여 위반 정도가 심할수록 벌점이 크게 부여되므로 다음 계산 과정에서 배제될 가능성이 커지게 되어 점차 적합한 영역에서의 해로 수렴하게 된다. Fig. 4는 구축된 유정압베어링 최적화 모듈(S/W)을 보여준다.

Fig. 4

Optimization module for hydrostatic bearings

3. 유정압베어링 설계 최적화 및 실험적 검증

3.1 최적화 문제 정의

유정압베어링에서 양면 베어링 타입인 경우 베어링 간극을 맞추기 위한 정밀가공 등의 문제로 실제 최적화 전/후에 대한 실험장치를 제작하여 확인하는 것은 쉽지 않다. 따라서 보다 현실적인 실험적 검증을 위하여 단면 베어링에 대해 최적화를 수행하고 실험적으로 검증하였다.

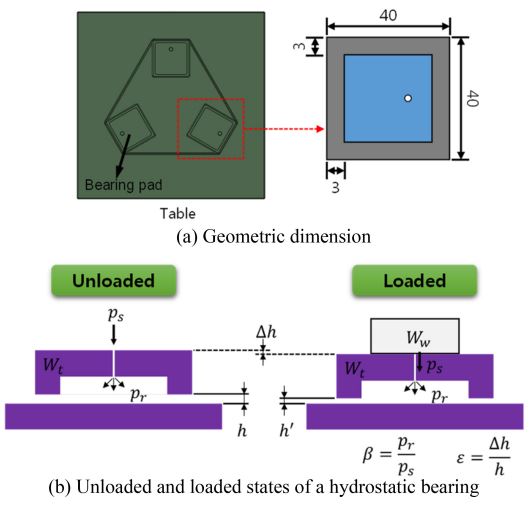
3개의 단면패드를 갖는 테이블에 대한 유정압베어링 설계를 대상으로 하였으며, 하나의 패드에 대한 치수는 Fig. 5와 같다. 테이블의 자중(W_t)만 고려한 경우를 무부하 상태로, 테이블의 자중에 공작물의 무게(W_w)가 추가로 작용하는 경우를 부하상태로 정의한다. 유정압베어링 테이블에 부하가 가해지게 되면 간극 h는 h'로 ∆h만큼 줄어들고, 이때 편심율 e는 ∆h/h로 정의한다.

Fig. 5

Specification of a hydrostatic bearing for design optimization

패드당 지지해야 하는 테이블과 공작물의 무게는 각각 60 kgf와, 30 kgf로 가정한다. 초기모델의 조건(공급압력 8 kgf/cm², 간극 22 μm, 압력비 0.5, 편심율 0.2)에 대해 무부하 상태와 부하상태의 해석을 통해 성능 기준을 선정하였다.

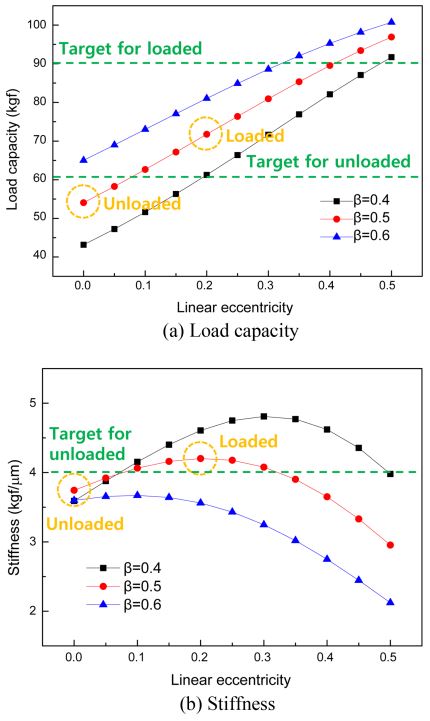
Fig. 6은 편심률 및 압력비에 따른 부하용량과 강성 변화를 보여준다. 테이블 자중만 고려된 무부하 상태인 경우(편심률 0), 압력비 0.5에서 부하용량은 54 kgf, 강성은 3.7 kgf/μm 정도 나오고 있으며, 부하 상태인 경우(편심률 0.2) 부하용량은 72 kgf, 강성은 4.2 kgf/μm를 보이고 있다. 설계하고자 하는 목표는 무부하상태에서 부하용량(C_p(unload))이 60 kgf 이상, 강성(K_unload)은 4 kgf/μm 이상, 부하상태에서의 부하용량(C_p(load))은 90 kgf이상, 강성(K_load)은 무부하상태의 80% 이상 되기를 원한다. 이를 위한 설계변수는 공급압력(p_s), 간극(h), 압력비(β), 편심율(ε)로, 이를 기존의 성능해석을 통해 결정하기는 쉽지 않다. 설계변수들에 따라 서로 상반되는 성능들이 도출될 수 있으므로 유정압베어링의 특성을 충분히 이해하고 설계 변수 값을 바꿔가며 반복적인 계산을 수행해야 하기 때문이다.

Fig. 6

Initial design results with eccentricity and pressure ratio

따라서 본 논문에서 개발한 유정압베어링의 설계 최적화 모듈을 통해 설계를 수행하였다. 목적함수는 식(2)와 같이, 부하상태의 부하용량(C_p(load)), 무부하 상태의 강성(K_unload), 유량(Q_in)을 두어, 부하용량과 강성은 최대화되고 유량은 최소화되도록 정의하였다. 수식 내에서 윗첨자 *는 각 변수의 무차원화 및 정규화(Normalization)를 위해 사용한 것을 의미한다. 설계변수들의 최대값 및 최소값의 범위는 식(2)에서 주어진다.

$\[ \begin{array}{c}\begin{array}{c}\text{◼Objective function} \hfill \\ \hfill \end{array}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}f\left(\stackrel{-}{x}\right)=\frac{1}{C_{p\left(load\right)}/C_p^{*}}+\frac{1}{K_{\left(unload\right)}/K^{*}}+\frac{Q_{in }}{Q^{*}}\hfill \\ ◼\text{ Design parameters} \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\stackrel{-}{x}=\left\{p_s,h,\beta ,\epsilon \right\}\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} 5\le p_s\le 12\left(kgf/{cm}^2\right)\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} 15\le h\le 25\left(\mu m\right)\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} 0.4\le \beta \le 0.6\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} 0\le \epsilon \le 0.3\hfill \\ \text{◼Constraints }\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} W_t\le C_{p\left(unload\right)}\le W_t+5\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} C_{p\left(load\right)}\ge W_t+W_w\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} K_{\left(unload\right)}\ge 4\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} 0.8K_{\left(unload\right)}\le K_{\left(load\right)}\le 1.2K_{\left(unload\right)}\hfill \\ \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em} k_c\ge 2.5\times {10}^{-5}\hfill \end{array} \]$

(2)

제한조건은 모세관 계수(k_c)를 포함하여 무부하 상태와 부하상태에서의 부하용량과 강성을 설계 목표치 범위에 맞게 설정하였다. 제한조건 위배 시 벌점을 부가하였으며, 벌점함수 $$ p\left(\stackrel{-}{x}\right)$$는 식(3)과 같이 정의하였다. λ_j는 j번째 제한조건의 위배된 크기로 제한조건을 만족하면 0, 만족하지 않으면 위배된 양에 비례하여 커지게 된다. λ_j*는 정규화를 위해 사용한 변수이며, c_j는 각 제한조건들의 상대적인 비중을 나타내는 값으로, 본 논문에서는 동일한 비중으로 설정하였다.

$\[ p\left(\stackrel{-}{x}\right)=\sum _{j=1}^5{c}_j\frac{{\lambda }_j}{{\lambda }_j^{*}} \]$

(3)

최종적으로, 적합도(fitness)를 목적함수와 벌점함수의 합으로 정의하여, 적합도 값을 최소화하는 최적화 문제를 정의하였다. c는 목적함수가 벌점함수에 비해 상대적으로 차지하는 비중을 나타내는 변수로, 본 논문에서는 0.3으로 설정하였다.

$\[ fitness=c\bullet f\left(\stackrel{-}{x}\right)+\left(1-c\right)\bullet p\left(\stackrel{-}{x}\right) \]$

(4)

3.2 최적화 결과

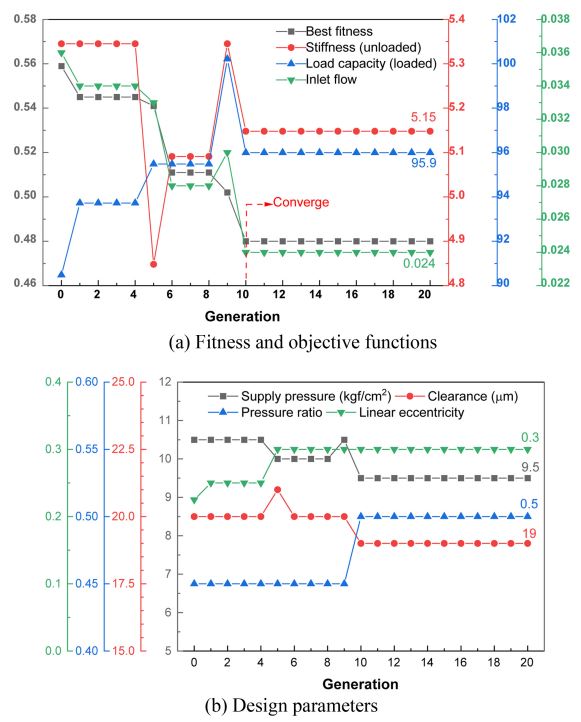
Fig. 7에서 보여진 바와 같이 최적화가 진행됨에 따라 적합도 값은 작아지고 있으며, 10세대만에 목적함수의 변수들은 제한조건을 만족하면서 잘 수렴하고 있으며, 설계변수도 주어진 설계 범위 내에서 잘 수렴하는 것을 확인할 수 있다.

Fig. 7

Optimization process with generation

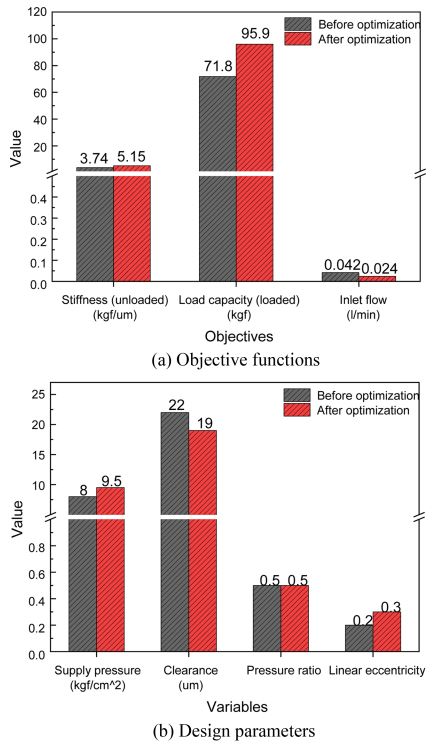
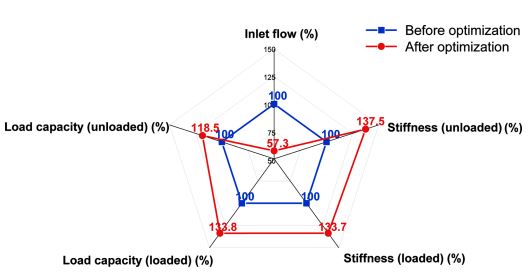
Fig. 8은 설계 최적화 전/후 목적함수 및 설계변수들의 변화를 보여주고 있다. 설계 최적화 후 강성과 부하용량은 초기 설계에 비해 모두 증가하고 있으며, 유량은 감소하는 결과를 볼 수 있다.

Fig. 8

Comparison of results before and after optimization

Table 1과 Fig. 9는 설계 최적화 전/후에 대한 무부하/부하상태에서의 부하용량 및 강성, 유량을 비교해서 보여주고 있으며, 최적설계 모델이 초기 모델에 비해 19-43% 정도 향상된 것을 확인할 수 있다.

Table 1

Comparison between initial design and optimal design

Fig. 9

Comparison between initial design and optimal design

참고로, 유전자 알고리즘과 입자 군집 최적화 알고리즘을 모두 사용하여 유정압베어링에 대한 최적화를 수행해 본 결과, 어느 알고리즘을 적용하던 제한조건을 만족하면서 최적화가 잘 수행되는 것을 확인할 수 있었다. 그러나 계산 속도면에서는 입자 군집 최적화 알고리즘이 유전자 알고리즘에 비해 2배 이상 빠른 계산능력을 보여주었다.

3.3 실험적 검증

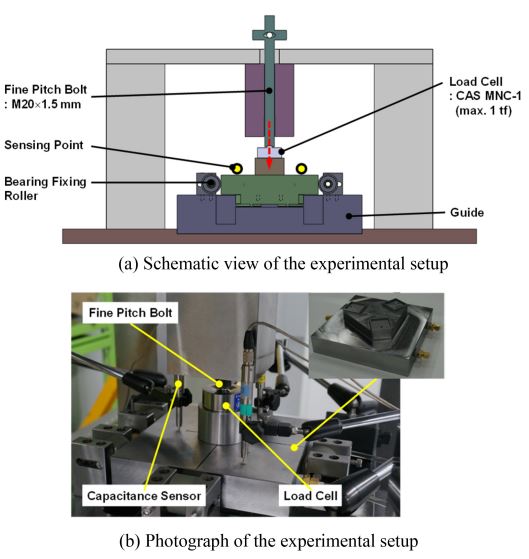
최적화 결과를 검증하기 위해 유정압베어링 실험장치를 설계하고 제작하였다. 유정압베어링은 Fig. 5(a)에서 보여진 바와 같이 패드 3개로 구성된 테이블로 구성하여 부하를 가할 때 모멘트에 의한 영향이 최소가 되도록 하였다. Fig. 10은 실험장치의 셋업을 보여주는 것으로, 정밀한 부하 조절나사를 이용하여 테이블에 수직하중을 부가한 후 로드셀을 이용하여 부하용량을 측정하였고, 이때 발생하는 베어링의 간극 변화량은 정전용량형 변위센서를 이용하여 측정하였다. 패드의 압력비는 모세관계수를 통해 조정하였다.

Fig. 10

Experimental setup for design optimization verification

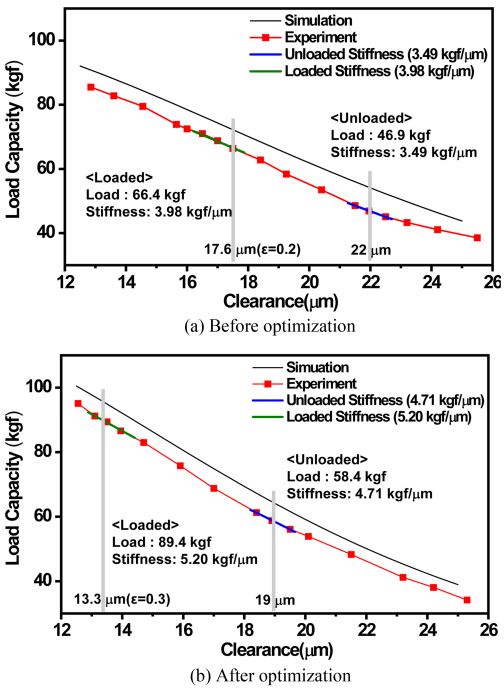
Figs. 11(a), 11(b)는 각각 설계 최적화 전/후 간극에 대해 부하용량을 측정한 결과를 시뮬레이션 값과 같이 보여준다. 강성은 부하용량을 간극에 대해 미분하여 계산하였다. 설계 최적화 전 무부하 상태에서의 간극은 22 μm이며, 부하상태에서는 편심율 0.2이 적용되어 17.6 μm가 되며, 최적화 후에는 무부하 상태에서의 간극은 19 μm, 부하상태에서는 편심율 0.3에 의해 13.3μm가 된다. 따라서 무부하 상태에서 부하용량 및 강성은 각각 최적화 전(초기설계) 46.9 kgf, 3.49 kgf/μm에서 설계 최적화 후 58.4 kgf, 4.71 kgf/μm까지 향상되었으며, 부하상태에서는 부하용량 및 강성이 각각 66.4 kgf, 3.98 kgf/μm에서 89.4 kgf, 5.20 kgf/μm까지 향상된 것을 볼 수 있다.

Fig. 11

Experiment and simulation results of load capacity and stiffness before and after optimization

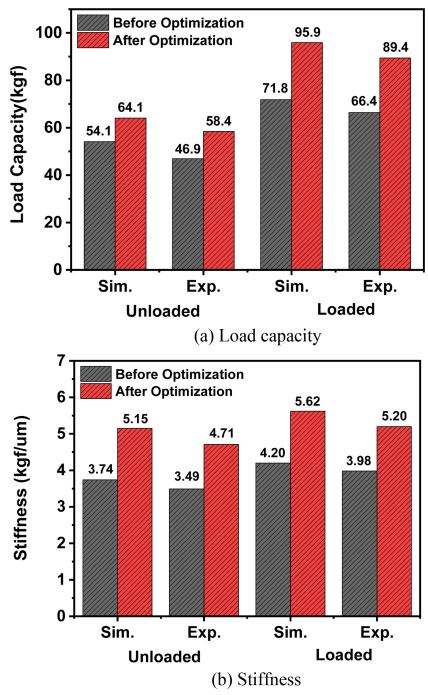
Table 2 및 Fig. 12는 무부하 상태 및 부하 상태에서의 부하용량과 강성에 대해 해석값 및 측정값을 설계 최적화 전/후에 대해 비교한 것이다. 부하용량 및 강성의 측정값은 해석값의 86.7-94.8% 수준을 보이고 있으며, 설계 최적화 전/후 해석값의 향상률 대비 측정값의 향상률의 비는 97.6-105.1% 수준을 보이고 있어 최적화가 잘 수행된 것을 확인할 수 있다.

Table 2

Comparison between initial design and optimal design

Fig. 12

Comparison between initial design and optimal design

4. 결론

본 논문에서는 사용자의 직접 설계가 필요한 유정압 베어링에 대한 최적설계를 수행하기 위해 유정압 베어링의 설계 최적화 모듈을 개발하였다. 최적화 문제를 정의한 후, 부하용량과 강성 등에 대해 최적화를 수행하고, 실험장치를 제작하여 실험적으로 검증하였다. 초기설계 모델에 비해 최적설계 모델은 모든 항목에서 최적설계 조건을 만족하면서 우수한 성능을 보이고 있어 본 논문에서 개발한 설계 최적화 모듈이 효과적으로 사용될 수 있음을 확인하였다. 결과를 정리하면 다음과 같다.

• 1. 무부하 상태에서 초기설계 모델의 부하용량과 강성은 각각 46.9 kgf, 3.49 kgf/μm에서 설계 최적화 후 58.4 kgf, 4.71 kgf/μm까지 향상되었으며, 부하 상태에서는 부하용량과 강성이 각각 66.4 kgf, 3.98 kgf/μm에서 89.4 kgf, 5.20 kgf/μm까지 향상되었다.
• 2. 부하용량 및 강성의 측정값은 해석값의 86.7-94.8% 수준이며, 설계 최적화 전/후 해석값의 향상률 대비 측정값의 향상률 비는 97.6-105.1% 수준을 보이고 있어 최적화가 잘 수행된 것을 확인하였다.
• 3. 본 연구에서 개발한 설계 최적화 모듈은 유정압 베어링 뿐만 다른 종류의 베어링이나 스테이지의 성능해석 모듈과도 연동할 수 있기 때문에 다양한 분야에서 최적설계 시 유용하게 활용될 수 있을 것으로 기대된다.

Acknowledgments

이 연구는 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20021902).

REFERENCES

• Rowe, W. B., (2012). Hydrostatic, aerostatic and hybrid bearing design, Elsevier.
• Liu, Z., Wang, Y., Cai, L., Zhao, Y., Cheng, Q., Dong, X., (2017), A review of hydrostatic bearing system: Researches and applications, Advances in Mechanical Engineering, 9(10), 1687814017730536. [https://doi.org/10.1177/1687814017730536]
• Michalec, M., Svoboda, P., Křupka, I., Hartl, M., (2021), A review of the design and optimization of large-scale hydrostatic bearing systems, Engineering Science and Technology, an International Journal, 24(4), 936-958. [https://doi.org/10.1016/j.jestch.2021.01.010]
• Rowe, W. B., O'Donoghue, J., Cameron, A., (1970), Optimization of externally pressurized bearings for minimum power and low temperature rise, Tribology, 3(3), 153-157. [https://doi.org/10.1016/0041-2678(70)90112-0]
• El-Sherbiny, M., Salem, F., El-Hefnawy, N., (1984), Optimum design of hydrostatic journal bearings Part I: Maximum load capacity, Tribology International, 17(3), 155-161. [https://doi.org/10.1016/0301-679X(84)90008-2]
• EI-Sherbiny, M., Salem, F., EI-Hefnawy, N., (1984), Optimum design of hydrostatic journal bearings Part II: Minimum power, Tribology International, 17(3),162-166. [https://doi.org/10.1016/0301-679X(84)90009-4]
• Singh, C., Singh, D., (1977), Stiffness optimization of a variable restrictor-compensated hydrostatic thrust bearing system, Wear, 44(2), 223-230. [https://doi.org/10.1016/0043-1648(77)90141-7]
• Rowe, W., Koshal, D., (1980), A new basis for the optimization of hybrid journal bearings, Wear, 64(1), 115-131. [https://doi.org/10.1016/0043-1648(80)90097-6]
• Kentli, A., Sahbaz, M., (2014), Optimization of hydrostatic thrust bearing using sequential quadratic programming, Oxidation Communications, 37(4), 1144-1152.
• Sahin, I., Dorterler, M., Gokce, H., (2019), Optimization of hydrostatic thrust bearing using enhanced grey wolf optimizer, Mechanika, 25(6), 480-486. [https://doi.org/10.5755/j01.mech.25.6.22512]
• Rehman, W. U., Wang, X., Cheng, Y., Chen, Y., Shahzad, H., Chai, H., Abbas, K., Ullah, Z., Kanwal, M., (2021), Model-based design approach to improve performance characteristics of hydrostatic bearing using multivariable optimization, Mathematics, 9(4), 388. [https://doi.org/10.3390/math9040388]
• Michalec, M., Ondra, M., Svoboda, M., Chmelík, J., Zeman, P., Svoboda, P., Jackson, R. L., (2023), A novel geometry optimization approach for multi-recess hydrostatic bearing pad operating in static and low-speed conditions using CFD simulation, Tribology Letters, 71(52), 1-14. [https://doi.org/10.1007/s11249-023-01726-3]
• Lee, C., Park, C., Lee, H., (1996), The optimization of a hydrostatic spindle system for grinding machines, Journal of the Korean Society for Precision Engineering, 13(7), 140-147.
• Mareš, M., Stach, E., Holkup, T., (2012), Applied method for design optimization of hydrostatic guideway on real machine tool, Engineering Mechanics, 857-868.
• Wang, Y., Liu, Z., Cheng, Q., Zhao, Y., Wang, Y., Cai, L., (2019), Analysis and optimization of nonlinear carrying performance of hydrostatic ram based on finite difference method and Runge–Kutta method, Advances in Mechanical Engineering, 11(6), 1-12. [https://doi.org/10.1177/1687814019856128]
• Jin, K. G., (2000), Genetic algorithms and their applications 2^nd edition, Kyowoo. ISBN: 8981721912, 9788981721916
• Nahvi, H., Mohagheghian, I., (2011), A particle swarm optimization algorithm for mixed variable nonlinear problems, International Journal of Engineering (IJE) Transactions A: Basics, 65-78.