Implementation and Verification of Fresnel Zone Plate Patterns Designed by Optimization of Surface Phase
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, we present a numerical simulation approach for designing Fresnel zone plate (FZP) patterns. By optimizing surface phase parameters using desired merit functions in ray-tracing software, the obtained surface phase was converted into an FZP pattern through a 5-step procedure. A comparison between our numerical simulation approach and the traditional analytical method showed a negligible zone size difference of 0.606 nm and nearly absolute agreement of 17.549 μm in focal spot size. The FZP pattern was experimentally verified by an expected focal spot size of 18.55 μm. Our approach demonstrated design flexibility and has potential applications in simulating various functionalities in FZP patterns and refractive-diffractive hybrid lenses to address specific optical challenges. The surface phase can be freely modified based on optimization objectives that cannot be achieved using the analytical approach, ensuring high-precision design for accurate extraction.
Keywords:
Numerical simulation, Fresnel zone plate patterns, Kinoform, Phase plate, Physical optics propagation1. Introduction
The trend of shrinking and thinning optical systems has always been a priority in the design of optical devices. In recent years, flat lenses have emerged as leading candidates to realize this trend [1-3]. Unlike conventional bulk lenses that use refractive theory to modulate the phase and control light propagation, Fresnel Zone Plates (FZP) is one of the most basic flat lenses that utilize diffraction theory to control waves [4,5]. They serve as the basis for modifying various diffractive patterns to address specific optical issues, such as depth of focus (DOF) extension, freeform wavefront metrology, compact imaging systems, and aberration correction [6-9]. They are widely applied in microscopy, astronomy, and telecommunications due to their thin structure.
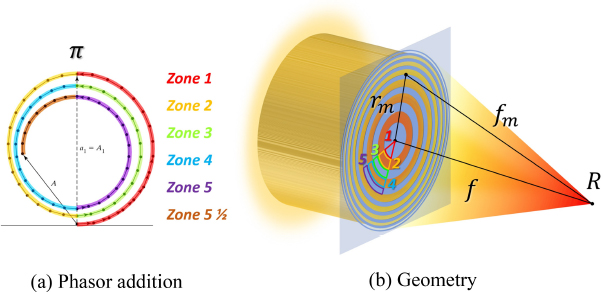
The fundamental principle of FZP is established in dividing concentric rings into alternating transparent and opaque zones to generate out-of-phase π depicted in Fig. 1(a), allowing them to superpose diffraction rays as foci [10]. Most of the FZP is designed through an analytical representative of the exact size of zones rm2 +f2 = (f + mλ)2, where rm is a radius of mth ring zone (m = 1,2, 3...), f and fm is the foci position of FZPs and mth zones, respectively, λ is the designed wavelength, and fm = f + mλ. Then, the light propagation is considered based on Rayleigh-Sommerfeld diffraction theory as Fig. 1(b) [11].
Indeed, with the rapid advancement of photolithography and laser writer technique, the FZP is a high-resolution solution for an optical promise, but its major drawback is low efficiency [12-14]. Various ideas have been proposed to improve this issue, such as kinoform, binary phase plate, and refractive-diffractive hybrid optics [15-18]. However, the analytical design approach is quite rigid and inflexible, making it challenging to vary the size of the zones to achieve the desired combined performance.
In this study, we introduce a numerical approach for designing the FZP patterns, that can be easily modified through an optimization of surface phase using optical ray-tracing software [19]. The flexible numerical approach allows the FZP pattern to exhibit multifunctionality and adapt to various applications. We will discuss the detailed design procedure, evaluate performance, conduct a comparison with the analytical solution, and then validate it through experimentation.
2. Design Method
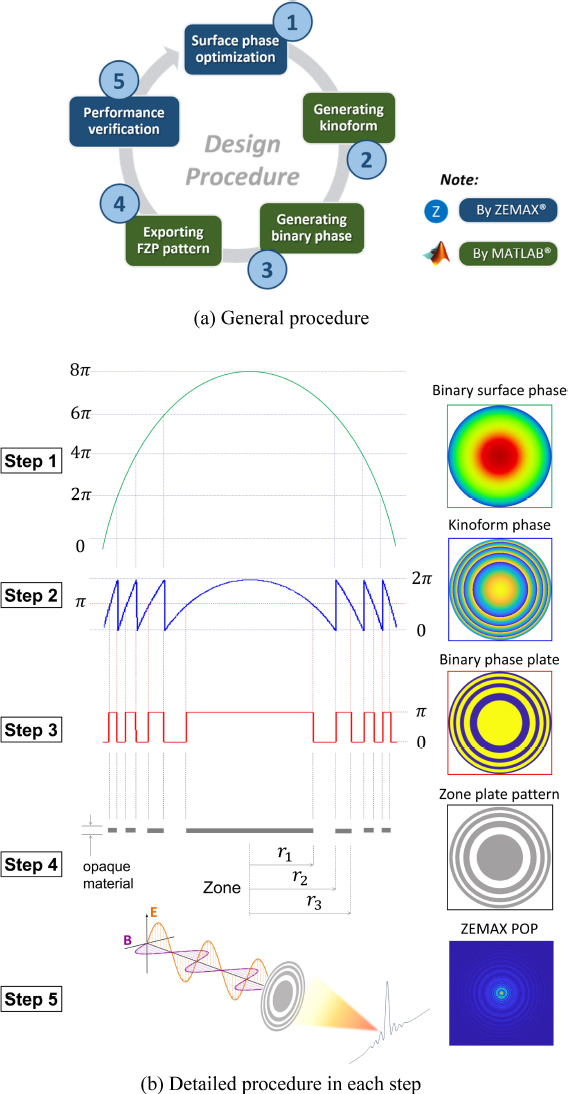
We introduce a general design procedure for the FZP pattern in Fig. 2(a) and their details in Fig. 2(b) include 5 main steps.
2.1 Procedure
The numerical simulation is performed using the design software ZEMAX®. Binary Optics does not directly model wavelength-scale grooves. Instead, ZEMAX employs the phase advance or delay represented by the surface locally to alter the direction of ray propagation. Binary surfaces can have zero thickness with no index change across the surface. A diffractive surface representing FZP is defined in ZEMAX by the Binary Optic 2 surface (ϕ), which adds a symmetrical phase to the ray according to the following polynomial expansion [20].
| (1) |
where N is the number of polynomial coefficients in the series, Ai is the coefficient on the 2ith power of valuable ρ, which is the normalized radial aperture coordinate, and M is the diffraction order.
Using multiple polynomials to model FZP enhances accuracy, but it increases complexity for the surface and optimization time. The coefficients Ai represent the design parameters in the numerical simulation, corresponding to the terms used. The surface phase is optimized with the target operands to achieve specific optical performance.
A kinoform phase profile ϕK is a continuous surface phase profile divided at 2π ambiguity given by
| (2) |
There are several methods to divide the surface phase at the 2π level. However, in this study, we employ a pair of inverse functions, tan and tan?¹, which ensures the precise calculation for each pixel in the numerical simulation approach. The kinoform is recognized to achieve 100% diffraction efficiency of the ideal ZEMAX surface phase [20].
A binary phase ϕB is a phase profile structure closest to the FZP pattern, it is also known as a 2-step phase in which kinoform profile is generated as 0 and 1 binary index corresponding to 0 and π phase level as follows:
| (3) |
Different from phase plates, Fresnel Zone Plate patterns are implemented using opaque materials with negligible thickness. There is no distinction in terms of where the opaque and transparent regions are placed; they simply need to be designed alternately. If the OFF and ON modes allow the rays can block and pass, respectively, the FZP pattern can be defined as follows:
| (4) |
The radii of the zones rm will be determined in Step 4 as depicted in Fig. 2(b) and evaluate rays propagation using ZEMAX® physical optics propagation (POP) which is calculated by scalar diffraction theory. The FZP pattern is implemented by the concentric circular apertures with corresponding radii that are entered sequentially in a user-defined aperture (UDA).
2.2 Numerical Design and Simulation
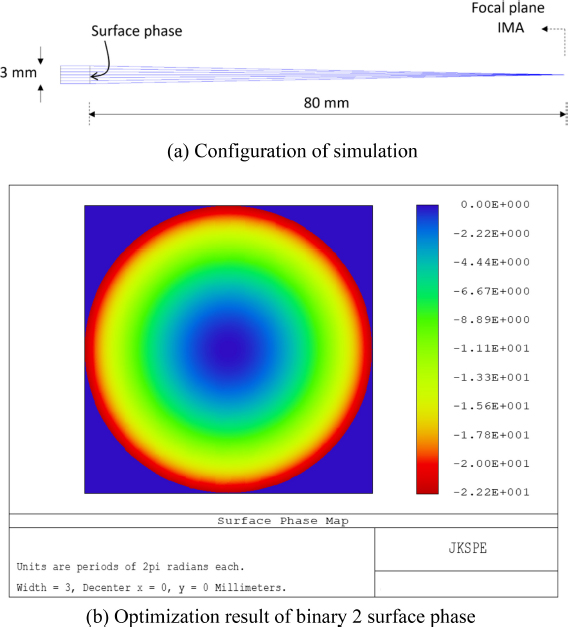
We demonstrate our procedure through a specific design with the specifications given in Table 1. Fig. 3(a) shows the ZEMAX simulation configuration in which the surface phase with a size of 3 mm diameter represents the FZP pattern. We use the 5 terms of polynomial expansion of the surface phase as optimization parameters of the default merit function for spot radius. Besides, the EFFL operand is added to constrain the 80 mm of focal length, and the RWCE operand is used to optimize the RMS wavefront error with a target of 0; Both are considered with the weight factor of 1 shown in Table 2. The diffraction order 1 is implicit in this study. The optimized surface phase obtained with the peak to valley (PV) of 22.2 periods of 2π is performed in Fig. 3(b) and the polynomial coefficients (Ai) obtained are presented in Table 3.
2.3 Performance
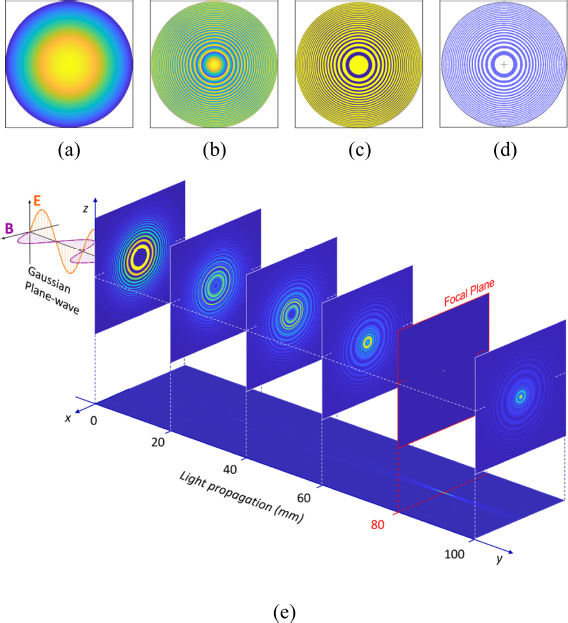
We successfully apply the 5-step procedure presented in section 2.1 and evaluate the performance of the designed FZP pattern by the 3D results presented in Fig. 4. Fig. 4(a) is the ZEMAX surface phase obtained after the optimization process presented in section 2.2, then they are divided by equation (2) at a level of 2π as Fig. 4(b). The phase plate obtained in Fig. 4(c) from binarizing the kinoform surface and then obtaining the FZP pattern. Fig. 4(d) is the footprint of the FZP pattern modeled by UDA and it is used to evaluate light propagation by ZEMAX-POP as Fig. 4(e). The input Gaussian light source is implemented by a plane wave perpendicular to the light propagation direction. We show the beam shape through the FZP pattern to the focal plane and the xy plane’s light propagation. At the focal plane, we obtain the beam expressed as a delta function.
3. Verification
3.1 Comparison
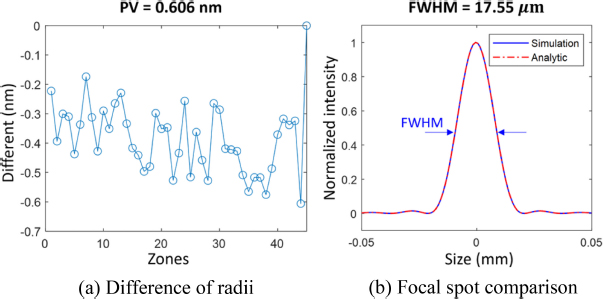
The comparison of the FZP pattern design performance between our proposal numerical simulation approach and the traditional analytical approach is important to demonstrate flexibility in this study. By step 4, some specific zones in radii (rm) implemented by the two approaches described are compared in Table 4. The difference between whole designed zones is shown in Fig. 5(a) with a PV of 0.606 nm and goes further if the calculation resolution of increased. This sub-nm difference is dismissed compared to the most current advanced manufacturing technologies which are at the nanometer level. The evaluation is also carried out considering propagation at the focal plane (80 mm of displacement) of the FZP designed by both approaches. Fig. 5(b) shows a near-absolute agreement of the focal spot size in both, which has a confirmed FWHM = 17.55 μm equality.
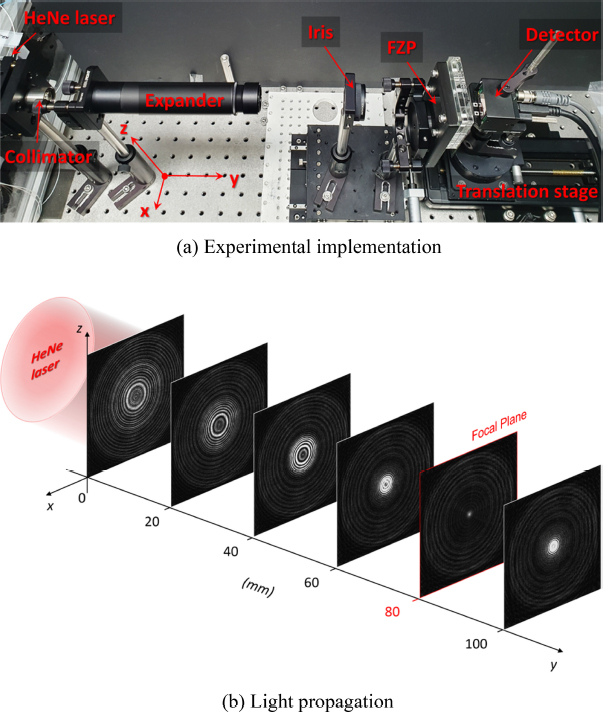
3.2 Experiment
The FZP pattern design by our numerical simulation is more verified by experiment. The practical FZP pattern is realized by photomasks technology and the fabrication positioning accuracy is used by 0.15 μm. A HeNe standard laser source (632.8 nm wavelength) is prepared from a fiber and collimated using a collimator. An expander, which is a pair of lenses in a Galilean configuration, is placed to increase the original beam size. A freespace beam from the collimator will pass through the expander and align with a displacement of 3 meters which guarantees plane wave characteristic within the experimental setup. This plane wave beam size is controlled by a precise iris and illuminates the FZP pattern as implemented in Fig. 6(a). A monochromatic detector with a resolution of 4,096 × 3,000 and pixel size of 3.45 μm is mounted on a translation stage to capture the beam shape along the light propagation y. The displacement accuracy of the translation stage is employed by 0.1 m and operated by a servo motor. The beam shapes at the different positions corresponding to the evaluation in ZEMAX-POP are taken and performed in Fig. 6(b). Beam propagation images are shown every 20 mm in each and a long displacement of 100 mm. At the focal plane in the experiment, the concentric faint sidelobes appear around the focal spot as a result of refraction of the light source obtained on the detector through the FZP pattern. They are considered dark current noise and negligible in this study. The number of data points taken by the detector is interpolated by MATLAB function to tens of thousands of data points to determine the FWHM of the focal spot. The focal spot size was recorded at FWHM = 18.55 μm and was also compared with the simulation result as shown in Fig. 7. The difference from the focal spot size in simulation by 1 μm that is the expected result based on manufacturing capability and alignment issues.
4. Conclusion
In this study, we present a flexible procedure to design the FZP pattern using the numerical simulation approach. By optimizing the surface phase with the desired target operands in ZEMAX® software, the extracted surface phase is converted to the FZP pattern. Our approach is demonstrated by a near-absolute agreement of the focal spot size of 17.549 μm and the sub-nm difference of the zones in radii with the analytical approach. Furthermore, it was also verified by the practical experiment, and the focal spot size was expected as 18.55 μm. There have been many attempts to simulate various functionality FZP patterns and combine refractive-diffractive hybrid lenses to solve optical issues such as DOF modulation, aberration correction, or freeform wavefront metrology. Our approach has the potential to be applied in the above combination design and can be freely modified depending on optimization targets that cannot be met by the traditional analytical approach. Besides, a high-precision FZP pattern design is implemented that far exceeds the fabrication capabilities currently available with typical technologies.
Acknowledgments
This study was supported by the National Research Foundation with the government, Ministry of Science and ICT (No. 2021R1A4A1031660), “Fanout semiconductor PR pattern highspeed automatic inspection equipment development (No. 20018441)”, a part of the Ministry of Trade, Industry and Energy's mechanical equipment industrial technology development project, and “Development of Ultra-Small Satellite with Hyperspectral and Visible Dual-Sensor Camera (No. RS-2022-00155901)”, a part of the space innovation project funded by the National Research Foundation of Korea.
REFERENCES
-
Tuan, P. T., Hai, V. N., Shin, S., (2016), A novel technique to design flat fresnel lens with uniform irradiance distribution, International Journal of Energy and Power Engineering, 5(2), 73-82.
[https://doi.org/10.11648/j.ijepe.20160502.17]

-
Banerji, S., Meem, M., Majumder, A., Vasquez, F. G., Sensale-Rodriguez, B., Menon, R., (2019), Imaging with flat optics: Metalenses or diffractive lenses?, Optica, 6(6), 805-810.
[https://doi.org/10.1364/OPTICA.6.000805]

-
Huang, K., Qin, F., Liu, H., Ye, H., Qiu, C., Hong, M., Luk'yanchuk, B., Teng, J., (2018), Advanced Material, WILEY, 30(26), 1704556.
[https://doi.org/10.1002/adma.201704556]

-
Moreno, V., Román, J. F., Salgueiro, J. R., (1997), High efficiency diffractive lenses: Deduction of kinoform profile, American Journal of Physics, 65(6), 556-562.
[https://doi.org/10.1119/1.18587]

-
Menz, B., Bräuninger, H., Burwitz, V., Hartner, G., Predehl, P., (2015), A Fresnel zone plate collimator: Potential and aberrations, Optics for EUV, X-Ray, and Gamma-Ray Astronomy VII, 9603, 454-467.
[https://doi.org/10.1117/12.2187996]

-
Tarrazó-Serrano, D., Castiñeira-Ibáñez, S., Minin, O. V., Candelas, P., Rubio, C., Minin, I. V., (2019), Design of acoustical Bessel-like beam formation by a pupil masked Soret zone plate lens, Sensors, 19(2), 378.
[https://doi.org/10.3390/s19020378]

-
Banerji, S., Meem, M., Majumder, A., Sensale-Rodriguez, B., Menon, R., (2020), Extreme-depth-of-focus imaging with a flat lens, Optica, 7(3), 214-217.
[https://doi.org/10.1364/OPTICA.384164]

-
Hao, C., Gao, S., Ruan, Q., Feng, Y., Li, Y., Yang, J. K., Li, Z., Qiu, C. W., (2020), Single?layer aberration?compensated flat lens for robust wide?angle imaging, Laser & Photonics Reviews, 14(6), 2000017.
[https://doi.org/10.1002/lpor.202000017]

-
Yamada, K., Watanabe, W., Li, Y., Itoh, K., Nishii, J., (2004), Multilevel phase-type diffractive lenses in silica glass induced by filamentation of femtosecond laser pulses, Optics Letters, 29(16), 1846-1848.
[https://doi.org/10.1364/OL.29.001846]

- Hecht, E., (2021), Optics 5th edition, Pearson. https://www.pearson.com/en-us/subject-catalog/p/optics/P200000006793/9780137526420
-
Liu, T., Wang, L., Zhang, J., Fu, Q., Zhang, X., (2018), Numerical simulation and design of an apodized diffractive optical element composed of open-ring zones and pinholes, Applied Optics, 57(1), 25-32.
[https://doi.org/10.1364/AO.57.000025]

-
Siemion, A., (2019), Terahertz diffractive optics—Smart control over radiation, Journal of Infrared, Millimeter, and Terahertz Waves, 40(5), 477-499.
[https://doi.org/10.1007/s10762-019-00581-5]

-
Park, S. Y., Lee, S., Yang, J., Kang, M. S., (2023), Patterning quantum dots via photolithography: A review, Advanced Materials, 2300546.
[https://doi.org/10.1002/adma.202300546]

-
Low, M. J., Lee, H., Lim, C. H. J., Sandeep, C. S., Murukeshan, V. M., Kim, S.-W., KIm, Y.-J., (2020), Laser-induced reduced-graphene-oxide micro-optics patterned by femtosecond laser direct writing, Applied Surface Science, 526, 146647.
[https://doi.org/10.1016/j.apsusc.2020.146647]

-
Low, M. J., Rohith, T. M., Kim, B., Kim, S.-W., Sandeep, C. S., Murukeshan, V. M., Kim, Y.-J., (2022), Refractive-diffractive hybrid optics array: comparative analysis of simulation and experiments, Journal of Optics, 24(5), 055401.
[https://doi.org/10.1088/2040-8986/ac5926]

-
Wiltse, J. C., (2004), Diffraction optics for terahertz waves, Terahertz for Military and Security Applications II, 127-135.
[https://doi.org/10.1117/12.541237]

-
Siemion, A., (2021), The magic of optics—An overview of recent advanced terahertz diffractive optical elements, Sensors, 21(1), 100.
[https://doi.org/10.3390/s21010100]

-
Hazra, L., Han, Y., Delisle, C., (1995), Kinoform lenses: Sweatt model and phase function, Optics Communications, 117(1-2), 31-36.
[https://doi.org/10.1016/0030-4018(95)00071-F]

- Ansys, Ansys Zemax OpticStudio. https://www.ansys.com/products/optics-vr/ansys-zemax-opticstudio
- ZEMAX®, (2011), Optical design program user’s manual. https://neurophysics.ucsd.edu/Manuals/Zemax/ZemaxManual.pdf

Ph.D. candidate in the Department of Mechanical System Design Engineering, Seoul National University of Science and Technology. His research interest His research interests are optical design, surface metrology, diffractive optics.
E-mail: cd.quanghuy@gmail.com

Associate Professor in the Department of Mechanical System Design Engineering, Seoul National University of Science and Technology University. His research interests are precision metrology, optical design, diffractive optics, space optics, laser pulse, spectroscopy.
E-mail: JLee@seoultech.ac.kr