터널링 효과를 이용한 초정밀 공작기계에서 공구 좌표계 설정
1홍익대학교 기계시스템디자인공학과Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Work coordinate setup is a time-consuming and difficult task in ultraprecision machining. The setup process determines the precision and tolerance of the machined parts. In ultraprecision machining, the table can be moved in the nanometer range, but the accuracy of the measuring device has not reached the nanometer accuracy range. Although several measurement methods have been proposed, the attained precision is still insufficient. Some methods also lose the precision when the sensor is changed with the tool after the work coordinate setup is completed. A work coordinate setup method proposed in this study could improve the precision and the measurement process using electron tunneling. Since the method can use the tool as a sensor probe, the changing process does not degrade the measurement precision. In addition, the proposed method can theoretically detect the distance between the tool and the workpiece in sub-nanometers like a scanning tunneling microscope. The simple system requires a precision current amplifier capable of measuring electron tunneling current in the picoampere to nanoampere range and a power supply. The method, installed on an ultra-precision machine tool, was tested on WC and aluminum material. The accuracy of the method was evaluated for applied voltage.
Keywords:
Tunneling effect, Work coordinate setup, Measurement, Machine tool키워드:
터널링 현상, 공구 좌표계 설정, 측정, 공작기계1. 서론
광학 부품과 정밀 부품을 사용하는 제품의 수요가 증가하면서 초정밀 가공 기술의 수요 또한 증가하고 있다[1,2]. 수십에서 수백 나노미터 수준의 정밀도를 요구하는 부품을 가공하기 위해 공작기계의 정밀도는 발전하고 있지만, 공작기계의 부가 장치들의 정밀도는 공작기계의 정밀도에 미치지 못하는 상황이다[3]. 부가장치 중 공구와 공작물 사이의 거리를 측정하여 공구 좌표계를 설정하는 시스템은 가공 정밀도에 영향을 미치는 중요한 장치이다[4]. 터치 프로브 타입의 공구 좌표계 설정 시스템은 공작기계에서 산업에서 널리 사용되고 있지만, 측정 시스템의 정밀도는 초정밀 공작기계의 정밀도에 미치지 못하는 상황이다. 이러한 간극을 좁히기 위하여 여러 연구팀에서 공구 좌표계를 설정하기 위한 여러 센서를 이용한 측정 방법을 개발하였다.
공구와 공작물 사이의 거리를 측정하는 센서의 방식은 접촉 방식과 비접촉 방식으로 나뉜다. 접촉 측정 방식은 공구와 공작물이 접촉하면서 발생하는 물리적 혹은 전기적 반응을 관측하여 접촉 여부를 판단하는 방식이다. 가속도 센서, 음파 센서, 전류 센서, 공구 동력계와 같이 공구와 공작물이 접촉하면서 발생하는 진동이나 반발력, 전기 저항의 변화를 측정하여 접촉 여부를 판단한다. Roy et al.은 가속도 센서를 머시닝 센터의 스핀들에 장착하여 공구와 공작물이 접촉할 때 발생하는 스핀들의 떨림을 관측하여 공구와 공작물 사이의 접촉여부를 판단하였다[5]. Min et al.은 공구와 공작물이 접촉할 때 공작물을 통해 전달되는 진동을 감지하여 공구와 공작물의 접촉을 감지하였다[6]. Chen et al.은 선반에서 공구동력계를 이용하고 공구가 공작물을 누를 때 반발력을 측정하여 접촉 위치를 측정하였다[7]. Castano et al.은 전도체인 공구와 재료가 밀링 중에 접하는 순간 저항을 측정하여 접촉 여부를 판단하였다[8]. 접촉방식은 기본적으로 접촉을 기반으로 하는 측정이기 때문에 공구와 공작물의 접촉으로 인해 공구나 공작물 표면에 상처를 입힐 가능성이 높다.
반면 비접촉 측정 방식은 공구와 공작물이 접촉하지 않고 측정하기 때문에 두 재료의 표면에 상처를 입힐 가능성이 낮다. 비접촉 측정 방식은 카메라, 레이저 센서, 방전, 전기용량과 같이 빛이나 전자를 매개체로 이용하여 공구와 공작물 사이의 거리를 측정한다. Clark et al.은 비전을 이용하여 공구와 공작물 사이의 거리를 5 μm 수준의 정밀도로 관측하였다[9]. Yoshioka et al.이 제안한 방법은 투명한 다이아몬드 공구를 사용할 경우 레이저를 이용하여 공구와 공작물 사이의 거리를 측정하였다[10]. Maeng et al.은 공구와 공작물 사이에 방전이 일어나는 것을 관측하여 두 재료 사이의 거리를 측정하였다[11]. Wang et al.은 캐패시터 센서를 이용하여 마이크로미터 단위에서 두 물체 사이의 거리를 측정하는 방법을 제안하였다[12]. 비접촉 방식은 접촉이 일어나지 않기 때문에 두 물체 표면에 상처를 입히는 가능성은 낮지만 상대적으로 접촉식 방식에 비하여 정밀도와 신뢰도가 떨어진다.
두 물체 사이의 거리를 측정하는 방법은 직접적이나 간접적인 방법으로 분류할 수 있다. 대표적인 간접 측정 방법은 터치 프로브를 이용한 공구 좌표계 설정 시스템이다[13]. 터치 프로브 센서는 공작기계 내의 공구 홀더에 장착되어 공작물과 거리를 측정한 뒤 공구와 교체된다. 프로브 센서와 교체한 공구 사이의 거리는 외부에 장착된 거리 측정 센서를 이용하여 측정한다. 공구와 센서 사이의 거리와 센서와 공작물 사이의 거리 정보를 바탕으로 간접적으로 공구와 공작물 사이의 거리를 계산한다. 직접적인 측정방법은 공구나 공작물을 센서와 교체하지 않고 공작기계에 장착한 상태로 외부 센서를 이용하거나 공구 자체를 센서 프로브로 사용하여 두 물체 사이의 거리를 측정한다. 접촉 방식 센서 중 음파 센서나 가속도 센서는 센서 프로브 없이 공구와 공작물의 접촉을 감지한다. 비접촉 방식 중 레이저 센서는 외부에 센서가 설치되어 공구와 공작물 사이의 거리를 직접 측정한다. 일반적으로 간접적인 측정 방법은 센서와 공구가 교체되는 과정에서 오차가 발생하는 문제가 있다. 따라서 정밀 측정에는 직접 측정방법을 선호한다.
본 연구에서는 양자역학 중 터널링 효과를 이용하여 공구와 공작물 사이의 거리를 비접촉 상태에서 직접적으로 측정하고 이를 바탕으로 공구 좌표계를 설정하는 방법을 제안한다. 전도체 재료 사이에서 발생하는 터널링으로 거리를 측정하는 연구는 수행되었지만 공작기계에서 공구와 공작물 사이의 거리를 측정한 연구는 미미하다. 제안하는 방법으로 전도체인 공구와 공작물 사이의 거리를 나노 미터 수준으로 이동하면서 공구와 공작물 사이에 발생하는 터널링 전류를 측정하고 이를 바탕으로 두 전도체 사이의 거리를 측정하였다. 초경 공구와 알루미늄 공작물에서 터널링 전류를 측정하며 재료에 따른 차이를 관찰하였다. 그리고 공작기계의 불확실성 분석을 통해 측정 방법의 정밀도에 미치는 요인들의 영향도를 확인하였다.
2. 터널링
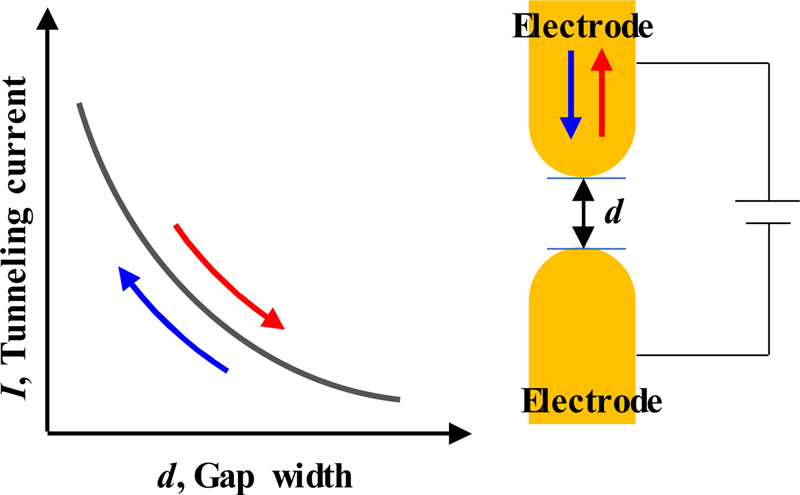
양자역학 현상 중 하나인 터널링 현상은 전위차가 있는 두 원자 사이에 비전도체가 나노미터 정도 간격으로 존재할 때 전자가 비전도체를 통과하여 두 원자사이에 미세한 전류가 흐르는 현상을 말한다[14]. 이러한 미세한 전류를 터널링 전류라 하고 전류의 크기를 식(1)과 같이 두 원자 사이의 거리에 대한 함수로 표현할 수 있다.
| I∝f(V)exp(-A√ˉϕd) | (1) |
여기서 I는 터널링 전류, V는 두 전도체 사이의 인가전압, d는 두 전극 사이의 거리이다. A와 ϕ는 두 전도체와 전도체 사이의 절연체의 전기적 특성을 나타내는 상수이다[15]. 터널링 이론에 따르면 터널링 전류는 전압에 비례하고 두 전극 재료의 거리에 반비례한다. Fig. 1과 같이 두 전극 사이의 거리가 멀어지면 터널링 전류 크기는 지수비율로 감소한다. 터널링 전류와 두 전도체 사이 거리에 대한 관계를 이용하여 원자 단위로 거리 측정이 가능한 Scanning Tunneling Microscopy (STM)가 개발되었다. 이론적으로 STM을 이용하여 측정 가능한 깊이 방향의 해상도는 0.01 nm이다[16]. 폭 방향의 해상도는 사용하는 프로브의 날카로움으로 결정되고 프로브 끝단이 날카로워 끝단에 존재하는 원자의 개수가 작아질수록 폭 방향의 해상도가 높다.
터널링 현상을 관측하기 위해서는 두 전도체 사이의 거리를 수 나노미터 이하로 제어할 수 있고 10-100 pA 수준의 미세한 전류를 측정할 수 있어야 한다. STM은 나노미터 수준으로 두 전도체의 상대 위치를 제어하고 미세한 터널링 전류를 측정할 수 있는 정밀 전류계를 탑재하고 있다. 또한 외부의 진동을 차폐하고 산화막 형성을 늦추며, 열수축/팽창을 최소화하기 위한 시스템을 갖추고 있다. STM과 비슷하게 초정밀 공작기계는 나노미터급으로 이송축을 제어하기 위하여 외부와 진동을 차폐하는 시스템과 공작기계 주변의 온도를 일정하게 유지할 수 있는 시스템이 존재한다. 이러한 환경은 터널링 현상을 측정하기에 적합한 환경이다. 공구와 공작물에 전위차를 발생시키며 두 전도체 사이의 거리를 나노미터로 제어하면 정밀 전류계를 이용하여 공작기계 상에서 터널링 전류를 관측할 수 있다.
3. 실험
초정밀 공작기계에서 터널링 현상을 이용하여 공구 좌표계를 설정하는 방법을 검증하기 위하여 실험을 수행하였다. 피에조 정밀 이송장치를 이용하여 절삭 공구와 공작물 사이의 거리를 제어하며 재료와 인가 전압에 따라 터널링 전류를 측정하는 거리-전류 실험을 수행하였다. 그리고 초정밀 공작기계에 절삭 공구와 공작물 사이의 거리를 이동하며 터널링 전류를 측정하여 터널링 측정 기반 공구 좌표계 설정 방법의 정밀도를 검증하는 불확실성 분석 실험을 하였다.
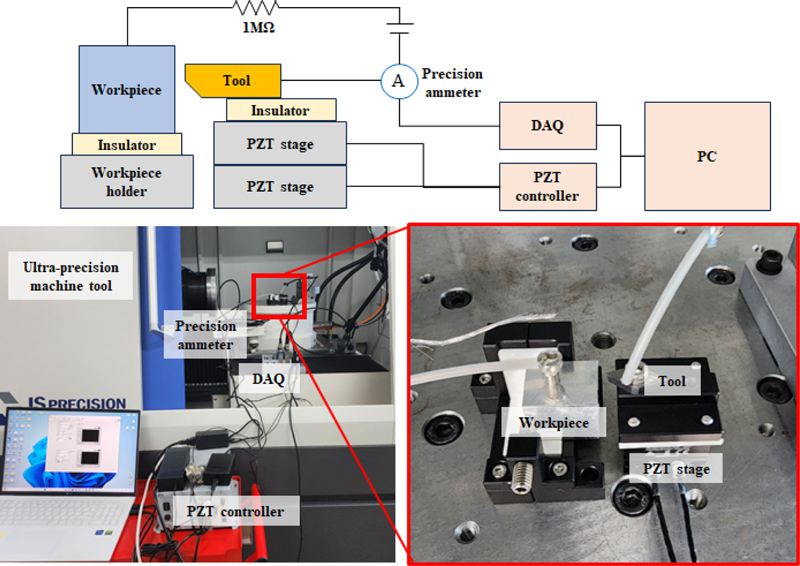
거리-전류 실험은 피에조 정밀 이송장치를 초정밀 공작기계 위에 Fig. 2와 같이 설치하여 수행되었다. 0.1 nm의 이송분해능을 갖는 2축 피에조 스테이지(P-620, PI, 독일)위에 공구를 설치하고 공작물은 그 반대쪽에 설치하였다. 공구과 공작물에는 Analog Output 모듈(NI-9260, NI, 미국)을 이용하여 전압을 인가하였고 공구와 공작물 사이에 흐르는 터널링 전류는 정밀전류증폭기(DLPCA-200, FEMTO, 독일)을 이용하여 증폭한 뒤 디지타이저(NI-9775, NI, 미국)에서 전압을 측정하였다. 터널링 전류의 값이 매우 작기 때문에 외부에서 발생하는 노이즈를 차폐해야 하므로 공구와 공작물을 고정하는 부분은 비전도체인 세라믹으로 격리하였다. 또한 동축 전선을 이용하여 외부의 노이즈를 최소화하고자 하였다. 실험장치는 4축 초정밀 공작기계(DTM-150, JS Precision, 한국) 상에서 실험하여 외부에서 발생하는 진동 영향을 최소화하고자 하였다.
거리-전류 실험은 Table 1과 같은 조건으로 수행하였다. 인가 전압은 0.2-1 V까지 0.2 V 간격으로 변경하며 수행하였다. 공구는 텅스텐카바이드(WC)를 이용하였고 공작물 재료는 알루미늄을 사용하였다. 공구와 공작물 사이의 접촉 위치는 공구를 움직이면서 측정되는 전류값이 급격하게 커지는 것을 관측하여 정의하였다. 공구와 공작물 사이의 거리가 가까워지면 터널링 효과에 의해서 10 pA-10 nA 사이의 전류가 측정된다. 공구와 공작물이 가까워지다 접촉하게 되는 순간 공작물과 공구는 통전이 되고 전류는 저항과 인가전압을 고려하여 0.1-1 μA이 된다. 이렇게 완전히 통전되는 위치를 접촉점이라 가정하였다. 이 과정을 10번 반복하여 전류값이 급격하게 커지는 접촉점의 평균 위치를 구하여 공구와 공작물의 기준점으로 정의하였다. 나노미터 단위에서 기준점을 설정하기 어렵기 때문에 접촉하였을 때 발생하는 급격한 전류를 관측하여 기준점을 정의하고 그 후 그 기준점을 바탕으로 떨어진 거리를 측정하였다. 제안한 방법은 비접촉한 상태로 거리를 측정하는 방식이지만 기준점 정의를 위해서 접촉하였을 때 발생하는 신호를 사용하였다. 기준점으로부터 멀어지는 방향으로 공구를 1 nm/s의 속도로 기준점에서부터 30 nm까지 이송하며 전류 변화를 측정하였다. 각 조건별로 10회 수행 실험을 수행하였다.
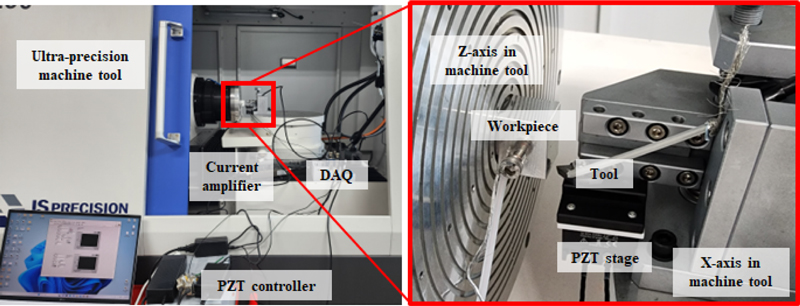
공작기계상에서 적용 가능성을 확인하기 위하여 초정밀 공작기계 상에서 실험을 수행하였다. 실험에 사용한 4축 공작기계는 x축과 z축 방향으로 1 nm, B축과 C축으로 1 μ° 단위로 제어가 가능하다. 초정밀 공작기계의 x축 위에 공구, z축 위에 공작물을 부착한 후 터널링 전류 측정 실험을 수행하였다. 인가 전압은 0.6 V, 공구는 WC, 공작물은 알루미늄으로 수행하였다. Fig. 3와 같이 x축 위에 피에조 정밀 이송장치를 설치하고 나머지 전류 측정 장치는 이전 정밀 이송 측정 실험과 동일하게 구성하였다. 피에조 정밀 이송장치를 이용하여 공구와 공작물의 접촉위치를 정의한 후 공작기계의 z축을 이동하며 터널링 전류를 측정하였다. 공작기계의 이송축을 1 nm/s로 같은 조건으로 이송하며 60 nm 떨어진 부분까지 이동하였다. 위 실험은 20회 반복하며 반복성을 평가하였다. 또한 공작기계의 불확실성을 평가하기 위하여 공작기계의 반복성과 진동을 측정하였다.
4. 실험 결과
거리-전류 실험에서 피에조 정밀 이송장치를 이용하여 공구과 공작물 사이를 떨어지게 하면서 터널링 전류를 측정하였다. Fig. 4와 같이 공구와 공작물의 거리가 멀어질수록 전류의 크기는 급격하게 낮아지는 것을 관찰할 수 있다. 측정된 전류의 크기는 10 nA 수준이며 일반적인 STM 장치에서 측정되는 터널링 전류의 크기에 비하여 10-100배 크다. 이는 STM 장치에 사용하는 프로브와 공구 끝단 형상에 의해 발생한 것으로 예상한다. 일반적인 STM 프로브의 끝단은 날카롭게 제작되지만 일반 절삭 공구의 끝단은 나노미터 단위에서는 뭉툭하다. 이는 공구의 끝단과 공작물 사이에 터널링 현상을 일으키는 원자의 개수에 영향을 미친다. 뭉툭한 공구는 일반적인 STM의 프로브에 비하여 공작물과 터널링 효과를 만드는 원자의 개수가 많아 일반적인 STM에서 관측되는 터널링 전류보다 공구와 공작물 사이에서 관측되는 터널링 전류가 10-100배 정도 높을 것으로 예상한다. 10-100배 정도 높은 전류인 1-10 nA는 공구와 공작물이 통전할 경우 발생하는 전류인 1 μA에 비하여 100배 이하로 낮은 수치이기 때문에 공작물과 공구 사이의 터널링 효과로 나타나는 효과로 판단된다.
Fig. 4(a)에서 일부 구간에서 터널링 전류가 급격하게 감소하지 않고 크게 변동이 생기는 영역이 존재한다. 이는 측정 중 외부에서 발생하는 진동이나 재료의 열변형 등 외란 요소에 의해서 공구와 공작물 사이의 거리가 변하게 되고 이 변동이 터널링 전류 변화에 영향을 미쳤을 것으로 예상한다. 또한 Fig. 4(b)에서 관찰할 수 있는 터널링 전류 측정 구간의 변화는 피에조 정밀 이송장치의 반복정밀도에 영향을 받은 것으로 예상한다.
터널링 전류의 이론적 모델에서도 확인할 수 있듯이 인가전압의 크기에 따라 터널링 전류의 크기도 비례하여 커진다. 인가전압이 클수록 전류의 크기가 커지기 때문에 전류를 바탕으로 거리를 측정할 때 거리에 따른 전류의 변화를 민감하게 측정할 수 있다. 그러나 인가 전압이 일정 수준 이상일 경우 공구와 공작물 사이에 터널링 현상이 일어나지 않고 방전이 일어나게 된다. 기존 연구에서 2-3 V 이상의 인가전압이 가해지면 공구와 공작물 사이에 방전이 일어나고 재료 표면에 손상이 일어나는 것을 확인하였다[11]. 따라서, 터널링 현상을 일으키는 적절한 인가전압 범위는 1 V 이하로 설정해야 한다.
터널링 전류를 바탕으로 공구와 공작물 사이의 거리를 측정하는 방식의 정밀도를 평가하기 위하여 같은 터널링 전류값이 발생하는 거리를 측정하고 편차를 계산하였다. 임계값으로 설정한 터널링 전류는 4 nA로 하였고 전류증폭기에서 4 nA 이하의 전류값을 측정할 때 공구와 공작물 사이의 거리를 기록하였다. 10회 반복하며 인가 전압과 공작물 재료에 따른 거리의 평균과 표준편차를 Fig. 5와 같이 정리하였다. 표준편차는 1 V일 경우 약 3.1 nm이고 0.2 V에서는 4.2 nm이다. 표준편차는 인가전압이 클수록 낮아지고 작을수록 커지는 모습을 보인다. 이는 인가전압이 높을수록 측정정밀도가 높음을 시사한다. Fig. 4에서 볼 수 있듯이 전압이 높은 경우에 터널링 전류 변화 민감도가 높아 거리 정밀도가 높아졌을 것으로 예상한다. 터널링이 관측된 위치의 평균값은 약 10-12 nm 수준에 위치하며 인가전압에는 영향을 받지 않는 것으로 보인다.
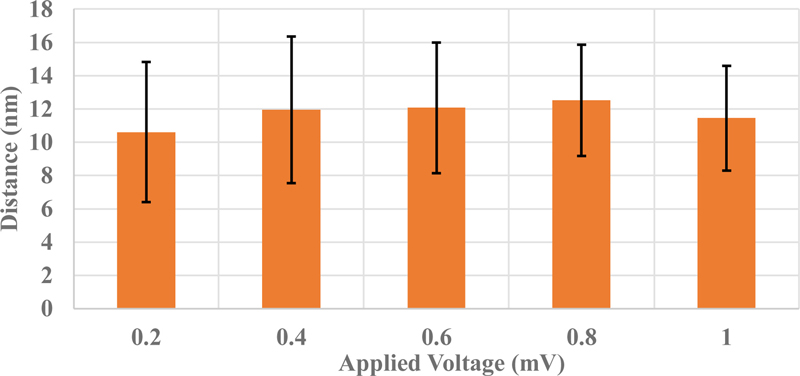
Averaged distance where the tunneling current is detected; error bars indicate the standard deviation
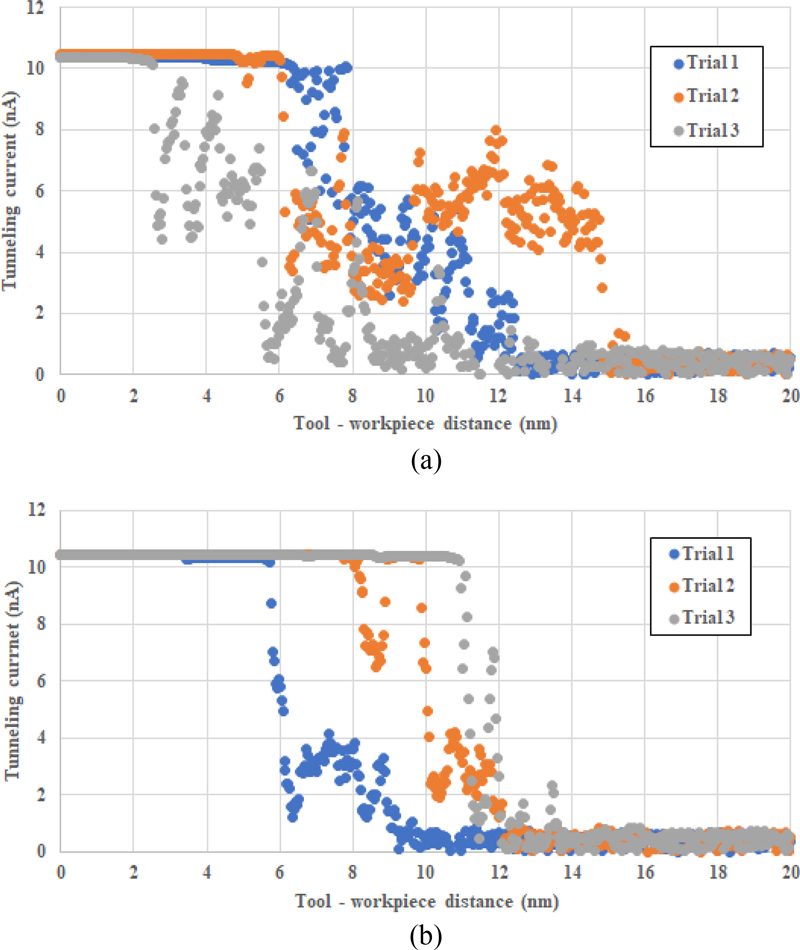
초정밀 공작기계 상에서 제안한 터널링 측정 방법으로 공구와 공작물 거리를 측정 가능한지 실험을 통해 검증하였다. Fig. 6은 초정밀 공작기계의 이송축을 이송하며 터널링 전류를 측정한 결과이다. 피에조 스테이지를 움직이면서 실험한 결과에 비하여 전류의 변동이 큰 것을 확인할 수 있다. 이는 초정밀 공작기계 이송축의 진동에 의해 발생하는 것으로 예상한다. 이송축의 레이저 인코더에서 측정하는 각 축의 위치를 측정하면 Fig. 7과 같다. 이송축의 진동은 x축의 경우 6 nm, z축의 경우 7 nm로 터널링 현상이 일어나는 간격에서는 큰 영향이 미친다.
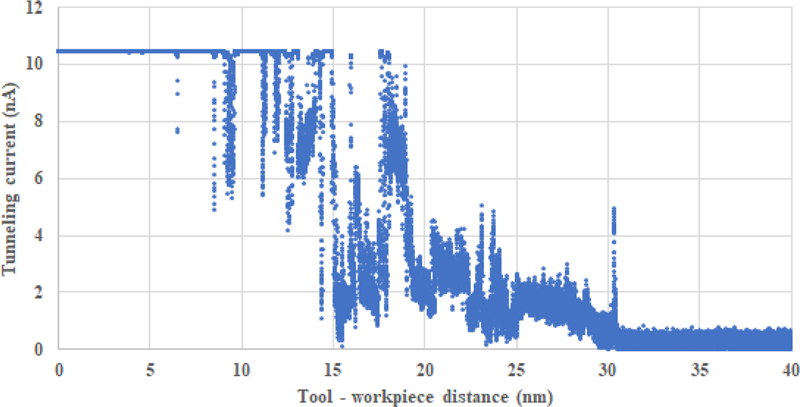
Tunneling current for tool – workpiece distance in an ultra-precision machine tool at applied voltage of 0.6 V
공작기계의 z축을 움직여 기준점으로부터 공작물을 공구로 멀어질 때 터널링 전류가 4 nA 이하로 측정될 경우 공작물의 위치를 기록하였다. 20회 실험에서 공작물의 위치의 평균은 16.5 nm이고 표준편차는 각각 9.8 nm로 측정되었다. 피에조 정밀 이송장치에서 수행한 실험결과에 비하여 초정밀 공작기계에서 큰 표준편차를 보인다. 편차가 더 커지는 이유는 공작기계의 진동과 이송반복도로 판단된다. 공작기계의 이송축 정밀도가 높아지면 제안한 방법을 이용한 측정 방법의 정밀도도 향상될 것으로 예상한다.
5. 결론
본 연구에서는 터널링 현상을 이용하여 초정밀 공작기계에서 공구 좌표계를 설정하는 방법에 대해 제안하였다. 나노 단위의 거리에서 발생하는 터널링 전류를 관측하여 공구와 공작물 사이의 거리를 예상하고 이를 바탕으로 공구 좌표계를 설정하였다. 제안한 방법의 측정 정밀도를 확인하기 위하여 피에조 정밀 이송장치 위에서 거리-전류 실험을 수행하였다. 인가전압을 변경하며 터널링 전류를 측정하고 조건별 터널링 전류 변화를 관찰하였다. 터널링 전류의 변화를 감지하여 표준편차 4.2 nm 수준을 갖는 정밀도로 공구와 공작물의 거리를 예측할 수 있음을 보였다. 인가전압이 높아질수록 측정거리 표준편차는 감소하였다. 이는 높은 인가전압에서 터널링 전류가 공구와 공작물 사이 거리에 민감하게 반응하기 때문으로 예측한다.
터널링 현상을 이용하여 거리를 측정하는 방법을 초정밀 공작기계에 적용하여 공구와 공작물 사이의 거리를 예측하였다. 초정밀 공작기계 이송축의 진동과 반복도는 제안한 방법의 측정 정밀도를 낮추는 주요한 요인이었다. 제안하는 방법은 높은 정밀도를 갖는 이송축에서 효과적으로 사용할 수 있는 것으로 보인다.
향후 연구에서는 CBN, HSS로 이루어진 공구와 여러 전도체 공작물의 조합에서 터널링 현상을 관찰하고자 한다. 또한, 전도체 재료에서만 사용할 수 있는 한계를 극복하기 위하여 비전도체인 재료에 정전기를 관측하거나 비전도체 위에 금속 증착을 하여 제안한 방법을 적용할 예정이다.
NOMENCLATURE
| I : | Tunneling Current |
| ϕ : | Average Barrier Height (Work Function) |
| V : | Bias Potential between Two Electrodes |
| d : | Gap Width between Two Materials |
| A : | Tunneling Material Constant, 1 at ϕ in eV and d in Å |
Acknowledgments
이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2022R1F1A1074622).
REFERENCES
-
Abdulkadir, L. N., Abou-El-Hossein, K., Jumare, A. I., Odedeyi, P. B., Liman, M. M., Olaniyan, T. A., (2018), Ultra-precision diamond turning of optical silicon—A review, The International Journal of Advanced Manufacturing Technology, 96(1), 173-208.
[https://doi.org/10.1007/s00170-017-1529-x]

-
Binnig, G., Rohrer, H., (1983), Scanning tunneling microscopy, Surface Science, 126(1-3), 236-244.
[https://doi.org/10.1016/0039-6028(83)90716-1]

-
Brinksmeier, E., Gläbe, R., Osmer, J., (2006), Ultra-precision diamond cutting of steel molds, CIRP Annals, 55(1), 551-554.
[https://doi.org/10.1016/S0007-8506(07)60480-6]

-
Castaño, F., del Toro, R. M., Haber, R. E., Beruvides, G., (2015), Conductance sensing for monitoring micromechanical machining of conductive materials, Sensors and Actuators A: Physical, 232, 163-171.
[https://doi.org/10.1016/j.sna.2015.05.015]

-
Chen, Y.-L., Shimizu, Y., Cai, Y., Wang, S., Ito, S., Ju, B.-F., Gao, W., (2015), Self-evaluation of the cutting edge contour of a microdiamond tool with a force sensor integrated fast tool servo on an ultra-precision lathe, The International Journal of Advanced Manufacturing Technology, 77, 2257-2267.
[https://doi.org/10.1007/s00170-014-6580-2]

-
Clark, L., Shirinzadeh, B., Bhagat, U., Smith, J., (2013), A vision-based measurement algorithm for micro/nano manipulation, Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 100-105.
[https://doi.org/10.1109/AIM.2013.6584075]

-
Kane, E. O., (1961), Theory of tunneling, Journal of Applied Physics, 32(1), 83-91.
[https://doi.org/10.1063/1.1735965]

-
Kuk, Y., Silverman, P., (1989), Scanning tunneling microscope instrumentation, Review of Scientific Instruments, 60(2), 165-180.
[https://doi.org/10.1063/1.1140457]

-
Küng, A., Meli, F., Thalmann, R., (2007), Ultraprecision micro-CMM using a low force 3D touch probe, Measurement Science and Technology, 18(2), 319.
[https://doi.org/10.1088/0957-0233/18/2/S01]

-
Maeng, S., Min, S., (2023), Work coordinate setup in the ultra-precision machine tool using electrical breakdown, International Journal of Precision Engineering and Manufacturing, 24(5), 745-753.
[https://doi.org/10.1007/s12541-023-00779-7]

-
Min, S., Lidde, J., Raue, N., Dornfeld, D., (2011), Acoustic emission based tool contact detection for ultra-precision machining, CIRP Annals, 60(1), 141-144.
[https://doi.org/10.1016/j.cirp.2011.03.079]

-
Roy, S., Mandal, S., Nagahanumaiah, N., (2016), Tool–workpiece contact detection in micro-milling using wirelessaided accelerometer sensor, Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 230(1), 182-187.
[https://doi.org/10.1177/0954405415573850]

-
Schneider, F., Das, J., Kirsch, B., Linke, B., Aurich, J. C., (2019), Sustainability in ultra precision and micro machining: A review, International Journal of Precision Engineering and Manufacturing-Green Technology, 6(3), 601-610.
[https://doi.org/10.1007/s40684-019-00035-2]

-
Trapet, E., Wäldele, F., (1991), A reference object based method to determine the parametric error components of coordinate measuring machines and machine tools, Measurement, 9(1), 17-22.
[https://doi.org/10.1016/0263-2241(91)90022-I]

-
Wang, D.-C., Chou, J.-C., Wang, S.-M., Lu, P.-L., Liao, L.-P., (2003), Application of a fringe capacitive sensor to small-distance measurement, Japanese Journal of Applied Physics, 42(9R), 5816.
[https://doi.org/10.1143/JJAP.42.5816]

-
Yoshioka, H., Shinno, H., Sawano, H., Tanigawa, R., (2014), Monitoring of distance between diamond tool edge and workpiece surface in ultraprecision cutting using evanescent light, CIRP Annals, 63(1), 341-344.
[https://doi.org/10.1016/j.cirp.2014.03.129]


B.S. student in the Department of Mechanical and System Design Engineering, Hongik University. His research interest is precision measurement.
E-mail: gksemf7@gmail.com

Assistant Professor in the Department of Mechanical and System Design Engineering, Hongik University. His research interests are precision manufacturing, machine tool, and precision measurement.
E-mail: sjmaeng@hongik.ac.kr